Active Assistive Design and Multiaxis Self-Tuning Control of a Novel Lower Limb Rehabilitation Exoskeleton
Abstract
:1. Introduction
- A mechanical design involving a stepless (continuous variable lengths) adjustable length was adopted in the novel exoskeleton. To ensure the fit and comfort of the wearer, the axes of rotation were designed on the waist and ankle joints. The entire LLRE-II system weighed 16 kg.
- A multiaxis (multiple motor control) system was established. Planar motors were installed at the hips and knees of the LLRE-II. Harmonic drives (HDs) were fixed using a connecting plate to the motors to enhance the torque of each joint. The motor drive strategy was based on field-oriented control, including Clarke and Park transformations.
- The performance of the control system was evaluated. The trajectory tracking of the exoskeleton hip joint and knee during movement was achieved via a designed self-tuning controller. The responses of the exoskeleton system were analyzed.
2. Materials and Methods
2.1. DOF and Range of Motions
2.1.1. Sagittal Plane
2.1.2. Coronal Plane
2.1.3. Transverse Plane
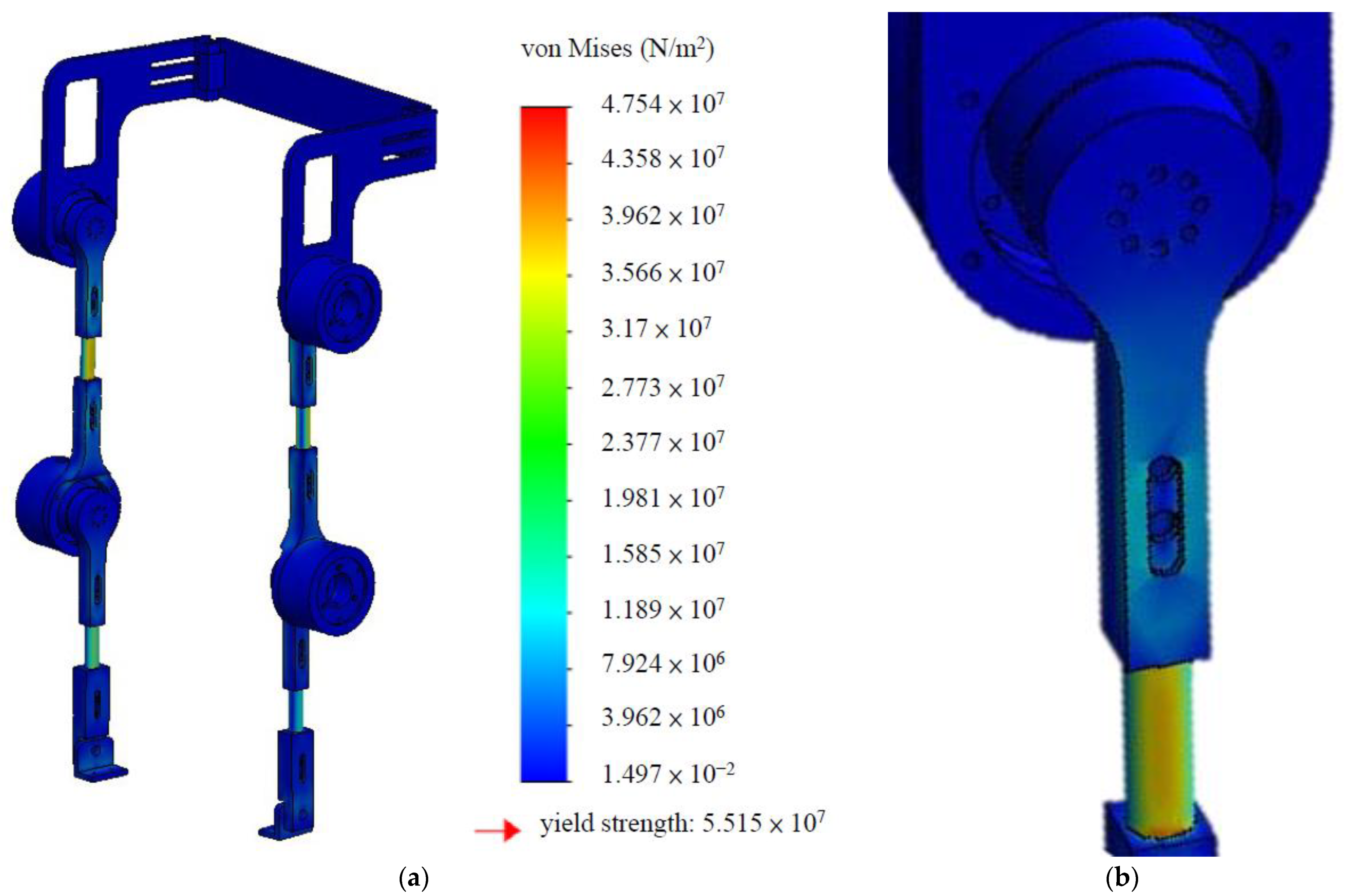
2.2. Mechanical Design and Simulation
- (1)
- Simple and impactful design for ergonomics
- (2)
- Flexibility for wearers
- (3)
- Wearer safety
- (4)
- High strength and lightweight
- (5)
- Economical and easy component renewal
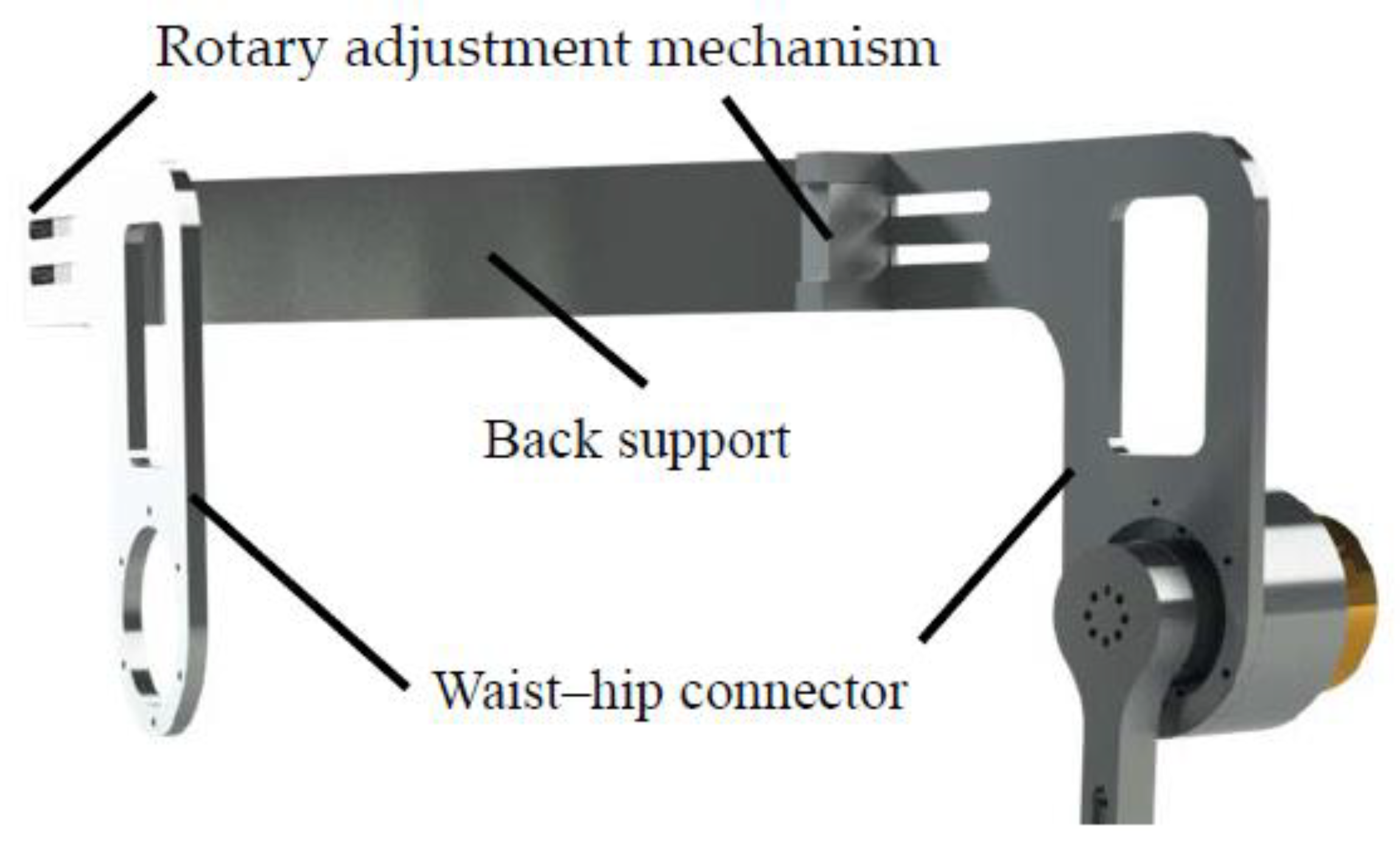
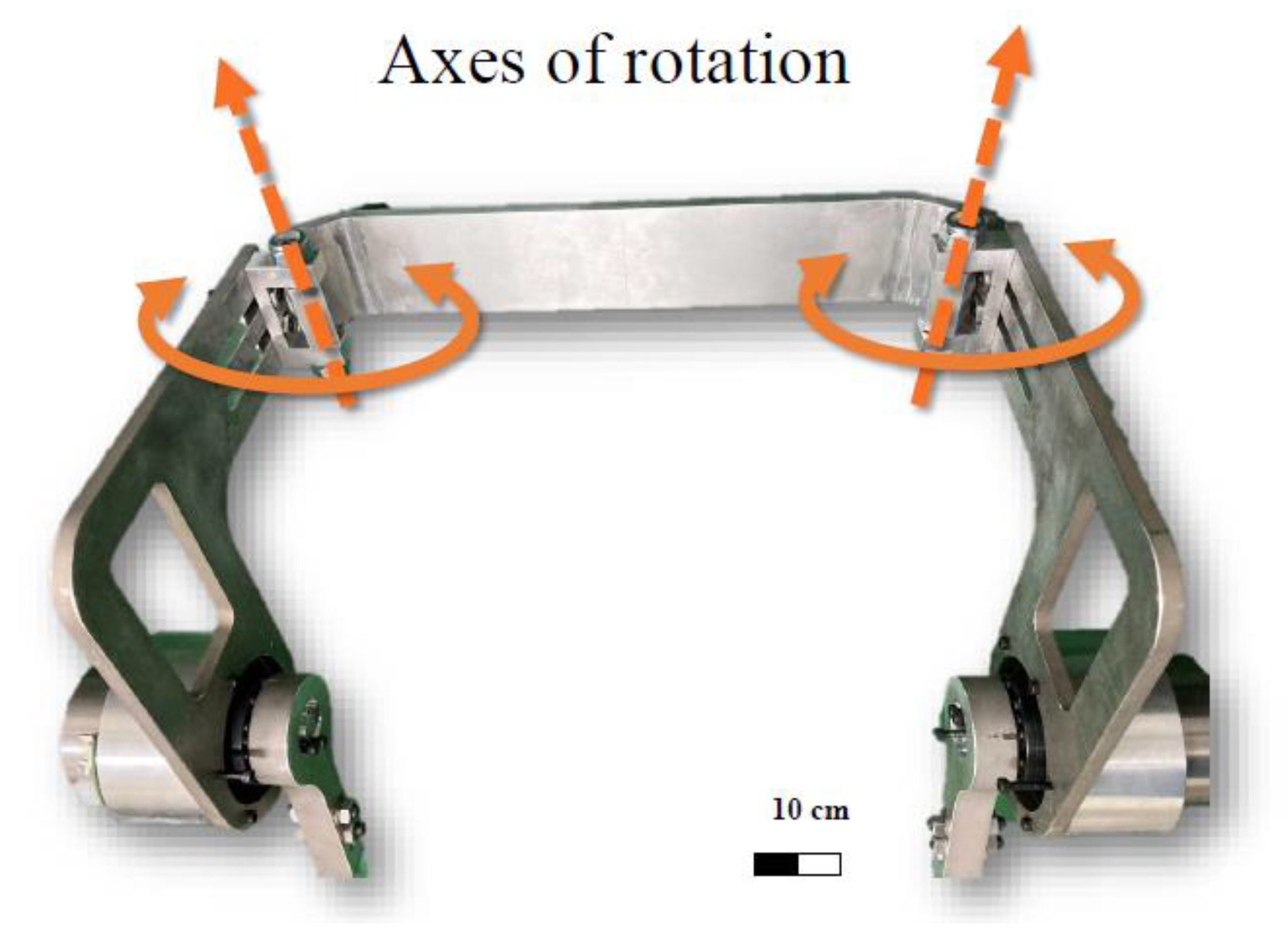
2.2.1. Waist Design
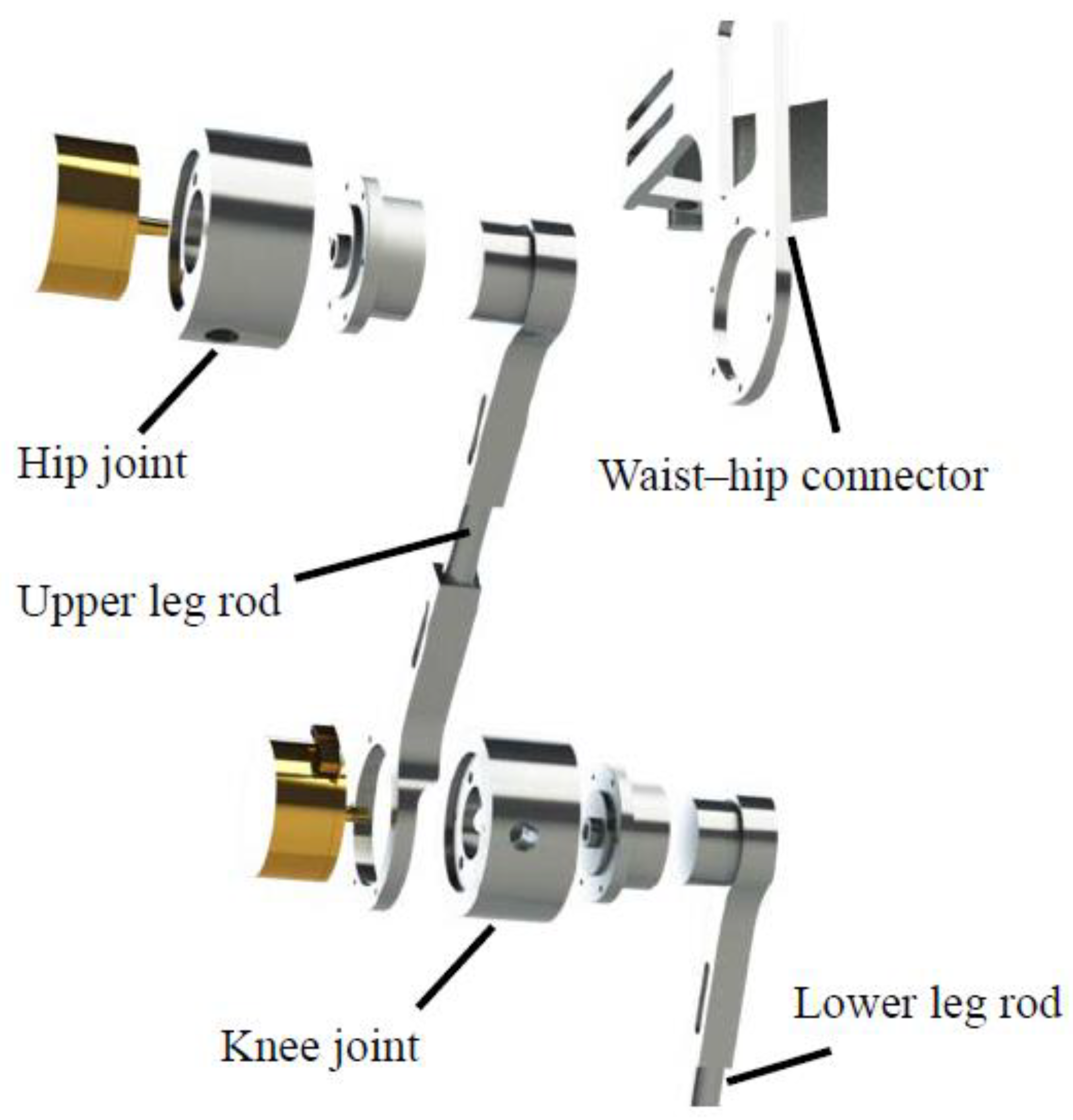
2.2.2. Leg Rod, Motor Plate, and Foot Designs
2.2.3. Hip Joint and Knee Joint Designs
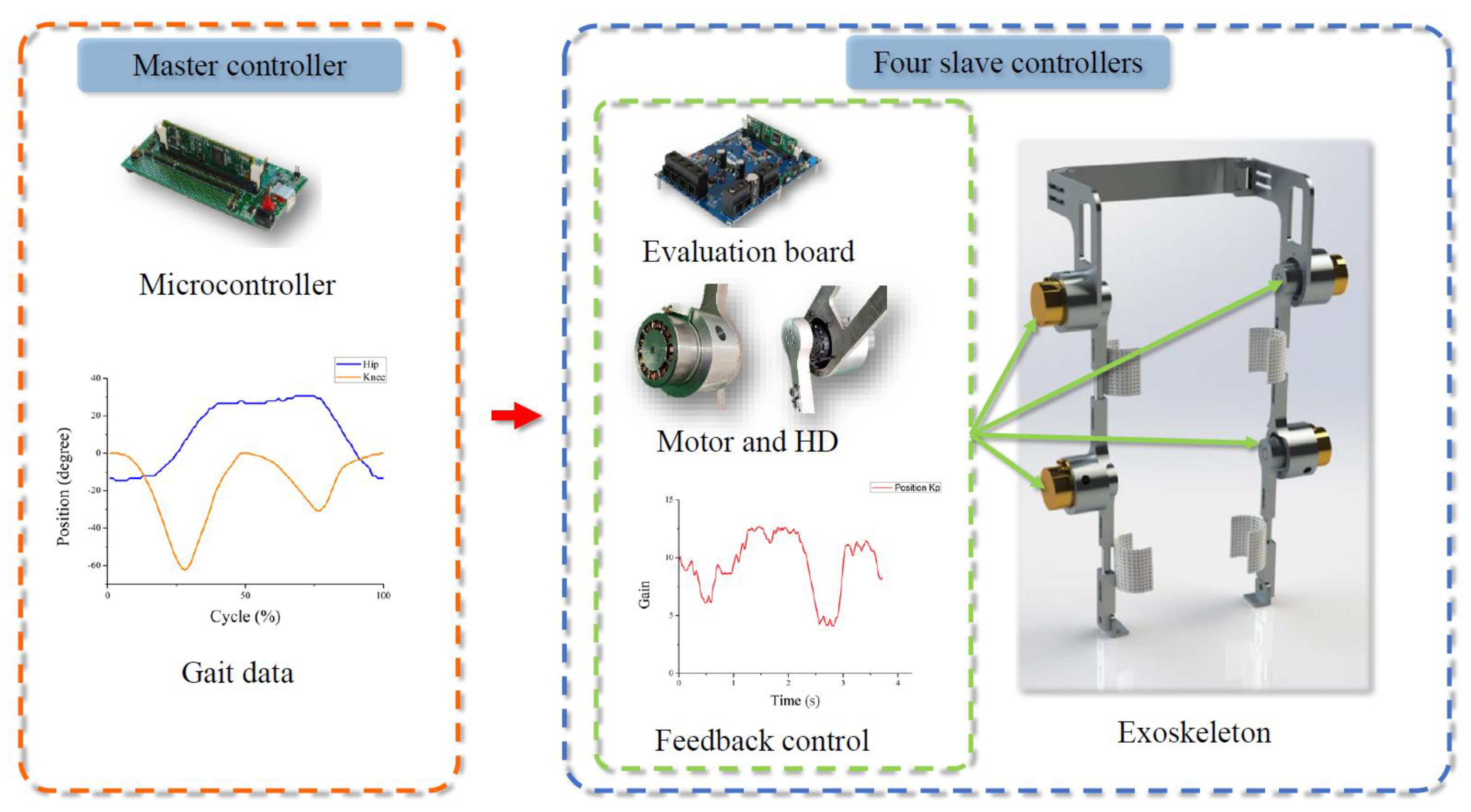
2.3. Multiaxis Control System
2.3.1. Motor-Driven System Design
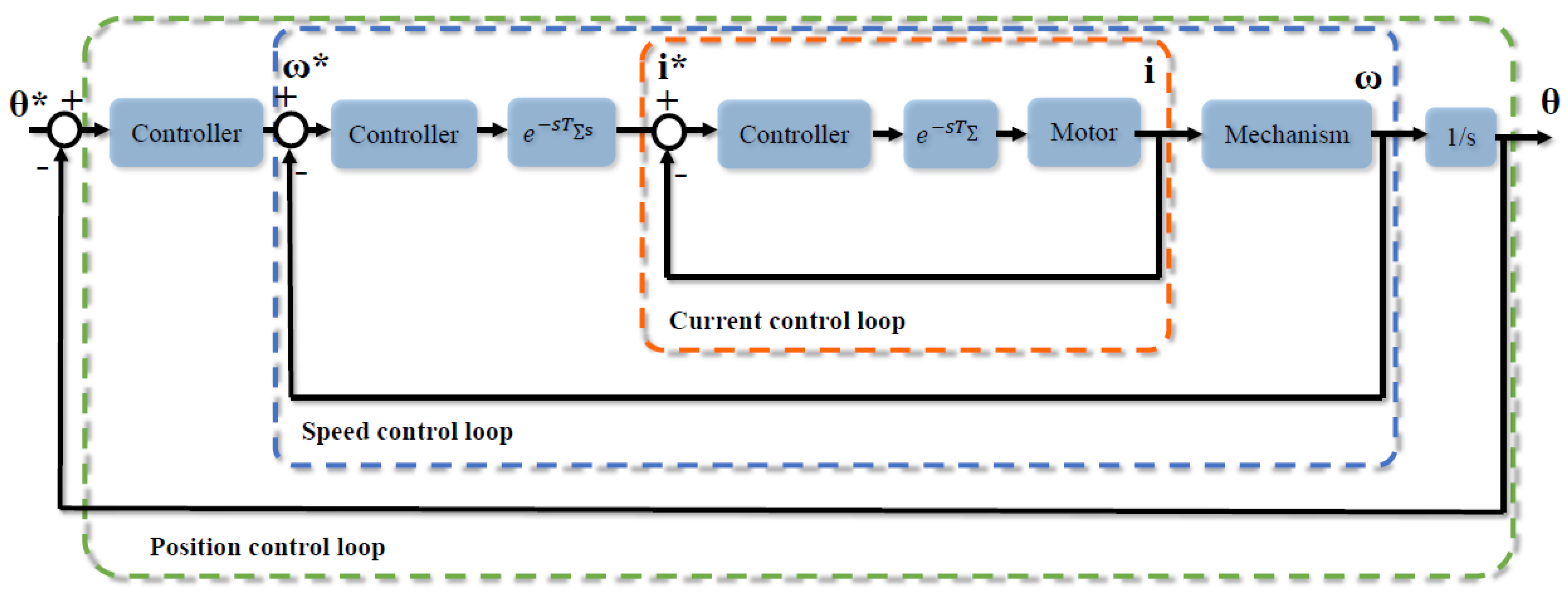
2.3.2. Control System Design
3. Results and Discussion
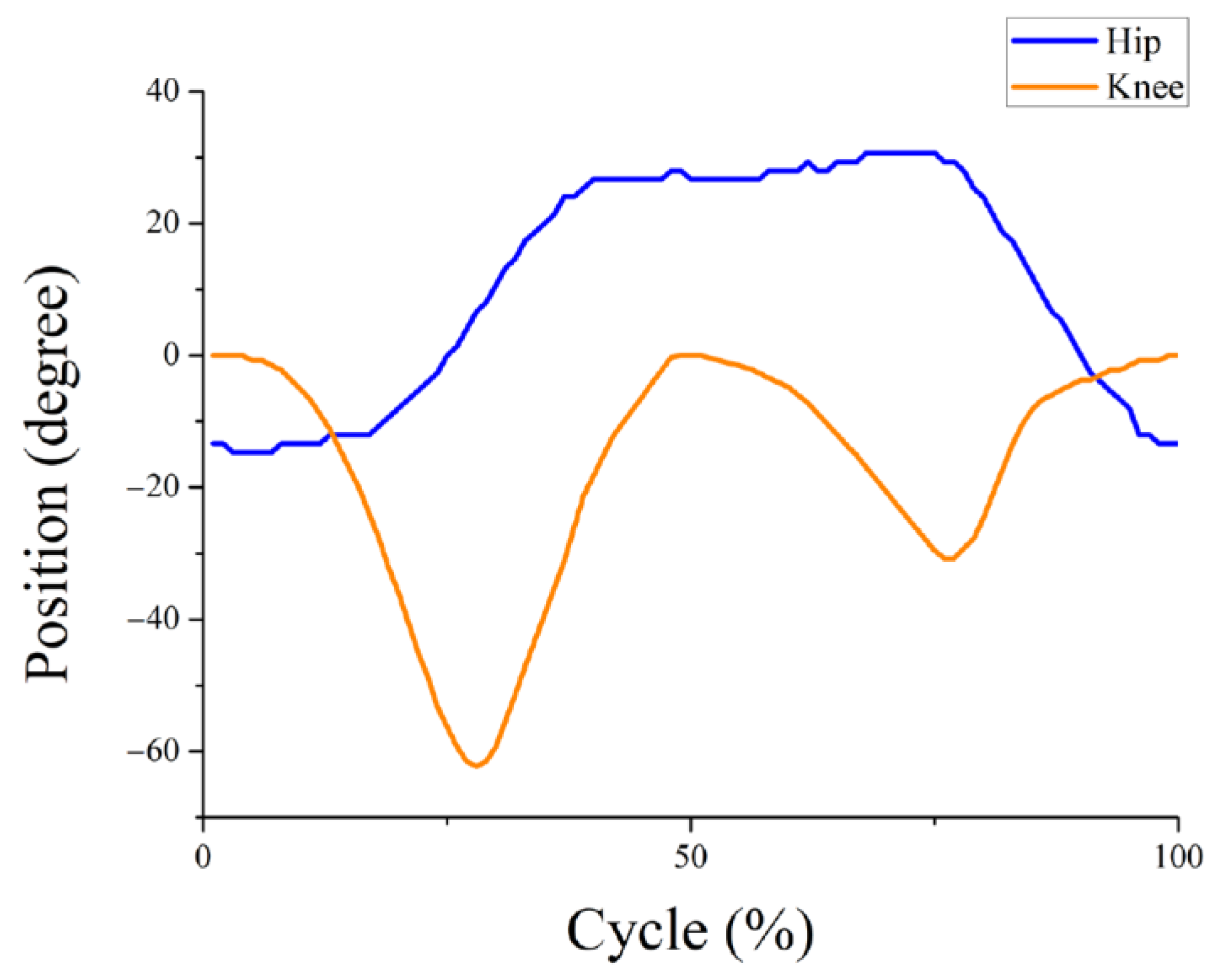
3.1. Test of the Exoskeleton Worn by the Participant
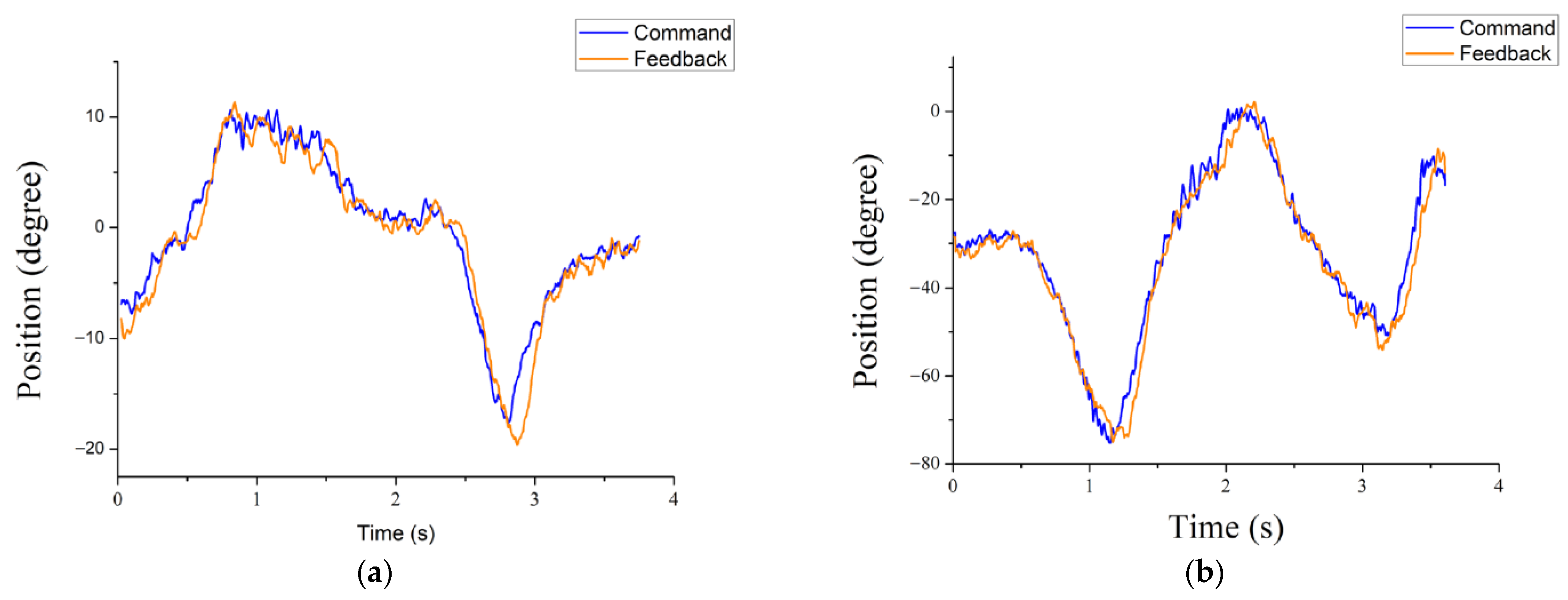
3.2. Conventional PI Controller
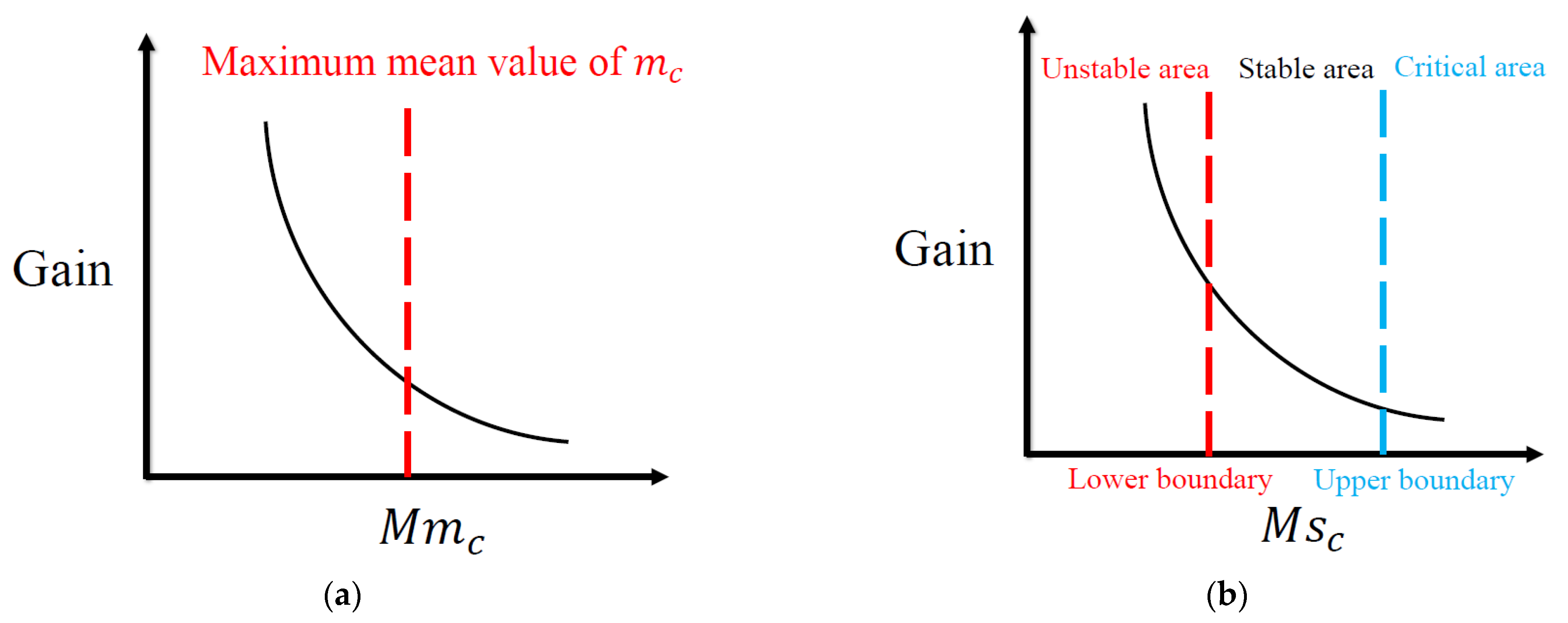
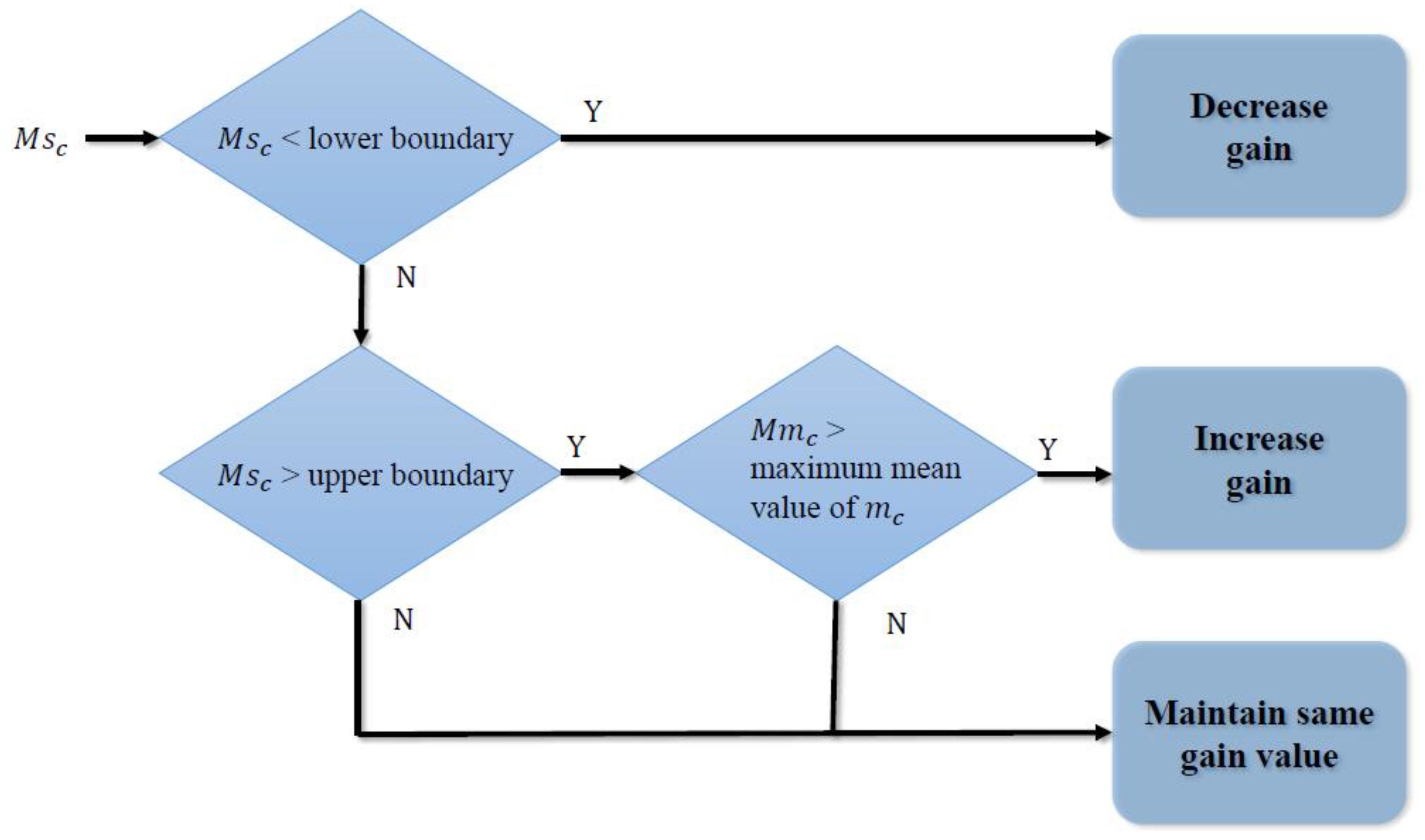
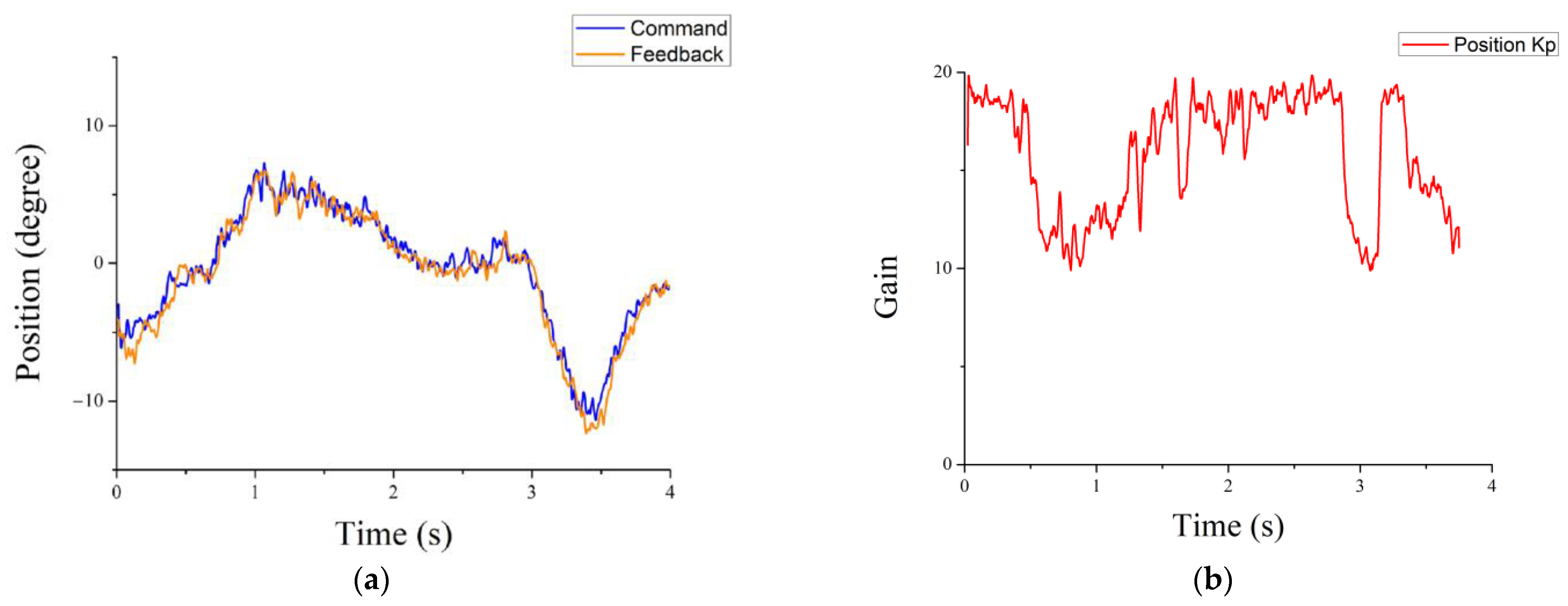
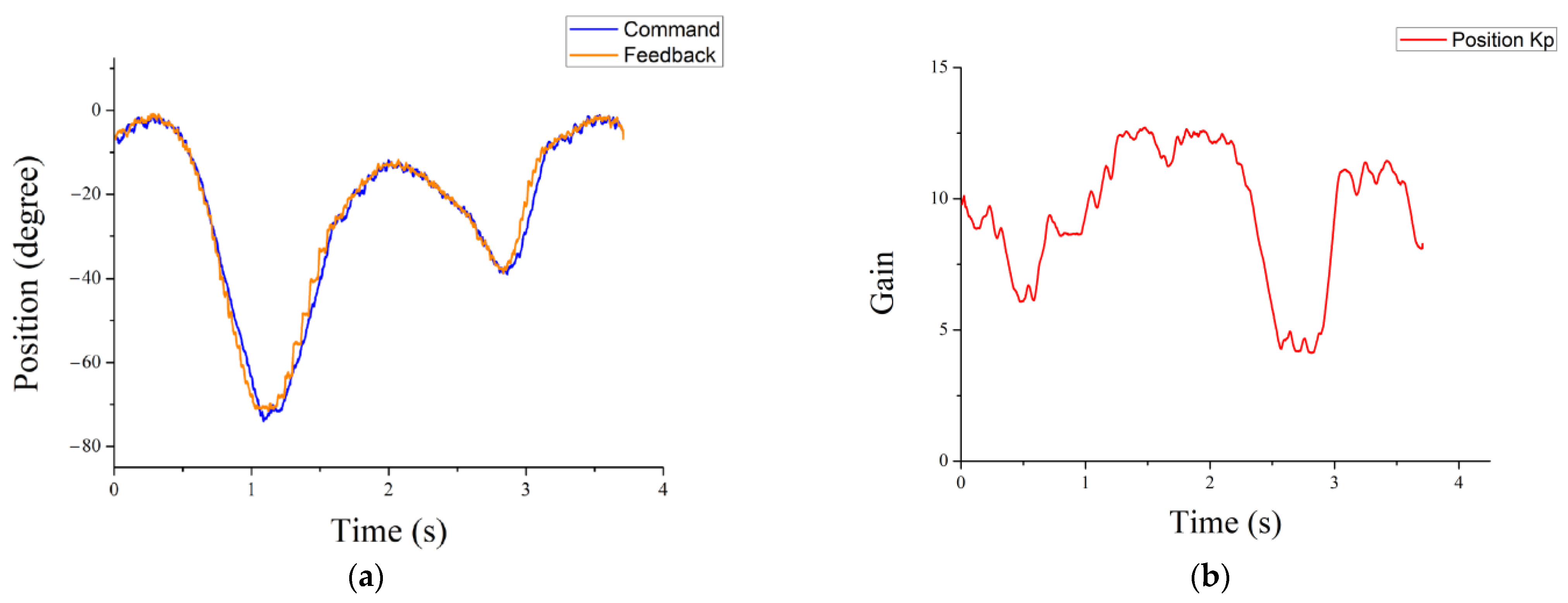
3.3. Self-Tuning Controller
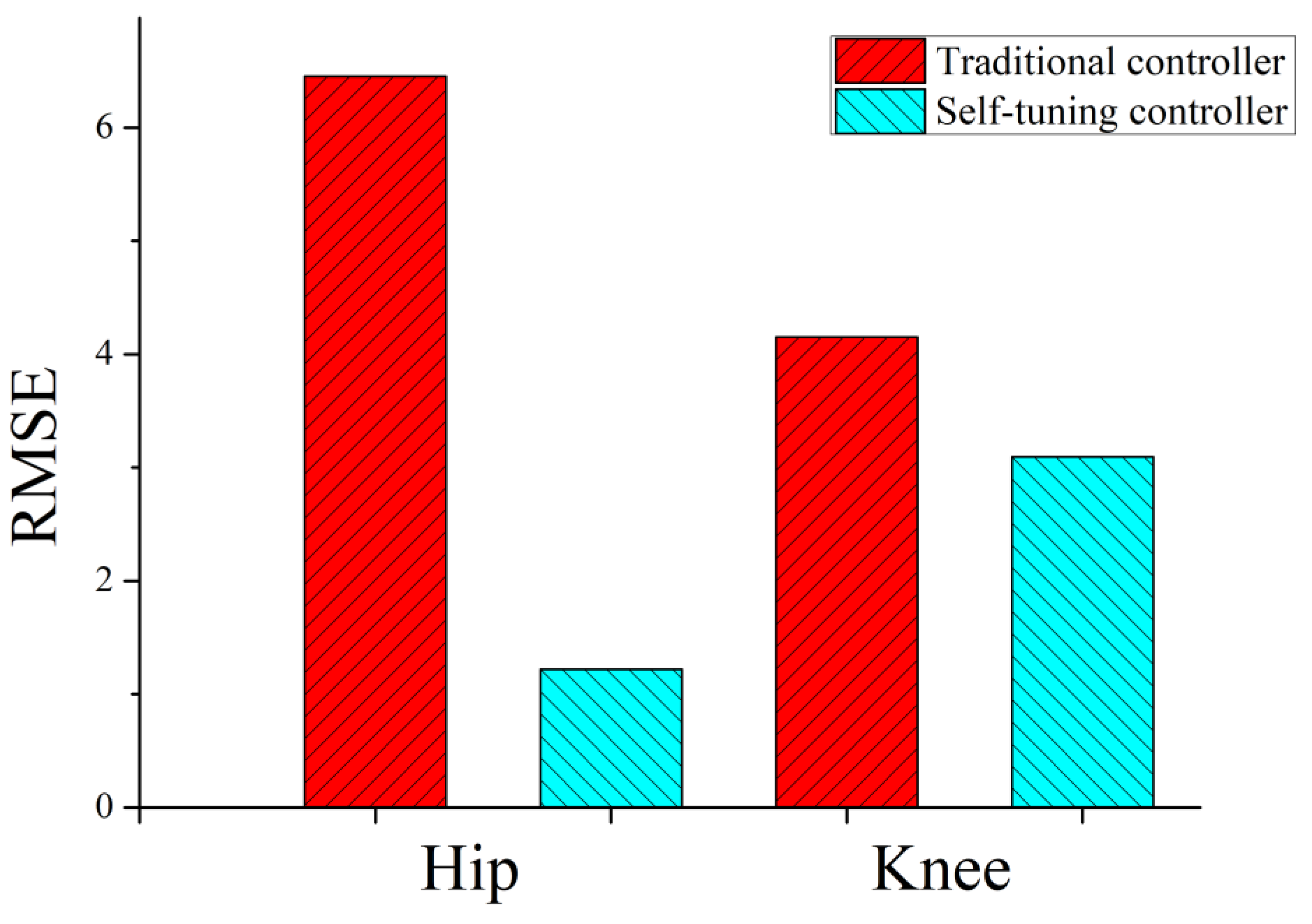
3.4. Discussion and Related Studies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cenciarini, M.; Dollar, A.M. Biomechanical Considerations in the Design of Lower Limb Exoskeletons. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June 2011; p. 5975366. [Google Scholar] [CrossRef]
- Jatsun, S.; Savin, S.; Yatsun, A.; Postolnyi, A. Control system parameter optimization for lower limb exoskeleton with integrated elastic elements. In Advances in Cooperative Robotics; World Scientific Publishing: Singapore, 2017; pp. 797–805. [Google Scholar]
- Liu, D.X.; Wu, X.; Du, W.; Wang, C.; Chen, C.; Xu, T. Deep spatial-temporal model for rehabilitation gait: Optimal trajectory generation for knee joint of lower-limb exoskeleton. Assem. Autom. 2017, 37, 369–378. [Google Scholar] [CrossRef]
- Kirtley, C. CGA Normative Gait Database; Hong Kong Polytechnic University: Hong Kong, China, 2005. [Google Scholar]
- Zheng, X.; Jia, S.; Gao, Y.; Hou, M.; Xi, D.; Yang, H. Modern Sports Biomechanics; National Defense Industry Press: Beijing, China, 2002; pp. 100–163. [Google Scholar]
- Makinson, B.J. Research and Development Prototype for Machine Augmentation of Human Strength Endurance, Hardiman I Project; Tech. Rep. S-71-1056; General Electric Company: Schenectady, NY, USA, 1971. [Google Scholar]
- Yamamoto, K.; Hyodo, K.; Ishii, M.; Matsuo, T. Development of power assisting suit for assisting nurse labor. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2002, 45, 703–711. [Google Scholar] [CrossRef] [Green Version]
- Kazerooni, H.; Steger, R.; Huang, L. Hybrid control of the Berkeley lower extremity exoskeleton (BLEEX). Int. J. Robot. Res. 2006, 25, 561–573. [Google Scholar] [CrossRef]
- Zoss, A.B.; Kazerooni, H.; Chu, A. Biomechanical design of the Berkeley lower extremity exoskeleton (BLEEX). IEEE ASME Trans. Mechatron. 2006, 11, 128–138. [Google Scholar] [CrossRef]
- Chen, C.-F.; Du, Z.; He, L.; Shi, Y.; Wang, J.; Xu, G.; Zhang, Y.; Wu, D.; Dong, W. Development and hybrid control of an electrically actuated lower limb exoskeleton for motion assistance. IEEE Access 2019, 7, 169107–169122. [Google Scholar] [CrossRef]
- Han, J.; Yang, S.; Xia, L.; Chen, Y. Deterministic adaptive robust control with a novel optimal gain design approach for a fuzzy 2DOF lower limb exoskeleton robot system. IEEE Trans. Fuzzy Syst. 2020, 29, 2373–2387. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Ovur, S.E.; Chen, Z.; Li, X.; Hu, Z.; Hu, Y. Novel design and adaptive fuzzy control of a lower-limb elderly rehabilitation. Electronics 2020, 9, 343. [Google Scholar] [CrossRef] [Green Version]
- Bocker, J.; Beineke, S.; Bahr, A. On the Control Bandwidth of Servo Drives. In Proceedings of the 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009. [Google Scholar]
- Hsu, C.-J.; Lai, Y. Novel online optimal bandwidth search and autotuning techniques for servo motor drives. IEEE Trans. Ind. Appl. 2017, 53, 3635–3642. [Google Scholar] [CrossRef]
- Pan, C.-T.; Chang, C.-C.; Yang, Y.-S.; Yen, C.-K.; Liu, C.-C.; Lee, C.-L.; Shiue, Y.-L. Development a multi-loop modulation method on the servo drives for lower limb rehabilitation exoskeleton. Mechatronics 2020, 68, 102360. [Google Scholar] [CrossRef]
- Liu, J.; Fang, H.; Xu, J. Online Adaptive PID control for a multi-joint lower extremity exoskeleton system using improved particle swarm optimization. Machines 2022, 10, 21. [Google Scholar] [CrossRef]
- Lu, Z.; Ye, D.; Chen, Q.; Liu, C.; Dong, H.; Cheng, D. Adaptive adjustment strategy for walking characteristics of single-legged exoskeleton robots. Machines 2022, 10, 134. [Google Scholar] [CrossRef]
- Chen, S.; Han, T.; Dong, F.; Lu, L.; Liu, H.; Tian, X.; Han, J. Precision interaction force control of an underactuated hydraulic stance leg exoskeleton considering the constraint from the wearer. Machines 2021, 9, 96. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, A.; Lobo-Prat, J.; Font-Llagunes, J.M. Systematic review on wearable lower-limb exoskeletons for gait training in neuromuscular impairments. J. Neuroeng. Rehabil. 2021, 18, 22. [Google Scholar] [CrossRef] [PubMed]
- Li, W.-Z.; Cao, G.-Z.; Zhu, A.-B. Review on control strategies for lower limb rehabilitation exoskeletons. IEEE Access 2021, 9, 123040–123060. [Google Scholar] [CrossRef]
- Lovrenovic, Z.; Doumit, M. Review and Analysis of Recent Development of Lower Extremity Exoskeletons for Walking Assist. In Proceedings of the 2016 IEEE EMBS International Student Conference (ISC), Ottawa, ON, Canada, 29–31 May 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Del-Ama, A.J.; Koutsou, A.D.; Moreno, J.C.; de-los-Reyes, A.; Gil-Agudo, N.; Pons, J.L. Review of hybrid exoskeletons to restore gait following spinal cord injury. JRRD 2012, 49, 497. [Google Scholar] [CrossRef]
- Arya, K.N.; Pandian, S.; Kumar, V. Effect of activity-based mirror therapy on lower limb motor-recovery and gait in stroke: A randomised controlled trial. Neuropsychol. Rehabil. 2019, 29, 1193–1210. [Google Scholar] [CrossRef]
- Önen, Ü.; Botsalı, F.M.; Kalyoncu, M.; Tınkır, M.; Yılmaz, N.; Şahin, Y. Design and actuator selection of a lower extremity exoskeleton. IEEE/ASME Trans. Mechatron. 2014, 19, 623–632. [Google Scholar] [CrossRef]
- Xia, L.; Feng, Y.; Chen, F.; Wu, X. A Bio-Signal Enhanced Adaptive Impedance Controller for Lower Limb Exoskeleton. In Proceedings of the IEEE International Conference of Robotic Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 4739–4744. [Google Scholar]
- Wang, C.; Wu, X.; Wang, Z.; Ma, Y. Implementation of a braincomputer interface on a lower-limb exoskeleton. IEEE Access 2018, 6, 38524–38534. [Google Scholar] [CrossRef]
- Molazadeh, V.; Zhang, Q.; Bao, X.; Sharma, N. An iterative learning controller for a switched cooperative allocation strategy during sit-tostand tasks with a hybrid exoskeleton. IEEE Trans. Control Syst. Technol. 2021, 30, 1021–1036. [Google Scholar] [CrossRef]
- Cardona, M.; Cena, C.E.G.; Serrano, F.; Saltaren, R. ALICE: Conceptual development of a lower limb exoskeleton robot driven by an on-board musculoskeletal simulator. Sensors 2020, 20, 789. [Google Scholar] [CrossRef] [Green Version]
- Song, B.; Lee, D.; Park, S.Y.; Baek, Y.S. A novel method for designing motion profiles based on a fuzzy logic algorithm using the hip joint angles of a lower-limb exoskeleton robot. Appl. Sci. 2020, 10, 6852. [Google Scholar] [CrossRef]

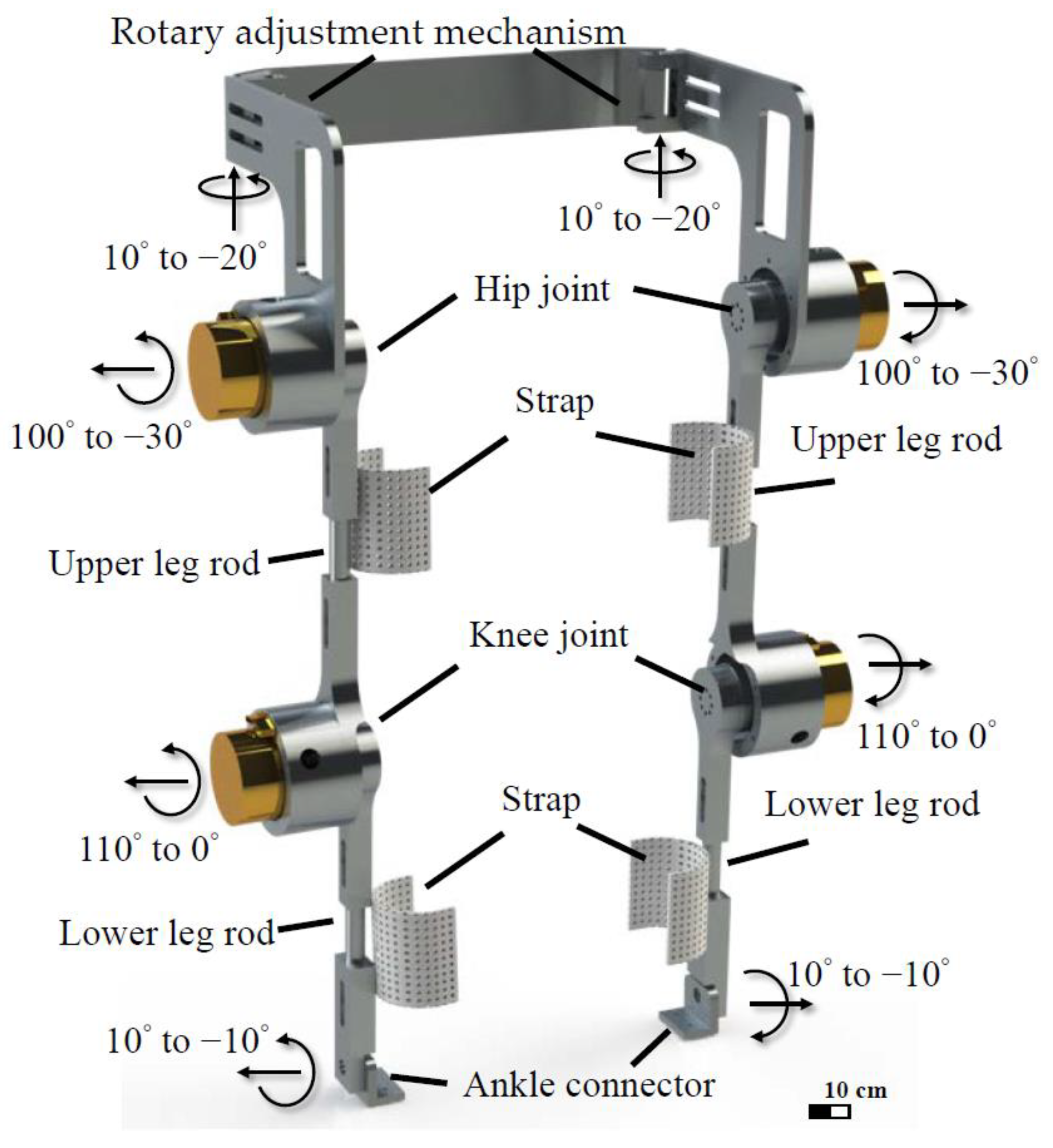









| Lower Limb Movements | Angle Range for Walking | Angle Range of Humans | Joint Angle Range of the LLRE-II Wearer |
|---|---|---|---|
| Waist medial/lateral rotation | 9° to 0° | 50° to −31° | 10° to −20° |
| Hip flexion/extension | 26° to −10° | 120° to −40° | 100° to −30° |
| Knee flexion/extension | 68° to 4° | 140° to 0° | 110° to 0° |
| Ankle plantarflexion/dorsiflexion | 14° to −12° | 20° to −50° | 10° to −10° |
| Target of Research | Participant in Research | Powered Joint | Actuator | Control Strategy | Optimization and Feature | |
|---|---|---|---|---|---|---|
| Ref. [25] | patients with muscle weakness | two healthy participants | hip and knee | DC motor | model-based control with radial basis function neural network | estimate joint torque using sEMG signals |
| Ref. [26] | --- | four healthy participants | hip and knee | DC motor | brain-computer interface (BCI) control | BCI based on motor imagery |
| Ref. [27] | people with paraplegia | four healthy and participants one participant with spinal cord injury | hip and knee | DC motor with transmission | iterative learning controller | iterative learning controller adapts to different musculoskeletal models |
| Ref. [28] | patients with impaired mobility | four participants with sclerosis | hip and knee | flat motor (EC 90 flat, Maxon) with HD | adaptive PID controller | musculoskeletal simulator to generator motion trajectories |
| Ref. [29] | --- | one healthy participant | knee | electro-hydraulic actuator | fuzzy logic control | knee joint is operated by a hydraulic cylinder |
| This work | people with muscle weakness | one healthy participant | hip and knee | flat motor (EC 90 flat, Maxon) with HD | self-tuning controller | stepless length adjustment mechanism; axes of rotation on the waist connectors |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, C.-T.; Lee, M.-C.; Huang, J.-S.; Chang, C.-C.; Hoe, Z.-Y.; Li, K.-M. Active Assistive Design and Multiaxis Self-Tuning Control of a Novel Lower Limb Rehabilitation Exoskeleton. Machines 2022, 10, 318. https://doi.org/10.3390/machines10050318
Pan C-T, Lee M-C, Huang J-S, Chang C-C, Hoe Z-Y, Li K-M. Active Assistive Design and Multiaxis Self-Tuning Control of a Novel Lower Limb Rehabilitation Exoskeleton. Machines. 2022; 10(5):318. https://doi.org/10.3390/machines10050318
Chicago/Turabian StylePan, Cheng-Tang, Ming-Chan Lee, Jhih-Syuan Huang, Chun-Chieh Chang, Zheng-Yu Hoe, and Kuan-Ming Li. 2022. "Active Assistive Design and Multiaxis Self-Tuning Control of a Novel Lower Limb Rehabilitation Exoskeleton" Machines 10, no. 5: 318. https://doi.org/10.3390/machines10050318
APA StylePan, C.-T., Lee, M.-C., Huang, J.-S., Chang, C.-C., Hoe, Z.-Y., & Li, K.-M. (2022). Active Assistive Design and Multiaxis Self-Tuning Control of a Novel Lower Limb Rehabilitation Exoskeleton. Machines, 10(5), 318. https://doi.org/10.3390/machines10050318






