A Fault Diagnosis Model for Coaxial-Rotor Unit Using Bidirectional Gate Recurrent Unit and Highway Network
Abstract
1. Introduction
- (1)
- A test rig for coaxial-rotor unit fault generation is established, based on which the working properties under different conditions are analyzed. Specifically, the bearing circlip failure is pronounced.
- (2)
- A novel fault diagnosis method is established, integrating the Bidirectional Gated Recurrent Unit and Highway Network. Our model aims to not just capture the internal features of the working state but also identify the faults of the coaxial-rotor unit with various rotating speeds.
- (3)
- In line with the practical working conditions, experiments are carried out on coaxial-rotor unit vibration signals to verify the effectiveness of the proposed model. Our model achieves decent working performance in the test.
2. Problem Formulation
2.1. Structure of Coaxial-Rotor Unit
2.2. System Establishment
3. Preliminary Analysis
4. Fault Diagnosis Approach
4.1. Model Architecture
4.2. Model Training
5. Empirical Study
5.1. Experimental Setting
5.2. Experimental Protocol
5.3. Main Results
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations and Nomenclature
| HEV | Hybrid Electric Vehicle |
| ICE | Internal Combustion Engine |
| GRU | Gate Recurrent Unit |
| ICP | Integrated Circuits Piezoelectric |
| PCB | Printed Circuit Board |
| HHT | Hilbert–Huang Transform |
| EMD | Empirical Mode Decomposition |
| HAS | Hilbert Spectrum Analysis |
| IMF | Intrinsic Mode Functions |
| Bi-GRU | Bidirectional Gated Recurrent Unit |
| ReLU | Rectified Linear Unit |
| RNN | Recurrent Neural Network |
| ADAM | Adaptive Moment Estimation |
| TP | True Positive |
| TN | True Negative |
| FP | False Positive |
| FN | False Negative |
| KNN | K-Nearest Neighbor |
| SVM | Support Vector Machine |
| CNN | Convolutional Neural Network |
| LSTM | Long Short-Term Memory |
| i-th IMF | |
| n-th residual function | |
| A | instantaneous amplitude |
| instantaneous phase | |
| instantaneous frequency | |
| the marginal spectrum energy value of IMF | |
| energy normalization value | |
| output of Bi-GRU | |
| forward hidden state | |
| backward hidden state | |
| transform gate of Highway Network | |
| carry gate of Highway Network | |
| parametric matrices optimized during training | |
| trainable matrix | |
| offset vector | |
| regularization |
References
- Tran, D.D.; Vafaeipour, M.; Baghdadi, M.E.; Barrero, R.; Hegazy, O. Thorough state-of-the-art analysis of electric and hybrid vehicle powertrains: Topologies and integrated energy management strategies. Renew. Sustain. Energy Rev. 2019, 119, 109596. [Google Scholar] [CrossRef]
- Haley, P. Effect of Electric Vehicles on Residential Distribution Systems. Bachelor’s Thesis, Louisiana State University, Baton Rouge, LA, USA, 2010. [Google Scholar]
- Tate, E.D. Techniques for Hybrid Electric Vehicle Controller Synthesis. Doctor’s Dissertation, University of Michigan, Ann Arbor, MI, USA, 2007. [Google Scholar]
- Borthakur, S.; Subramanian, S.C. Optimized Design and Analysis of a Series-Parallel Hybrid Electric Vehicle Powertrain for a Heavy Duty Truck. IFAC-PapersOnLine 2018, 51, 184–189. [Google Scholar] [CrossRef]
- Samuel; Ashwin, V. Energy Management System for a Hybrid Electric Vehicle. Master’s Dissertation, Lamar University, Beaumont, TX, USA, 2015. [Google Scholar]
- Canadian Automobile Association. Types of Electric Vehicles. Available online: https://electricvehicles.caa.ca/types-of-electric-vehicles/ (accessed on 29 May 2015).
- Zhao, Y.P.; Hu, Q.K.; Xu, J.G.; Bing, L.; Gong, H.; Pan, Y.T. A robust extreme learning machine for modeling a small-scale turbojet engine. Appl. Energy 2018, 218, 22–35. [Google Scholar] [CrossRef]
- Chen, Z.; Yuan, X.; Sun, M.; Gao, J.; Li, P. A Hybrid Deep Computation Model for Feature Learning on Aero-engine Data—Applications to Fault Detection. Appl. Math. Model. 2020, 83, 487–496. [Google Scholar] [CrossRef]
- Ji, Z.; Qin, J.; Guo, F.; Dang, C.; Zhang, S.; Dong, P. Effect of operating parameters on a hybrid propulsion system with high efficiency fueled by Kerosene for high altitude long endurance unmanned aerial vehicles. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis with Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Dan, Q.; Liu, X.; Yi, C.; Ke, Z.; Hao, L. A Fault Diagnosis Approach Based on Deep Belief Network and Its Application in Bearing Fault. In Proceedings of the 2018 Chinese Intelligent Systems Conference; Springer: Singapore, 2018; pp. 289–300. [Google Scholar]
- Lu, S.; Wang, X. A new methodology to estimate the rotating phase of a BLDC motor with its application in variable-speed bearing fault diagnosis. IEEE Trans. Power Electron. 2018, 33, 3399–3410. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Huang, P.; Li, Q. Fault diagnosis of rolling bearing using symmetrized dot pattern and density-based clustering. Measurement 2020, 152, 107293. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part II: Fault Diagnosis With Knowledge-Based and Hybrid/Active Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar] [CrossRef]
- Yin, J.; Zhao, W. Fault diagnosis network design for vehicle on-board equipment of high-speed railway: A deep learning approach. Eng. Appl. Artif. Intell. 2016, 56, 250–259. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Song, F.Q.; Pan, Y.T.; Li, B. Retargeting extreme learning machines for classification and their applications to fault diagnosis of aircraft engine. Aerosp. Sci. Technol. 2017, 71, 603–618. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.H.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Yang, C.; Jiang, M.; Jiang, B.; Zhou, W.; Li, K. Co-Attention Network with Question Type for Visual Question Answering. IEEE Access 2019, 7, 40771–40781. [Google Scholar] [CrossRef]
- Lin, L.; Luo, H.; Huang, R.; Ye, M. Recurrent Models of Visual Co-Attention for Person Re-Identification. IEEE Access 2019, 7, 8865–8875. [Google Scholar] [CrossRef]
- Ji, Z.; Qin, J.; Cheng, K.; Liu, H.; Zhang, S.; Dong, P. Performance evaluation of a turbojet engine integrated with inter-stage turbine burner and solid oxide fuel cell. Energy 2019, 168, 702–711. [Google Scholar] [CrossRef]
- Dadouche, A.; Rezaei, A.; Wickramasinghe, V.; Dmochowski, W.; Bird, J.W.; Nitzsche, F. Sensitivity of Air-Coupled Ultrasound and eddy current sensors to bearing fault detection. Tribol. Trans. 2008, 51, 310–323. [Google Scholar] [CrossRef]
- Rezaei, A.; Dadouche, A.; Wickramasinghe, V.; Dmochowski, W. A comparison study between acoustic sensors for bearing fault detection under different speed and load using a variety of signal processing techniques. Tribol. Trans. 2010, 54, 179–186. [Google Scholar] [CrossRef]
- Rezaei, A.; Dadouche, A. Development of a turbojet engine gearbox test rig for prognostics and health management. Mech. Syst. Signal Processing 2012, 33, 299–311. [Google Scholar] [CrossRef]
- Jin, X.; Yang, H.; Wang, H. Fault Diagnosis for Civil Aviation Engine Test Based on the Vibration Signal. Procedia Eng. 2012, 29, 3002–3006. [Google Scholar] [CrossRef][Green Version]
- PCB Model 356A33. Available online: https://www.pcb.com/products?m=356A33 (accessed on 25 September 2017).
- Zhao, X.; Jia, M.; Lin, M. Deep laplacian auto-encoder and its application into imbalanced fault diagnosis of rotating machinery. Measurement 2019, 152, 107320. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.A. The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Song, D.; Liu, X.; Huang, J.; Zhang, J. Energy-based analysis of seismic failure mechanism of a rock slope with discontinuities using Hilbert-Huang transform and marginal spectrum in the time-frequency domain. Landslides 2021, 18, 105–123. [Google Scholar] [CrossRef]
- Li, C.; Yu, G.; Fu, B.; Hu, H.; Zhu, Q. Fault Separation and Detection for Compound Bearing-Gear fault Condition Based on Decomposition of Marginal Hilbert Spectrum. IEEE Access 2019, 7, 110518–110530. [Google Scholar] [CrossRef]
- Jia, W.; Diao, M.; Jiang, L.; Huang, G. Fluctuating Characteristics of the Stilling Basin with a Negative Step Based on Hilbert-Huang Transform. Water 2021, 13, 2673. [Google Scholar] [CrossRef]
- Yi, C.; Lin, J.; Zhang, W.; Ding, J. Faults Diagnostics of Railway Axle Bearings Based on IMF’s Confidence Index Algorithm for Ensemble EMD. Sensors 2015, 15, 10991–11011. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A Critical Review of Recurrent Neural Networks for Sequence Learning. Available online: http://arxiv.org/abs/1506.00019 (accessed on 17 October 2015).
- Dey, R.; Salemt, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar]
- Dang, L.M.; Sadeghi-Niaraki, A.; Huynh, H.D.; Min, K.; Moon, H. Deep Learning Approach for Short-Term Stock Trends Prediction Based on Two-Stream Gated Recurrent Unit Network. IEEE Access 2018, 6, 55392–55404. [Google Scholar]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Highway networks. arXiv 2015, arXiv:1505.00387. [Google Scholar]
- Powers, D. Evaluation: From Precision, Recall and F-Measure to Roc, Informedness, Markedness & Correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
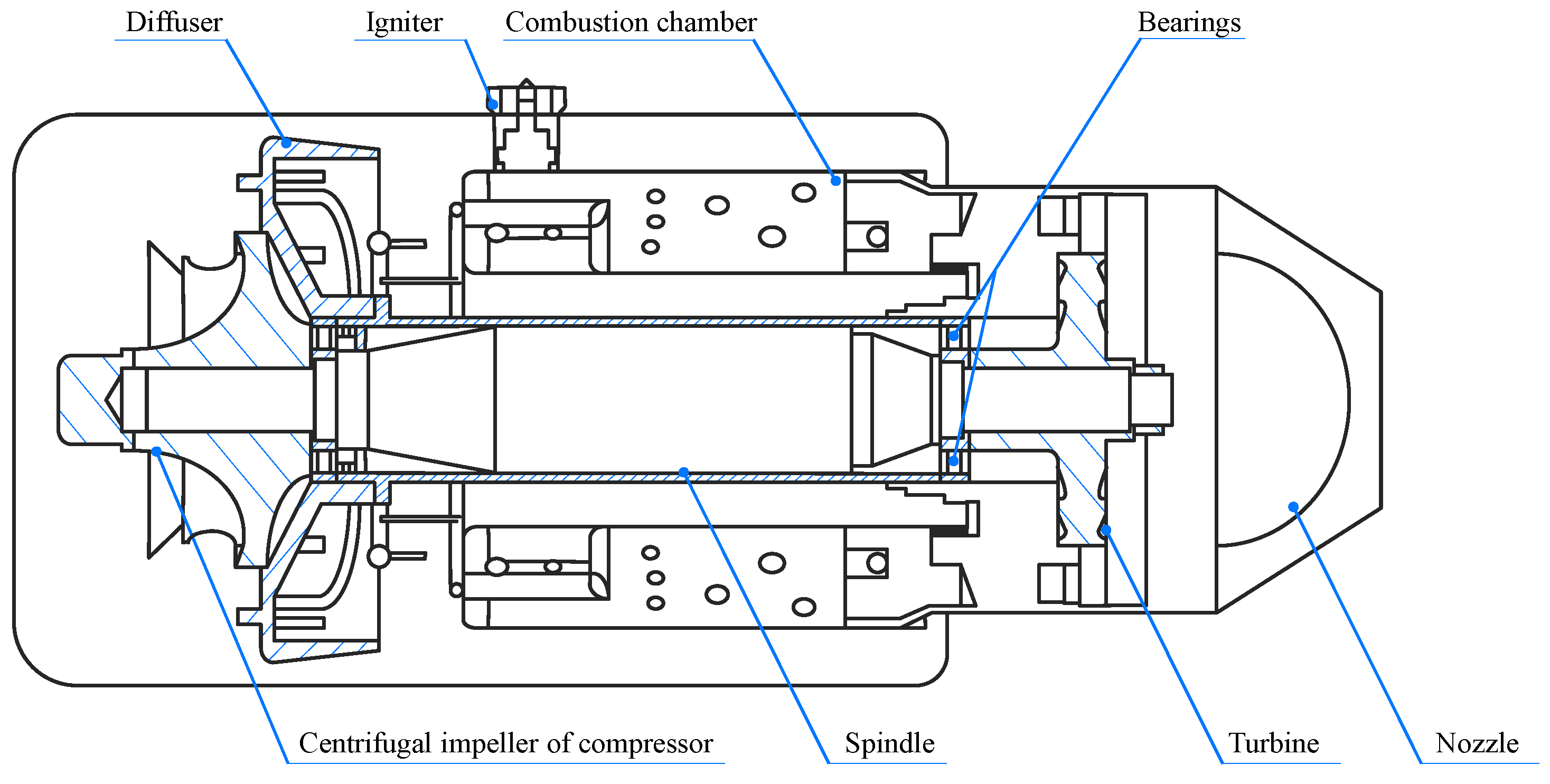
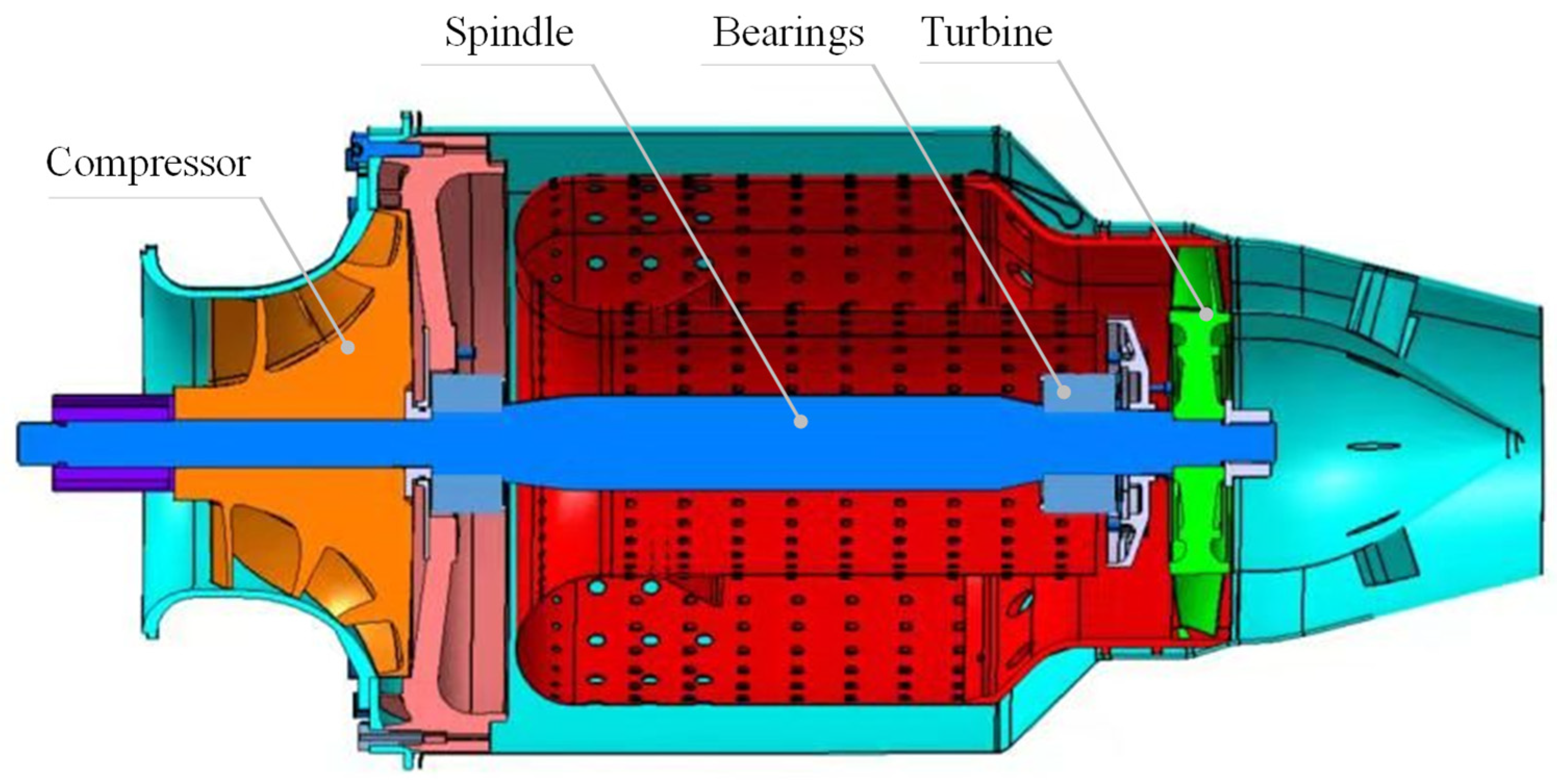

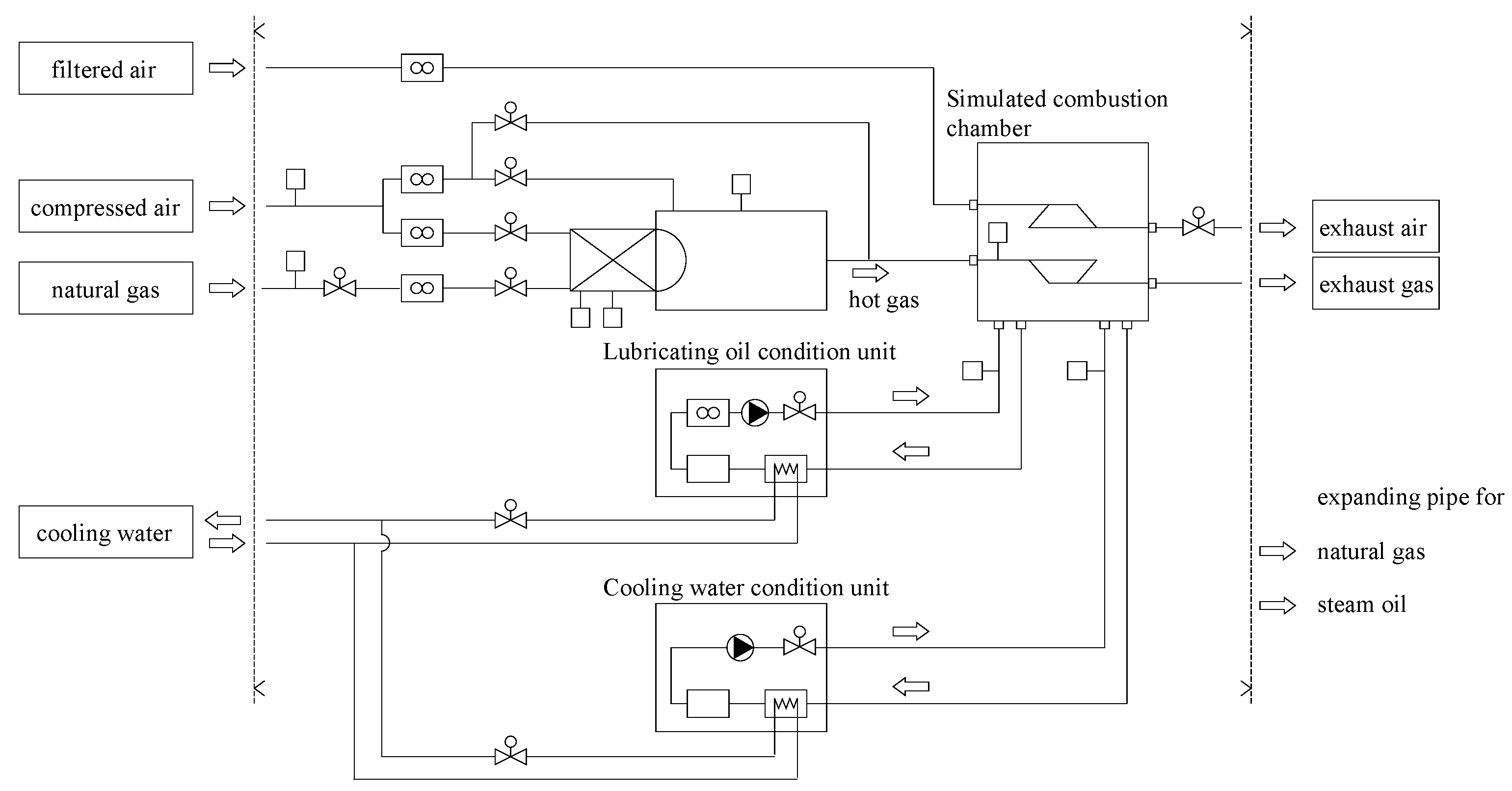


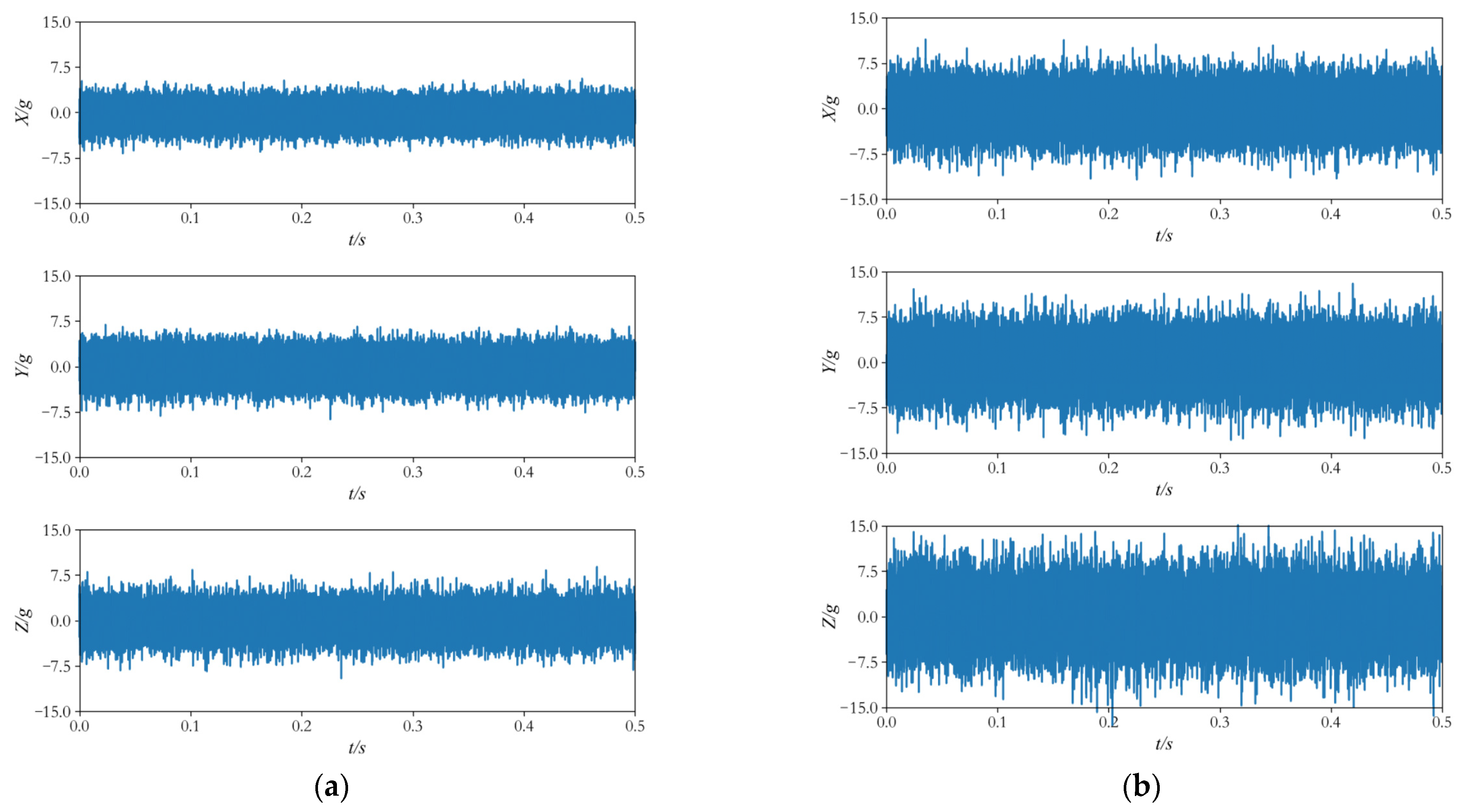



| Device | Model | Range | Precision | Quantity |
|---|---|---|---|---|
| Vibration sensor | ICP 356A33 | (−500~+500) g | 10 mg/V | 3 |
| Temperature sensor | W-Re5/26 | (0~1800) | 0.5% F.S. | 1 |
| Speed sensor | SS443A | (0–20 k) Hz | 1% F.S. | 1 |
| Vibration analyzer | LMS830A | (0–102.4 k) Hz | 1% F.S. | 1 |
| Predicted/Actual | Actual: YES | Actual: NO |
|---|---|---|
| Predicted: YES Predicted: NO | TP(True Positive) FN(False Negative) | FP(False Positive) TN(True Negative) |
| Rotating Speed (r/min) | KNN | SVM | CNN | LSTM | GRU | Bi-GRU | Our Model |
|---|---|---|---|---|---|---|---|
| 20,000 | 85.0% | 72.8% | 89.5% | 82.4% | 81.5% | 99.9% | 100% |
| 25,000 | 75.0% | 64.4% | 86.7% | 99.3% | 94.0% | 95.9% | 99.4% |
| 30,000 | 94.4% | 95.6% | 95.0% | 95.5% | 92.0% | 97.8% | 98.0% |
| 35,000 | 81.1% | 72.2% | 100% | 100% | 99.5% | 99.9% | 99.6% |
| 40,000 | 100% | 100% | 90.2% | 100% | 98.3% | 99.9% | 99.2% |
| 45,000 | 100% | 100% | 94.5% | 100% | 100% | 100% | 100% |
| 50,000 | 86.1% | 91.1% | 100% | 99.8% | 99.6% | 100% | 100% |
| 55,000 | 77.8% | 76.7% | 99.4% | 98.5% | 100% | 99.1% | 99.3% |
| 60,000 | 100% | 100% | 99.7% | 100% | 99.7% | 99.9% | 99.1% |
| Average | 88.8% | 85.7% | 95.0% | 97.3% | 96.0% | 99.1% | 99.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Dong, K.; Wang, Y.; Huang, X. A Fault Diagnosis Model for Coaxial-Rotor Unit Using Bidirectional Gate Recurrent Unit and Highway Network. Machines 2022, 10, 313. https://doi.org/10.3390/machines10050313
Peng Z, Dong K, Wang Y, Huang X. A Fault Diagnosis Model for Coaxial-Rotor Unit Using Bidirectional Gate Recurrent Unit and Highway Network. Machines. 2022; 10(5):313. https://doi.org/10.3390/machines10050313
Chicago/Turabian StylePeng, Zhaoqin, Kunyu Dong, Yan Wang, and Xucong Huang. 2022. "A Fault Diagnosis Model for Coaxial-Rotor Unit Using Bidirectional Gate Recurrent Unit and Highway Network" Machines 10, no. 5: 313. https://doi.org/10.3390/machines10050313
APA StylePeng, Z., Dong, K., Wang, Y., & Huang, X. (2022). A Fault Diagnosis Model for Coaxial-Rotor Unit Using Bidirectional Gate Recurrent Unit and Highway Network. Machines, 10(5), 313. https://doi.org/10.3390/machines10050313





