An Unscented Kalman Filter Online Identification Approach for a Nonlinear Ship Motion Model Using a Self-Navigation Test
Abstract
:1. Introduction
- (a)
- The time-varying problem of motion parameters is overcome. Based on a self-navigation model test, unknown parameters in the ship motion system are identified online by using a combination of receding horizon denoising and a UKF algorithm while collecting relevant data of the ship’s motion system.
- (b)
- The nonlinear problem of the ship motion system is overcome and the motion system of a specific type of ship model is identified based on a nonlinear ship motion model. The practical application of the UKF in parameter identification provides data support for ship control problems.
2. System Modeling
3. Online Identification Modeling and UKF Application
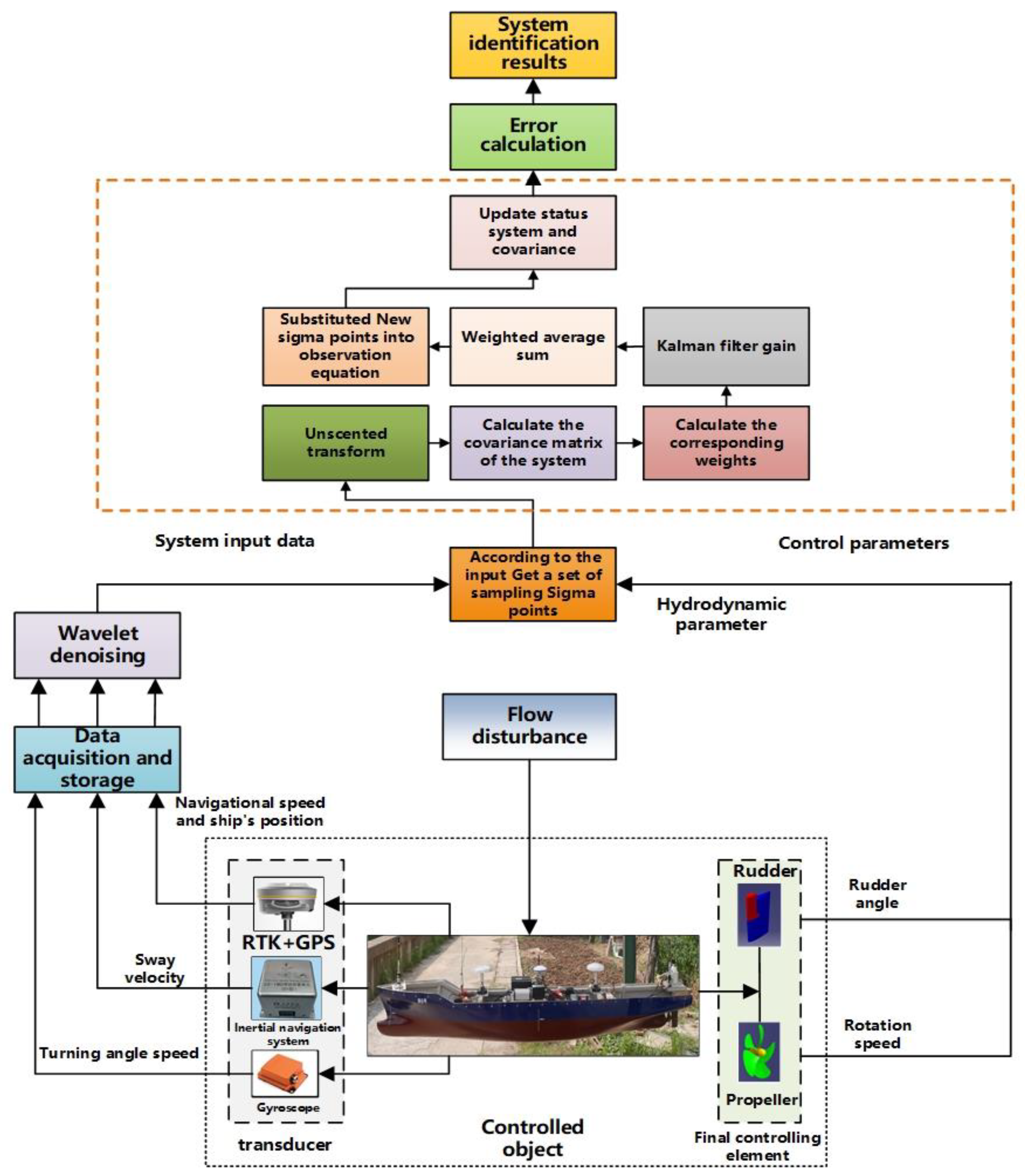
3.1. Online Identification Framework Design
3.2. Application of the UKF Algorithm
- Obtain a set of sampling points and their corresponding weights using Formulas (2) and (3).
- 2.
- Calculate the one-step prediction of the 2𝑛 + 1 sampling points, 𝑖 = 1,2... 𝑛 + 1,2.
- 3.
- Calculate the one-step prediction and covariance matrix of the system state obtained from the weighted sum of the predicted values of the sigma point set.
- 4.
- According to the one-step predicted value of the system state, an unscented transformation is used again to generate a new set of sigma points.
- 5.
- By substituting the new set of sigma points into the observation equation, the one-step predicted value of the observed quantity can be obtained, 𝑖 = 1,2... 2𝑛 + 1.
- 6.
- By summing the one-step prediction observation value of the sigma point set, the one-step prediction means, covariance and one-step prediction covariance of the system state are obtained.
- 7.
- Calculate Kalman filter gain.
- 8.
- Finally, the state and covariance update of the system are calculated.
| Algorithm 1 Unscented Kalman filter identification algorithm. |
| Principle of the UKF Online Identification Algorithm |
| 1: Set the sampling rule of sigma points 2: Set the weight of sampling points 3: Set the original initial value of the parameters |
| 4: Obtain the initial filter value |
| 5: for i = 1:𝑛 |
| 6: Set state space 𝑋(𝑘) 𝑍(𝑘) |
| 7: Enter the ship movement parameters 𝑢, 𝑣, 𝑟, and |
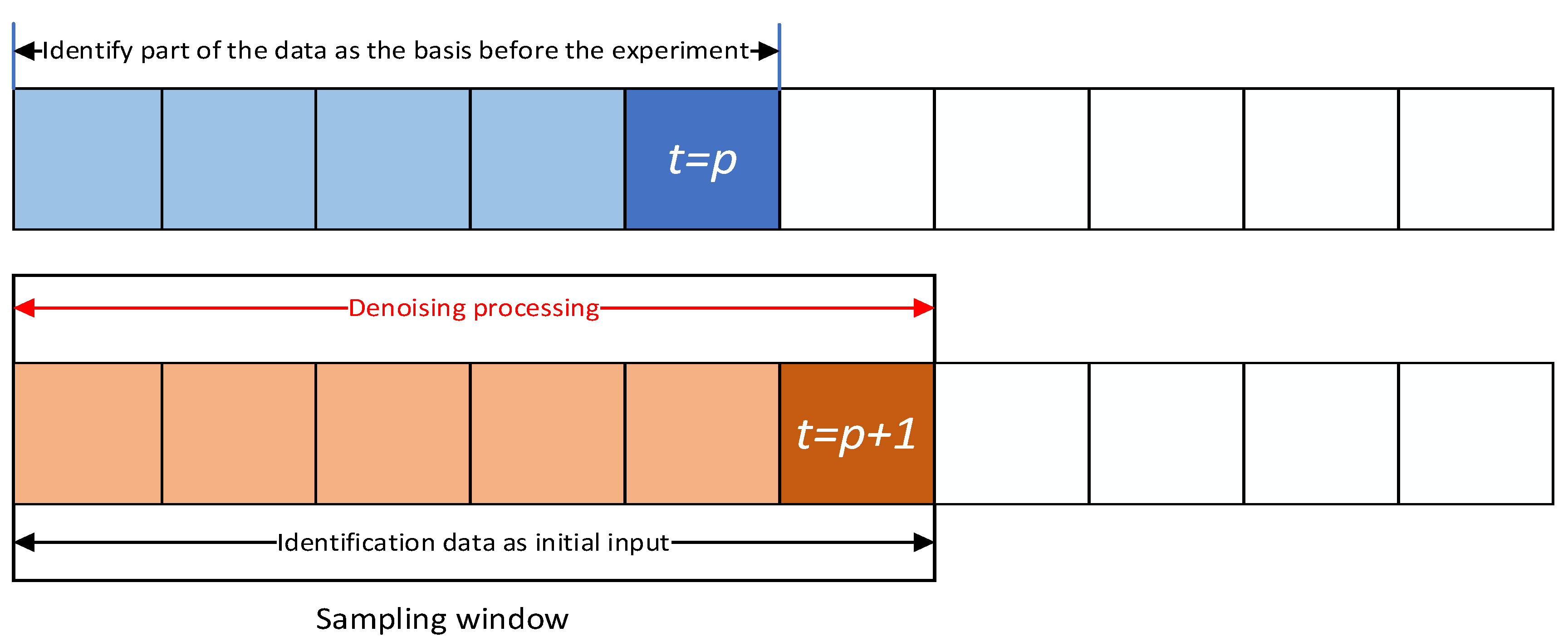
| 8: Sliding time window (1) |
| 9: Unscented Kalman filter (1) |
| 10: Wavelet denoising |
| 11: Sliding time window (2) |
| 12: Unscented Kalman filter (2) |
| 13: end 14: Calculated identification error |
4. Experiment Description
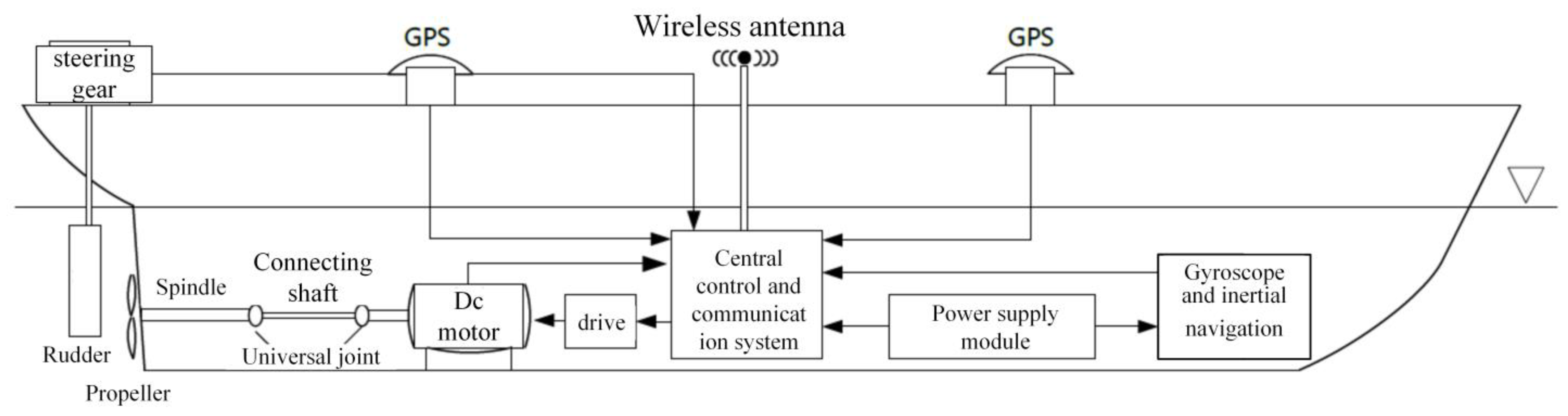
4.1. Free-Running Test Platform and Design
4.2. Contrasting Experiments before and after Denoising
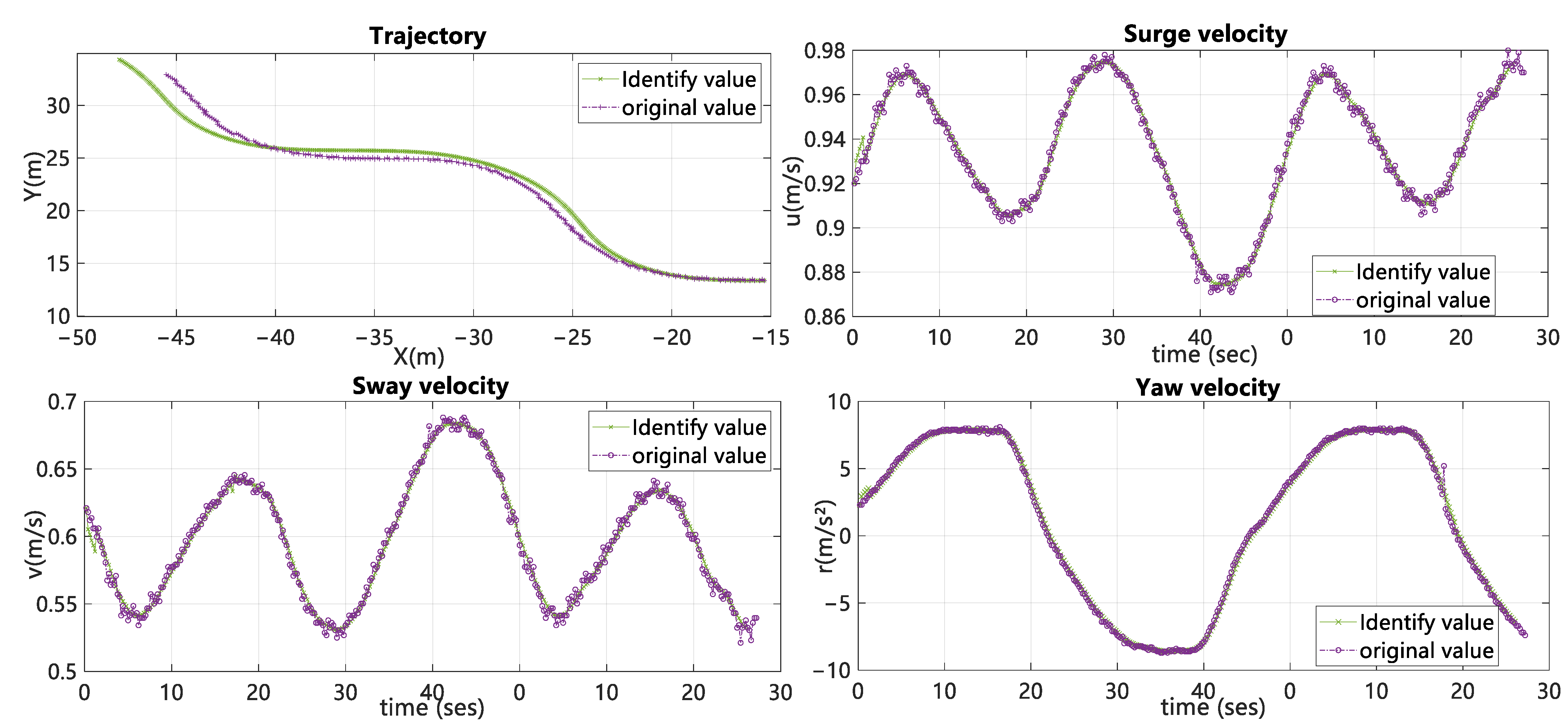
4.3. Comparison of the Identification Effects to Other Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, W.; Soares, C.G.; Zou, Z. Parameter Identification of Ship Maneuvering Model Based on Support Vector Machines and Particle Swarm Optimization. J. Offshore Mech. Arct. Eng. 2016, 138, 031101. [Google Scholar] [CrossRef]
- Luo, W.L.; Zou, Z.J. Identification of Response Models of Ship Maneuvering Motion Using Support Vector Machines. J. Ship Mech. 2007, 11, 832–838. [Google Scholar]
- Zhang, X.G.; Zou, Z.J. Black-box modeling of vessel manoeuvring motion based on feed-forward neural network with Chebyshev orthogonal basis function. J. Mar. Sci. Technol. 2013, 18, 42–49. [Google Scholar] [CrossRef]
- Wang, X.-G.; Zou, Z.-J.; Hou, X.-R. System identification modelling of vessel manoeuvring motion based on epsilon—Support vector regression. J. Hydrodyn. 2015, 27, 502–512. [Google Scholar] [CrossRef]
- Xue, Y.; Liu, Y.; Ji, C.; Xue, G.; Huang, S. System identification of ship dynamic model based on Gaussian process regression with input noise. Ocean. Eng. 2020, 216, 107862. [Google Scholar] [CrossRef]
- Wang, N.; Dong, N.; Liu, Y.; Han, M. Vessel maneuvering model identification using multi-output dynamic fuzzy neural networks. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 5144–5149. [Google Scholar] [CrossRef]
- Moreira, L.; Soares, C.G. Dynamic model of manoeuvrability using recursive neural networks. Ocean. Eng. 2003, 30, 1669–1697. [Google Scholar] [CrossRef]
- Yin, J.; Wang, N.; Perakis, A.N. A Real-Time Sequential Ship Roll Prediction Scheme Based on Adaptive Sliding Data Window. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 2115–2125. [Google Scholar] [CrossRef]
- Huang, B.G.; Zou, Z.J.; Ding, W.W. Online prediction of ship roll motion based on a coarse and fine tuning fixed grid wavelet network. Ocean. Eng. 2018, 160, 425–437. [Google Scholar] [CrossRef]
- Yoon, H.K.; Rhee, K.P. Identification of hydrodynamic coefficients in vessel maneuvering equations of motion by Estimation-Before-Modeling technique. Ocean. Eng. 2003, 30, 2379–2404. [Google Scholar] [CrossRef]
- Deng, F.; Levi, C.; Yin, H.; Duan, M. Identification of an Autonomous Underwater Vehicle hydrodynamic model using three Kalman filters. Ocean. Eng. 2021, 229, 108962. [Google Scholar] [CrossRef]
- Zheng, J.; Yan, M.; Li, Y.; Huang, C.; Ma, Y.; Meng, F. An online identification approach for a nonlinear ship motion model based on a receding horizon. Trans. Inst. Meas. Control. 2021, 43, 3000–3012. [Google Scholar] [CrossRef]
- Perera, L.P.; Oliveira, P.; Guedes Soares, C. Dynamic parameter estimation of a nonlinear vessel steering model for ocean navigation. In Proceedings of the 30th International Conference on Ocean, Offshore and Arctic Engineering, OMAE 2011, Rotterdam, The Netherlands, 19–24 June 2011. OMAE 2011-50249. [Google Scholar]
- Skjetne, R.; Smogeli, Y.; Fossen, T.I. Modeling, identification, and adaptive maneuvering of CyberShip II: A complete design with experiments. IFAC Proc. Vol. 2004, 37, 203–208. [Google Scholar] [CrossRef]
- Cui, R.; Ge, S.S.; How, B.V.E.; Choo, Y.S. Leader–follower formation control of underactuated autonomous underwater vehicles. Ocean. Eng. 2010, 37, 1491–1502. [Google Scholar] [CrossRef]
- Chang, L.; Hu, B.; Li, A.; Qin, F. Transformed Unscented Kalman Filter. IEEE Trans. Autom. Control. 2013, 58, 252–257. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, D.; Zhang, J.; Zhang, M.; Soares, C.G. A novel real-time collision risk awareness method based on velocity obstacle considering uncertainties in ship dynamics. Ocean. Eng. 2020, 220, 108436. [Google Scholar] [CrossRef]
- Islam, H.; Soares, C.G. Estimation of hydrodynamic derivatives of a container ship using PMM simulation in OpenFOAM. Ocean. Eng. 2018, 164, 414–425. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X.; Pang, H. Multi-innovation auto-constructed least squares identification for 4 DOF ship manoeuvring modelling with full-scale trial data. Isa Trans. 2015, 58, 186–195. [Google Scholar] [CrossRef] [PubMed]
- Bo, C.; Zhang, S.; Wang, Z.; Lu, A. Research on the Modeling Method Based on Sliding Time Window for Support Vector Machine Soft-Sensing. Process Autom. Instrum. 2006, 027, 45–48. [Google Scholar]


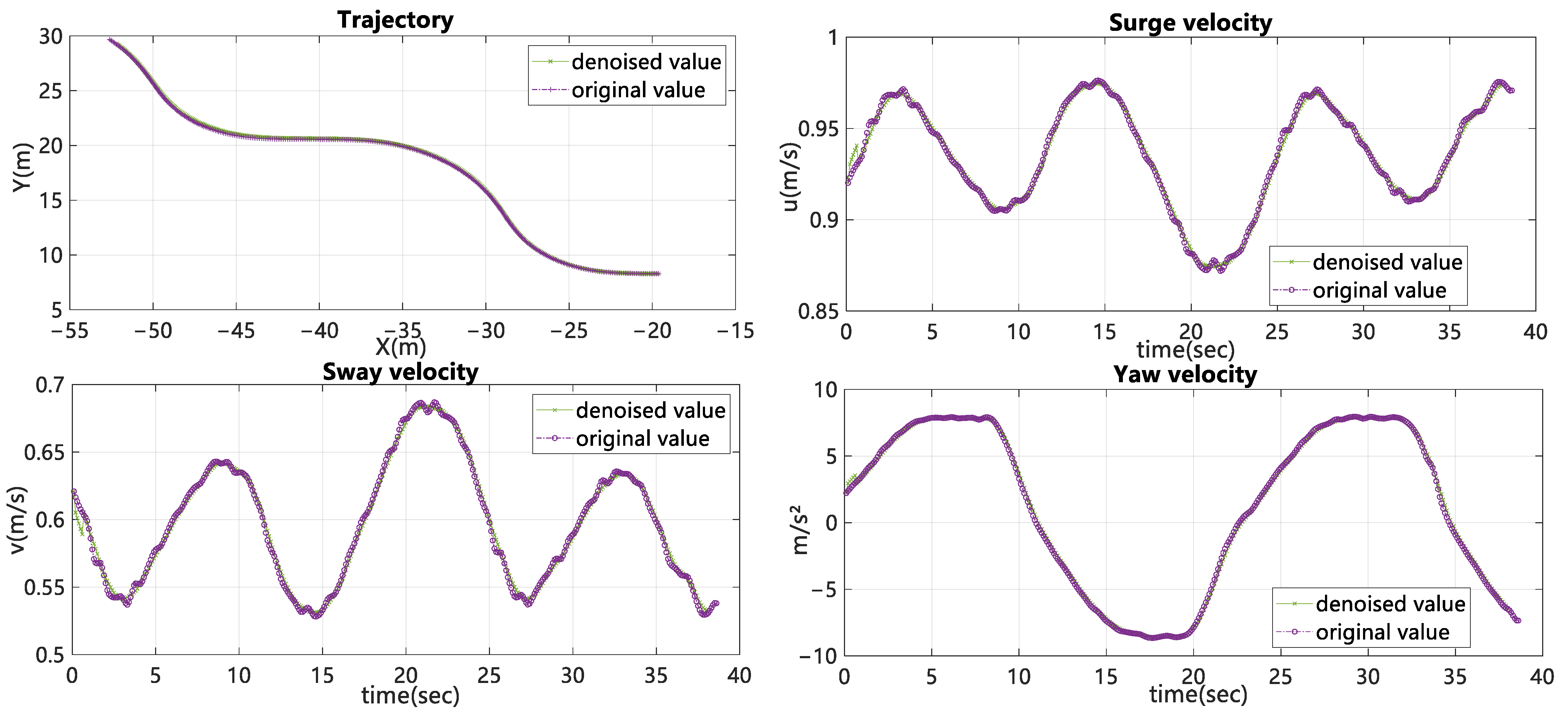
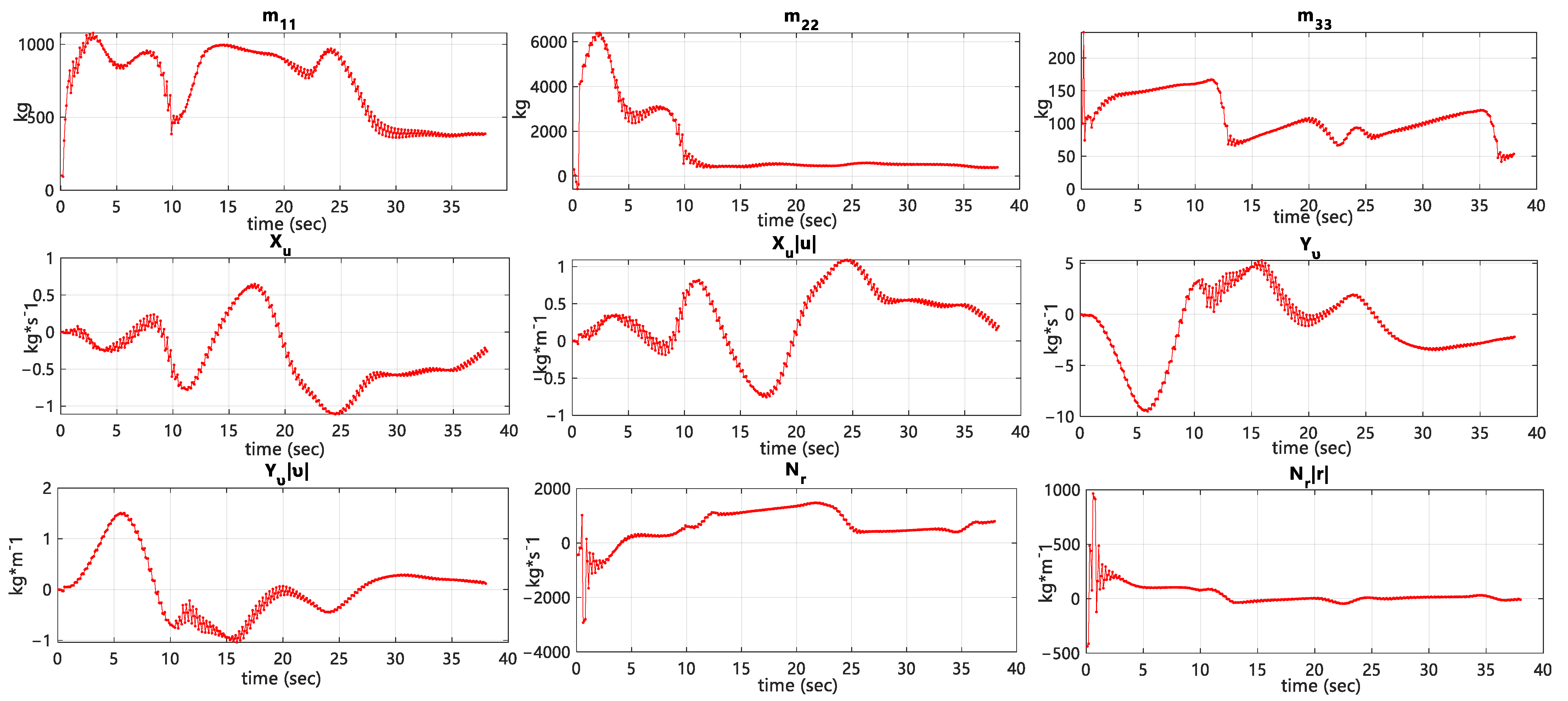
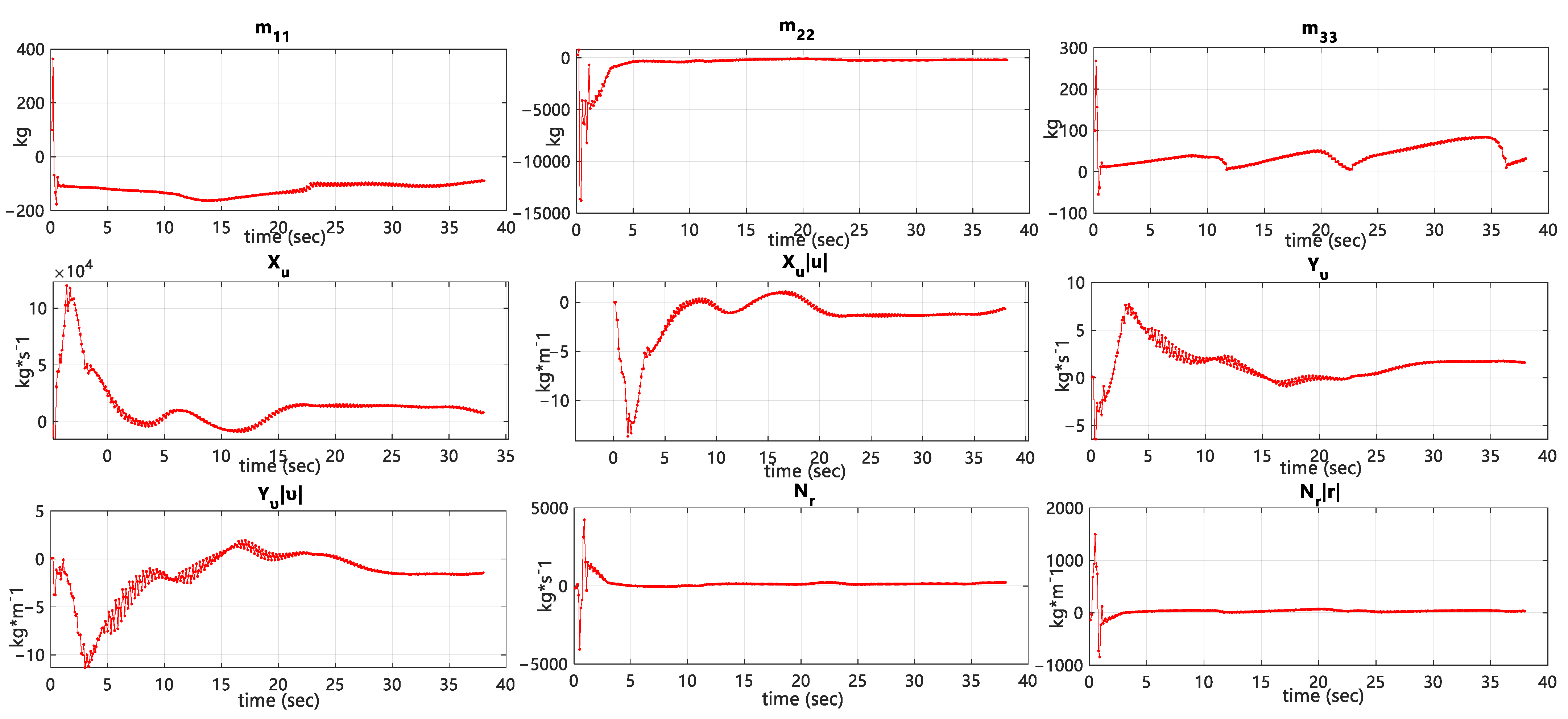
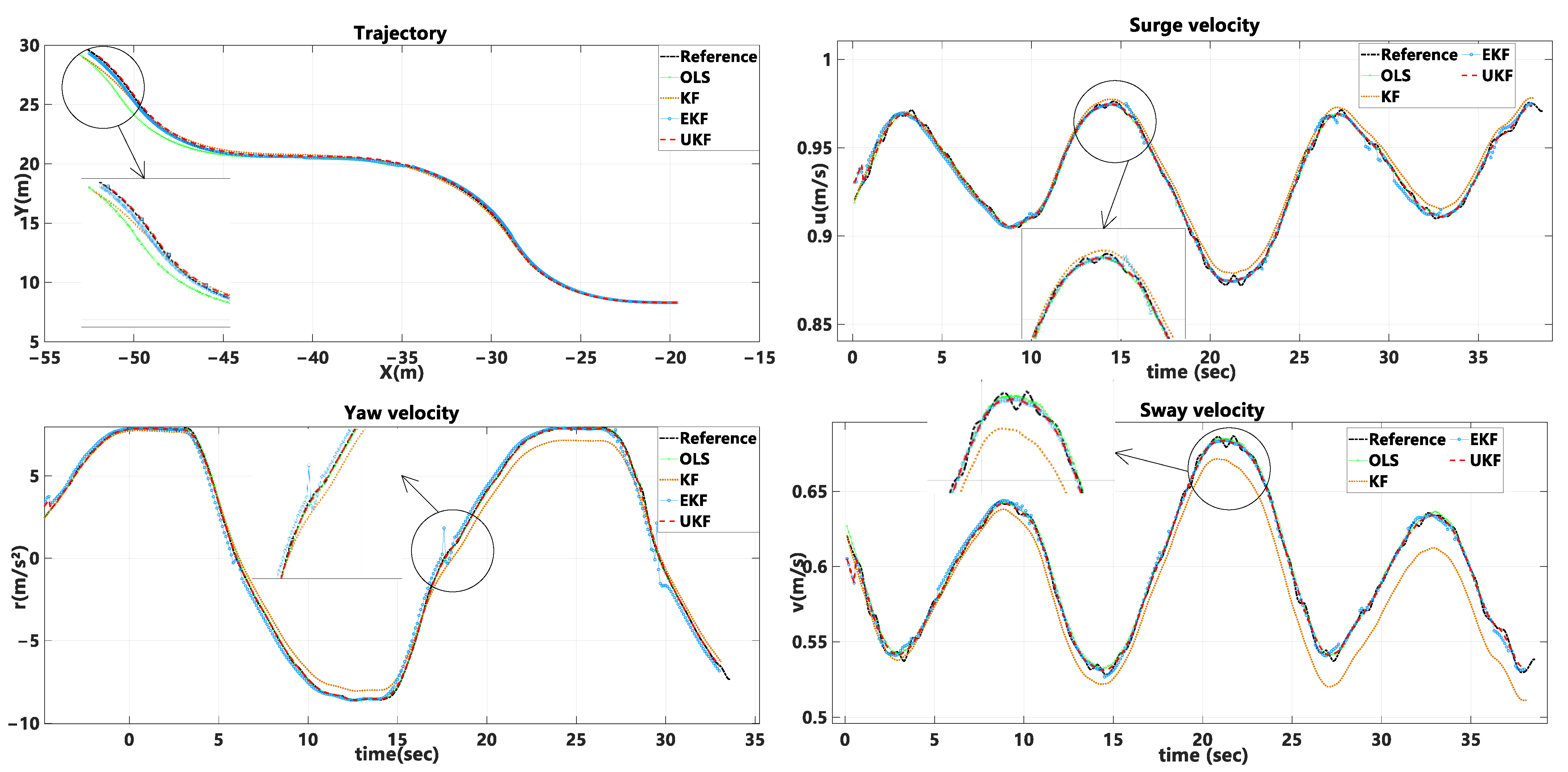
| Parameters | Real Ship | Free-Running Ship |
|---|---|---|
| Hull parameter | ||
| Lpp (m) | 230.0 | 3.0464 |
| Lwl (m) | 232.5 | 3.0791 |
| Breadth (m) | 32.2 | 0.4265 |
| Depth (m) | 19.0 | 0.2517 |
| Draft (m) | 10.8 | 0.1430 |
| Displacement (m3) | 52,030 | 0.1209 |
| Longitudinal center on buoyancy (%) | −1.48 | −1.48 |
| Hull surface area without rudder (m2) | 9530 | 1.6719 |
| Block coefficient (Cb) | 0.651 | 0.651 |
| Midship Section coefficient (CM) | 0.985 | 0.985 |
| Rudder parameter | ||
| S of the rudder (m2) | 115 | 0.0202 |
| Projected area of rudder side (m2) | 54.45 | 0.0096 |
| Rudder height (m) | 9.90 | 0.1311 |
| Mean chord (m) | 5.50 | 0.0728 |
| Mean thickness (m) | 0.99 | 0.0131 |
| Turning rate (deg/s) | 2.32 | 20.2 |
| Propeller parameter | ||
| Type | KP505 | KP505 |
| No. of blades | 5 | 5 |
| Diameter (m) | 7.9 | 0.105 |
| Pitch ratio of 0.7R (P/D) | 0.997 | 0.997 |
| Section line | α = 0.8 | α = 0.8 |
| Hub ratio | 0.180 | 0.180 |
| Rotation | Right hand | Right hand |
| Expended Area ratio (AE/A0) | 0.800 | 0.800 |
| Algorithm | System Input | Surge Velocity (m/s) | Sway Velocity (m/s) | Yaw Velocity (m/s) | Coordinate Distance (m) |
|---|---|---|---|---|---|
| EKF | Denoised data | 0.0032 | 0.0049 | 0.1852 | 0.1122 |
| Original data | 0.0042 | 0.0046 | 0.2344 | 1.8444 | |
| KF | Denoised data | 0.0037 | 0.0150 | 0.4869 | 0.1517 |
| Original data | 0.0063 | 0.0135 | 0.5508 | 1.5448 | |
| OLS | Denoised data | 0.0253 | 0.0537 | 0.5319 | 0.6668 |
| UKF | Denoised data | 0.0024 | 0.0036 | 0.1042 | 0.0850 |
| Original data | 0.0030 | 0.0047 | 0.1480 | 0.1050 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Yan, D.; Yan, M.; Li, Y.; Zhao, Y. An Unscented Kalman Filter Online Identification Approach for a Nonlinear Ship Motion Model Using a Self-Navigation Test. Machines 2022, 10, 312. https://doi.org/10.3390/machines10050312
Zheng J, Yan D, Yan M, Li Y, Zhao Y. An Unscented Kalman Filter Online Identification Approach for a Nonlinear Ship Motion Model Using a Self-Navigation Test. Machines. 2022; 10(5):312. https://doi.org/10.3390/machines10050312
Chicago/Turabian StyleZheng, Jian, Duowen Yan, Ming Yan, Yun Li, and Yabing Zhao. 2022. "An Unscented Kalman Filter Online Identification Approach for a Nonlinear Ship Motion Model Using a Self-Navigation Test" Machines 10, no. 5: 312. https://doi.org/10.3390/machines10050312
APA StyleZheng, J., Yan, D., Yan, M., Li, Y., & Zhao, Y. (2022). An Unscented Kalman Filter Online Identification Approach for a Nonlinear Ship Motion Model Using a Self-Navigation Test. Machines, 10(5), 312. https://doi.org/10.3390/machines10050312






