Progressive Improvement of the Model of an Exoskeleton for the Lower Limb by Applying the Modular Modelling Methodology
Abstract
:1. Introduction
2. The Modular Modelling Methodology
3. The Lower Limb Exoskeleton
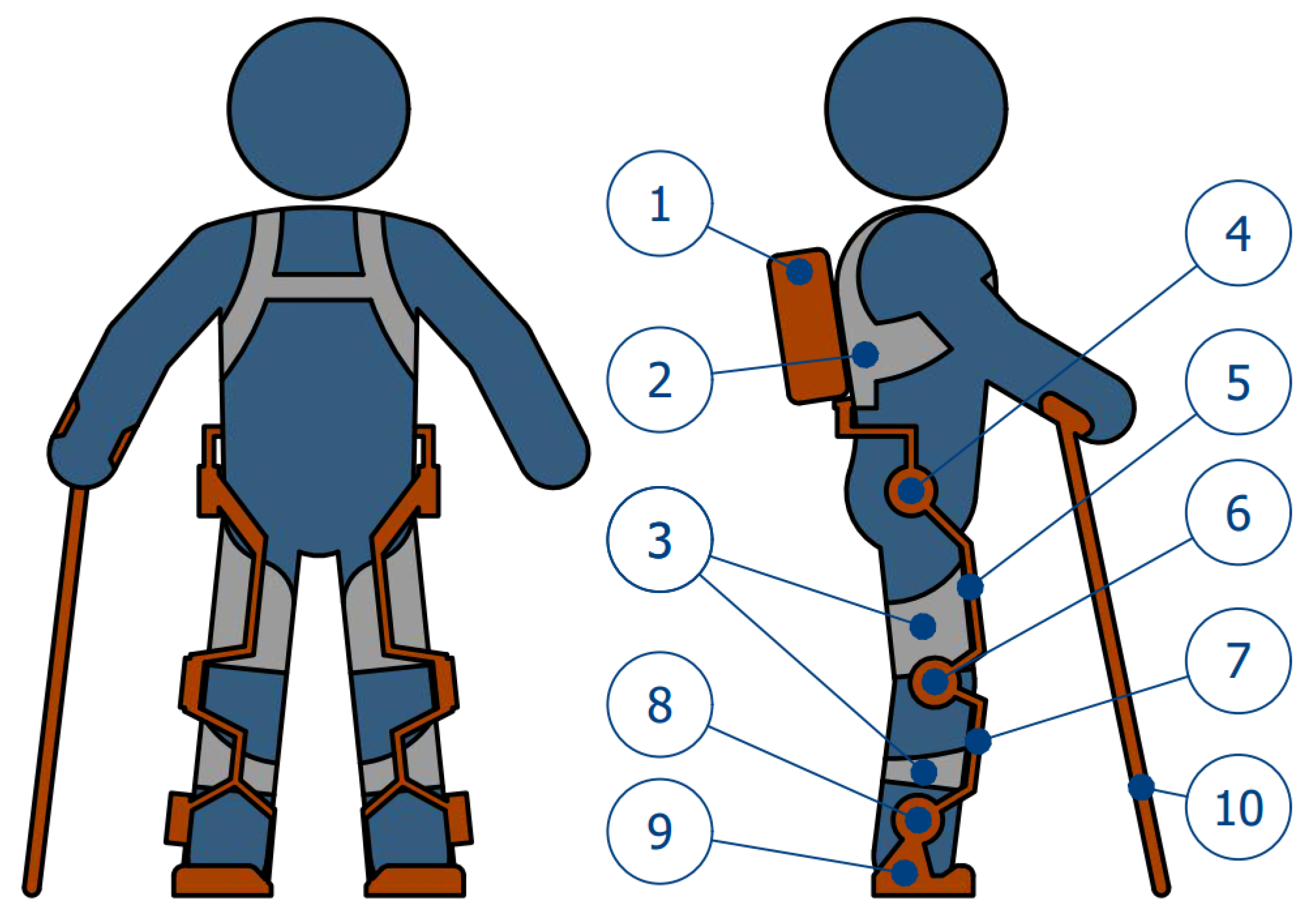
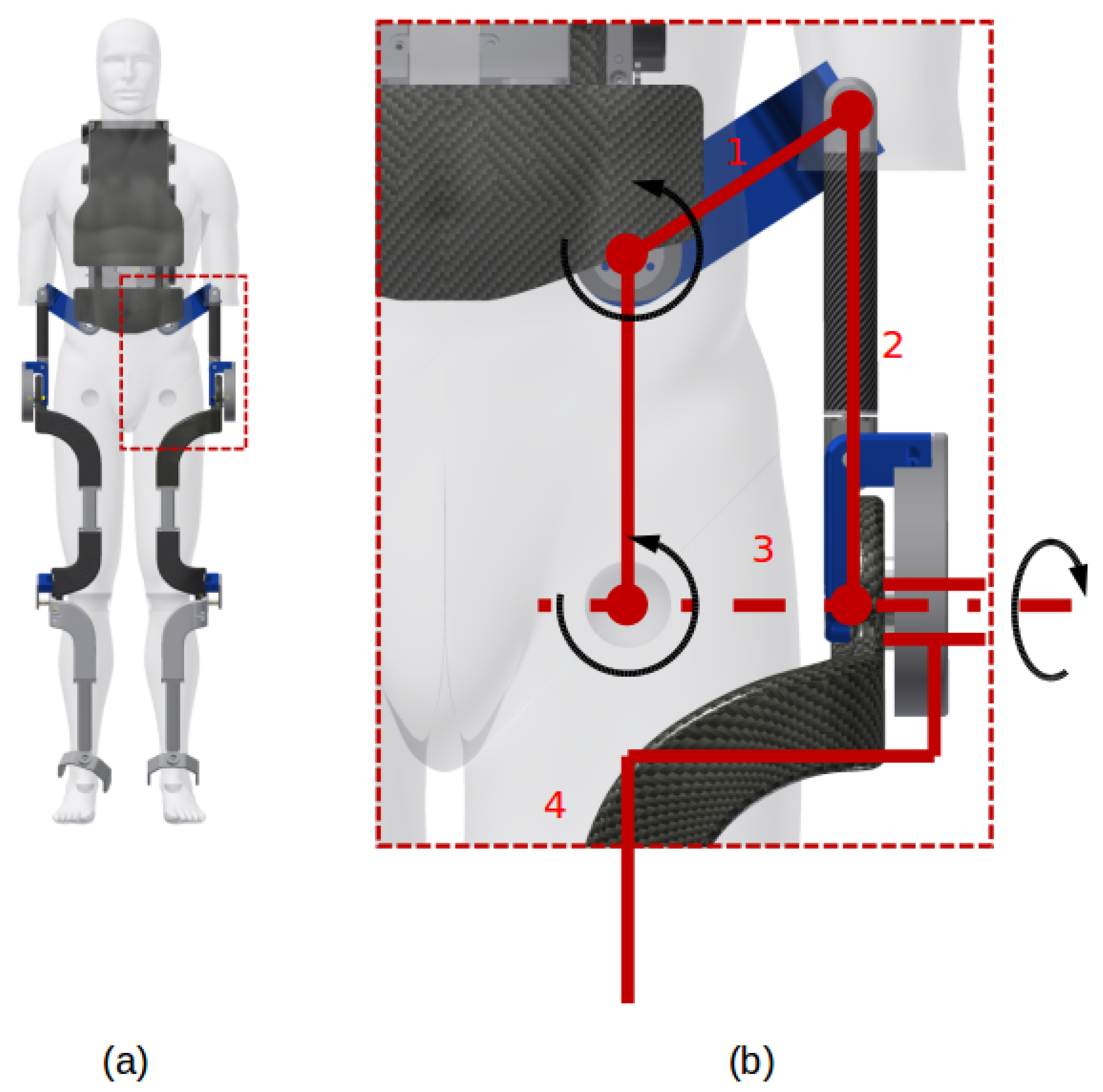
3.1. Conceptual Design
3.2. Mobility Analysis
4. The Exoskeleton Modelling
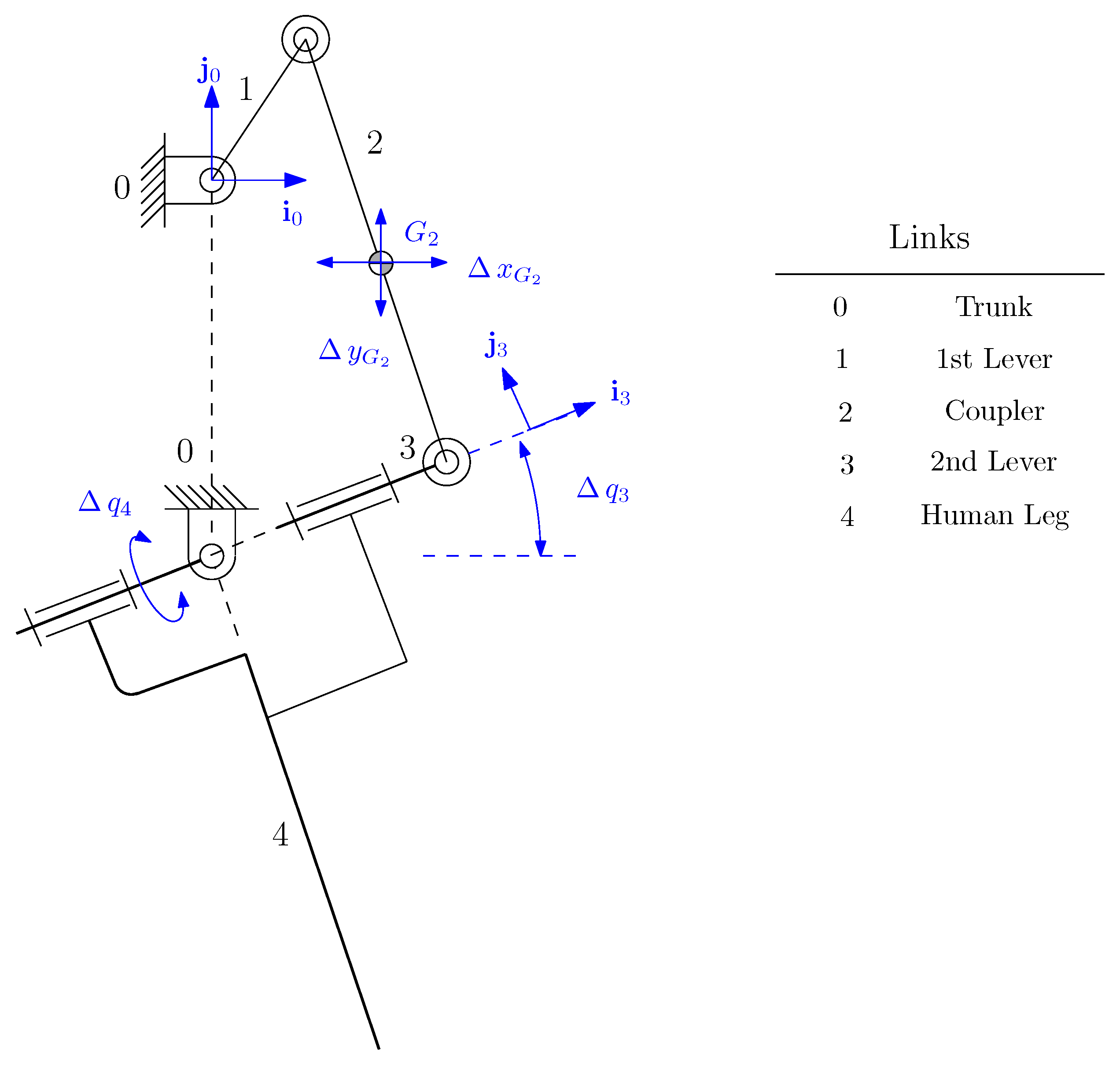
4.1. Kinematic Model
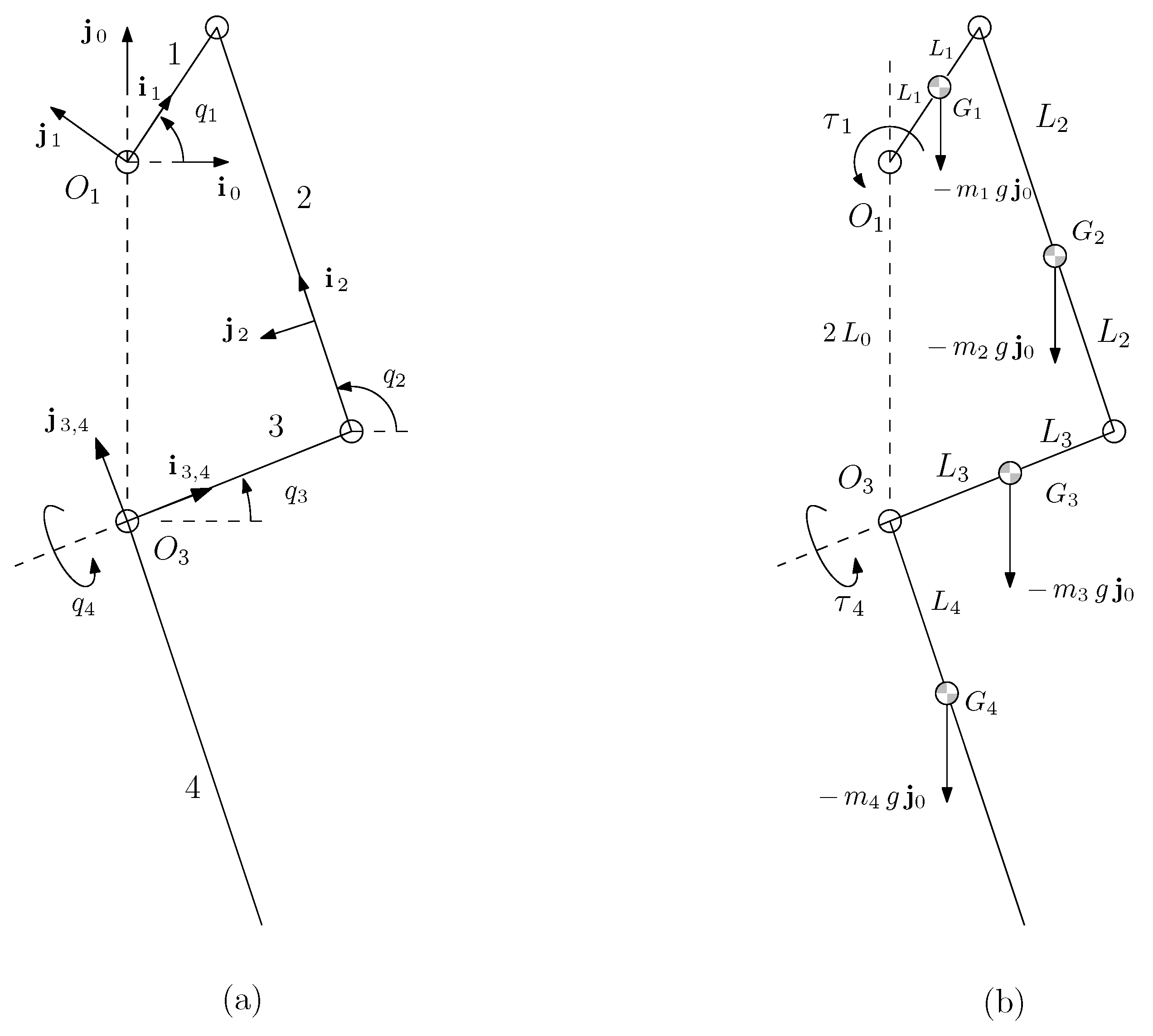
4.2. Dynamic Model
4.3. Modifying the Dynamic Model
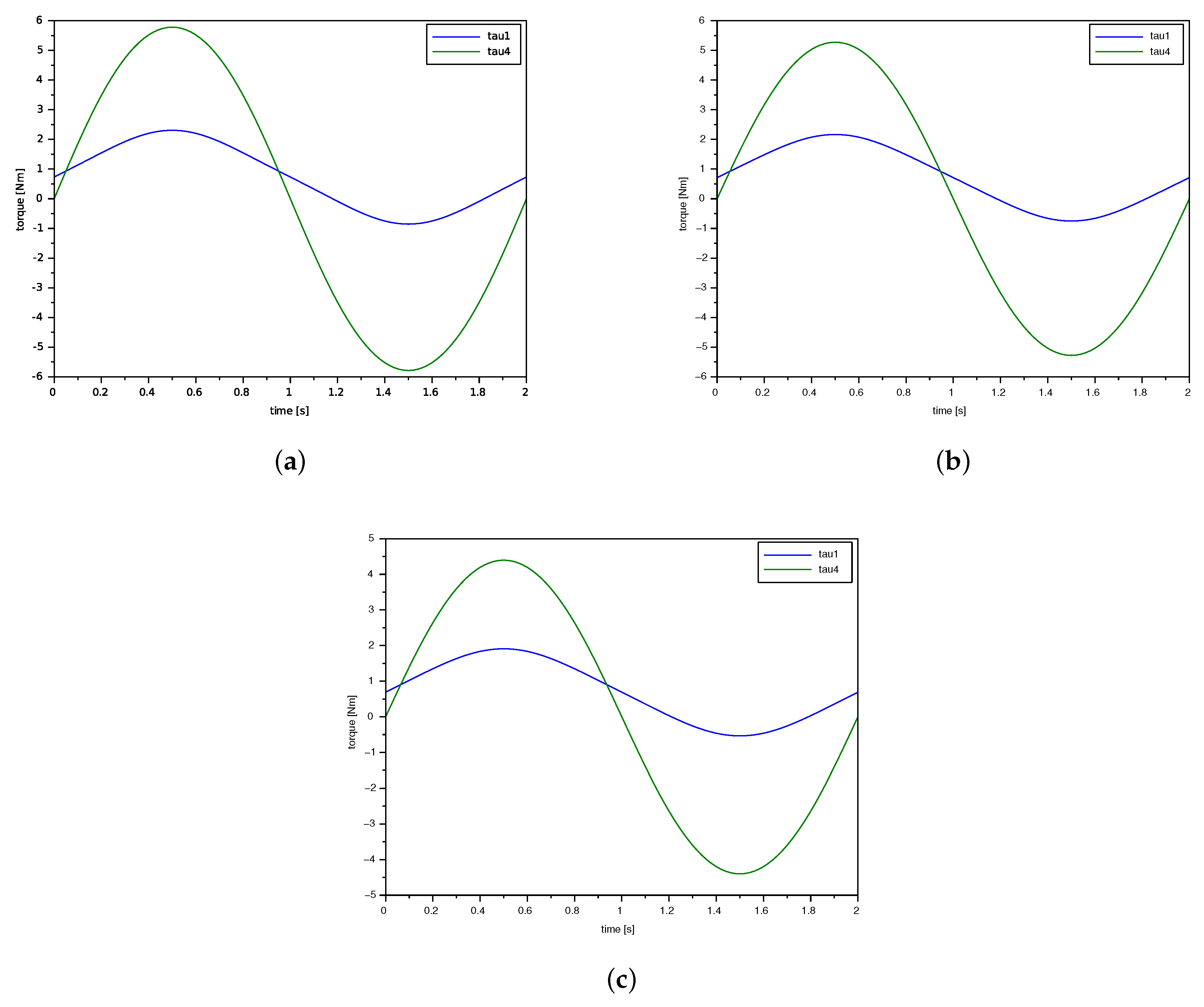
5. Simulations and Results
5.1. First Simulation: Inverse Dynamics
5.2. Second Simulation: Direct Dynamics
5.3. Third Simulation: Inverse Dynamics
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Pons, J.L. Wearable Robots: Biomechatronic Exoskeletons; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Souza, R.S.; Sanfilippo, F.; Silva, J.R.; Forner-Cordero, A. Modular exoskeleton design: Requirement engineering with KAOS. In Proceedings of the IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016; pp. 978–983. [Google Scholar]
- Perry, J.C.; Rosen, J. Design of a 7 degree-of-freedom upper-limb powered exoskeleton. The First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics. BioRob 2006, 2006, 805–810. [Google Scholar]
- Apkarian, J.; Naumann, S.; Cairns, B. A three-dimensional kinematic and dynamic model of the lower limb. J. Biomech. 1989, 22, 143–155. [Google Scholar] [CrossRef]
- Miranda, A.B.W. Exoesqueleto Robótico de Membro Superior com três Graus de Liberdade Ativos. Master’s Thesis, University of Sao Paulo, Sao Paulo, Brazil, 2014. [Google Scholar]
- Hogan, N. Impedance Control: An Approach to manipulation: Part I, Part II, Part III. J. Dyn. Syst. Meas. Control 1985, 107, 1–24. [Google Scholar] [CrossRef]
- Zoss, C.A.; Kazerooni, H.; Chu, A. Biomechanical Design of the Berkeley Lower Extremity exoskeleton (BLEEX). IEEE/ASME Trans. Mechatron. 2006, 11, 128–138. [Google Scholar] [CrossRef]
- Guizzo, E.; Goldstein, H. The Rise of the Boots; IEEE Spectrum: New York, NY, USA, 2005; pp. 52–56. [Google Scholar]
- Kazerooni, H.; Steger, R. The Berkeley lower extremity exoskeleton. J. Dyn. Syst. Meas. Control Trans. ASME 2006, 128, 14–25. [Google Scholar] [CrossRef]
- Acosta-Marquez, C.; Bradley, D.A. The Analysis, Design and Implementation of a Model of an exoskeleton to Support Mobility. In Proceedings of the IEEE 9th International Conference on Rehabilitation Robotics, Chicago, IL, USA, 28 June–1 July 2005; pp. 99–102. [Google Scholar]
- Altuzarra, O.; Eggers, P.M.; Campa, F.; Roldan-Paraponiaris, C.; Pinto, C. Dynamic modelling of lower-mobility parallel manipulators using the Boltzmann-Hammel equations. In Mechanisms, Transmissions and Applications; Springer: Berlin/Heidelberg, Germany, 2015; pp. 157–165. [Google Scholar]
- Featherstone, R. Rigid Body Dynamics Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; 272p. [Google Scholar]
- Tsai, L.-W. Robot Analysis: The Mechanics of Serial and Parallel Manipulators; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Anam, K.; Al-Jumaily, A.A. Active exoskeleton Control Systems: State of the Art. Procedia Eng. 2012, 41, 988–994. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, S.K.; Banala, S.K.; Fattah, A.; Sangwan, V.; Krishnamoorthy, V.; Scholz, J.P.; Hsu, W.-L. Assessment of Motion of a Swing Leg and Gait Rehabilitation With a Gravity Balancing exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 410–420. [Google Scholar] [CrossRef] [PubMed]
- Collins, S.H.; Wiggin, M.B.; Sawicki, G.S. Reducing the energy cost of human walking using an unpowered exoskeleton. Nature 2015, 522, 212–215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baruh, H. Analytical Dynamics; WCB/Mc Graw Hill: New York, NY, USA, 1999. [Google Scholar]
- Kane, T.R.; Levinson, D.A. Dynamics: Theory and Applications; Mc Graw Hill: New York, NY, USA, 1985. [Google Scholar]
- Orsino, R.M.M. A Contribution on Modelling Methodologies for Multibody Systems. Ph.D. Thesis, Escola Politécnica-University of São Paulo, São Paulo, Brazil, 2016; 213p. [Google Scholar]
- Orsino, R.M.M.; Hess-Coelho, T.A. A contribution for developing more efficient dynamic modelling algorithms of parallel robots. Int. J. Mech. Robot. Syst. 2013, 1, 15–34. [Google Scholar] [CrossRef]
- Orsino, R.M.M.; Hess-Coelho, T.A. A contribution on the modular modelling of multibody systems. Proc. R. Soc. A 2015, 471, 20150080. [Google Scholar] [CrossRef]
- Hess-Coelho, T.A.; Orsino, R.M.M.; Malvezzi, F. Modular modelling methodology applied to the dynamic analysis of parallel mechanisms. Mech. Mach. Theory 2021, 161, 104332. [Google Scholar] [CrossRef]
- Young, A.J.; Ferris, D.P. State of the Art and Future Directions for Lower Limb Robotic exoskeletons. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Hervé, J.M. The Lie group of rigid body displacements, a fundamental tool for mechanism design. Mech. Mach. Theory 1999, 34, 719–730. [Google Scholar] [CrossRef]
- Angeles, J. Qualitative Synthesis of Parallel Manipulators. ASME J. Mech. Des. 2004, 126, 617–624. [Google Scholar] [CrossRef]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; Wiley: Hoboken, NJ, USA, 2009; 370p. [Google Scholar]
- Winter, D.A. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J. Biomech. 1996, 29, 1223–1230. [Google Scholar]



| Joint | Dof | Actuated | Passive |
|---|---|---|---|
| Hip | 3 | Flex-extension | Rotation |
| Adduction–abduction | Internal–external | ||
| Knee | 1 | Flex–extension | – |
| Ankle | 2 | Flex–extension | Inversion–eversion |
| Metatarsophalangeal | 1 | – | Flex–extension |
| Link 1 | Link 2 | Link 3 | |||
|---|---|---|---|---|---|
| 0.18 | 0.15 | 0.2 | |||
| 0.09 | 0.2 | 0.1 | |||
| 0.00068 | 0.0014 | 0.00072 | |||
| Link 4 | |||||
| 1.8 m, 80 kg | 13.3 | 0.36 | 0.819 | 0.0062 | 0.819 |
| 1.7 m, 60 kg | 11.1 | 0.36 | 0.51 | 0.006 | 0.51 |
| 1.6 m, 50 kg | 9.3 | 0.34 | 0.38 | 0.006 | 0.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hess-Coelho, T.A.; Cortez, M.; Moura, R.T.; Forner-Cordero, A. Progressive Improvement of the Model of an Exoskeleton for the Lower Limb by Applying the Modular Modelling Methodology. Machines 2022, 10, 248. https://doi.org/10.3390/machines10040248
Hess-Coelho TA, Cortez M, Moura RT, Forner-Cordero A. Progressive Improvement of the Model of an Exoskeleton for the Lower Limb by Applying the Modular Modelling Methodology. Machines. 2022; 10(4):248. https://doi.org/10.3390/machines10040248
Chicago/Turabian StyleHess-Coelho, Tarcisio Antonio, Milton Cortez, Rafael Traldi Moura, and Arturo Forner-Cordero. 2022. "Progressive Improvement of the Model of an Exoskeleton for the Lower Limb by Applying the Modular Modelling Methodology" Machines 10, no. 4: 248. https://doi.org/10.3390/machines10040248
APA StyleHess-Coelho, T. A., Cortez, M., Moura, R. T., & Forner-Cordero, A. (2022). Progressive Improvement of the Model of an Exoskeleton for the Lower Limb by Applying the Modular Modelling Methodology. Machines, 10(4), 248. https://doi.org/10.3390/machines10040248







