Fault Detection and Diagnosis with Imbalanced and Noisy Data: A Hybrid Framework for Rotating Machinery
Abstract
1. Introduction
2. Review of Current Models
3. Background Theory
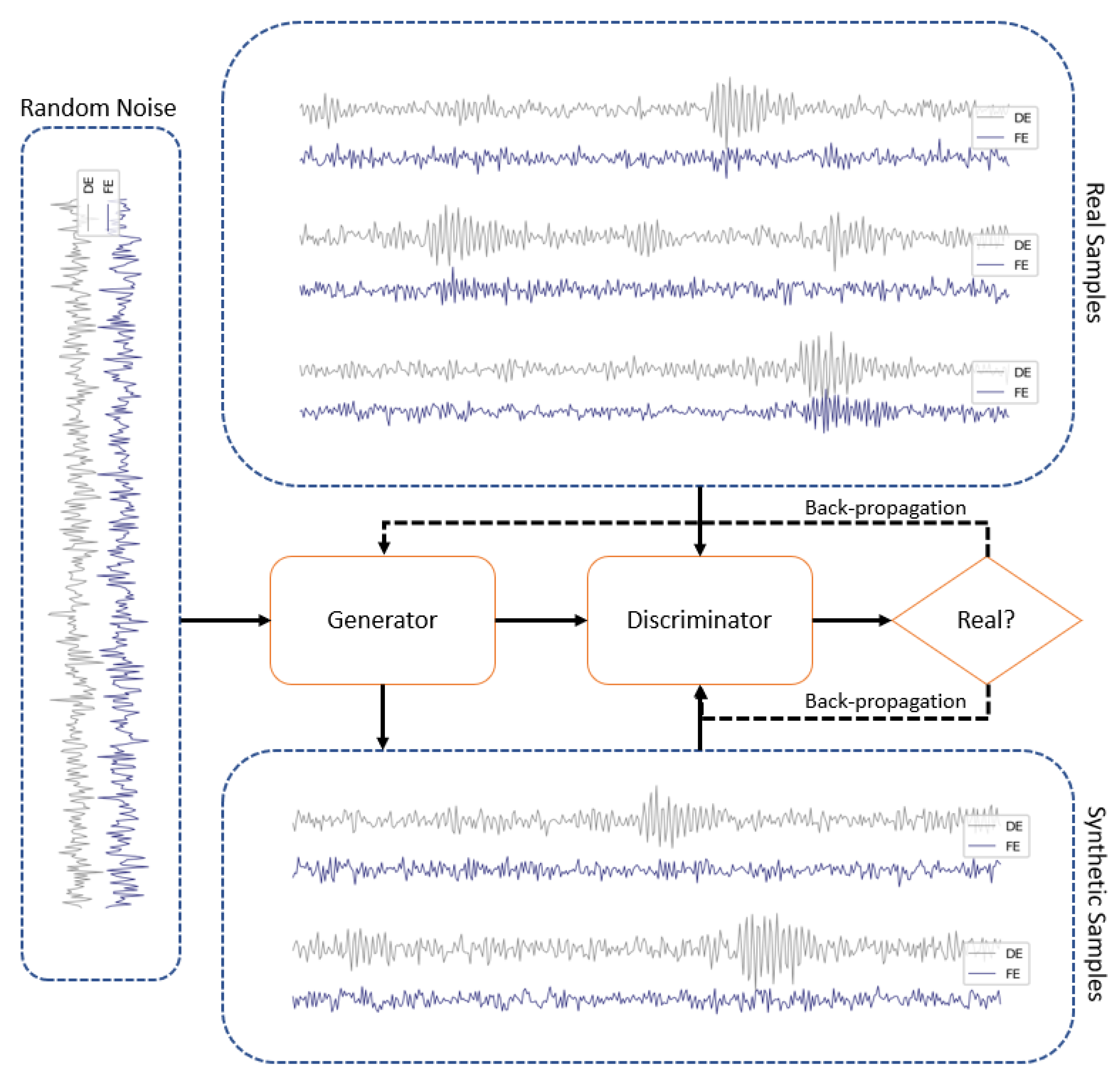
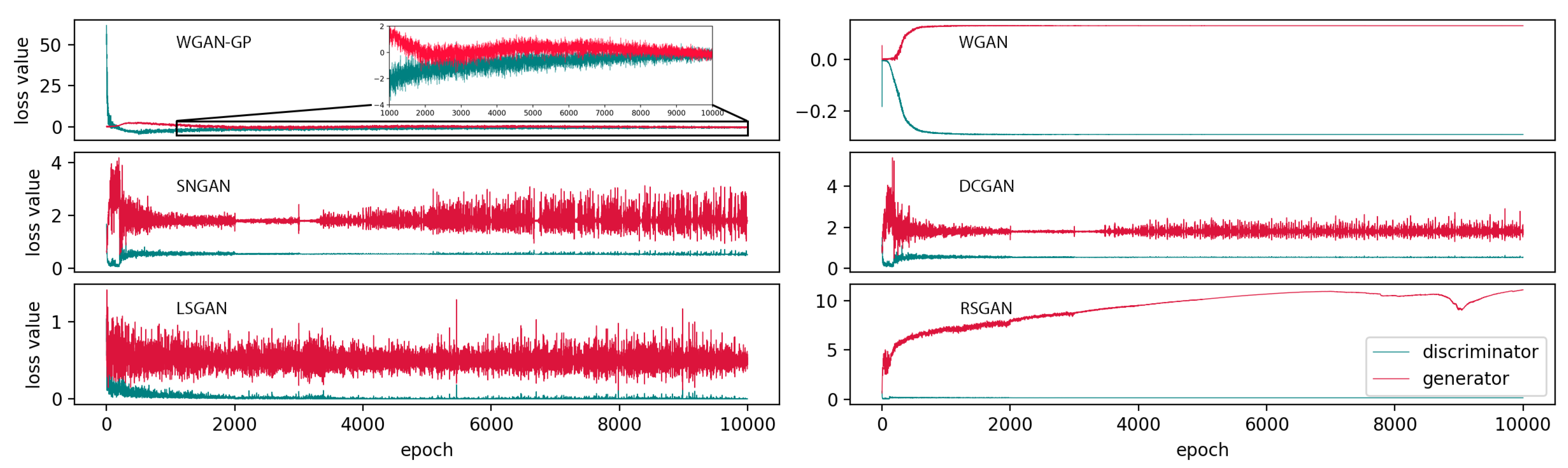
3.1. WGAN-GP
3.2. CLSTM
3.3. W-ELM
4. The Proposed FDD Model
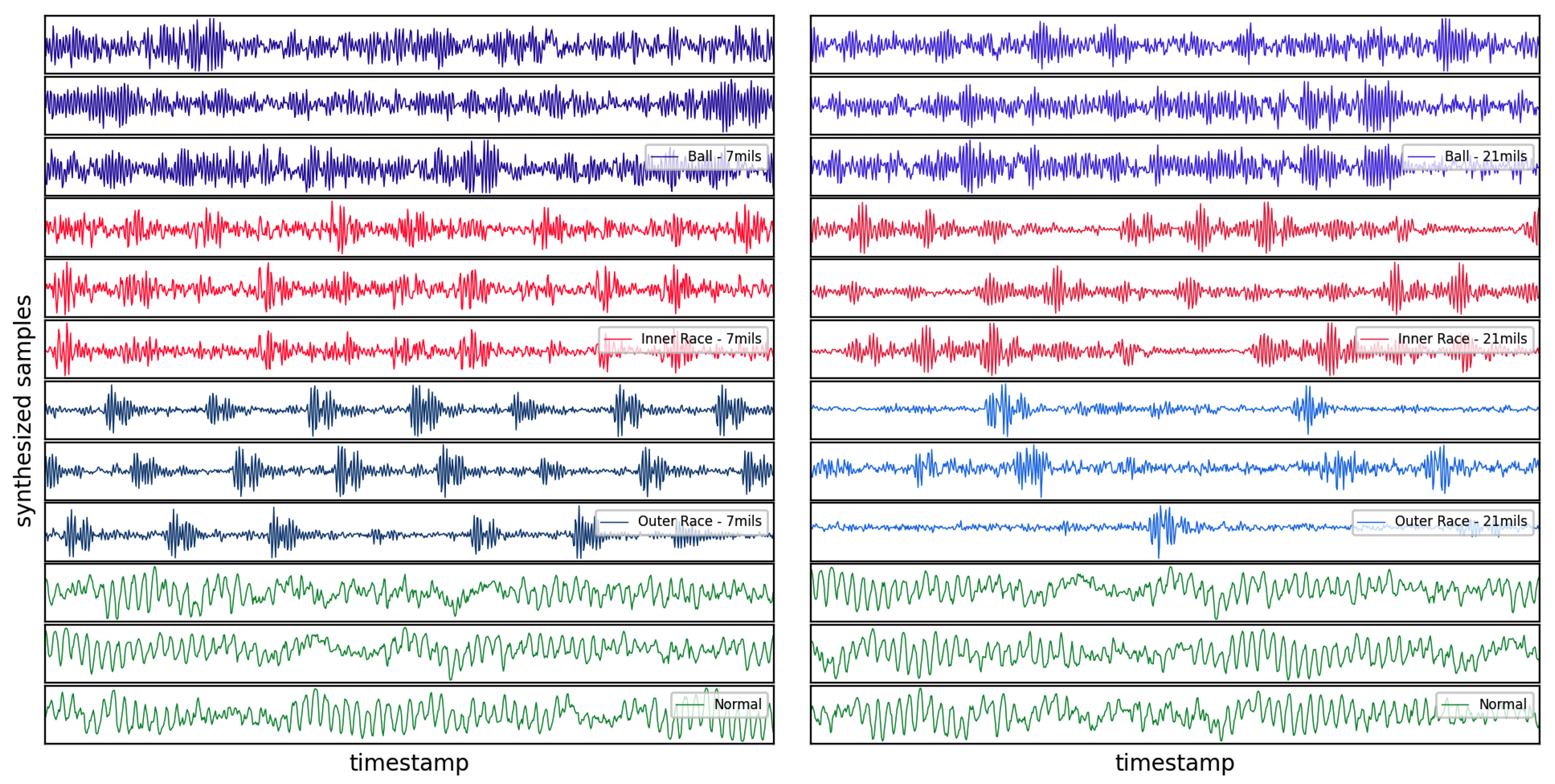
4.1. Sample Generation Model Design
| Algorithm 1: WGAN-GP |
Input:  |
4.2. Fault Diagnosis Model Design
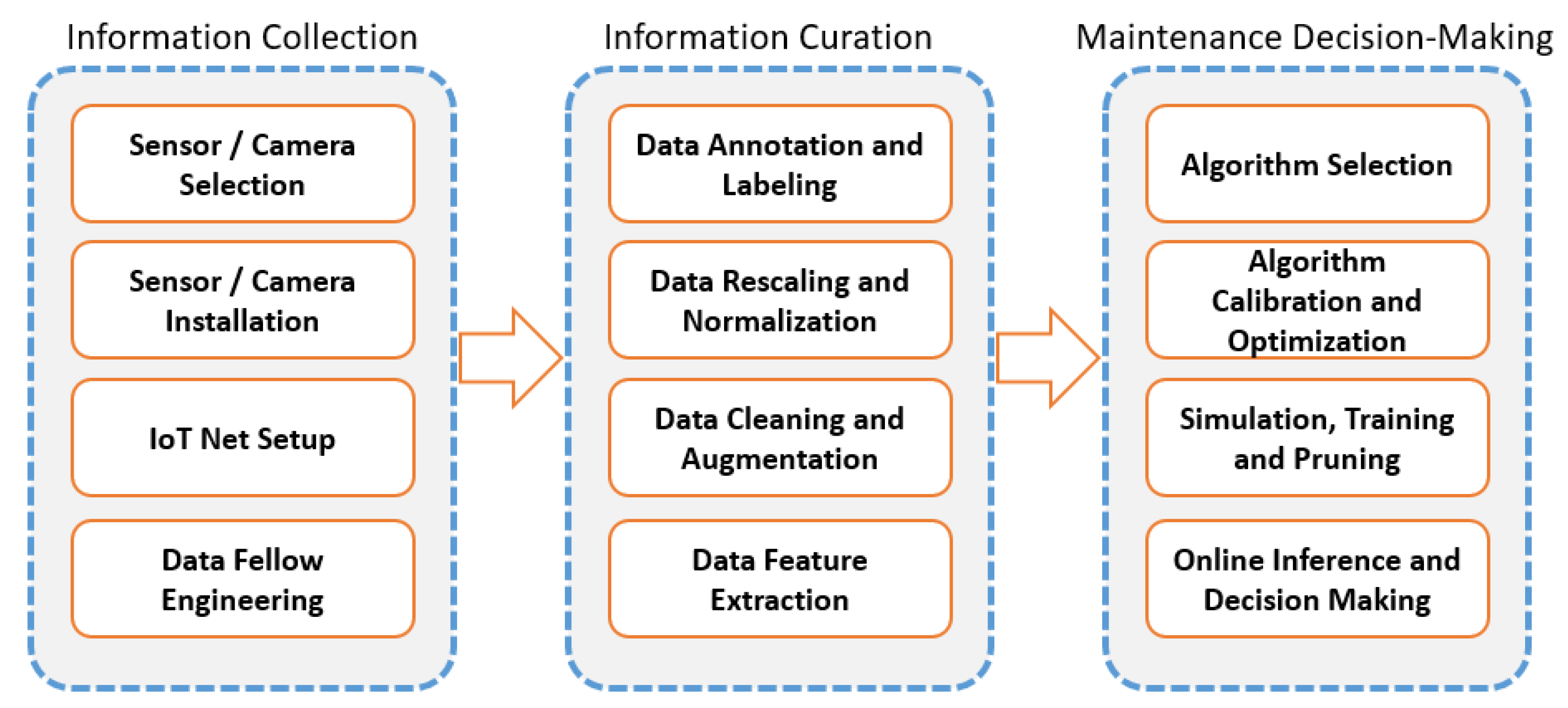
4.3. General Procedure of the Proposed Model
- Step 1: The sensory signals are collected from the accelerometers mounted on the rotating machinery.
- Step 2: The training, the test, and the validation datasets are constructed from the raw signals to separate bursts by resampling.
- Step 3: The training dataset is augmented using WGAN-GP introduced in Section 3.1 on the minority classes. The fake samples are added to the real samples to make the training dataset balanced.
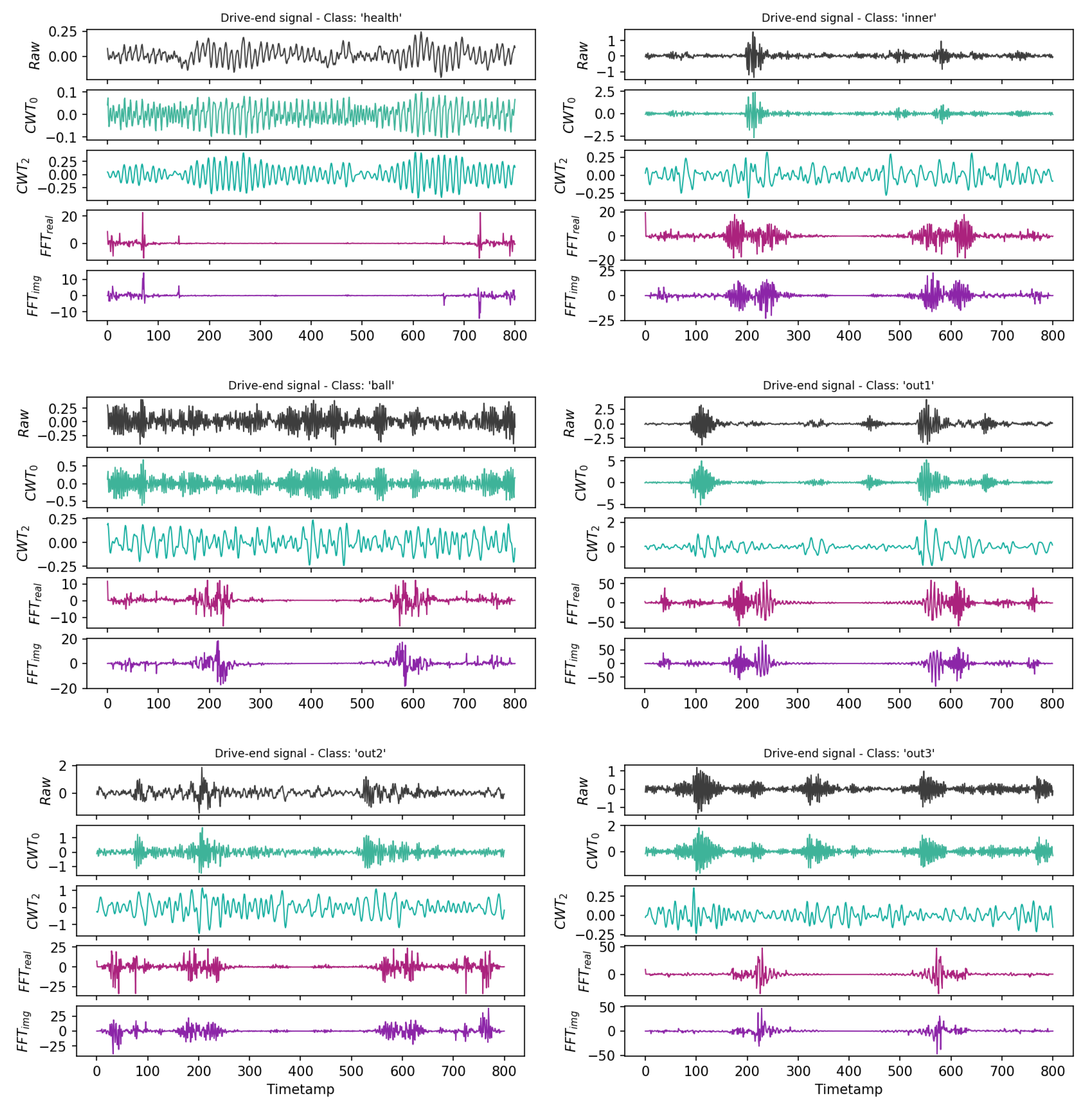
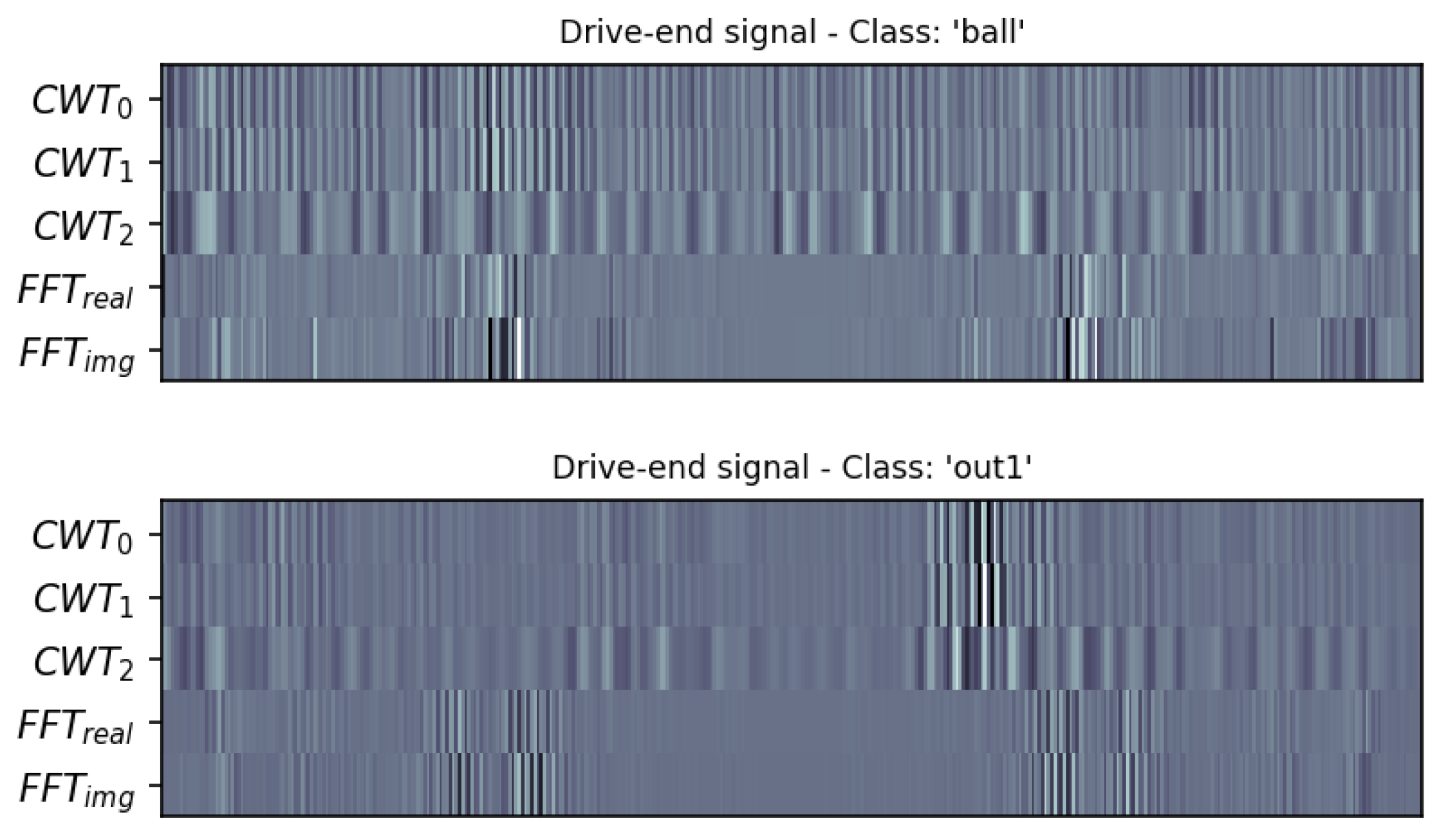
- Step 4: By employing FFT and CWT techniques the model can extract fault signatures which were hidden in the raw signals. The extracted Fourier and Wavelet transform-based diagrams are concatenated to form three-dimensional tensors (such as Figure 5) which will be given in input to the deep learning blocks.
- Step 5: These pre-processed samples go through two different paths of deep learning blocks: (1) a one-dimensional convolutional layer followed by an LSTM block, and (2) three blocks of CNN architectures followed by flatten and dense layers.
- Step 6: After concatenating the outputs of the two deep learning paths, a W-ELM technique is used to classify the extracted deep features and diagnose the fault type.
5. Results
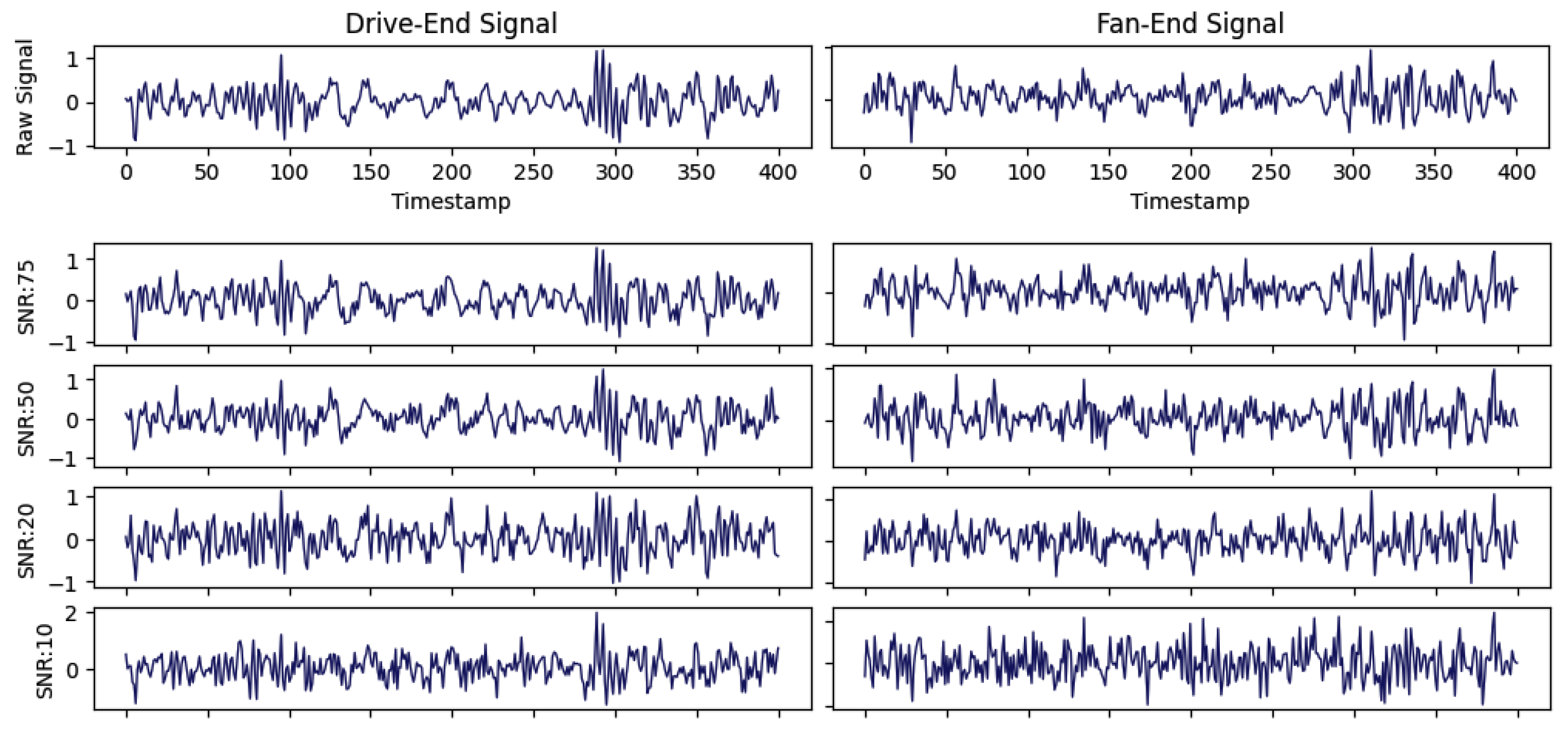
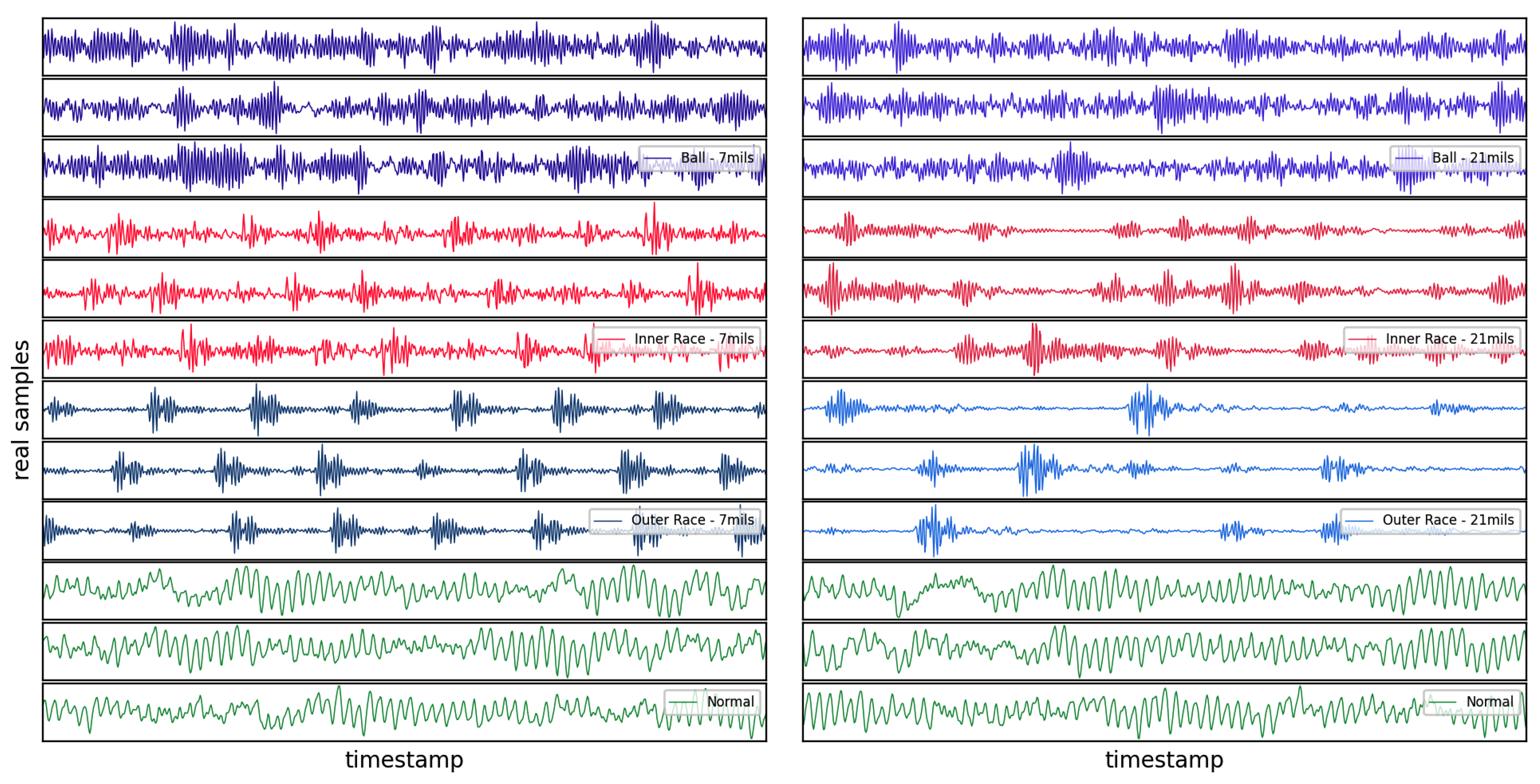
5.1. Dataset Description
5.2. GAN Model Selection
5.3. The Sensitivity Analysis
5.4. Model Performance Evaluation
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Glowacz, A.; Glowacz, W.; Glowacz, Z.; Kozik, J. Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals. Measurement 2018, 113, 1–9. [Google Scholar] [CrossRef]
- Shojaeinasab, A.; Charter, T.; Jalayer, M.; Khadivi, M.; Ogunfowora, O.; Raiyani, N.; Yaghoubi, M.; Najjaran, H. Intelligent manufacturing execution systems: A systematic review. J. Manuf. Syst. 2022, 62, 503–522. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Zhao, G.; Zhang, G.; Ge, Q.; Liu, X. Research Advances in Fault Diagnosis and Prognostic based on Deep Learning. In Proceedings of the Prognostics and System Health Management Conference, Chengdu, China, 19–21 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Balderston, H. Incipient Failure Detection: Incipient Failure Detection in Ball Bearings; Technical Report; Boeing Co Seattle Wa Aerospace Systems Div.: Seattle, MA, USA, 1969. [Google Scholar]
- Weichbrodt, B.; Smith, K.A. Signature Analaysis. Non-Intrusive Techniques for Incipient Failure Identification; General Electric Technical Information Series; October 1970. Available online: https://www.govinfo.gov/content/pkg/GOVPUB-C13-003e8bb93c2efe1b83a1da16f27f8e21/pdf/GOVPUB-C13-003e8bb93c2efe1b83a1da16f27f8e21.pdf (accessed on 21 February 2022).
- Li, C.J.; Ma, J. Wavelet decomposition of vibrations for detection of bearing-localized defects. NDT E Int. 1997, 30, 143–149. [Google Scholar] [CrossRef]
- Raghav, M.S.; Sharma, R.B. A Review on Fault Diagnosis and Condition Monitoring of Gearboxes by Using AE Technique. Arch. Comput. Methods Eng. 2020, 28, 2845–2859. [Google Scholar] [CrossRef]
- Mao, W.; He, L.; Yan, Y.; Wang, J. Online sequential prediction of bearings imbalanced fault diagnosis by extreme learning machine. Mech. Syst. Signal Process. 2017, 83, 450–473. [Google Scholar] [CrossRef]
- Lee, H. Framework and development of fault detection classification using IoT device and cloud environment. J. Manuf. Syst. 2017, 43, 257–270. [Google Scholar] [CrossRef]
- Zhang, T.; Ye, H.; Zhang, H.; Li, M. PCA-LMNN-Based Fault Diagnosis Method for Ironmaking Processes with Insufficient Faulty Data. ISIJ Int. 2016, 56, 1779–1788. [Google Scholar] [CrossRef]
- Liu, G.; Bao, H.; Han, B. A Stacked Autoencoder-Based Deep Neural Network for Achieving Gearbox Fault Diagnosis. Math. Probl. Eng. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Haidong, S.; Hongkai, J.; Huiwei, Z.; Fuan, W. A novel deep autoencoder feature learning method for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2017, 95, 187–204. [Google Scholar] [CrossRef]
- Lu, C.; Wang, Z.Y.; Qin, W.L.; Ma, J. Fault diagnosis of rotary machinery components using a stacked denoising autoencoder-based health state identification. Signal Process. 2017, 130, 377–388. [Google Scholar] [CrossRef]
- Li, K.; Wang, Q. Study on signal recognition and diagnosis for spacecraft based on deep learning method. In Proceedings of the 2015 Prognostics and System Health Management Conference (PHM), Beijing, China, 21–23 October 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Guo, L.; Lin, J.; Xing, S. A neural network constructed by deep learning technique and its application to intelligent fault diagnosis of machines. Neurocomputing 2018, 272, 619–628. [Google Scholar] [CrossRef]
- Lei, Y.; Jia, F.; Lin, J.; Xing, S.; Ding, S.X. An Intelligent Fault Diagnosis Method Using Unsupervised Feature Learning Towards Mechanical Big Data. IEEE Trans. Ind. Electron. 2016, 63, 3137–3147. [Google Scholar] [CrossRef]
- Li, K.; Kong, X.; Lu, Z.; Wenyin, L.; Yin, J. Boosting weighted ELM for imbalanced learning. Neurocomputing 2014, 128, 15–21. [Google Scholar] [CrossRef]
- Vong, C.M.; Ip, W.F.; Wong, P.K.; Chiu, C.C. Predicting minority class for suspended particulate matters level by extreme learning machine. Neurocomputing 2014, 128, 136–144. [Google Scholar] [CrossRef]
- Zong, W.; Huang, G.B.; Chen, Y. Weighted extreme learning machine for imbalance learning. Neurocomputing 2013, 101, 229–242. [Google Scholar] [CrossRef]
- Mirza, B.; Lin, Z.; Toh, K.A. Weighted online sequential extreme learning machine for class imbalance learning. Neural Process. Lett. 2013, 38, 465–486. [Google Scholar] [CrossRef]
- Mirza, B.; Lin, Z.; Cao, J.; Lai, X. Voting based weighted online sequential extreme learning machine for imbalance multi-class classification. In Proceedings of the IEEE International Symposium on Circuits and Systems, Lisbon, Portugal, 24–27 May 2015; pp. 565–568. [Google Scholar] [CrossRef]
- Hao, W.; Liu, F. Imbalanced Data Fault Diagnosis Based on an Evolutionary Online Sequential Extreme Learning Machine. Symmetry 2020, 12, 1204. [Google Scholar] [CrossRef]
- Chen, Y.J.; Wang, B.C.; Wu, J.Z.; Chien, C.F. Big Data Analytic for Multivariate Fault Detection and Classification in Semiconductor Manufacturing. In Proceedings of the 2017 13th IEEE Conference on Automation Science and Engineering (CASE), Xi’an, China, 20–23 August 2017. [Google Scholar]
- Cheng, J.; Chen, J.; Guo, Y.N.; Cheng, S.; Yang, L.; Zhang, P. Adaptive CCR-ELM with variable-length brain storm optimization algorithm for class-imbalance learning. Nat. Comput. 2021, 20, 11–22. [Google Scholar] [CrossRef]
- Xu, Q.; Lu, S.; Jia, W.; Jiang, C. Imbalanced fault diagnosis of rotating machinery via multi-domain feature extraction and cost-sensitive learning. J. Intell. Manuf. 2020, 31, 1467–1481. [Google Scholar] [CrossRef]
- Zhao, X.; Jia, M.; Liu, Z. Fault Diagnosis Framework of Rolling Bearing Using Adaptive Sparse Contrative Auto-Encoder with Optimized Unsupervised Extreme Learning Machine. IEEE Access 2020, 8, 99154–99170. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Huang, G.; Hu, Q.K.; Tan, J.F.; Wang, J.J.; Yang, Z. Soft extreme learning machine for fault detection of aircraft engine. Aerosp. Sci. Technol. 2019, 91, 70–81. [Google Scholar] [CrossRef]
- Han, B.; Jia, S.; Liu, G.; Wang, J. Imbalanced Fault Classification of Bearing via Wasserstein Generative Adversarial Networks with Gradient Penalty. Shock Vib. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Ding, Y.; Ma, L.; Ma, J.; Wang, C.; Lu, C. A generative adversarial network-based intelligent fault diagnosis method for rotating machinery under small sample size conditions. IEEE Access 2019, 7, 149736–149749. [Google Scholar] [CrossRef]
- Zhang, Y.; Xing, K.; Bai, R.; Sun, D.; Meng, Z. An enhanced convolutional neural network for bearing fault diagnosis based on time–frequency image. Measurement 2020, 157, 107667. [Google Scholar] [CrossRef]
- He, W.; He, Y.; Li, B. Generative Adversarial Networks with Comprehensive Wavelet Feature for Fault Diagnosis of Analog Circuits. IEEE Trans. Instrum. Meas. 2020, 69, 6640–6650. [Google Scholar] [CrossRef]
- Liang, P.; Deng, C.; Wu, J.; Yang, Z. Intelligent fault diagnosis of rotating machinery via wavelet transform, generative adversarial nets and convolutional neural network. Measurement 2020, 159, 107768. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar] [CrossRef]
- Ren, J.; Liu, Y.; Liu, J. EWGAN: Entropy-Based Wasserstein GAN for Imbalanced Learning. Proc. AAAI Conf. Artif. Intell. 2019, 33, 10011–10012. [Google Scholar] [CrossRef][Green Version]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GaN. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Zhou, F.; Lin, X.; Liu, C.; Zhao, Y.; Xu, P.; Ren, L.; Xue, T.; Ren, L. A survey of visualization for smart manufacturing. J. Vis. 2019, 22, 419–435. [Google Scholar] [CrossRef]
- Jalayer, M.; Jalayer, R.; Kaboli, A.; Orsenigo, C.; Vercellis, C. Automatic Visual Inspection of Rare Defects: A Framework based on GP-WGAN and Enhanced Faster R-CNN. In Proceedings of the 2021 IEEE International Conference on Industry 4.0, Artificial Intelligence, and Communications Technology (IAICT), Bandung, Indonesia, 27–28 July 2021; pp. 221–227. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schraudolph, N.N. Learning Precise Timing with LSTM Recurrent Networks. J. Mach. Learn. Res. 2002, 3, 115–143. [Google Scholar]
- Healy, M.J.R.; Rao, C.R.; Mitra, S.K. Generalized Inverse of Matrices and its Applications. J. R. Stat. Soc. Ser. A (Gen.) 1972, 135, 439. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Fletcher, R. Practical Methods of Optimization, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2000; p. 436. [Google Scholar] [CrossRef]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved training of wasserstein GANs. Adv. Neural Inf. Process. Syst. 2017, 30, 5768–5778. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008; p. 832. [Google Scholar]
- Jalayer, M.; Orsenigo, C.; Vercellis, C. Fault detection and diagnosis for rotating machinery: A model based on convolutional LSTM, Fast Fourier and continuous wavelet transforms. Comput. Ind. 2021, 125, 103378. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H. Insights into lstm fully convolutional networks for time series classification. IEEE Access 2019, 7, 67718–67725. [Google Scholar] [CrossRef]
- Mao, W.; Feng, W.; Liu, Y.; Zhang, D.; Liang, X. A new deep auto-encoder method with fusing discriminant information for bearing fault diagnosis. Mech. Syst. Signal Process. 2021, 150, 107233. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M. A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing. Neurocomputing 2018, 313, 47–64. [Google Scholar] [CrossRef]


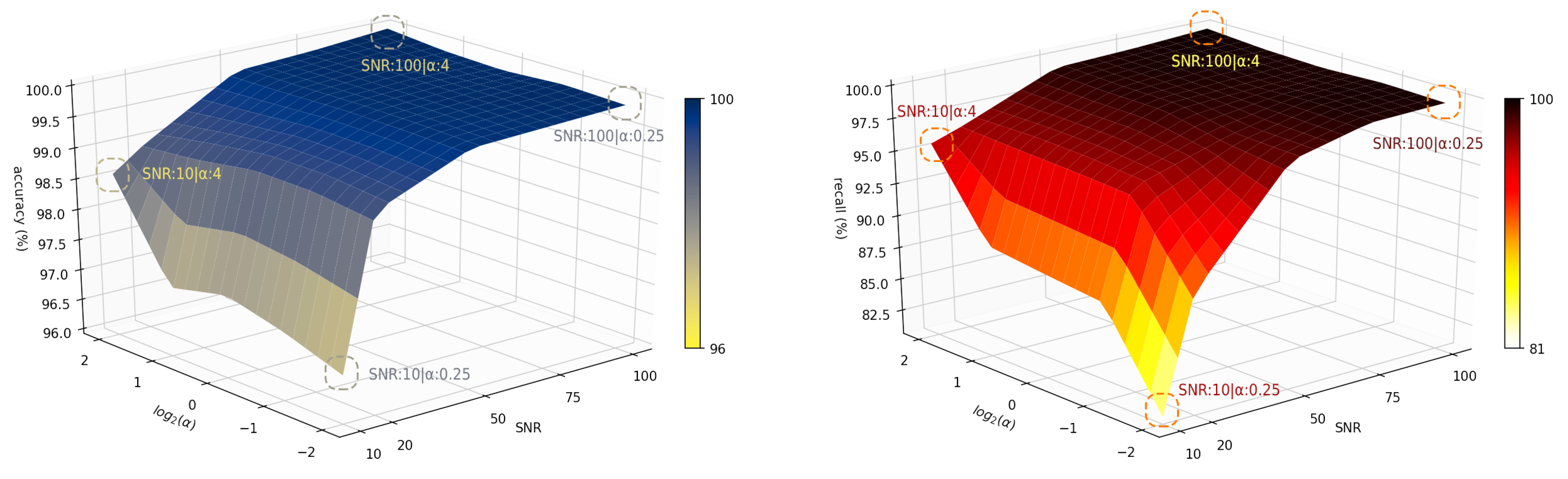
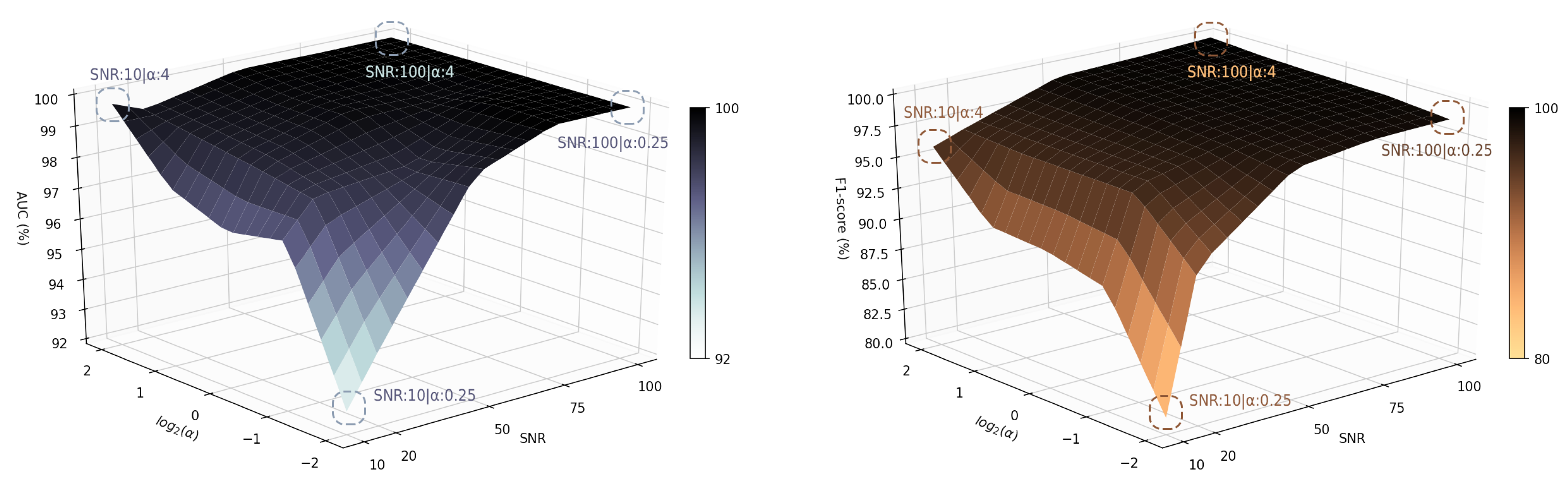
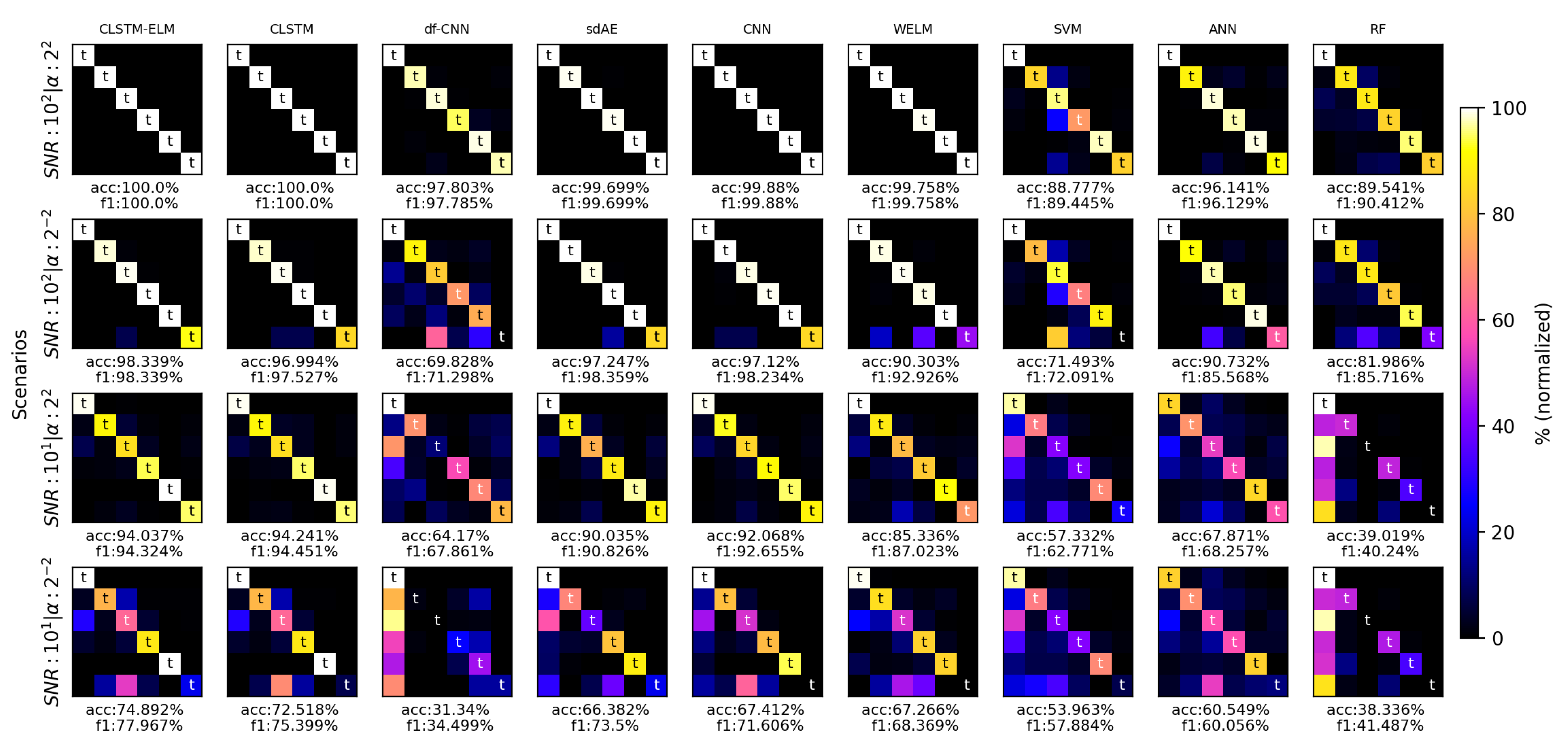
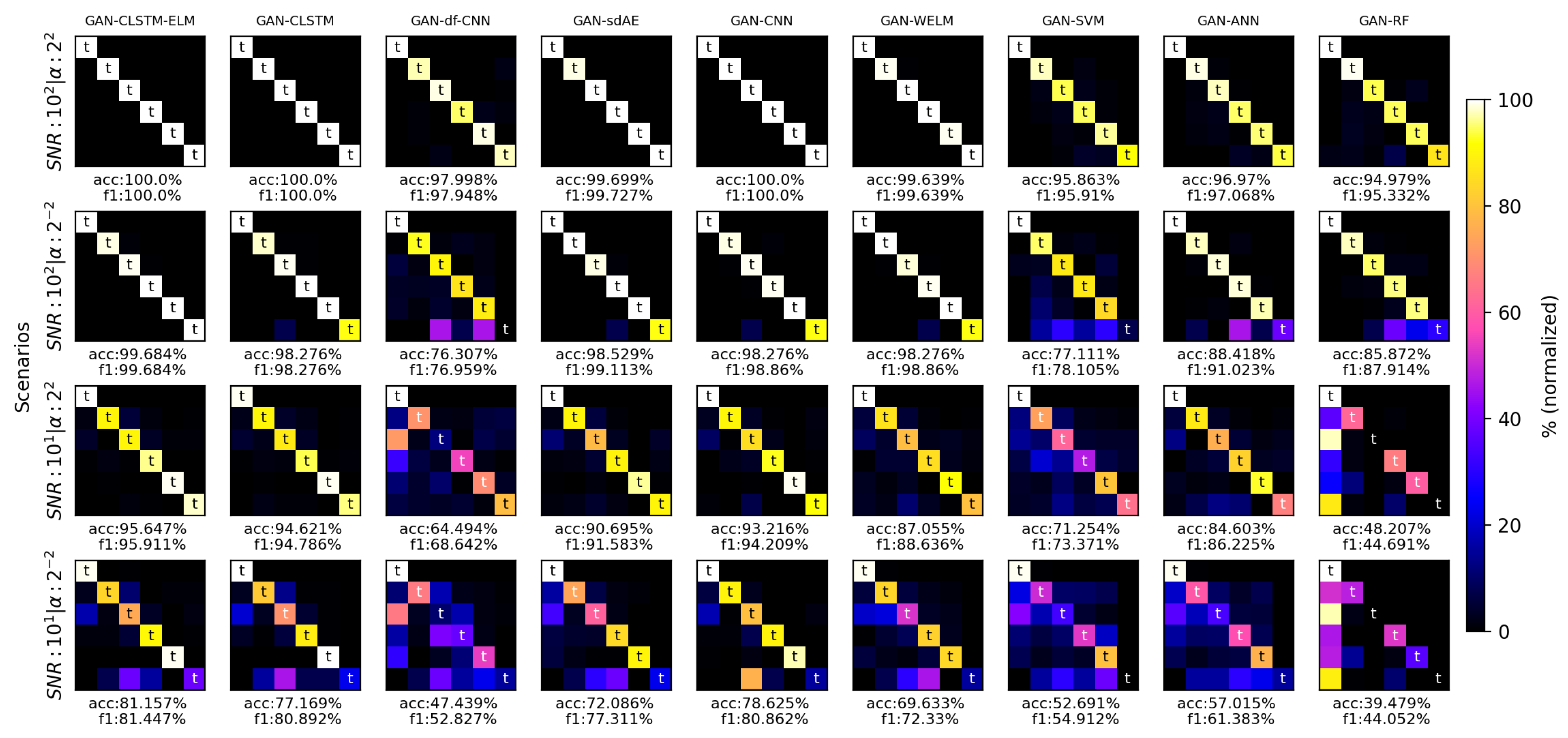
| Block | Layer | Specifications |
|---|---|---|
| CNN Block1 | 1D-Convolutinoal | filters: 16; kernel size: 5; stride: 2; padding: 0 |
| Batch Normalization | momentum: 0.99; epsilon: 0.001 | |
| 1D-Max Pooling | pool size: 2, padding: 0, stride: 1 | |
| CNN Block2 | 1D-Convolutinoal | filters: 32; kernel size: 3; stride: 1; padding: 0 |
| Batch Normalization | momentum: 0.99; epsilon: 0.001 | |
| 1D-Max Pooling | pool size: 2, padding: 0, stride: 1 | |
| CNN Block3 | 1D-Convolutinoal | filters: 64; kernel size: 3; stride: 1; padding: 0 |
| Batch Normalization | momentum: 0.99; epsilon: 0.001 | |
| 1D-Max Pooling | pool size: 2, padding: 0, stride: 1 | |
| Convolutional LSTM | 1D-Convolutinoal | filters: 20; kernel size: 8; stride: 3; padding: 0 |
| Embedding | input dimension: 200; output dimension: 64 | |
| LSTM | units: 64; activation function: tanh; | |
| ELM unit | WELM | #nuerons: 150; activation function: sigmoid; |
| Minority Share (%) | Percentage of Training Samples in Each Condition | |||||
|---|---|---|---|---|---|---|
| Health | Inner | Ball | Out1 | Out2 | Out3 | |
| 76% | 5% | 5% | 5% | 5% | 4% | |
| 78% | 5% | 5% | 5% | 5% | 2% | |
| 79% | 5% | 5% | 5% | 5% | 1% | |
| 79.5% | 5% | 5% | 5% | 5% | 0.5% | |
| 79.75% | 5% | 5% | 5% | 5% | 0.25% | |
| Framework | Preprossecing | Description | References |
|---|---|---|---|
| CLSTM | FFT + CWT + Statistical features | Its architecture comprises two CNN blocks (containing 1D-Convolutional layers, Batch Normalization, ReLU and Max Pooling), a LSTM block, a Logarithmic SoftMax, a concatenation which adds statistical features and three fully connected neural networks for the classification. | [46] |
| CLSTM-ELM | FFT + CWT + Statistical features | Its CNN and LSTM architecture are the same as in CLSTM; yet, the fully connected layers are substituted for W-ELM with 150 nodes. | N/A |
| df-CNN | raw signals | It is proposed to make an abstract 2-dimensional image out of raw signals. Its architecture comprises two CNN blocks (containing 2D-Convolutional layers, Batch Normalization, ReLU and Max Pooling), and three fully connected neural networks for the classification. df-CNN works directly on the raw vibration signals. | [48] |
| sdAE | raw signals | It is a multilayered architecture composed of four auto-associative neural network layers, which contain one input layer and three AEs. The input of this framework are raw signals. | [14] |
| CNN | FFT | The architecture consists of three CNN blocks (containing one 1D-Convolutional layer and a Pooling layer), two fully connected layers, and a SoftMax classification layer. It takes short-term Fourier transform (STFT) form of the signals as its input. | [16,31,33] |
| W-ELM | FFT + VMD + Statistical features | It takes a combination of FFT, VMD [49] and some statistical features. | [20] |
| SVM | Statistical features | SVM with polynomial kernel and degree of 2 is selected | N/A |
| ANN | Statistical features | 3 fully connected layers with a grid search to find optimal number of neurons per layer and the activation functions | N/A |
| RF | Statistical features | A grid search is designed to find the optimal number of estimators, and criteria (between ‘gini’ and ‘entropy’) parameters | N/A |
| Algorithm | Runtime/Step (ms) | #Epochs to Converge | Batch Size | Learning Rate |
|---|---|---|---|---|
| CLSTM-ELM | 104.7 ± 8.6 | 10 | 64 | |
| CLSTM | 116.4 ± 10.5 | 12 | 64 | |
| df-CNN | 12.1 ± 1.8 | 8 | 64 | |
| sdAE | 43.3 ± 4.1 | 6 | 64 | |
| CNN | 21.8 ± 1.7 | 7 | 64 | |
| WELM | 17.2 ±1.4 | 7 | 32 |
| Algorithm | Training Time (min) | |||
|---|---|---|---|---|
| SVM | 8.73 ± 0.45 | 8.90 ± 0.37 | 18.67 ± 1.32 | 19.40 ± 1.49 |
| ANN | 1.97 ± 0.22 | 1.72 ± 0.31 | 2.06 ± 0.38 | 2.17 ± 0.42 |
| RF | 2.13 ± 0.40 | 1.55 ± 0.36 | 3.06 ± 0.33 | 3.21 ± 0.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jalayer, M.; Kaboli, A.; Orsenigo, C.; Vercellis, C. Fault Detection and Diagnosis with Imbalanced and Noisy Data: A Hybrid Framework for Rotating Machinery. Machines 2022, 10, 237. https://doi.org/10.3390/machines10040237
Jalayer M, Kaboli A, Orsenigo C, Vercellis C. Fault Detection and Diagnosis with Imbalanced and Noisy Data: A Hybrid Framework for Rotating Machinery. Machines. 2022; 10(4):237. https://doi.org/10.3390/machines10040237
Chicago/Turabian StyleJalayer, Masoud, Amin Kaboli, Carlotta Orsenigo, and Carlo Vercellis. 2022. "Fault Detection and Diagnosis with Imbalanced and Noisy Data: A Hybrid Framework for Rotating Machinery" Machines 10, no. 4: 237. https://doi.org/10.3390/machines10040237
APA StyleJalayer, M., Kaboli, A., Orsenigo, C., & Vercellis, C. (2022). Fault Detection and Diagnosis with Imbalanced and Noisy Data: A Hybrid Framework for Rotating Machinery. Machines, 10(4), 237. https://doi.org/10.3390/machines10040237








