Partial Shaking Moment Balancing of Spherical Parallel Robots by a Combined Counterweight and Adjusting Kinematic Parameters Approach

Abstract

Spherical parallel robots (SPR) are widely used in industries and robotic rehabilitation. Designing such systems for better balance properties is still a challenge. This paper presents a work to minimize the shaking moment for a fully force-balanced SPR by combining the counterweight (CW) and adjusting the kinematic parameters (AKP). An approximate model of the shaking moment of the SPR is proposed for computational efficiency (specifically allowing for a gradient-based optimization algorithm available in MATLAB) yet without the loss of much accuracy. The effectiveness of the proposed approach has been confirmed based on simulation, especially with the software system SPACAR due to its high reliability and easy availability. Specifically, the simulation result shows that compared with the unbalanced SPR, the shaking moment of the balanced SPR can decrease by more than 90%. It is worth mentioning that the AKP approach is an excellent example of mechatronics by combining the capability of re-planning the joint motion from the end-effector motion and adjusting the kinematic parameters to redistribute the mass of the whole robot for canceling the shaking force and shaking moment—inertia-induced force and moment to the ground. In short, the main contributions of this paper are: (1) a combined CW and AKP approach to the partial moment balancing of the SPR enhanced with a simplified mathematical model of the shaking moment of the SPR, and (2) a new design of the SPR which can be fully force balanced yet partially moment balanced. A note is taken that the simplified model is under the condition that the parameters of the link have certain geometric relations, which is a limitation of our approach.

1. Introduction

The dynamic balancing of the parallel manipulator is crucial to the quality of the parallel and closed-loop manipulator. In the operation of such a manipulator, forces and moments on the ground are generated due to the inertia of the components of the manipulator, which are called shaking force and shaking moment [1,2,3,4]. This paper will present a new approach to the partial moment balancing yet fully force balancing of the spherical parallel robot (SPR).

Methods for balancing the shaking force and shaking moment for planar mechanisms have been developed in recent decades. In general, there are two strategies to achieve a balanced mechanism, namely (1) balancing integrated with the design and (2) balancing after the design. Fisher’s method [5], proposed in 1906, is perhaps the first published method for the force balancing of the mechanism integrated with design. The main idea of Fisher’s method is to make the COM of the mechanism stationary by adding auxiliary parallelograms. Wijk expanded Fisher’s method for dynamic balancing [6]. The limitation in Wijk’s work is that the method for the moment balancing technique is restricted to special types of mechanisms; especially, there may be some challenges in avoiding interference among links at the embodied mechanism design phase [7]. Most of the dynamic balancing methods in the literature fall into the category of balancing after design [8].

The first well-known approach of this kind to the shaking force balancing of the mechanism is the counterweights (CW) approach, which was applied in Berkof’s work for the complete force and moment balancing of an inline four-bar linkage [9]. The main idea with the CW approach is to add additional lumped objects (or weights) to the mechanism or manipulator such that the center of the mass (COM) of the mechanism, including the added weights, does not change its location during the operation of the mechanism. As such, the inertia-induced force (i.e., shaking force) of the whole mechanism is zero. For the shaking moment balancing of the mechanism, device objects that create the moment of inertia are added to the mechanism such that the angular momentum of the mechanism, including the added objects, keeps a constant with respect to a fixed point on the ground [10,11,12]. The method by combining add-of-springs (AOS) and counterweights (CW) to achieve force-balanced robotic mechanisms was proposed in several studies [13,14], and this method can be said to be an application of the engineering hybridization principle, resulting in a trade-off between the increase in the weight of the system (with the CW approach) and the increase in the complexity of the configuration of the system (with the AOS approach). A screw theory-based methodology, which addresses a new dynamic balancing problem, i.e., instantaneous dynamic balance conditions for planar and spatial mechanisms [15]. An alternative approach by satisfying all higher-order derivatives of the balance conditions was presented in [16], which potentially leads to simpler and more cost-effective solutions for the dynamic balancing of a small set of closed-loop linkages.

Another approach for the shaking force balancing of robotic mechanisms is called adjusting kinematic parameters (AKP) [17,18]. The idea with the AKP is to change the kinematic parameter of the link so as to change the mass distribution as well as the distribution of the moment of inertia, together with re-planning the servomotor in the robotic mechanism to off-set the altered workspace of the robot due to the change of the kinematic parameters. However, in the case of a particular task along with its required workspace, the changed workspace may not be able to meet the required workspace, which is the limitation of the AKP approach. AKP has never been explored for the dynamic balancing of spatial mechanisms. This paper concerns the dynamic balancing of SPR with the AKP method combined with the CW method.

It must be noted that the balancing of spatial mechanisms is less studied in the literature due to its complexity in finding the balancing equations. Kaufman and Sandor proposed a CW method for fully force balancing spatial mechanisms [19]. Moore presented a CW approach to statically balance spherical four-bar linkages as well [20]. Wu and Gosselin designed a reactionless parallelepiped 3-DOF spatial mechanism by adding a counter-rotating gear on it [21]. The foregoing methods inevitably increase the weight of the mechanism, resulting in an increase in the driving torque fluctuation as well as the joint force and shaking moment. Besides, the spatial mechanism of Wu and Gosselin is with a special configuration of the spherical mechanism or robot, which limits its application. Gosselin studied the dynamic balancing of the spatial parallel mechanism with six legs by using the CW approach [22], but the mechanism in their study is a special configuration of SPR.

The partial moment balancing refers to the situation wherein the shaking moment is not completely annulled. In practice, full dynamic balancing i.e., fully canceling the shaking force and moment of mechanisms is a challenge, especially the full balancing of the shaking moment. The underlying reason is that the shaking moment is related to the moment of inertia, which depends on both the mass and mass distribution of the link and mechanism. The approach based on the concept of “counter” to the moment of inertia, as opposed to “counter” to the inertia of the mass, requires complicated structures of added objects to a moment-unbalanced mechanism, and sometimes added objects are auxiliary linkages, which greatly complicate the whole mechanism. By a trade-off between the benefit of a fully moment-balanced mechanism and the complexity of the structure of added objects along with the original mechanism, the idea of partial moment balancing makes sense in the research community of dynamic balancing of mechanisms.

The philosophy behind partial moment balancing is to select the best one among many options that can fully balance the force of the mechanism to minimize the shaking moment. Arakelian and Da Han proposed a CW method for the partial moment balancing of a fully force balanced spatial linkage, which can reduce the torque fluctuation as well [23]. The spatial linkage in their work is an RSS’R spatial linkage. Besides, the shaking moment in their work is an exact expression, which can lead to computation overhead in the optimization process.

A promising strategy for the balancing of mechanisms is to combine different methods by following the engineering hybridization principle [24]. Due to the complementary advantages of CW and AKP, a combined CW and AKP approach (called hybrid approach for balancing, CW-AKP for short) was proposed for the shaking force balancing of a five-bar planar mechanism [25]. In the study reported in this paper, the combined CW-AKP approach was extended to the partially shaking moment balancing of a spatial mechanism (while being fully force balanced), the SPR in this case. It is noted that the SPR in our study is with a general configuration as opposed to the special configuration of the SPR studied by other researchers in the literature [26,27,28]. Therefore, our work has two contributions: (1) a new approach, by combining the CW and the AKP, to the partial moment balancing of a spatial mechanism, demonstrated by the SPR of a general configuration, and (2) a new design of the SPR which can be fully force balanced yet partially moment balanced.

The remaining part of this paper is organized as follows. Section 2 introduces the structure of the SPR. Section 3 introduces the process of partially moment balancing the SPR by using the combined CW-AKP approach. Section 4 illustrates the effectiveness of the proposed approach. Section 5 presents conclusions with a discussion of future work.

2. The SPR along with Its D-H Coordinate System

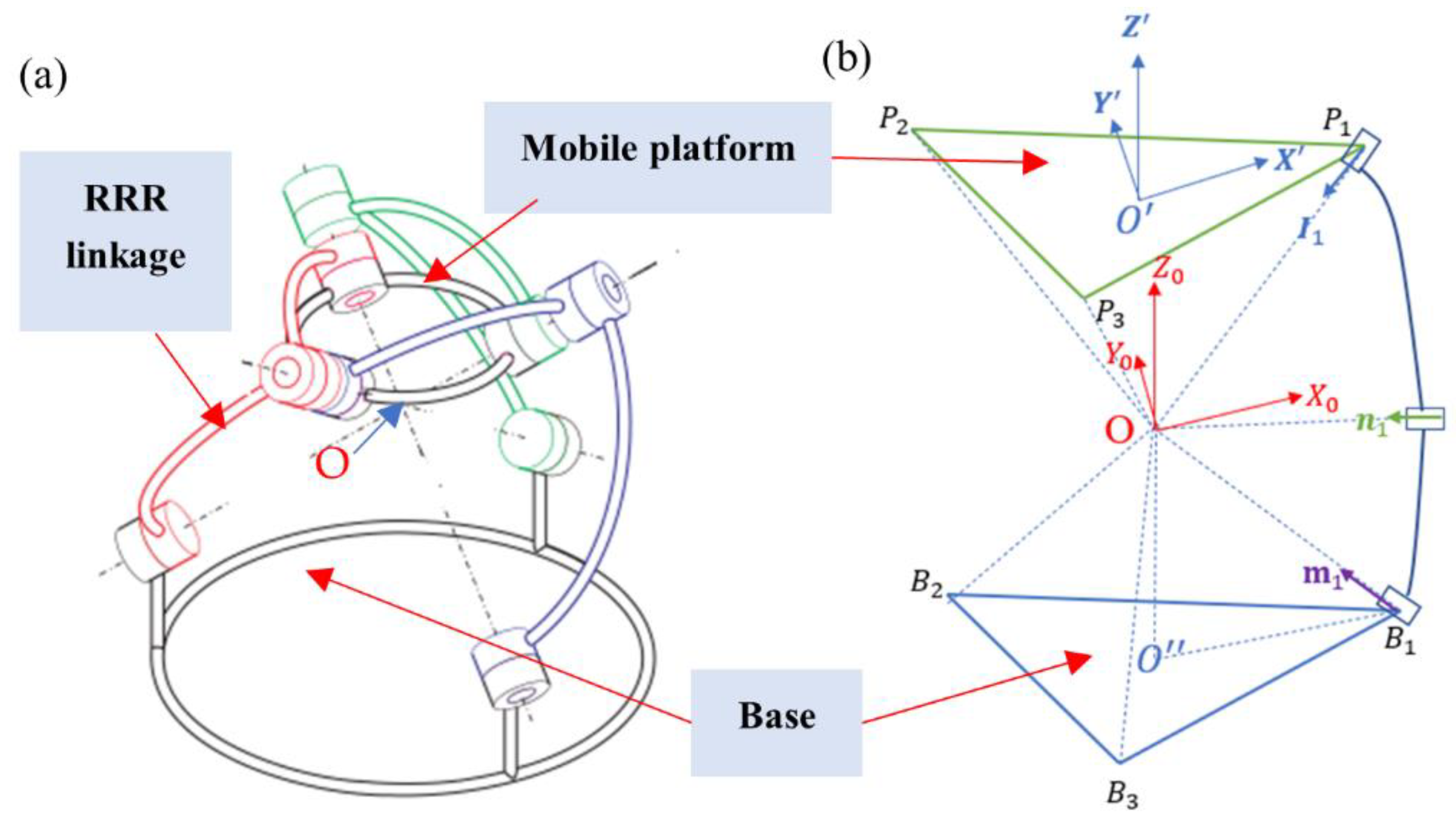
As stated earlier, without the loss of generality, the general configuration of the SPR, as shown in Figure 1a, is used throughout this paper. This mechanism contains nine revolute joints in total and three RRR linkages between its base and mobile platform. In this mechanism, all the nine revolute joint axes meet at a common center, O, which is a fixed point on the ground. The axes of three servo motors are on the ground at $B_i$, distributed by an angle of 120°. There are three joint axes on the mobile platform at $P_i$, distributed by an angle of 120°, and through these joints are the three upper links connected with the mobile platform, i = 1, 2, 3.

Define ${\mathit{Z}}_0$ as perpendicular to the base with its origin being at the center O of the SPR. Notice that the point O″ is the intersection point of the axis ${\mathit{Z}}_0$ with the triangle B₁B₂B₃. Define ${\mathbf{X}}_0$ as perpendicular to ${\mathit{Z}}_0$ and parallel to the line O″B₁. Define ${\mathit{Y}}_0$ from ${\mathit{Z}}_0$ and ${\mathbf{X}}_0$ by following the right-hand rule. The coordinate system O-${\mathit{X}}_0$(${\mathit{Y}}_0$)${\mathit{Z}}_0$ is fixed to the ground and taken as a global reference coordinate system for the SPR. For the convenience of later discussions, denote this coordinate system as the frame O.

Define a local coordinate system O′-$\mathit{X}$′($\mathit{Y}$′)$\mathit{Z}$′ on the mobile platform as the frame M. Specifically, define O′ at the center of the mobile platform and define the axis $\mathit{Z}$′ as perpendicular to the mobile platform at the point O’. Define the axis $\mathit{X}$′ as perpendicular to the axis $\mathit{Z}$′ and as passing through one of the three points, $P_i$, say $P_1$. Initially, ${\mathbf{X}}_0$ is parallel to $\mathit{X}$′, namely the mobile platform is in the horizontal position, parallel to the triangle B₁B₂B₃ (Figure 1b).

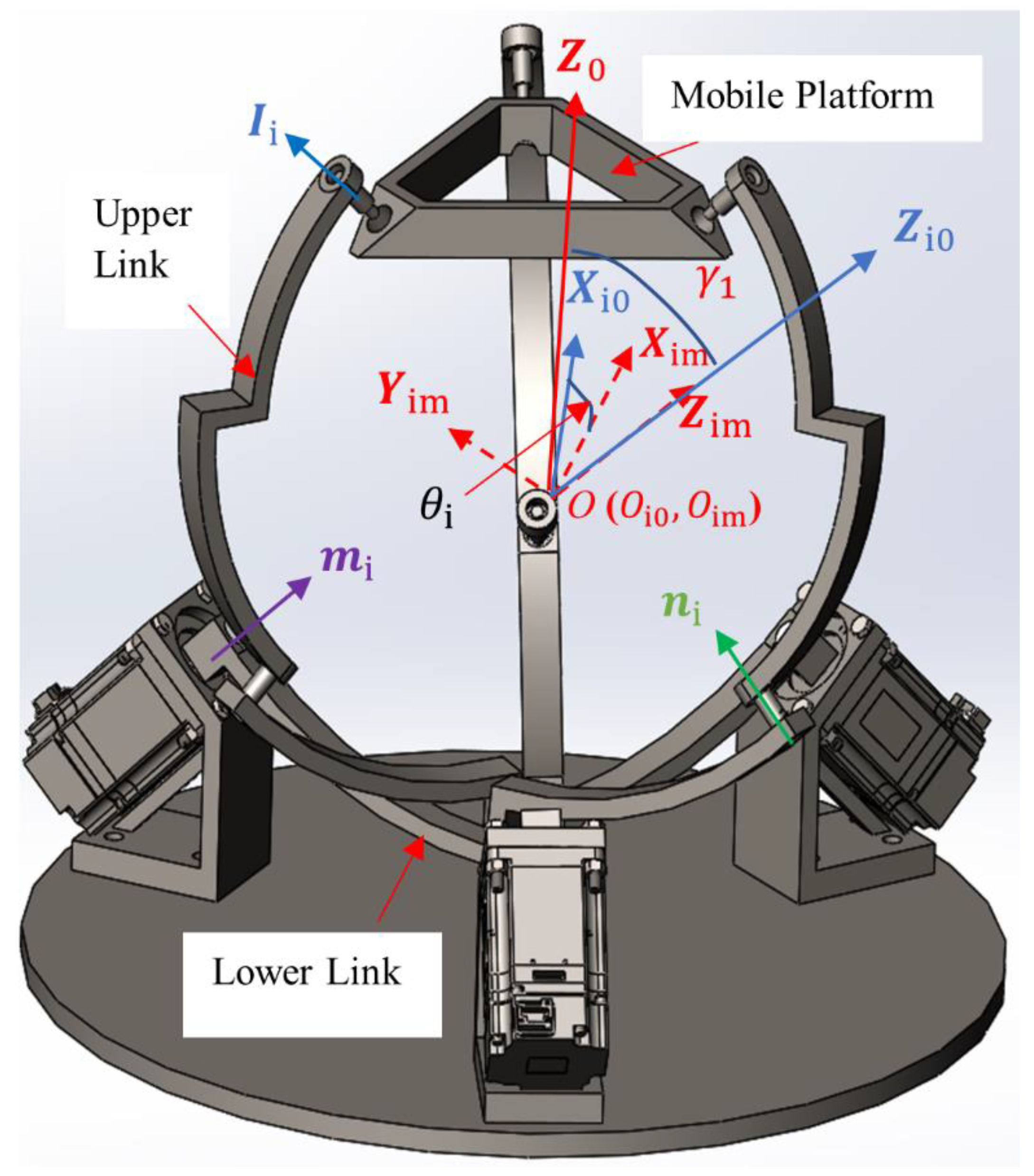
2.1. The D-H Kinematic Model of the SPR

Denote i for the i-th leg (i = 1, 2, 3), $u_i$ for the upper link, $l_i$ for the lower link. As shown in Figure 2, denote ${\mathit{I}}_{\mathrm{i}}$ for the joint axis between the i-th upper link and the mobile platform, ${\mathit{n}}_{\mathrm{i}}$ for the joint axis between the upper link and lower link, and ${\mathit{m}}_{\mathrm{i}}$ for the joint axis between the lower link and base (i = 1, 2, 3), see Figure 2. Note that ${\mathit{I}}_{\mathrm{i}}$, ${\mathit{n}}_{\mathrm{i}}$, and ${\mathit{m}}_{\mathrm{i}}$ are unit vectors. Since all three legs are identical and symmetrical to the center O of the SPR, it is sufficient to take one leg as an example to illustrate how to assign the D-H coordinate system to the leg. Define ${\mathit{Z}}_{\mathrm{il}}$ along the ${\mathit{I}}_{\mathrm{i}}$ axis, ${\mathit{Z}}_{\mathrm{in}}$ along the ${\mathit{n}}_{\mathrm{i}}$ axis, and ${\mathit{Z}}_{\mathrm{im}}$ along the ${\mathit{m}}_{\mathrm{i}}$ axis. Define ${\mathit{X}}_{\mathrm{il}}$as perpendicular to both ${\mathit{Z}}_{\mathrm{il}}$ and $\mathit{Z}$′. The origin of the frame ${\mathit{X}}_{\mathrm{il}}$(${\mathit{Y}}_{\mathrm{il}}$)${\mathit{Z}}_{\mathrm{il}}$ is at O, denoted as $O_{\mathrm{il}}$, due to the spherical property of the SPR. Define${\mathit{X}}_{\mathrm{in}}$ as perpendicular to both ${\mathit{Z}}_{\mathrm{in}}$ and ${\mathit{Z}}_{\mathrm{il}}$. The origin of the frame ${\mathit{X}}_{\mathrm{in}}$(${\mathit{Y}}_{\mathrm{in}}$)${\mathit{Z}}_{\mathrm{in}}$ is at O, denoted as $O_{\mathrm{in}}$, due to the spherical property of the SPR. Define ${\mathit{X}}_{\mathrm{im}}$ as perpendicular to both ${\mathit{Z}}_{\mathrm{im}}$ and ${\mathit{Z}}_{\mathrm{in}}$. The origin of the frame ${\mathit{X}}_{\mathrm{im}}$(${\mathit{Y}}_{\mathrm{im}}$)${\mathit{Z}}_{\mathrm{im}}$ is at O, denoted as $O_{\mathrm{im}}$, due to the spherical property of the SPR.

Define ${\mathit{Z}}_{\mathrm{i}0}$ along the ${\mathit{m}}_{\mathrm{i}}$ axis, and further define ${\mathit{X}}_{\mathrm{i}0}$ as perpendicular to ${\mathit{Z}}_{\mathrm{i}0}$ and along the direction such that initially, ${\mathit{X}}_{\mathrm{im}}$ is coincident with ${\mathit{X}}_{\mathrm{i}0}$, where the mobile platform is at the horizontal state. The origin of the frame ${\mathit{X}}_{\mathrm{i}0}$(${\mathit{Y}}_{\mathrm{i}0}$)${\mathit{Z}}_{\mathrm{i}0}$ is also at O, denoted as $O_{\mathrm{i}0}$, due to the spherical property of the SPR.

For the convenience of later discussions, denote the frame $O_{\mathrm{i}0}$-${\mathit{X}}_{\mathrm{i}0}$(${\mathit{Y}}_{\mathrm{i}0}$)${\mathit{Z}}_{\mathrm{i}0}$ as the frame ${\mathrm{O}}_{\mathrm{i}}$, denote the frame $O_{\mathrm{il}}$-${\mathit{X}}_{\mathrm{il}}$(${\mathit{Y}}_{\mathrm{il}}$)${\mathit{Z}}_{\mathrm{il}}$ as the frame I, denote the frame $O_{\mathrm{im}}$-${\mathit{X}}_{\mathrm{im}}$(${\mathit{Y}}_{\mathrm{im}}$)${\mathit{Z}}_{\mathrm{im}}$ as the frame L, the frame $O_{\mathrm{in}}$-${\mathit{X}}_{\mathrm{in}}$(${\mathit{Y}}_{\mathrm{in}}$)${\mathit{Z}}_{\mathrm{in}}$ as the frame U.

Define ${\theta }_{\mathrm{i}}$ as the angle between ${\mathit{X}}_{\mathrm{i}0}$ and ${\mathit{X}}_{\mathrm{im}}$, see Figure 2. Define ${\mu }_{\mathrm{i}}$ as the angle between ${\mathit{X}}_{\mathrm{im}}$ and ${\mathit{X}}_{\mathrm{in}}$, see Figure 3. Further from Figure 2 and Figure 3, ${\beta }_1$ is the angle between ${\mathit{Z}}_{\mathrm{im}}$ and ${\mathit{Z}}_{\mathrm{in}}$; ${\beta }_2$is the angle between ${\mathit{Z}}_{\mathrm{in}}$ and ${\mathit{Z}}_{\mathrm{il}}$; ${\gamma }_1$ is the angle between ${\mathit{Z}}_{\mathrm{i}0}$ and ${\mathit{Z}}_0$; and ${\gamma }_2$ is the angle between $\mathit{Z}$′ and ${\mathit{Z}}_{\mathrm{il}}$. It is noted that these four angles are identical to each leg.

Table 1. Parameters of the link established by the D-H method.

Link i	${\mathbf{a}}_{\mathbf{i}-1}$	${\alpha }_{\mathbf{i}-1}$	${\mathit{d}}_{\mathit{i}}$	${\mathsf{\theta }}_{\mathbf{i}}$
${\mathit{Z}}_{\mathrm{i}0}$	0	${\gamma }_1$	0	${\delta }_i$
${\mathit{Z}}_{\mathrm{im}}$	0	$0$	0	${\mathsf{\theta }}_{\mathrm{i}}$
${\mathit{Z}}_{\mathrm{in}}$	0	${\mathsf{\beta }}_1$	0	${\mathsf{\mu }}_{\mathrm{i}}$

shows the D-H parameters of the lower link and upper link, which are associated with the three coordinate systems, namely the frame ${\mathrm{O}}_{\mathrm{i}}$, the frame L, and the frame U.

The rotation matrix from the frame O to the frame ${\mathrm{O}}_{\mathrm{i}}$ can be written as:

$${\mathit{R}}_{\mathrm{i}}=\left[\begin{array}{ccc}c{\delta }_i\hfill & -s{\delta }_{i}c{\gamma }_1& s{\delta }_{i}s{\gamma }_1 \\ s{\delta }_i\hfill & c{\delta }_{i}c{\gamma }_1& -c{\delta }_{i}s{\gamma }_1 \\ 0\hfill & s{\gamma }_1& c{\gamma }_1\end{array}\right]$$

(1)

where ${\delta }_i$ = 2(i $-$ 1) π/3 implies that the three motor axes are separated by 120° and where c and s are cosine and sine functions of trigonometric functions (all the c and s representations in the following text have the same meaning as here). The transformation matrix from frame ${\mathrm{O}}_{\mathrm{i}}$to frame L using the parameters from Table 1 is as follows:

$${\mathit{T}}_{\mathrm{li}}=\left[\begin{array}{cccc}c{\theta }_i\hfill & -s{\theta }_i& 0& 0\\ s{\theta }_i\hfill & c{\theta }_i& 0& 0\\ 0\hfill & 0& 1& 0\\ 0\hfill & 0& 0& 1\end{array}\right]$$

(2)

The transformation matrix from frame L to frame U using the parameters from Table 1 is as follows:

$${\mathit{T}}_{\mathrm{ui}}=\left[\begin{array}{cccc}c{\mu }_i\hfill & -s{\mu }_{i}c{\beta }_1& s{\mu }_{i}s{\beta }_1& 0\\ s{\mu }_i\hfill & c{\mu }_{i}c{\beta }_1& -c{\mu }_{i}s{\beta }_1& 0\\ 0\hfill & s{\beta }_1& c{\beta }_1& 0\\ 0\hfill & 0& 0& 1\end{array}\right]$$

(3)

The rotation matrix ${\mathit{R}}_{\mathrm{li}}$ (3 × 3) is a submatrix of ${\mathit{T}}_{\mathrm{li}}$ (take the first three rows and the first three columns), which represents the orientation relation among the axes in the frame ${\mathrm{O}}_{\mathrm{i}}$ and the frame L. Define ${}_{ }{}^O\mathit{r}{}_{il }$as the position of the center of mass (COM) of the lower link with respect to the global reference frame O, then ${}_{ }{}^O\mathit{r}{}_{il }$can be written as:

$${}_{ }{}^O\mathit{r}{}_{il }={}_{ }{}^O\mathit{O}{}_{im}+{\mathit{R}}_i{\mathit{R}}_{li}{}_{ }{}^L\mathit{C}{}_{il}$$

(4)

$${}_{ }{}^O\mathit{O}{}_{im}=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]\mathrm{and}{}_{ }{}^L\mathit{C}{}_{il}=\left[\begin{array}{c}{x}_{ic}\\ y_{ic}\\ z_{ic}\end{array}\right](i=1,2\&3)$$

(5)

where ${}_{ }{}^O\mathit{O}{}_{im}$ is the position of $O_{im}$ with respect to the frame O, and ${}_{ }{}^{L}C{}_{il}$represents the COM of the lower link with respect to the local frame L.

The rotation matrix ${\mathit{R}}_{ui}$ (3 × 3) is a submatrix of ${\mathit{T}}_{\mathrm{ui}}$ (take the first three rows and the first three columns), which represents the orientation relation among the axes in frame L and frame U. Define ${}_{ }{}^O\mathit{r}{}_{iu }$ as the COM of the upper link with respect to the global reference frame O, and ${}_{ }{}^O\mathit{r}{}_{iu }$ is expressed as follows:

$${}_{ }{}^O\mathit{r}{}_{iu }={}_{ }{}^O\mathit{O}{}_{in}+{\mathit{R}}_i{\mathit{R}}_{li}{\mathit{R}}_{ui}{}_{ }{}^U\mathit{C}{}_{iu}$$

(6)

$${}_{ }{}^L\mathit{C}{}_{iu}=\left[\begin{array}{c}{x}_{iuc}\\ y_{iuc}\\ z_{iuc}\end{array}\right](i=1,2\&3)$$

(7)

where ${}_{ }{}^O\mathit{O}{}_{in}$ is the position of $O_{\mathrm{in}}$ with respect to frame O. ${}_{ }{}^U\mathit{C}{}_{iu}$ represents the COM of the upper link with respect to its local frame U.

Define ${}_{ }{}^O\mathit{r}{}_p$ as the COM of the mobile platform with respect to frame O, which is a column matrix, and ${}_{ }{}^O\mathit{r}{}_p$ can be written as:

$${}_{ }{}^O\mathit{r}{}_p={}_{ }{}^O{\mathit{O}}^{\prime }+{\mathit{R}}_{TT}{}_{ }{}^M\mathit{C}_p$$

(8)

where ${}_{ }{}^M\mathit{C}_p$ represents the COM of the mobile platform with respect to frame M, which is a column matrix, and ${}_{ }{}^O{\mathit{O}}^{\prime }$ represents the origin of frame M with respect to frame O, which is a column matrix. ${\mathit{R}}_{\mathrm{TT}}$ represents the orientation of the mobile platform with respect to the global frame O. Calculating the rotation matrix ${\mathit{R}}_{\mathrm{TT}}$ using the Euler angle (φ, σ, Ψ), The matrix ${\mathit{R}}_{\mathrm{TT}}$ is expressed as follows:

$${\mathit{R}}_{TT}=\left[\begin{array}{ccc}c\phi c\sigma (\phi -\Psi )\hfill & c\phi c\sigma s(\phi -\Psi )-s\phi c(\phi -\Psi )& c\phi s\sigma \\ s\phi c\sigma c(\phi -\Psi )+s\phi c(\phi -\Psi )\hfill & s\phi c\sigma c(\phi -\Psi )+s\phi c(\phi -\Psi )& s\phi s\sigma \\ -s\sigma c(\phi -\Psi )\hfill & s\sigma s(\phi -\Psi )& c\sigma \end{array}\right]$$

(9)

$${}_{ }{}^M\mathit{C}{}_{p }=\left[\begin{array}{c}{x}_p\\ y_p\\ z_p\end{array}\right],{}_{ }{}^O{\mathit{O}}^{\prime }=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]$$

(10)

2.2. The Force Balancing Equations for the SPR

The principle of the force balancing of the mechanism is to keep the COM of the mechanism stationary for any configuration of the mechanism. With this principle, the COM of the SPR with respect to the global reference frame O is expressed as follows:

$$M\mathit{r}=m_{\mathrm{p}}{}_{ }{}^O\mathit{r}{}_p+{\displaystyle \sum }_{i=1}^3\left(m_{\mathrm{il}}{}_{ }{}^O\mathit{r}{}_{il }+m_{\mathrm{iu}}{}_{ }{}^O\mathit{r}{}_{iu }\right)$$

(11)

where M is the total mass of SPR, $m_{\mathrm{p}}$ is the mass of the mobile platform, $m_{\mathrm{iu}}$ is the mass of the upper link of the i-th leg, and $m_{\mathrm{il}}$is the mass of the lower link of the i-th leg. That is:

$$M=m_{\mathrm{p}}+{\displaystyle \sum }_{i=1}^3\left(m_{\mathrm{il}}+m_{\mathrm{iu}}\right)$$

(12)

In the above equations, r is the position of the COM of the mechanism, i.e.,

$$\mathit{r}=\left[\begin{array}{c}{r}_x\\ r_y\\ r_z\end{array}\right]$$

(13)

Consequently, the SPR is force balanced if the time-dependent terms of Equation (11) are equated to zero. Substituting Equations (4), (6) and (8) into Equation (11), and then along the X, Y, and Z directions, equates the time-dependent terms to zero. The detailed derivation can be found in Appendix A.

It is noted that the equations for force balancing are only the necessary condition. To reach both the necessary and sufficient conditions, the loop equations of the mechanism need to be derived. There are three independent loop equations for the SPR, namely (a) Loop 1 (base platform—leg 1—mobile platform—leg 2), (b) Loop 2 (base platform—leg 2—mobile platform—leg 3), and (c) Loop 3 (base platform—leg 1—mobile platform—leg 3). The three-loop equations can be expressed by (see Appendix B for details):

$$\begin{gathered} {}_{ }{}^O\mathit{O}{}_{im}+{\mathit{R}}_i{\mathit{R}}_{li}{\mathit{l}}_{il}+{\mathit{R}}_i{\mathit{R}}_{li}{\mathit{R}}_{ui}{\mathit{l}}_{iu}+{\mathit{R}}_{pi}{\mathit{R}}_{TT}{\mathit{l}}_p={}_{ }{}^O\mathit{O}{}_{jm}+{\mathit{R}}_j{\mathit{R}}_{l\mathrm{j}}{\mathit{l}}_{\mathrm{j}l}+{\mathit{R}}_j{\mathit{R}}_{l\mathrm{j}}{\mathit{R}}_{u\mathrm{j}}{\mathit{l}}_{\mathrm{j}u} \\ (for i=1, j=3, or i=2, j=3, or i=1, j=2) \end{gathered}$$

(14)

where ${\mathit{l}}_{il}$ is a column vector defined as ${\left[0,0,l_{il}\right]}^T$ and $l_{il}$ is the length of the i-th lower link. ${\mathit{l}}_{iu}$ is a column vector defined as ${\left[0,0,l_{iu}\right]}^T$ and $l_{iu}$ is the length of the i-th upper link. ${\mathit{l}}_p$ is a column vector defined as ${\left[0,0,l_p\right]}^T$ and $l_p$ is the distance between the point $O^{\prime }$ and the point $P_i$. ${\mathit{R}}_{pi}$ is the rotation matrix from frame M to frame I.

$${\mathit{R}}_{pi}=\left[\begin{array}{ccc}c{\delta }_i\hfill & -s{\delta }_{i}c{\gamma }_2& s{\delta }_{i}s{\gamma }_2 \\ s{\delta }_i\hfill & c{\delta }_{i}c{\gamma }_2& -c{\delta }_{i}s{\gamma }_2 \\ 0\hfill & s{\gamma }_2& c{\gamma }_2\end{array}\right]$$

(15)

2.3. The Shaking Moment of the SPR

According to Newton’s law for angular momentum, we have the following equation:

$${\displaystyle \sum }{M}_0=\dot{L_0}$$

(16)

where $M_0$is the sum of the external moment at a reference point O, $L_0$ is the total angular momentum considered at O, and $\dot{L_0}$ is the first derivative of $L_0$. The angular momentum of the SPR with respect to its center point O can be expressed by:

$$L_0=(m_{\mathrm{p}}\left({\mathit{r}}_{\mathrm{p}}\times \dot{{\mathit{r}}_{\mathrm{p}}}\right)+L_{\mathrm{p}})+{{\displaystyle \sum }}_{i=1}^3\left(L_{\mathrm{il}}+m_{\mathrm{il}}\left({\mathit{r}}_{\mathrm{il}}\times \dot{{\mathit{r}}_{\mathrm{il}}}\right)+L_{\mathrm{iu}}+m_{\mathrm{iu}}\left({\mathit{r}}_{\mathrm{iu}}\times \dot{{\mathit{r}}_{\mathrm{iu}}}\right)\right)$$

(17)

$$L_{\mathrm{p}}=6{{\displaystyle \int }}_0^{\frac{\pi }{3}}\frac{m_p}{3\sqrt{3}{l}_p}{(\frac{l_p}{2\cos \left(\theta \right)})}^{2}d\theta \dot{{\theta }_p}=\frac{\sqrt{3}}{9}{m}_p{l}_p{}^2\dot{{\theta }_p}$$

(18)

$$\left\{\begin{array}{cc}\hfill L_{\mathrm{iu}}& =\frac{r_{\mathrm{i}2}}{r_{\mathrm{i}2}+r_{\mathrm{i}1}}{m}_{\mathrm{iu}}\left({\left|r_{\mathrm{i}2}\right|}^2-{\left|r_{\mathrm{iu}}\right|}^2\right)\dot{{\theta }_{lu}}+\frac{r_{\mathrm{i}1}}{r_{\mathrm{i}2}+r_{\mathrm{i}1}}{m}_{\mathrm{iu}}\left({\left|r_{\mathrm{i}1}\right|}^2-{\left|r_{\mathrm{iu}}\right|}^2\right)\dot{{\theta }_{lu}}\hfill \\ \hfill L_{\mathrm{i}l}& =\frac{r_{\mathrm{i}2}}{r_{\mathrm{i}2}+r_{\mathrm{i}1}}{m}_{\mathrm{il}}\left({\left|r_{\mathrm{i}2}\right|}^2-{\left|r_{\mathrm{i}1}\right|}^2\right)\dot{{\theta }_{ll}}+\frac{r_{\mathrm{i}1}}{r_{\mathrm{i}2}+r_{\mathrm{i}1}}{m}_{\mathrm{il}}\left({\left|r_{\mathrm{i}1}\right|}^2-{\left|r_{\mathrm{i}1}\right|}^2\right)\dot{{\theta }_{ll}}\hfill \end{array}\right.$$

(19)

where $L_{\mathrm{p}}$is the angular momentum of the mobile platform with respect to its COM, $l_p$ is the length between $P_i$ and the COM of the mobile platform, and $r_{i2}$ and $r_{i11}$ are the outer sphere radius and inner sphere radius of the upper link, respectively. $\dot{{\theta }_p}$is the angular velocity of the mobile platform, ${\mathit{r}}_{\mathrm{p}}$ is the vector from point O to the COM of the mobile platform and $\dot{{\mathit{r}}_{\mathrm{p}}}$ is the first derivative of ${\mathit{r}}_{\mathrm{p}}$. ${\mathit{r}}_{\mathrm{il}}$ is the vector from point O to the COM of the lower link and $\dot{{\mathit{r}}_{\mathrm{il}}}$ is the first derivative of ${\mathit{r}}_{\mathrm{il}}$. ${\mathit{r}}_{\mathrm{iu}}$ is the vector from the point O to the COM of the upper link and $\dot{{\mathit{r}}_{\mathrm{iu}}}$ is the first derivative of ${\mathit{r}}_{\mathrm{iu}}$.$L_{\mathrm{iu}}$ is the angular momentum of the upper link with respect to its COM, $L_{\mathrm{il}}$ is the angular momentum of the lower link with respect to its COM, $\dot{{\theta }_{il}} and \dot{{\theta }_{iu}}$ are the angular velocity of the lower link and upper link, and $m_{\mathrm{il}}$ and $m_{\mathrm{iu}}$are the mass of the lower link and upper link.

Figure 4a shows the structure of the mobile platform, and Figure 4b shows the structure of the upper link of the SPR. ${}_{ }{}^O\mathit{r}{}_{iu}$is the COM of the upper link with respect to the frame O, ${\mathit{Z}}_{\mathrm{o}}$ is the rotation axis passing through the point O, and ${\mathit{Z}}_{cu}$ is the rotation axis passing through the point ${}_{ }{}^{O}r{}_{iu}$. Due to the characteristics of the spherical mechanism, it can be calculated that the angular momentum around the ${\mathit{Z}}_{\mathrm{o}}$ axis is $\frac{r_{\mathrm{i}2}}{r_{\mathrm{i}2}+r_{\mathrm{i}1}}{m}_{\mathrm{iu}}{\left|r_{\mathrm{i}2}\right|}^2\dot{{\theta }_{iu}}+\frac{r_{\mathrm{i}1}}{r_{\mathrm{i}2}+r_{\mathrm{i}1}}{m}_{\mathrm{iu}}{\left|r_{\mathrm{i}1}\right|}^2\dot{{\theta }_{iu}}$, according to the parallel axis theorem. Then the angular momentum around the ${\mathit{Z}}_{cu}$ axis is $\frac{r_{\mathrm{i}2}}{r_{\mathrm{i}2}+r_{\mathrm{i}1}}{m}_{\mathrm{iu}}({\left|r_{\mathrm{i}2}\right|}^2-|r_{\mathrm{iu}}{|}^2)\dot{{\theta }_{iu}}+\frac{r_{\mathrm{i}1}}{r_{\mathrm{i}2}+r_{\mathrm{i}1}}{m}_{\mathrm{iu}}({\left|r_{\mathrm{i}1}\right|}^2-|r_{\mathrm{iu}}{|}^2)\dot{{\theta }_{iu}}.$

3. Partial Moment Balancing of the SPR Using the CW-AKP Approach

The CW approach is used to modify the lower link. Using Equation (A6) in Appendix A, the length of the lower link is expressed by

$$l_{\mathrm{il}}=\frac{m_{1l}{y}_{1c}c{\beta }_1-m_{1l}{z}_{1c}s{\beta }_1}{m_{1u}s{\beta }_1}$$

(20)

The length of the link adjustment is given as $v_{1\mathrm{l}}$. Due to the symmetry of the SPR, we have $v_{\mathrm{il}}$=$v_{1\mathrm{l}}$.

$$v_{1l}=l_{1l}^0-l_{1l}=l_{1l}^0-\frac{m_{1l}{y}_{1c}c{\beta }_1-m_{1l}{z}_{1c}s{\beta }_1}{m_{1u}s{\beta }_1}$$

(21)

Consequently, Equation (21) gives the mass redistribution of the lower link based on the CW approach.

The AKP approach is used to adjust the upper link. Equation (A29) in Appendix B is used to derive the length of the upper link. The equation to calculate the adjustment is:

$$v_{\mathrm{iu}}=v_{1\mathrm{u}}=l_{1u}^0-\frac{\left(y_{10}-y_{30}\right)}{s{\beta }_2}$$

(22)

where $l_{1l}^0$ and $l_{1u}^0$ are the initial value of the lower link and upper link length.

The shaking moment is considered as the objective function for optimization, that is, to minimize the shaking moment. The shaking moment is derived from Equation (16) and expressed by:

$$M=m_p|r_p{|}^2\ddot{{\theta }_p}+\frac{\sqrt{3}}{9}{m}_{\mathrm{p}}{l}_p{}^2\ddot{{\theta }_{\mathrm{p}}}+{\displaystyle \sum }_{i=1}^3(m_{il}|r_{\mathrm{il}}{|}^2\ddot{{\theta }_{il}}+m_{iu}|r_{\mathrm{iu}}{|}^2\ddot{{\theta }_{iu}}+\dot{L_{il}}+\dot{L_{iu}})$$

(23)

where $\dot{L_{il}}$ is the first derivative of $L_{\mathrm{il}}$, and $\dot{L_{iu}}$ is the first derivative of $L_{\mathrm{iu}}$. $\ddot{{\theta }_p}$, $\ddot{{\theta }_{il}}$, and $\ddot{{\theta }_{iu}}$ are the accelerations of the mobile platform, of the lower link, and of the upper link, respectively.

In the following, we consider an SPR mechanism in which the $r_{i2}$ and $r_{i1}$ of the links are nearly equal and defined as r. $l_{il}$ and $l_{iu}$ are the spherical length of the upper link and lower link of Leg i, respectively, therefore $l_{il}=l_{iu}=$ $r{\beta }_1$ and ${\beta }_1={90}^{°}$ (${\beta }_1$ is defined previously in Section 2). Then, we can obtain:

$$|r_{\mathrm{iu}}|=r\frac{\sin (\frac{{\beta }_1}{2})}{\frac{{\beta }_1}{2}}=\frac{l_{iu}}{{\beta }_1}\frac{\sin (\frac{{\beta }_1}{2})}{\frac{{\beta }_1}{2}}$$

(24)

Subsequently, we have:

$${\displaystyle \sum }_{i=1}^3{r}_{iu}={\displaystyle \sum }_{i=1}^3\frac{l_{iu}}{{\beta }_1}\frac{\sin (\frac{{\beta }_1}{2})}{\frac{{\beta }_1}{2}}={\displaystyle \sum }_{i=1}^{3}0.537l_{iu}$$

(25)

Similarly:

$${\displaystyle \sum }_{i=1}^3{r}_{il}={\displaystyle \sum }_{i=1}^{3}0.537l_{il}$$

(26)

Using Equations (24)–(26), Equation (23) can be written as follows:

$$M=m_p{r}_p{}^2\ddot{{\theta }_p}+{\displaystyle \sum }_{i=1}^3\left(0.537+0.124\right)m_{il}{l}_{il}^2\ddot{{\theta }_{il}}+{\displaystyle \sum }_{i=1}^3\left(0.537+0.124\right)m_{iu}{l}_{iu}^2\ddot{{\theta }_{iu}}+\frac{\sqrt{3}}{9}{m}_{\mathrm{p}}{l}_p{}^2\ddot{{\theta }_{\mathrm{p}} }$$

(27)

The optimal variables are the added masses and their locations (for the lower link) with the CW method, and the adjustment of the length of the links (for the upper link) with the AKP method. Therefore, only the last four terms of Equation (27) are considered. The objective function can therefore be simplified as follows:

$$M={\displaystyle \sum }_{i=1}^3\left(0.661m_{il}{l}_{il}^2+0.661m_{iu}{l}_{iu}^2\right)$$

(28)

From Equation (28), the variables of the objective function are $m_{il}$, $m_{iu}$, $l_{il}$, and $l_{iu}$. Further, Equation (A6) in Appendix A and Equation (A29) in Appendix B are selected as the constraint equations in the optimization model, which is explained in the following. From Appendix A, there are 18 force-balancing equations, though only Equations (A6)–(A10) are the functions of $m_{il}$, $m_{iu}$, $l_{il}$, and $l_{iu}$. Since the three legs are identical, only Equation (A6) is selected as the constraint equation by taking Leg 1 as an example. Equation (A29) is the loop equation, and therefore, it is defined as a constraint equation. For the convenience of later discussions, the two constraint equations, Equations (A6) and (A29), are put below as Equations (29) and (30), respectively.

$$m_{1l}{y}_{1c}c{\beta }_1-m_{1l}{z}_{1c}{\beta }_1-m_{1u}{l}_{1\mathrm{l}}s{\beta }_1=0$$

(29)

$$l_{3u}s{\beta }_2=y_{10}-y_{30}$$

(30)

The specific parameters of the SPR can be extracted from the SolidWorks CAD model of the SPR, and they are shown in

Table 2. CAD data of SPR.

Unbalanced Linkage	Value	Units
Length (Lower Link)	313	mm
Mass (Lower Link)	641.6	g
$\mathrm{Point}{B}_1$	(0.0, 162.1, −64.3)
$\mathrm{Point}{B}_2$	(−140.3, −81.1, −64.3)
$\mathrm{Point}{B}_3$	(140.3, −81.1, −64.3)
Length (Upper Link)	243	mm
Mass (Upper Link)	483.5	g
$\mathrm{Point}{O}_{1n}$	(−16.8, −149.3, −37.1)
$\mathrm{Point}{O}_{2n}$	(129.8, 74.9, −37.1)
$\mathrm{Point}{O}_{3n}$	(−129.8, 74.9, −37.1)
Length (Mobile Platform)	189.7	mm
Mass (Mobile Platform)	313	g
$\mathrm{Point} P_1$	(0.0, −109.5, 202.5)
$\mathrm{Point} P_2$	(94.8, 54.8, 202.5)
$\mathrm{Point} P_3$	(−94.8, 54.8, 202.5)
$\mathrm{Point}{O}^{\prime }$	(0, 0, 0.202)

. Rows 1 and 2 give details of the length and the mass of the lower link. Rows 3, 4, and 5 show the values of the coordinate points $B_1$, $B_2$, and $B_3$, with respect to frame O. Rows 6 and 7 give details of the length and the mass of the upper link. Rows 8, 9, and 10 show the values of the coordinate points $O_{1n}$, $O_{2n}$, and $O_{3n}$ considered with respect to frame O in the initial state. Rows 11 and 12 give details of the length and the mass of the mobile platform. Rows 13, 14, and 15 show coordinates for the points$P_1$, $P_2$, and $P_3$ with respect to frame O in the initial state. Row 16 shows the coordinates for the COM of the platform with respect to frame O in the initial state. Figure 5 shows the details of these points.

The following equation can be obtained by substituting the values of M (1438 g) and $m_{\mathrm{p}}$= 313 g into Equation (12):

$$m_{iu}=1.125-m_{il}$$

(31)

Substituting the values of $z_{\mathrm{ic}}$ = 157 (mm) and ${\beta }_1$ = 90° into Equation (29) gives the constraint equation (g1). Substituting the values of $y_{10}$ = 162.1 (mm), $y_{30}$ = −81.1 (mm), and ${\beta }_2$ = 90° into Equation (30) gives the constraint equation (g2). Substituting Equation (31) into Equation (28), $m_{\mathrm{iu}}$ is eliminated and the number of variables in the objective function is reduced to three. In summary, the optimization problem is formulated as follows:

$$\begin{gathered} \min f\left(m_{il},l_{il},l_{iu}\right)=0.661m_{il}{l}_{il}^2+0.7436l_{iu}^2-0.661m_{il}{l}_{iu}^2 \\ \mathrm{s}.\mathrm{t}{g}_1: 0.157m_{il}+1.125l_{il}-m_{il}{l}_{il}=0 \\ {g}_2: l_{iu}-0.243=0 \end{gathered}$$

4. Simulation Verification

The MATLAB optimization toolbox functions or solvers were used to solve this optimization problem. In the MATLAB toolbox, the “fmincon” command was used as an optimization function. The “fmincon” function uses four different algorithms, of which the sequential quadratic programming (SQP) algorithm was used here due to its applicability to our optimization problem as well as its efficiency in solving such a kind of optimization. Using the SQP solver, the results were found to be $m_{\mathrm{il}}$ = 475.6 (g), $l_{\mathrm{il}}$ = 115 (mm), and $l_{\mathrm{iu}}$ = 243.3 (mm). The results were verified for not being local minima by trying different starting points and by using the interior-point solver in MATLAB. The shaking moment was found to be 0.0093 (Nm) only, while the shaking moment of the unbalanced result was found to be 0.073 (Nm).

The simulation was carried out with SPACAR [29]. SPACAR is a reliable software that has been used as a tool for simulation-based experiments by many other researchers in the literature [30]. The initial parameters of the unbalanced SPR are shown in Table 2, using the optimized values of $m_{\mathrm{il}}$ = 475.6 (g) and length $l_{\mathrm{il}}$ = 115 (mm) for the balanced lower link. The INVDYN module in SPACAR was used for the simulation. The input parameters are the trajectory. The outputs (i.e., shaking force and shaking moment) were obtained from SPACAR. The SPR was defined using a data file, which is the input file of SPACAR, containing specific SPACAR keywords and parameters (see Supplementary Materials S1). The input file contains the details of kinematic data, dynamics data, and inverse dynamics data.

For the convenience of simulation but without the loss of the purpose of verification, we chose the input motion to the system as this: the center of the mobile platform goes around a closed-form trajectory (named trajectory 1), A → B → C → D → A. The coordinates of these points are as follows: A (0, 0, 0.0905), B (0.0002, −0.0001, 0.0903), C (0.0002, 0, 0.0903), and D (−0.0001, 0, 0.0901) (see Figure 6). To increase the reliability of the verification, we consider two situations (see Figure 7).

Situation (1): Initially, the mobile platform is at rest at point A for 0.05 s. Next, the mobile platform starts from point A, (i) accelerates uniformly for 0.03 s to a speed of 0.0176 m/s, (ii) maintains the speed of 0.0176 m/s for 0.14 s, and (iii) decelerates uniformly for 0.03 s to a speed of 0 m/s and in the meantime reaches point B. Next, the mobile platform starts from point B, (i) accelerates uniformly for 0.03 s to a speed of 0.0059 m/s, (ii) maintains the speed of 0.0059 m/s for 0.14 s, and (iii) decelerates uniformly for 0.03 s to a speed of 0 m/s and in the meantime reaches point C. Next, the mobile platform starts from point C, (i) accelerates uniformly for 0.03 s to a speed of 0.0212 m/s, (ii) maintains the speed of 0.0212 m/s for 0.14 s, and (iii) decelerates uniformly for 0.03 s to a speed of 0 m/s while in the meantime reaching point D. Finally, it takes 0.05 s for the mobile platform to accelerate uniformly from point D to point A.

Situation (2): Initially, the mobile platform is at rest at point A for 0.05 s. Next, the mobile platform starts from point A, (i) accelerates uniformly for 0.1 s to a speed of 0.03 m/s, and (ii) decelerates uniformly for 0.1 s to a speed of 0 m/s while in the meantime reaching point B. Next, the mobile platform starts from point B, (i) accelerates uniformly for 0.1 s to a speed of 0.01 m/s, and (ii) decelerates uniformly for 0.1 s to a speed of 0 m/s while in the meantime reaching point C. Next, the mobile platform starts from point C, (i) accelerates uniformly for 0.1 s to a speed of 0.0357 m/s, and (ii) decelerates uniformly for 0.1 s to a speed of 0 m/s while in the meantime reaching point D. Finally, it takes 0.05 s for the mobile platform to accelerate uniformly from point D to point A.

For the convenience of subsequent discussions, we call Situation (1) “high” (in terms of rise time, which is 0.03 s), and Situation (2) “low” (in terms of acceleration time, which is 0.1 s). The simulation results are presented below.

$F$ represents the magnitude of the shaking force of the SPR (notice that the shaking force is a vector with components in all X, Y, Z directions). M represents the magnitude of the shaking moment of the SPR (notice that the shaking moment is a vector with its components in all X, Y, Z directions). Figure 8a shows the result of the shaking force of the SPR at “low”. It can be found that the shaking force of the unbalanced SPR fluctuates significantly between −1.616 N and 0.890 N while the optimized SPR has no shaking force. Figure 8b shows the result of the shaking force of the SPR at “high”, which has the same pattern of reduction by applying our method. Figure 9a shows the result of the shaking moment of the SPR at “low”. From Figure 9a, it can be found that the shaking moment of the unbalanced SPR fluctuates significantly between −5.9 Nm and 3.8 Nm while the shaking moment of the optimized SPR only fluctuates between −0.15 Nm and 0.15 Nm. Figure 9b shows the result of the shaking moment of the SPR at “high”, which has the same pattern of reduction by applying our method. In summary, the shaking moment of the optimized SPR is reduced by more than 95% for “high” and by more than 97% for “low” by comparing with that of the unbalanced SPR. Figure 10 shows the result of the torque fluctuation of the three motors installed on the base at (a) “low” and (b) “high”. It is apparent that the torque fluctuation of the three motors of the optimized SPR at both “high” and “low” have reduced by more than 25% compared with the unbalanced SPR.

In order to increase the reliability of the verification, another path (named trajectory 2) in space is randomly selected, as shown in Figure 11. We consider two situations as well: Situation 1: the mobile platform tracking the path within 1 s (named “high”), Situation 2, the mobile platform tracking the path within 10 s (named “low”). The simulation results are presented below.

From Figure 12 and Figure 13, it is apparent that the shaking force and shaking moment of the optimized SPR at both “high” and “low” are reduced by more than 90% compared with the unbalanced SPR. From Figure 14, it is apparent that the torque of the three motors at the base of the optimized SPR at both “high” and “low” have reduced by more than 20% compared with the unbalanced SPR.

5. Conclusions

This paper presented a study on the dynamic balance of spatial robotic mechanisms. The spherical parallel robot (SPR) was chosen as a study vehicle. The goal of the study was to extend the CW-AKP approach to the partial moment balancing of mechanisms with the goal of making the shaking moment as small as possible. This approach was applied to SPR. A simplified mathematical expression of the shaking moment under a certain condition was described, which has only three variables and is a quadratic form. An efficient solver for such optimization is available. This will greatly benefit the real-time control of the SPR concerning the shaking moment. The verification of the effectiveness of our approach was made with the help of SPACAR in the MATLAB environment, namely a simulation-based experiment. The result from the experiment shows that the approach is effective, especially for the example system used for analysis: a 90% reduction in the shaking moment has been achieved. The main contributions of this paper are: (1) a combined CW and AKP approach to the partial moment balancing of the SPR enhanced with a simplified mathematical model of the shaking moment of the SPR, and (2) a new design of the SPR which can be fully force balanced yet partially moment balanced.

However, a note is taken that the simplified model is under the condition that the parameters of the link have certain geometric relations, which is a limitation of this study.

There are several future studies to be based upon the current study described in this paper. First, an effort is to be taken toward the physical-based experiment of the proposed partial moment balance by the CW-AKP approach. Second, the balancing of machines, especially so-called soft machines or soft robots, is with a growing interest in soft robots [31] and compliant mechanisms [32,33,34], since both soft robots and compliant mechanisms are more complex when external loads are added to them (dimensional deformation). It is worth mentioning that the balancing of mechanisms in the contemporary literature refers to the cancellation of the inertia-induced force to the ground. Balancing an external force on the mechanism is a relatively new issue. Third, the balancing of micro-motion manipulators with two or multi-degrees of freedom (micro-surgical robots) [35] needs attention, as the micro-motion system demands high accuracy [36] and the shaking moment may become a significant factor that compromises the accuracy.