The Modelling and Analysis of Micro-Milling Forces for Fabricating Thin-Walled Micro-Parts Considering Machining Dynamics
Abstract
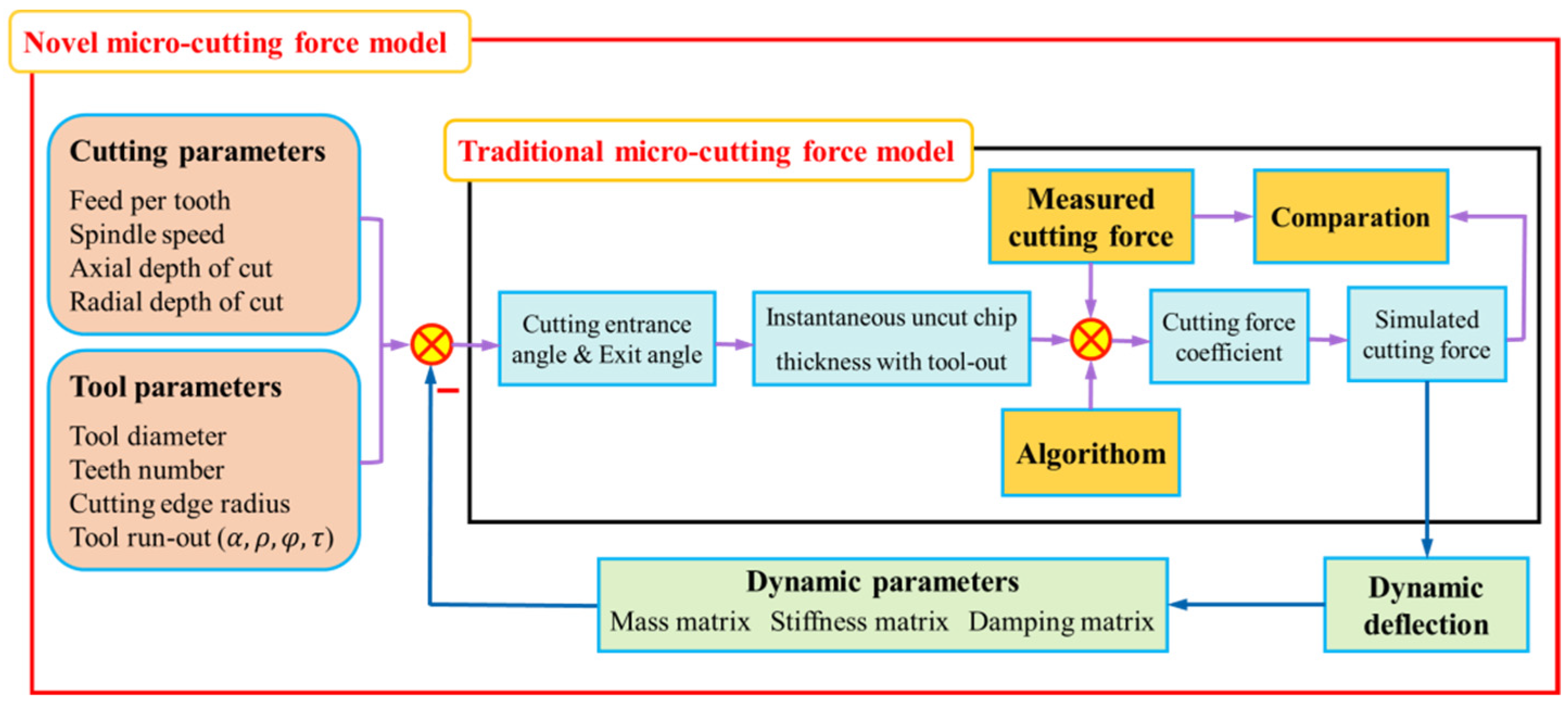
:1. Introduction
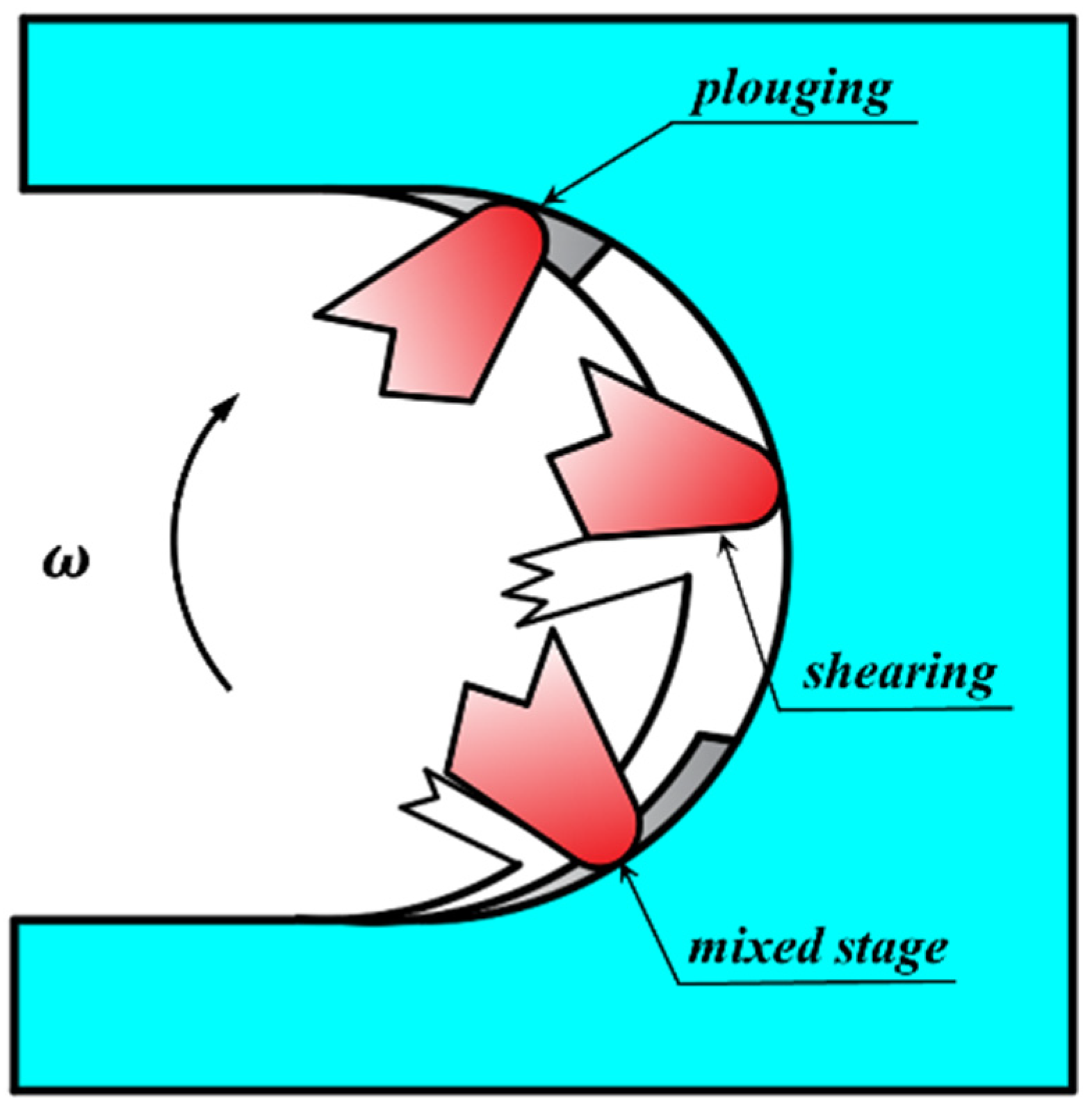
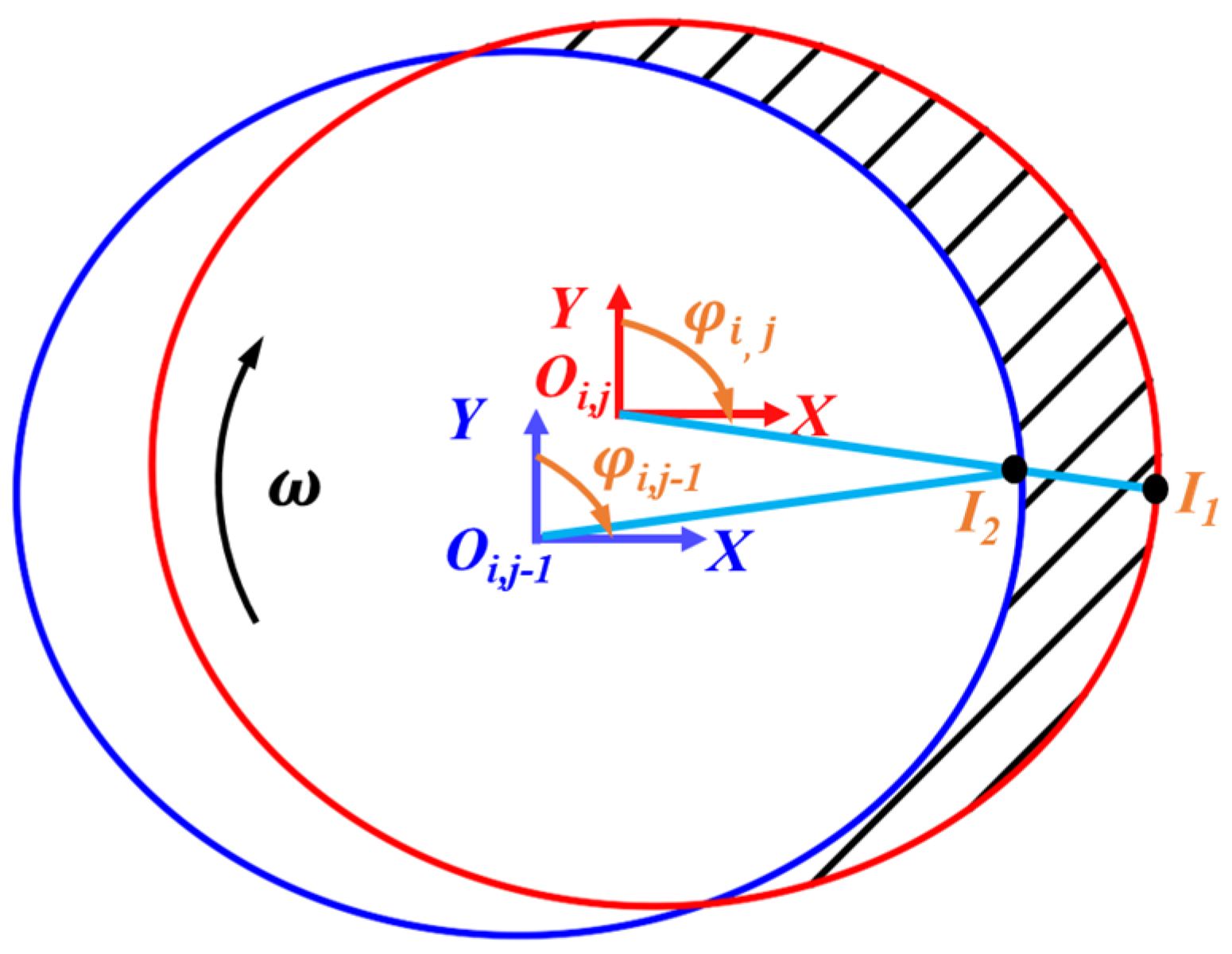
2. Modelling of IUCT
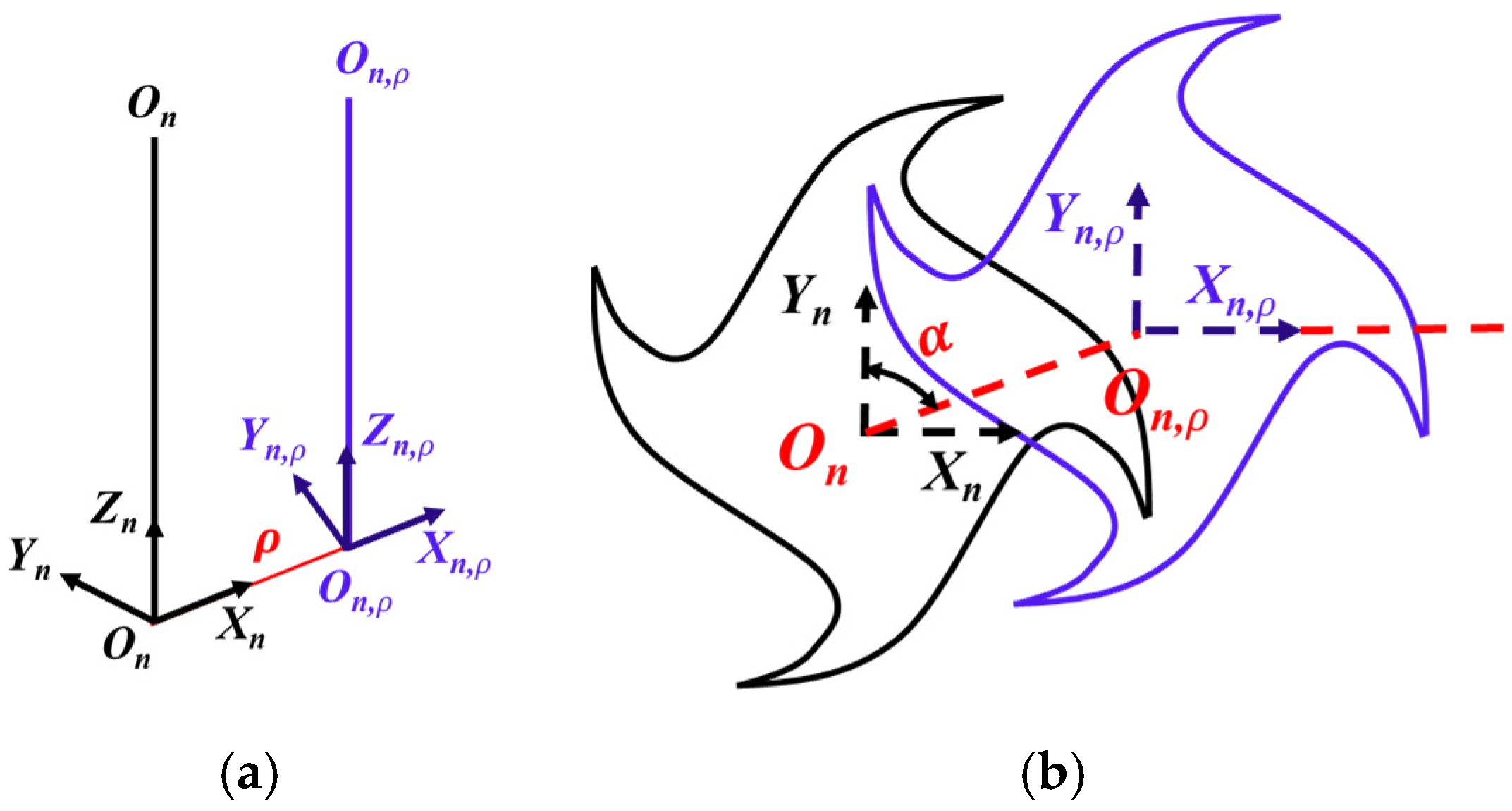
2.1. Modelling of the Cutting-Edge Trajectories
2.2. IUCT Modelling Considering the Tool Runout
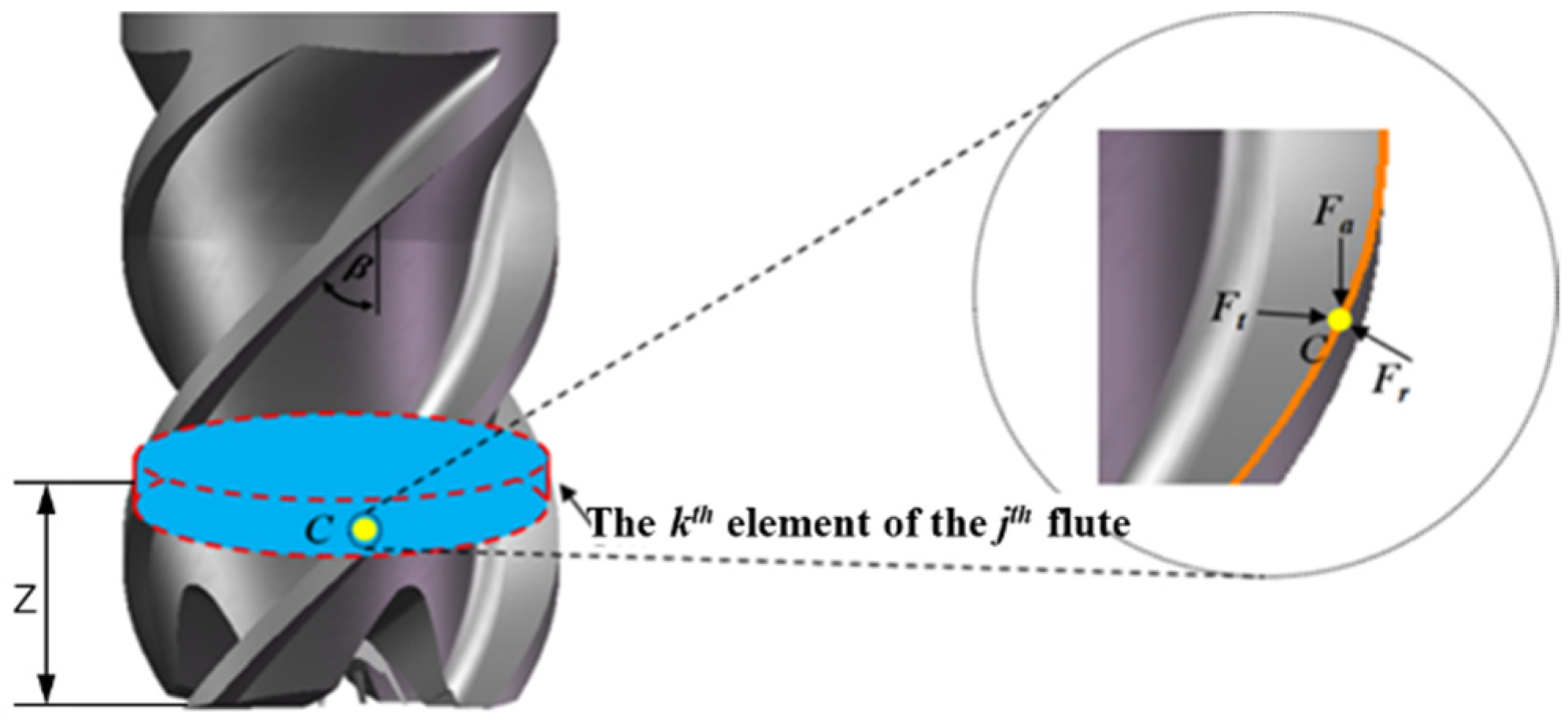
3. Micro-Milling Forces Modelling
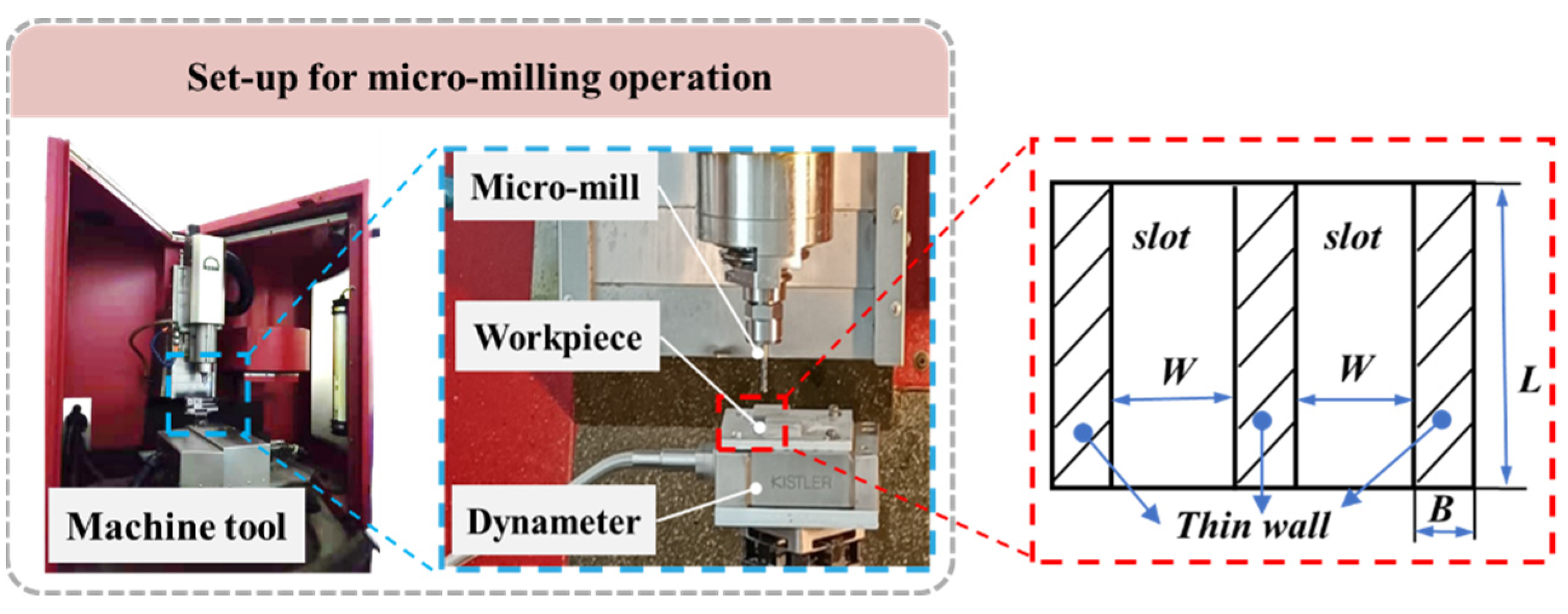
4. Validation of the Cutting Forces Modelling
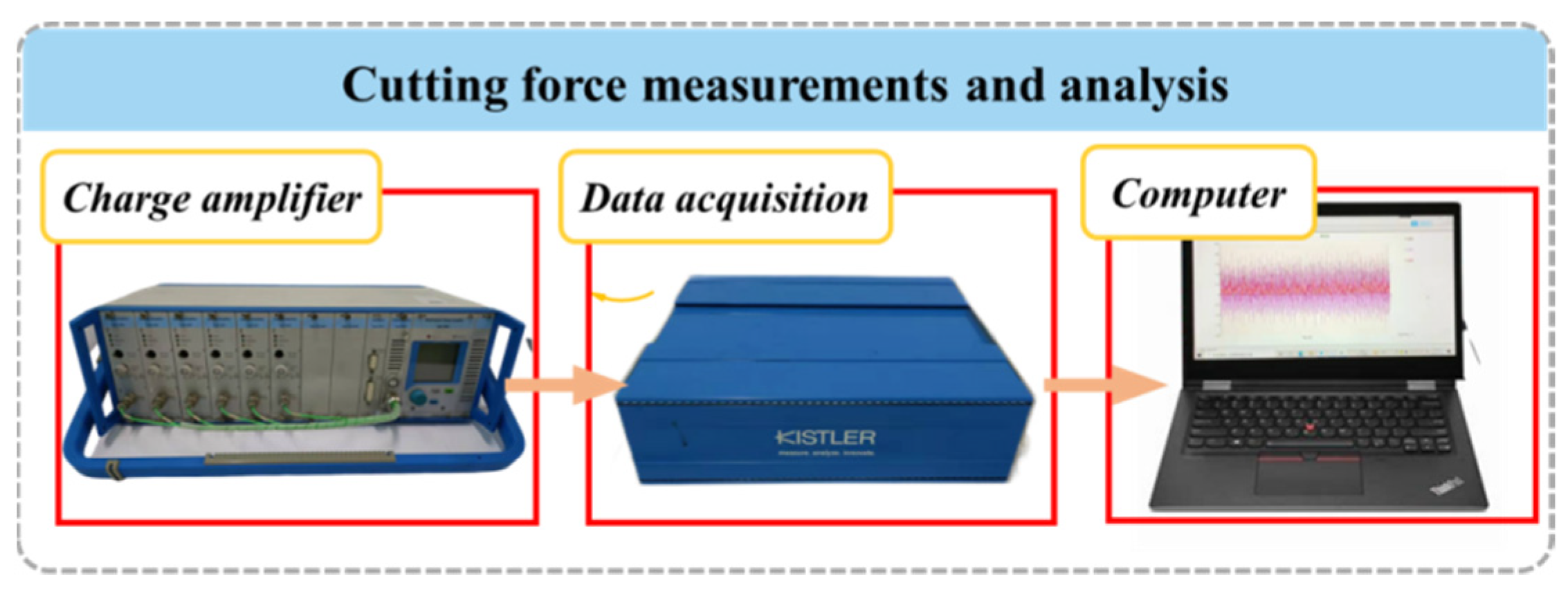
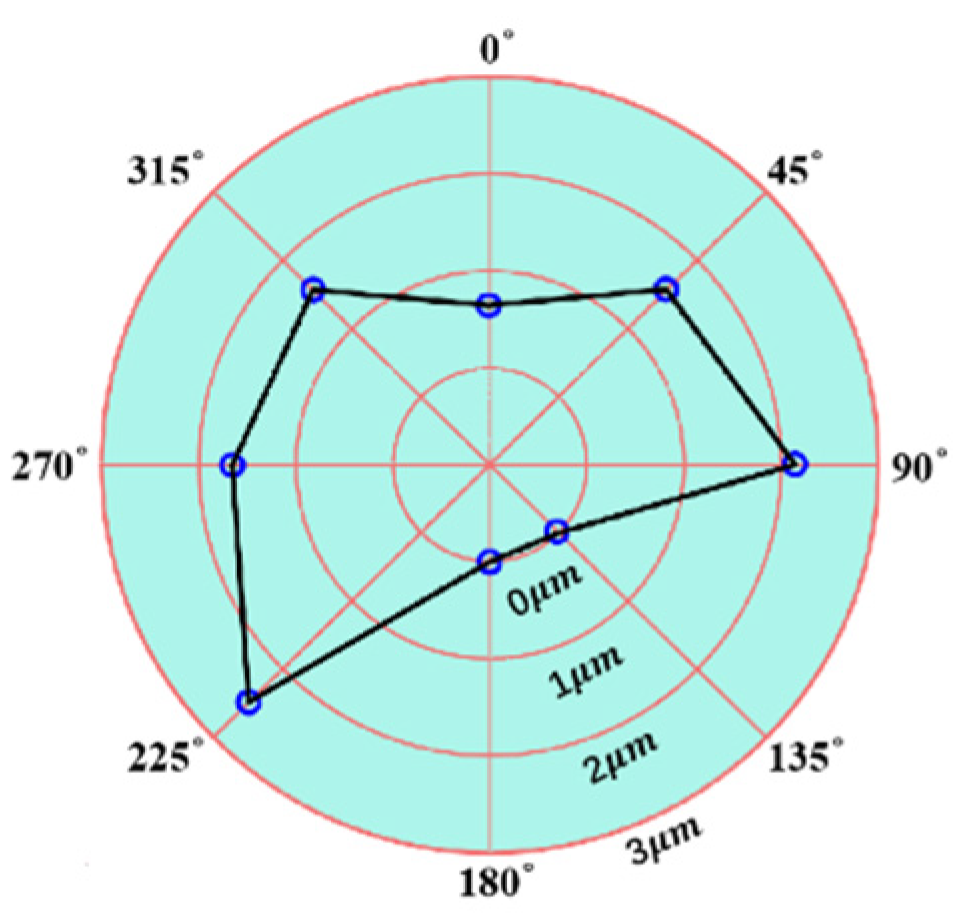
4.1. Cutting Force Experiments and Runout Error Measurement
4.2. Identification of Dynamic Parameters
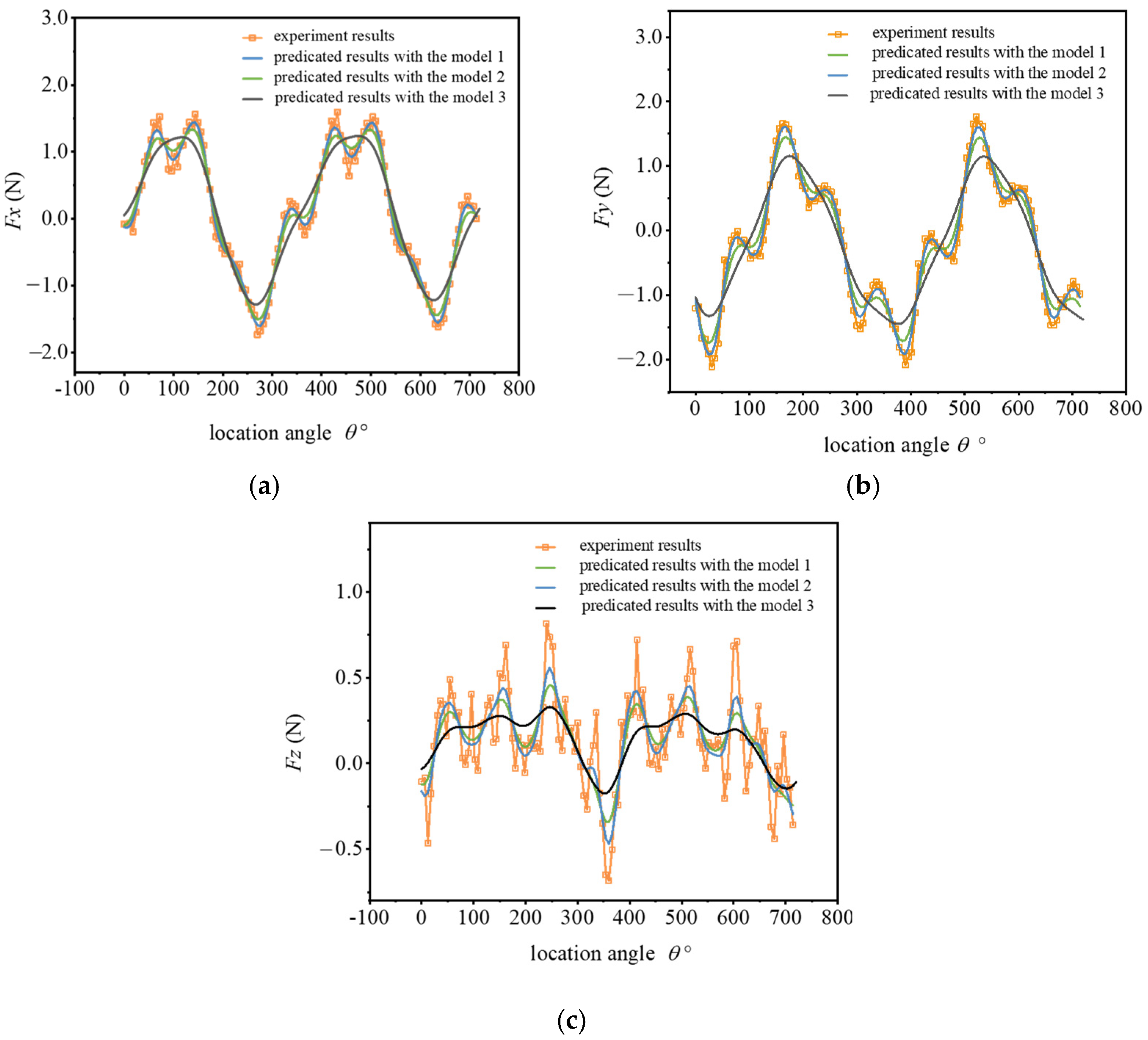
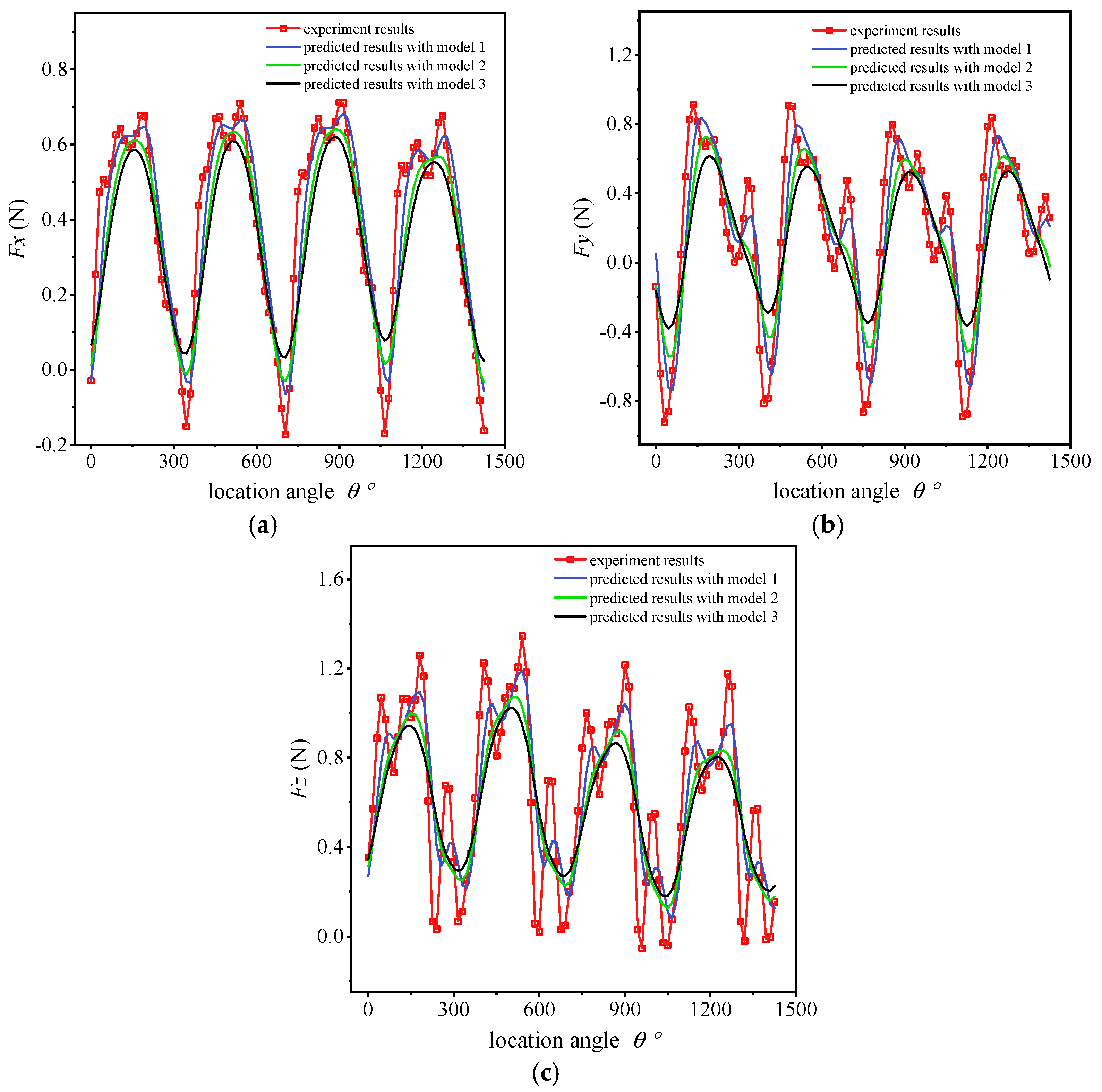
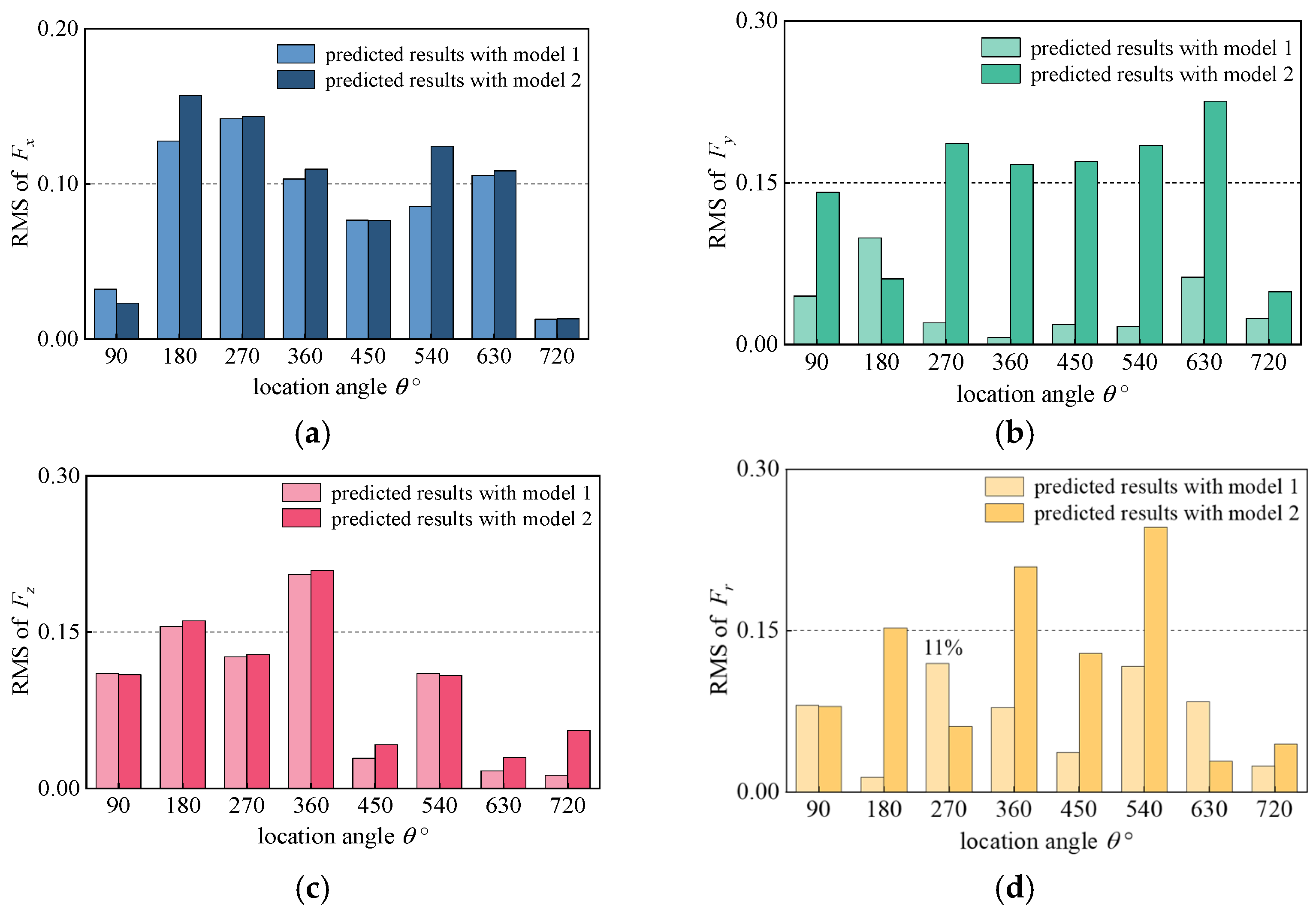
4.3. Results and Discussion
5. Conclusions
- (1)
- In the micro-milling of thin-walled parts, the actual trajectories of the cutting edge were analysed by considering the tool runout error and the dynamic deformation. On this basis, the instantaneous undeformed chip thickness model was established, which also considers the “tooth skipping” phenomenon.
- (2)
- Based on the proposed instantaneous undeformed chip thickness model, a mechanistic cutting force model was established. The tool runout errors were measured by a dial indicator. The dynamic parameters of the micro-cutter and thin-walled micro-parts were obtained by the receptance method.
- (3)
- The micro-milling forces were simulated by MATLAB. Additionally, the proposed model was validated by two groups of dry micro-milling experiments. The results show that the simulated cutting forces are in good consistency with the experimental results. Compared with Model 2 and Model 3, the cutting forces simulated by the proposed method were much closer to the experimental cutting forces. Additionally, the RMS errors of the resultant force between the measured values and the simulated values obtained from the proposed model were all less than 11%. It can be concluded that the cutting forces are significantly influenced by dynamic chatter and tool runout.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, X.; Cheng, X.; Ling, S.; Zheng, G.; Li, Y.; Liu, H. Research on optimization of micro-milling process for curved thin wall structure. Precis. Eng. 2022, 73, 296–312. [Google Scholar] [CrossRef]
- Li, G.; Wang, F.; Wang, H.; Cheng, J. Microstructure and Mechanical Properties of TC4 Titanium Alloy Subjected to High Static Magnetic Field. Trans Tech. Publ. 2017, 898, 345–354. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Zhu, K. Generic instantaneous force modeling and comprehensive real engagement identification in micro-milling. Int. J. Mech. Sci. 2022, 176, 105504. [Google Scholar] [CrossRef]
- Lee, H.U.; Cho, D.; Ehmann, K.F. A Mechanistic model of cutting forces in micro-end-milling with cutting-condition-independent cutting force coefficients. ASME J. Manuf. Sci. Eng. 2008, 3, 031102. [Google Scholar] [CrossRef]
- Bao, W.Y.; Tansel, I.N. Modeling micro-end-milling operations. Part I: Analytical cutting force model. International Journal of Machine Tools and Manufacture. Int. J. Mach. Tools Manuf. 2000, 40, 2155–2173. [Google Scholar] [CrossRef]
- Zhang, X.; Ehmann, K.F.; Yu, T.; Wang, W. Cutting forces in micro-end-milling processes. Int. J. Mach. Tools Manuf. 2016, 107, 21–40. [Google Scholar] [CrossRef]
- Sahoo, P.; Patra, K. Mechanistic modeling of cutting forces in micro-end-milling considering tool run out, minimum chip thickness and tooth overlapping effects. Mach. Sci. Technol. 2018, 23, 407–430. [Google Scholar] [CrossRef]
- Jing, X.; Tian, Y.; Yuan, Y.; Wang, F. A runout measuring method using modeling and simulation cutting force in micro end-milling. Int. J. Adv. Manuf. Technol. 2017, 91, 4191–4201. [Google Scholar] [CrossRef]
- Li, G.; Li, S.; Zhu, K. Micro-milling force modeling with tool wear and runout effect by spatial analytic geometry. Int. J. Adv. Manuf. Technol. 2020, 107, 631–643. [Google Scholar] [CrossRef]
- Afazov, S.M.; Ratchev, S.M.; Segal, J. Modelling and simulation of micro-milling cutting forces. J. Mater. Processing Technol. 2010, 210, 2154–2162. [Google Scholar] [CrossRef]
- Rodríguez, P.; Labarga, J.E. A new model for the prediction of cutting forces in micro-end-milling operations. J. Mater. Processing Technol. 2013, 213, 261–268. [Google Scholar] [CrossRef]
- Li, K.; Zhu, K.; Mei, T. A generic IUCT model for the cutting force modeling in micromilling. Int. J. Mach. Tools Manuf. 2016, 105, 23–31. [Google Scholar] [CrossRef]
- Liu, K.; Melkote, S.N. Finite element analysis of the influence of tool edge radius on size effect in orthogonal micro-cutting process. Int. J. Mech. Sci. 2007, 49, 650–660. [Google Scholar] [CrossRef]
- Varghese, A.; Kulkarni, V.; Joshi, S.S. Modeling cutting edge degradation by chipping in micro-milling. Wear 2022, 488–489, 204141. [Google Scholar] [CrossRef]
- Lucca, D.A.; Rhorer, R.L.; Komanduri, R. Energy Dissipation in the Ultraprecision Machining of Copper. CIRP Ann. 1991, 40, 69–72. [Google Scholar] [CrossRef]
- Lai, X.; Li, H.; Li, C.; Lin, Z.; Ni, J. Modelling and analysis of micro scale milling considering size effect, micro cutter edge radius and minimum chip thickness. Int. J. Mach. Tools Manuf. 2008, 48, 1–14. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, T.; Li, P.; Wang, S.; To, S.; Wang, H. Analytical modelling of the trans-scale cutting forces in diamond cutting of polycrystalline metals considering material microstructure and size effect. Int. J. Mech. Sci. 2021, 204, 106575. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, W.; Huang, D.; Wang, W. Cutting force modeling and experimental validation for micro end milling. Int. J. Adv. Manuf. Technol. 2021, 117, 933–947. [Google Scholar] [CrossRef]
- Malekian, M.; Park, S.S.; Jun, M.B.G. Modeling of dynamic micro-milling cutting forces. Int. J. Mach. Tools Manuf. 2009, 49, 586–598. [Google Scholar] [CrossRef]
- Chen, W.; Teng, X.; Huo, D.; Wang, Q. An improved cutting force model for micro milling considering machining dynamics. Int. J. Adv. Manuf. Technol. 2017, 93, 3005–3016. [Google Scholar] [CrossRef] [Green Version]
- Afazov, S.M.; Ratchev, S.M.; Segal, J.; Popov, A.A. Chatter modelling in micro-milling by considering process nonlinearities. Int. J. Mach. Tools Manuf. 2012, 56, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Jin, X.; Cao, H. Chatter stability analysis in Micro-milling with aerostatic spindle considering speed effect. Mech. Syst. Signal Processing 2022, 169, 108620. [Google Scholar] [CrossRef]
- Cao, Z.; Li, H. Investigation of machining stability in micro milling considering the parameter uncertainty. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Mascardelli, B.A.; Park, S.S.; Freiheit, T. Substructure Coupling of Micro End Mills. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, IMECE2006, Chicago, IL, USA, 5–10 November 2006. [Google Scholar]
- Kanh, M. Modeling of Cutting Forces in Micro Milling Including Run-Out. Master’s Thesis, Bilkent University, Ankara, Turkey, 2014. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Niu, Z.; Jiao, F.; Cheng, K. An innovative investigation on chip formation mechanisms in micro-milling using natural diamond and tungsten carbide tools. J. Manuf. Processes 2018, 31, 382–394. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, T.; Wang, W. Chatter stability of micro end milling by considering process nonlinearities and process damping. Int. J. Adv. Manuf. Technol. 2016, 87, 2785–2796. [Google Scholar] [CrossRef]





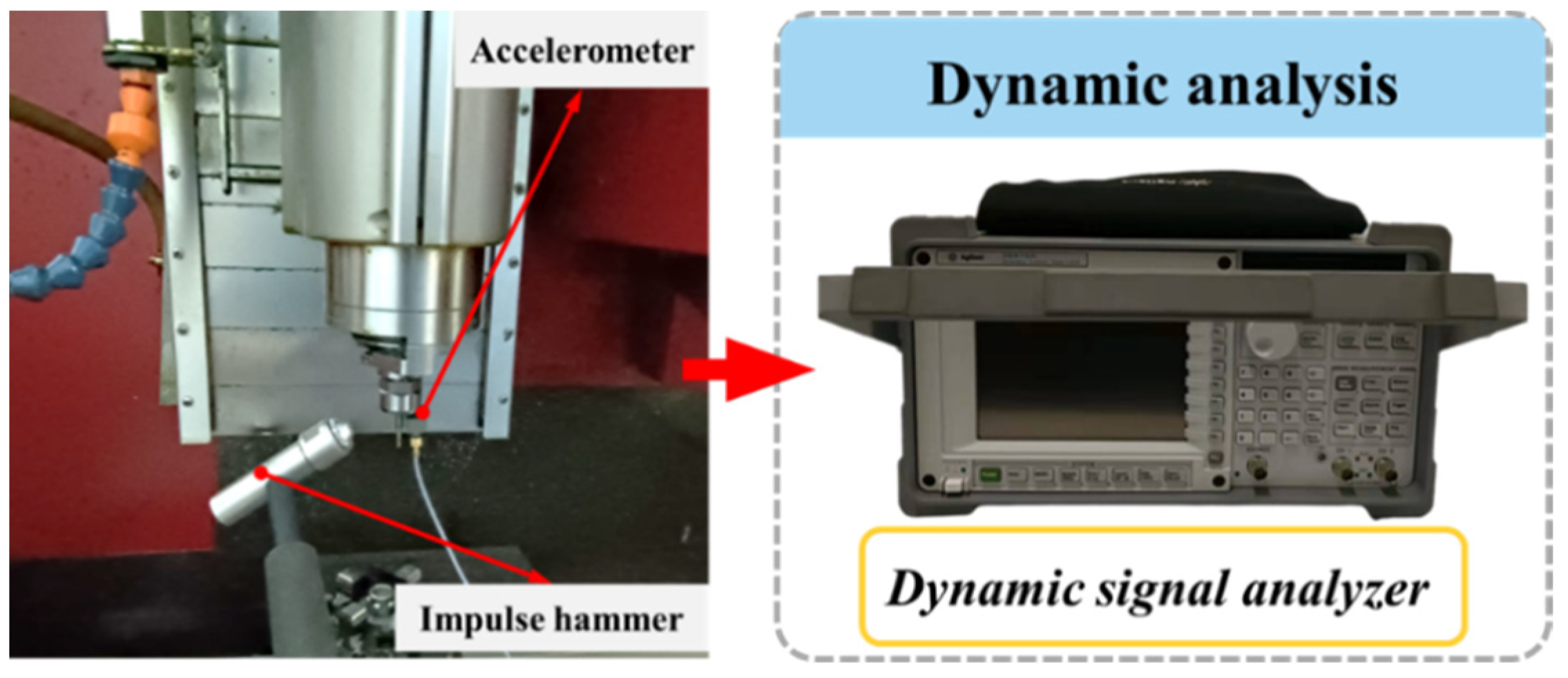

| Cutter 1 | Cutter 2 | |
|---|---|---|
| Material | Carbide | Carbide |
| Helix angle | 45° | 45° |
| Edge diameter | 1 mm | 0.6 mm |
| Tool length | 20.5 mm | 20.5 mm |
| Edge radius | 1.9 μm | 2.0 μm |
| Teeth number | 4 | 2 |
| n (r/mim) | ae (μm) | ap (μm) | fz (μm/Tooth) |
|---|---|---|---|
| 10,000 | 1000 | 50 | 5 |
| 25,000 | 600 | 20 | 5 |
| Direction | ωn (Hz) | K (N/μm) | M (Kg) | c (%) |
|---|---|---|---|---|
| xt | 2500 | 5 | 0.15 | 0.8 |
| yt | 2500 | 5 | 0.15 | 1.1 |
| xw | 1500 | 21 | 0.2 | 1 |
| yw | 4300 | 140 | 0.2 | 0.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Bai, Q.; Cheng, K.; Zhao, L.; Ding, H. The Modelling and Analysis of Micro-Milling Forces for Fabricating Thin-Walled Micro-Parts Considering Machining Dynamics. Machines 2022, 10, 217. https://doi.org/10.3390/machines10030217
Wang P, Bai Q, Cheng K, Zhao L, Ding H. The Modelling and Analysis of Micro-Milling Forces for Fabricating Thin-Walled Micro-Parts Considering Machining Dynamics. Machines. 2022; 10(3):217. https://doi.org/10.3390/machines10030217
Chicago/Turabian StyleWang, Peng, Qingshun Bai, Kai Cheng, Liang Zhao, and Hui Ding. 2022. "The Modelling and Analysis of Micro-Milling Forces for Fabricating Thin-Walled Micro-Parts Considering Machining Dynamics" Machines 10, no. 3: 217. https://doi.org/10.3390/machines10030217
APA StyleWang, P., Bai, Q., Cheng, K., Zhao, L., & Ding, H. (2022). The Modelling and Analysis of Micro-Milling Forces for Fabricating Thin-Walled Micro-Parts Considering Machining Dynamics. Machines, 10(3), 217. https://doi.org/10.3390/machines10030217








