Discussion on Ball Screw Slide–Roll Ratio and Entrainment Velocity Calculation
Abstract
:1. Introduction
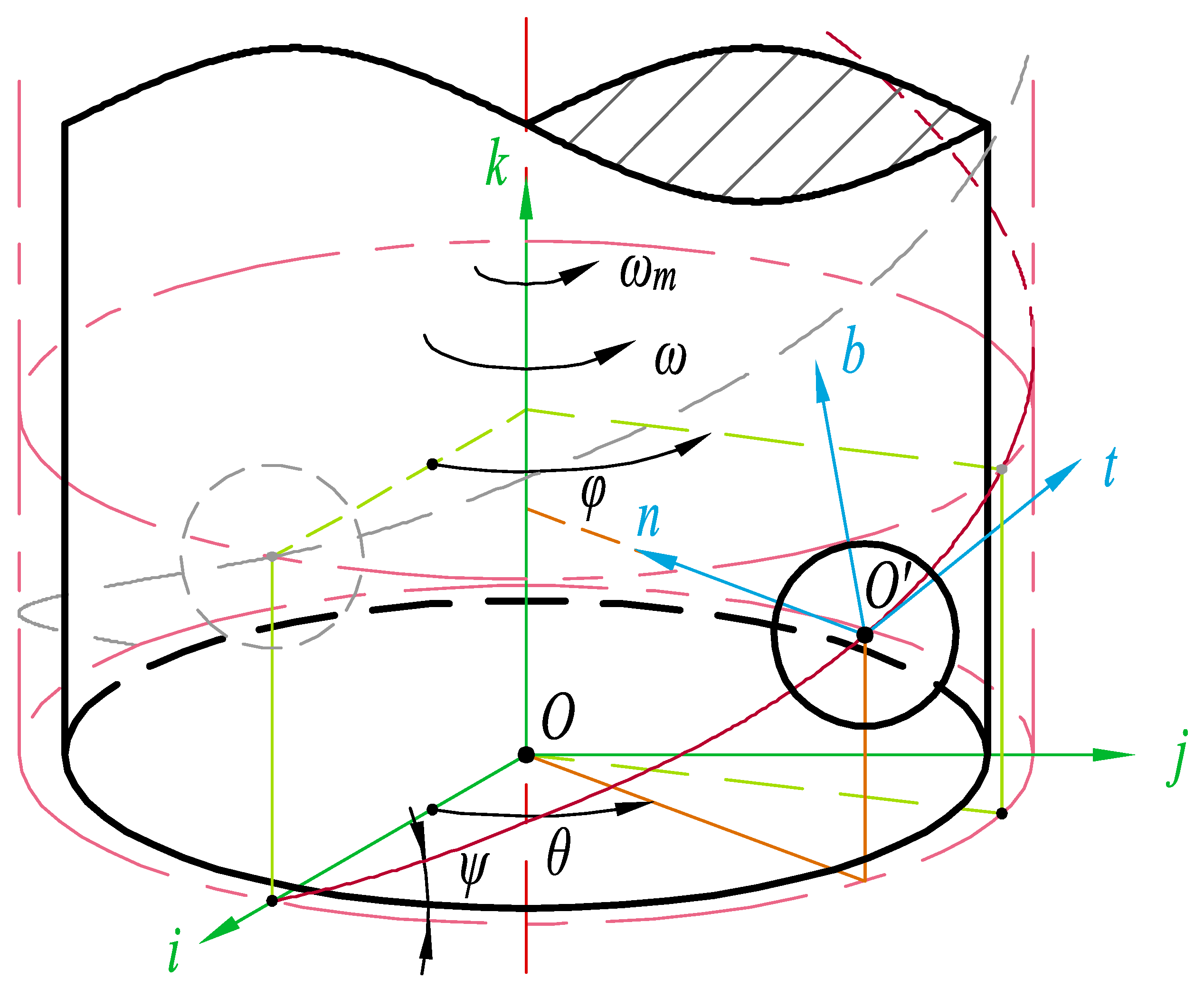
2. Theoretical Analysis
2.1. Slide–Roll Ratio and Entrainment Velocity
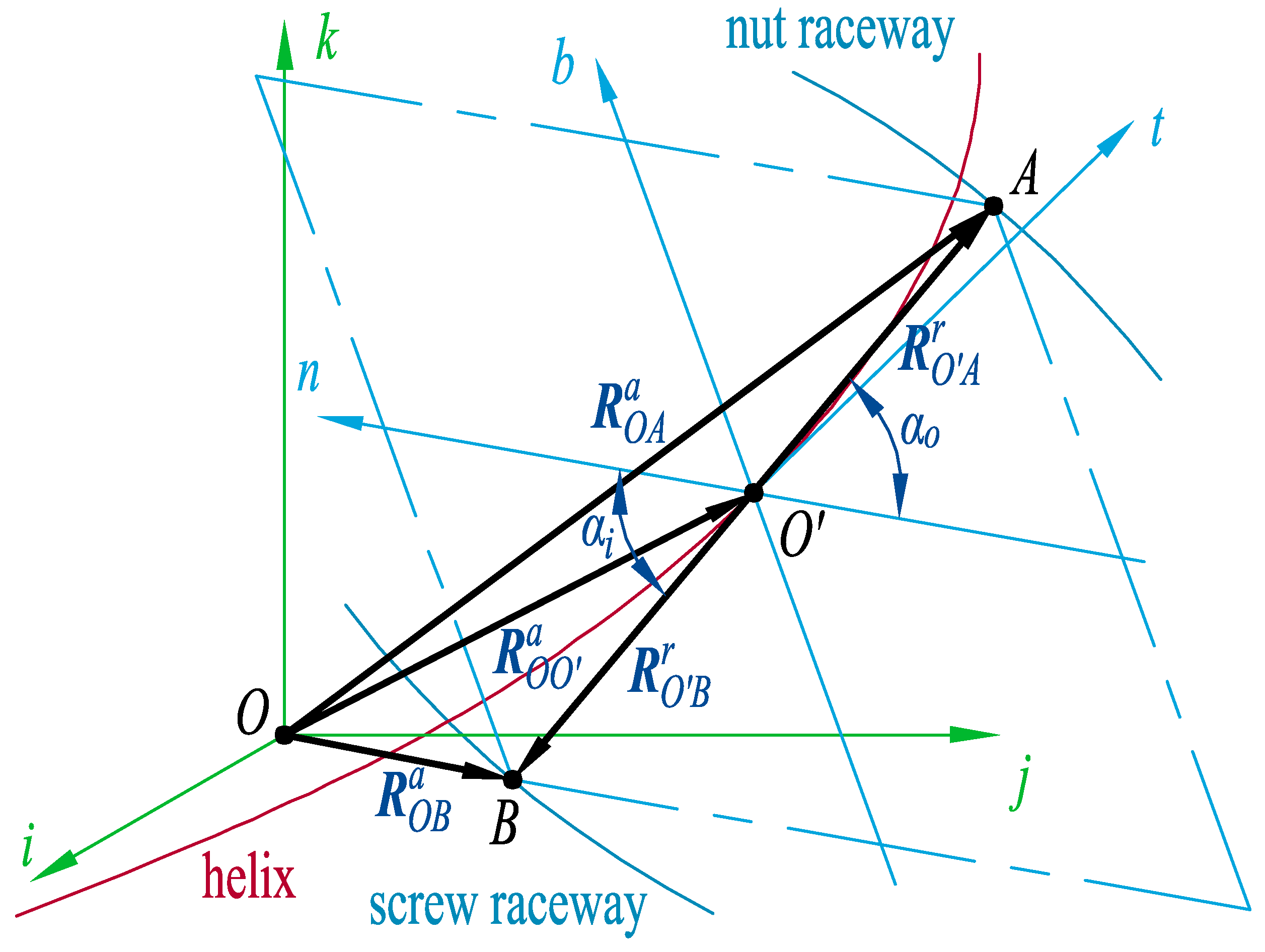
2.2. Position of Contact Points
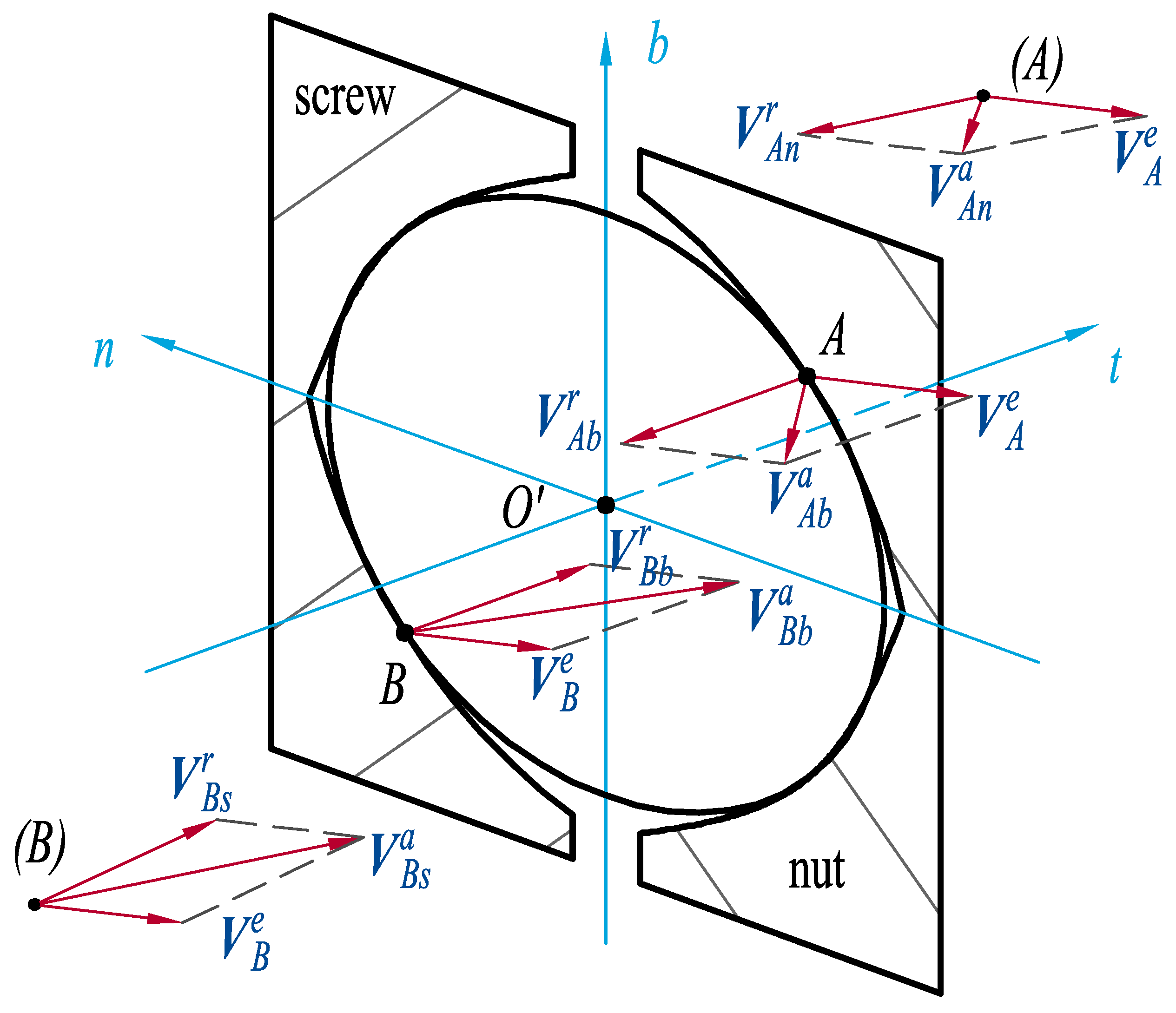
2.3. Absolute Velocity
2.4. Relative Velocity
3. Results and Discussion
3.1. Verification Based on a Ball Bearing
3.2. BSM-Based Discussion
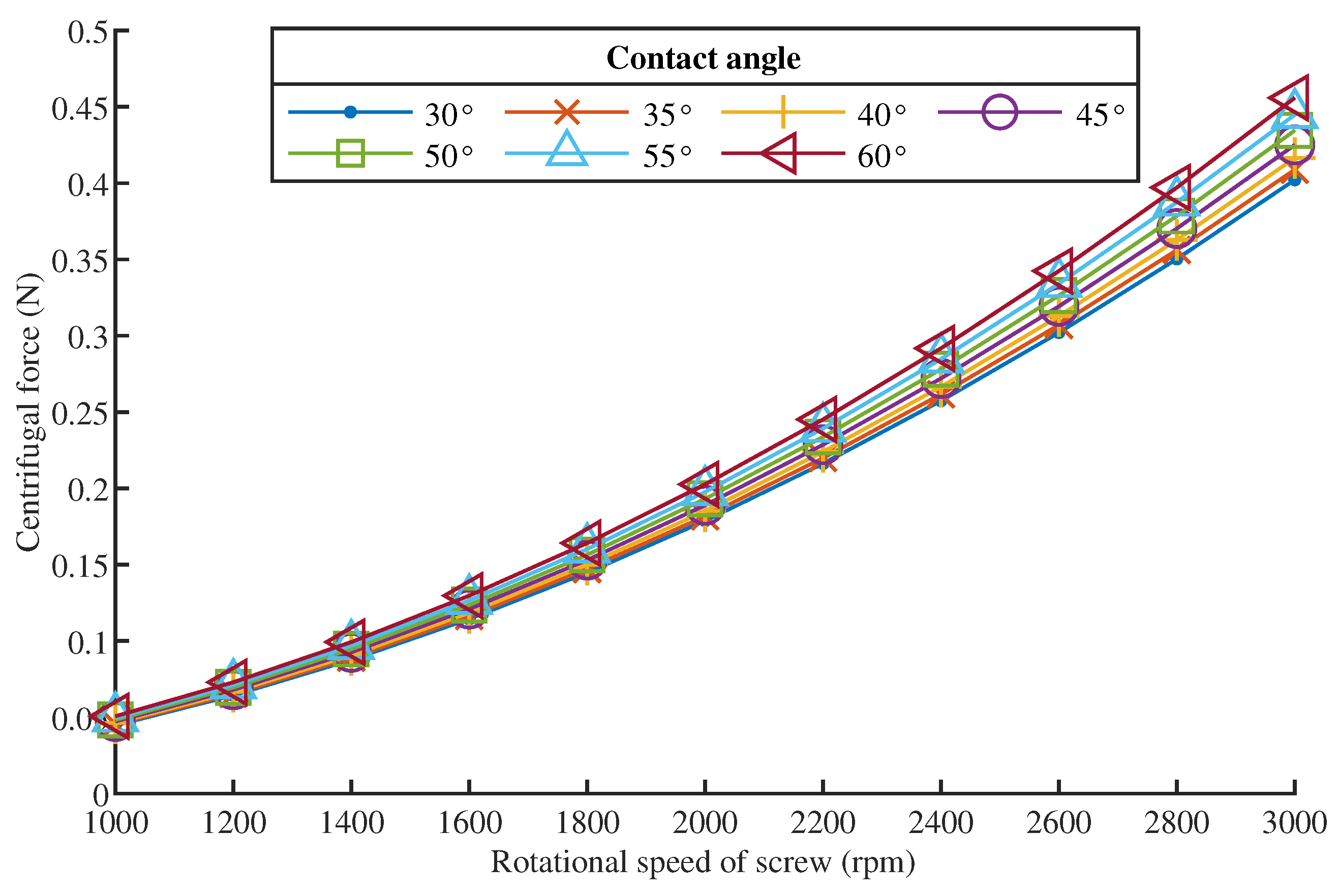
3.3. Centrifugal Force
3.4. Slide–Roll Ratio and Entrainment Velocity
3.4.1. Effect of Screw Rotational Speed
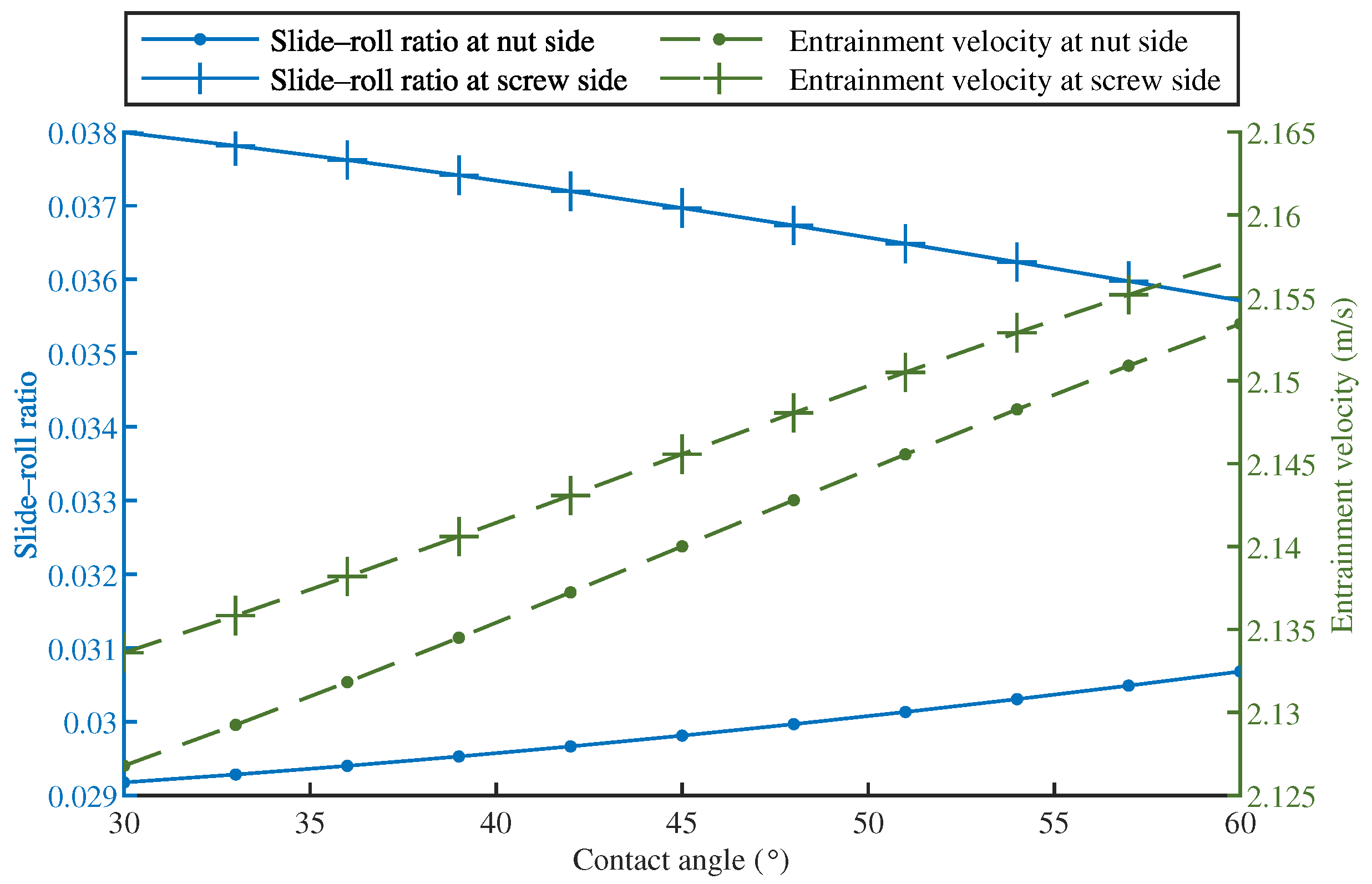
3.4.2. Effect of Contact Angle
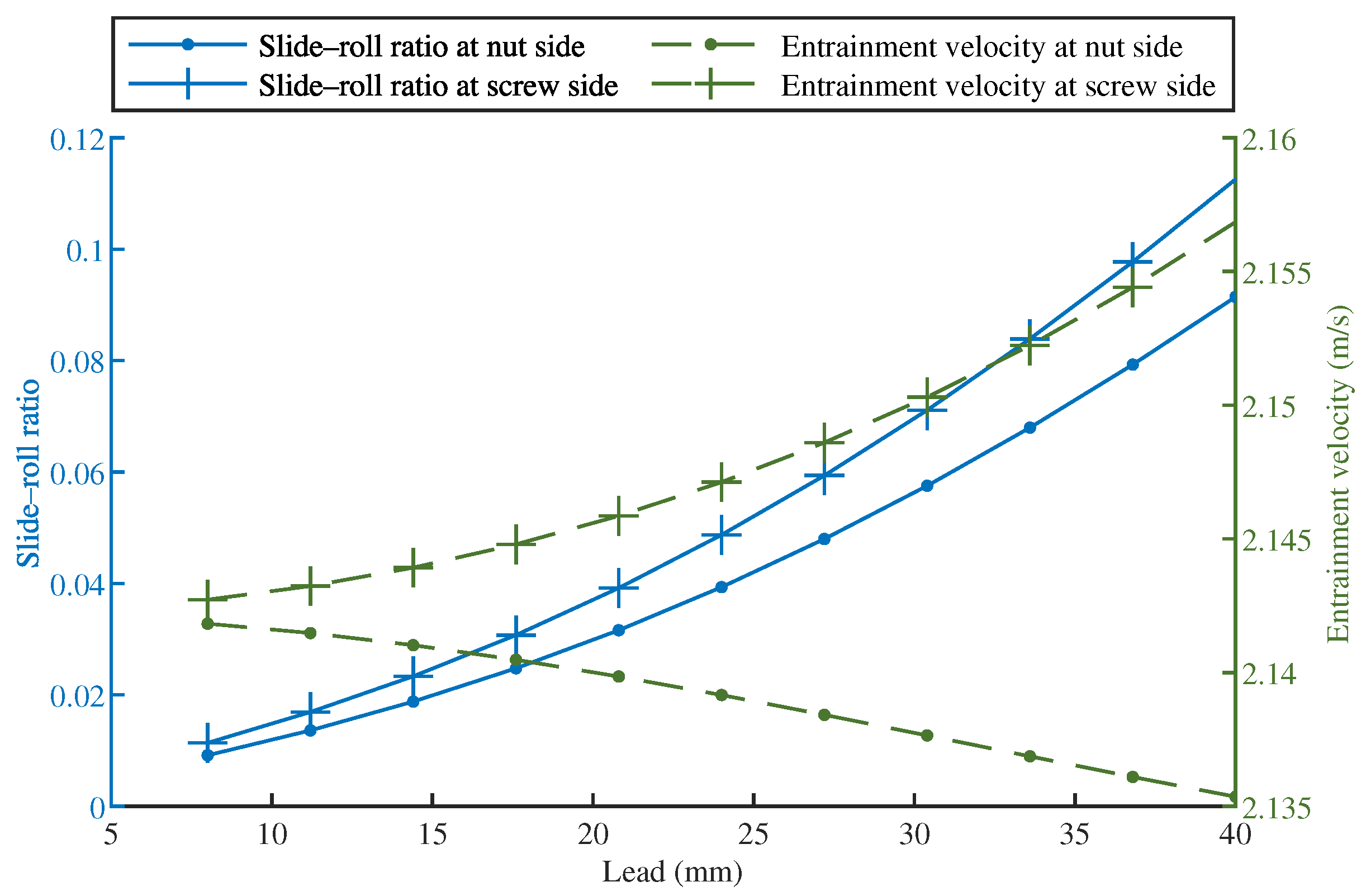
3.4.3. Effect of Lead Length
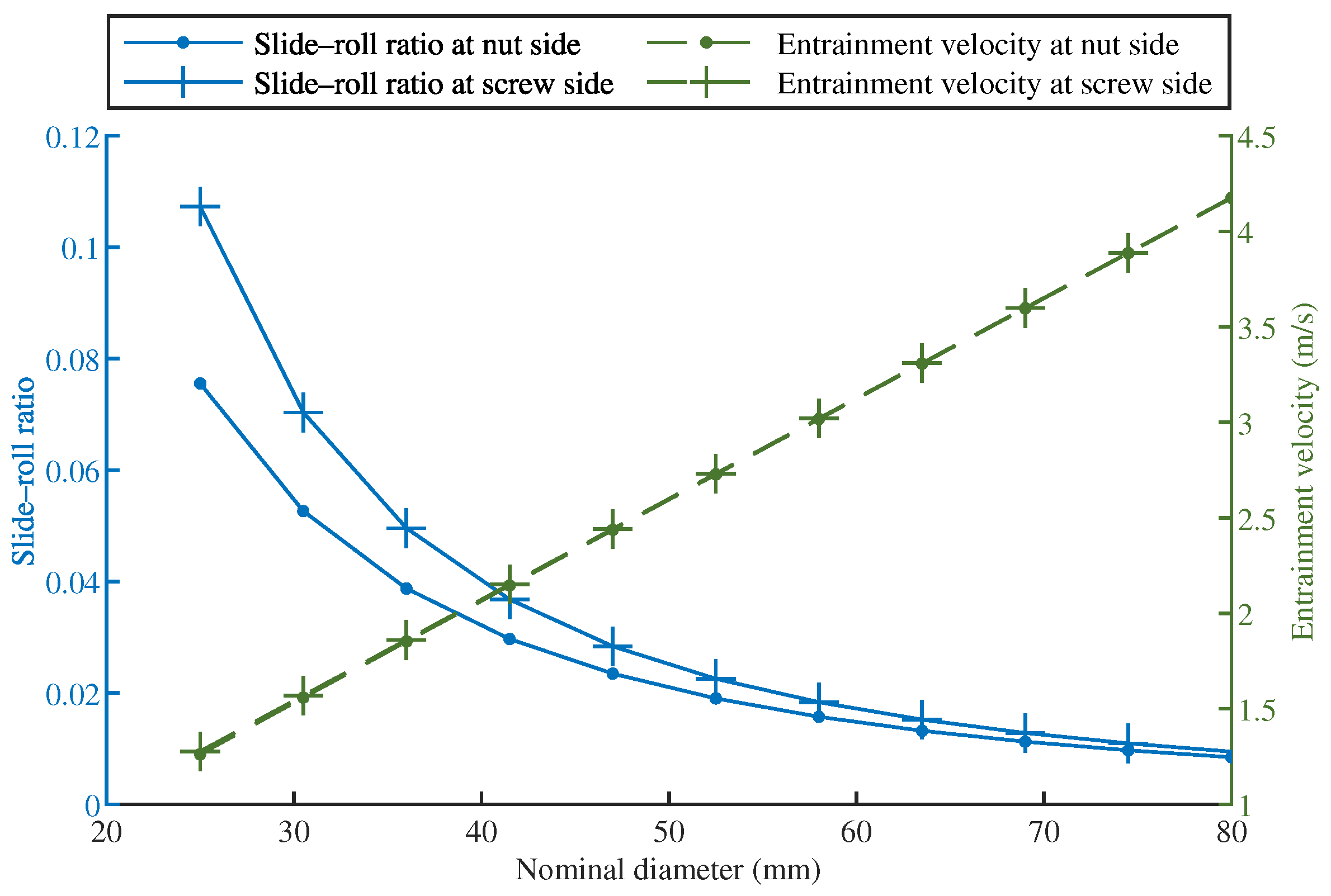
3.4.4. Effect of Nominal Diameter
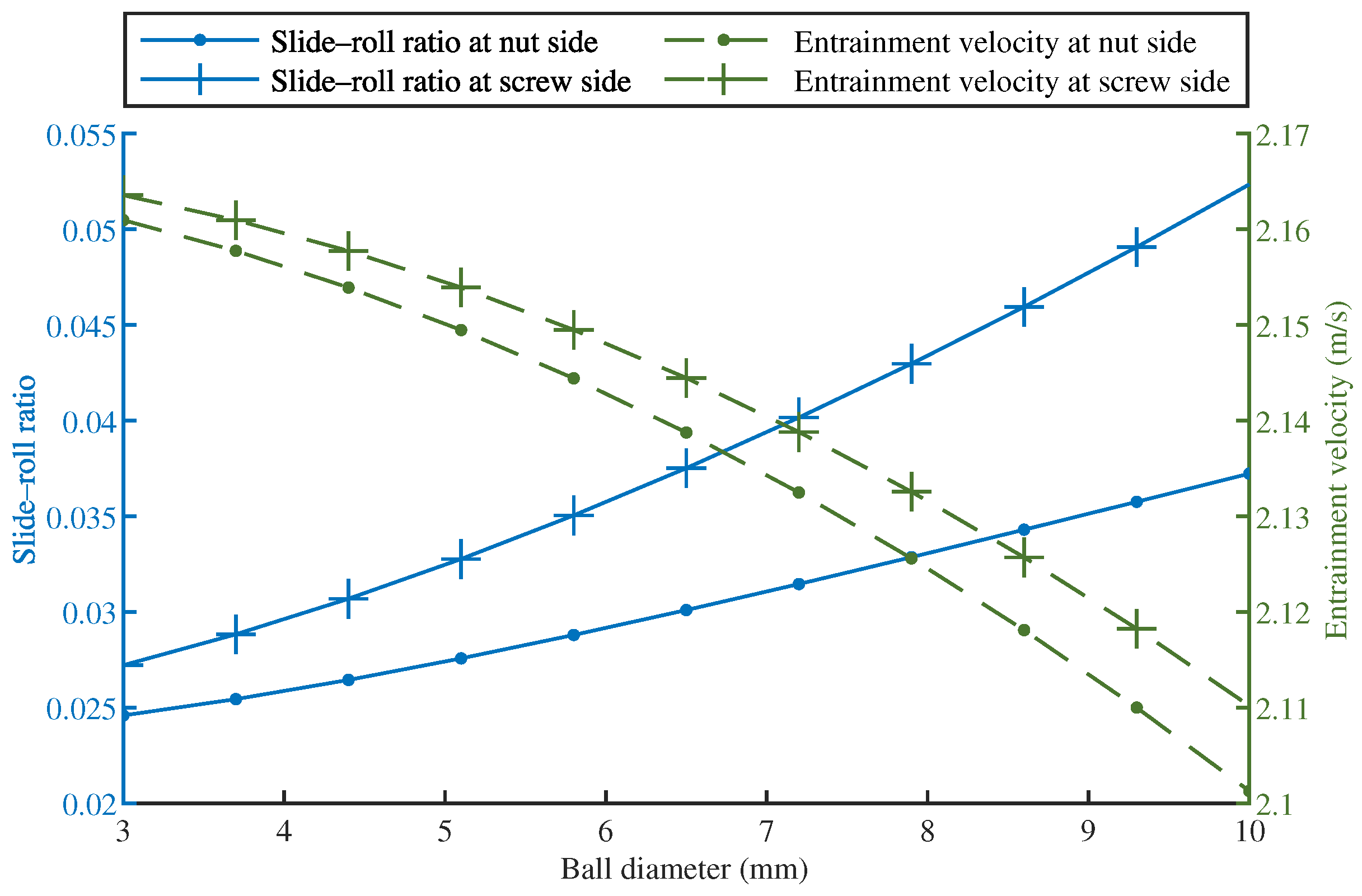
3.4.5. Effect of Ball Diameter
4. Conclusions
- The ball’s centrifugal force was negligible in comparison with the contact load. Centrifugal force had a minor influence on medium-to high-speed operating or small BSMs;
- The variation of the contact angle had a negligible influence on the centrifugal force and a minor effect on the slide–roll ratio and entrainment velocity. When determining the BSM’s kinematic characteristics, the contact angle at the inner and outer sides can be considered to be equal to the nominal contact angle;
- The slide–roll ratio and entrainment velocity were close on the inner and outer sides. The slide–roll ratio was usually slightly higher on the screw side than on the nut side, as was the entrainment velocity;
- The helix angle had the greatest impact on the sliding behavior at the contact points. When either the lead increases or the nominal diameter decreases, the helix angle will be increased, resulting in a significant increase in the slide–roll ratio;
- The entrainment velocity rose linearly with the screw rotation speed and nominal diameter, while all other construction parameters had a negligible influence. Lubrication can be enhanced and sliding decreased in high-speed BSMs with a long lead by increasing the nominal diameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CS | global coordinate system fixed to the base |
| CS | Frenet coordinate system moved to the ball center |
| centrifugal force of the ball | |
| L | lead of the ball screw |
| m | ball’s mass |
| N | number of loaded balls |
| absolute coordinates of the nut contact point | |
| absolute coordinates of the screw contact point | |
| absolute position of the ball center | |
| vector from the ball’s center to the nut contact point | |
| vector from the ball’s center to the screw contact point | |
| radius of the ball | |
| nominal radius of the ball screw | |
| slide–roll ratio at the nut contact point | |
| slide–roll ratio at the screw contact point | |
| coordinate transformation matrix from CS to CS | |
| coordinate transformation matrix from CS to CS when | |
| entrainment velocity at the nut contact point | |
| entrainment velocity at the screw contact point | |
| convected velocity at the nut contact point | |
| convected velocity at the screw contact point | |
| ball’s absolute linear velocities at the contact point with the nut | |
| ball’s relative linear velocities at the contact point with the nut | |
| ball’s absolute linear velocities at the contact point with the screw | |
| ball’s relative linear velocities at the contact point with the screw | |
| nut’s absolute linear velocities at the contact point | |
| nut’s relative linear velocities at the contact point | |
| nut’s absolute linear velocities at the contact point | |
| screw’s relative linear velocities at the contact point | |
| sliding velocity at the nut contact point | |
| sliding velocity at the screw contact point | |
| base vector of the global coordinate system CS | |
| base vector of the Frenet coordinate system CS | |
| nominal contact angle of the ball screw | |
| contact angle of ball–screw contact | |
| contact angle of ball–nut contact | |
| ball pitch angle relative to the Frenet frame | |
| ball yaw angle | |
| ratio of to | |
| rotating angular speed of the screw | |
| orbital angular speed of the ball | |
| rotation angular speed of the ball along its own axis | |
| vector of the ball’s rotation angular speed | |
| components of the ball’s angular speed along the t-, n-, and b-axis | |
| rotation angle of the screw | |
| helix angle of the ball screw | |
| azimuth angle of the ball | |
| Superscripts | |
| a | absolute velocity or coordinates |
| e | convected velocity |
| r | relative velocity or coordinates |
| Subscripts | |
| A | values of the contact point at the nut side |
| B | values of the contact point at the screw side |
| b | values of the ball (except for pointing along the b-axis) |
| n | values of the nut (except and for pointing along the n-axis) |
| s | values of the screw |
| contact between the ball and the nut/screw raceway | |
| Endings | |
| vectors expressed in the global coordinate system CS | |
| vectors expressed in the Frenet coordinate system CS |
Appendix A
| Parameter (Symbol) | Value | Unit |
|---|---|---|
| Helix angle () | deg | |
| Lead (L) | 20 | mm |
| Nominal diameter () | mm | |
| Ball’s diameter () | mm | |
| Ball’s mass (m) | g | |
| Number of loaded balls (N) | 52 | |
| Nominal contact angle () | 45 | deg |
| Screw’s rotational speed | 2000 | rpm |
References
- Wei, C.C.; Lin, J.F. Kinematic Analysis of the Ball Screw Mechanism Considering Variable Contact Angles and Elastic Deformations. J. Mech. Des. 2003, 125, 717–733. [Google Scholar] [CrossRef]
- Oyanguren, A.; Larrañaga, J.; Ulacia, I. Thermo-Mechanical Modelling of Ball Screw Preload Force Variation in Different Working Conditions. Int. J. Adv. Manuf. Technol. 2018, 97, 723–739. [Google Scholar] [CrossRef]
- Lin, M.C.; Ravani, B.; Velinsky, S.A. Kinematics of the Ball Screw Mechanism. J. Mech. Des. 1994, 116, 849–855. [Google Scholar] [CrossRef]
- Jiang, H.K. Research on Machining Method and Dynamic Performance of Steep-Lead Ball Screw Mechanism. Ph.D. Thesis, Shandong University, Jinan, China, 2007. [Google Scholar]
- Mu, S.G. Research on Dynamic Characteristics of High-speed Ball Screw with Nut Driven. Ph.D. Thesis, Shandong University, Jinan, China, 2013. [Google Scholar]
- Zhang, L.C.; Zhou, C.G. Experimental Study on the Coefficient of Friction of the Ball Screw. J. Tribol. 2022, 144, 031601. [Google Scholar] [CrossRef]
- Wei, C.C.; Lai, R.S. Kinematical Analyses and Transmission Efficiency of a Preloaded Ball Screw Operating at High Rotational Speeds. Mech. Mach. Theory 2011, 46, 880–898. [Google Scholar] [CrossRef]
- Hu, J.; Wang, M.; Zan, T. The Kinematics of Ball-Screw Mechanisms via the Slide–Roll Ratio. Mech. Mach. Theory 2014, 79, 158–172. [Google Scholar] [CrossRef]
- Mei, X.; Tsutsumi, M.; Tao, T.; Sun, N. Study on the Load Distribution of Ball Screws with Errors. Mech. Mach. Theory 2003, 38, 1257–1269. [Google Scholar] [CrossRef]
- Lin, B.; Okwudire, C.E.; Wou, J.S. Low Order Static Load Distribution Model for Ball Screw Mechanisms Including Effects of Lateral Deformation and Geometric Errors. J. Mech. Des. 2018, 140, 022301. [Google Scholar] [CrossRef]
- Zhen, N.; An, Q. Analysis of Stress and Fatigue Life of Ball Screw with Considering the Dimension Errors of Balls. Int. J. Mech. Sci. 2018, 137, 68–76. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, M.; Song, X.; Guo, Q. Investigation of Load Distribution and Deformations for Ball Screws with the Effects of Turning Torque and Geometric Errors. Mech. Mach. Theory 2019, 141, 95–116. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, C.; Meng, X.; Wen, B. Static Load Distribution Analysis of Ball Screws with Nut Position Variation. Mech. Mach. Theory 2020, 151, 103893. [Google Scholar] [CrossRef]
- Wei, C.C.; Lin, J.F.; Horng, J.H. Analysis of a Ball Screw with a Preload and Lubrication. Tribol. Int. 2009, 42, 1816–1831. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, L.; Jiang, H.K. Study on the Lubrication of the Precision Ball Screw Mechanism. J. Mech. Transm. 2015, 39, 22–26. [Google Scholar]
- Chaudhary, R.; Pandey, R.; Mazumdar, S. Tribological Studies of Low and High Viscous Oils Lubricated Heavily Loaded Textured Point Contacts under the Reciprocating Motion. Proc. Inst. Mech. Eng. Part J. J. Eng. Tribol. 2020, 234, 229–246. [Google Scholar] [CrossRef]
- Maldonado-Cortés, D.; Peña-Parás, L.; Leyva, C.L.; Guerrero, A.; Garza, A.; Quintanilla-Correa, D.; Coronado-Quintanilla, J.; González Aguirre, P. Improvement of Tribological Properties through the Application of Laser Surface Texturing and Nanolubricants in CNC Equipment Elements. Tribol. Ind. 2020, 42, 159–164. [Google Scholar] [CrossRef]
- Harris, T.A. An Analytical Method to Predict Skidding in Thrust-Loaded, Angular-Contact Ball Bearings. J. Lubr. Technol. 1971, 93, 17–23. [Google Scholar] [CrossRef]
- Harris, T.A. Ball Motion in Thrust-Loaded, Angular Contact Bearings With Coulomb Friction. J. Lubr. Technol. 1971, 93, 32–38. [Google Scholar] [CrossRef]
- Harris, T.A.; Kotzalas, M.N. Rolling Bearing Analysis-2 Volume Set; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar] [CrossRef]
- Meng, F.; Zheng, Y.; Liu, Y.; Gong, J.; Wang, B. Multi-Ellipsoid Contact Elastohydrodynamic Lubrication Performance for Deep Groove Ball Bearing. Tribol. Int. 2020, 150, 106367. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts: Part III—Fully Flooded Results. J. Lubr. Technol. 1977, 99, 264–275. [Google Scholar] [CrossRef]
- Dowson, D.; Taylor, C.M.; Xu, H. Elastohydrodynamic Lubrication of Elliptical Contacts with Spin and Rolling. Proc. Inst. Mech. Eng. Part C Mech. Eng. Sci. 1991, 205, 165–174. [Google Scholar] [CrossRef]
- Zhu, D. Elastohydrodynamic Lubrication in Extended Parameter Ranges—Part I: Speed Effect. Tribol. Trans. 2002, 45, 540–548. [Google Scholar] [CrossRef]
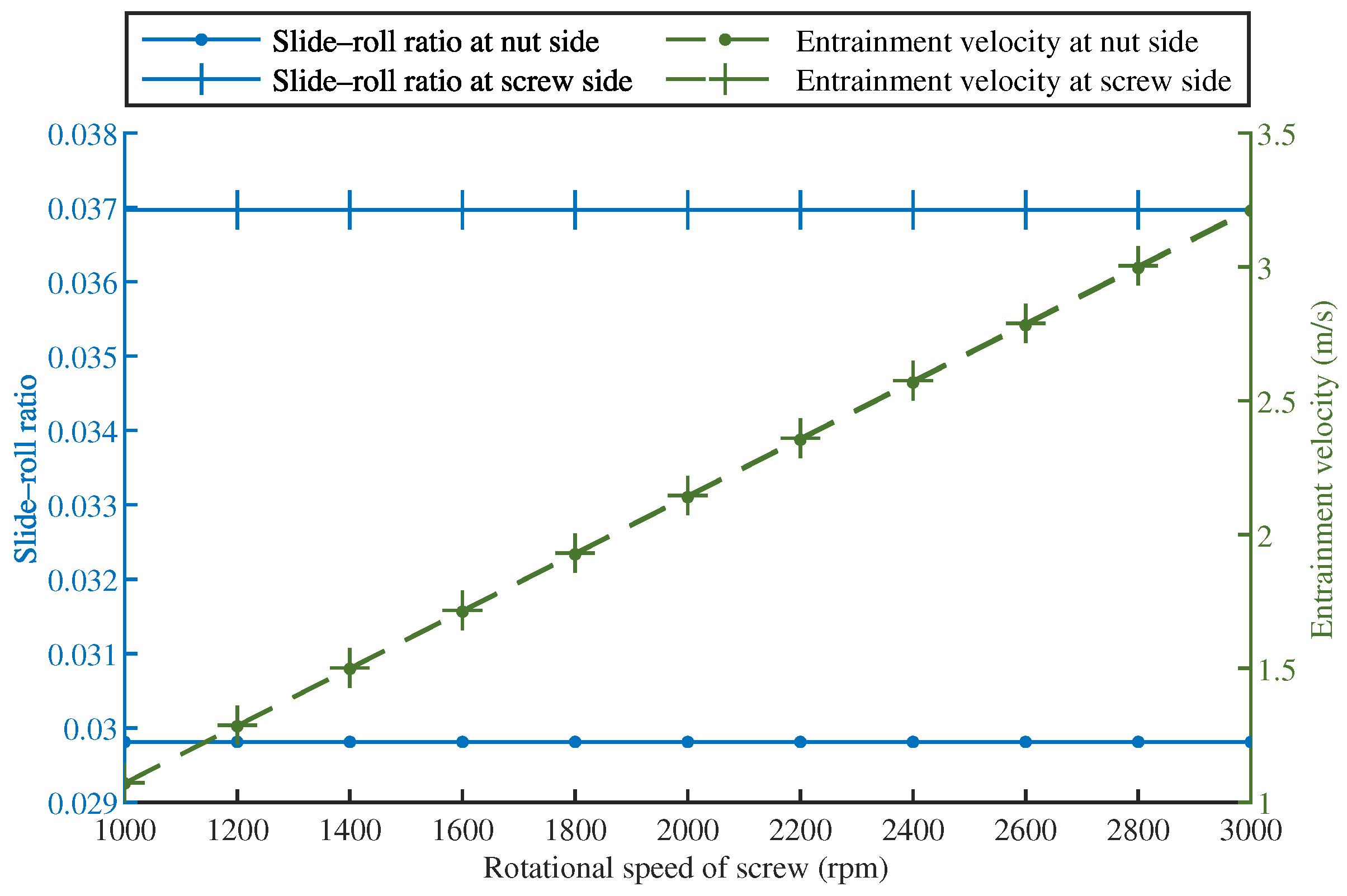
| Item (Unit) | Present Model | Wei’s Model | Harris Method |
|---|---|---|---|
| (m/s) | 15.994 | 7.971 | 15.994 |
| (m/s) | 15.994 | 22.740 | 15.994 |
| 0.000 | 2.000 | 0.000 | |
| 0.000 | 0.701 | 0.000 |
| Item (Unit) | Present Model | Wei’s Model |
|---|---|---|
| (m/s) | ||
| (m/s) | ||
| (m/s) | ||
| (m/s) | ||
| (m/s) | ||
| (m/s) | ||
| (m/s) | 2.140 | 1.071 |
| (m/s) | 2.146 | 2.937 |
| 0.030 | 1.766 | |
| 0.037 | 0.648 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Chen, S.; Lu, C.; Lv, L. Discussion on Ball Screw Slide–Roll Ratio and Entrainment Velocity Calculation. Machines 2022, 10, 203. https://doi.org/10.3390/machines10030203
Wang W, Chen S, Lu C, Lv L. Discussion on Ball Screw Slide–Roll Ratio and Entrainment Velocity Calculation. Machines. 2022; 10(3):203. https://doi.org/10.3390/machines10030203
Chicago/Turabian StyleWang, Weike, Shujiang Chen, Changhou Lu, and Lei Lv. 2022. "Discussion on Ball Screw Slide–Roll Ratio and Entrainment Velocity Calculation" Machines 10, no. 3: 203. https://doi.org/10.3390/machines10030203
APA StyleWang, W., Chen, S., Lu, C., & Lv, L. (2022). Discussion on Ball Screw Slide–Roll Ratio and Entrainment Velocity Calculation. Machines, 10(3), 203. https://doi.org/10.3390/machines10030203






