Multi-Objective Optimal Design and Development of a Four-Bar Mechanism for Weed Control
Abstract
1. Introduction
2. Literature Review
2.1. Four-Bar Mechanism
2.2. Four-Bar Mechanism for Weeding
3. Operational Requirements
- (1)
- The weeding blade of cultivator (the coupler point of four-bar mechanism) should be capable of tracking the path shown in Figure 1 while the cultivator is operating in the field.
- (2)
- (3)
- The proposed mechanism should have a reasonable size considering its in-field application.
4. Theoretical Framework
4.1. The Path Identification of Weeding Blade
4.2. Standard Mathematical Model for Multi-Objective Optimization
4.3. Objective Functions
4.4. The Constraints of Cultivator Design Problem
4.5. Four-Bar Mechanism Formulation
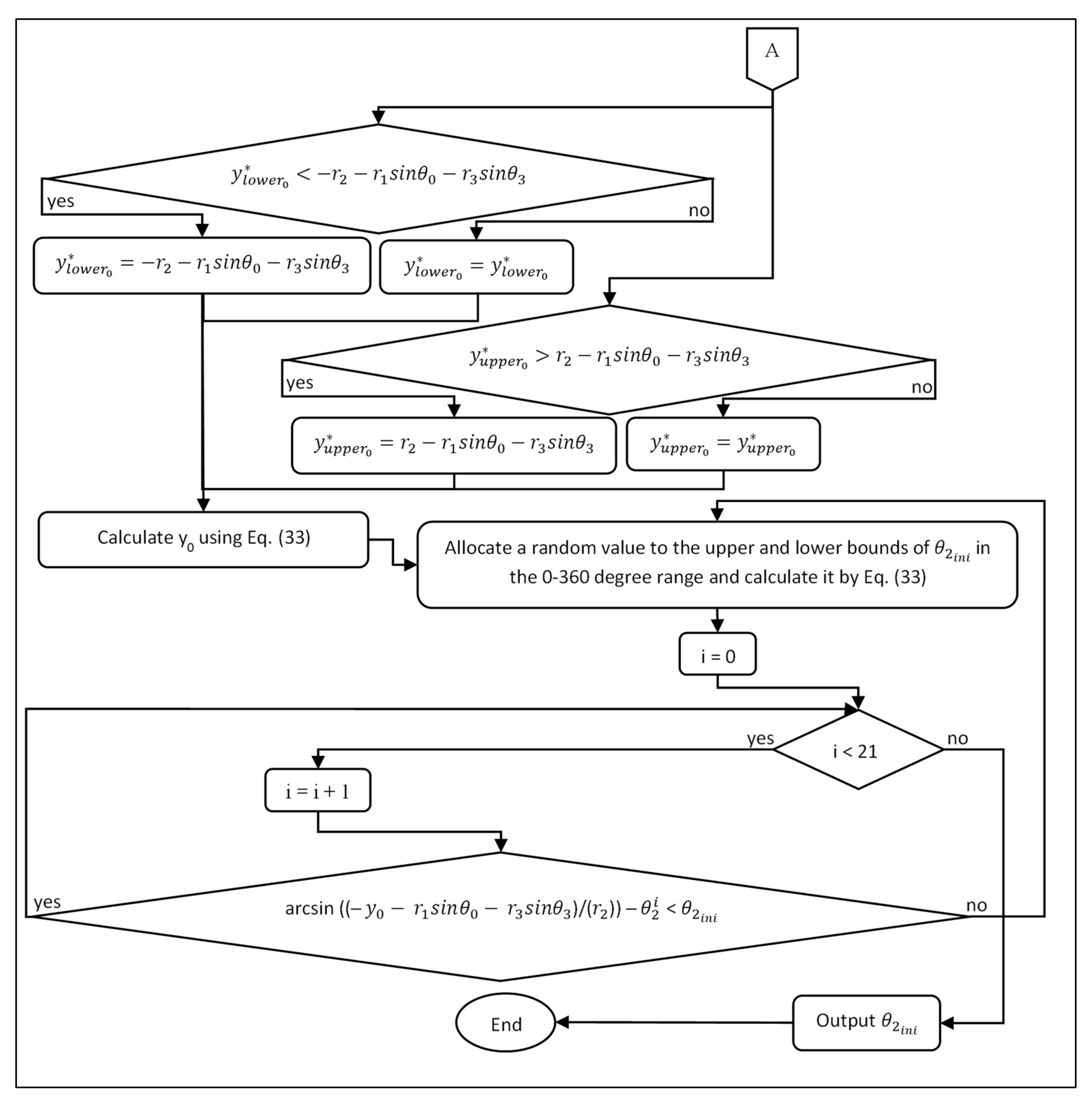
4.6. HGA-Based Optimal Design Process
4.6.1. Goal Attainment Method
- (1)
- The decision-maker defines the vector of ideal objective functions (b). Each component of this vector represents a utopian value associated with a counterpart objective function. During the optimization process, the goal is that any objective function approaches its corresponding utopian value.
- (2)
- The decision-maker also defines the vector of weights (w). Each component of this vector represents a value associated with a counterpart objective function. The value of each component is in proportion to the importance of the corresponding objective function.
- (3)
- The optimization process tries to minimize the scalar α in order to minimize the gap between the ideal objective functions and real objective functions.
4.6.2. Non-Dominated Sorting Genetic Algorithm (NSGA-II)
- (1)
- Randomly generate an initial population () of size N regarding the constraints governing the problem.
- (2)
- Evaluate the objective functions of each individual in .
- (3)
- Apply GA operators, such as selection, mutation and crossover, to produce the offspring population () of size N from .
- (4)
- Evaluate the objective functions of each individual in .
- (5)
- Combine and to produce of size 2N.
- (6)
- Classify the entire population of into different fronts based on non-dominated sorting method.
- (7)
- Form the new generation () of size N by individual from better fronts. Firstly, fill by the individuals of first front. Then, fill it by the individuals of second front, and so on. As there exist N slots in and, on the other hand, have 2N individuals, the extra fronts cannot transfer to new generation and must be eliminated. Regarding the last allowed front, calculate the crowding distance of each individual by Equation (30) [62] and transfer the individuals with highest values into the . The selection of individuals based on crowding distance keeps the diversity of new population.
- (8)
- Go to step 2 and repeat the procedure provided that the stopping criterion is not satisfied.
- (9)
- Stop and output the pareto solutions if the stopping criterion is satisfied.
4.6.3. The Hybrid of NSGA-II and Goal Attainment Method
4.7. QNM-Based Optimal Design Process
5. Experimental Study
5.1. Cultivation Depth
5.2. Weeding Performance
5.3. Mechanical Damage
6. Results and Discussion
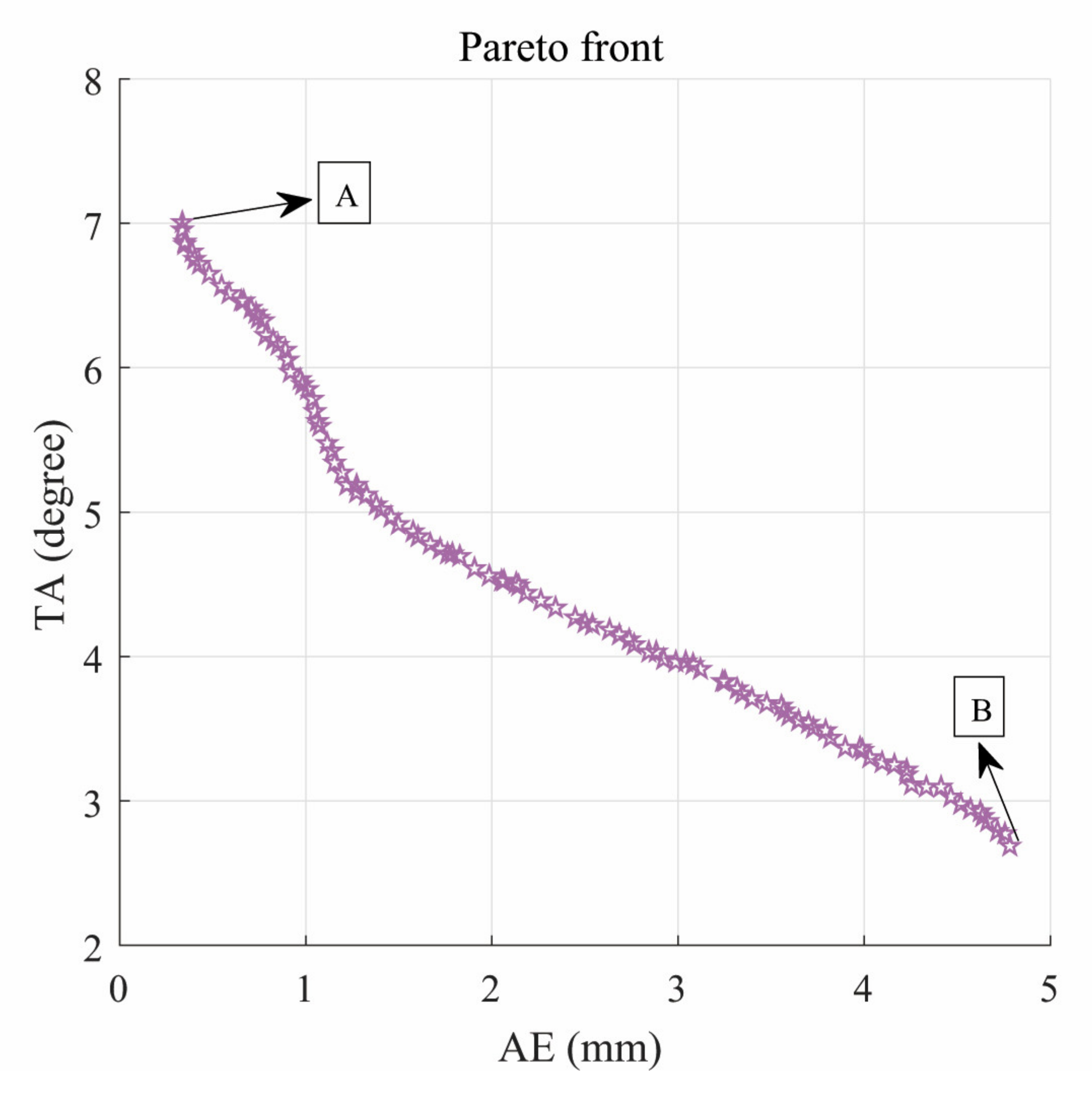
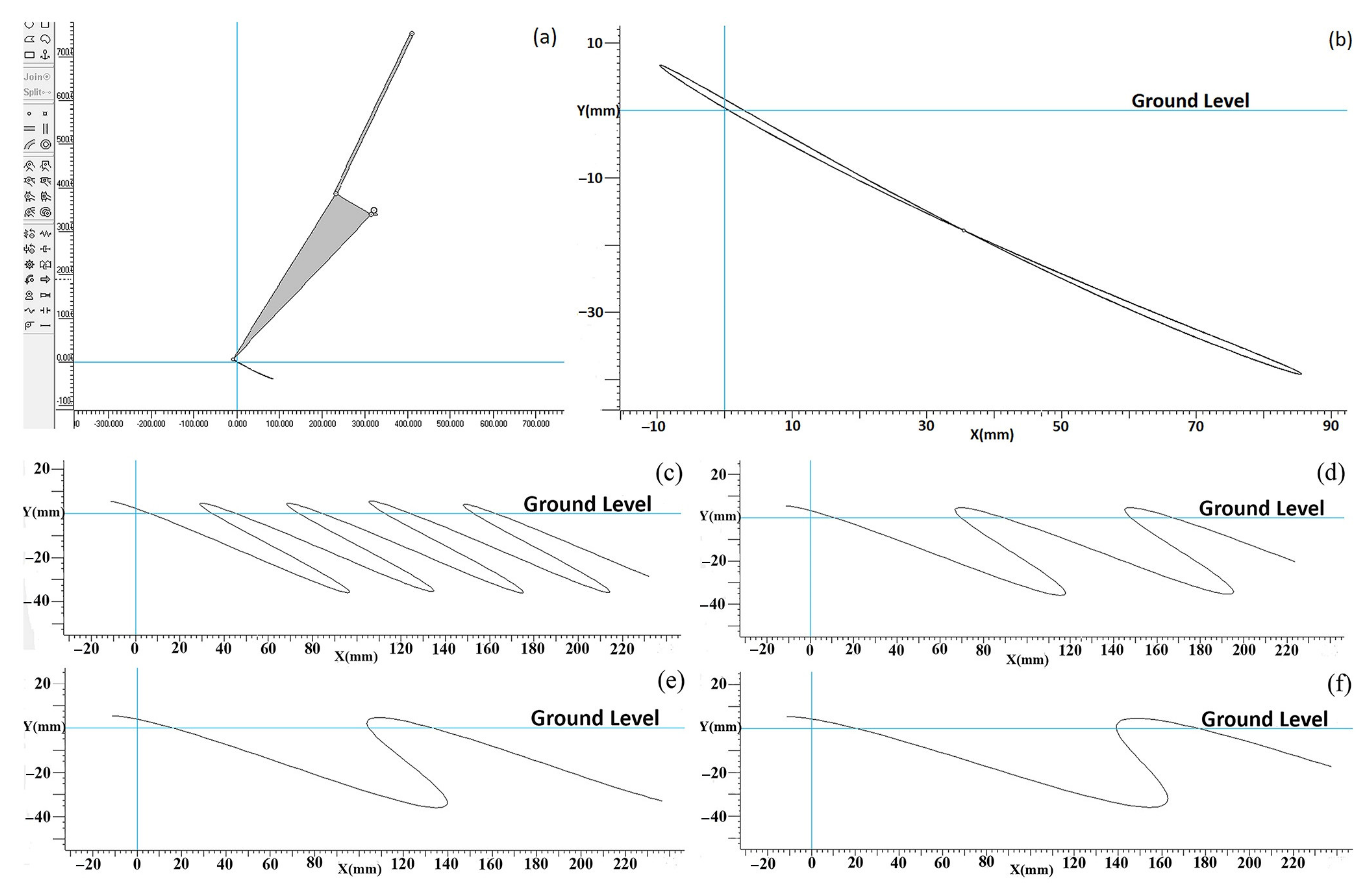
6.1. Generated Mechanisms and Paths
6.2. Average Tracking Error
6.3. Transmission Angle’s Deviation from Right Angle (TA)
6.4. The Effective Stroke of Weeding Blade
6.5. The Results of Dynamic Simulation
6.6. Experimental Results
7. Conclusions and Further Studies
- (1)
- The proposed methods synthesized an active tool powered by PTO, which avoids waste of energy through the drawbar of the tractor.
- (2)
- A predefined path, inspired by the hand motion of farmers during hand weeding, was introduced to the mechanism synthesis process so that the weeding blade tracked a targeted path and did not exceed the allowable depth (40 mm), which reduces the risk of mechanical damage to the crop roots.
- (3)
- The maximum closeness of penetration and return stroke of the blade, achieved through displacement and velocity vector analysis, tries to maximize weeding efficiency. On the contrary, conventional cultivators indiscriminately plough the soil, which can lead to a large amount of soil disturbance.
- (4)
- Unlike the analytical–graphical approaches formerly used to synthesize four-bar mechanisms for weeding, the proposed methods in this study overcame the limited-precision-point problem, which leads to synthesizing a four-bar mechanism whose blade is capable of tracking a more precise path through the soil.
- (5)
- Compared with the transmission angle’s deviation of the mechanisms developed based on analytical–graphical approaches in Refs. [14,25], that of the proposed mechanism has decreased by 85.2% and 88.9%, respectively. The decrease in the value of the transmission angle’s deviation from a right angle (90 degrees) is an indicator of smooth rotations in the joints of a four-bar mechanism and then good torque and energy transmission.
- (6)
- Compared with the effective stroke of the mechanisms developed based on analytical–graphical approaches in Refs. [14,25], that of the proposed mechanism has increased by 113% and 300%, respectively. The effective stroke of the weeding blade is an indicator of the interaction time between the weeding blade and soil during a weeding cycle.
- (7)
- In terms of weeding performance and mechanical damage to crop plants, the proposed mechanism is more effective than conventional tools and four-bar cultivators developed based on classic methods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. BFGS Algorithm with FLS
References
- Bohne, B.; Hensel, O. Application of thermoplastics to increase efficiency during thermal weed control. Landtechnik 2012, 67, 441–444. [Google Scholar] [CrossRef]
- Mohidem, N.A.; Che’Ya, N.N.; Juraimi, A.S.; Ilahi, W.F.F.; Roslim, M.H.M.; Sulaiman, N.; Saberioon, M.; Noor, N.M. How can unmanned aerial vehicles be used for detecting weeds in agricultural fields? Agriculture 2021, 11, 1004. [Google Scholar] [CrossRef]
- Chang, C.; Xie, B.; Chung, S. Mechanical control with a deep learning method for precise weeding on a farm. Agriculture 2021, 11, 1049. [Google Scholar] [CrossRef]
- Gharde, Y.; Singh, P.K.; Dubey, R.P.; Gupta, P.K. Assessment of yield and economic losses in agriculture due to weeds in India. Crop Prot. 2018, 107, 12–18. [Google Scholar] [CrossRef]
- Pannacci, E.; Tei, F.; Guiducci, M. Evaluation of mechanical weed control in legume crops. Crop Prot. 2018, 104, 52–59. [Google Scholar] [CrossRef]
- Tellaeche, A.; Pajares, G.; Burgos-Artizzu, X.P.; Ribeiro, A. A computer vision approach for weeds identification through support vector machines. Appl. Soft Comput. 2011, 11, 908–915. [Google Scholar] [CrossRef]
- Rob, M.M.; Hossen, K.; Khatun, M.R.; Iwasaki, K.; Iwasaki, A.; Suenaga, K.; Kato-Noguchi, H. Identification and Application of Bioactive Compounds from Garcinia xanthochymus Hook. for Weed Management. Appl. Sci. 2021, 11, 2264. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y. Soil disturbance and cutting forces of four different sweeps for mechanical weeding. Soil Tillage Res. 2017, 168, 167–175. [Google Scholar] [CrossRef]
- Le Bellec, F.; Velu, A.; Fournier, P.; Le Squin, S.; Michels, T.; Tendero, A.; Bockstaller, C. Helping farmers to reduce herbicide environmental impacts. Ecol. Indic. 2015, 54, 207–216. [Google Scholar] [CrossRef]
- Carrubba, A.; Militello, M. Nonchemical weeding of medicinal and aromatic plants. Agron. Sustain. Dev. 2013, 33, 551–561. [Google Scholar] [CrossRef]
- Melander, B.; Lattanzi, B.; Pannacci, E. Intelligent versus non-intelligent mechanical intra-row weed control in transplanted onion and cabbage. Crop Prot. 2015, 72, 1–8. [Google Scholar] [CrossRef]
- Nieuwenhuizen, A.T.; Tang, L.; Hofstee, J.W.; Muller, J.; van Henten, E.J. Colour based detection of volunteer potatoes as weeds in sugar beet fields using machine vision. Precis. Agric. 2007, 8, 267–278. [Google Scholar] [CrossRef][Green Version]
- Nieuwenhuizen, A.T.; Hofstee, J.W.; van Henten, E.J. Performance evaluation of an automated detection and control system for volunteer potatoes in sugar beet fields. Biosyst. Eng. 2010, 107, 46–53. [Google Scholar] [CrossRef]
- Hosseini, A.A.M.; Akhijahani, H.S.; Mehravar, H.; Massah, J. Design of a mechanism for a new cultivator (part 1: Path generation and dimensional synthesis). Agric. J. 2007, 9, 63–76, (In Persian, with English abstract). [Google Scholar]
- Nosrattia, I.; Sabeti, P.; Chaghamirzaee, G.; Heidari, H. Weed problems, challenges, and opportunities in Iran. Crop Prot. 2020, 134, 104371. [Google Scholar] [CrossRef]
- O’Dogherty, M.J.; Godwin, R.J.; Dedousis, A.P.; Brighton, J.L.; Tillett, N.D. A mathematical model of the kinematics of a rotating disc for inter- and intra-row hoeing. Biosyst. Eng. 2007, 96, 169–179. [Google Scholar] [CrossRef]
- Pullen, D.W.M.; Cowell, P.A. An Evaluation of the Performance of Mechanical Weeding Mechanisms for use in High Speed Inter-Row Weeding of Arable Crops. J. Agric. Eng. Res. 1997, 67, 27–34. [Google Scholar] [CrossRef]
- Sedara, A.M.; Sedara, O.S. A review on inter-row crops mechanical weeder. Turk. J. Agric. Eng. Res. 2020, 1, 200–221. [Google Scholar]
- Cloutier, D.C.; van der Weide, R.Y.; Peruzzi, A.; Leblanc, M.L. Mechanical Weed Management. In Non-Chemical Weed Management: Principles, Concepts and Technology; Upadhyaya, M.K., Blachshaw, R.E., Eds.; CAB International: Oxfordshire, UK, 2007; pp. 111–134. [Google Scholar]
- Van der Linden, S.; Mouazen, A.M.; Anthonis, J.; Ramon, H.; Saeys, W. Infrared laser sensor for depth measurement to improve depth control in intra-row mechanical weeding. Biosyst. Eng. 2008, 100, 309–320. [Google Scholar] [CrossRef]
- Bowman, G. Steel in the Field: A Farmer’s Guide to Weed Management Tools; Sustainable Agriculture Network: Beltsville, MD, USA, 2002. [Google Scholar]
- Mohler, C.L. Mechanical management of weeds. In Ecological Management of Agricultural Weeds, Liebman, M., Mohler, C.L., Staver, C.P., Eds.; Cambridge University Press: Cambridge, UK, 2004; pp. 139–209. [Google Scholar]
- Prasertkan, K.; Usaborisut, P. Power requirements of combination tillage tool operating on two different fields. In Proceedings of the 110th The IRES International Conference, Osaka, Japan, 27–28 April 2018; pp. 25–29. [Google Scholar]
- Rao, N.R.N.V.G.; Chaudhary, H.; Sharma, A.K. Design and development of vibratory cultivator using optimization algorithms. SN Appl. Sci. 2019, 1, 1287. [Google Scholar] [CrossRef]
- Kwon, T.H.; Ashtiani-Araghi, A.; Lee, C.; Kang, T.G.; Lee, B.; Rhee, J. Evaluation of a crank-type walking cultivator for upland farming. J. Biosyst. Eng. 2014, 39, 1–10. [Google Scholar] [CrossRef]
- Khorshidi, M.; Soheilypour, M.; Peyro, M.; Atai, A.; Shariat Panahi, M. Optimal design of four-bar mechanisms using a hybrid multi-objective GA with adaptive local search. Mech. Mach. Theory 2011, 46, 1453–1465. [Google Scholar] [CrossRef]
- Kim, J.W.; Seo, T.; Kim, J. A new design methodology for four-bar linkage mechanisms based on derivations of coupler curve. Mech. Mach. Theory 2016, 100, 138–154. [Google Scholar] [CrossRef]
- Thomas, E.V. Development of a mechanism for transplanting rice seedlings. Mech. Mach. Theory 2002, 37, 395–410. [Google Scholar] [CrossRef]
- Jiang, Y.; Bian, B.; Li, L. Integrated harvest and farm-to-door distribution scheduling with postharvest quality deterioration for vegetable online retailing. Agronomy 2019, 9, 724. [Google Scholar] [CrossRef]
- Jamal, A.; Linker, R. Genetic operator-based particle filter combined with markov chain monte carlo for data assimilation in a crop growth model. Agriculture 2020, 10, 606. [Google Scholar] [CrossRef]
- Hwang, S.; Park, J.; Lee, J.; Shim, S.; Nam, J. Optimization of main link lengths of transplanting device of semi-automatic vegetable transplanter. Agriculture 2020, 10, 1938. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, J.; Li, K.; Dai, L.; Chen, J. Optimal design and experiment of 2-DoF five-bar mechanism for flower seedling transplanting. Comput. Electron. Agric. 2020, 178, 105746. [Google Scholar] [CrossRef]
- Cabrera, J.A.; Simon, A.; Prado, M. Optimal synthesis of mechanisms with genetic algorithms. Mech. Mach. Theory 2002, 37, 1165–1177. [Google Scholar] [CrossRef]
- Calva-Yanez, M.B.; Nino-Suarez, P.A.; Portilla-Flores, E.A.; Aponte-Rodriguez, J.A.; Santiago-Valentin, E. Reconfigurable mechanical system design for tracking an ankle trajectory using an evolutionary optimization algorithm. IEEE Access 2017, 5, 5480–5493. [Google Scholar] [CrossRef]
- Lin, W.Y. A GA–DE hybrid evolutionary algorithm for path synthesis of four-bar linkage. Mech. Mach. Theory 2010, 45, 1096–1107. [Google Scholar] [CrossRef]
- Nariman-Zadeh, N.; Felezi, M.; Jamali, A.; Ganji, M. Pareto optimal synthesis of four-bar mechanisms for path generation. Mech. Mach. Theory 2009, 44, 180–191. [Google Scholar] [CrossRef]
- Chanekar, P.V.; Ghosal, A. Optimal synthesis of adjustable planar four-bar crank-rocker type mechanisms for approximate multi-path generation. Mech. Mach. Theory 2013, 69, 263–277. [Google Scholar] [CrossRef]
- Krishnamurty, S.; Turcic, D.A. Optimal synthesis of mechanisms using nonlinear goal programming techniques. Mech. Mach. Theory 1992, 27, 599–612. [Google Scholar] [CrossRef]
- Felezi, M.E.; Vahabi, S.; Nariman-zadeh, N. Pareto optimal design of reconfigurable rice seedling transplanting mechanisms using multi-objective genetic algorithm. Neural Comput. Appl. 2016, 27, 1907–1916. [Google Scholar] [CrossRef]
- Molari, G.; Mattetti, M.; Guarnieri, A. Optimal three-point hitch design to maximize lifting performance. Trans. ASABE 2014, 57, 371–379. [Google Scholar] [CrossRef]
- Rao, G.; Mall, N.K.; Chaudhary, H.; Kumar, A. Design of four bar mechanism for transplanting paddy seedlings. In Proceedings of the International Conference on Sustainable Computing in Science, Technology and Management (SUSCOM), Jaipur, India, 26–28 February 2019; pp. 330–335. [Google Scholar]
- Hettiaratchi, D.R.P. The development of a powered low draught tine cultivator. Soil Tillage Res. 1993, 28, 159–177. [Google Scholar] [CrossRef]
- Nokleby, S.B.; Podhorodeski, R.P. Optimization-based synthesis of a deep-digging tillage mechanism. Trans. CSME 2000, 24, 61–78. [Google Scholar] [CrossRef]
- Podhorodeski, R.P.; Fang, X. Optimization-based Grashof-mechanism synthesis via sub-type specific parameter transforms. In Proceedings of the ASME Design Engineering Technical Conference and Computers in Engineering Conference, Irvine, CA, USA, 18–22 August 1996. [Google Scholar]
- Rao, N.R.N.V.G.; Chaudhary, H.; Sharma, A. Design and analysis of vibratory mechanism for tillage application. Open Agric. 2018, 3, 437–443. [Google Scholar] [CrossRef]
- Rao, N.R.N.V.G.; Chaudhary, H.; Sharma, A.K. Optimal design and analysis of oscillatory mechanism for agricultural tillage operation. SN Appl. Sci. 2019, 1, 1003. [Google Scholar] [CrossRef]
- Akhijahani, H.S.; Arabhosseini, A.; Kianmehr, M.H. Effects of vehicle and rotational speeds on performance and mechanical damage of new a mechanical inter-row weeder. Middle-East J. Sci. Res. 2011, 7, 869–875. [Google Scholar]
- Nie, L.; Ding, H.; Gan, J. Dead center identification of single-DOF multi-loop planar manipulator and linkage based on graph theory and transmission angle. IEEE Access 2019, 7, 77161–77173. [Google Scholar] [CrossRef]
- Balli, S.S.; Chand, S. Transmission angle in mechanisms (Triangle in mech). Mech. Mach. Theory 2002, 37, 175–195. [Google Scholar] [CrossRef]
- Martin, P.J.; Russell, K.; Sodhi, R.S. On mechanism design optimization for motion generation. Mech. Mach. Theory 2007, 42, 1251–1263. [Google Scholar] [CrossRef]
- Norton, R.L. Design of Machinery: An Introduction to the Synthesis and Analysis of Mechanisms and Machines, 6th ed.; McGraw-Hill: New York, NY, USA, 2020. [Google Scholar]
- Coello, C.A.C.; Lamont, G.B.; Van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Objective Problems, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Collette, Y.; Siarry, P. Multiobjedive Optimization: Principles and Case Studies; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Flores-Pulido, L.; Portilla-Flores, E.A.; Santiago-Valentin, E.; Vega-Alvarado, E.; Yanez, M.B.C.; Nino-Suarez, P.A. A comparative study of improved harmony search algorithm in four bar mechanisms. IEEE Access 2020, 8, 148757–148778. [Google Scholar] [CrossRef]
- Zhang, Y.; Arakelian, V. Design and synthesis of single-actuator walking robots via coupling of linkages. Front. Mech. Eng. 2021, 6, 109. [Google Scholar] [CrossRef]
- Freudenstein, F. An analytical approach to the design of four-link mechanisms. Trans. ASME 1954, 76, 483–492. [Google Scholar]
- Waldron, K.J.; Kinzel, G.L. Kinematics, Dynamics, and Design of Machinery, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Jahn, J. Vector Optimization: Theory, Applications, and Extensions, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Gembicki, F.W.; Haimes, Y.Y. Approach to performance and sensitivity multiobjective optimization: The goal attainment method. IEEE Trans. Automat. Control 1975, 20, 769–771. [Google Scholar] [CrossRef]
- Jiang, R.; Jin, Z.; Liu, D.; Wang, D. Multi-objective lightweight optimization of parameterized suspension components based on NSGA-II algorithm coupling with surrogate model. Machines 2021, 9, 107. [Google Scholar] [CrossRef]
- Jiang, R.; Ci, S.; Liu, D.; Cheng, X.; Pan, Z. A hybrid multi-objective optimization method based on NSGA-II algorithm and entropy weighted TOPSIS for lightweight design of dump truck carriage. Machines 2021, 9, 165. [Google Scholar] [CrossRef]
- Ogbemhe, J.; Mpofu, K.; Tlale, N. Optimal trajectory scheme for robotic welding along complex joints using a hybrid multi-objective genetic algorithm. IEEE Access 2019, 7, 158753–158769. [Google Scholar] [CrossRef]
- Arora, J.S. Introduction to Optimum Design, 2nd ed.; Elsevier Academic Press: San Diego, CA, USA, 2004. [Google Scholar]
- Pulkkinen, S. A Review of Methods for Unconstrained Optimization: Theory, Implementation and Testing. Master’s Thesis, University of Helsinki, Helsinki, Finland, 2008. [Google Scholar]
- Asgari, S.; Sahari, M.A.; Barzegar, M. Practical modeling and optimization of ultrasound-assisted bleaching of olive oil using hybrid artificial neural network-genetic algorithm technique. Comput. Electron. Agric. 2017, 140, 422–432. [Google Scholar] [CrossRef]
- Van Henten, E.J.; Schenk, E.J.; van Willigenburg, L.G.; Meuleman, J.; Barreiro, P. Collision-free inverse kinematics of the redundant seven-link manipulator used in a cucumber picking robot. Biosyst. Eng. 2010, 106, 112–124. [Google Scholar] [CrossRef]
- Van Henten, E.J.; Van’t Slot, D.A.; Hol, C.W.J.; Van Willigenburg, L.G. Optimal manipulator design for a cucumber harvesting robot. Comput. Electron. Agric. 2009, 65, 247–257. [Google Scholar] [CrossRef]
- Walther, C.; Wenzel, A.; Beneke, F.; Hensel, O.; Huster, J. Determination of working states of the rotating cutting assembly in forage harvesters by artificial neural networks. Automatisierungstechnik 2017, 65, 198–206. [Google Scholar] [CrossRef]

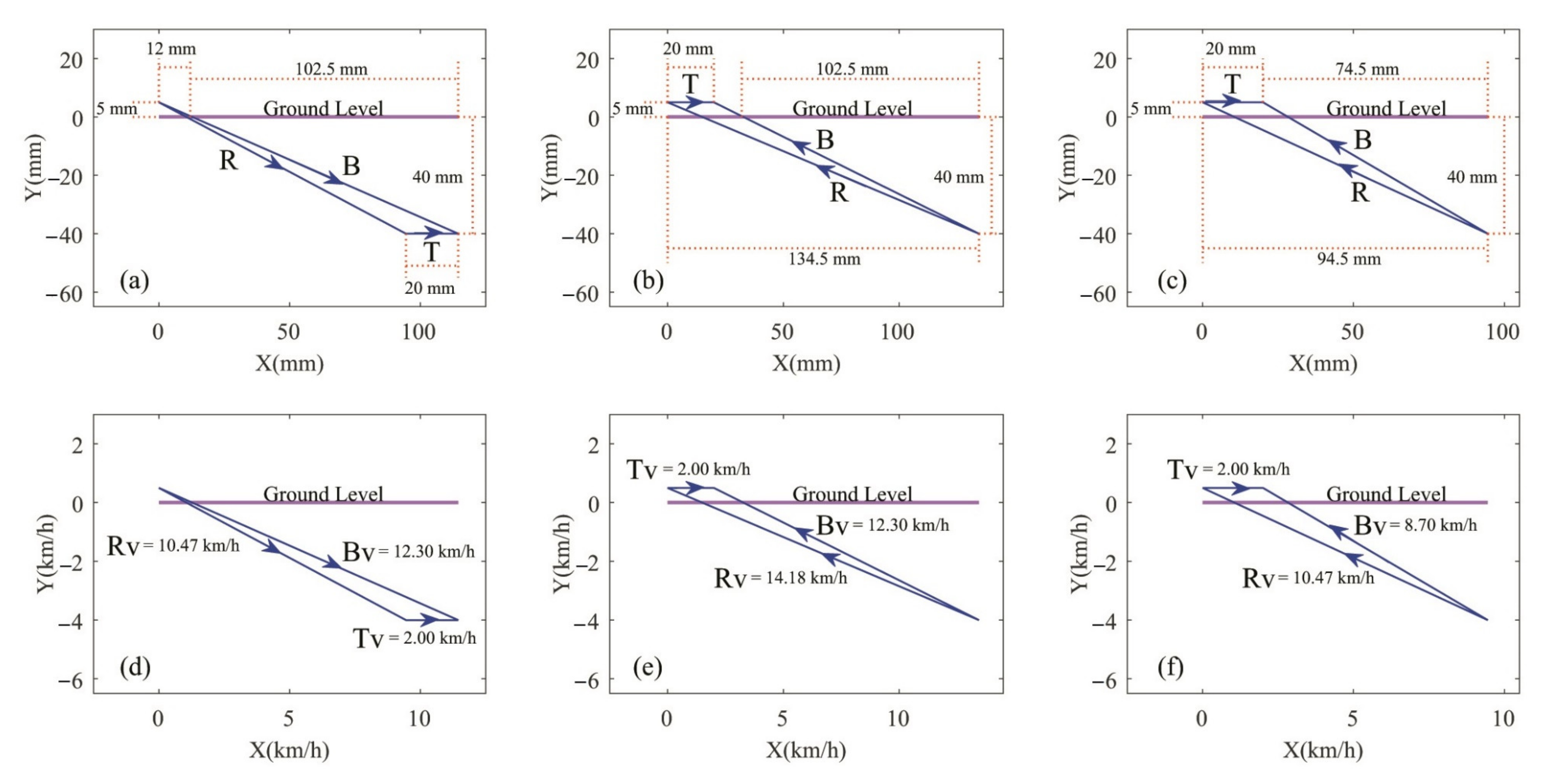
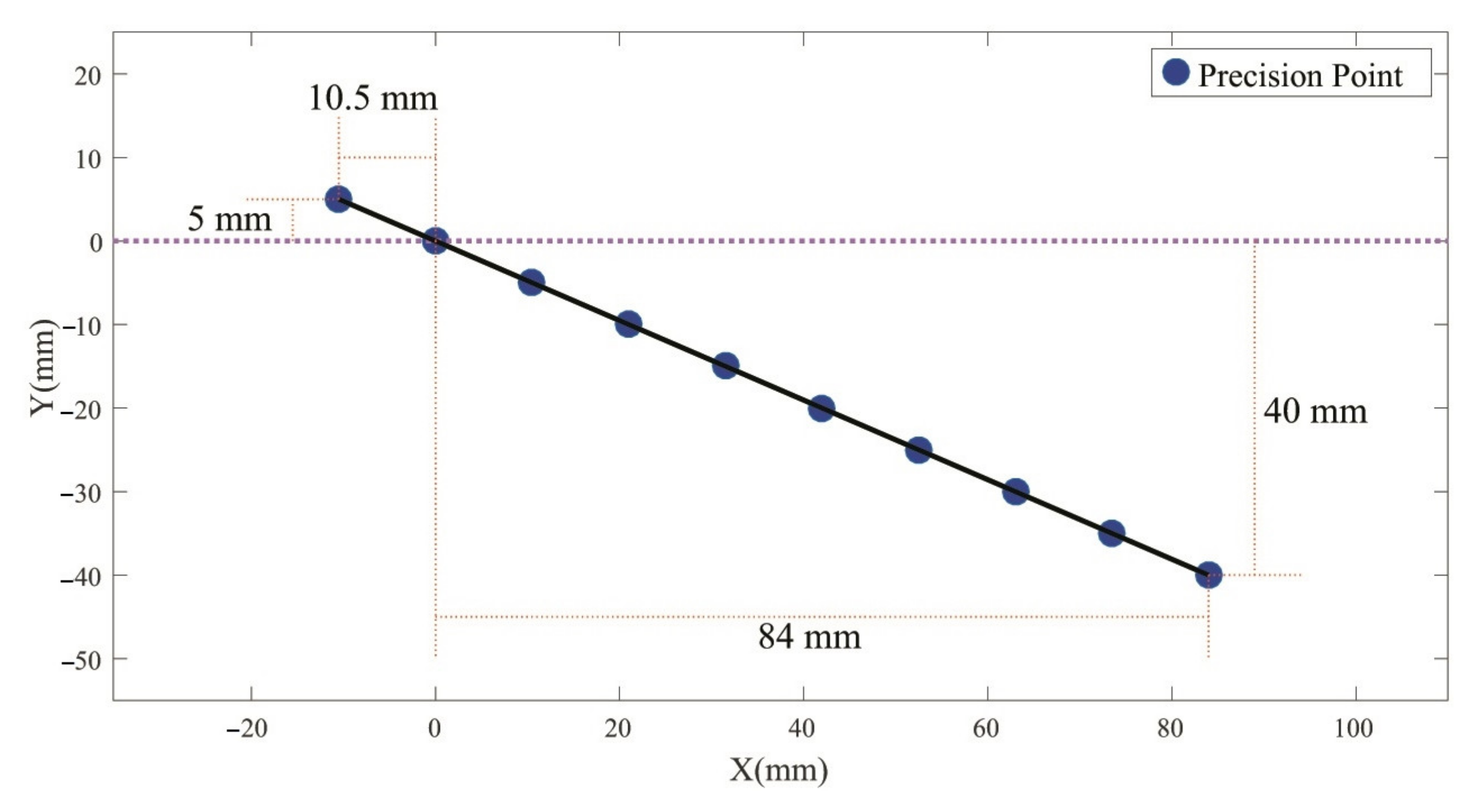



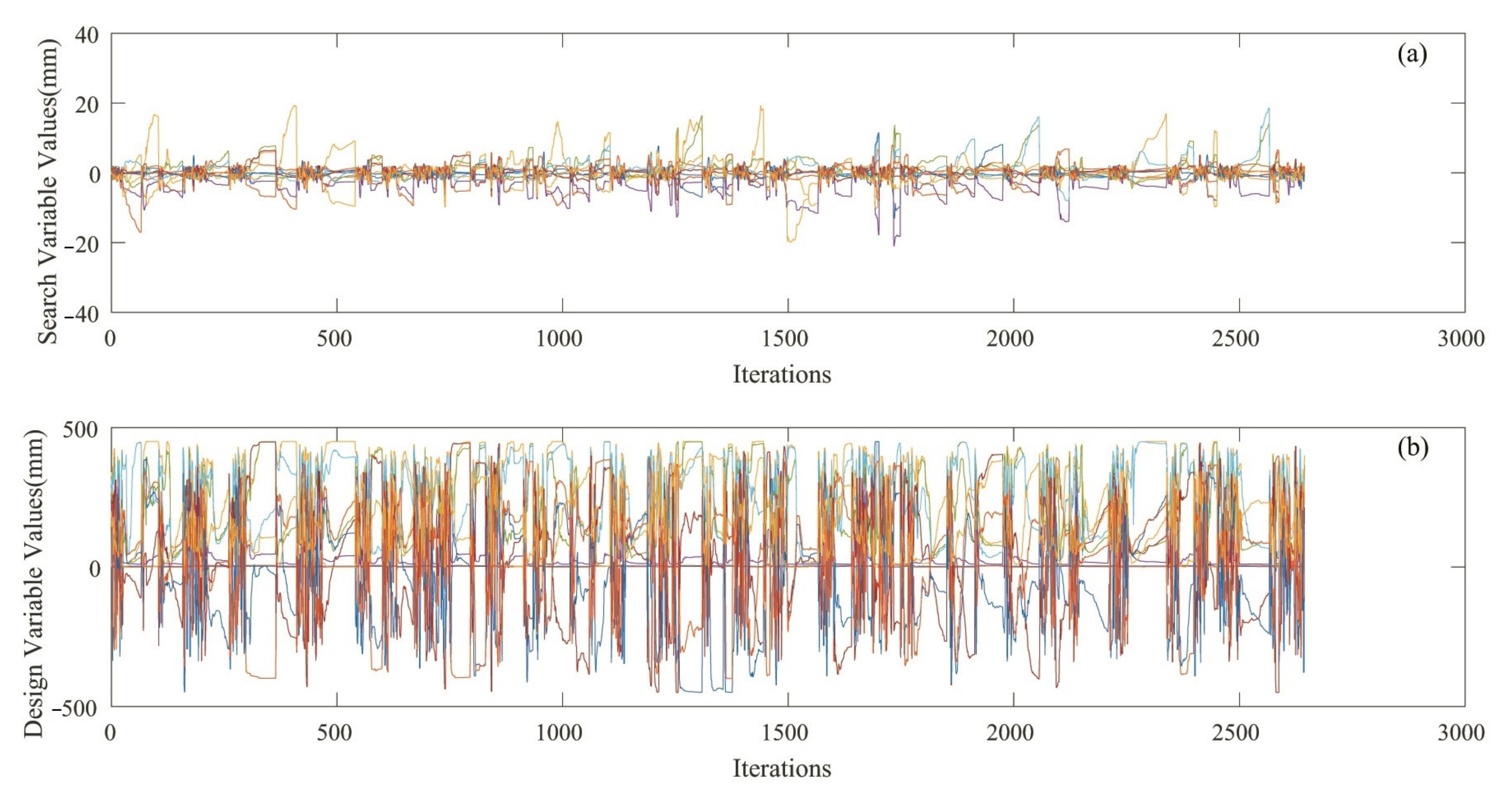
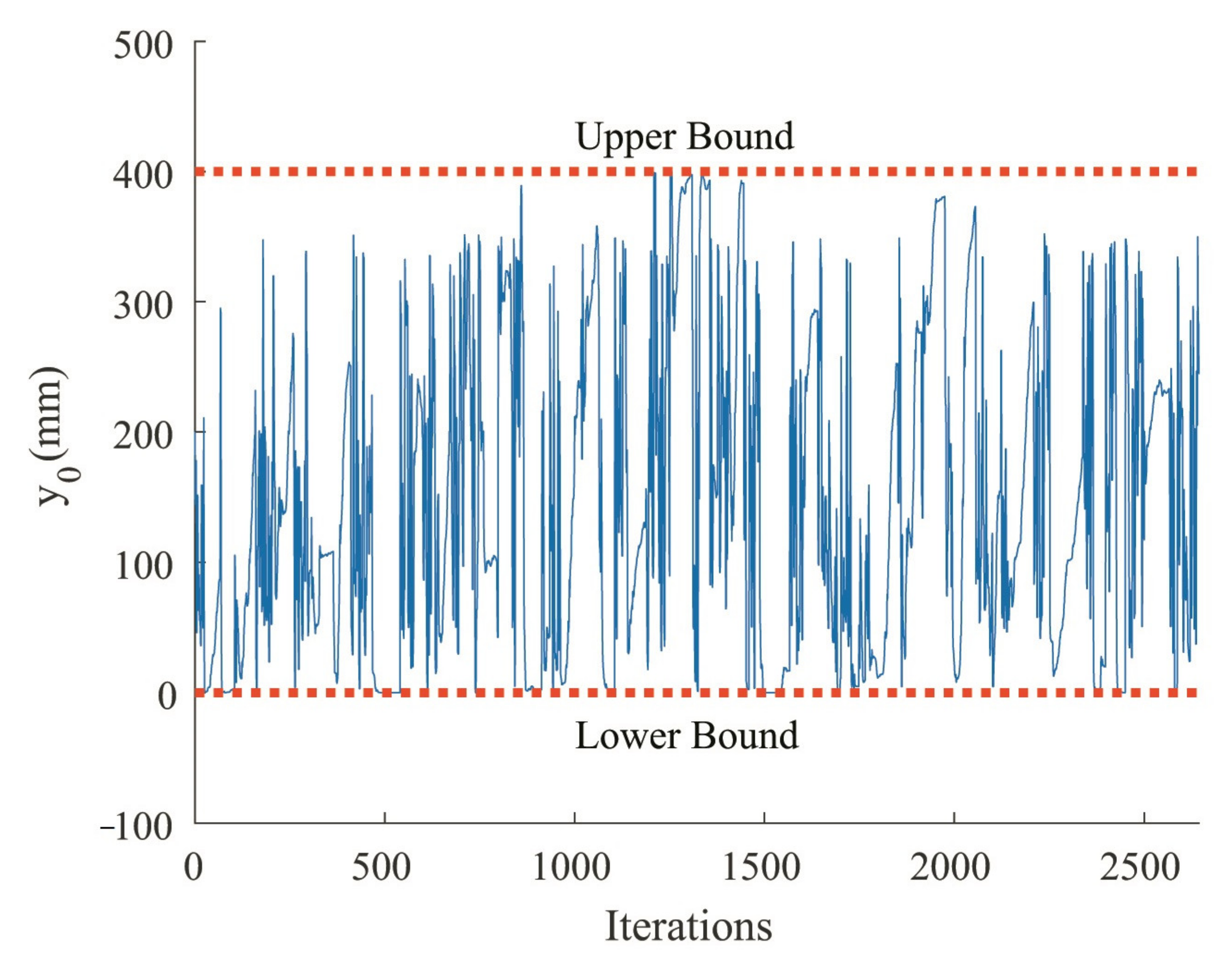

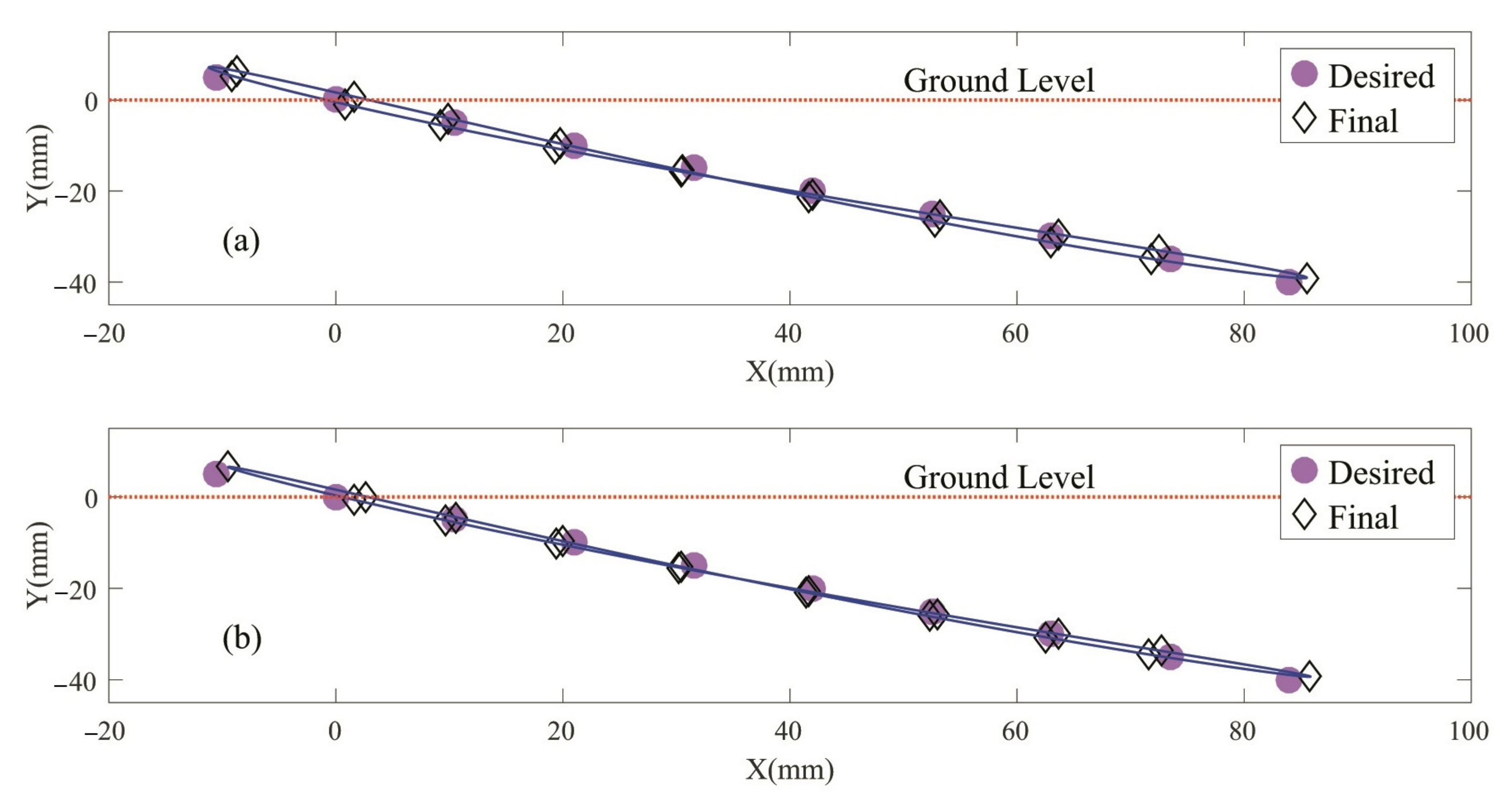
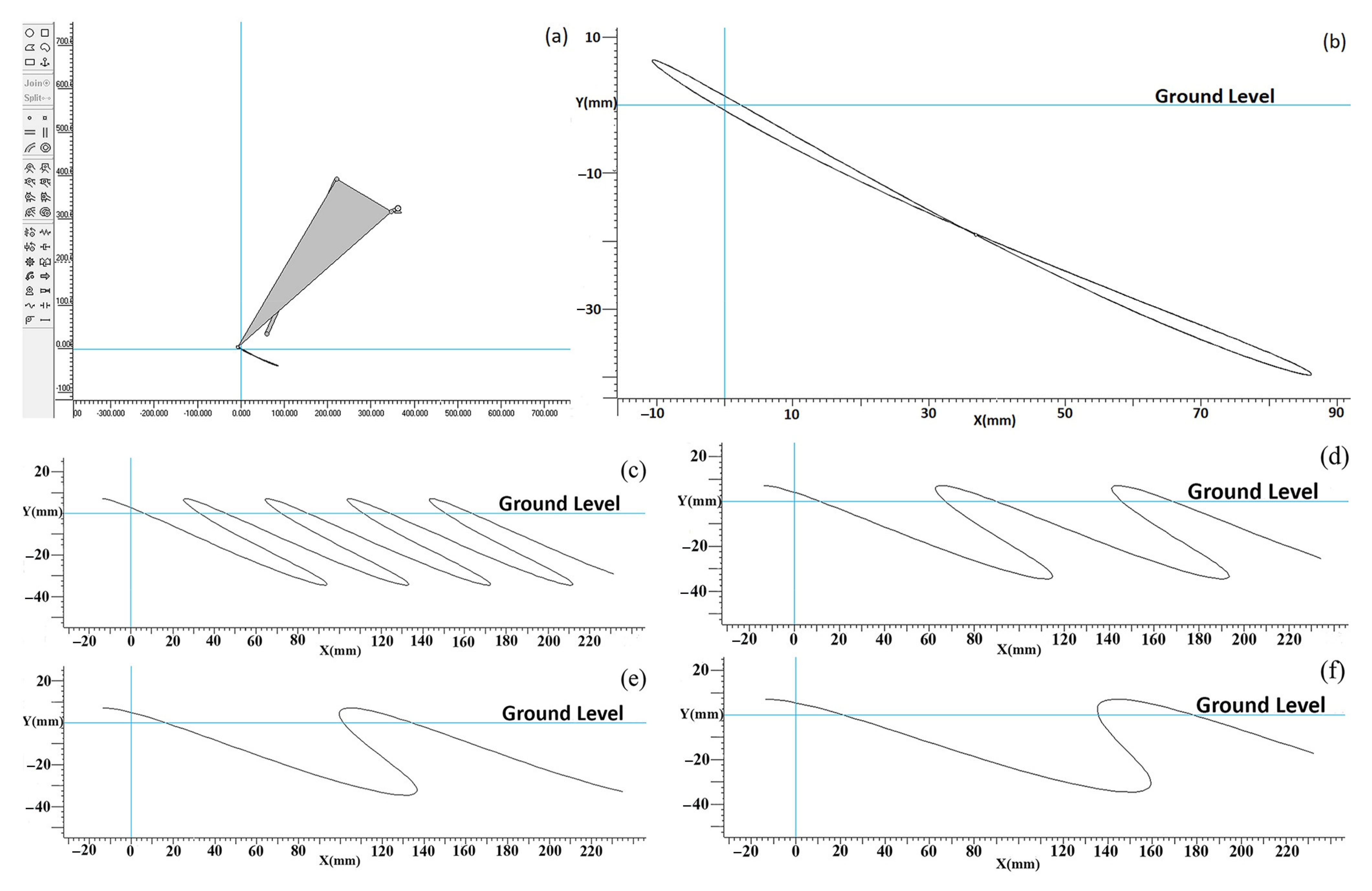


| Order of Points | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x—coordinate (mm) | −10.5 | 0 | 10.5 | 21 | 31.5 | 42 | 52.5 | 63 | 73.5 | 84 |
| y—coordinate (mm) | 5 | 0 | −5 | −10 | −15 | −20 | −25 | −30 | −35 | −40 |
| Order of Points | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| x—coordinate (mm) | 84 | 73.5 | 63 | 52.5 | 42 | 31.5 | 21 | 10.5 | 0 | −10.5 |
| y—coordinate (mm) | −40 | −35 | −30 | −25 | −20 | −15 | −10 | −5 | 0 | 5 |
| Design Variable | r1 (mm) | r2 (mm) | r3 (mm) | r4 (mm) | r5 (mm) | r6 (mm) | x0 (mm) | y0 (mm) | θ0 (degree) | (degree) |
|---|---|---|---|---|---|---|---|---|---|---|
| Upper bound | 450 | 450 | 450 | 450 | 450 | 450 | 400 | 400 | 360 | 360 |
| Lower bound | 10 | 10 | 10 | 10 | −450 | −450 | −400 | 0 | 0 | 0 |
| Parameter | Value |
|---|---|
| Population size | 200 |
| Initial range | [10; 390] |
| Crossover probability | 0.80 |
| Mutation probability | 0.20 |
| Pareto front population fraction | 0.55 |
| Generation | 1000 |
| Design Variable | r1 (mm) | r2 (mm) | r3 (mm) | r4 (mm) | r5 (mm) | r6 (mm) | x0 (mm) | y0 (mm) | θ0 (degree) | (degree) |
|---|---|---|---|---|---|---|---|---|---|---|
| GA | 448 | 18.2 | 162.4 | 416.8 | 163.1 | 450 | 375.9 | 318.4 | 223.1 | 19.4 |
| HGA | 418.8 | 16.7 | 147.4 | 392.2 | 145.7 | 450 | 362.1 | 324 | 223.8 | 20.5 |
| QNM | 416.1 | 11.1 | 97.5 | 408.1 | 113.1 | 449.9 | 321.0 | 347.7 | 77.7 | 154.4 |
| This Study (GA) | This Study (HGA) | This Study (QNM) | Ref. [14] | Ref. [25] | |
|---|---|---|---|---|---|
| AE (mm) | 0.33 | 0.33 | 0.33 | ||
| TA (degree) | 7.3 | 7.0 | 8.7 | 47.2 | 63.1 |
| Effective stroke of the mechanism (degree) | 320 | 320 | 320 | 150 | 80 |
| This Study (State 1) | This Study (State 2) | This Study (State 3) | This Study (State 4) | Four-Bar [47] | Four-Bar [25] | Brush Weeder [17] | Harrow Comb [17] | Ducksfoot Cultivator [17] | Ground Driven [17] | Rotary Powered [17] | Sweep Weeder [17] | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Weeding performance (%) | 98 | 94 | 85 | 96 | 90 | 61 | 51–60 | 52–77 | 65–99 | 58–90 | 60–99 | 88–90 |
| Mechanical damage (%) | 8 | 3 | 1 | 6 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseini, H.; Farzad, A.; Majeed, F.; Hensel, O.; Nasirahmadi, A. Multi-Objective Optimal Design and Development of a Four-Bar Mechanism for Weed Control. Machines 2022, 10, 198. https://doi.org/10.3390/machines10030198
Hosseini H, Farzad A, Majeed F, Hensel O, Nasirahmadi A. Multi-Objective Optimal Design and Development of a Four-Bar Mechanism for Weed Control. Machines. 2022; 10(3):198. https://doi.org/10.3390/machines10030198
Chicago/Turabian StyleHosseini, Hooman, Abdulali Farzad, Faizan Majeed, Oliver Hensel, and Abozar Nasirahmadi. 2022. "Multi-Objective Optimal Design and Development of a Four-Bar Mechanism for Weed Control" Machines 10, no. 3: 198. https://doi.org/10.3390/machines10030198
APA StyleHosseini, H., Farzad, A., Majeed, F., Hensel, O., & Nasirahmadi, A. (2022). Multi-Objective Optimal Design and Development of a Four-Bar Mechanism for Weed Control. Machines, 10(3), 198. https://doi.org/10.3390/machines10030198






