Micromechanism of Plastic Accumulation and Damage Initiation in Bearing Steels under Cyclic Shear Deformation: A Molecular Dynamics Study
Abstract
:1. Introduction
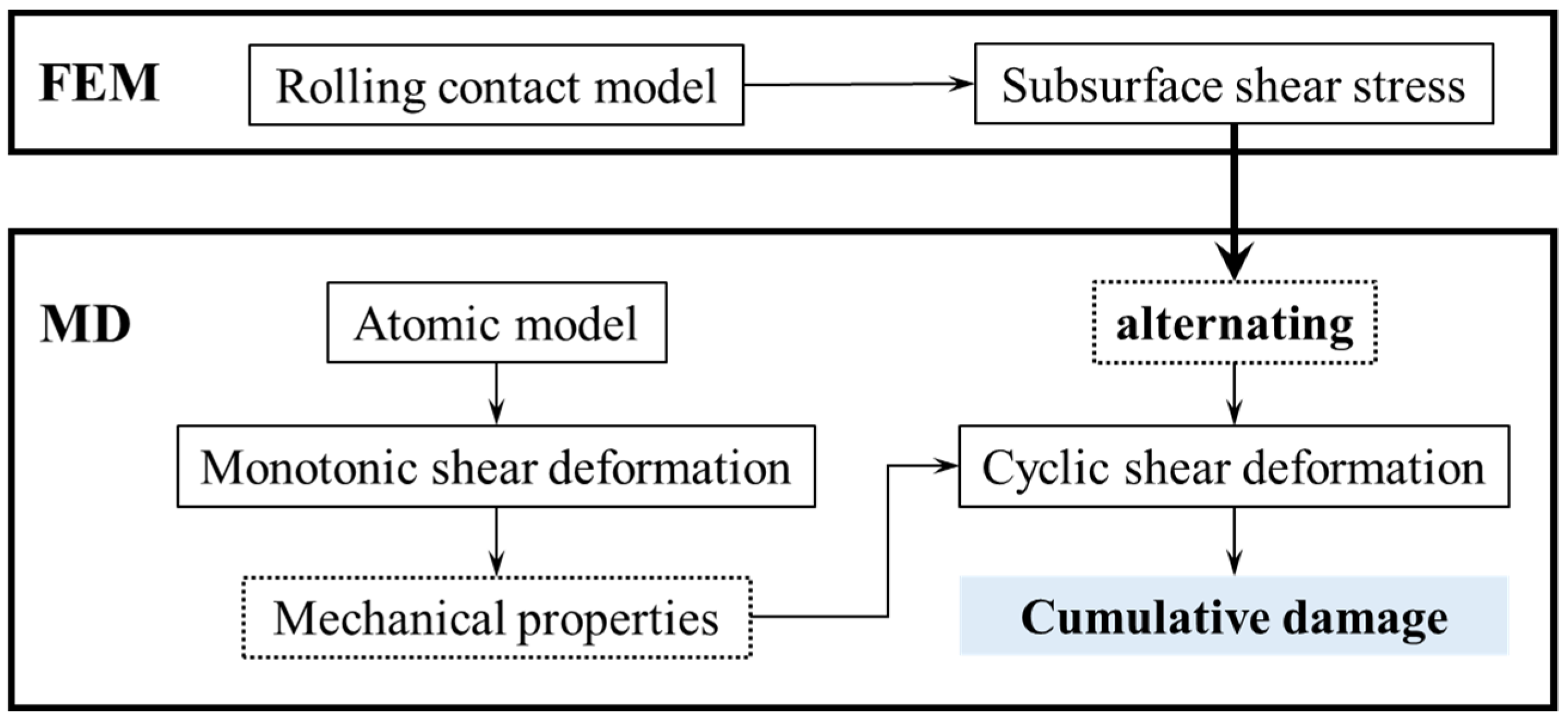
2. Methodology
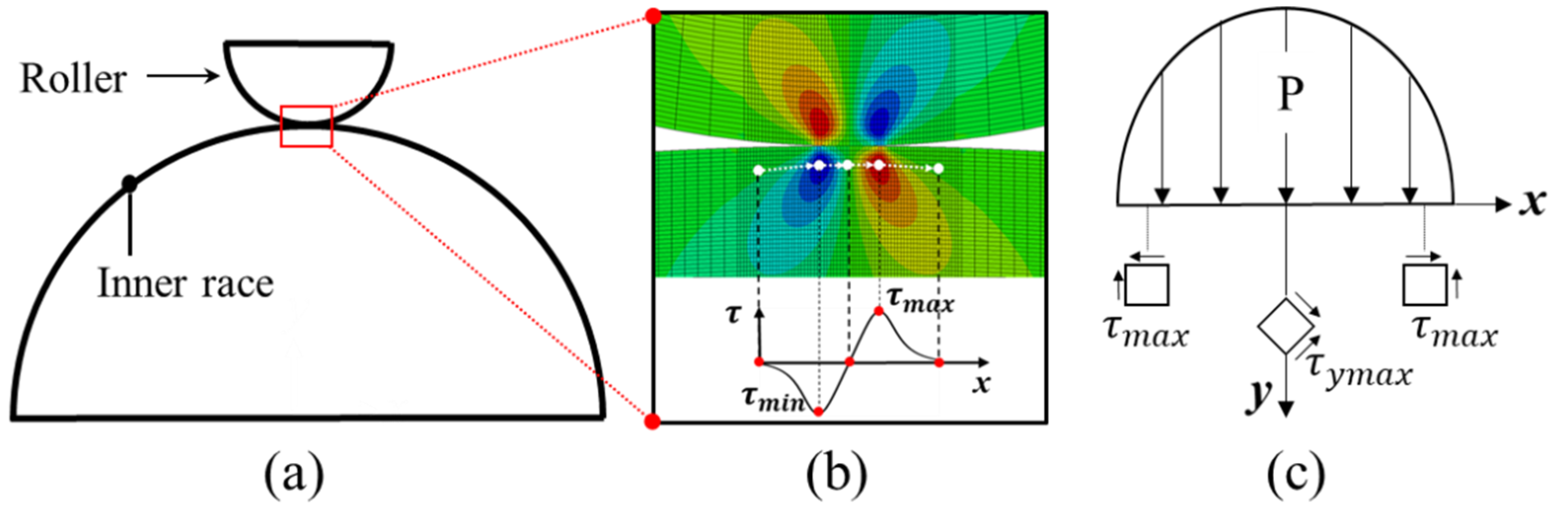
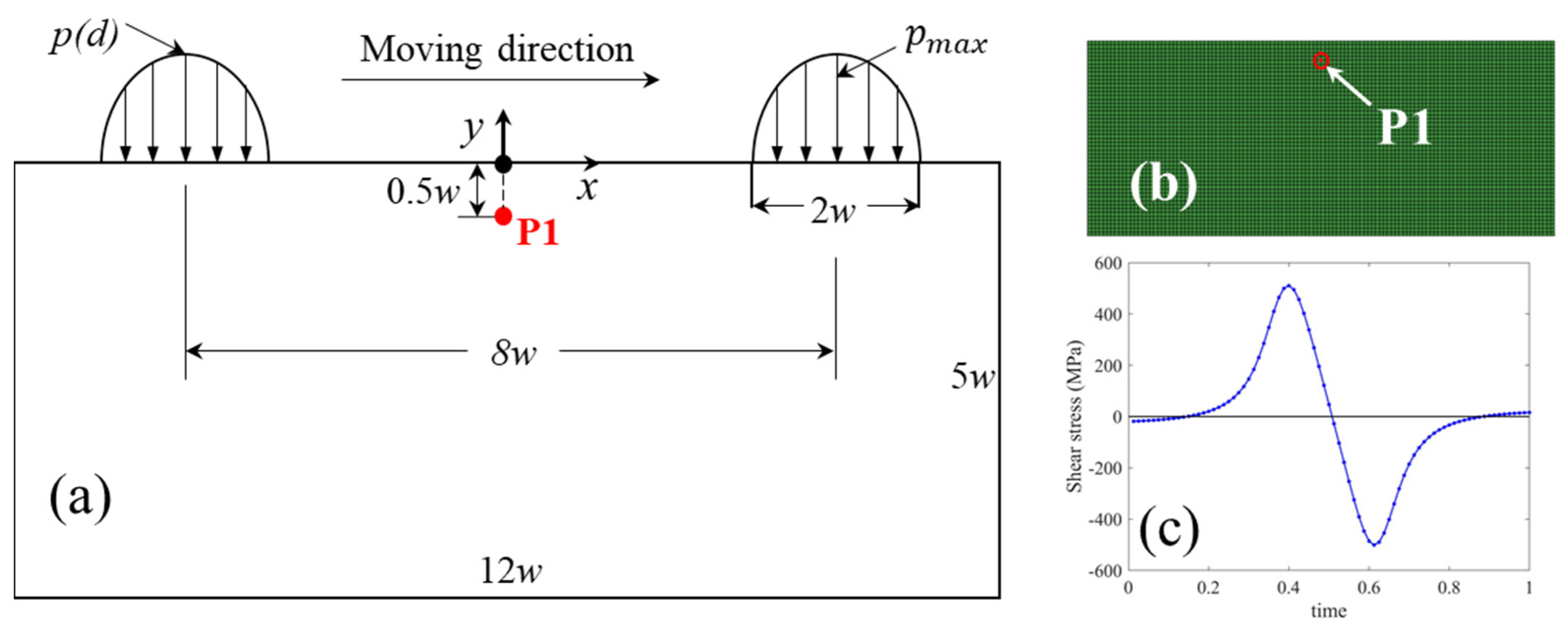
2.1. Subsurface Shear Stress
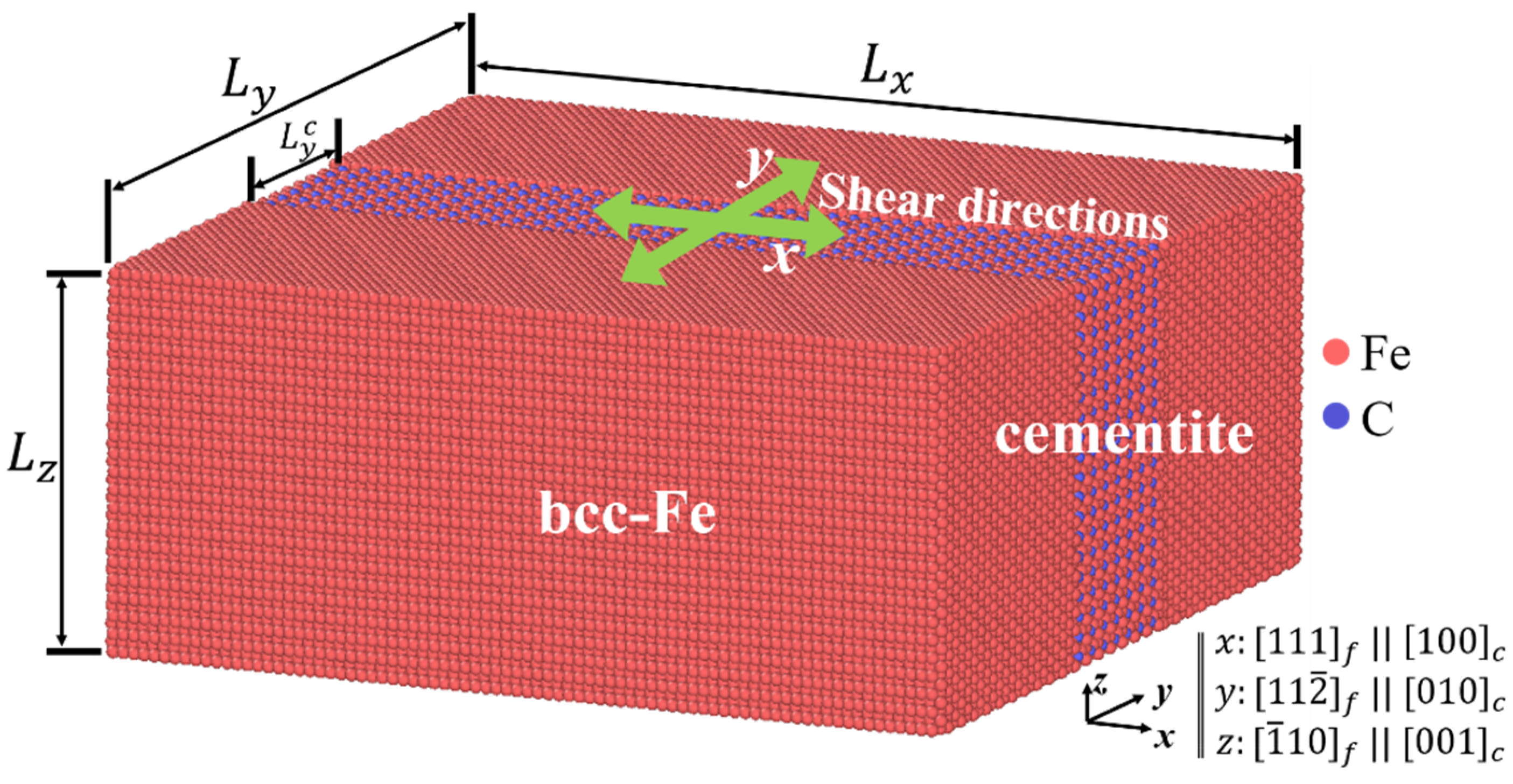
2.2. Atomic Model
2.3. Loading Conditions
3. Results and Discussion
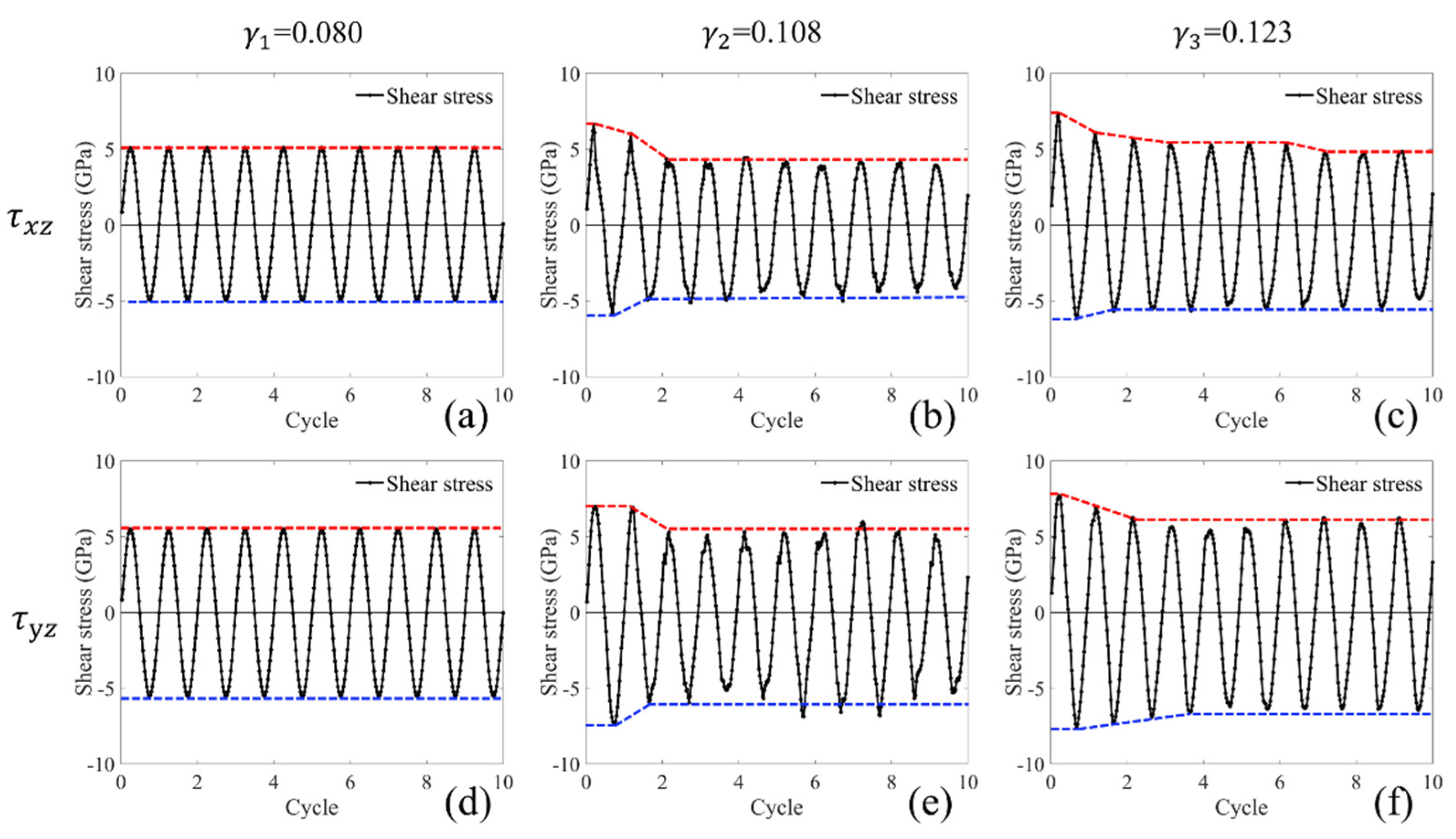
3.1. Shear Stress Responses
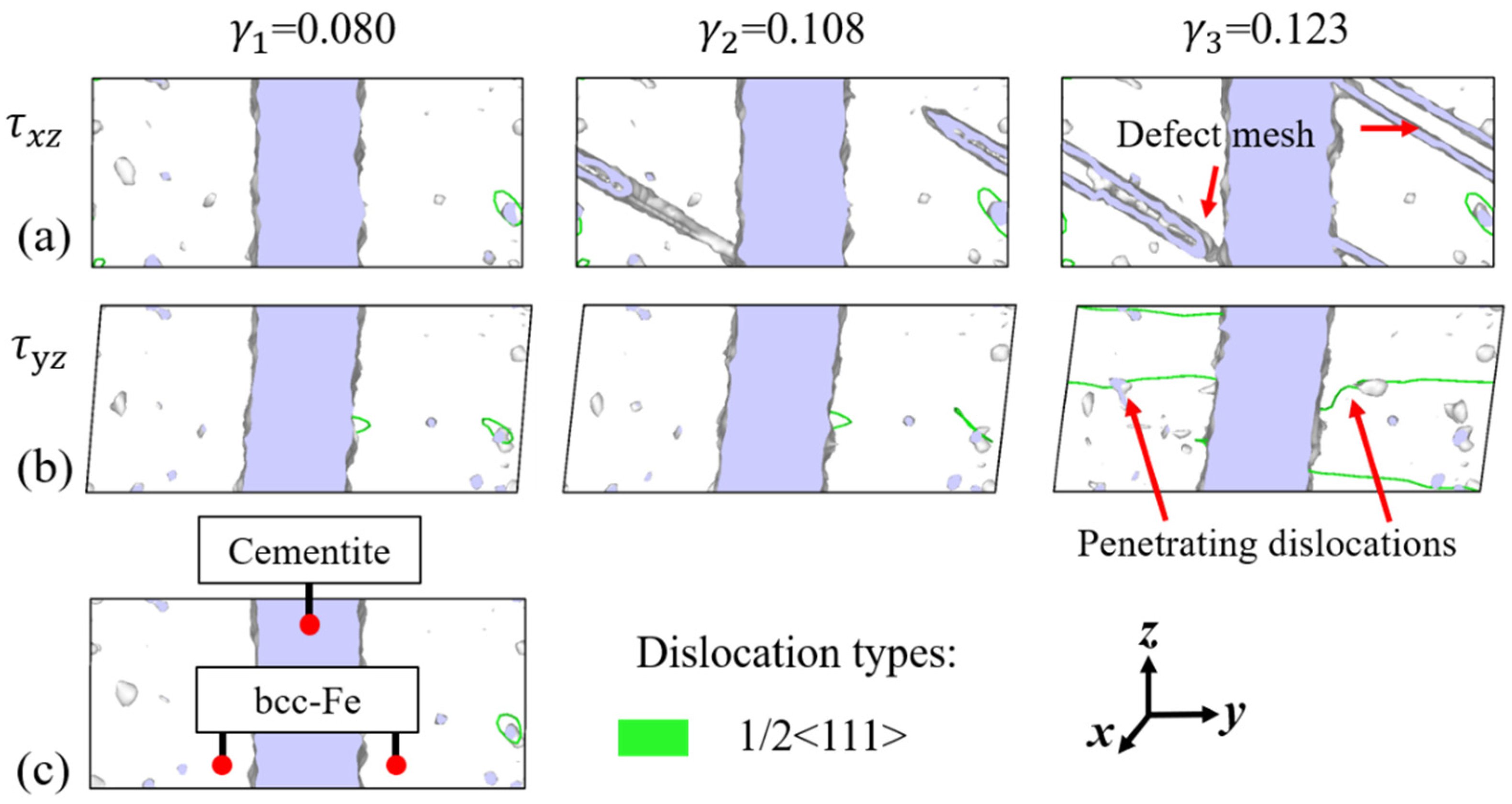
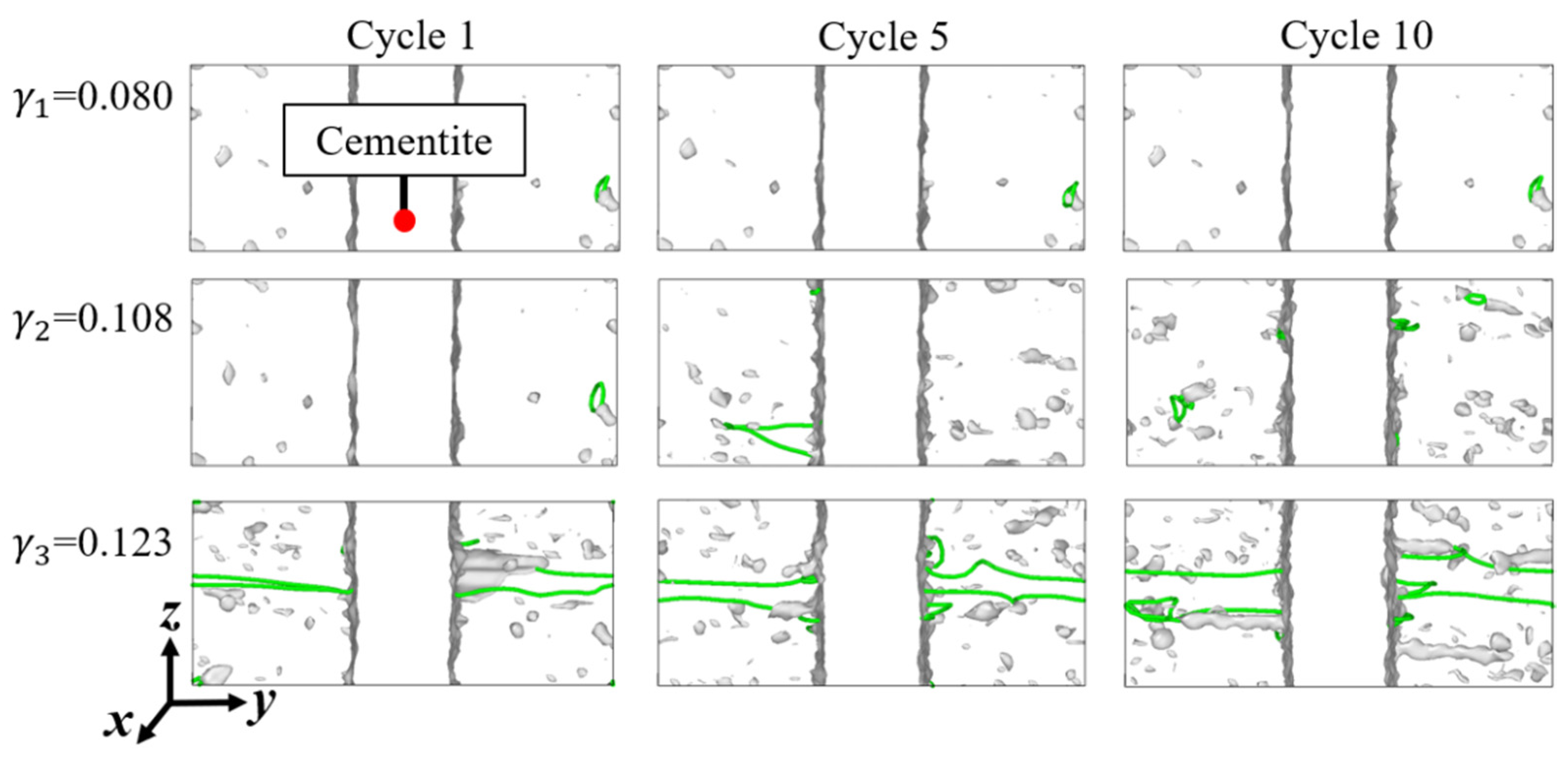
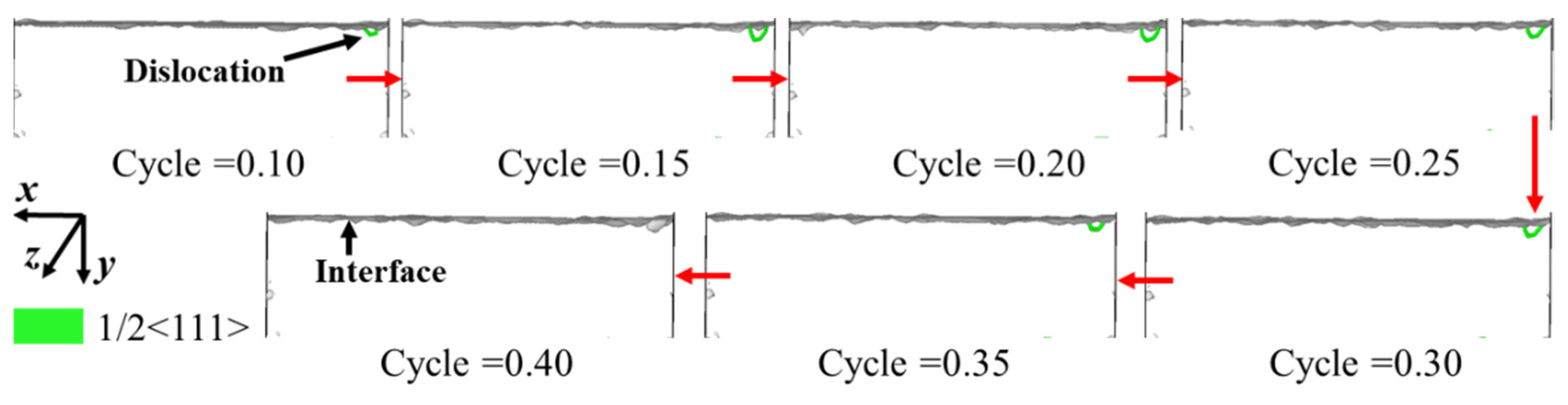
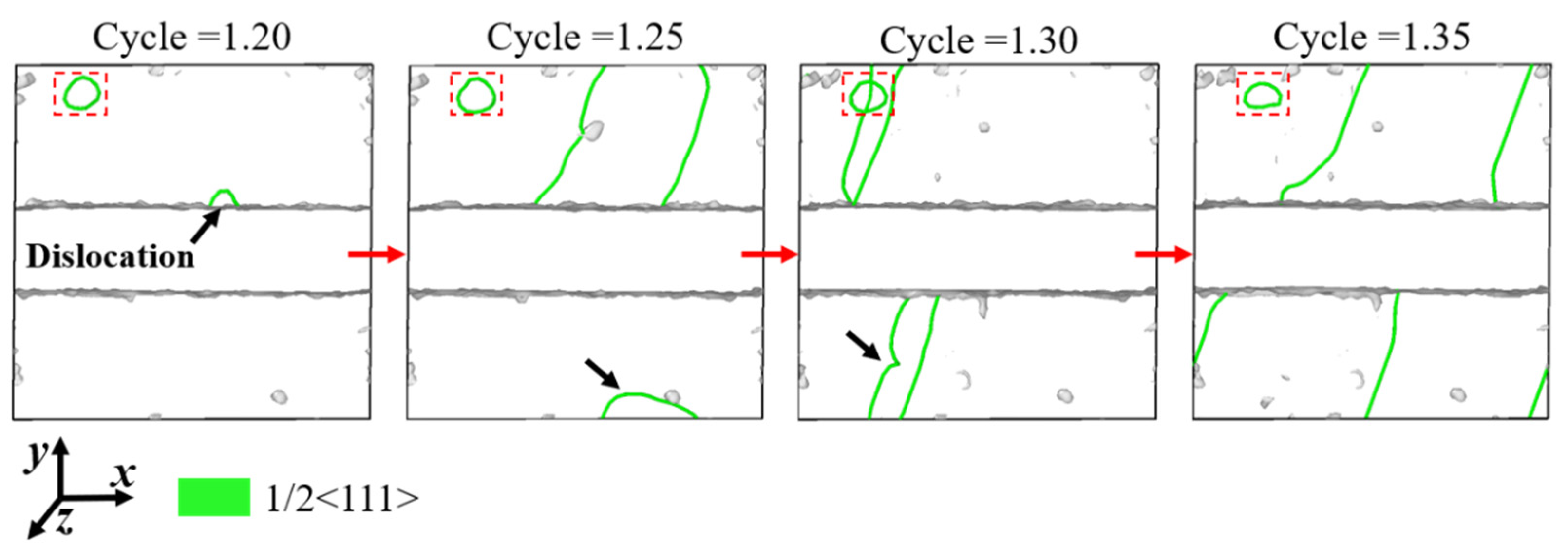
3.2. Evolution of Dislocations and Defect Meshes
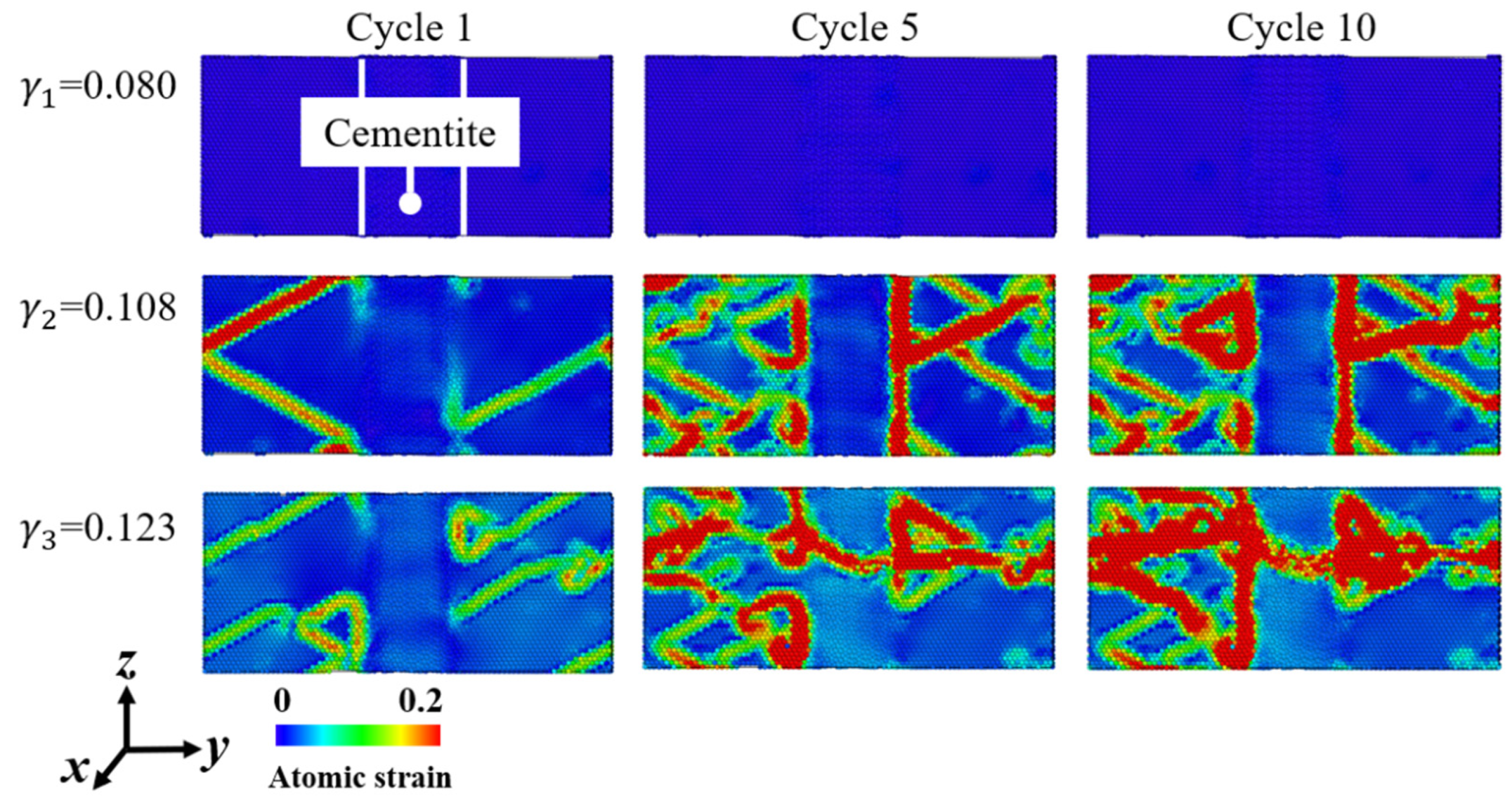
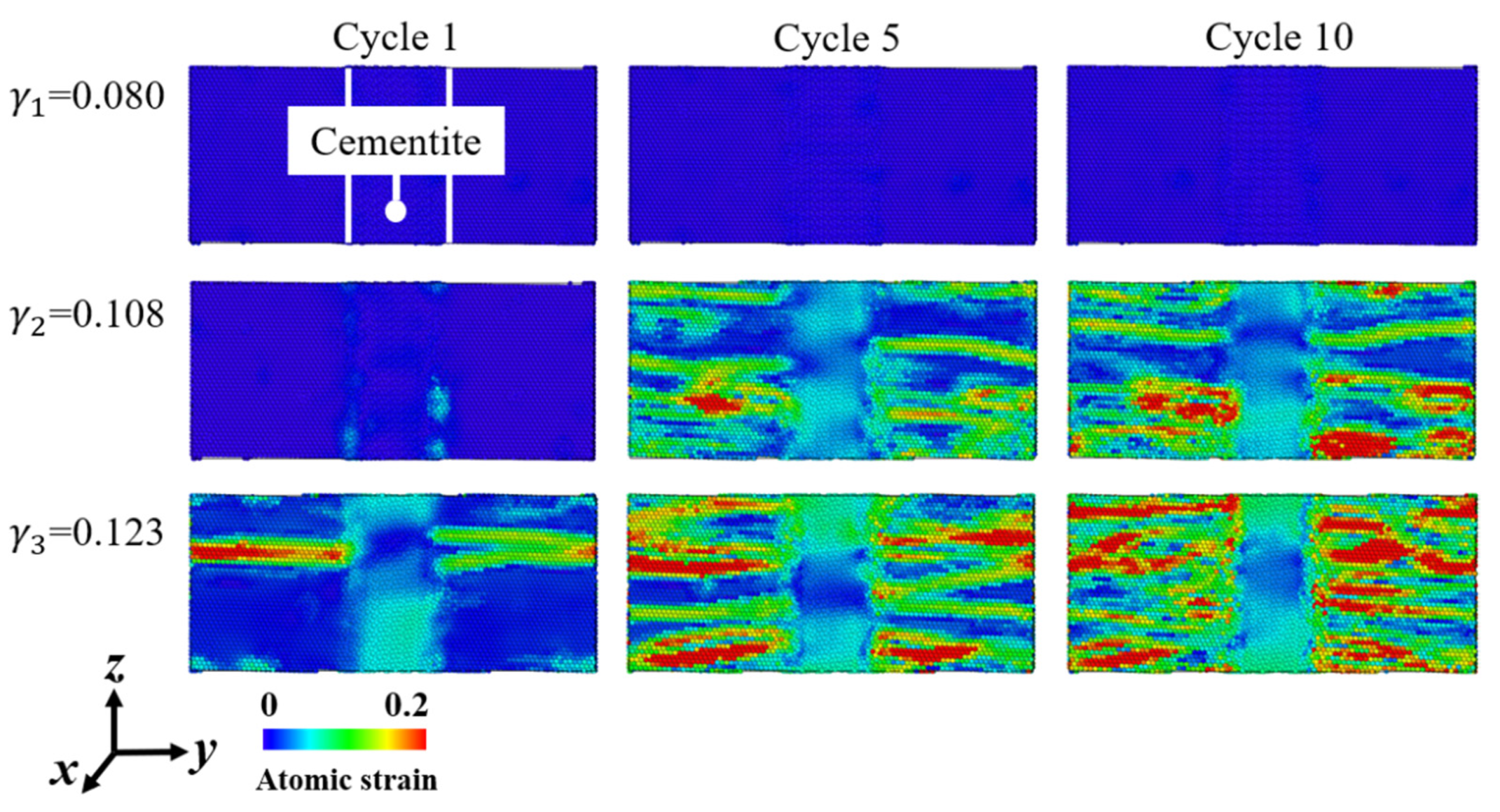
3.3. Evolution of High-Strain Atoms
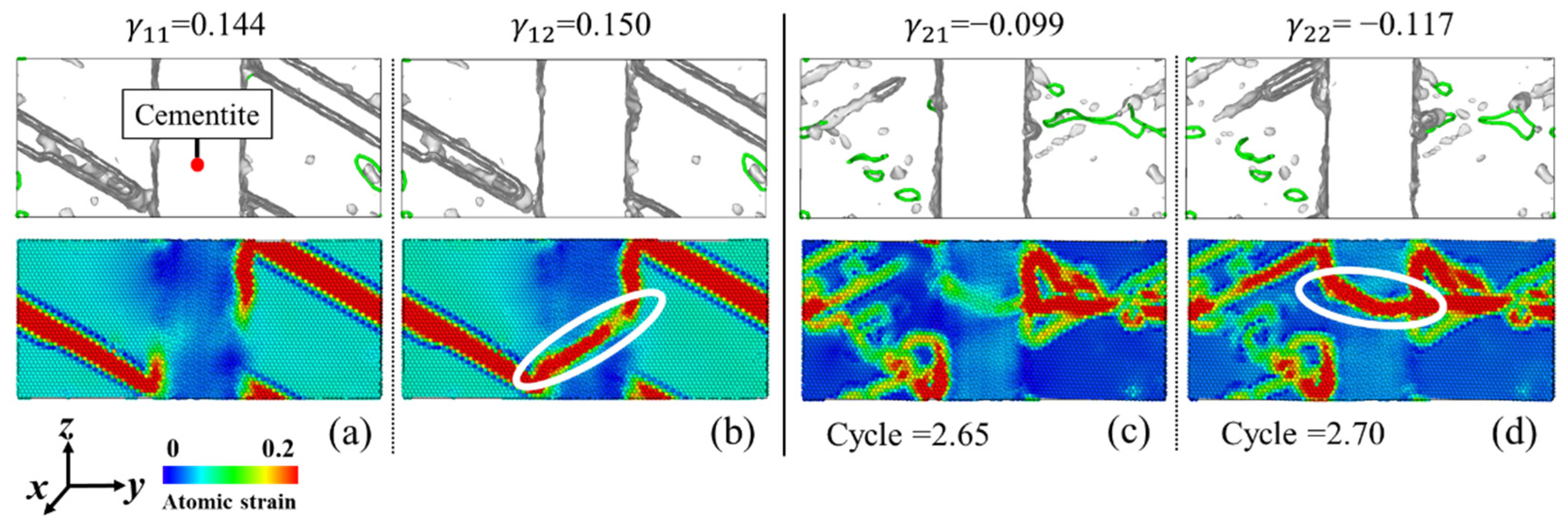
3.4. Shear Deformation of Cementite Phase and Damage Initiation
4. Conclusions
- The stress response of the atomic model is cyclic softening when the model is in the plastic stage, and shear deformation along x-axis is more likely to appear cyclic softening than that along the y-axis.
- Dislocations nucleate and are annihilated on the interface when shear strain amplitude and cycle index are small. When the amplitude and index are large enough, regular structures of the material are destroyed, and dislocations and defect meshes are retained in the model, resulting in the gradual accumulation of plasticity.
- Highly strained atoms appear in the bcc-Fe phase and cementite phase when shear strain amplitude and cycle index are large enough. The direction parallel to the two-phase interface is more likely to induce residual strain in the model, and is beneficial to the shear slip of the cementite phase, thus resulting in cumulative damage.
- Cyclic shear deformation can accelerate the plastic accumulation of the atomic model and thus result in an earlier shear slip of the cementite phase than that under monotonic shear deformation. When the cementite phase is damaged under severe shear deformation, the material is usually in a dangerous state, which indicates the origin of microscopic damage near inclusion. Since cementite is brittle and difficult to deform, it can represent a series of brittle inclusions in bearing steels. Therefore, plastic accumulation and defect initiation are more likely to occur on the interface between inclusions and bearing steel matrix under cyclic shear deformation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Breidenstein, B.; Denkena, B.; Krödel, A.; Prasanthan, V.; Poll, G.; Pape, F.; Coors, T. Production-Related Surface and Subsurface Properties and Fatigue Life of Hybrid Roller Bearing Components. Metals 2020, 10, 1339. [Google Scholar] [CrossRef]
- Fu, H.; Rivera-Díaz-del-Castillo, P. Evolution of White Etching Bands in 100Cr6 Bearing Steel under Rolling Contact-Fatigue. Metals 2019, 9, 491. [Google Scholar] [CrossRef] [Green Version]
- Rycerz, P.; Olver, A.; Kadiric, A. Propagation of surface initiated rolling contact fatigue cracks in bearing steel. Int. J. Fatigue 2017, 97, 29–38. [Google Scholar] [CrossRef] [Green Version]
- Darisuren, S.; Park, J.; Pyun, Y.; Amanov, A. A Study on the Improvement of the Fatigue Life of Bearings by Ultrasonic Nanocrystal Surface Modification Technology. Metals 2019, 9, 1114. [Google Scholar] [CrossRef] [Green Version]
- Lundberg, G.; Palmgren, A. Dynamic capacity of rolling bearings. J. Appl. Mech. Trans. ASME 1947, 196, 12. [Google Scholar] [CrossRef]
- Romanowicz, P. Numerical assessment of fatigue load capacity of cylindrical crane wheel using multiaxial high-cycle fatigue criteria. Arch. Appl. Mech. 2017, 87, 1707–1726. [Google Scholar] [CrossRef]
- Romanowicz, P.J.; Szybinski, B. Fatigue Life Assessment of Rolling Bearings Made from AISI 52100 Bearing Steel. Materials 2019, 12, 371. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, F.; Jalalahmadi, B.; Slack, T.S.; Raje, N.; Arakere, N.K. A Review of Rolling Contact Fatigue. J. Tribol. Trans. ASME 2009, 131, 220. [Google Scholar] [CrossRef]
- Ebert, F.J. Fundamentals of Design and Technology of Rolling Element Bearings. Chin. J. Aeronaut. 2010, 23, 123–136. [Google Scholar] [CrossRef] [Green Version]
- Warhadpande, A.; Sadeghi, F.; Evans, R.D. Microstructural Alterations in Bearing Steels under Rolling Contact Fatigue Part 1—Historical Overview. Tribol. Trans. 2013, 56, 349–358. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Steels for bearings. Prog. Mater. Sci. 2012, 57, 268–435. [Google Scholar] [CrossRef]
- Arakere, N.K. Gigacycle rolling contact fatigue of bearing steels: A review. Int. J. Fatigue 2016, 93, 238–249. [Google Scholar] [CrossRef]
- Harris, T.A.; Kotzalas, M.N. Advanced Concepts of Bearing Technology: Rolling Bearing Analysis, 5th ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Shanyavskiy, A.A. Mechanisms and modeling of subsurface fatigue cracking in metals. Eng. Fract. Mech. 2013, 110, 350–363. [Google Scholar] [CrossRef]
- Dey, R.; Tarafder, S.; Sivaprasad, S. Influence of proportional and non-proportional loading on deformation behaviour of austenitic stainless steel-macro and micro analysis. Theor. Appl. Fract. Mech. 2019, 100, 342–353. [Google Scholar] [CrossRef]
- Kachit, M.; Courbon, J.; Boulnat, X.; Adrien, J.; Verdu, C. Non-symmetrical fatigue life of nodular graphite cast iron under non-proportional multi-axial cyclic loading. Int. J. Fatigue 2019, 125, 128–137. [Google Scholar] [CrossRef]
- Romanowicz, P.J.; Smolarski, D.; Kozien, M.S. Using the Effect of Compression Stress in Fatigue Analysis of the Roller Bearing for Bimodal Stress Histories. Materials 2021, 15, 196. [Google Scholar] [CrossRef]
- Akama, M. Fatigue Crack Growth under Non-Proportional Mixed Mode Loading in Rail and Wheel Steel Part 1: Sequential Mode I and Mode II Loading. Appl. Sci. 2019, 9, 2006. [Google Scholar] [CrossRef] [Green Version]
- Akama, M.; Kiuchi, A. Fatigue Crack Growth under Non-Proportional Mixed Mode Loading in Rail and Wheel Steel Part 2: Sequential Mode I and Mode III Loading. Appl. Sci. 2019, 9, 2866. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Shao, E.; Zhao, D.; Guo, J.; Fan, Z. Measurement of the critical size of inclusions initiating contact fatigue cracks and its application in bearing steel. Wear 1991, 147, 285–294. [Google Scholar] [CrossRef]
- Xia, Z.; Kujawski, D.; Ellyin, F. Effect of mean stress and ratcheting strain on fatigue life of steel. Int. J. Fatigue 2015, 18, 335–341. [Google Scholar] [CrossRef]
- Pandkar, A.S.; Arakere, N.; Subhash, G. Ratcheting-based microstructure-sensitive modeling of the cyclic hardening response of case-hardened bearing steels subject to Rolling Contact Fatigue. Int. J. Fatigue 2015, 73, 119–131. [Google Scholar] [CrossRef]
- Arakere, N.K.; Subhash, G. Work hardening response of M50-NiL case hardened bearing steel during shakedown in rolling contact fatigue. Mater. Sci. Technol. 2012, 28, 34–38. [Google Scholar] [CrossRef]
- Trojahn, W.; Valentin, P. Bearing steel quality and bearing performance. Mater. Sci. Technol. 2013, 28, 55–57. [Google Scholar] [CrossRef]
- Šmeļova, V.; Schwedt, A.; Wang, L.; Holweger, W.; Mayer, J. Electron microscopy investigations of microstructural alterations due to classical Rolling Contact Fatigue (RCF) in martensitic AISI 52100 bearing steel. Int. J. Fatigue 2017, 98, 142–154. [Google Scholar] [CrossRef]
- Chakraborty, J.; Bhattacharjee, D.; Manna, I. Development of ultrafine bainite + martensite duplex microstructure in SAE 52100 bearing steel by prior cold deformation. Scr. Mater. 2009, 61, 604–607. [Google Scholar] [CrossRef]
- Lobodyuk, V.A.; Meshkov, Y.; Pereloma, E.V. On Tetragonality of the Martensite Crystal Lattice in Steels. Metall. Mater. Trans. A 2018, 50, 97–103. [Google Scholar] [CrossRef] [Green Version]
- Decaudin, B.; Djega-Mariadassou, C.; Cizeron, G. Structural study of M50 steel carbides. J. Alloy. Compd. 1995, 226, 208–212. [Google Scholar] [CrossRef]
- Lian, J.; Zheng, L.; Wang, F.; Zhang, H. Evolution of carbides on surface of carburized M50NiL bearing steel. J. Iron Steel Res. Int. 2018, 25, 1198–1211. [Google Scholar] [CrossRef]
- Wang, K.; Jing, H.; Xu, L.; Han, Y.; Zhao, L.; Hu, W.; Deng, H. Carbide effects on tensile deformation behavior of [001] symmetric tilt grain boundaries in bcc Fe. Model. Simul. Mater. Sci. Eng. 2020, 28, 035006. [Google Scholar] [CrossRef]
- Liang, L.; Wang, Y.; Chen, Y.; Wang, H.; Dai, L. Dislocation nucleation and evolution at the ferrite-cementite interface under cyclic loadings. Acta Mater. 2020, 186, 267–277. [Google Scholar] [CrossRef]
- Luu, H.T.; Gunkelmann, N. Pressure-induced phase transformations in Fe-C: Molecular dynamics approach. Comput. Mater. Sci. 2019, 162, 295–303. [Google Scholar] [CrossRef]
- Ghaffarian, H.; Karimi Taheri, A.; Ryu, S.; Kang, K. Nanoindentation study of cementite size and temperature effects in nanocomposite pearlite: A molecular dynamics simulation. Curr. Appl. Phys. 2016, 16, 1015–1025. [Google Scholar] [CrossRef] [Green Version]
- Ghaffarian, H.; Taheri, A.K.; Kang, K.; Ryu, S. Molecular Dynamics Simulation Study on the Effect of the Loading Direction on the Deformation Mechanism of Pearlite. Multiscale Sci. Eng. 2019, 1, 47–55. [Google Scholar] [CrossRef] [Green Version]
- Guziewski, M.; Coleman, S.P.; Weinberger, C.R. Atomistic investigation into the mechanical properties of the ferrite-cementite interface: The Bagaryatskii orientation. Acta Mater. 2017, 144, 656–665. [Google Scholar] [CrossRef]
- Pandkar, A.S.; Arakere, N.; Subhash, G. Microstructure-sensitive accumulation of plastic strain due to ratcheting in bearing steels subject to Rolling Contact Fatigue. Int. J. Fatigue 2014, 63, 191–202. [Google Scholar] [CrossRef]
- Sackfield, A.; Hills, D.A. Some useful results in the classical Hertz contact problem. J. Strain Anal. Eng. Des. 1983, 18, 101–105. [Google Scholar] [CrossRef]
- Radzimovsky, E.I. Stress distribution and strength condition of two rolling cylinders pressed together. Univ. Ill. Bull. 1953, 50, 1–40. [Google Scholar]
- Moghaddam, S.M.; Sadeghi, F.; Paulson, K.; Weinzapfel, N.; Correns, M.; Bakolas, V.; Dinkel, M. Effect of non-metallic inclusions on butterfly wing initiation, crack formation, and spall geometry in bearing steels. Int. J. Fatigue 2015, 80, 203–215. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Kang, K.; Ryu, S. Characterization of the misfit dislocations at the ferrite/cementite interface in pearlitic steel: An atomistic simulation study. Int. J. Plast. 2016, 83, 302–312. [Google Scholar] [CrossRef]
- Bhadeshia, H. Solution to the Bagaryatskii and Isaichev ferrite–cementite orientation relationship problem. Mater. Sci. Technol. 2018, 34, 1666–1668. [Google Scholar] [CrossRef] [Green Version]
- Liyanage, L.S.I.; Kim, S.G.; Houze, J.; Kim, S.; Tschopp, M.A.; Baskes, M.I.; Horstemeyer, M.F. Structural, elastic, and thermal properties of cementite (Fe3C) calculated using a modified embedded atom method. Phys. Rev. B 2014, 89, 094102. [Google Scholar] [CrossRef] [Green Version]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heyes, D.M. Pressure tensor of partial-charge and point-dipole lattices with bulk and surface geometries. Phys. Rev. B Condens Matter 1994, 49, 755. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 2154–2162. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Yuan, X.; Yu, W.; Fu, S.C.; Yu, D.; Chen, X. Effect of mean stress and ratcheting strain on the low cycle fatigue behavior of a wrought 316LN stainless steel. Mater. Sci. Eng. A 2016, 677, 193–202. [Google Scholar] [CrossRef]
- Kang, G.; Dong, Y.; Liu, Y.; Wang, H.; Cheng, X. Uniaxial ratchetting of 20 carbon steel: Macroscopic and microscopic experimental observations. Mater. Sci. Eng. A 2011, 528, 5610–5620. [Google Scholar] [CrossRef]
- Matthews, J.W.; Blakeslee, A.E. Defects in Epitaxial Multilayers. I. Misfit Dislocations. J. Cryst. Growth 1974, 27, 118–125. [Google Scholar] [CrossRef]
- Stukowski, A.; Albe, K. Extracting dislocations and non-dislocation crystal defects from atomistic simulation data. Model. Simul. Mater. Sci. Eng. 2010, 119, 2131–2145. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, S.; Zhu, X.; Zhao, Y. Mechanisms of crack propagation in nanoscale single crystal, bicrystal and tricrystal nickels based on molecular dynamics simulation. Results Phys. 2017, 7, 1722–1733. [Google Scholar] [CrossRef]
- Liang, L.; Xiang, L.; Wang, Y.; Chen, Y.; Wang, H.; Dai, L. Ratchetting in cold-drawn pearlitic steel wires. Metall. Mater. Trans. A 2019, 50, 4561–4568. [Google Scholar] [CrossRef]
- Shimizu, F.; Ogata, S.; Li, J. Theory of Shear Banding in Metallic Glasses and Molecular Dynamics Calculations. Mater. Trans. 2007, 48, 2923–2927. [Google Scholar] [CrossRef] [Green Version]
- Shibanuma, K.; Aihara, S.; Ohtsuka, S. Observation and Quantification of Crack Nucleation in Ferrite-Cementite Steel. ISIJ Int. 2013, 99, 582–591. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Cao, H.; Wei, X. Micromechanism of Plastic Accumulation and Damage Initiation in Bearing Steels under Cyclic Shear Deformation: A Molecular Dynamics Study. Machines 2022, 10, 199. https://doi.org/10.3390/machines10030199
Sun Y, Cao H, Wei X. Micromechanism of Plastic Accumulation and Damage Initiation in Bearing Steels under Cyclic Shear Deformation: A Molecular Dynamics Study. Machines. 2022; 10(3):199. https://doi.org/10.3390/machines10030199
Chicago/Turabian StyleSun, Yachao, Hongrui Cao, and Xunkai Wei. 2022. "Micromechanism of Plastic Accumulation and Damage Initiation in Bearing Steels under Cyclic Shear Deformation: A Molecular Dynamics Study" Machines 10, no. 3: 199. https://doi.org/10.3390/machines10030199
APA StyleSun, Y., Cao, H., & Wei, X. (2022). Micromechanism of Plastic Accumulation and Damage Initiation in Bearing Steels under Cyclic Shear Deformation: A Molecular Dynamics Study. Machines, 10(3), 199. https://doi.org/10.3390/machines10030199





