A Comparative Study to Predict Bearing Degradation Using Discrete Wavelet Transform (DWT), Tabular Generative Adversarial Networks (TGAN) and Machine Learning Models
Abstract
:1. Introduction
2. Materials and Method
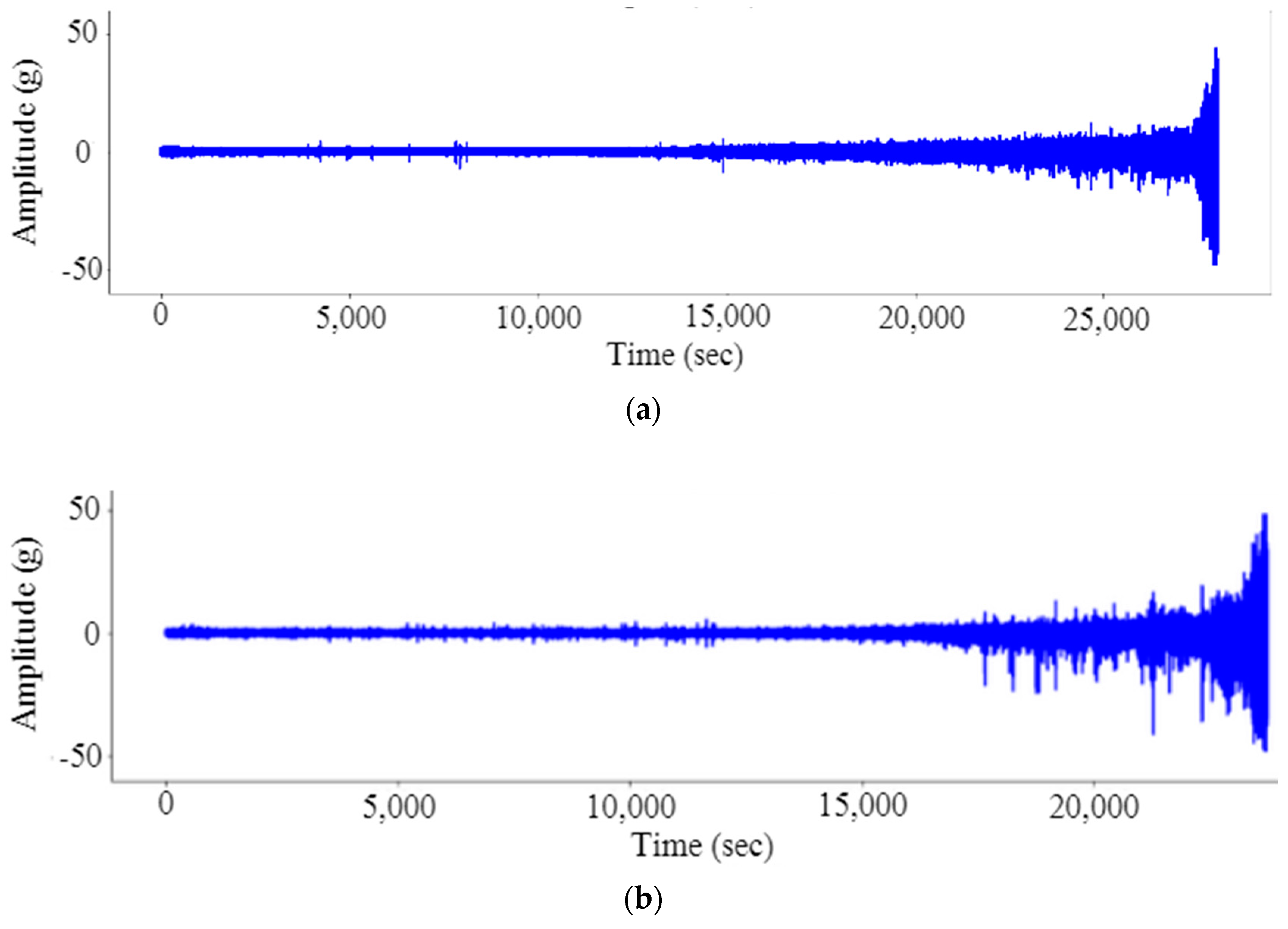
2.1. Dataset
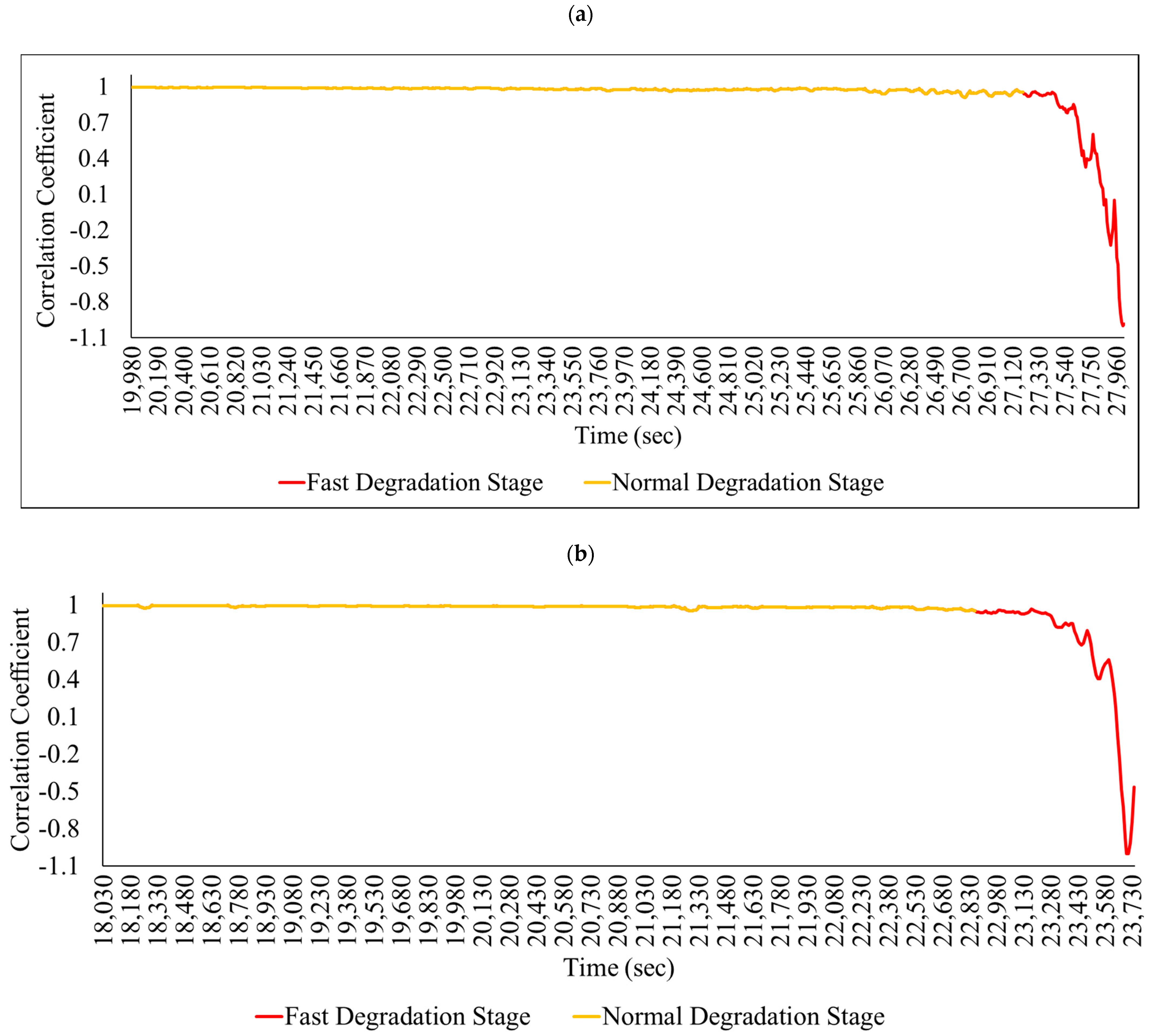
2.2. Health Assessment
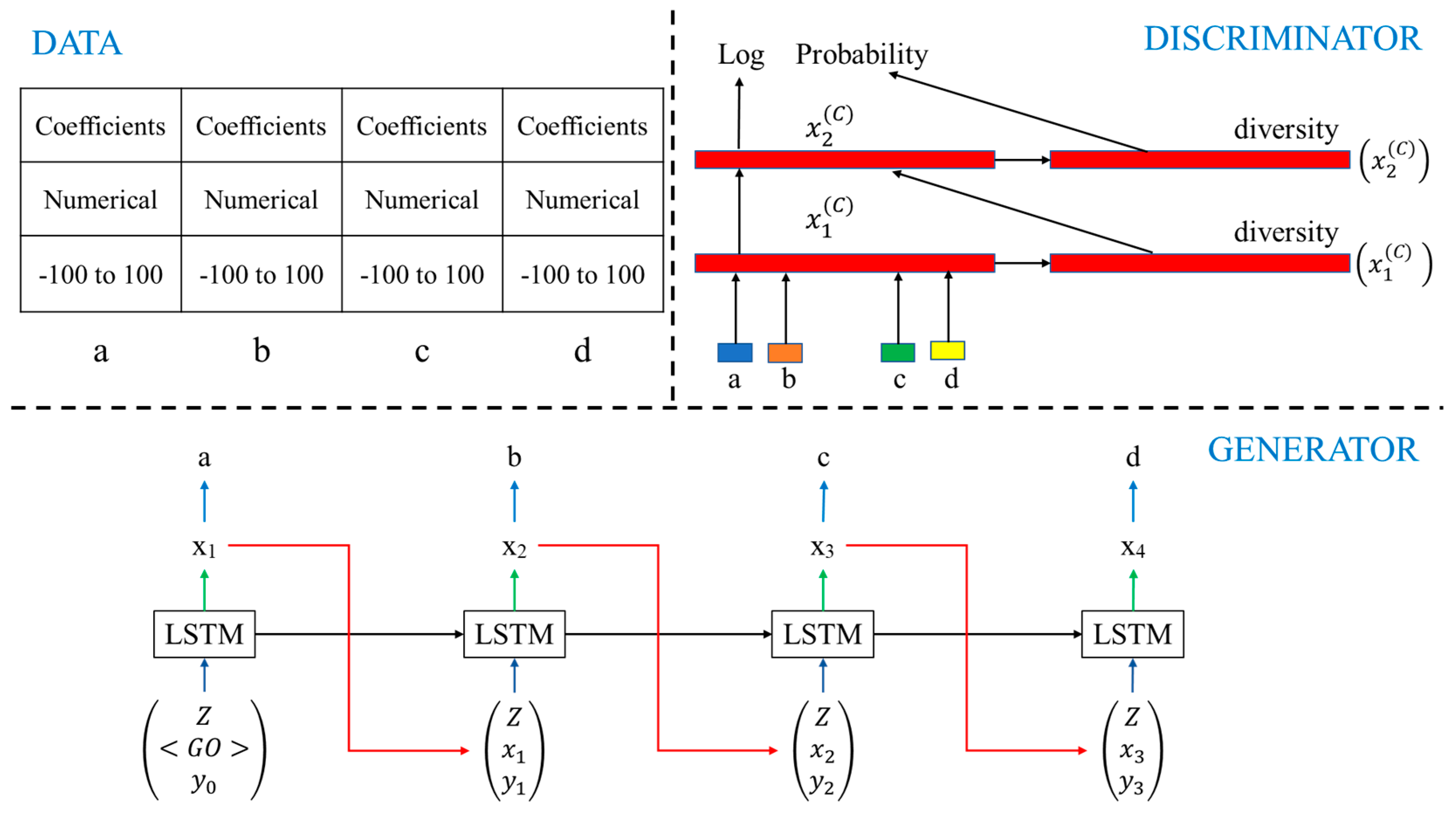
2.3. Tabular Generative Adversarial Networks
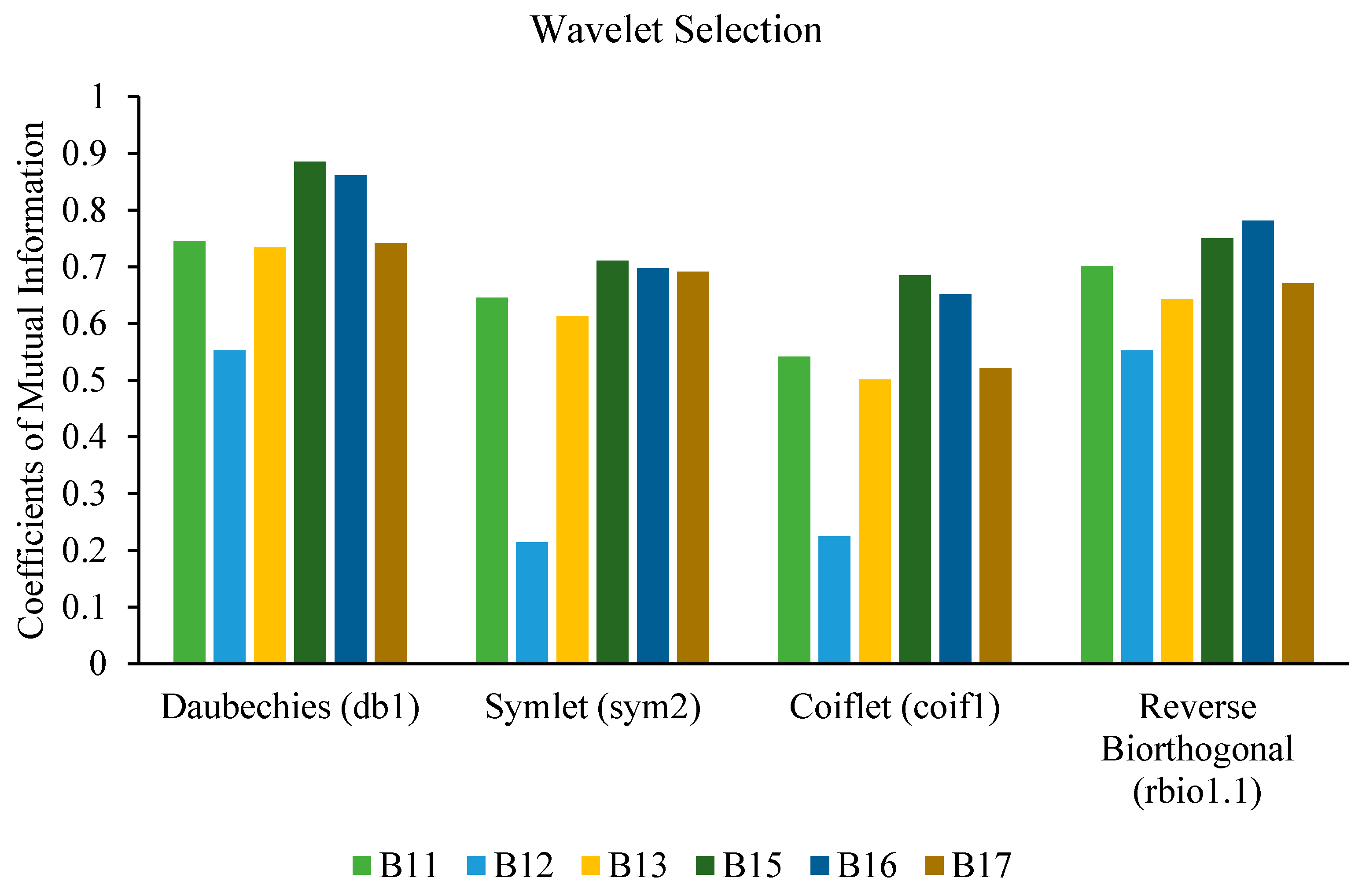
2.4. Feature Extraction
2.5. Machine Learning Models
2.5.1. Ensemble Bagged Trees
2.5.2. Squared Exponential Gaussian Processes Regression (SEGPR)
3. Results and Discussions
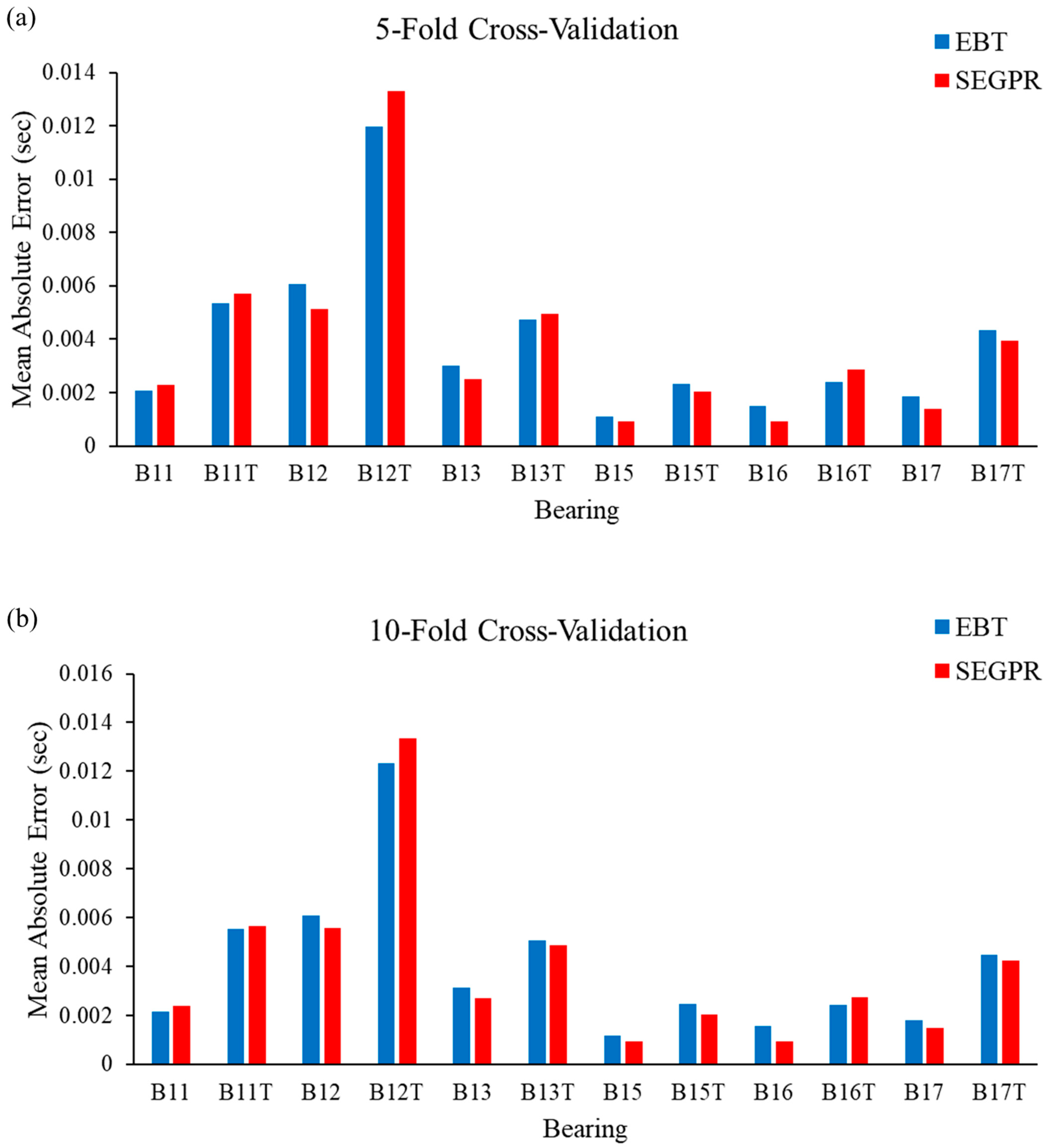
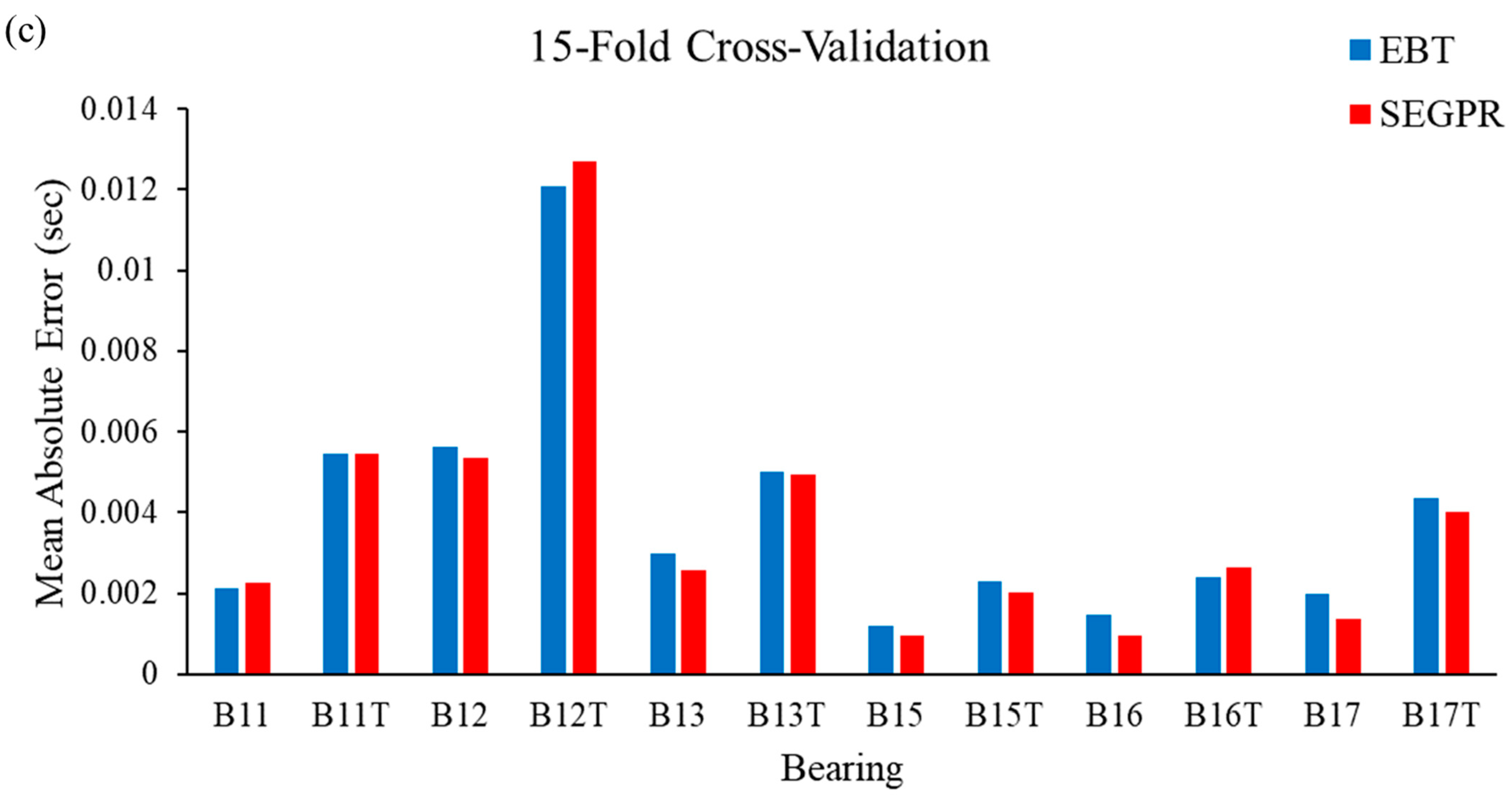
3.1. Mean Absolute Error (MAE)
3.2. Root Mean Square Error (MAE)
4. Conclusions
- The effectiveness of ML models was assessed with two standard performance metrics: RMSE and MAE. Least errors have been observed to predict bearing degradation from both the EBT and SEGPR models.
- The lowest RMSE value of 0.0045 was observed with the SEGPR model when fifteen-fold cross-validation was implemented, whereas with the EBT model, the lowest RMSE was observed as 0.0047 when five-fold cross-validation was implemented.
- With the SEGPR model, the lowest MAE value observed was 0.0037 when fifteen-fold cross-validation was implemented, whereas with the EBT model, the lowest MAE was observed as 0.0038 with five-fold cross-validation.
- The methodology developed based on hybrid TGAN–SEGPR, which is least explored for bearing degradation, can be useful to various applications including fault diagnosis, fault severity, and manufacturing parameter assessments, when the availability of experimental data is limited, which makes difficult to develop ML models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PHM | Prognostics and Health Management |
| MI | Mutual Information |
| RUL | Remaining Useful Life |
| CNN | Convolution Neural Network |
| DWT | Discrete Wavelet Transform |
| GAN | Generative Neural Network |
| TGAN | Tabular Generative Neural Network |
| BN | Batch Normalization |
| NASA | National Aeronautics and Space Administration |
| SVD | Singular Value Decomposition |
| db | Daubechies Wavelet |
| sym | Symlet Wavelet |
| coif | Coiflet Wavelet |
| rbio | Reverse Biorthogonal Wavelet |
| LSTM | Long Short-Term Memory |
| MLP | Multi-Layer Perceptron |
| ML | Machine Learning |
| EBT | Ensemble Bagged Trees |
| SEGPR | Squared Exponential Gaussian Processes Regression |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| KL | Kullback–Leibler |
Notation
| xt | Hidden Vector |
| ki | Output of LSTM, k = a, b, c |
| K | Total number of samples |
| k | Current sample |
| j | 1…N, q represent the length of singular value vectors |
| x(k) | Value of current sample |
| s(ui,uj) | Output of squared exponential kernel function |
| ui | Value of signal at location i |
| uj | Value of signal at location j |
| Vt | Learned parameter in the network |
| diversity | Mini-batch discrimination vector |
| xm | Mean |
| xstd | Standard deviation |
| xvar | Variance |
| xskew | Skewness |
| xkurt | Kurtosis |
| xrms | Root mean square |
| xppv | Peak to peak value |
| xmax | Maximum amplitude |
| xmin | Minimum amplitude |
| xIF | Impulse factor |
| xCF | Crest factor |
| xSF | Shape factor |
| y | Weight vector |
| z | Random noise |
| ⊕ | Concatenation operator |
| σlc | Characteristic length scale |
| σstd | Standard deviation of the signal |
| Tsynth | Synthetic table |
| C1, C2, C3 …, Cnr | Continuous variable |
| Dmr1, Dmr2, Dmr3 ……, Dnr | Multinomial discrete random variables |
| x, y | Singular value vectors of the signal |
References
- Heng, A.; Zhang, S.; Tan, A.C.; Mathew, J. Rotating machinery prognostics: State of the art, challenges and opportunities. Mech. Syst. Signal Process. 2009, 23, 724–739. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Fault diagnosis of ball bearings using machine learning methods. Expert Syst. Appl. 2011, 38, 1876–1886. [Google Scholar] [CrossRef]
- Vakharia, V.; Gupta, V.; Kankar, P. Nonlinear dynamic analysis of ball bearings due to varying number of balls and centrifugal force. In Proceedings of the 9th IFToMM International Conference on Rotor Dynamics; Springer: Milan, Italy, 2015; pp. 1831–1840. [Google Scholar]
- Benkedjouh, T.; Medjaher, K.; Zerhouni, N.; Rechak, S. Remaining useful life estimation based on nonlinear feature reduction and support vector regression. Eng. Appl. Artif. Intell. 2013, 26, 1751–1760. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Robust performance degradation assessment methods for enhanced rolling element bearing prognostics. Adv. Eng. Inform. 2003, 17, 127–140. [Google Scholar] [CrossRef]
- Albrecht, P.; Appiarius, J.; McCoy, R.; Owen, E.; Sharma, D. Assessment of the reliability of motors in utility applications-Updated. IEEE Trans. Energy Convers. 1986, EC-1, 39–46. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Gontarz, S.; Lin, J.; Radkowski, S.; Dybala, J. A model-based method for remaining useful life prediction of machinery. IEEE Trans. Reliab. 2016, 65, 1314–1326. [Google Scholar] [CrossRef]
- Omoregbee, H.O.; Heyns, P.S. Fault classification of low-speed bearings based on support vector machine for regression and genetic algorithms using acoustic emission. J. Vib. Eng. Technol. 2019, 7, 455–464. [Google Scholar] [CrossRef]
- Jardine, A.K.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Bustillo, A.; Pimenov, D.Y.; Matuszewski, M.; Mikolajczyk, T. Using artificial intelligence models for the prediction of surface wear based on surface isotropy levels. Robot. Comput.-Integr. Manuf. 2018, 53, 215–227. [Google Scholar] [CrossRef]
- Dave, V.; Singh, S.; Vakharia, V. Diagnosis of bearing faults using multi fusion signal processing techniques and mutual information. Indian J. Eng. Mater. Sci. 2021, 27, 878–888. [Google Scholar]
- Akhenia, P.; Bhavsar, K.; Panchal, J.; Vakharia, V. Fault severity classification of ball bearing using SinGAN and deep convolutional neural network. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.; An, W.; Liu, H.; Jiang, T. Rolling Bearing Performance Degradation Prediction Based on FBG Signal. IEEE Sens. J. 2021, 21, 24134–24141. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Deep learning-based remaining useful life estimation of bearings using multi-scale feature extraction. Reliab. Eng. Syst. Saf. 2019, 182, 208–218. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, N.; Peng, W. Estimation of bearing remaining useful life based on multiscale convolutional neural network. IEEE Trans. Ind. Electron. 2018, 66, 3208–3216. [Google Scholar] [CrossRef]
- Behzad, M.; Arghand, H.A.; Rohani Bastami, A. Remaining useful life prediction of ball-bearings based on high-frequency vibration features. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 3224–3234. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Tang, J.; Li, Y. Predicting remaining useful life of rolling bearings based on deep feature representation and long short-term memory neural network. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Yoo, Y.; Baek, J.-G. A novel image feature for the remaining useful lifetime prediction of bearings based on continuous wavelet transform and convolutional neural network. Appl. Sci. 2018, 8, 1102. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Lei, Y.; Li, N.; Li, N. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings. IEEE Trans. Reliab. 2018, 69, 401–412. [Google Scholar] [CrossRef]
- Ye, X.; Li, G.; Meng, L.; Lu, G. Dynamic health index extraction for incipient bearing degradation detection. ISA Trans. 2021. [Google Scholar] [CrossRef]
- Savić, B.; Urošević, V.; Ivković, N.; Popović, M.; Gubeljak, N.; Šiniković, G. Implementation of a Non-Linear Regression Model in Rolling Bearing Diagnostics. Teh. Vjesn. 2022, 29, 314–321. [Google Scholar]
- Blaut, J.; Breńkacz, Ł. Application of the Teager-Kaiser energy operator in diagnostics of a hydrodynamic bearing. Eksploat. I Niezawodn. 2020, 22, 757–765. [Google Scholar] [CrossRef]
- Kubik, A.; Stanik, Z.; Hadryś, D.; Csiszár, C. Impact of Selected Operational Parameters on Measures of Technical Condition of Rolling Bearings in Means of Transport Built Based on Analysis of Vibration Signals. Sci. J. Silesian Univ. Technol. Ser. Transp. 2021, 111, 89–98. [Google Scholar] [CrossRef]
- Verstraete, D.; Droguett, E.; Modarres, M. A deep adversarial approach based on multi-sensor fusion for semi-supervised remaining useful life prognostics. Sensors 2020, 20, 176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Zhang, W.; Ma, H.; Luo, Z.; Li, X. Data alignments in machinery remaining useful life prediction using deep adversarial neural networks. Knowl.-Based Syst. 2020, 197, 105843. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management, PHM’12, Denver, CO, USA, 18–21 June 2012; pp. 1–8. [Google Scholar]
- Bustillo, A.; Pimenov, D.Y.; Mia, M.; Kapłonek, W. Machine-learning for automatic prediction of flatness deviation considering the wear of the face mill teeth. J. Intell. Manuf. 2021, 32, 895–912. [Google Scholar] [CrossRef]
- Bustillo, A.; Reis, R.; Machado, A.R.; Pimenov, D.Y. Improving the accuracy of machine-learning models with data from machine test repetitions. J. Intell. Manuf. 2020, 1–19. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.Y.; Wang, Z.; Paul Smolley, S. Least squares generative adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2794–2802. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, Sydney, NSW, Australia, 11 August 2017; pp. 214–223. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. Available online: https://arxiv.org/abs/1411.1784 (accessed on 26 January 2022).
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. Infogan: Interpretable representation learning by information maximizing generative adversarial nets. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2180–2188. [Google Scholar]
- Odena, A.; Olah, C.; Shlens, J. Conditional image synthesis with auxiliary classifier gans. In Proceedings of the International Conference on Machine Learning, Sydney, NSW, Australia, 10 April 2017; pp. 2642–2651. [Google Scholar]
- Odena, A. Semi-supervised learning with generative adversarial networks. arXiv 2016, arXiv:1606.01583. Available online: https://arxiv.org/abs/1606.01583 (accessed on 26 January 2022).
- Xu, L.; Veeramachaneni, K. Synthesizing tabular data using generative adversarial networks. arXiv 2018, arXiv:1811.11264. Available online: https://arxiv.org/abs/1811.11264 (accessed on 26 January 2022).
- Zheng, Y.-J.; Zhou, X.-H.; Sheng, W.-G.; Xue, Y.; Chen, S.-Y. Generative adversarial network based telecom fraud detection at the receiving bank. Neural Netw. 2018, 102, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Malla, C.; Panigrahi, I. Review of condition monitoring of rolling element bearing using vibration analysis and other techniques. J. Vib. Eng. Technol. 2019, 7, 407–414. [Google Scholar] [CrossRef]
- Vakharia, V.; Gupta, V.; Kankar, P. Efficient fault diagnosis of ball bearing using ReliefF and Random Forest classifier. J. Braz. Soc. Mech. Sci. Eng. Appl. Artif. Intell. 2017, 39, 2969–2982. [Google Scholar] [CrossRef]
- Upadhyay, R.; Padhy, P.; Kankar, P. A comparative study of feature ranking techniques for epileptic seizure detection using wavelet transform. Comput. Electr. Eng. 2016, 53, 163–176. [Google Scholar] [CrossRef]
- Duvenaud, D. Automatic Model Construction with Gaussian Processes. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2014. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, UK, 2006. [Google Scholar]
- Vakharia, V.; Gupta, V.; Kankar, P. A multiscale permutation entropy based approach to select wavelet for fault diagnosis of ball bearings. J. Vib. Control 2015, 21, 3123–3131. [Google Scholar] [CrossRef]
- Ross, B.C. Mutual information between discrete and continuous data sets. PLoS ONE 2014, 9, e87357. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.-R.; Lee, J.-E.; Zeng, Y.-M. Time series multiple channel convolutional neural network with attention-based long short-term memory for predicting bearing remaining useful life. Sensors 2020, 20, 166. [Google Scholar] [CrossRef] [Green Version]
- Niu, Q.; Tong, Q.; Cao, J.; Zhang, Y.; Liu, F. On-line prediction remaining useful life for ball bearings via grey NARX. J. Vibroeng. 2019, 21, 82–96. [Google Scholar]






| Operating Condition | |||
|---|---|---|---|
| Condition 1 | Condition 2 | Condition 3 | |
| Radial load (N) | 4000 | 4200 | 5000 |
| Speed (RPM) | 1800 | 1650 | 1500 |
| Dataset | Bearing11 | Bearing21 | Bearing31 |
| Bearing12 | Bearing22 | Bearing32 | |
| Bearing13 | Bearing23 | Bearing33 | |
| Bearing14 | Bearing24 | ||
| Bearing15 | Bearing25 | ||
| Bearing16 | Bearing26 | ||
| Bearing17 | Bearing27 | ||
| Name | Description | Formula | |
|---|---|---|---|
| Mean | The average value of the vibration signal | (3) | |
| Standard Deviation | Deviation from the mean value of the vibration signal | (4) | |
| Variance | Square of standard deviation | (5) | |
| Sum | Sum of signal | (6) | |
| Skewness | A measure of lack of symmetry | (7) | |
| Kurtosis | A measure of the spikiness of the signal relative to a normal distribution | (8) | |
| Root Mean Square (RMS) | The square root of the mean of squares of a signal | (9) | |
| Peak to Peak Value | Difference between maximum and minimum peak values | (10) | |
| Maximum Amplitude | Value of the maximum amplitude of the signal | ) | (11) |
| Minimum Amplitude | Value of the minimum amplitude of the signal | ) | (12) |
| Crest Factor | The ratio of peak value to RMS value | (13) | |
| Shape Factor | The ratio of RMS value and mean-value | (14) | |
| Impulse Factor | The ratio of max value and mean value | (15) | |
| Mean | Mean | Std | Std | Var | Var | RMS | RMS | |
|---|---|---|---|---|---|---|---|---|
| Original Features | Generated Features | Original Features | Generated Features | Original Features | Generated Features | Original Features | Generated Features | |
| Mean | 0.048 | 0.058 | 5.863 | 5.22 | 42.744 | 42.985 | 5.869 | 5.855 |
| Std | 0.381 | 0.351 | 2.908 | 2.887 | 43.260 | 43.842 | 2.915 | 2.896 |
| Min | 2.205 | 1.986 | 2.730 | 3.442 | 7.4578 | 6.987 | 2.730 | 2.425 |
| 25 | 0.033 | 0.092 | 3.455 | 3.885 | 11.937 | 11.845 | 3.454 | 3.198 |
| 50 | 0.010 | 0.012 | 4.950 | 5.441 | 24.513 | 23.854 | 4.955 | 4.287 |
| 75 | 0.088 | 0.089 | 7.930 | 8.661 | 62.901 | 61.825 | 7.984 | 7.511 |
| Max | 0.852 | 0.885 | 13.479 | 13.479 | 181.68 | 181.68 | 13.475 | 13.47 |
| Max | Max | Min | Min | P2P | P2P | Skew | Skew | |
| Original Features | Generated Features | Original Features | Generated Features | Original Features | Generated Features | Original Features | Generated Features | |
| Mean | 26.376 | 26.88 | 34.254 | 33.158 | 60.630 | 58.251 | 0.624 | 0.584 |
| Std | 13.575 | 13.896 | 13.029 | 12.586 | 24.980 | 23.420 | 0.566 | 0.486 |
| Min | 11.343 | 11.969 | 63.257 | 62.884 | 24.224 | 23.884 | 3.076 | 2.871 |
| 25 | 15.799 | 15.966 | 44.578 | 43.857 | 41.883 | 40.458 | 0.843 | 0.824 |
| 50 | 21.854 | 22.236 | 31.44 | 30.548 | 51.500 | 50.898 | 0.575 | 0.564 |
| 75 | 34.472 | 36.001 | 24.029 | 22.885 | 81.257 | 80.750 | 0.259 | 0.249 |
| Max | 68.063 | 69.012 | 12.881 | 13.987 | 131.32 | 131.32 | 0.524 | 0.514 |
| Kurt | Kurt | SF | SF | IF | IF | CF | CF | |
| Original Features | Generated Features | Original Features | Generated Features | Original Features | Generated Features | Original Features | Generated Features | |
| Mean | 9.084 | 8.854 | 1.467 | 1.384 | 6.672 | 6.445 | 4.539 | 4.586 |
| Std | 4.088 | 3.475 | 0.085 | 0.076 | 1.168 | 1.075 | 0.713 | 0.816 |
| Min | 3.292 | 2.745 | 1.269 | 1.148 | 4.189 | 4.096 | 3.191 | 3.091 |
| 25 | 6.293 | 6.110 | 1.413 | 1.388 | 5.957 | 5.348 | 4.043 | 4.055 |
| 50 | 7.888 | 7.550 | 1.463 | 1.446 | 6.571 | 6.412 | 4.388 | 4.281 |
| 75 | 10.742 | 10.314 | 1.529 | 1.498 | 7.525 | 7.539 | 5.047 | 4.889 |
| Max | 25.546 | 250.546 | 1.700 | 1.622 | 10.024 | 10.024 | 6.331 | 5.996 |
| References | Model | Dataset | MAE | RMSE |
|---|---|---|---|---|
| Xiang Li et al. [15] | CNN | 17 | 19.65882 | 23.61765 |
| Wentao Mao et al. [18] | CNN + LSTM | 4 | - | 80 |
| David Verstraete et al. [25] | Adversarial–Variational Model | 3 | - | 8.173333 |
| Xiang Li et al. [26] | GAN + CNN | 17 | - | 34.05882 |
| Jehn-Ruey Jiang et al. [46] | TSMC + CNN + ALSTM | - | 0.0186 | 0.0268 |
| Qiming Niu et al. [47] | NARX | 6 | 1.60 | 2.94 |
| Proposed | TGAN + SEGPR | 6 | 0.00225 (Real) | 0.00285 (Real) |
| 0.00529 (Artificial) | 0.00629 (Artificial) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhavsar, K.; Vakharia, V.; Chaudhari, R.; Vora, J.; Pimenov, D.Y.; Giasin, K. A Comparative Study to Predict Bearing Degradation Using Discrete Wavelet Transform (DWT), Tabular Generative Adversarial Networks (TGAN) and Machine Learning Models. Machines 2022, 10, 176. https://doi.org/10.3390/machines10030176
Bhavsar K, Vakharia V, Chaudhari R, Vora J, Pimenov DY, Giasin K. A Comparative Study to Predict Bearing Degradation Using Discrete Wavelet Transform (DWT), Tabular Generative Adversarial Networks (TGAN) and Machine Learning Models. Machines. 2022; 10(3):176. https://doi.org/10.3390/machines10030176
Chicago/Turabian StyleBhavsar, Keval, Vinay Vakharia, Rakesh Chaudhari, Jay Vora, Danil Yurievich Pimenov, and Khaled Giasin. 2022. "A Comparative Study to Predict Bearing Degradation Using Discrete Wavelet Transform (DWT), Tabular Generative Adversarial Networks (TGAN) and Machine Learning Models" Machines 10, no. 3: 176. https://doi.org/10.3390/machines10030176
APA StyleBhavsar, K., Vakharia, V., Chaudhari, R., Vora, J., Pimenov, D. Y., & Giasin, K. (2022). A Comparative Study to Predict Bearing Degradation Using Discrete Wavelet Transform (DWT), Tabular Generative Adversarial Networks (TGAN) and Machine Learning Models. Machines, 10(3), 176. https://doi.org/10.3390/machines10030176











