Integrated Conceptual Mechatronic Design of a Delta Robot
Abstract
:1. Introduction
1.1. Structural and Control Design
1.2. Mechatronic Design
1.3. Model-Based Systems Engineering
- A clarifying view for the recurrent process of black-box/white-box analysis during the design process, allowing a natural integration of multicriteria decision making tools for a mechatronic robot design;
- An integrated framework for mechatronic conceptual design considering both theoretical and numerical engineering tools such as complex decision making, automated optimization, mathematical, and CAD/CAE modeling techniques;
- An MBSE methodology that enables to capture knowledge in a systematic way from the user needs to successfully design a Delta robot in terms of requirements, functionality, design synthesis, validation, and other aspects of interest for the system itself;
- It is important to highlight that this design proposal renders a more general framework for automated design, although in this paper it is implemented for a conceptual Delta robot design.
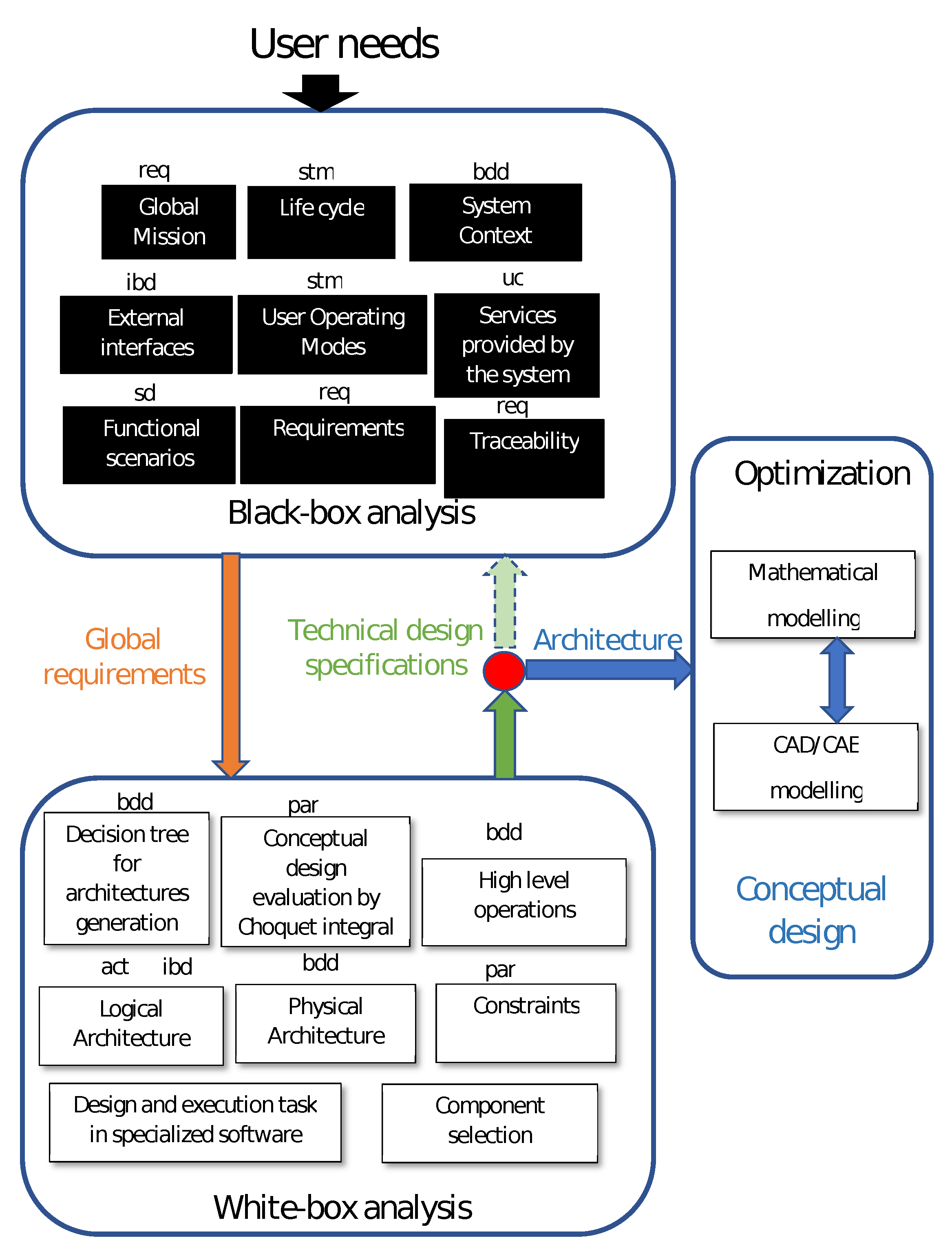
2. Methodology Overview
3. Delta Robot Design
3.1. Black-Box Analysis
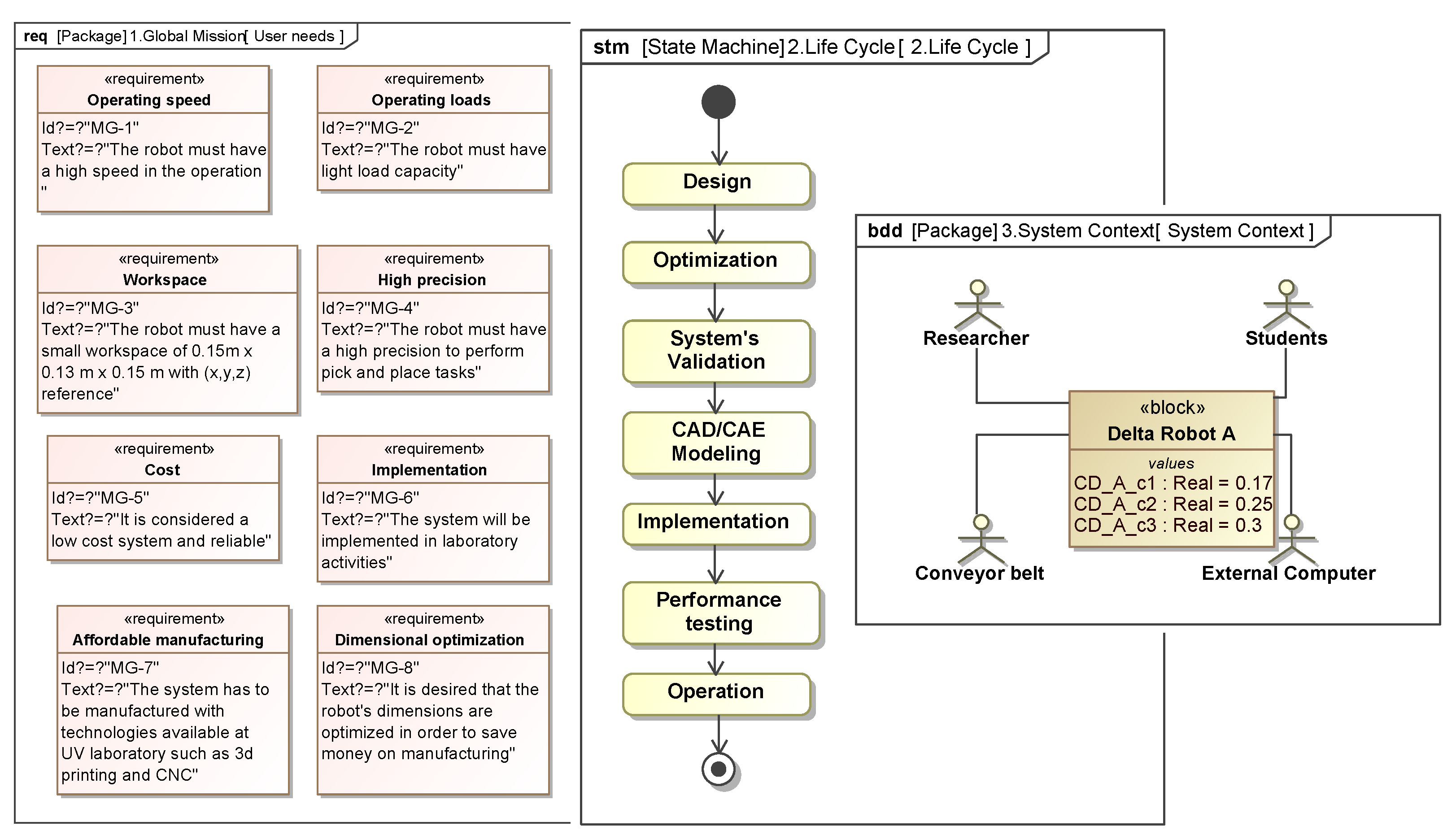
3.1.1. Global Mission
3.1.2. Life Cycle
3.1.3. System Context
3.1.4. External Interfaces
3.1.5. User Operation Modes
3.1.6. Services Provided by the System
3.1.7. Functional Scenarios
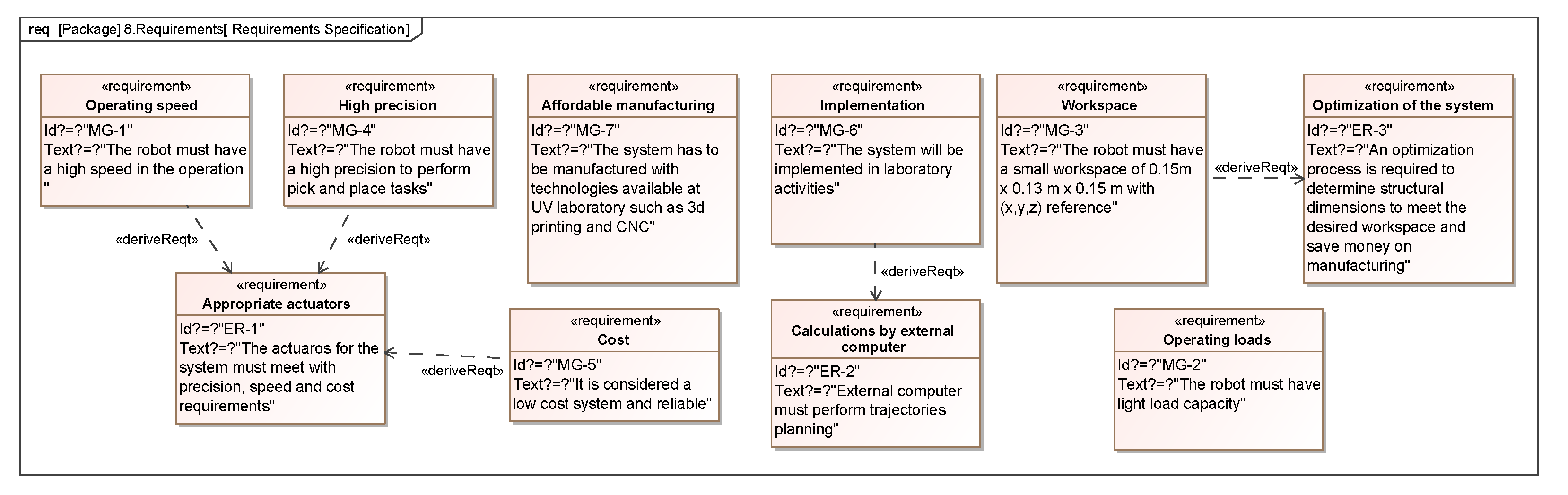
3.1.8. Requirements
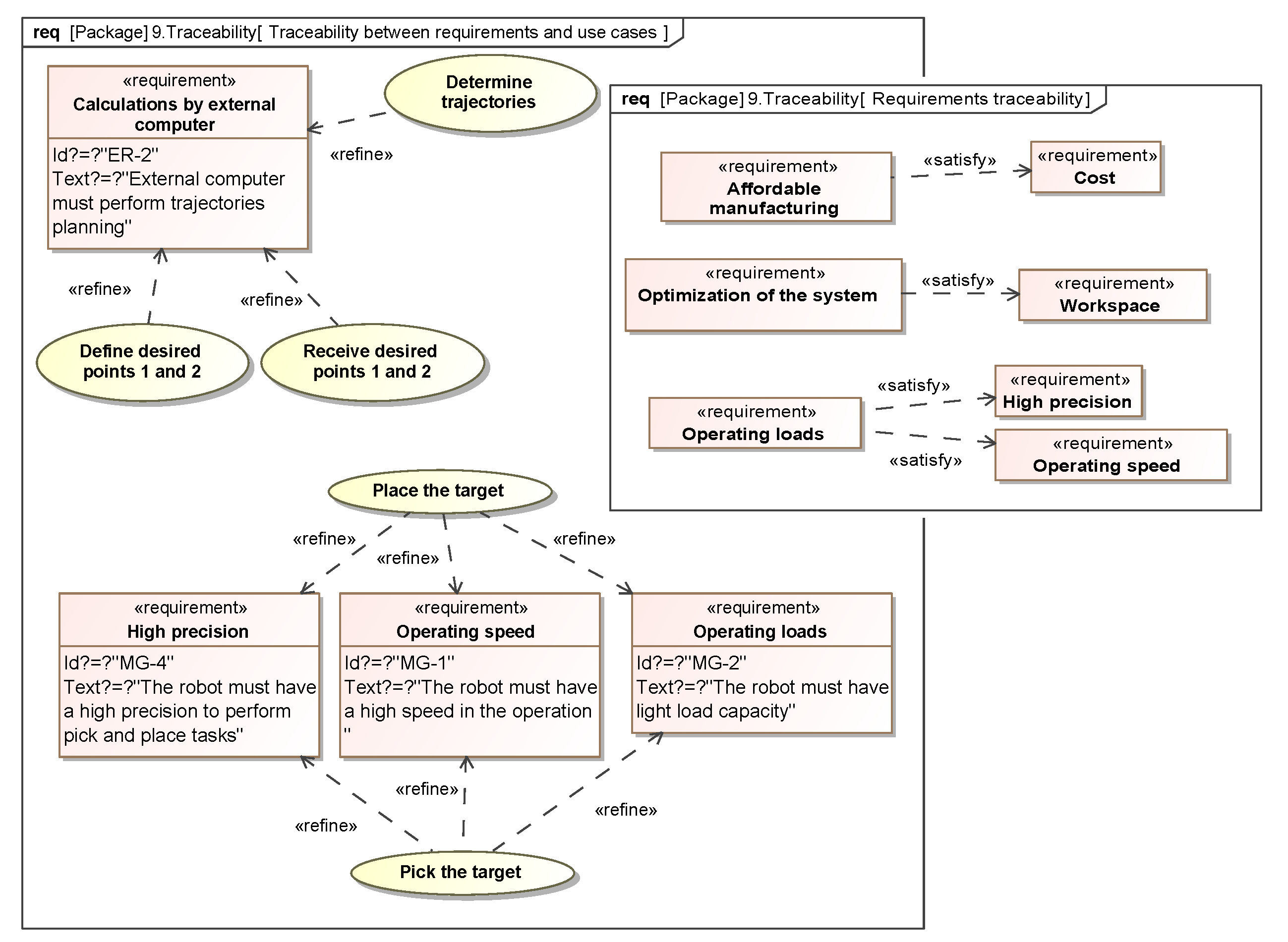
3.1.9. Traceability
3.2. White-Box Analysis
3.2.1. Decision Tree for Architectures Generation
3.2.2. Conceptual Design Evaluation
3.2.3. High Level Operations
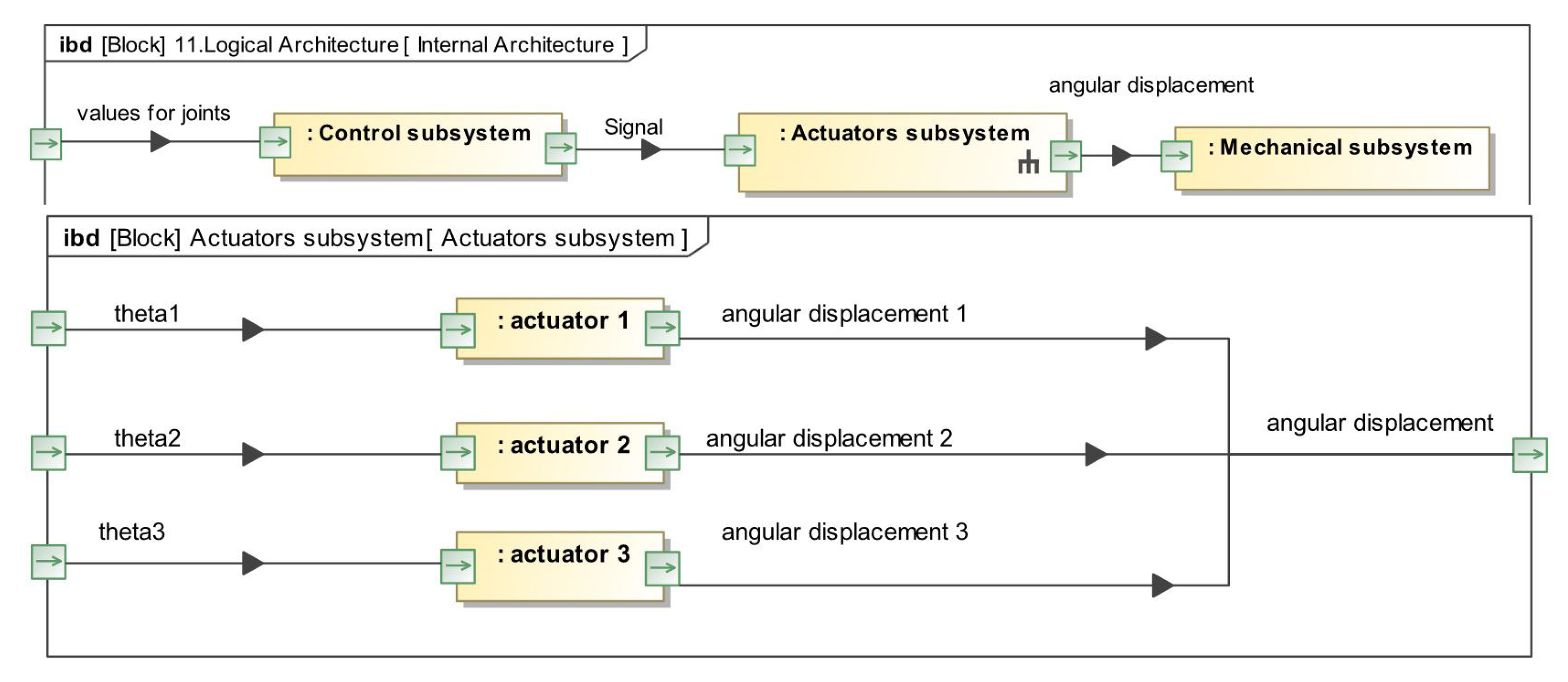
3.2.4. Logical Architecture
3.2.5. Physical Architecture
3.2.6. Constraints
3.2.7. Design and Execution Task
3.2.8. Component Selection
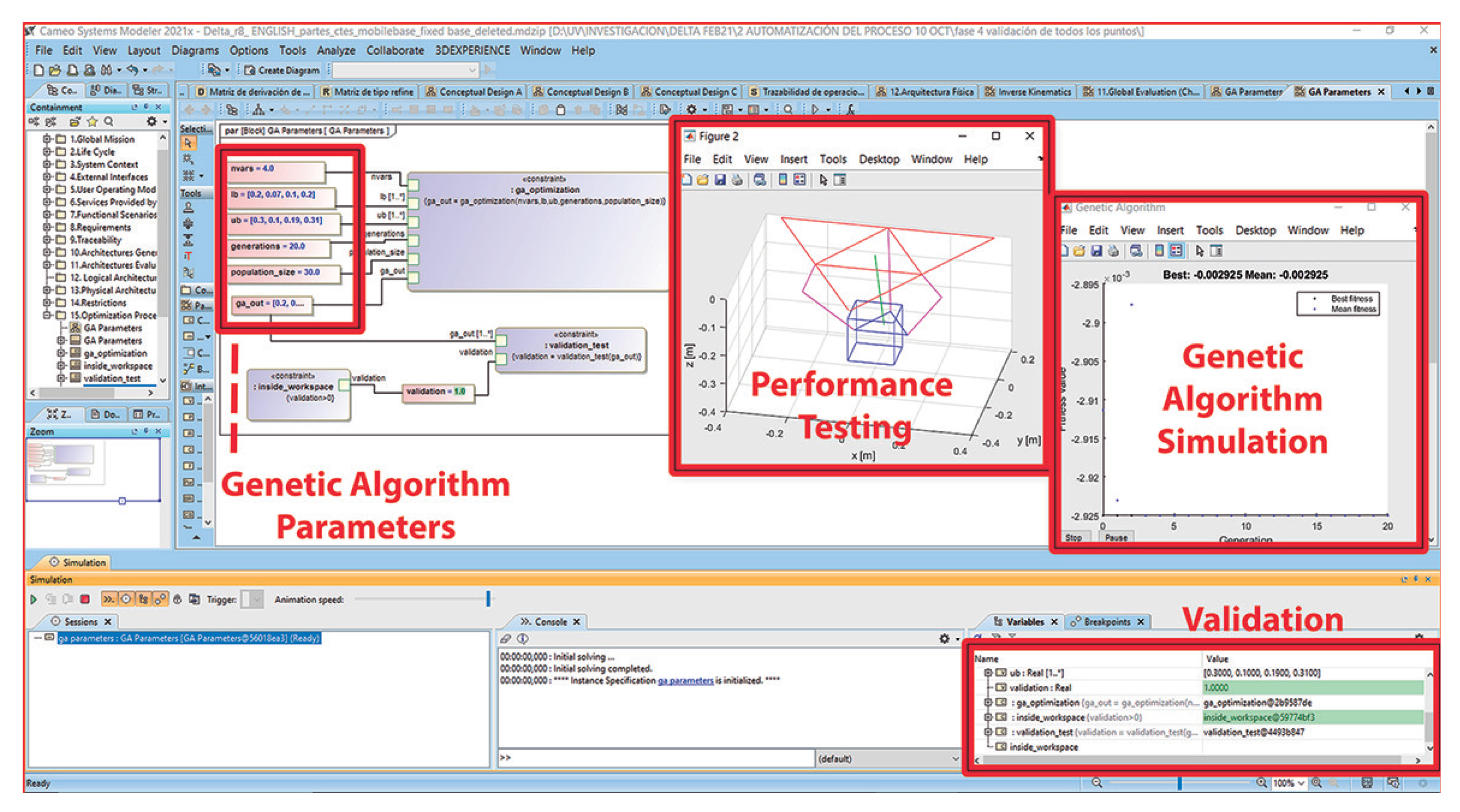
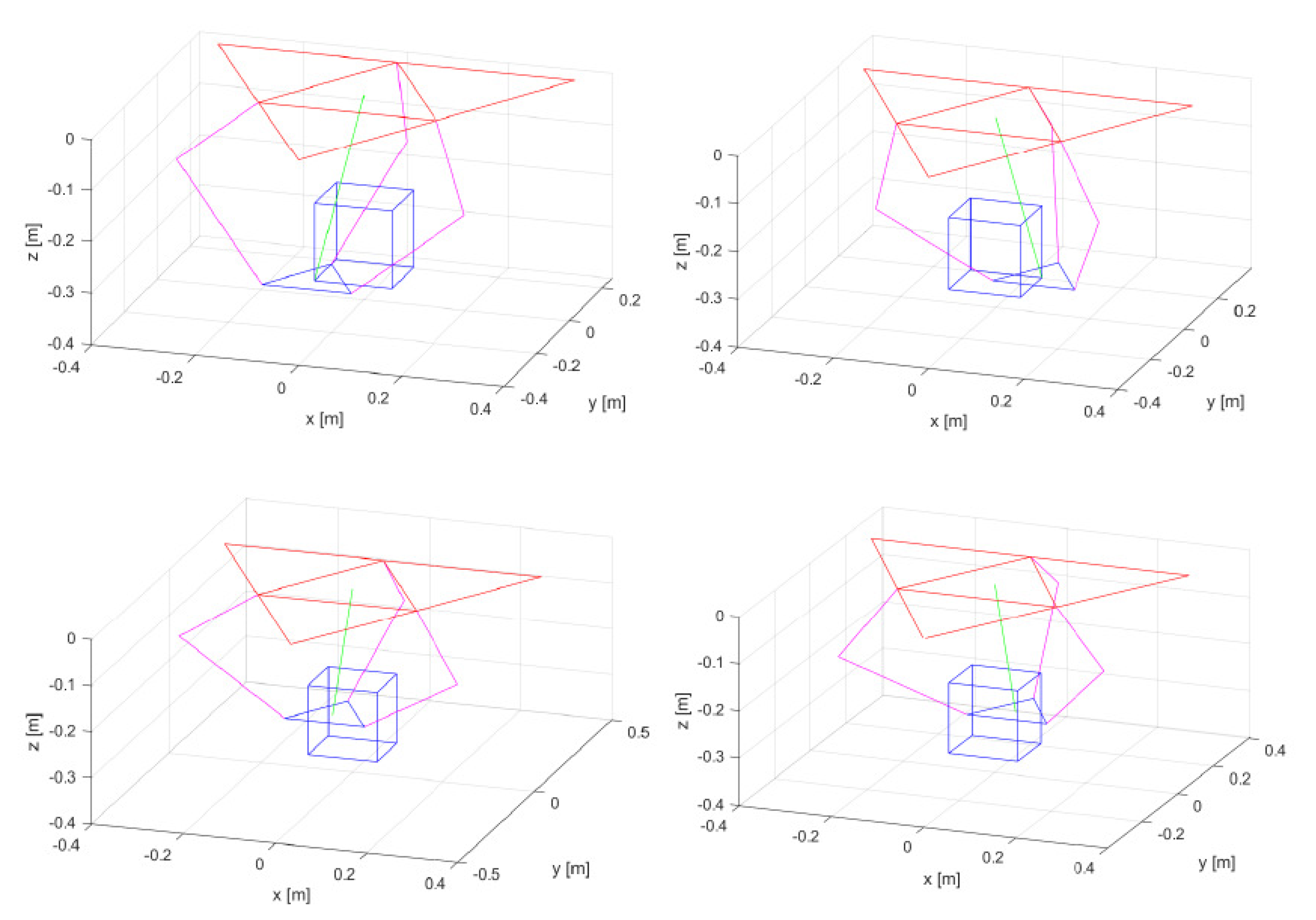
3.3. Optimization
Tools Integration
4. Validation of the Optimized System and Discussion
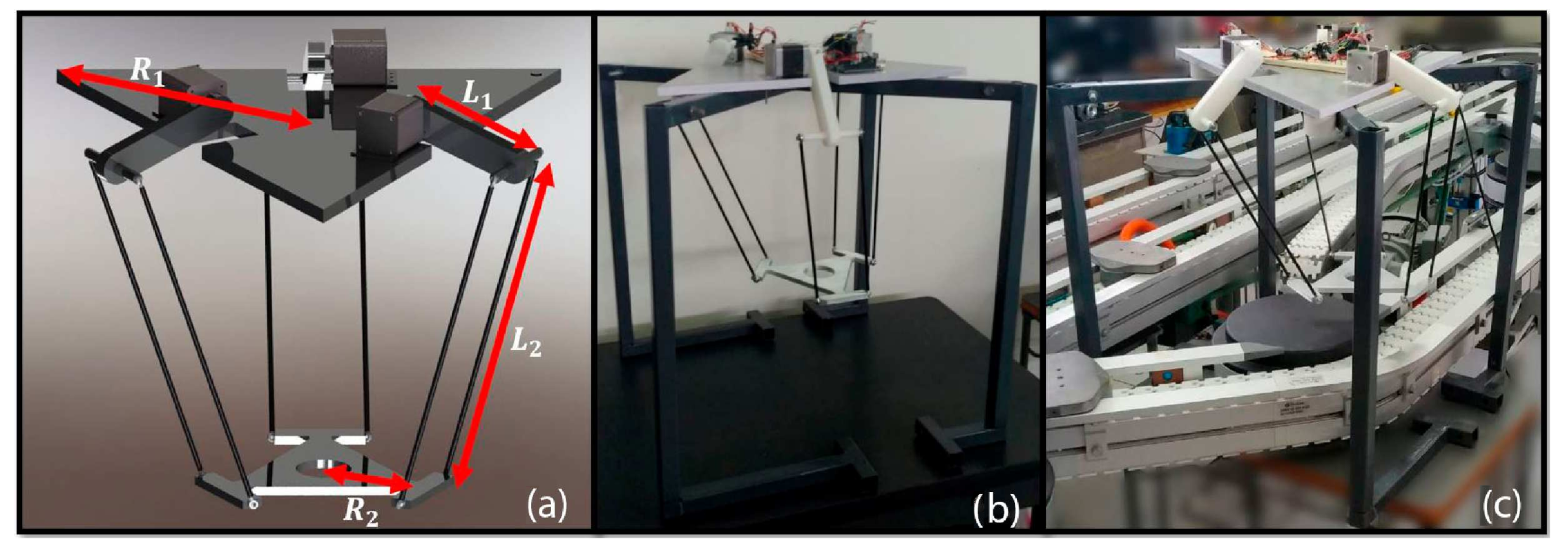
4.1. Prototyping
4.2. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| MBSE | Model-Based Systems Engineering |
| QFD | Quality Function Deployment |
| DOF | Degrees of Freedom |
| CAD | Computer Aided Design |
| CAE | Computer Aided Engineering |
| MDQ | Mechatronic Design Quotient |
| MDI | Mechatronic Design Indicator |
| CNC | Computer Numeric Control |
| PCB | Printed Circuit Board |
References
- Dehong, C.; Chengyao, L.; Ruchao, W.; Chen, S.; Chang, T.; Zhijian, Q. Innovative design and realization of lightweight delta robot platform. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 6068–6071. [Google Scholar]
- Chablat, D.; Kong, X.; Zhang, C. Kinematics, Workspace, and Singularity Analysis of a Parallel Robot with Five Operation Modes. J. Mech. Robot. 2018, 10, 035001. [Google Scholar] [CrossRef] [Green Version]
- Mahmoodi, M.; Tabrizi, M.G.; Alipour, K. A new approach for Kinematics-based design of 3-RRR delta robots with a specified workspace. In Proceedings of the 2015 AI Robotics (IRANOPEN), Qazvin, Iran, 12 April 2015; pp. 1–6. [Google Scholar]
- Patel, Y.D.; George, P. Parallel Manipulators Applications—A Survey. Mod. Mech. Eng. 2012, 40, 57–64. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Ye, W.; Li, Q. Review of the performance optimization of parallel manipulators. Mech. Mach. Theory 2022, 170, 104725. [Google Scholar] [CrossRef]
- Botello-Aceves, S.; Valdez, S.I.; Becerra, H.M.; Hernandez, E. Evaluating concurrent design approaches for a Delta parallel manipulator. Robotica 2018, 36, 697–714. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, C. Hybrid algorithm for multi-objective optimization design of parallel manipulators. Appl. Math. Model. 2021, 98, 245–265. [Google Scholar] [CrossRef]
- Meng, Q.; Li, J.; Shen, H.; Deng, J.; Wu, G. Kinetostatic design and development of a non-fully symmetric parallel Delta robot with one structural simplified kinematic linkage. Mech. Based Des. Struct. Mach. 2021, 1–21. [Google Scholar] [CrossRef]
- Préault, C.; Saafi, H.; Laribi, M.A.; Zeghloul, S. Optimal design and evaluation of a dexterous 4 DoFs haptic device based on delta architecture. Robotica 2019, 37, 1267–1288. [Google Scholar] [CrossRef]
- Llopis-Albert, C.; Valero, F.; Mata, V.; Pulloquinga, J.L.; Zamora-Ortiz, P.; Escarabajal, R.J. Optimal Reconfiguration of a Parallel Robot for Forward Singularities Avoidance in Rehabilitation Therapies. A Comparison via Different Optimization Methods. Sustainability 2020, 12, 5803. [Google Scholar] [CrossRef]
- Dastjerdi, A.H.; Sheikhi, M.M.; Masouleh, M.T. A complete analytical solution for the dimensional synthesis of 3-DOF delta parallel robot for a prescribed workspace. Mech. Mach. Theory 2020, 153, 103991. [Google Scholar] [CrossRef]
- Jiang, J.; Wu, D.; He, T.; Zhang, Y.; Li, C.; Sun, H. Kinematic analysis and energy saving optimization design of parallel lifting mechanism for stereoscopic parking robot. Energy Rep. 2022, 8, 2163–2178. [Google Scholar] [CrossRef]
- Yang, X.; Wang, S.; Dong, Y.; Yang, H. D2 Delta Robot Structural Design and Kinematics Analysis. IOP Conf. Ser. Mater. Sci. Eng. 2017, 274, 012009. [Google Scholar] [CrossRef]
- Stepanenko, O.; Bonev, I.A.; Zlatanov, D. A New 4-DOF Fully Parallel Robot with Decoupled Rotation for Five-Axis Micromachining Applications. J. Mech. Robot. 2019, 11, 031010. [Google Scholar] [CrossRef]
- McClintock, H.; Temel, F.Z.; Doshi, N.; Koh, J.S.; Wood, R.J. The milliDelta: A high-bandwidth, high-precision, millimeter-scale Delta robot. Sci. Robot. 2018, 3, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, J.; Luo, C.H.; Lin, K.H. Design and Implementation of a New DELTA Parallel Robot in Robotics Competitions. Int. J. Adv. Robot. Syst. 2015, 12, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Valles, M.; Araujo-Gómez, P.; Mata, V.; Valera, A.; Díaz-Rodríguez, M.; Page, Á.; Farhat, N.M. Mechatronic design, experimental setup, and control architecture design of a novel 4 DoF parallel manipulator. Mech. Based Des. Struct. Mach. 2018, 46, 425–439. [Google Scholar] [CrossRef]
- Alvares, A.J.; Gasca, E.A.R.; Jaimes, C.I.R. Development of the Linear Delta Robot for Additive Manufacturing. In Proceedings of the 2018 5th International Conference on Control, Decision and Information Technologies (CoDIT), Thessaloniki, Greece, 10–13 April 2018; pp. 187–192. [Google Scholar]
- Rodriguez, E.; Alvares, A.J.; Jaimes, C.I. Conceptual design and dimensional optimization of the linear delta robot with single legs for additive manufacturing. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2019, 233, 855–869. [Google Scholar] [CrossRef]
- Li, J.; Liu, L. Conceptual Design of Mechatronics System Based on Intelligent Control. J. Phys. Conf. Ser. 2021, 1982, 1–6. [Google Scholar] [CrossRef]
- Curcio, E.; Carbone, G. Mechatronic Design of a Robot for Upper Limb Rehabilitation at Home. J. Biomed. Eng. 2021, 18, 857–871. [Google Scholar] [CrossRef]
- Morales-Cruz, C.; Ceccarelli, M.; Portilla-Flores, E.A. An Innovative Optimization Design Procedure for Mechatronic Systems with a Multi-Criteria Formulation. Appl. Sci. 2021, 11, 8900. [Google Scholar] [CrossRef]
- Huldt, T.; Stenius, I. State-of-practice survey of model-based systems engineering. Syst. Eng. 2019, 22, 134–145. [Google Scholar] [CrossRef]
- Furterer, S. Systems Engineering; CRC-Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Mabrouk, A.; Penas, O.; Plateaux, R.; Barkallah, M.; Choley, J.Y.; Akrout, A. Integration of agility in a MBSE methodology for multidisciplinary systems design. In Proceedings of the 2018 IEEE International Systems Engineering Symposium (ISSE), Rome, Italy, 1–3 October 2018; pp. 1–5. [Google Scholar]
- Barbedienne, R.; Penas, O.; Choley, J.Y.; Hehenberger, P. Modeling Framework for a Consistent Integration of Geometry Knowledge during Conceptual Design. J. Comput. Inf. Sci. Eng. 2019, 19, 021009. [Google Scholar] [CrossRef]
- Kass, N.; Kolozs, J. Getting Started with MBSE in Product Development. In Proceedings of the 26th Annual INCOSE International Symposium (IS 2016), Edinburgh, UK, 18–21 July 2016. [Google Scholar]
- Morkevicius, A.; Aleksandraviciene, A.; Mazeika, D.; Bisikirskiene, L.; Strolia, Z. MBSE Grid: A Simplified SysML Based Approach for Modeling Complex Systems. INCOSE Int. Symp. 2017, 27, 136–150. [Google Scholar] [CrossRef]
- Delligatti, L. SysML Distilled: A Brief Guide to the Systems Modeling Language, 1st ed.; Addison-Wesley Professional: Boston, MA, USA, 2013. [Google Scholar]
- Vazquez-Santacruz, J.; Torres-Figueroa, J.; Portillo-Vélez, R.D.J. Design of a human-like biped locomotion system based on a novel mechatronic methodology. Concurr. Eng. 2019, 27, 249–267. [Google Scholar] [CrossRef]
- Basnet, S.; Bahootoroody, A.; Chaal, M.; Valdez Banda, O.A.; Lahtinen, J.; Kujala, P. A decision-making framework for selecting an MBSE language–A case study to ship pilotage. Expert Syst. Appl. 2022, 193, 116451. [Google Scholar] [CrossRef]
- Silva, C.D.; Behbahani, S. A design paradigm for mechatronic systems. Mechatronics 2013, 23, 960–966. [Google Scholar] [CrossRef]
- Hammadi, M.; Choley, J.; Penas, O.; Riviere, A.; Louati, J.; Haddar, M. A new multi-criteria indicator for mechatronic system performance evaluation in preliminary design level. In Proceedings of the 2012 9th France-Japan & 7th Europe-Asia Congress on Mechatronics (MECATRONICS)/13th Int’l Workshop on Research and Education in Mechatronics (REM), Paris, France, 21–23 November 2012; pp. 409–416. [Google Scholar]
- Grabisch, M. The application of fuzzy integrals in multicriteria decision making. Eur. J. Oper. Res. 1996, 89, 445–456. [Google Scholar] [CrossRef]
- Katrantzis, E.; Moulianitis, V.C.; Miatliuk, K. Conceptual Design Evaluation of Mechatronic Systems; IntechOpen: Rijeka, Croatia, 2020; Chapter 2. [Google Scholar]
- Rastegar, J.; Fardanesh, B. Manipulation workspace analysis using the Monte Carlo Method. Mech. Mach. Theory 1990, 25, 233–239. [Google Scholar] [CrossRef]
- Sinha, A.; Malo, P.; Deb, K. A Review on Bilevel Optimization: From Classical to Evolutionary Approaches and Applications. IEEE Trans. Evol. Comput. 2018, 22, 276–295. [Google Scholar] [CrossRef]

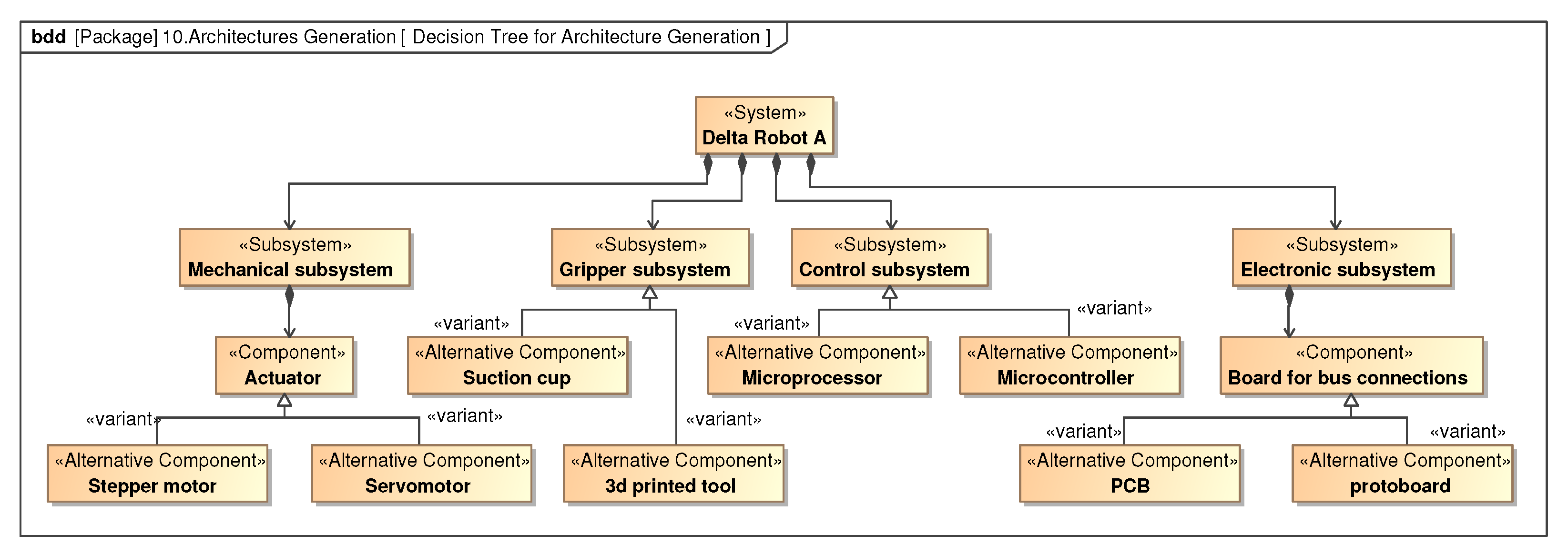
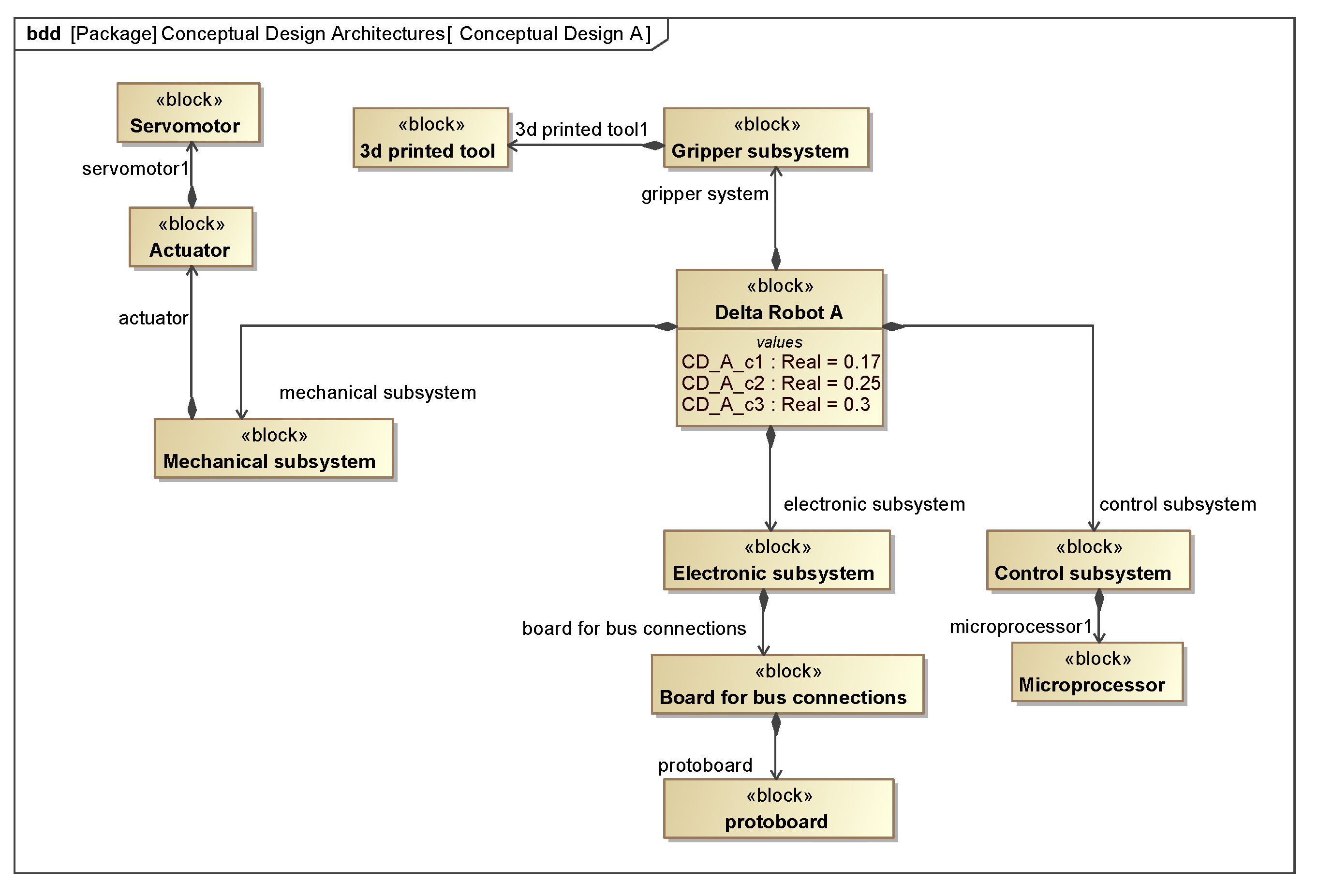
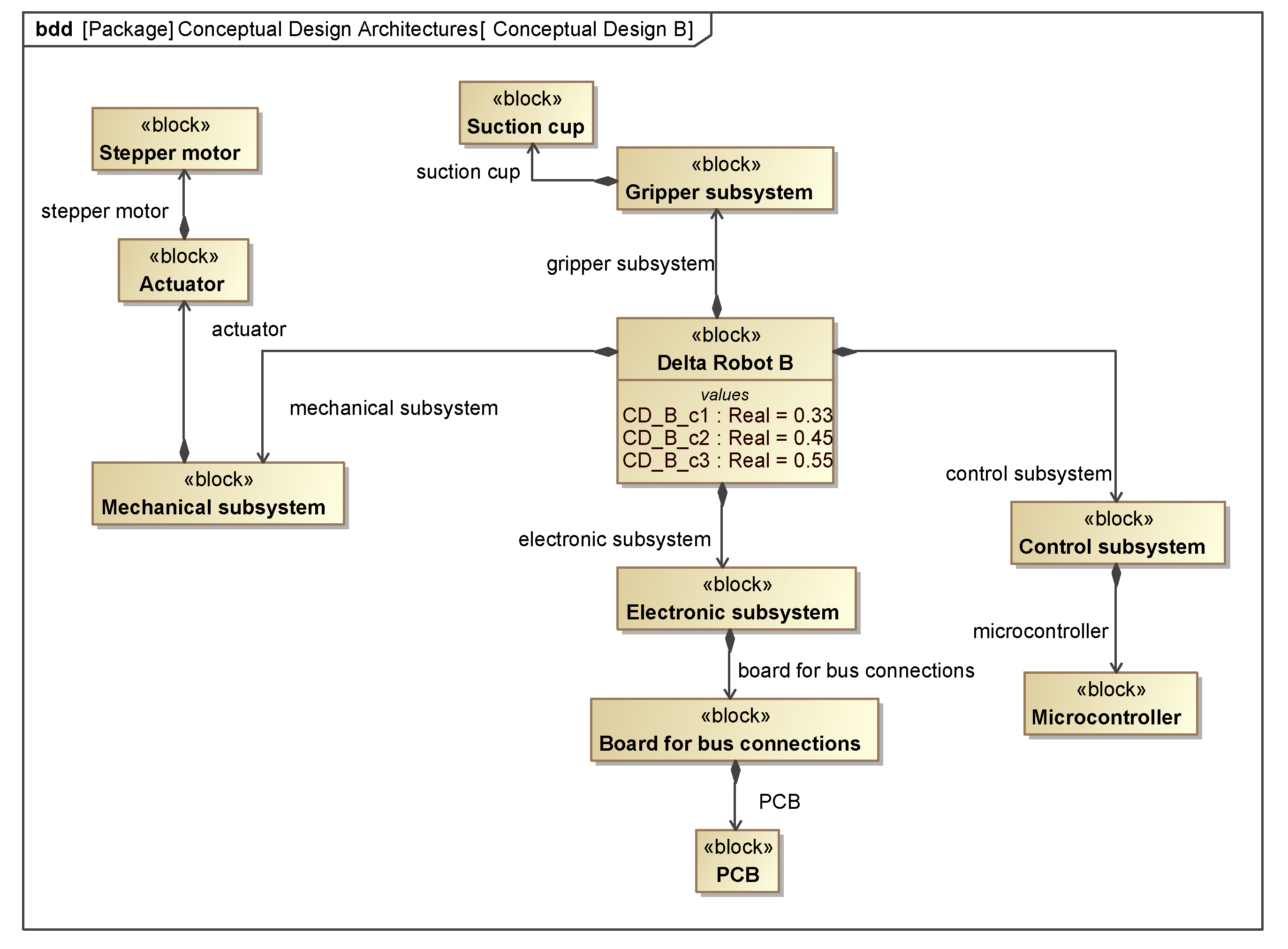
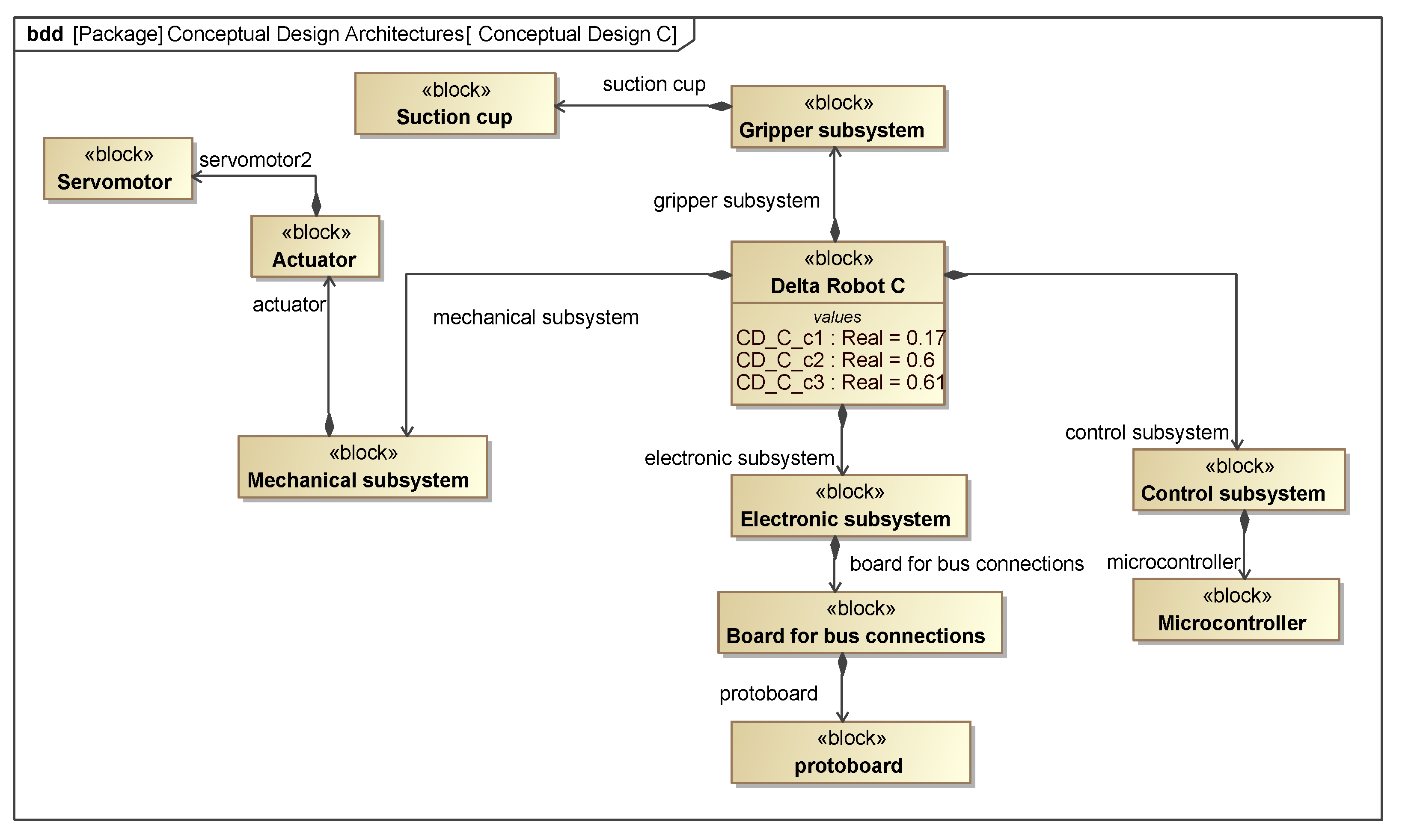

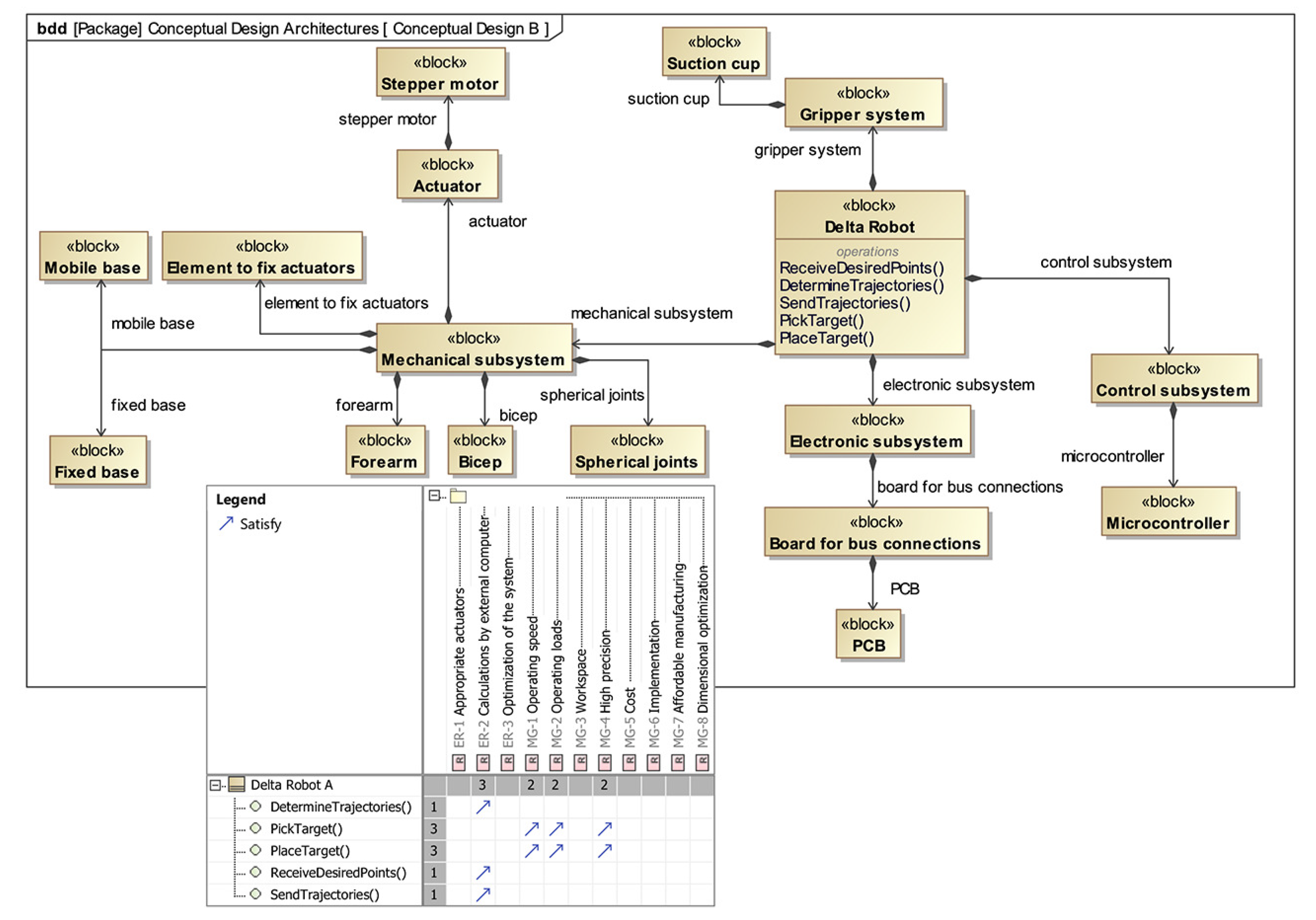

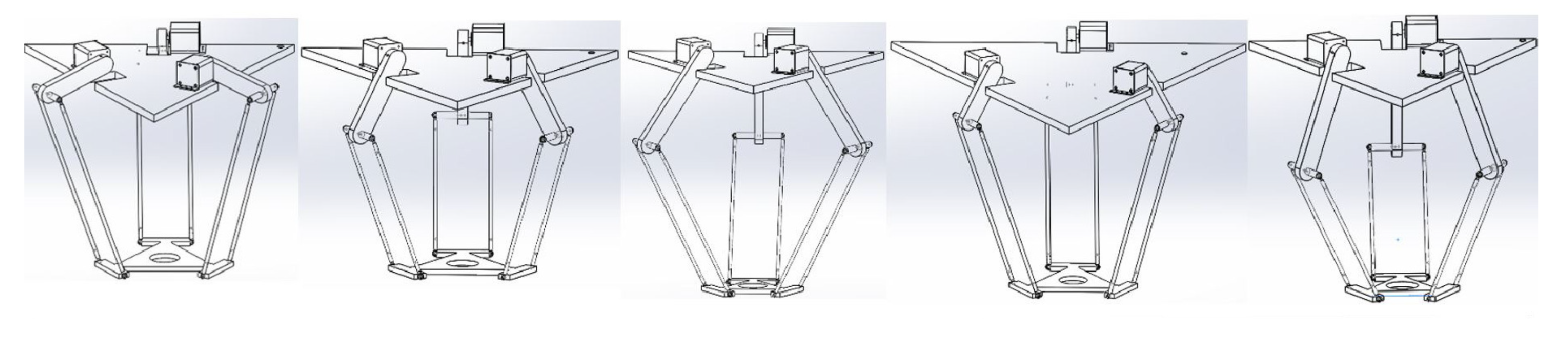
| Conceptual Design | Mechanical Subsystem | Gripper Subsystem | Electronic Subsystem | Control Subsystem |
|---|---|---|---|---|
| A | Servomotor | 3D Printed | Protoboard | Microprocessor |
| B | Stepper motor | Suction cup | PCB | Microcontroller |
| C | Servomotor | Suction cup | Protoboard | Microcontroller |
| Conceptual Design | Dependability | Cost | Complexity | Choquet Integral |
|---|---|---|---|---|
| A | 0.17 | 0.25 | 0.30 | 0.2185 |
| B | 0.33 | 0.45 | 0.55 | 0.4090 |
| C | 0.17 | 0.60 | 0.61 | 0.3660 |
| Subsystem | Component | Number of Parts |
|---|---|---|
| Mobile base | 1 | |
| Fixed base | 1 | |
| Element to fix actuator | 3 | |
| Bicep | 3 | |
| Forearm | 6 | |
| Mechanical | SA3T/K (M3) spherical bearing | 12 |
| Stepper motor Nema 17 | 3 | |
| Hex nut (1/8" diameter) | +15 | |
| wire, 22 gauge | 50 [cm] | |
| M3 screw (1/8" diam. × 5/8" long) | +9 | |
| M3 screw (1/8" diam. × 1.5" long) | +6 | |
| Electronic | PCB | 1 |
| Controller | Microcontroller (Arduino uno) | 1 |
| Gripper | Suction cup | 1 |
| Simulation | Number of Points N | Number of Generations | Number of Individuals | Vector of Solution x | Workspace Maximization [m] |
|---|---|---|---|---|---|
| 8 | 100 | 50 | 50 | [0.2, 0.1, 0.1122, 0.31] | 0.0029 |
| 20 | 100 | 50 | 10 | [0.2011, 0.0983, 0.1277, 0.2095] | 0.0029 |
| 22 | 50 | 50 | 10 | [0.2, 0.07, 0.19, 0.2738] | 0.0029 |
| 25 | 50 | 100 | 50 | [0.2986, 0.0964, 0.1003, 0.3082] | 0.0029 |
| 27 | 100 | 100 | 50 | [0.2, 0.07, 0.19, 0.2] | 0.0029 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Portillo-Vélez, R.d.J.; Burgos-Castro, I.A.; Vásquez-Santacruz, J.A.; Marín-Urías, L.F. Integrated Conceptual Mechatronic Design of a Delta Robot. Machines 2022, 10, 186. https://doi.org/10.3390/machines10030186
Portillo-Vélez RdJ, Burgos-Castro IA, Vásquez-Santacruz JA, Marín-Urías LF. Integrated Conceptual Mechatronic Design of a Delta Robot. Machines. 2022; 10(3):186. https://doi.org/10.3390/machines10030186
Chicago/Turabian StylePortillo-Vélez, Rogelio de Jesús, Iván Andrés Burgos-Castro, José Alejandro Vásquez-Santacruz, and Luis Felipe Marín-Urías. 2022. "Integrated Conceptual Mechatronic Design of a Delta Robot" Machines 10, no. 3: 186. https://doi.org/10.3390/machines10030186
APA StylePortillo-Vélez, R. d. J., Burgos-Castro, I. A., Vásquez-Santacruz, J. A., & Marín-Urías, L. F. (2022). Integrated Conceptual Mechatronic Design of a Delta Robot. Machines, 10(3), 186. https://doi.org/10.3390/machines10030186






