PSTO: Learning Energy-Efficient Locomotion for Quadruped Robots
Abstract
:1. Introduction
2. Materials and Methods
2.1. Physics Simulation and Robot Platform
2.2. Deep Reinforcement Learning
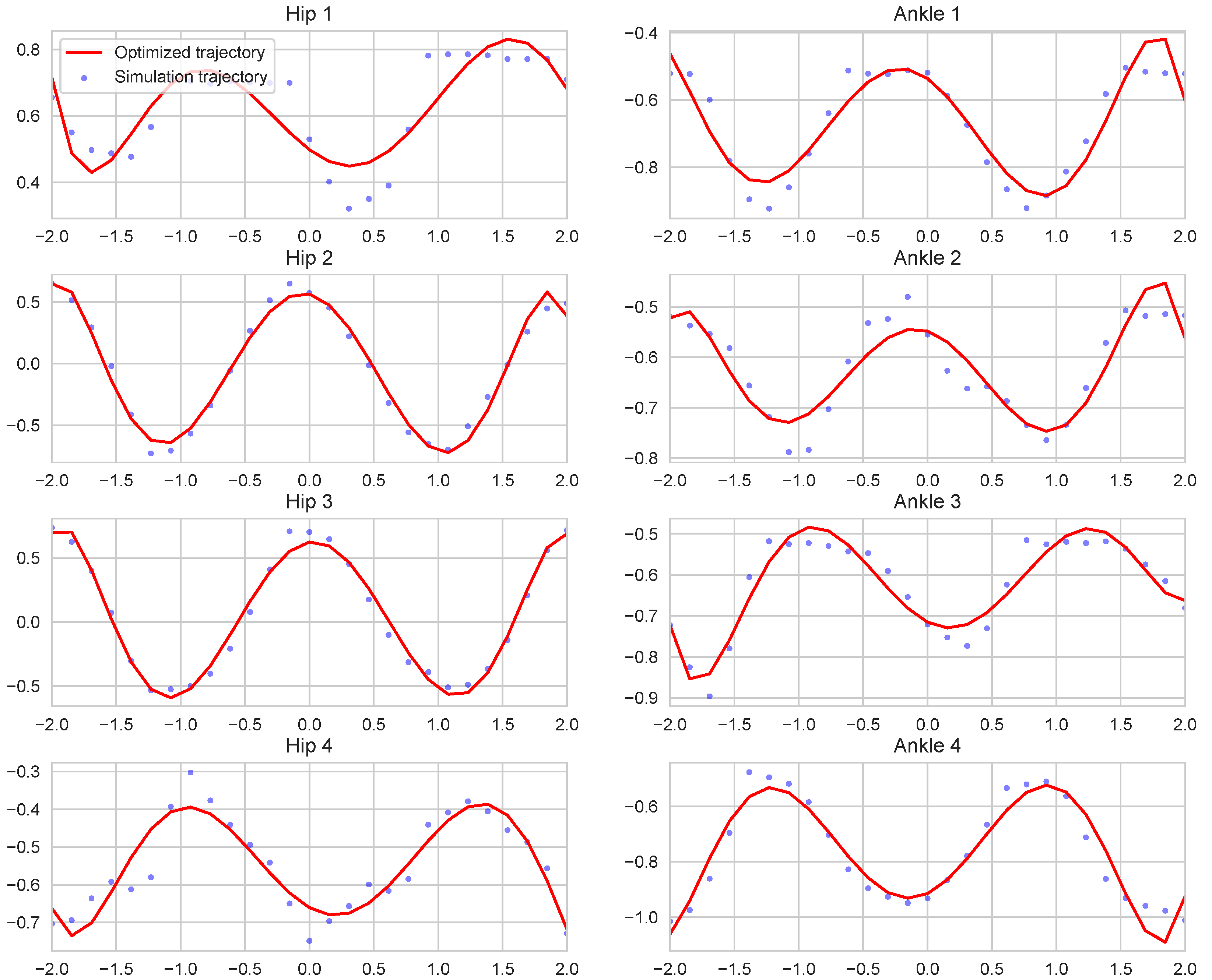
2.3. Trajectory Optimization
| Algorithm 1 PSTO with TD3. |
|
2.4. Experiment Setup
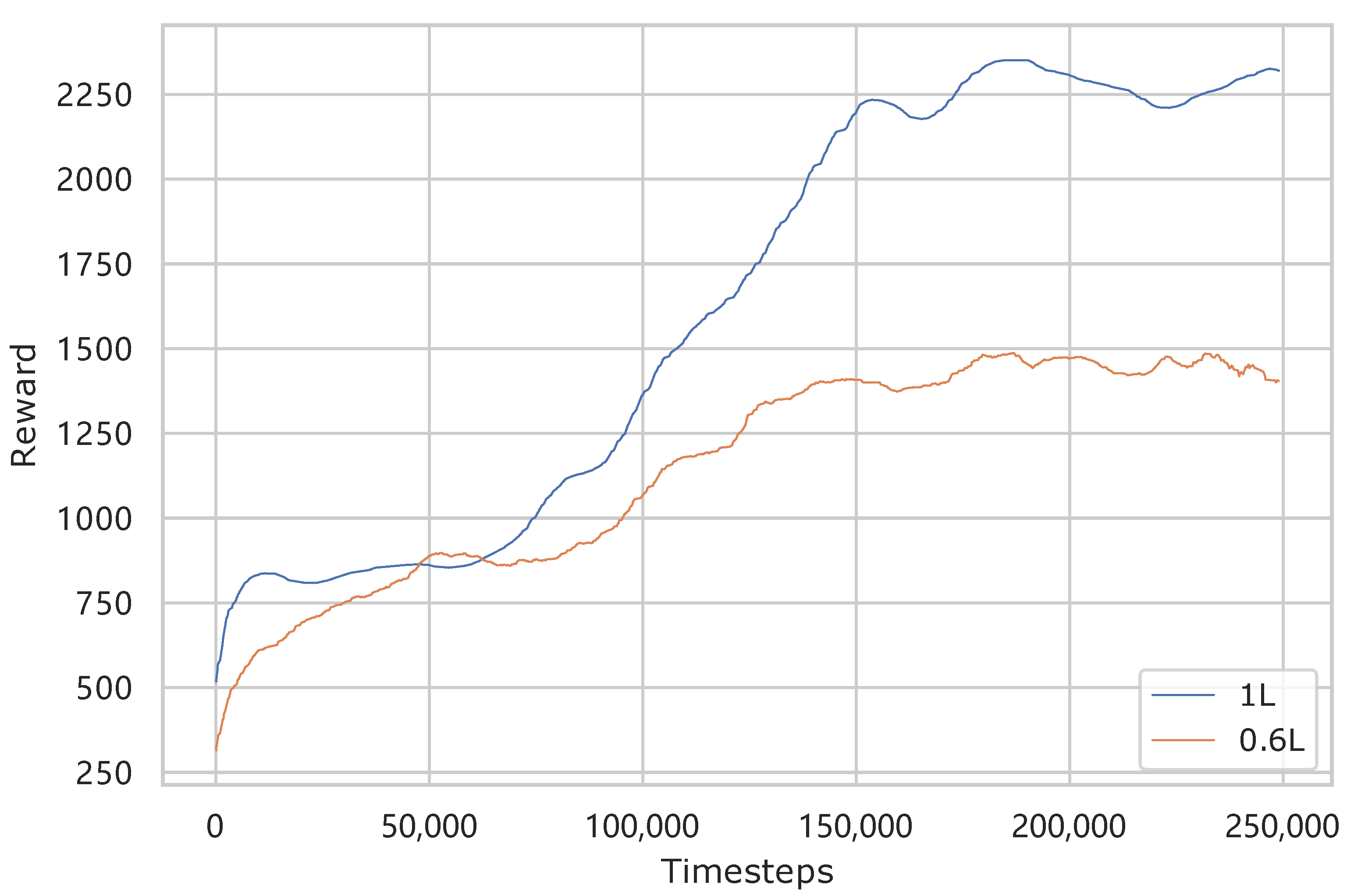
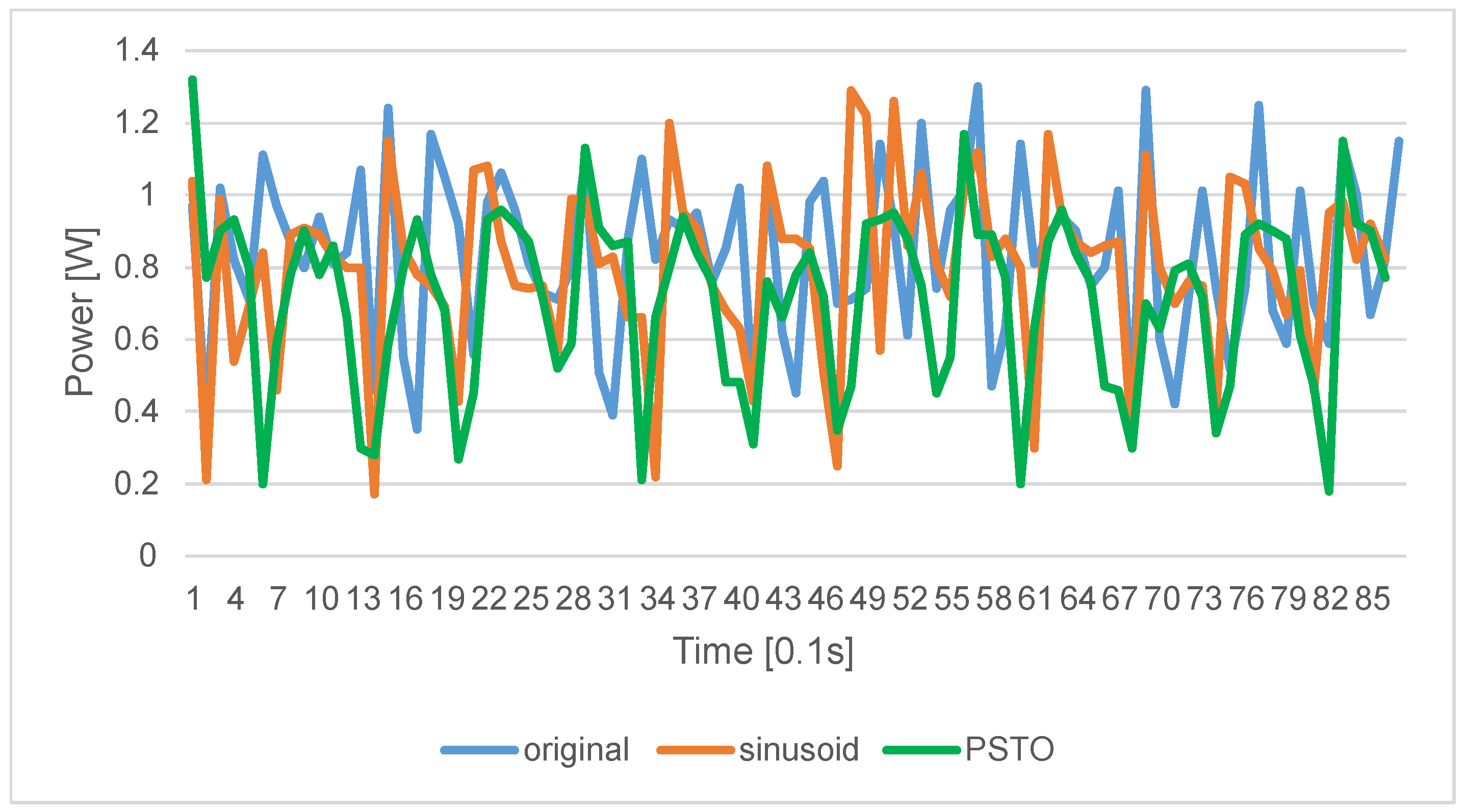
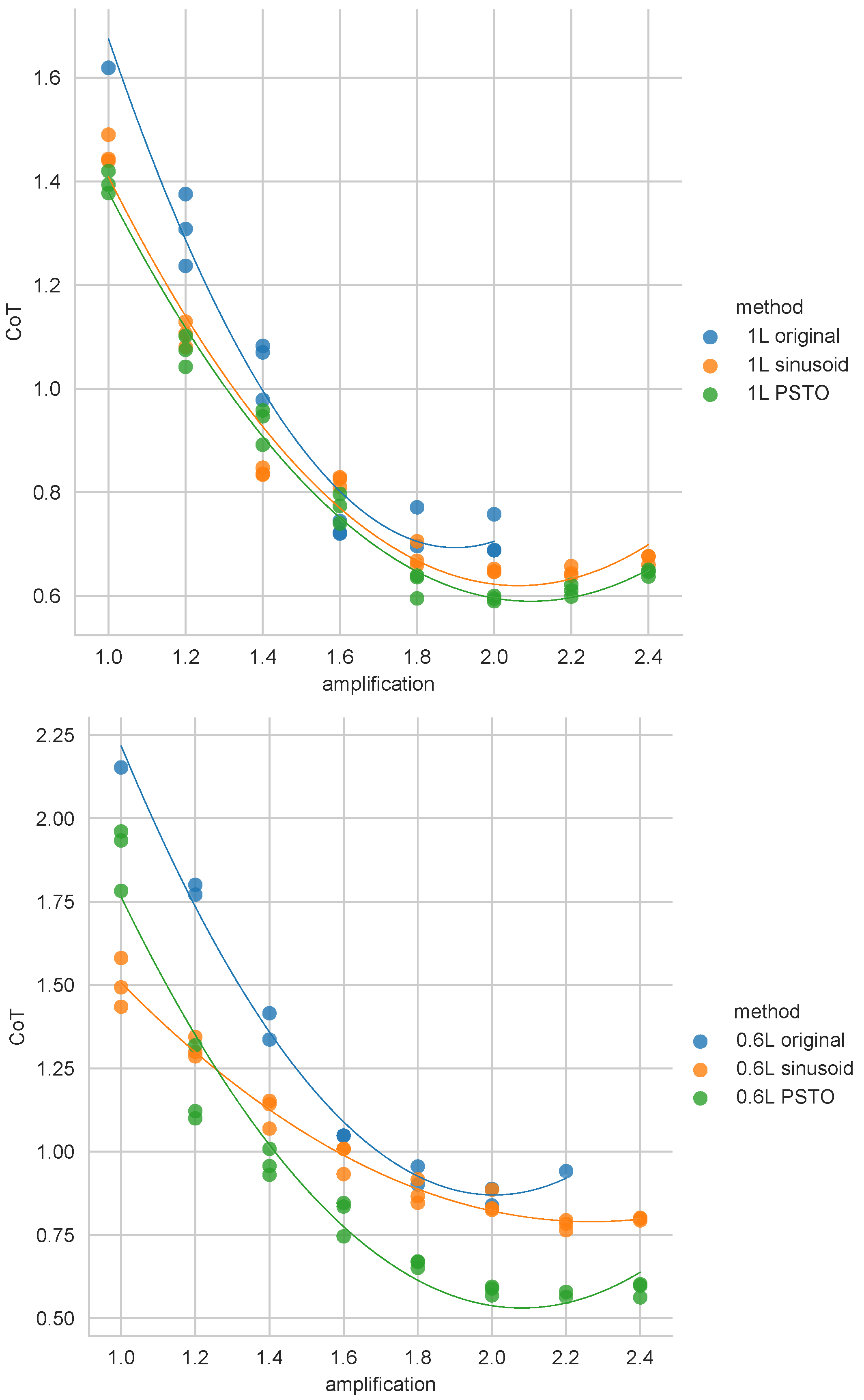
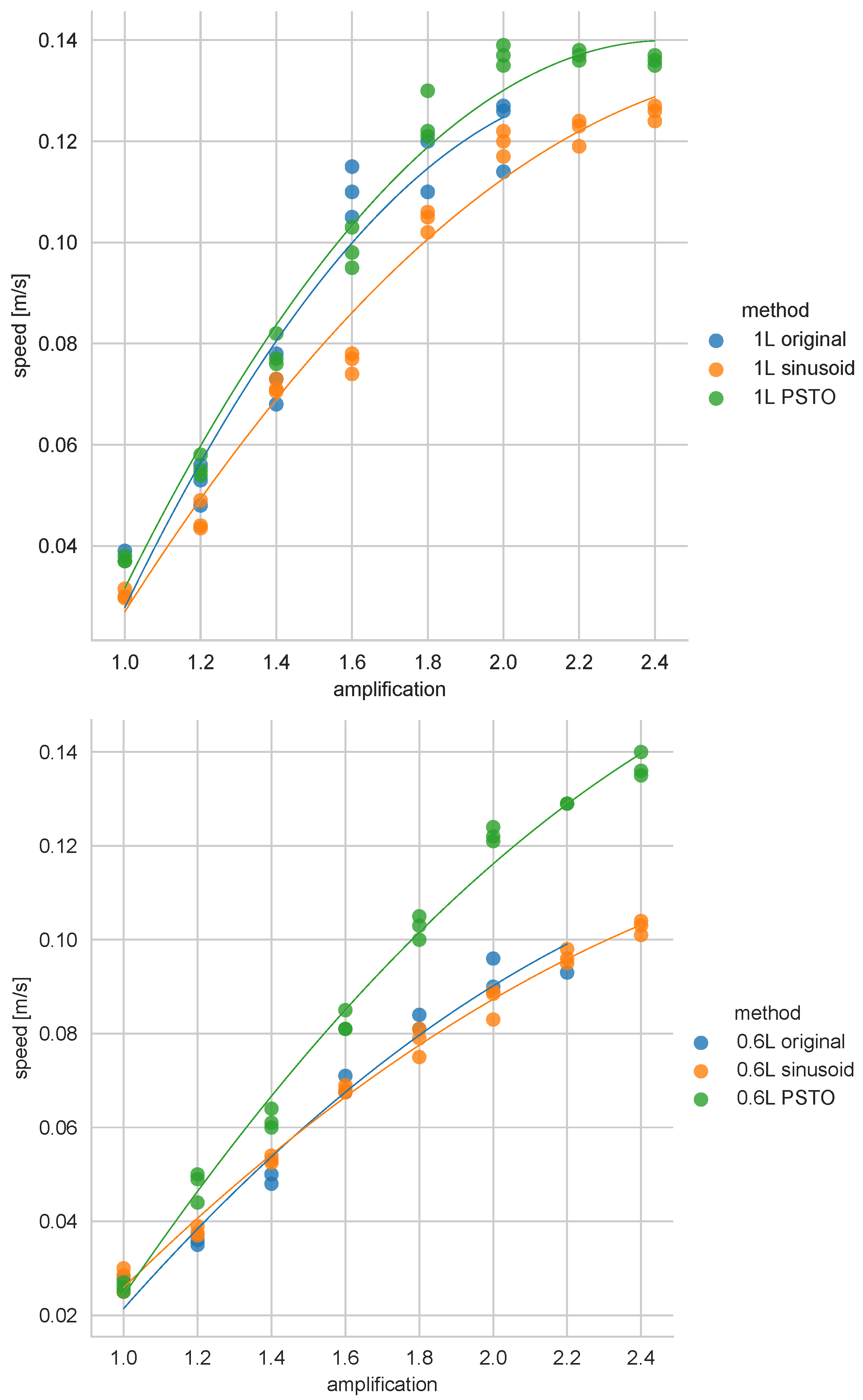
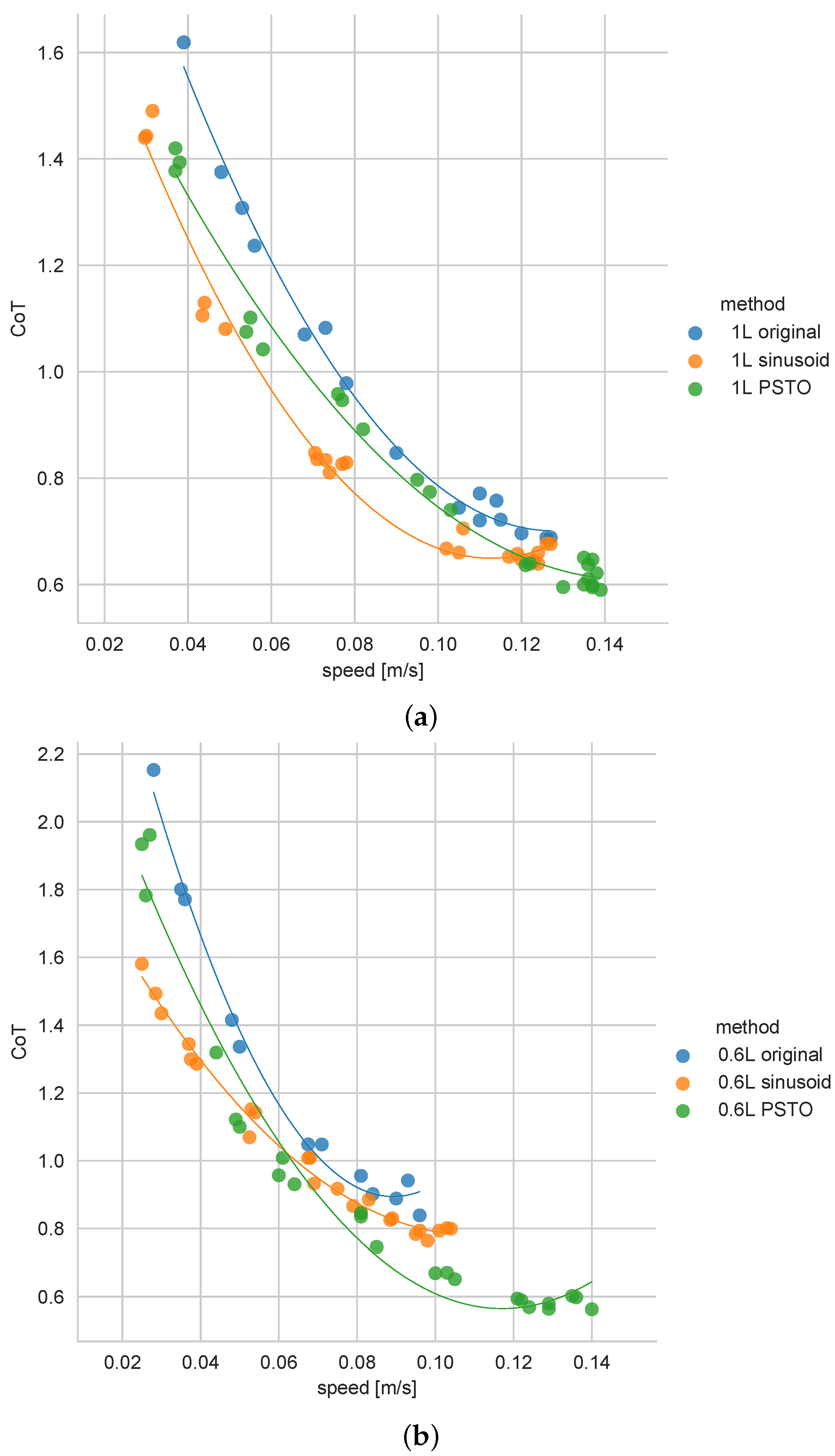
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raibert, M.H. Legged Robots that Balance; Massachusetts Institute of Technology: Cambridge, MA, USA, 1986; ISBN 0-262-18117-7. [Google Scholar]
- Pratt, J.; Pratt, G. Intuitive control of a planar bipedal walking robot. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), Leuven, Belgium, 20 May 1998; Volume 3, pp. 2014–2021. [Google Scholar]
- Kolter, J.Z.; Rodgers, M.P.; Ng, A.Y. A control architecture for quadruped locomotion over rough terrain. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 811–818. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1889–1897. [Google Scholar]
- Duan, Y.; Chen, X.; Houthooft, R.; Schulman, J.; Abbeel, P. Benchmarking deep reinforcement learning for continuous control. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1329–1338. [Google Scholar]
- Bing, Z.; Lemke, C.; Cheng, L.; Huang, K.; Knoll, A. Energy-efficient and damage-recovery slithering gait design for a snake-like robot based on reinforcement learning and inverse reinforcement learning. Neural Netw. 2020, 129, 323–333. [Google Scholar] [CrossRef] [PubMed]
- Peters, J.; Schaal, S. Reinforcement learning of motor skills with policy gradients. Neural Netw. 2008, 21, 682–697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Levine, S. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]
- Boeing, A.; Bräunl, T. Leveraging multiple simulators for crossing the reality gap. In Proceedings of the 2012 12th International Conference on Control Automation Robotics Vision (ICARCV), Guangzhou, China, 5–7 December 2012; pp. 1113–1119. [Google Scholar]
- Levine, S.; Pastor, P.; Krizhevsky, A.; Ibarz, J.; Quillen, D. Learning hand-eye coordination for robotic grasping with deep learning and large-scale data collection. Int. J. Robot. Res. 2018, 37, 421–436. [Google Scholar] [CrossRef]
- Haarnoja, T.; Ha, S.; Zhou, A.; Tan, J.; Tucker, G.; Levine, S. Learning to Walk Via Deep Reinforcement Learning. arXiv 2018, arXiv:1812.11103. [Google Scholar]
- Rosendo, A.; Von Atzigen, M.; Iida, F. The trade-off between morphology and control in the co-optimized design of robots. PLoS ONE 2017, 12, e0186107. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Zhang, T.; Coumans, E.; Iscen, A.; Bai, Y.; Hafner, D.; Vanhoucke, V. Sim-to-Real: Learning Agile Locomotion for Quadruped Robots. arXiv 2018, arXiv:1804.10332. [Google Scholar]
- Li, T.; Geyer, H.; Atkeson, C.G.; Rai, A. Using deep reinforcement learning to learn high-level policies on the atrias biped. In Proceedings of the 2019 International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 263–269. [Google Scholar]
- Nagabandi, A.; Clavera, I.; Liu, S.; Fearing, R.S.; Abbeel, P.; Levine, S.; Finn, C. Learning to Adapt in Dynamic, Real-World Environments through Meta-Reinforcement Learning. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Tsujita, K.; Tsuchiya, K.; Onat, A. Adaptive gait pattern control of a quadruped locomotion robot. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the Next, Millennium (Cat. No. 01CH37180), Maui, HI, USA, 29 October–3 November 2001; Volume 4, pp. 2318–2325. [Google Scholar]
- Erden, M.S. Optimal protraction of a biologically inspired robot leg. J. Intell. Robot. Syst. 2011, 64, 301–322. [Google Scholar] [CrossRef]
- de Santos, P.G.; Garcia, E.; Ponticelli, R.; Armada, M. Minimizing energy consumption in hexapod robots. Adv. Robot. 2009, 23, 681–704. [Google Scholar] [CrossRef] [Green Version]
- Hunt, J.; Giardina, F.; Rosendo, A.; Iida, F. Improving efficiency for an open-loop-controlled locomotion with a pulsed actuation. IEEE/ASME Trans. Mechatron. 2016, 21, 1581–1591. [Google Scholar] [CrossRef]
- Sulzer, J.S.; Roiz, R.A.; Peshkin, M.A.; Patton, J.L. A highly backdrivable, lightweight knee actuator for investigating gait in stroke. IEEE Trans. Robot. 2009, 25, 539–548. [Google Scholar] [CrossRef] [PubMed]
- Wensing, P.M.; Wang, A.; Seok, S.; Otten, D.; Lang, J.; Kim, S. Proprioceptive actuator design in the mit cheetah: Impact mitigation and high-bandwidth physical interaction for dynamic legged robots. IEEE Trans. Robot. 2017, 33, 509–522. [Google Scholar] [CrossRef]
- Nygaard, T.F.; Martin, C.P.; Torresen, J.; Glette, K.; Howard, D. Real-world embodied AI through a morphologically adaptive quadruped robot. Nat. Mach. Intell. 2021, 3, 410–419. [Google Scholar] [CrossRef]
- Choromanski, K.; Iscen, A.; Sindhwani, V.; Tan, J.; Coumans, E. Optimizing simulations with noise-tolerant structured exploration. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2970–2977. [Google Scholar]
- Cully, A.; Clune, J.; Tarapore, D.; Mouret, J.B. Robots that can adapt like animals. Nature 2015, 521, 503–507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Calandra, R.; Seyfarth, A.; Peters, J.; Deisenroth, M.P. Bayesian optimization for learning gaits under uncertainty. Ann. Math. Artif. Intell. 2015, 76, 5–23. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Li, S.; Wang, Z.; Rosendo, A. Bayesian optimization of a quadruped robot during three-dimensional locomotion. In Proceedings of the Conference on Biomimetic and Biohybrid Systems, Nara, Japan, 9–12 July 2019; pp. 295–306. [Google Scholar]
- Coumans, E.; Bai, Y. Pybullet, a Python Module for Physics Simulation in Robotics, Games and Machine Learning. 2016–2017. Available online: http://pybullet.org (accessed on 2 February 2021).
- Weng, J.; Chen, H.; Duburcq, A.; You, K.; Zhang, M.; Yan, D.; Su, H.; Zhu, J. GitHub Repository. 2020. Available online: https://github.com/thu-ml/tianshou (accessed on 2 February 2021).
- Tucker, V.A. The Energetic Cost of Moving About: Walking and running are extremely inefficient forms of locomotion. Much greater efficiency is achieved by birds, fish—And bicyclists. Am. Sci. 1975, 63, 413–419. [Google Scholar] [PubMed]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]


| Hyperparameter | Value |
|---|---|
| buffer size | 20,000 |
| actor learning rate | 0.0003 |
| critic learning rate | 0.001 |
| 0.99 | |
| tau | 0.005 |
| update actor frequency | 2 |
| policy noise | 0.2 |
| exploration noise | 0.1 |
| epoch | 2500 |
| step per epoch | 100 |
| collect per step | 10 |
| batch size | 128 |
| hidden layer number | 3 |
| hidden neurons per layer | 128 |
| training number | 8 |
| test number | 50 |
| joint gear | 45 |
| joint control range | −45∼45 |
| Method | CoT | Speed [m/s] |
|---|---|---|
| 1 L original | 0.688 | 0.127 |
| 1 L sinusoid | 0.639 | 0.127 |
| 1 L PSTO | 0.595 | 0.139 |
| 0.6 L original | 0.839 | 0.096 |
| 0.6 L sinusoid | 0.764 | 0.104 |
| 0.6 L PSTO | 0.563 | 0.139 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Rosendo, A. PSTO: Learning Energy-Efficient Locomotion for Quadruped Robots. Machines 2022, 10, 185. https://doi.org/10.3390/machines10030185
Zhu W, Rosendo A. PSTO: Learning Energy-Efficient Locomotion for Quadruped Robots. Machines. 2022; 10(3):185. https://doi.org/10.3390/machines10030185
Chicago/Turabian StyleZhu, Wangshu, and Andre Rosendo. 2022. "PSTO: Learning Energy-Efficient Locomotion for Quadruped Robots" Machines 10, no. 3: 185. https://doi.org/10.3390/machines10030185
APA StyleZhu, W., & Rosendo, A. (2022). PSTO: Learning Energy-Efficient Locomotion for Quadruped Robots. Machines, 10(3), 185. https://doi.org/10.3390/machines10030185







