Denoising and Feature Extraction for Space Infrared Dim Target Recognition Utilizing Optimal VMD and Dual-Band Thermometry
Abstract
:1. Introduction
2. Theoretical Background
2.1. Dragonfly Algorithm Description
| Algorithm 1 The Pseudo-code of the DA [22]. |
| Initialize the dragonflies population Xi(i = 1, 2, …, n); |
| Initialize the step vectors ∆Xi(i = 1, 2, …, n); |
| while the end condition is not satisfied do |
| Calculate the objective values of all dragonflies |
| Update the food source and enemy |
| Update w, s, a, c, f, and e |
| Calculate S, A, C, F, and E using Equations (1)–(5) |
| Update neighboring radius r |
| if a dragonfly has at least one neighboring dragonfly then |
| Update velocity vector using Equation (6) |
| Update position vector using Equation (7) |
| else |
| Update position vector using Equation (8) |
| end if |
| Check and correct the new positions based on the boundaries of variables |
| end while |
2.2. Variational Mode Decomposition
3. Methodology
3.1. DA-VMD Parameter Optimization
- (1)
- Fitness function construction
- (2)
- Related modes selection method
3.2. Target Temperature and Emissivity-Area Product Feature Extraction Based on DBT
3.3. The Proposed Methodology DA-VMD-DBT
3.4. Infrared Bands Selection Criteria
4. Simulation Parameters Setting and Construction of Infrared Simulation Signal
5. Denoising and Feature Extraction of Simulation Signal
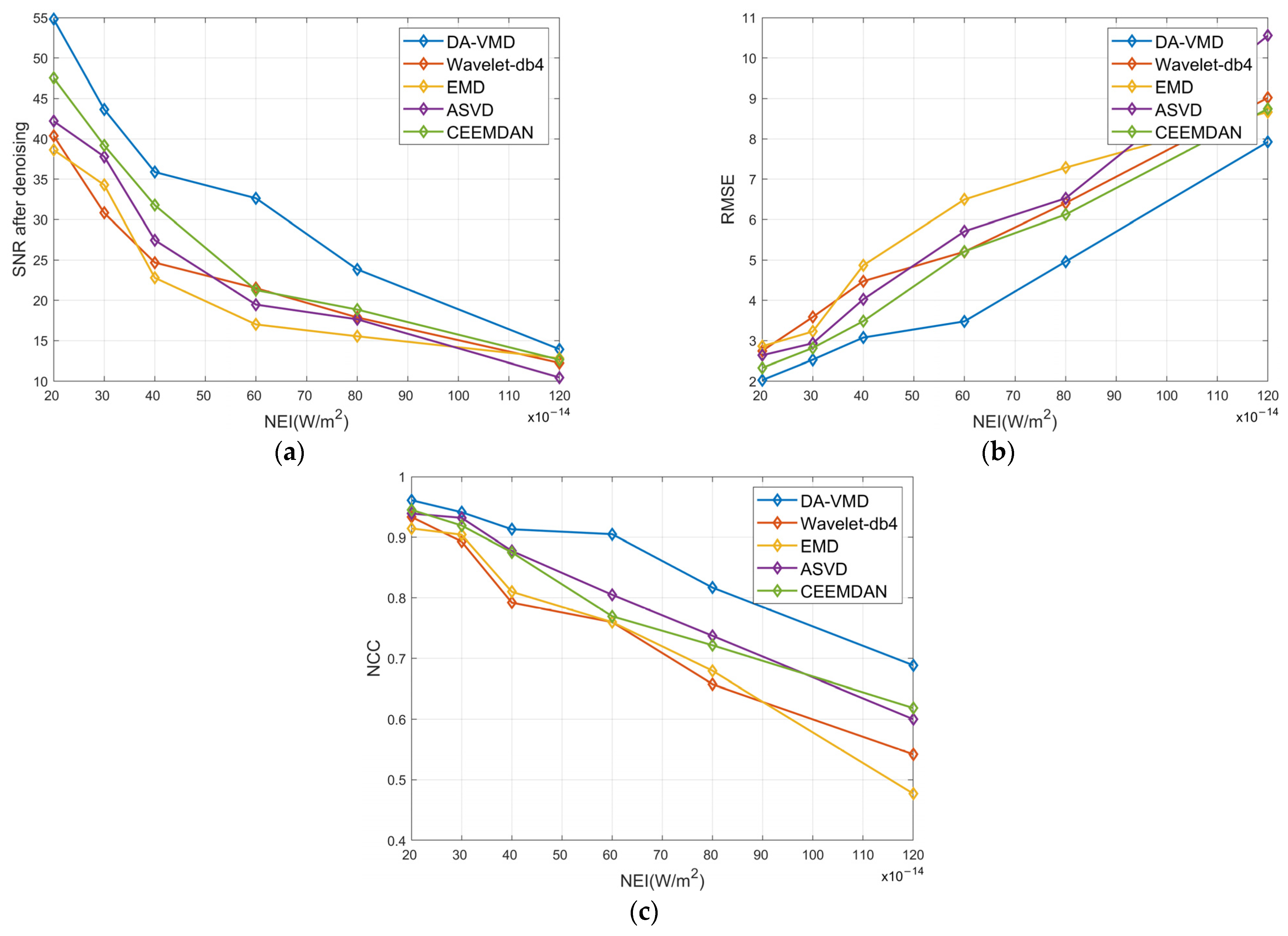
5.1. Denoising Result and Performance Comparison with Other Methods
5.2. Feature Extraction Based on DA-VMD-DBT
6. Experimental Verification of the Proposed Algorithm
6.1. Introduction of Experiment
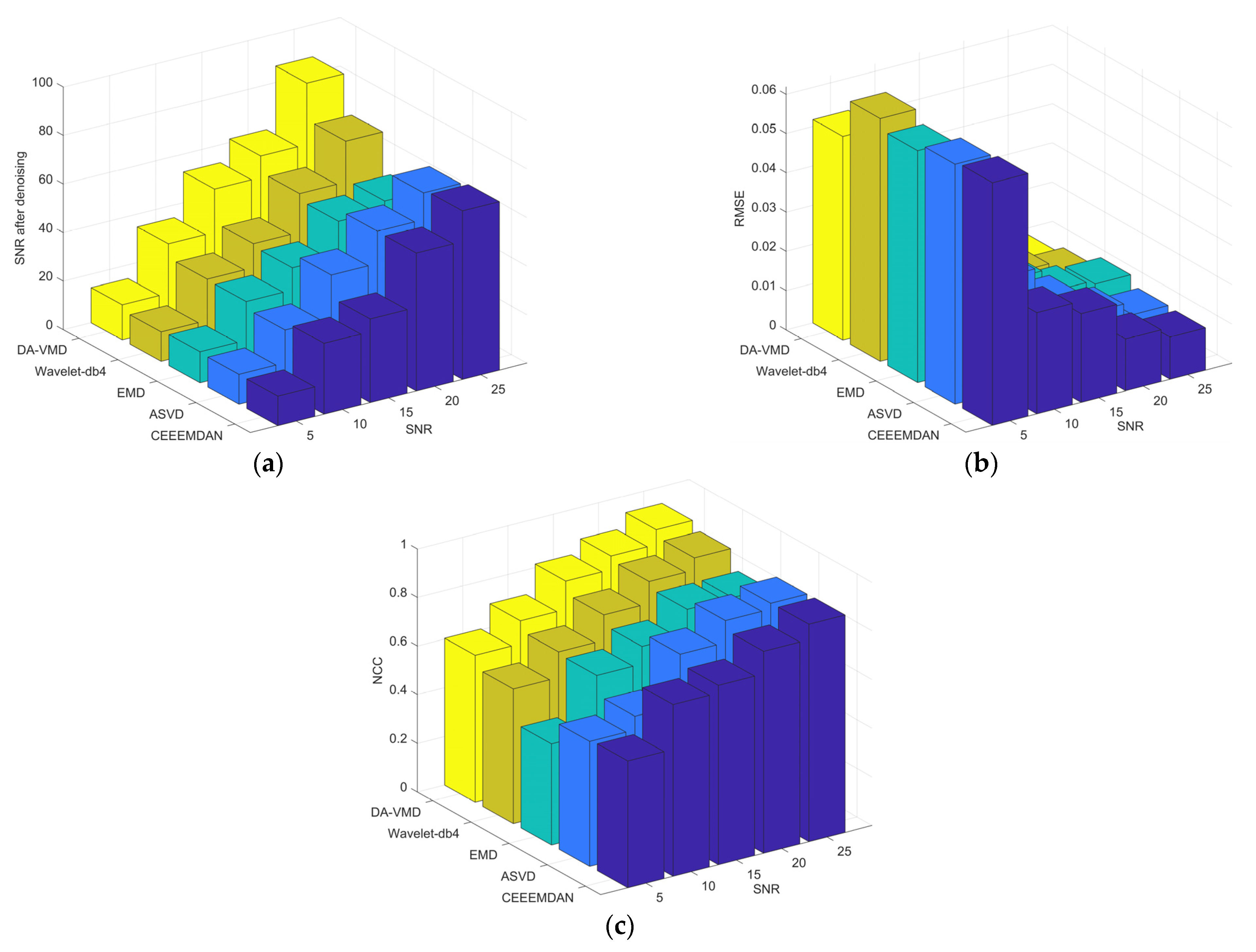
6.2. Denoising and Extracting Features of Experiment Data
7. Discussion
8. Conclusions
- (1)
- The selection of infrared band combination is carried out. By analyzing the accuracy of feature extraction of space targets with different emissivity and absorptivity under different band combinations, 8–12/6–7 μm is regarded as ideal selection. Using this band combination can reduce the influence of external radiation reflected by target on feature extraction.
- (2)
- The DA-VMD module is used for denoising signal. For the denoising, the DA and the mean weighted FuzzDistEn are used to search for the optimal combination of parameters (K, α). The VMD with the optimal parameters decomposes the infrared noisy signal to K BLIMFs, and the effective BLIMFs are selected by the PCC to reconstruct the denoising signal. The effectiveness of the module is analyzed and compared with Wavelet-db4, ASVD, EMD, and CEEMDAN by using the simulated infrared radiation intensity signal of the cone-cylinder and the measured signal of the ball-base-cone in the laboratory. The simulation and experimental results demonstrate that the DA-VMD outperforms four methods in terms of SNR, RMSE, NCC and gets better performance of denoising.
- (3)
- The DBT module is introduced to measure the features of the temperature and the emissivity-area product. The DA-VMD-DBT outperform other algorithms in the paper. The result can be concluded that the proposed algorithm can effectively extract the features of temperature and emissivity-area product from the infrared dim noisy signals.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Erlandson, R.E.; Taylor, J.C.; Michaelis, C.H.; Edwards, J.L.; Brown, R.C.; Swaminathan, P.K.; Kumar, C.K.; Hargis, C.B.; Goldberg, A.C.; Klatt, E.M.; et al. Development of Kill Assessment Technology for Space-Based Applications. Johns Hopkins APL Tech. Dig. 2010, 29, 289. [Google Scholar]
- Yılmaz, Ö.; Aouf, N.; Checa, E.; Majewski, L.; Sanchez-Gestido, M. Thermal analysis of space debris for infrared-based active debris removal. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 811–822. [Google Scholar] [CrossRef]
- Chen, L.; Rao, P.; Chen, X. Infrared dim target detection method based on local feature contrast and energy concentration degree. Optik 2021, 248, 167651. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Y.; Hu, T. Key parameters design of an aerial target detection system on a space-based platform. Opt. Eng. 2018, 57, 023107. [Google Scholar] [CrossRef]
- Deng, Q.; Lu, H.; Hu, M.; Zhao, B. Exo-atmospheric infrared objects classification using recurrence-plots-based convolutional neural networks. Appl. Opt. 2019, 58, 164–171. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Y.; Lu, H.; Zhao, B. Micromotion dynamics and geometrical shape parameters estimation of exo-atmospheric infrared targets. Opt. Eng. 2016, 55, 113103. [Google Scholar] [CrossRef]
- Reddy, T.S. Noise reduction in LIDAR signal using wavelets. Int. J. Eng. Technol. 2009, 2, 21–28. [Google Scholar]
- Yuan, R.; Lv, Y.; Song, G. Fault diagnosis of rolling bearing based on a novel adaptive high-order local projection denoising method. Complexity 2018, 2018, 3049318. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Luo, M.; Tan, Z.; Pei, R. Echo signal extraction method of laser radar based on improved singular value decomposition and wavelet threshold denoising. Infrared Phys. Technol. 2018, 92, 327–335. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Ahmed, W.A.; Wu, F.; Marlia, D.; Ednofri; Zhao, Y. Mitigation of Ionospheric Scintillation Effects on GNSS Signals with VMD-MFDFA. Remote Sens. 2019, 11, 2867. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Zhou, Y.; Xiang, J. Optimization of VMD using kernel-based mutual information for the extraction of weak features to detect bearing defects. Measurement 2021, 168, 108402. [Google Scholar] [CrossRef]
- Fu, J.; Cai, F.; Guo, Y.; Liu, H.; Niu, W. An Improved VMD-Based Denoising Method for Time Domain Load Signal Combining Wavelet with Singular Spectrum Analysis. Math. Probl. Eng. 2020, 2020, 1485937. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. Denoising and feature extraction algorithms using NPE combined with VMD and their applications in ship-radiated noise. Symmetry 2017, 9, 256. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Li, C.; Fu, W.; Liu, J.; Yu, T.; Chen, H. A modified variational mode decomposition method based on envelope nesting and multi-criteria evaluation. J. Sound Vib. 2020, 468, 115099. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, G.; Li, M.; Yin, H. Variational mode decomposition denoising combined the detrended fluctuation analysis. Signal Process. 2016, 125, 349–364. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Yu, J.; Yang, X.; Yang, H. The data-driven optimization method and its application in feature extraction of ship-radiated noise with sample entropy. Energies 2019, 12, 359. [Google Scholar] [CrossRef] [Green Version]
- Lian, J.; Liu, Z.; Wang, H.; Dong, X. Adaptive variational mode decomposition method for signal processing based on mode characteristic. Mech. Syst. Signal Process. 2018, 107, 53–77. [Google Scholar] [CrossRef]
- Li, C.; Peng, T.; Zhu, Y. A Novel Approach for Acoustic Signal Processing of a Drum Shearer Based on Improved Variational Mode Decomposition and Cluster Analysis. Sensors 2020, 20, 2949. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Kumar, S.; Rajamani, D.; Balsubramanian, E. Experimental Investigations and Multi-Objective Optimization of Selective Inhibition Sintering Process Using the Dragonfly Algorithm. Applications of Artificial Intelligence in Additive Manufacturing. In Advances in Computational Intelligence and Robotics; IGI Global: Hershey, PA, USA, 2022; pp. 96–113. [Google Scholar]
- Zhang, H.; Rao, P.; Xia, H.; Weng, D.; Chen, X.; Li, Y. Modeling and analysis of infrared radiation dynamic characteristics for space micromotion target recognition. Infrared Phys. Technol. 2021, 116, 103795. [Google Scholar] [CrossRef]
- Araújo, A.; Martins, N. Monte Carlo simulations of ambient temperature uncertainty determined by dual-band pyrometry. Meas. Sci. Technol. 2015, 26, 085016. [Google Scholar] [CrossRef]
- Araújo, A.; Silvano, S.; Martins, N. Monte Carlo uncertainty simulation of surface emissivity at ambient temperature obtained by dual spectral infrared radiometry. Infrared Phys. Technol. 2014, 67, 131–137. [Google Scholar] [CrossRef]
- Araújo, A. Analysis of multi-band pyrometry for emissivity and temperature measurements of gray surfaces at ambient temperature. Infrared Phys. Technol. 2016, 76, 365–374. [Google Scholar] [CrossRef]
- Duan, J.; Wang, P.; Ma, W.; Tian, X.; Fang, S.; Cheng, Y.; Chang, Y.; Liu, H. Short-term wind power forecasting using the hybrid model of improved variational mode decomposition and Correntropy Long Short-term memory neural network. Energy 2021, 214, 118980. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, J.; Zhou, T.; Qiu, Y.; Jia, H.; Lin, J. A parameter-adaptive variational mode decomposition approach based on weighted fuzzy-distribution entropy for noise source separation. Meas. Sci. Technol. 2020, 31, 125004. [Google Scholar] [CrossRef]
- Li, P.; Liu, C.; Li, K.; Zheng, D.; Liu, C.; Hou, Y. Assessing the complexity of short-term heartbeat interval series by distribution entropy. Med. Biol. Eng. Comput. 2015, 53, 77–87. [Google Scholar] [CrossRef]
- Chang, Y.; Bao, G.; Cheng, S.; He, T.; Yang, Q. Improved VMD-KFCM algorithm for the fault diagnosis of rolling bearing vibration signals. IET Signal Process. 2021, 15, 238–250. [Google Scholar] [CrossRef]
- Zhou, S. Introduction to Advanced Infrared Photoelectricity Engineering, 1st ed.; Science Press: Beijing, China, 2016; pp. 23–24. [Google Scholar]
- Wang, Y. On-orbit Radiometric Calibration Method for Gaze Camera with Large Planar Array. Ph.D. Thesis, Shanghai Institute of Technical Physics, Chinese Academy of Sciences, Shanghai, China, 2019. [Google Scholar]
- Resch, C. Exo-atmospheric discrimination of thrust termination debris and missile segments. Johns Hopkins APL Tech. Dig. 1998, 19, 315. [Google Scholar]
- Lu, Q.; Pang, L.; Huang, H.; Shen, C.; Cao, H.; Shi, Y.; Liu, J. High-G calibration denoising method for high-G MEMS accelerometer based on EMD and wavelet threshold. Micromachines 2019, 10, 134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lei, Z.; Su, W.; Hu, Q. Multimode decomposition and wavelet threshold denoising of mold level based on mutual information entropy. Entropy 2019, 21, 202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashtiani, M.B.; Shahrtash, S.M. Partial discharge de-noising employing adaptive singular value decomposition. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 775–782. [Google Scholar] [CrossRef]

















| Combination Number | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Band combination (μm) | 12–14 /8–12 | 12–14 /6–7 | 12–14 /3–5 | 8–12 /6–7 | 8–12 /3–5 | 6–7 /3–5 |
| Absorptivity and Emissivity Combination Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Value | 0.1/0.5 | 0.3/0.5 | 0.5/0.5 | 0.7/0.5 | 0.9/0.5 |
| Band Combinations (μm) | Temperature Error Percentage | Temperature RMSE | Emissivity-Area Product Error Percentage | Emissivity-Area Product RMSE |
|---|---|---|---|---|
| 12–14/8–12 | 0 | 0 | 0 | 0 |
| 12–14/6–7 | 2 | 2 | 0 | 0 |
| 12–14/3–5 | 0 | 0 | 5 | 0 |
| 8–12/6–7 | 23 | 23 | 20 | 20 |
| 8–12/3–5 | 0 | 0 | 0 | 2 |
| 6–7/3–5 | 0 | 0 | 0 | 3 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Radius | 1 m | Thickness | 1 mm |
| Height-1 | 1 m | Visible absorptivity | 0.45 |
| Height-2 | 1 m | Emissivity | 0.8 |
| Coning rate | π rad/s | Density | 2700 kg/m3 |
| Spinning rate | 4π rad/s | Specific capacity | 904 J/(kg·K) |
| Flight environment | sunlight | Initial temperature | 300 K |
| Frame rate | 10 Hz | Observation bands | 8–12 μm/6–7 μm |
| Observation duration | 30 s | Distance | [4550.92 km, 4352.92 km] |
| Indicators | DA-VMD with PCC | DA-VMD with MIE | DA-VMD with CMSE |
|---|---|---|---|
| SNR | 32.63 | 18.55 | 17.18 |
| RMSE | 3.48 | 6.01 | 6.48 |
| NCC | 0.91 | 0.78 | 0.76 |
| NEI (W·m−2) | SNR | RMSE |
|---|---|---|
| 120 × 10−14 | 4.69 | 24.80 |
| 80 × 10−14 | 6.75 | 16.39 |
| 60 × 10−14 | 9.25 | 11.92 |
| 40 × 10−14 | 13.33 | 9.01 |
| 30 × 10−14 | 17.11 | 6.44 |
| 20 × 10−14 | 22.42 | 4.98 |
| Infrared Band | NEI (W∗m−2) | SNR | MV-TE (%) | SD-TE (%) | RMSE-T | MV-EAP (%) | SD-EAP (%) | RMSE-EAP | NCC-EAP | |
|---|---|---|---|---|---|---|---|---|---|---|
| 8–12 μm 6–7 μm | 120∗10−14 200∗10−15 | 4.69 4.56 | DBT | 10.05 | 8.35 | 44.58 | 88.36 | 117.35 | 3.77 | −0.04 |
| ASVD-DBT | 3.37 | 2.59 | 12.81 | 25.14 | 21.32 | 0.90 | 0.14 | |||
| Wd-DBT | 3.93 | 2.98 | 14.74 | 31.51 | 28.57 | 1.17 | 0.12 | |||
| CEEMDAN-DBT | 3.35 | 3.41 | 13.52 | 30.22 | 25.00 | 1.08 | 0.05 | |||
| EMD-DBT | 3.94 | 3.07 | 14.94 | 31.58 | 27.43 | 1.14 | 0.13 | |||
| DA-VMD-DBT | 3.19 | 2.22 | 13.14 | 27.07 | 21.64 | 0.85 | 0.15 | |||
| 8–12 μm 6–7 μm | 80∗10−14 130∗10−15 | 6.75 6.49 | DBT | 6.96 | 5.07 | 25.96 | 52.07 | 50.02 | 1.86 | 0.065 |
| ASVD-DBT | 2.80 | 2.32 | 10.89 | 19.26 | 17. 80 | 0.72 | 0.19 | |||
| Wd-DBT | 2.64 | 1.77 | 9.51 | 18.56 | 12.97 | 0.62 | 0.28 | |||
| CEEMDAN-DBT | 2.63 | 1.93 | 9.76 | 19.19 | 15.08 | 0.67 | 0.21 | |||
| EMD-DBT | 3.61 | 2.60 | 11.31 | 25.82 | 21.57 | 0.92 | 0.19 | |||
| DA-VMD-DBT | 1.89 | 1.53 | 9.73 | 15.74 | 13.59 | 0.77 | 0.25 | |||
| 8–12 μm 6–7 μm | 60∗10−14 90∗10−15 | 9.25 10.02 | DBT | 5.14 | 3.64 | 18.22 | 35.34 | 29.01 | 1.24 | 0.16 |
| ASVD-DBT | 2.21 | 1.60 | 8.16 | 16.99 | 13.25 | 0.60 | 0.34 | |||
| Wd-DBT | 1.92 | 1.38 | 7.09 | 16.30 | 11.22 | 0.54 | 0.39 | |||
| CEEMDAN-DBT | 1.99 | 1.63 | 7.70 | 15.17 | 13.68 | 0.57 | 0.47 | |||
| EMD-DBT | 2.36 | 1.93 | 9.11 | 18.53 | 14.99 | 0.65 | 0.37 | |||
| DA-VMD-DBT | 1.34 | 0.87 | 5.57 | 11.37 | 7.18 | 0.41 | 0.52 | |||
| 8–12 μm 6–7 μm | 40∗10−14 65∗10−15 | 13.33 14.62 | DBT | 3.22 | 2.52 | 11.56 | 23.16 | 21.68 | 0.88 | 0.19 |
| ASVD-DBT | 1.78 | 1.42 | 6.81 | 12.76 | 10.49 | 0.46 | 0.39 | |||
| Wd-DBT | 1.01 | 0.79 | 3.85 | 8.93 | 6.99 | 0.31 | 0.45 | |||
| CEEMDAN-DBT | 1.02 | 0.75 | 3.79 | 8.55 | 6.32 | 0.30 | 0.52 | |||
| EMD-DBT | 1.84 | 1.32 | 6.79 | 12.95 | 9.35 | 0.44 | 0.48 | |||
| DA-VMD-DBT | 0.83 | 0.65 | 4.34 | 8.37 | 5.44 | 0.38 | 0.63 | |||
| 8–12 μm 6–7 μm | 30∗10−14 45∗10−15 | 17.11 17.88 | DBT | 2.45 | 1.89 | 9.01 | 18.18 | 15.31 | 0.64 | 0.36 |
| ASVD-DBT | 0.96 | 0.67 | 4.23 | 8.87 | 5.97 | 0.33 | 0.64 | |||
| Wd-DBT | 0.90 | 0.67 | 3.3 | 8.92 | 6.54 | 0.30 | 0.50 | |||
| CEEMDAN-DBT | 1.17 | 0.79 | 4.23 | 9.38 | 7.27 | 0.33 | 0.64 | |||
| EMD-DBT | 1.72 | 1.33 | 5.53 | 11.05 | 9.95 | 0.42 | 0.75 | |||
| DA-VMD-DBT | 0.73 | 0.48 | 3.01 | 8.28 | 4.39 | 0.28 | 0.77 | |||
| 8–12 μm 6–7 μm | 20∗10−14 30∗10−15 | 22.42 21.67 | DBT | 1.71 | 1.34 | 6.39 | 13.38 | 10.43 | 0.47 | 0.43 |
| ASVD-DBT | 0.97 | 0.65 | 3.49 | 10.60 | 5.91 | 0.33 | 0.67 | |||
| Wd-DBT | 0.79 | 0.53 | 2.86 | 8.30 | 5.09 | 0.27 | 0.70 | |||
| CEEMDAN-DBT | 0.96 | 0.60 | 3.38 | 10.16 | 5.61 | 0.32 | 0.67 | |||
| EMD-DBT | 1.30 | 0.91 | 4.77 | 10.71 | 7.90 | 0.38 | 0.76 | |||
| DA-VMD-DBT | 0.64 | 0.36 | 2.16 | 7.64 | 3.48 | 0.24 | 0.79 |
| Infrared Band | NEI (W∗m−2) | SNR | MV-TE (%) | SD-TE (%) | RMSE-T | MV-EAP (%) | SD-EAP (%) | RMSE-EAP | NCC-EAP | |
|---|---|---|---|---|---|---|---|---|---|---|
| 8–12 μm 3–5 μm | 120∗10−14 200∗10−15 | 4.69 1.67 | DBT | 10.10 | 7.25 | 37.17 | 96.38 | 170.67 | 6.42 | 0.055 |
| ASVD-DBT | 4.94 | 3.37 | 16.85 | 24.42 | 24.05 | 0.95 | 0.21 | |||
| Wd-DBT | 4.62 | 2.87 | 16.29 | 18.30 | 13.88 | 0.63 | 0.24 | |||
| CEEMDAN-DBT | 5.11 | 3.44 | 17.91 | 24.21 | 19.16 | 0.84 | 0.21 | |||
| EMD-DBT | 4.32 | 3.17 | 14.17 | 16.76 | 10.98 | 0.54 | 0.30 | |||
| DA-VMD-DBT | 4.19 | 2.30 | 14.29 | 20.08 | 15.78 | 0.69 | 0.28 | |||
| 8–12 μm 3–5 μm | 80∗10−14 130∗10−15 | 6.75 2.43 | DBT | 7.44 | 6.16 | 28.86 | 46.29 | 71.62 | 2.40 | 0.076 |
| ASVD-DBT | 4.32 | 3.37 | 17.18 | 19.74 | 14.86 | 0.68 | 0.42 | |||
| Wd-DBT | 3.52 | 2.65 | 13.18 | 14.83 | 10.13 | 0.49 | 0.39 | |||
| CEEMDAN-DBT | 4.15 | 2.46 | 14.41 | 16.68 | 11.42 | 0.56 | 0.46 | |||
| EMD-DBT | 3.81 | 2.79 | 13.09 | 10.35 | 8.41 | 0.47 | 0.49 | |||
| DA-VMD-DBT | 3.41 | 2.31 | 12.32 | 16.78 | 11.59 | 0.68 | 0.51 | |||
| 8–12 μm 3–5 μm | 60∗10−14 90∗10−15 | 9.25 3.50 | DBT | 5.32 | 3.93 | 19.77 | 29.14 | 38.83 | 1.34 | 0.34 |
| ASVD-DBT | 3.41 | 2.31 | 12.34 | 14.59 | 10.44 | 0.50 | 0.47 | |||
| Wd-DBT | 2.92 | 1.84 | 10.33 | 11.79 | 7.68 | 0.38 | 0.57 | |||
| CEEMDAN-DBT | 3.45 | 1.76 | 11.47 | 13.38 | 9.05 | 0.43 | 0.60 | |||
| EMD-DBT | 3.01 | 1.78 | 10.46 | 13.13 | 7.72 | 0.43 | 0.62 | |||
| DA-VMD-DBT | 2.96 | 1.74 | 10.28 | 11.01 | 6.88 | 0.36 | 0.65 | |||
| 8–12 μm 3–5 μm | 40∗10−14 65∗10−15 | 13.33 4.54 | DBT | 4.16 | 2.85 | 15.07 | 20.17 | 16.71 | 0.73 | 0.38 |
| ASVD-DBT | 3.22 | 2.17 | 11.62 | 13.48 | 9.94 | 0.46 | 0.52 | |||
| Wd-DBT | 3.02 | 1.68 | 9.79 | 11.25 | 6.07 | 0.33 | 0.58 | |||
| CEEMDAN-DBT | 2.49 | 1.76 | 9.14 | 10.44 | 6.72 | 0.31 | 0.68 | |||
| EMD-DBT | 3.08 | 1.63 | 10.42 | 10.69 | 7.35 | 0.38 | 0.66 | |||
| DA-VMD-DBT | 2.97 | 1.53 | 9.99 | 9.89 | 5.59 | 0.31 | 0.74 | |||
| 8–12 μm 3–5 μm | 30∗10−14 45∗10−15 | 17.11 6.15 | DBT | 3.52 | 2.32 | 12.61 | 15.50 | 10.70 | 0.52 | 0.46 |
| ASVD-DBT | 2.71 | 1.56 | 9.35 | 9.01 | 6.16 | 0.29 | 0.73 | |||
| Wd-DBT | 3.07 | 1.22 | 9.89 | 10.04 | 5.03 | 0.31 | 0.72 | |||
| CEEMDAN-DBT | 2.87 | 1.63 | 9.86 | 8.93 | 6.03 | 0.29 | 0.75 | |||
| EMD-DBT | 3.08 | 1.57 | 10.34 | 10.01 | 6.85 | 0.34 | 0.71 | |||
| DA-VMD-DBT | 2.75 | 1.29 | 9.07 | 8.76 | 5.51 | 0.29 | 0.80 | |||
| 8–12 μm 3–5 μm | 20∗10−14 30∗10−15 | 22.42 9.88 | DBT | 3.00 | 1.92 | 10.65 | 11.17 | 7.48 | 0.37 | 0.61 |
| ASVD-DBT | 2.91 | 1.05 | 9.25 | 8.64 | 5.03 | 0.27 | 0.88 | |||
| Wd-DBT | 3.02 | 1.14 | 9.68 | 8.89 | 5.30 | 0.28 | 0.76 | |||
| CEEMDAN-DBT | 2.90 | 1.22 | 9.42 | 8.45 | 4.32 | 0.28 | 0.81 | |||
| EMD-DBT | 2.96 | 1.44 | 10.23 | 9.68 | 6.23 | 0.31 | 0.84 | |||
| DA-VMD-DBT | 2.76 | 1.20 | 9.00 | 8.88 | 4.68 | 0.27 | 0.88 |
| Parameter Name | Infrared Detector 1 | Infrared Detector 2 |
|---|---|---|
| Spectral range (μm) | 8–11.7 | 3–5 |
| Resolution (pixel) | 320 × 256 | 640 × 512 |
| Pixel size (μm) | 30 | 15 |
| Focal length (mm) | 100 | 200 |
| Optical aperture (cm) | 5 | 5 |
| Infrared Band | SNR | MV-TE (%) | SD-TE (%) | RMSE-T | MV-EAP (%) | SD-EAP (%) | RMSE-EAP | NCC-EAP | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 8–11.7 μm 3–5 μm | 5 5 | DBT | 4.38 | 3.11 | 16.80 | 43.34 | 37.27 | 0.0084 | 0.018 | |
| ASVD-DBT | 2.37 | 1.39 | 8.59 | 22.89 | 15.52 | 0.0040 | 0.084 | |||
| Wd-DBT | 2.20 | 1.27 | 7.95 | 21.47 | 14.05 | 0.0037 | 0.11 | |||
| CEEMDAN-DBT | 2.49 | 1.10 | 8.54 | 22.83 | 11.99 | 0.0037 | 0.13 | |||
| EMD-DBT | 2.23 | 1.31 | 8.09 | 21.21 | 13.33 | 0.0036 | 0.09 | |||
| DA-VMD-DBT | 1.99 | 1.17 | 7.23 | 19.46 | 13.57 | 0.0035 | 0.11 | |||
| 8–11.7 μm 3–5 μm | 10 10 | DBT | 2.41 | 1.71 | 9.24 | 23.38 | 19.25 | 0.0045 | 0.10 | |
| ASVD-DBT | 2.32 | 0.74 | 7.65 | 20.15 | 6.68 | 0.0031 | 0.33 | |||
| Wd-DBT | 2.27 | 0.82 | 7.57 | 20.27 | 8.35 | 0.0032 | 0.42 | |||
| CEEMDAN-DBT | 2.27 | 0.78 | 7.51 | 19.53 | 7.84 | 0.0031 | 0.41 | |||
| EMD-DBT | 2.38 | 0.83 | 7.89 | 21.20 | 8.66 | 0.0034 | 0.31 | |||
| DA-VMD-DBT | 2.08 | 0.65 | 6.81 | 19.27 | 6.47 | 0.0030 | 0.47 | |||
| 8–11.7 μm 3–5 μm | 15 15 | DBT | 2.13 | 1.44 | 8.04 | 19.87 | 14.08 | 0.0036 | 0.21 | |
| ASVD-DBT | 2.20 | 0.53 | 7.09 | 19.69 | 4.62 | 0.0030 | 0.58 | |||
| Wd-DBT | 2.26 | 0.62 | 7.35 | 20.66 | 5.99 | 0.0032 | 0.50 | |||
| CEEMDAN-DBT | 2.24 | 0.50 | 7.18 | 20.04 | 4.66 | 0.0030 | 0.49 | |||
| EMD-DBT | 2.21 | 0.65 | 7.21 | 20.36 | 6.74 | 0.0032 | 0.53 | |||
| DA-VMD-DBT | 1.99 | 0.44 | 6.38 | 17.67 | 4.00 | 0.0027 | 0.61 | |||
| 8–11.7 μm 3–5 μm | 20 20 | DBT | 2.23 | 1.13 | 7.82 | 20.72 | 11.63 | 0.0035 | 0.28 | |
| ASVD-DBT | 2.23 | 0.42 | 7.12 | 19.36 | 3.63 | 0.0029 | 0.65 | |||
| Wd-DBT | 2.28 | 0.38 | 7.25 | 20.36 | 4.30 | 0.0031 | 0.62 | |||
| CEEMDAN-DBT | 2.23 | 0.48 | 7.01 | 20.04 | 3.01 | 0.0029 | 0.65 | |||
| EMD-DBT | 2.23 | 0.47 | 7.13 | 20.25 | 4.42 | 0.0031 | 0.56 | |||
| DA-VMD-DBT | 2.22 | 0.36 | 7.03 | 20.06 | 3.74 | 0.0030 | 0.74 | |||
| 8–11.7 μm 3–5 μm | 25 25 | DBT | 2.17 | 0.97 | 7.42 | 19.86 | 9.66 | 0.0033 | 0.32 | |
| ASVD-DBT | 2.17 | 0.37 | 6.84 | 19.65 | 2.90 | 0.0029 | 0.77 | |||
| Wd-DBT | 2.20 | 0.43 | 7.02 | 19.87 | 3.73 | 0.0030 | 0.64 | |||
| CEEMDAN-DBT | 2.19 | 0.47 | 7.01 | 19.70 | 4.15 | 0.0029 | 0.62 | |||
| EMD-DBT | 2.21 | 0.51 | 7.09 | 19.91 | 4.16 | 0.0030 | 0.74 | |||
| DA-VMD-DBT | 2.16 | 0.33 | 6.84 | 19.50 | 3.02 | 0.0029 | 0.87 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Rao, P.; Chen, X.; Xia, H.; Zhang, S. Denoising and Feature Extraction for Space Infrared Dim Target Recognition Utilizing Optimal VMD and Dual-Band Thermometry. Machines 2022, 10, 168. https://doi.org/10.3390/machines10030168
Zhang H, Rao P, Chen X, Xia H, Zhang S. Denoising and Feature Extraction for Space Infrared Dim Target Recognition Utilizing Optimal VMD and Dual-Band Thermometry. Machines. 2022; 10(3):168. https://doi.org/10.3390/machines10030168
Chicago/Turabian StyleZhang, Hao, Peng Rao, Xin Chen, Hui Xia, and Shenghao Zhang. 2022. "Denoising and Feature Extraction for Space Infrared Dim Target Recognition Utilizing Optimal VMD and Dual-Band Thermometry" Machines 10, no. 3: 168. https://doi.org/10.3390/machines10030168
APA StyleZhang, H., Rao, P., Chen, X., Xia, H., & Zhang, S. (2022). Denoising and Feature Extraction for Space Infrared Dim Target Recognition Utilizing Optimal VMD and Dual-Band Thermometry. Machines, 10(3), 168. https://doi.org/10.3390/machines10030168






