Recent Advancements in the Tribological Modelling of Rough Interfaces
Abstract
1. Introduction
2. BEM Formulation for Elastic Sliding Contacts
3. BEM Formulation for Viscoelastic Sliding Contacts
4. Results and Discussion
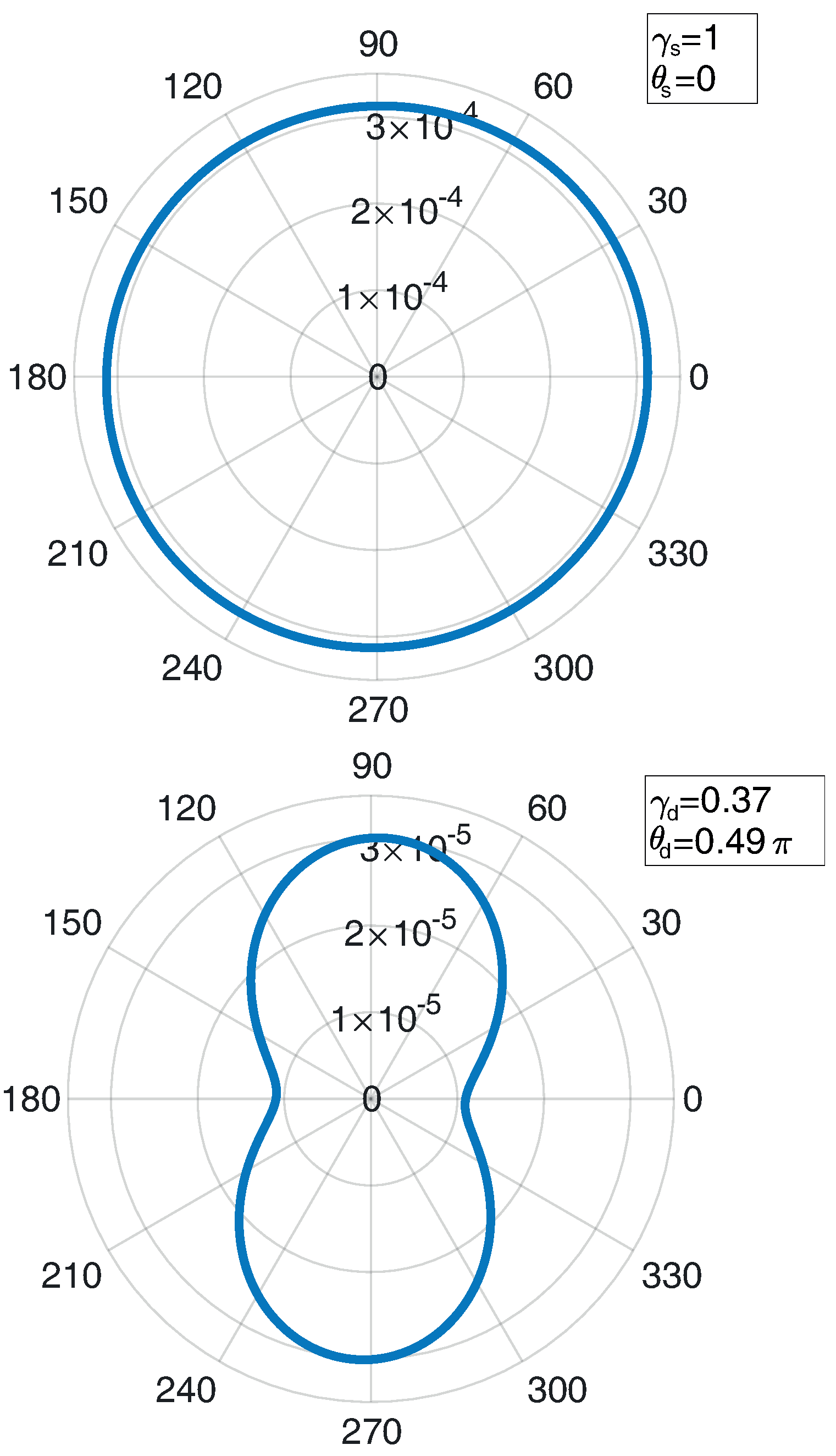
4.1. Two-Dimentional Viscoelastic Sliding Rough Contacts: The Role of Anisotropy
4.2. Adhesion in Elastic Contacts of Thin Layers
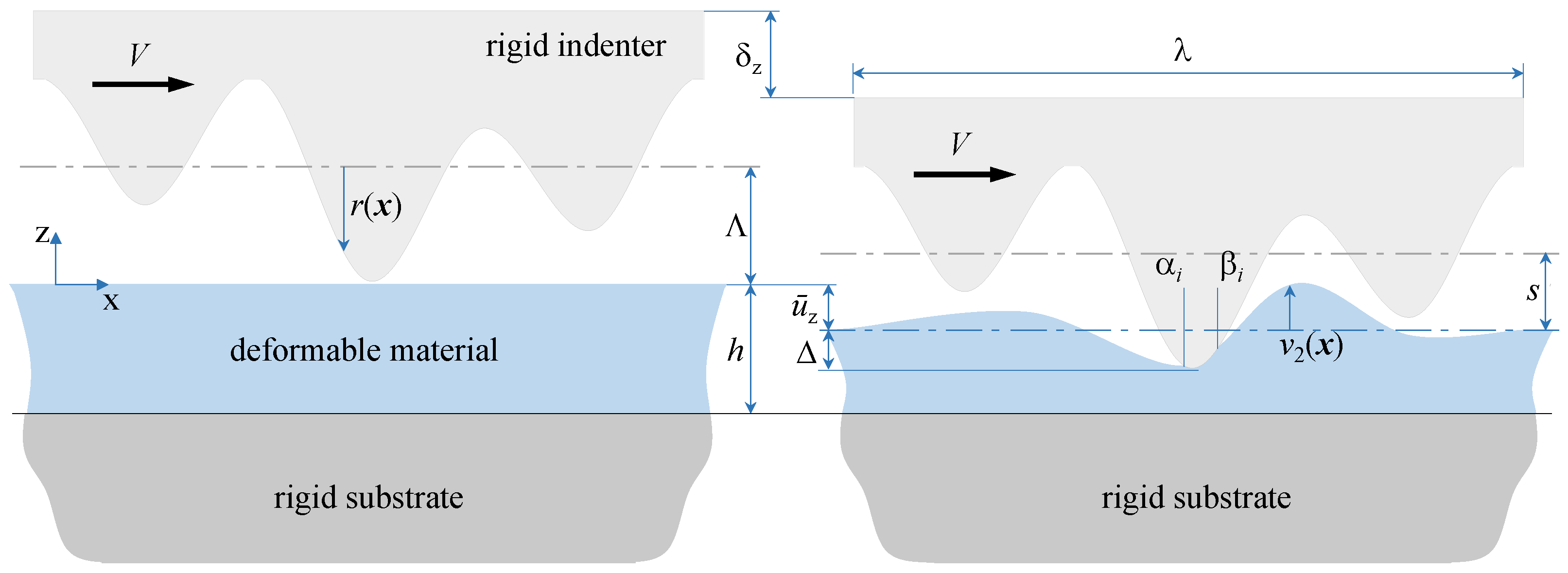
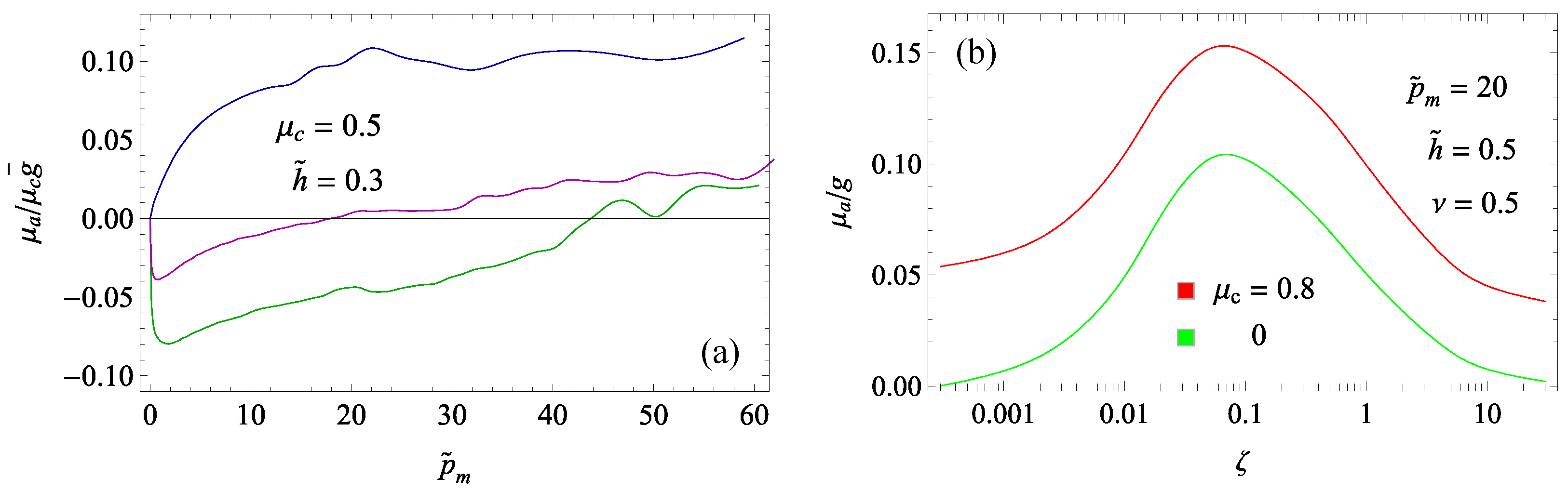
4.3. Frictional Elastic/Viscoelastic Sliding Rough Contacts of Thin Layers
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thatte, A.; Salant, R.F. Effects of multi-scale viscoelasticity of polymers on high-pressure, high-frequency sealing dynamics. Tribol. Int. 2012, 52, 75–86. [Google Scholar] [CrossRef]
- Shukla, A.; Datta, T. Optimal Use of Viscoelastic Dampers in Building Frames for Seismic Force. J. Struct. 1999, 125, 401–409. [Google Scholar] [CrossRef]
- Geim, A.K.; Dubonos, S.V.; Gricorieva, I.V.; Novoselov, K.S.; Zhukov, A.A.; Shapoval, S.Y. Microfabricated adhesive mimicking gecko foot-hair. Nat. Mater. 2003, 2, 461–463. [Google Scholar] [CrossRef] [PubMed]
- Dening, K.; Heepe, L.; Afferrante, L.; Carbone, G.; Gorb, S. Adhesion control by inflation: Implications from biology to artificial attachment device. Appl. Phys. A Mater. Sci. Process. 2014, 116, 567–573. [Google Scholar] [CrossRef]
- Arzt, E.; Gorb, S.; Spolenak, R. From micro to nano contacts in biological attachment devices. Proc. Natl. Acad. Sci. USA 2003, 100, 10603–10606. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Ryu, S.; Tokareva, O.; Gronau, G.; Jakobsen, M.M.; Huang, W.; Rizzo, D.J.; Li, D.; Stai, C.; Pugno, N.; et al. Predictive modelling-based design and experiments for synthesis and spinning of bioinspired silk fibres. Nat. Commun. 2015, 6, 6892. [Google Scholar] [CrossRef]
- Angelini, T.E.; Dunn, A.C.; Uruena, J.M.; Dickrell, D.J.; Burris, D.L.; Sawyer, W.G. Cell Friction. Faraday Discuss. 2012, 156, 31–39. [Google Scholar] [CrossRef]
- Dunn, A.C.; Cobb, J.A.; Kantzios, A.N.; Lee, S.J.; Sarntinoranont, M.; Tran-Son-Tay, R.; Sawyer, W.G. Friction Coefficient Measurement of Hydrogel Materials on Living Epithelial Cells. Tribol. Lett. 2008, 30, 13–19. [Google Scholar] [CrossRef]
- Chortos, A.; Liu, J.; Bao, Z. Pursuing prosthetic electronic skin. Nature 2016, 15, 937. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of Nominally Flat Surfaces. Proc. R. Soc. Lond. A 1966, 295, 300–319. [Google Scholar]
- Greenwood, J.A.; Putignano, C.; Ciavarella, M. A Greenwood & Williamson theory for line contact. Wear 2011, 270, 332–334. [Google Scholar]
- Bush, A.W.; Gibson, R.D.; Thomas, T.R. The elastic contact of a rough surface. Wear 1975, 35, 87–111. [Google Scholar] [CrossRef]
- Carbone, G.; Bottiglione, F. Asperity contact theories: Do they predict linearity between contact area and load? J. Mech. Phys. Solids 2008, 56, 2555–2572. [Google Scholar] [CrossRef]
- Sahlia, R.; Pallares, G.; Ducottet, C.; Ben Alid, I.E.; Al Akhrassd, S.; Guiberta, M.; Scheibert, J. Evolution of real contact area under shear and the value of static friction of soft materials. Proc. Natl. Acad. Sci. USA 2017, 115, 471–476. [Google Scholar] [CrossRef] [PubMed]
- Carbone, G.; Scaraggi, M.; Tartaglino, U. Adhesive contact of rough surfaces: Comparison between numerical calculations and analytical theories. Eur. Phys. J. E—Soft Matter 2009, 30, 65–74. [Google Scholar] [CrossRef]
- Putignano, C.; Afferrante, L.; Carbone, G.; Demelio, G. The influence of the statistical properties of self-affine surfaces in elastic contact: A numerical investigation. J. Mech. Phys. Solids 2012, 60, 973–982. [Google Scholar] [CrossRef]
- Putignano, C.; Afferrante, L.; Carbone, G.; Demelio, G. A new efficient numerical method for contact mechanics of rough surfaces. Int. J. Solids Struct. 2012, 49, 338–343. [Google Scholar] [CrossRef]
- Paggi, M.; Ciaveralla, M. The coefficient of proportionality k between real contact area and load, with new asperity models. Wear 2010, 268, 1020–1029. [Google Scholar] [CrossRef]
- Yastrebov, V.A.; Anciaux, G.; Molinari, J.F. Contact between representative rough surfaces. Phys. Rev. E 2012, 86, 035601(R). [Google Scholar] [CrossRef]
- Yastrebov, V.A.; Anciaux, G.; Molinari, J.F. The role of the roughness spectral breadth in elastic contact of rough surfaces. J. Mech. Phys. Solids 2017, 107, 469–493. [Google Scholar] [CrossRef]
- Ju, Y.; Farris, T.N. Spectral Analysis of Two-Dimensional Contact Problems. J. Tribol. 1996, 118, 320–328. [Google Scholar] [CrossRef]
- Stanley, H.M.; Kato, T. An FFT-Based Method for Rough Surface Contact. J. Tribol. 1997, 119, 481–485. [Google Scholar] [CrossRef]
- Campana, C.; Muser, M.H. Contact Mechanics of Real vs Randomly Rough Surfaces: A Green’s Function Molecular Dynamics Study. Europhys. Lett. 2007, 77, 38005. [Google Scholar] [CrossRef]
- Dapp, W.B.; Lücke, A.; Persson, B.N.J.; Müser, M.H. Self-affine elastic contacts: Percolation and leakage. Phys. Rev. Lett. 2012, 108, 244301. [Google Scholar] [CrossRef] [PubMed]
- Takewaki, I. Building Control with Passive Dampers: Optimal Performance-Based Design for Earthquakes; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Bao, G.; Suresh, S. Cell and molecular mechanics of biological materials. Nat. Mater. 2003, 2, 715–725. [Google Scholar] [CrossRef]
- Hunter, S.C. The rolling contact of a rigid cylinder with a viscoelastic half space. Trans. ASME Ser. E J. Appl. Mech. 1961, 28, 611–617. [Google Scholar] [CrossRef]
- Carbone, G.; Putignano, C. A novel methodology to predict sliding/rolling friction in viscoelastic materials: Theory and experiments. J. Mech. Phys. Solids 2013, 61, 1822–1834. [Google Scholar] [CrossRef]
- Grosch, K.A. The Relation between the Friction and Visco-Elastic Properties of Rubber. Proc. R. Soc. Lond. Ser. A Math. Phys. 1963, 274, 21–39. [Google Scholar]
- Putignano, C.; Reddyhoff, T.; Carbone, G.; Dini, D. Experimental investigation of viscoelastic rolling contacts: A comparison with theory. Tribol. Lett. 2013, 51, 105–113. [Google Scholar] [CrossRef]
- Putignano, C.; Reddyhoff, T.; Dini, D. The influence of temperature on viscoelastic friction properties. Tribol. Int. 2016, 100, 338–343. [Google Scholar] [CrossRef]
- Kusche, S. Frictional force between a rotationally symmetric indenter and a viscoelastic half-space. J. Appl. Math. Mech. 2017, 97, 226–239. [Google Scholar] [CrossRef]
- Carbone, G.; Putignano, C. Rough viscoelastic sliding contact: Theory and experiments. Phys. Rev. E 2014, 89, 032408. [Google Scholar] [CrossRef] [PubMed]
- Koumi, K.E.; Chaise, T.; Nelias, D. Rolling contact of a rigid sphere/sliding of a spherical indenter upon a viscoelastic half-space containing an ellipsoidal inhomogeneity. J. Mech. Phys. Solids 2015, 80, 1–25. [Google Scholar] [CrossRef]
- Putignano, C.; Carbone, G.; Dini, D. Mechanics of Rough Contacts in Elastic and Viscoelastic Thin Layers. Int. Solids Struct. 2015, 69–70, 507–517. [Google Scholar] [CrossRef]
- Putignano, C.; Carbone, G.; Dini, D. Theory of reciprocating contact for viscoelastic solids. Phys. Rev. E 2016, 93, 043003. [Google Scholar] [CrossRef]
- Putignano, C.; Carbone, G. Viscoelastic Damping in alternate reciprocating contacts. Sci. Rep. 2017, 7, 8333. [Google Scholar] [CrossRef]
- Putignano, C.; Carbone, G. Viscoelastic reciprocating contacts in presence of finite rough interfaces: A numerical investigation. J. Mech. Phys. Solids 2018, 114, 185–193. [Google Scholar] [CrossRef]
- Putignano, C.; Dini, D. Soft matter lubrication: Does solid viscoelasticity matter? Acs Appl. Mater. Interfaces 2017, 9, 42287–42295. [Google Scholar] [CrossRef]
- Putignano, C. Soft lubrication: A generalized numerical methodology. J. Mech. Phys. Solids 2020, 134, 103748. [Google Scholar] [CrossRef]
- Putignano, C.; Burris, D.L.; Moore, A.; Dini, D. Cartilage rehydration: The sliding-induced hydrodynamic triggering mechanism. Acta Biomater. 2021, 125, 90–99. [Google Scholar] [CrossRef]
- Putignano, C.; Menga, N.; Afferrante, L.; Carbone, G. Viscoelasticity induces anisotropy in contacts of rough solids. J. Mech. Phys. Solids 2019, 129, 147–159. [Google Scholar] [CrossRef]
- Bottiglione, F.; Carbone, G.; Mangialardi, L.; Mantriota, G. Leakage mechanism in flat seals. J. Appl. Phys. 2009, 106, 104902. [Google Scholar] [CrossRef]
- Lorenz, B.; Persson, B.N.J. Leak rate of seals: Effective-medium theory and comparison with experiment. Eur. Phys. J. E 2010, 31, 159–167. [Google Scholar] [CrossRef] [PubMed]
- Dapp, W.B.; Müser, M.H. Fluid leakage near the percolation threshold. Sci. Rep. 2016, 6, 19513. [Google Scholar] [CrossRef] [PubMed]
- Vladescu, S.; Putignano, C.; Marx, N.; Keppens, T.; Reddyhoff, T.; Dini, D. The percolation of liquid through a compliant seal—An experimental and theoretical study. J. Fluids Eng. 2019, 141, 031101. [Google Scholar] [CrossRef]
- Persson, B.N.J. Adhesion between an elastic body and a randomly rough hard surface. Eur. Phys. J. E 2002, 8, 385–401. [Google Scholar] [CrossRef]
- Pastewka, L.; Robbins, M.O. Contact between rough surfaces and a criterion for macroscopic adhesion. Proc. Natl. Acad. Sci. USA 2014, 111, 3298–3303. [Google Scholar] [CrossRef]
- Menga, N.; Carbone, G.; Dini, D. Do uniform tangential interfacial stresses enhance adhesion? J. Mech. Phys. Solids 2019, 133, 103744. [Google Scholar] [CrossRef]
- Violano, G.; Afferrante, L. Size effects in adhesive contacts of viscoelastic media. Eur. J. Mech.-A/Solids 2022, 96, 104665. [Google Scholar] [CrossRef]
- Violano, G.; Chateauminois, A.; Afferrante, L. Rate-dependent adhesion of viscoelastic contacts, Part I: Contact area and contact line velocity within model randomly rough surfaces. Mech. Mater. 2021, 160, 103926. [Google Scholar] [CrossRef]
- Violano, G.; Chateauminois, A.; Afferrante, L. Rate-dependent adhesion of viscoelastic contacts. Part II: Numerical model and hysteresis dissipation. Mech. Mater. 2021, 158, 103884. [Google Scholar] [CrossRef]
- Medina, S.; Dini, D. A numerical model for the deterministic analysis of adhesive rough contacts down to the nano-scale. Int. J. Solids Struct. 2014, 51, 2620–2632. [Google Scholar] [CrossRef]
- Persson, B.N.J. Theory of rubber friction and contact mechanics. J. Chem. Phys. 2001, 115, 3840–3861. [Google Scholar] [CrossRef]
- Yang, C.; Persson, B.N.J. Molecular Dynamics Study of Contact Mechanics: Contact Area and Interfacial Separation from Small to Full Contact. Phys. Rev. Lett. 2008, 100, 024303. [Google Scholar] [CrossRef]
- Hyun, S.; Pei, L.; Molinari, J.-F.; Robbins, M.O. Finite-element analysis of contact between elastic self-affine surfaces. Phys. Rev. E 2004, 70, 026117. [Google Scholar] [CrossRef] [PubMed]
- Campana, C.; Mueser, M.H.; Robbins, M.O. Elastic contact between self-affine surfaces: Comparison of numerical stress and contact correlation functions with analytic predictions. J. Phys. Condens. Matter 2008, 20, 354013. [Google Scholar] [CrossRef]
- Menga, N.; Putignano, C.; Carbone, G.; Demelio, G.P. The sliding contact of a rigid wavy surface with a viscoelastic half-space. Proc. R. Soc. A 2014, 470, 20140392. [Google Scholar] [CrossRef]
- Müser, M.H.; Dapp, W.B.; Bugnicourt, R.; Sainsot, P.; Lesaffre, N.; Lubrecht, T.A.; Persson, B.N.J.; Harris, K.; Bennett, A.; Schulze, K.; et al. Meeting the contact-mechanics challenge. Tribol. Lett. 2017, 65, 118. [Google Scholar] [CrossRef]
- Papangelo, A.; Putignano, C.; Hoffmann, N. Self-excited vibrations due to viscoelastic interactions. Mech. Syst. Signal Process. 2020, 144, 106894. [Google Scholar] [CrossRef]
- Papangelo, A.; Putignano, C.; Hoffmann, N. Critical thresholds for mode-coupling instability in viscoelastic contacts. Nonlinear Dyn. 2021, 104, 2995–3011. [Google Scholar] [CrossRef]
- Menga, N.; Afferrante, L.; Carbone, G. Effect of thickness and boundary conditions on the behavior of viscoelastic layers in sliding contact with wavy profiles. J. Mech. Phys. Solids 2016, 95, 517–529. [Google Scholar] [CrossRef]
- Carbone, G.; Mangialardi, L. Analysis of the adhesive contact of confined layers by using a Green’s function approach. J. Mech. Phys. Solids 2008, 56, 684–706. [Google Scholar] [CrossRef]
- Menga, N.; Afferrante, L.; Carbone, G. Adhesive and adhesiveless contact mechanics of elastic layers on slightly wavy rigid substrates. Int. J. Solids Struct. 2016, 88, 101–109. [Google Scholar] [CrossRef]
- Menga, N.; Foti, D.; Carbone, G. Viscoelastic frictional properties of rubber-layer roller bearings (RLRB) seismic isolators. Meccanica 2017, 52, 2807–2817. [Google Scholar] [CrossRef]
- Menga, N.; Afferrante, L.; Demelio, G.P.; Carbone, G. Rough contact of sliding viscoelastic layers: Numerical calculations and theoretical predictions. Tribol. Int. 2018, 122, 67–75. [Google Scholar] [CrossRef]
- Sackfield, A.; Hills, D.A.; Nowell, D. Mechanics of Elastic Contacts; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Barber, J.R. Contact Mechanics; Springer: Berlin/Heidelberg, Germany, 2018; Volume 250. [Google Scholar]
- Nowell, D.; Hills, D.A.; Sackfield, A. Contact of dissimilar elastic cylinders under normal and tangential loading. J. Mech. Phys. Solids 1988, 36, 59–75. [Google Scholar] [CrossRef]
- Chen, W.W.; Wang, Q.J. A numerical model for the point contact of dissimilar materials considering tangential tractions. Mech. Mater. 2008, 40, 936–948. [Google Scholar] [CrossRef]
- Chen, W.W.; Wang, Q.J. A numerical static friction model for spherical contacts of rough surfaces, influence of load, material, and roughness. J. Tribol. 2009, 131, 021402. [Google Scholar] [CrossRef]
- Wang, Z.J.; Wang, W.Z.; Wang, H.; Zhu, D.; Hu, Y.Z. Partial slip contact analysis on three-dimensional elastic layered half space. J. Tribol. 2010, 132, 021403. [Google Scholar] [CrossRef]
- Elloumi, R.; Kallel-Kamoun, I.; El-Borgi, S. A fully coupled partial slip contact problem in a graded half-plane. Mech. Mater. 2010, 42, 417–428. [Google Scholar] [CrossRef]
- Bentall, R.H.; Johnson, K.L. An elastic strip in plane rolling contact. Int. J. Mech. 1968, 10, 637–663. [Google Scholar] [CrossRef]
- Nowell, D.; Hills, D.A. Contact problems incorporating elastic layers. Int. J. Solids Struct. 1988, 24, 105–115. [Google Scholar] [CrossRef]
- Nowell, D.; Hills, D.A. Tractive rolling of tyred cylinders. Int. J. Mech. Sci. 1988, 30, 945–957. [Google Scholar] [CrossRef]
- Menga, N. Rough frictional contact of elastic thin layers: The effect of geometric coupling. Int. J. Solids Struct. 2019, 164, 212–220. [Google Scholar] [CrossRef]
- Menga, N.; Carbone, G.; Dini, D. Exploring the effect of geometric coupling on friction and energy dissipation in rough contacts of elastic and viscoelastic coatings. J. Mech. Phys. Solids 2021, 148, 104273. [Google Scholar] [CrossRef]
- Kogut, L.; Komvopoulos, K. Electrical contact resistance theory for conductive rough surfaces. J. Appl. Phys. 2003, 94, 3153–3162. [Google Scholar] [CrossRef]
- Menga, N.; Ciavarella, M. A Winkler solution for the axisymmetric Hertzian contact problem with wear and finite element method comparison. J. Strain Anal. Eng. 2015, 50, 156–162. [Google Scholar] [CrossRef]
- Piveteau, L.-D.; Girona, M.I.; Schlapbach, L.; Barboux, P.; Boilot, J.-P.; Gasser, B. Thin films of calcium phosphate and titanium dioxide by a sol-gel route: A new method for coating medical implants. J. Mater. Sci. Mater. Med. 1999, 10, 161–167. [Google Scholar] [CrossRef]
- Allen, M.; Myer, B.; Rushton, N. In Vitro and In Vivo Investigations into the Biocompatibility of Diamond-Like Carbon (DLC) Coatings for Orthopedic Applications. J. Biomed. Mater. 2001, 58, 319–328. [Google Scholar] [CrossRef]
- Kwak, M.K.; Jeong, H.-E.; Suh, K.Y. Rational design and enhanced biocompatibility of a dry adhesive medical skin patch. Adv. Mater. 2011, 23, 3949–3953. [Google Scholar] [CrossRef]
- Bacon, K.D.; Cummins, C.F. Pressure-Sensitive Adhesive. U.S. Patent US2285570 A, 9 June 1942. [Google Scholar]
- Peterson, D.R.; Stupp, S.I. Poly(amino Acid) Adhesive Tissue Grafts. U.S. Patent US5733868 A, 31 March 1998. [Google Scholar]
- Al-Harthi, M.A.; Bakather, O.Y.; De, S.C. Pressure Sensitive Adhesive. U.S. Patent US8697821 B1, 15 April 2014. [Google Scholar]
- Menga, N.; Afferrante, L.; Pugno, N.M.; Carbone, G. The multiple V-shaped double peeling of elastic thin films from elastic soft substrates. J. Mech. Phys. Solids 2018, 113, 56–64. [Google Scholar] [CrossRef]
- Menga, N.; Dini, D.; Carbone, G. Tuning the periodic V-peeling behavior of elastic tapes applied to thin compliant substrates. Int. J. Mech. Sci. 2020, 170, 105331. [Google Scholar] [CrossRef]
- Putignano, C.; Afferrante, L.; Mangialardi, L.; Carbone, G. Equilibrium states and stability of pretensioned adhesive tapes. Beilstein J. Nanotechnol. 2014, 5, 1725–1731. [Google Scholar] [CrossRef] [PubMed]
- Ceglie, M.; Menga, N.; Carbone, G. The role of interfacial friction on the peeling of thin viscoelastic tapes. J. Mech. Phys. Solids 2022, 159, 104706. [Google Scholar] [CrossRef]
- Johnson, K.L.J. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Menga, N.; Carbone, G. The surface displacements of an elastic half-space subjected to uniform tangential tractions applied on a circular area. Eur. J. Mech.-A/Solids 2019, 73, 137–143. [Google Scholar] [CrossRef]
- Christensen, R.M. Theory of Viscoelasticity; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701. [Google Scholar] [CrossRef]
- Putignano, C. Oscillating viscoelastic periodic contacts: A numerical approach. Int. J. Mech. Sci. 2021, 208, 106663. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. The statistical analysis of a random, moving surface. Philos. Trans. R. Soc. Lond. A 1957, 249, 321. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menga, N.; Putignano, C.; Carbone, G. Recent Advancements in the Tribological Modelling of Rough Interfaces. Machines 2022, 10, 1205. https://doi.org/10.3390/machines10121205
Menga N, Putignano C, Carbone G. Recent Advancements in the Tribological Modelling of Rough Interfaces. Machines. 2022; 10(12):1205. https://doi.org/10.3390/machines10121205
Chicago/Turabian StyleMenga, Nicola, Carmine Putignano, and Giuseppe Carbone. 2022. "Recent Advancements in the Tribological Modelling of Rough Interfaces" Machines 10, no. 12: 1205. https://doi.org/10.3390/machines10121205
APA StyleMenga, N., Putignano, C., & Carbone, G. (2022). Recent Advancements in the Tribological Modelling of Rough Interfaces. Machines, 10(12), 1205. https://doi.org/10.3390/machines10121205







