Abstract
Accurate identification of ultrasonic signals can effectively improve the accuracy of a defect detection and inversion. Current methods, based on machine learning and deep learning have been able to classify signals with significant differences. However, the ultrasonic internal detection signal is interspersed with a large number of anomalous signals of an unknown origin and is affected by the time shift of echo features and noise interference, which leads to the low recognition accuracy of the ultrasonic internal detection signal, at this stage. To address the above problems, this paper proposes a two-stage ultrasonic signal recognition method, based on the envelope and local similarity features (TS-ES). In the first stage, a normal signal classification method, based on the envelope feature extraction and fusion is proposed to solve the problem of the low ultrasonic signal classification accuracy under the conditions of the echo feature time shift and noise interference. In the second stage, an abnormal signal detection method, based on the local similarity feature extraction and enhancement is proposed to solve the problem of detecting abnormal signals in ultrasound internal detection data. The experimental results show that the accuracy of the two-stage ultrasonic signal recognition method, based on the envelope and local similarity features (TS-ES) in this paper is 97.43%, and the abnormal signal detection accuracy and recall rate are as high as 99.7% and 97.81%.
1. Introduction
Ultrasonic testing technology (UT) is the most successful nondestructive testing technique (NDT) for quality assessment and the defect detection of engineering materials [1,2]. Among them, the phased-array ultrasound detection (PAUT) is far more efficient and accurate than the conventional single-probe intra-ultrasound detection techniques by virtue of the multiple sensors in the array [3]. Due to the complexity of the pipeline environment, the phased-array ultrasound detector collects ultrasonic internal detection data as an array of data, containing different numbers of echoes and interspersed with abnormal signals. In industrial applications, the high-precision identification of ultrasonic internal detection data can effectively improve the identification and inversion accuracy of defect detection [4]. At present, many researchers have carried out a lot of research work around signal classification, It mainly includes machine learning based and deep learning based approaches.
The machine learning based approach first extracts features from the signal, according to the designed rules and then classifies the extracted features using machine learning methods. An unsupervised classification method was proposed in the literature [5], which uses the natural breakpoint method and ultrasound signal mechanism, by setting an energy threshold to obtain the peak position of the ultrasound signal echo for classification. The method has a high accuracy for signals with distinct echo characteristics. In the literature [6], the ultrasound signal is processed and its time domain, frequency and wavelet domain features are extracted using the fast Fourier transform and wavelet packet variation, and finally the particle swarm optimization support vector machine (PSO-SVM) is used for classification. The literature [7] uses the adaptive empirical wavelet transform (EWT) to decompose the ultrasound signal into a series of empirical modal functions and classify its features using the random forest (RF). The above machine learning methods can achieve a high accuracy using fewer samples, but the model accuracy overly relies on expert experience to adjust a large number of feature extraction parameters, resulting in a poor model stability and generalization ability, so the classification accuracy for the actual ultrasound internal detection data is low.
In recent years, deep learning methods using neural networks have evolved rapidly and have been successful in a variety of signal classification tasks. The literature [8] demonstrates that deep neural networks with the Dropout regularization have a higher accuracy and stability on ultrasound signal classification tasks, compared to single-hidden layer neural networks. In the literature [9], an auto-encoder for eliminating ultrasonic signal noise was designed to reduce the effect of noise on classification accuracy. A one-dimensional convolutional neural network, based on an improved Softmax function, is proposed in the literature [4] for the classification of ultrasound signals with a high degree of similarity. The literature [10] uses a wavelet transform to gradually divide the multiscale signals by dilation and translation, and reorganize them into a two-dimensional feature matrix, that automatically completes the feature extraction, using the powerful feature extraction capability of the convolutional neural networks for two-dimensional data, and completes the feature classification using support vector machines instead of Softmax functions.
Deep learning methods, based on neural networks, can automatically extract deep features of sample data and classify signals by learning class-specific patterns, so deep learning methods have accuracy advantages over the traditional methods in most cases. Figure 1 illustrates the typical signals from several sets of ultrasonic internal detection data. The ultrasonic signals can be classified into normal and abnormal signals, according to whether the signals have the conditions for wall thickness calculation. Normal ultrasonic signals have obvious echo characteristics and can calculate the pipe wall thickness, based on the echo position, while abnormal ultrasonic signals are usually generated by uneven surfaces, such as welds or defects, which do not have echo characteristics and cannot calculate the pipe wall thickness. Normal signals can be further classified into two-echo signals, three-echo signals and four-echo signals, according to the number of echoes. Figure 1a shows the ideal normal signal collected by the experimental platform. This signal is free from noise interference, while the signal echo features are obvious and the arrival time is stable, and the current deep learning method is able to accurately classify the signal under such conditions. Figure 1b–d show the normal and abnormal signals collected during the actual internal detection task, respectively. For such real-world signals, current deep learning methods have a low classification accuracy, which is mainly caused by two aspects.
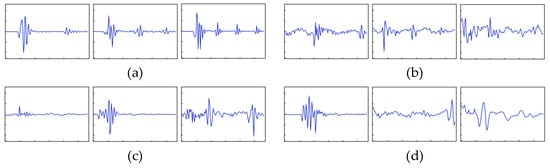
Figure 1.
Actual internal detection signal. The above signals are normalized. (a) Ideal signals in the experimental platform. (b) Actual internal detection normal signal. (c) Abnormal signals caused by welding seams. (d) Abnormal signals caused by defects.
(1) The severe noise interference and the time-shift phenomenon of the echo characteristics lead to the confusion of different types of normal signals. As shown in Figure 1b, the echo characteristics of various types of signals appear with different degrees of over-lagging, while the signals are accompanied by severe noise interference, which makes different classes of normal signals present an extremely high similarity in the high-dimensional space, thus affecting the classification accuracy.
(2) Anomalous signals occur for complex and diverse reasons, making it impossible to exhaust their patterns using sample labeling methods. As shown in Figure 1c,d, the absorption of ultrasound by the weld, the uneven surface of the defect on the ultrasound dispersion and other complex reasons caused by ultrasonic internal detection data interspersed with a large number of unknown abnormal signals, even if the same reason for the abnormal signal will have different patterns. Therefore, current deep learning methods tend to show a low classification accuracy when faced with unfamiliar anomalous signal patterns that have never appeared in the training set.
In order to solve the above problems, this paper proposes a two-stage ultrasonic signal recognition method, based on the envelope and local similarity features (TS-ES). The main contributions are as follows.
(1) An Akima-based data interpolation method is proposed for extracting the envelope features that are more correlated with the original signal.
(2) A convolution-based envelope feature fusion method is designed, which can automatically obtain the best fusion law between the envelope features and the original signal.
(3) A local similarity feature extraction method, based on dynamic time warping, is designed, which can still extract significant features without using anomalous signal samples.
(4) A probability-based similarity feature enhancement method is proposed to further strengthen the separability of the feature vectors in the embedding space.
2. Introduction of the Overall Approach
This paper proposes a two-stage ultrasonic signal recognition method, based on the envelope and local similarity features, which consists of two parts: normal signal classification, based on the envelope feature extraction and fusion, and the abnormal signal detection, based on the local similarity feature extraction and enhancement. The overall flow of the algorithm is shown in Figure 2.
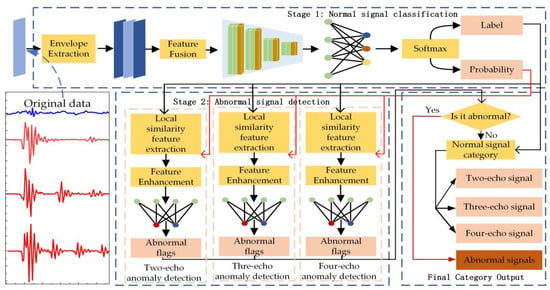
Figure 2.
Overall framework of the two-stage ultrasound signal recognition method, based on the envelope and local similarity features.
Stage 1: Normal signal classification method, based on the envelope feature extraction and fusion. This stage does not consider the existence of abnormal signals, and only classifies the signals to be detected into three types of normal signals with different numbers of echoes. Firstly, the envelope features of the signals are extracted, secondly, the envelope features are fused with the original signals, and finally, a one-dimensional convolutional neural network using the Softmax function as the top layer outputs the classes to which the signals belong and the probabilities of belonging to the classes.
Stage 2: Anomaly detection method, based on local similarity feature extraction and enhancement. In this stage, the anomaly detection is performed by using models with different parameters, according to the category to which the first stage belongs. The local similarity of the signal is first extracted and formed into a feature vector, and then the similarity feature vector is further enhanced and the anomaly detection is completed using the class probabilities from the first stage.
Finally, the final class of the signal to be detected is obtained by combining the classification and detection results of the two stages.
3. Normal Signal Classification Method, Based on the Envelope Feature Extraction and Fusion
In order to reduce the effects of the time shift of the normal signal echo features and strong noise interference, this paper proposes a normal signal classification method, based on the envelope feature extraction and fusion. Firstly, an Akima-based data interpolation method is proposed to extract the envelope features that are more correlated with the original signal, and secondly, a convolution-based envelope feature fusion method is designed, which automatically obtains the optimal fusion rule between the envelope and the original signal through network training. Then a one-dimensional convolutional neural network is used to complete the feature classification. Finally, a Softmax function is used to obtain the class to which the signal belongs and the corresponding class probability.
3.1. Envelope Feature Extraction
The envelope feature can eliminate the positive and negative amplitude oscillations of the ultrasound signal while preserving the echo position and intensity characteristics of the ultrasound signal, reducing the sensitivity of the algorithm to individual values and thus further reducing the effects of the time shifts and noise interference caused by the normal signal echo characteristics. Many methods have been developed to obtain the envelope of the signal, and the most representative technique is the interpolation of the local extrema, with linear, cubic spline, and Akima interpolation methods [11]. On the one hand, these methods are prone to downwash, overfilling, and edge effects [12]. On the other hand, the original data other than the extremal points are not involved in the computation, resulting in a reduced correlation between the generated envelopes and the original data. To solve these problems, an Akima-based data interpolation method is proposed in this paper to extract the envelope features that are more correlated with the original signal. The method includes two parts: local extremum extraction and the Akima-based data interpolation.
3.1.1. Local Extreme Point Extraction
The ultrasound signal X is a one-dimensional time-series signal, and X can be expressed in the following form.
The process of the extreme value point extraction is shown in Equations (2)–(5):
where MaxI, MinI, MaxI, MinV denote the local maximum sampling time, local maximum, local minimum sampling time and local minimum of the ultrasound signal, respectively. I denotes the position index, dif denotes the data differential operation and sign is the sign function.
The extracted local maxima are shown as red dots in Figure 3, and the local minima are shown as blue dots.
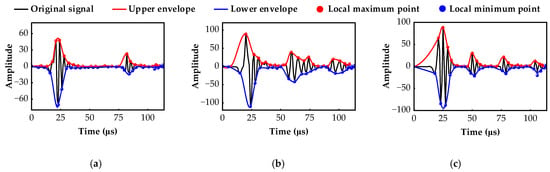
Figure 3.
Results of envelope feature extraction. (a) two echoes signal. (b) three echoes signal. (c) four echoes signal. The black line in the figure indicates the original ultrasound signal. The red line indicates the upper envelope derived using the Akima-based data interpolation method proposed in this paper. The black line indicates the lower envelope derived using the Akima-based data interpolation method proposed in this paper. The red points indicate the local maxima points. The black points indicate the local minima points.
3.1.2. Akima-Based Data Interpolation Method
Compared with the cubic spline interpolation method, the data obtained by the Akima interpolation method is smoother [13]. However, the Akima interpolation method only uses local extreme points to generate the envelope features. In order to involve the non-extreme points in the envelope calculation and further enhance the connection between the envelope and the original signal, this paper proposes an Akima-based data interpolation method, and the specific algorithm is shown in Equation (6).
where denotes the final envelope data, are the hyperparameters controlling the data smoothing and correlation, and the interpolation results are better when the values θ = 0.8, k = 2 are actually verified. is shown in Equation (7), which is the result after the interpolation using Akima.
The final acquired envelope features are shown as the red and blue lines in Figure 3. Considering that the raw ultrasound signal may still have irreplaceable features, the envelope data and the raw ultrasound signal are combined into a three-channel data output for the next stage of the feature fusion.
3.2. Feature Fusion and Classification
There must be a corresponding rule between the ultrasound signal and its upper and lower envelopes that can make the most significant features required by the classification network, but the optimal solution cannot be obtained by artificially specifying such a rule. In this paper, a convolution-based envelope feature fusion method is designed. The method fixes the position of the convolution kernel, and a convolution kernel is responsible for only one feature value in the fused feature vector, so as to find the optimal fusion law between the envelope and the original signal, and then uses a one-dimensional convolutional neural network to classify the fused features, as described in detail below.
3.2.1. Feature Fusion Method, Based on the Independent Convolution Kernel
As shown in equation (8), after the feature extraction, the obtained feature matrix with the 0 filled boundary can be represented as , using n convolution kernels for the fusion, according to Equation (10).
where is the value of the ith sampling moment after the feature fusion, and is the weight of the convolution kernel corresponding to the i sampling moment. The method obtains the optimal fusion parameters by gradient descent, and the post-fusion features of a certain sampling moment can take into account, not only the pre-fusion features of the current sampling moment, but also the pre-fusion features of the left and right neighboring moments, which makes the post-fusion features more comprehensive.
3.2.2. Normal Signal Classification
The fused features are classified using a one-dimensional convolutional neural network, and the network structure is shown in Table 1.

Table 1.
Structure of the one-dimensional convolutional neural network.
The network stacks multiple small convolutional kernels instead of large convolutional kernels, since multiple nonlinear layers increase the network depth to ensure learning more complex patterns with fewer parameters [14].
As shown in Equation (11), the network output of a single signal is , which is processed using the Softmax function to obtain the normal class (L) and the class probability (P) of the signal to be detected.
4. Anomalous Signal Detection Method, Based on the Local Similarity Feature Extraction and Enhancement
The expert system detects abnormal data in ultrasound intra-detection data by observing whether the signal to be detected has the echo characteristics of normal data. Inspired by this idea, this paper designs an abnormal signal detection method, based on the local similarity feature extraction and enhancement. First, a local similarity feature extraction method, based on the dynamic time regularization is designed to extract features in the absence of abnormal samples. Then a probability-based similarity feature enhancement method is proposed, which takes the category probability outputs in the first stage as inputs to further enhance the separability of the feature vectors in the embedding space. Finally, a two-layer fully connected neural network is used to complete the anomaly detection of the signal. Considering the relevance of the anomaly detection, this paper uses models with different parameters for each of the three categories of normal signals. The details are as follows.
4.1. Local Similarity Feature Extraction, Based on Dynamic Time Warping (DTW)
Dynamic time warping (DTW) is an algorithm used to measure the similarity between two sequences, and this sequence comparison method is commonly used for the time series classification [15]. As shown in Equation (12), X, Y are two time series with dimensions m and n, respectively.
D is the distance matrix, where D(i, j) is the distance between and , i.e.,
is the all aligned paths of X,Y. needs to satisfy the boundary condition, the continuity condition and the monotonicity condition [16]. The main idea of DTW is to find an optimal path on the distance matrix D using the dynamic programming (DP) algorithm that minimizes the cumulative value of the Euclidean distance on this path. As shown in Equation (14), this minimum distance is the DTW distance.
Compared to the Euclidean distance (ED), the DTW algorithm allows a one-to-many or many-to-one mapping of the data points of two sequences, enabling a degree of “warping” or “stretching” of the time axis, which makes it possible to make meaningful comparisons between two sequences that are similar in shape but differ locally. So this algorithm is suitable for the similarity comparison between ultrasound signals. Furthermore, considering that the ultrasonic normal signal features are mainly concentrated near the echo position, if the complete ultrasonic signal is used for matching, the similarity of the feature’s insignificant position will weaken the difference between different signal feature vectors, so a DTW-based local similarity feature extraction algorithm is designed in this paper. The details are described as follows.
4.1.1. Ultrasound Signal Pre-Processing
Different degrees of ultrasound signal amplitude attenuation can lead to large differences in the similarities between similar signals, and to eliminate this effect, the ultrasound signal is preprocessed using Equation (15).
where is the pre-processed ultrasound signal and is the original ultrasound signal. Following the pre-processing, the amplitude difference between the signals is eliminated and the shape information of the signals is retained.
4.1.2. Local Similarity Feature Extraction
As shown in Figure 4, the width of the DTW local similarity window is set to size, and the window moving step is str. XD is the ultrasound signal to be extracted, which can be expressed as Equation (16), where n is the ultrasound signal dimension.
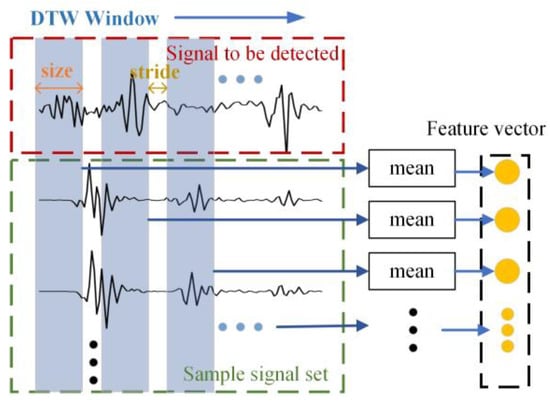
Figure 4.
DTW similarity feature extraction.
XS is the sample signal data set, which can be expressed as Equation (17), where m is the number of samples.
The DTW window extracts the similarity features, step by step, along the horizontal axis, and the feature vector F can be expressed as Equation (18), where k is the feature dimension, bounded by Equation (19). The feature extraction process can be expressed as Equation (20).
,is the local sub-signal of the ultrasound signal to be extracted and , is the local sub-signal of the Jth sample signal, which can be expressed as Equations (22) and (23).
In Equation (21), is the starting position of the window.
4.2. Probability-Based Similarity Feature Enhancement Method
To further enhance the separability of the local similarity features of the normal and abnormal signals in the embedding space, this section proposes a probability-based similarity feature enhancement method by combining the category of the probability outputs from the first stage normal signal classification method. The enhanced feature vector is , which can be expressed as Equation (24).
where is the eigenvalue in the enhanced eigenvector, which is calculated by Equation (25).
where is the enhancement coefficient, obtained by grid search, P is the category probability of the output of the signal to be detected after the first stage of the normal signal classification, and measures the probability that the signal to be detected is a certain normal signal. Following the processing by Equation (25), the mode of the abnormal signal feature vector will increase, expressed as a decrease in the degree of similarity, while the normal signal feature vector is unaffected, further widening the spacing between the two categories in the embedding space.
4.3. Abnormal Determination and Result Output
Considering that the low dimensionality of the similarity features, using a complex classifier will cause overfitting, this paper uses a two-layer fully connected neural network to determine the similarity features and finally determine whether the signal to be detected is anomalous or not.
Finally, as shown in Figure 2, we first determine whether the data is abnormal data, if the data is abnormal data, then we directly output the data as abnormal data, if not abnormal data, then we output the first stage of the normal signal classification results. Finally, the identification task of the detection data within the ultrasound is completed.
5. Experimental Verification
In this section, several sets of experiments are designed to demonstrate the effectiveness of the proposed method, and the sample data sets are given in Section 5.1. Section 5.2 demonstrates the effectiveness of the dynamic time regularization (DTW)-based local similarity feature extraction method proposed in Section 4.1 and the probability-based similarity feature enhancement method proposed in Section 4.2. Section 5.3 shows the performance comparison of the proposed method with other methods. Section 5.4 highlights the recognition power of the proposed method in this paper for unfamiliar anomalous signals. Finally, the performance of both the normal signal classification priority and anomaly detection priority approaches, is discussed in Section 5.5.
5.1. Experimental Setup
5.1.1. Description of the Experimental Sample Set
Two datasets are used in this paper, dataset 1 and dataset 2 are collected from two different oil pipelines in service. The basic information of the pipelines to which the data sets belong is shown in Table 2.

Table 2.
Basic information of the pipeline.
The number of samples of each type in dataset 1 and dataset 2 is shown in Table 3, where the difference between the samples of the abnormal signals is large. Dataset 1 consists mainly of abnormal signals caused by weld seams, and the signal is similar to Figure 5. Dataset 2 consists mainly of signal abnormalities caused by defects, and the signal is similar to Figure 6. Dataset 1 is used to verify the accuracy of the method proposed in this paper, and dataset 2 is used to verify the recognition of the method for unfamiliar abnormal signals. Dataset 1 is used to verify the accuracy of the proposed method, and data set 2 is used to verify the ability of the method to identify unfamiliar anomalous signals.

Table 3.
The number of samples in the dataset.
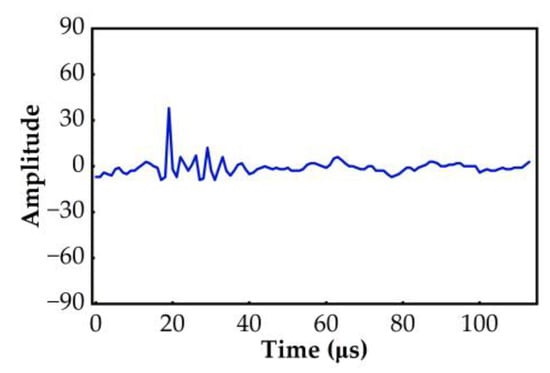
Figure 5.
Abnormal signal in dataset 1.
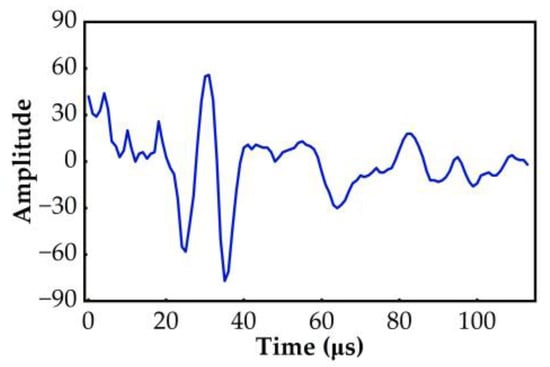
Figure 6.
Abnormal signal in dataset 2.
5.1.2. Parameter Settings
The hyperparameters θ, k in the first stage data interpolation method are empirical values that we have derived, based on testing a large amount of actual data. With the increase of θ and k, the smoother the output features, the less noise interference, and the classification accuracy of the normal signal will be improved, but with the further increase of θ and k, the output feature vector details will be weakened, which eventually leads to the decrease of the classification accuracy, so we set .
The hyperparameters of the second stage anomaly detection part perform a 3D grid search and a tri-fold cross-validation on the basis of dataset 1. The three sets of anomaly detection hyperparameters in the second stage are shown in Table 4.

Table 4.
Abnormal detection model parameter setting.
5.1.3. Comparison Method Introduction
In order to fully verify the feasibility of the method proposed in this paper, four machine learning and depth methods with a high accuracy for the ultrasound signal classification in the introduction are used to complete the comparison experiments with the method in this paper, and the four comparison methods are as follows.
- The method of the ultrasound signal classification, based on the mechanistic features and the natural breakpoint method proposed in the literature [5] (MFNB).
- The literature [6] proposed the classification method using time-frequency features of ultrasonic signals and PSO-SVM. (PSO-SVM).
- The literature [10] proposed the use of the wavelet transform to extract features and then use the two-dimensional convolutional neural network for the classification (WT-CNN).
- A one-dimensional convolutional neural network-based classification method proposed in the literature [4] (1-D CNN).
For the convenience of the presentation, this paper subsequently uses TS-ES to denote the two-stage ultrasound signal identification method, based on the envelope and local similarity features proposed in this paper.
5.2. Analysis of the Feature Enhancement Results
This part of the experiment is to fully demonstrate the effectiveness of the local similarity feature extraction method, based on the dynamic time regularization (DTW) proposed in 4.1 and the probability-based similarity feature enhancement method proposed in 4.2 of this paper. The experiments are as follows. A model is obtained using dataset 1 as the training set, and various types of similarity feature vectors in dataset 2 are extracted by the model, and then the feature vectors are augmented using the method proposed in 4.2. Finally, the T-distributed stochastic neighbor embedding (T_SNE) method is used to visualize and compare the feature vectors of the normal and abnormal signals. The final results are shown in Figure 7.
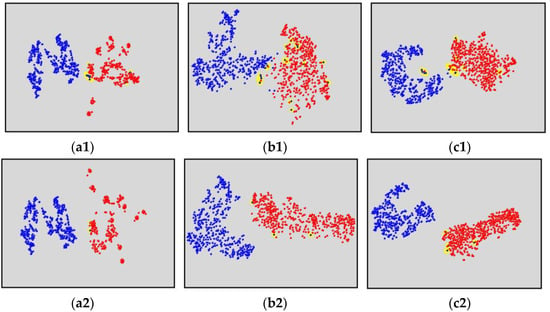
Figure 7.
Comparison of the feature enhancement results. The blue dots in the image indicate the normal signal feature vectors, the red dots indicate the abnormal signal feature vectors, and the yellow areas indicate the feature vector confusion locations. The sample size of both the normal and abnormal signals in the graph is 500. (a1) The distribution of the local similarity feature vectors in the embedding space of the two echoes signal and the anomalous signal before the feature enhancement. (a2) The distribution of the local similarity feature vectors in the embedding space of the two echoes signal and the anomalous signal after the feature enhancement. (b1) The distribution of the local similarity feature vectors in the embedding space of the three echoes signal and the anomalous signal before the feature enhancement. (b2) The distribution of the local similarity feature vectors in the embedding space of the three echoes signal and the anomalous signal after the feature enhancement. (c1) The distribution of the local similarity feature vectors in the embedding space of the four echoes signal and the anomalous signal before the feature enhancement. (c2) The distribution of the local similarity feature vectors in the embedding space of the four echoes signal and the anomalous signal after the feature enhancement.
Figure 7(a1–c1) shows the distribution of the similarity features without using the feature enhancement. As shown in the figure, the features are still clearly divided into two clusters, although more confusion occurs at the same time when the boundaries of the normal and abnormal features are connected. This indicates that the proposed DTW local similarity feature extraction method is effective.
Figure 7(a2–c2) shows the distribution of the similarity features using the feature enhancement. As shown in the figure, the spacing between the two categories of the constant and abnormal features becomes larger, the boundaries are clearer, and less confusion occurs. This indicates that the feature enhancement method proposed in this paper can improve the separability of the feature vectors in the high-dimensional space.
5.3. Accuracy Comparison
In order to fully verify the classification accuracy of the proposed method in this paper, three evaluation metrics were used, namely accuracy, precision (P), and recall (R), which were calculated as follows [17].
where TP, TN represent the true positive rate and the false positive rate. , , represent the true positive rate, the false positive rate and the false negative rate, respectively, if category i is a positive sample and the other categories are negative samples. S is the number of all samples and r represents the number of categories.
The experiments were conducted using dataset 1 for the 5-fold cross-validation of the above method. The accuracy of the classification results, are shown in Figure 8, the average precision and the average recall of each category are shown in Figure 9 and Figure 10.
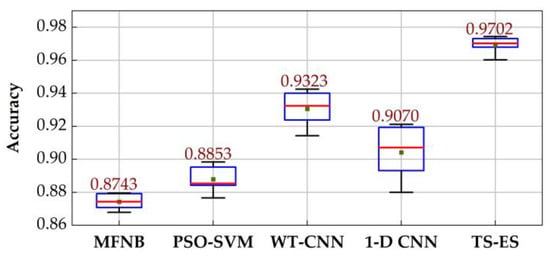
Figure 8.
Accuracy of each method.
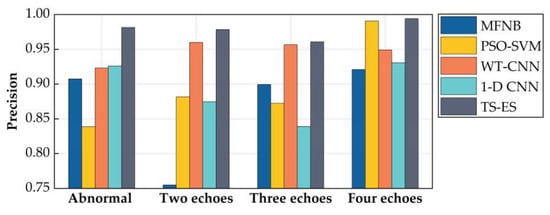
Figure 9.
Precision of each method.
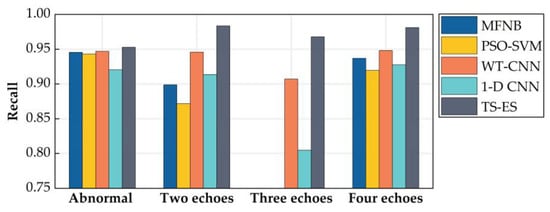
Figure 10.
Recall of each method.
As shown in the figure, the accuracy of the two-stage ultrasonic signal recognition method, based on the envelope and local similarity features (TS-ES) in this paper, reaches 97.02%, which is 4.07%~10.97% higher than the other methods, while the accuracy and recall of all kinds of ultrasonic signals are better than the other methods. This indicates that the TS-ES is capable of the accurate identification of various types of signals while having a high stability.
5.4. Analysis of the Abnormal Signal Detection Results
In order to fully validate the model’s ability to recognize unfamiliar anomalous signals, this section uses dataset 1 to train the model and dataset 2 to test the model. To highlight the demonstration, the secondary echo signals, tertiary echo signals, and quadratic echo signals are grouped into negative classes in this section, indicating non-anomalous signals, and positive classes for anomalous signals. To evaluate the ability of the model to recognize the unfamiliar anomalous data, five evaluation metrics were used: the receiver operating characteristic curve (ROC), the area under the curve (AUC) and accuracy (accuracy), the anomalous signal detection precision (P) and the anomaly detection recall (R) were evaluated. The comparison of ROC and AUC of the experimental results is shown in Figure 11, and the precision, anomaly detection accuracy and anomaly detection recall are shown in Table 5.
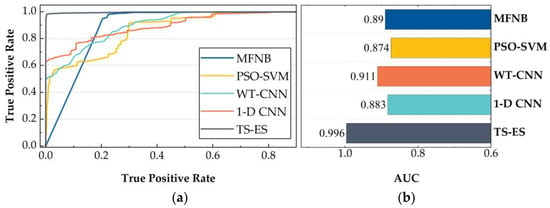
Figure 11.
ROC and AUC of each method. (a) ROC. (b) AUC.

Table 5.
Comparison of the accuracy, abnormal signal precision and abnormal signal recall.
As shown in Figure 11, compared with other methods, the ROC curve of TS-ES is closer to the (0, 1) point, while the AUC index of 0.996 is 9.33%–13.96% higher than that of the other methods, which indicates that this method has a higher accuracy in identifying the anomalous signals and less misclassification of non-anomalous signals when using the same threshold value. According to Table 4, the model accuracy of TS-ES is 98.99%, which is 20.26%–32.46% higher than other methods. In terms of the anomalous signal accuracy and recall, the method (WT-CNN) in the literature [9] achieves a 99.78% anomalous signal accuracy, but the recall is extremely low, only 39.17%. The method (MFNB) of the literature [4] has a 97.47% anomalous signal recall, but its precision is only 70.01%. The anomalous signal precision and recall of TS-ES in the text are 99.70% and 97.18%, which can meet the practical detection needs.
5.5. Comparison of the Normal Signal Classification Priority and the Abnormal Signal Detection Priority
The proposed two-stage ultrasound signal recognition method, based on the envelope and local feature similarity first classifies the normal signals and then detects the abnormal signals (normal signal classification priority). The corresponding common method is to first perform the abnormal signal detection and then the normal signal classification (abnormal signal detection priority). In this section we then perform a five-fold cross-validation of the two models (normal signal classification priority and abnormal signal detection priority) separately on dataset 1. In this section, the performance of the two models is evaluated using four indicators: accuracy, macor precision, macor recall and running time. The experimental results are shown in Table 6.

Table 6.
Performance comparison of the normal signal classification priority model and the abnormal signal detection priority model.
As can be seen from Table 6, the accuracy of the normal signal classification priority model used in this paper is significantly higher than that of the abnormal signal detection priority. We believe that using the abnormal signal detection priority approach, the model only needs to learn one pattern of normal signals when performing the anomaly detection, which greatly improves the focus of the model. For the abnormal signal detection priority, the model needs to learn three different types of normal signal patterns when performing the anomaly detection, which distracts the model’s attention and thus degrades the accuracy of the model.
Moreover, the normal signal classification priority model takes only half the computing time of the abnormal signal detection priority model. This is because if the normal signal classification is performed first, then only the local similarity features between the abnormal signal and a normal signal sample data set need to be computed. In contrast, if the anomaly detection is performed first, the local similarity features of the anomaly signal and three normal signal sample data sets need to be computed, which increases the running time of the algorithm.
6. Conclusions
An ultrasound signal classification and abnormality detection method is designed to address the problems of time-shifted echo features of normal ultrasound signals with severe noise interference and the inexhaustible variety of abnormal ultrasound signal patterns. Firstly, this paper elaborates on the implementation details of the method, classifies the normal signals by a one-dimensional convolutional neural network with a feature fusion, and then completes the detection of the abnormal ultrasound signals by using the idea of similarity comparison. The paper concludes with three sets of experiments to demonstrate the effectiveness of the proposed method. The experimental results show that the proposed method is able to accurately classify the ultrasound intra-detection data containing multiple types of interspersed abnormal signals with an accuracy of 97.02%. At the same time, it does not need to learn the characteristic patterns of the abnormal signals, and the accuracy reaches 98.99% for the abnormal and unfamiliar signals, which has a very high generalization performance. It provides favorable conditions for further effective analyses of ultrasound signals.
Author Contributions
Conceptualization, J.L.; methodology, L.W. and S.L.; software, L.W., S.L. and X.L.; validation, S.L.; data curation, L.W.; investigation, L.W.; writing—original draft, L.W. and X.L.; writing—review & editing, S.L.; visualization, X.L.; project administration, J.L.; supervision, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (U21A20481, 61973071).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, J.J.; Wen, Z.X.; Pei, H.Q.; Gu, S.N.; Zhang, C.J.; Yue, Z.F. Thermal damage evaluation of nickel-based superalloys based on ultrasonic nondestructive testing. Appl. Acoust. 2021, 183, 108329. [Google Scholar] [CrossRef]
- Yan, Y.; Liu, D.; Gao, B.; Tian, G.Y.; Cai, Z.C. A deep learning-based ultrasonic pattern recognition method for inspecting girth weld cracking of gas pipeline. IEEE Sens. J. 2020, 20, 7997–8006. [Google Scholar] [CrossRef]
- Dupont-Marillia, F.; Jahazi, M.; Lafreniere, S.; Belanger, P. Design and optimisation of a phased array transducer for ultrasonic inspection of large forged steel ingots. NDT E Int. 2019, 103, 119–129. [Google Scholar] [CrossRef]
- Gao, F.; Li, B.; Chen, L.; Shang, Z.; Wei, X.; He, C. A softmax classifier for high-precision classification of ultrasonic similar signals. Ultrasonics 2021, 112, 106344. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.X.; Xu, X.; Zhang, R.J. Small sample defect recognition method based on multi-dimensional selective search. Chin. J. Sci. Instrum. 2022, 43, 220–228. [Google Scholar]
- Wang, X.; Guan, S.; Hua, L.; Wang, B.; He, X. Classification of spot-welded joint strength using ultrasonic signal time-frequency features and PSO-SVM method. Ultrasonics 2019, 91, 161–169. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.; Zhang, Y.; Li, Z.; He, B.; Lang, X.; Liang, H.; Chen, J. Classification of red blood cell aggregation using empirical wavelet transform analysis of ultrasonic radiofrequency echo signals. Ultrasonics 2021, 114, 106419. [Google Scholar] [CrossRef] [PubMed]
- Munir, N.; Kim, H.J.; Song, S.J.; Kang, S.S. Investigation of deep neural network with drop out for ultrasonic flaw classification in weldments. J. Mech. Sci. Technol. 2018, 32, 3073–3080. [Google Scholar] [CrossRef]
- Munir, N.; Park, J.; Kim, H.J.; Song, S.J.; Kang, S.S. Performance enhancement of convolutional neural network for ultrasonic flaw classification by adopting autoencoder. NDT E Int. 2020, 111, 102218. [Google Scholar] [CrossRef]
- Meng, M.; Chua, Y.J.; Wouterson, E.; Ong, C.P.K. Ultrasonic signal classification and imaging system for composite materials via deep convolutional neural networks. Neurocomputing 2017, 257, 128–135. [Google Scholar] [CrossRef]
- Márquez-Figueroa, S.; Shmaliy, Y.S.; Ibarra-Manzano, O. Optimal extraction of EMG signal envelope and artifacts removal assuming colored measurement noise. Biomed. Signal Process. Control. 2020, 57, 101679. [Google Scholar] [CrossRef]
- Li, H.; Li, L. An improved EMD method with modified envelope algorithm based on C2 piecewise rational cubic spline interpolation for EMI signal decomposition. Appl. Math. Comput. 2018, 335, 112–123. [Google Scholar] [CrossRef]
- Chen, C.; Bei, Y.; Li, Y.; Zhou, W. Effect of interpolation methods on quantifying terrain surface roughness under different data densities. Geomorphology 2022, 417, 108448. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. Int. Conf. Learn. Represent. 2015, 1–14. [Google Scholar]
- Raheja, J.L.; Minhas, M.; Prashanth, D.; Shah, T.; Chaudhary, A. Robust gesture recognition using Kinect: A comparison between DTW and HMM. Optik 2015, 126, 1098–1104. [Google Scholar] [CrossRef]
- Guo, J.; Si, Z.; Liu, Y.; Li, J.; Li, Y.; Xiang, J. Dynamic time warping using graph similarity guided symplectic geometry mode decomposition to detect bearing faults. Reliab. Eng. Syst. Saf. 2022, 224, 108533. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Wu, Y.Q. Research progress of surface defect detection methods based on machine vision. Chin. J. Sci. Instrum. 2022, 43, 198–219. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).