On the Impact of Condensation and Liquid Water on the Radial Turbine of a Fuel Cell Turbocharger
Abstract
1. Introduction
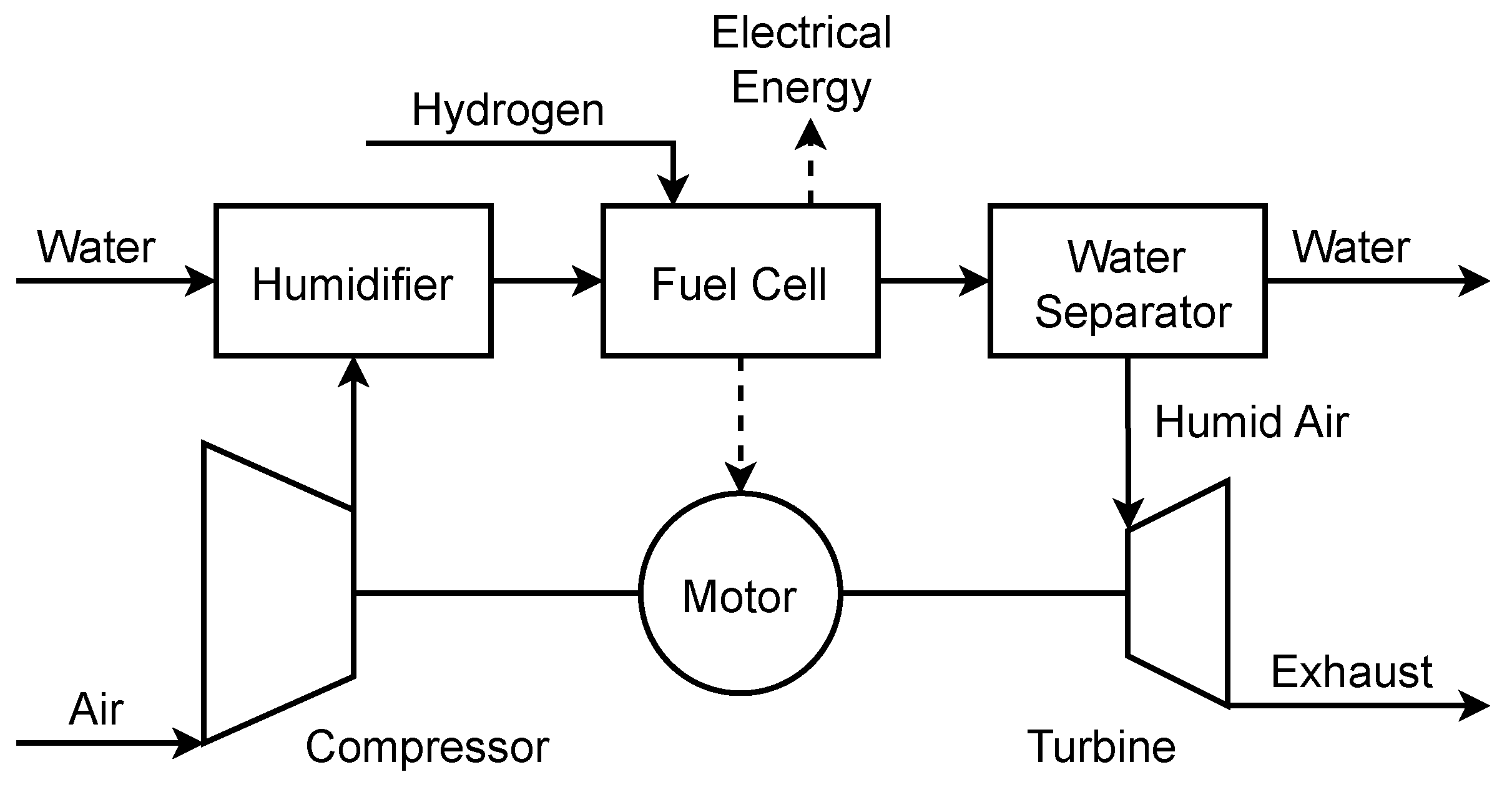
2. Materials and Methods
2.1. Condensation Theory and Numerics
2.2. Turbine Test Case
3. Results and Discussion
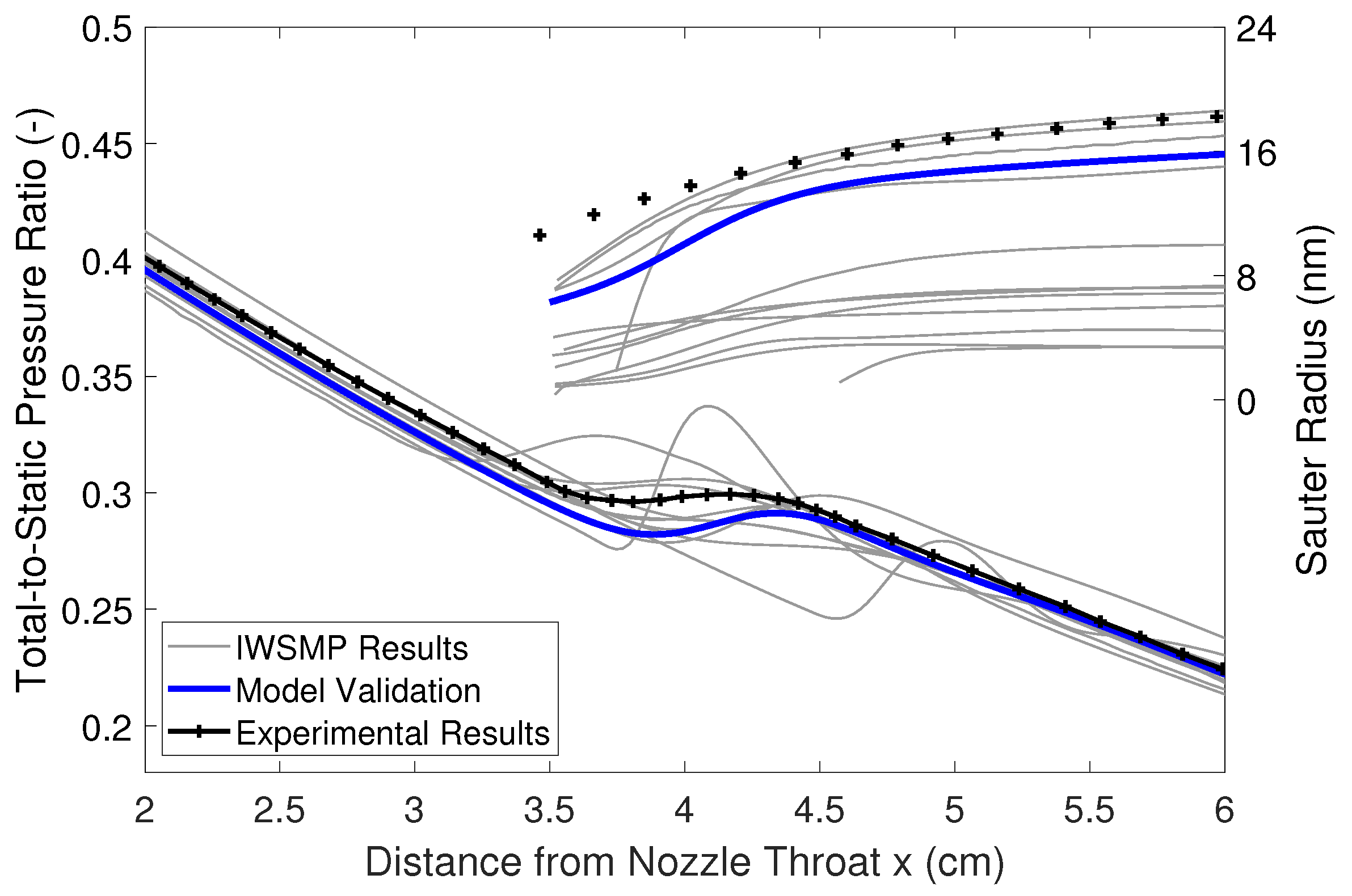
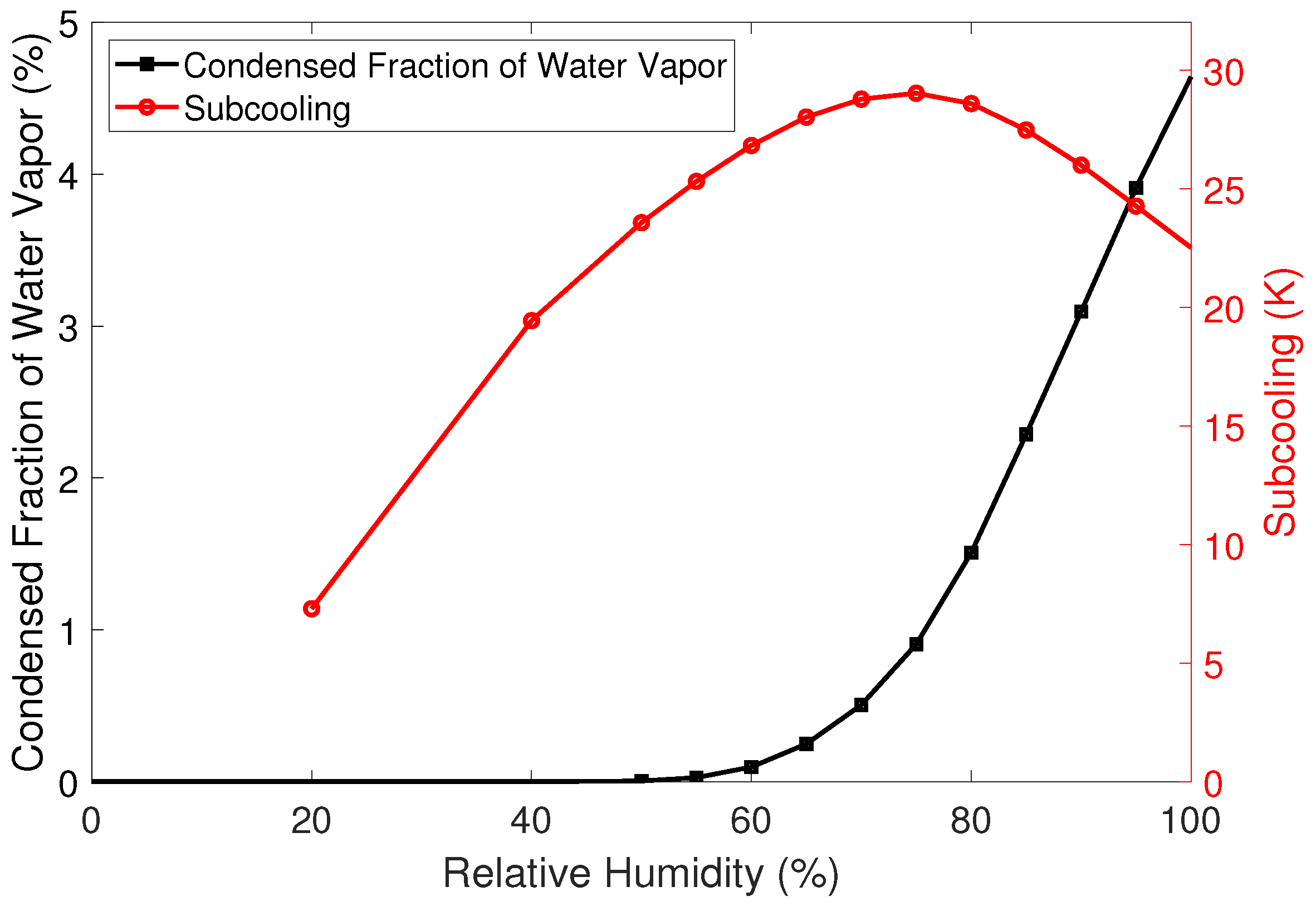
3.1. Phase Change of Water Vapor to Liquid Water
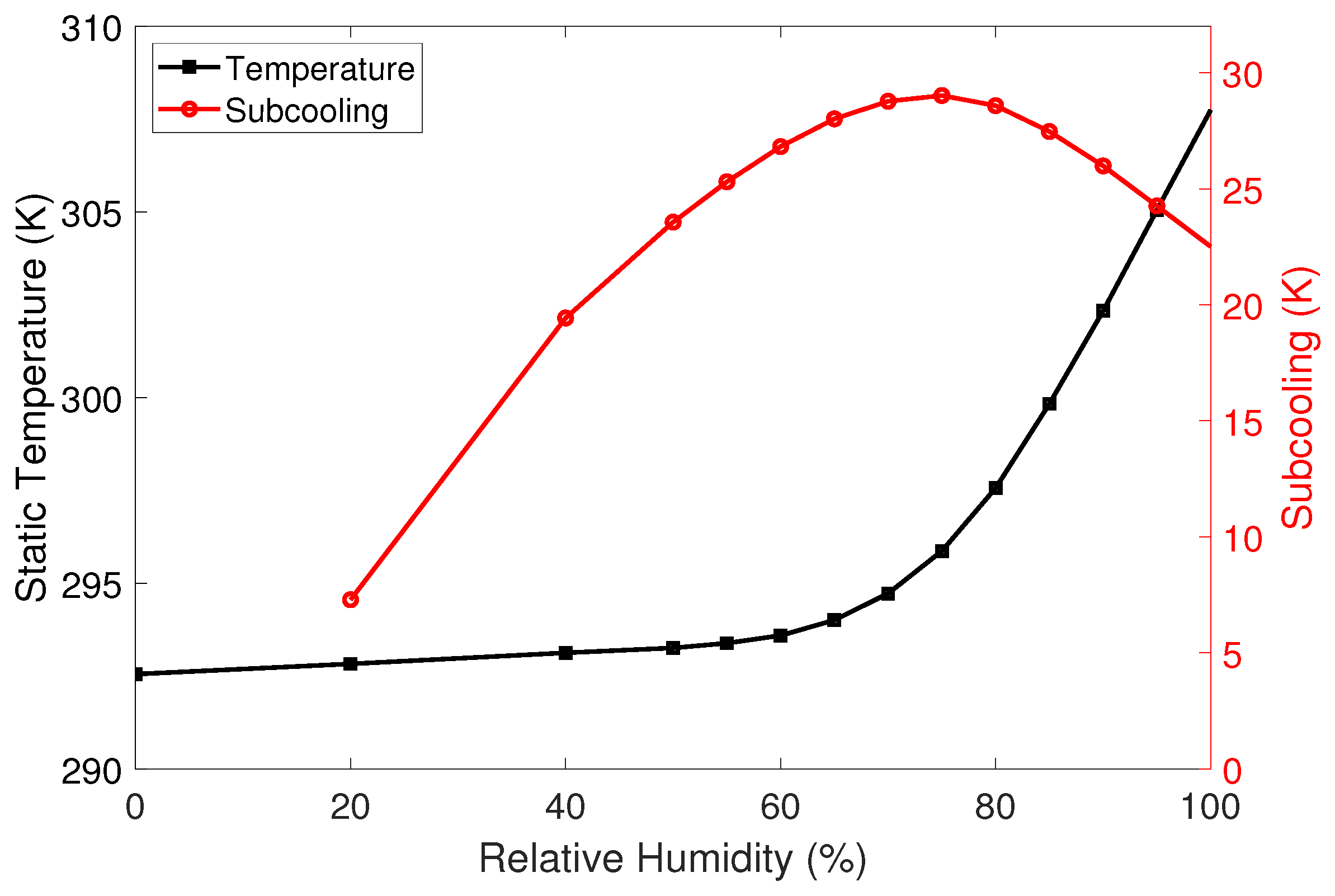
3.2. Release of Latent Heat
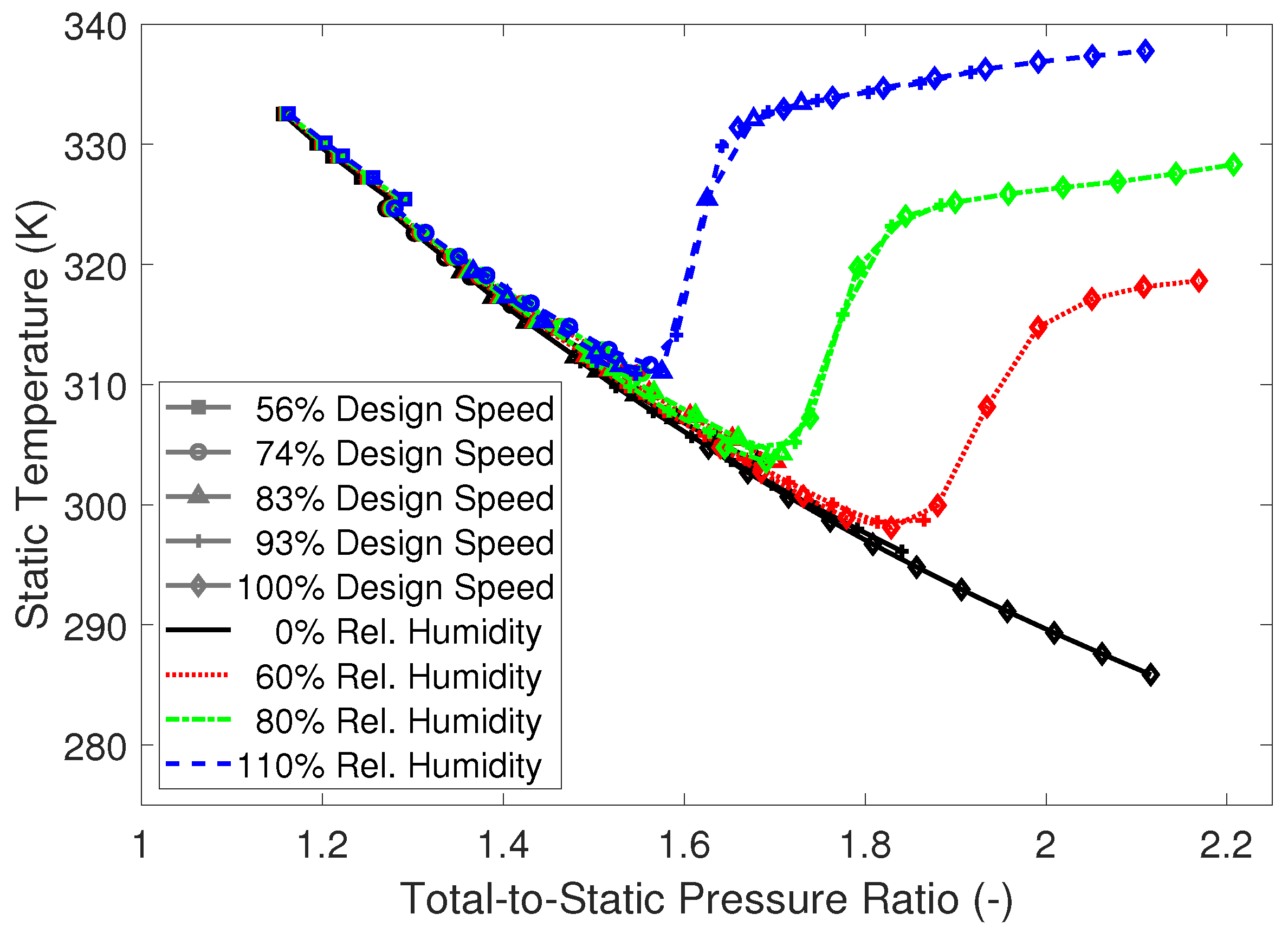
3.3. Thermal Throttling
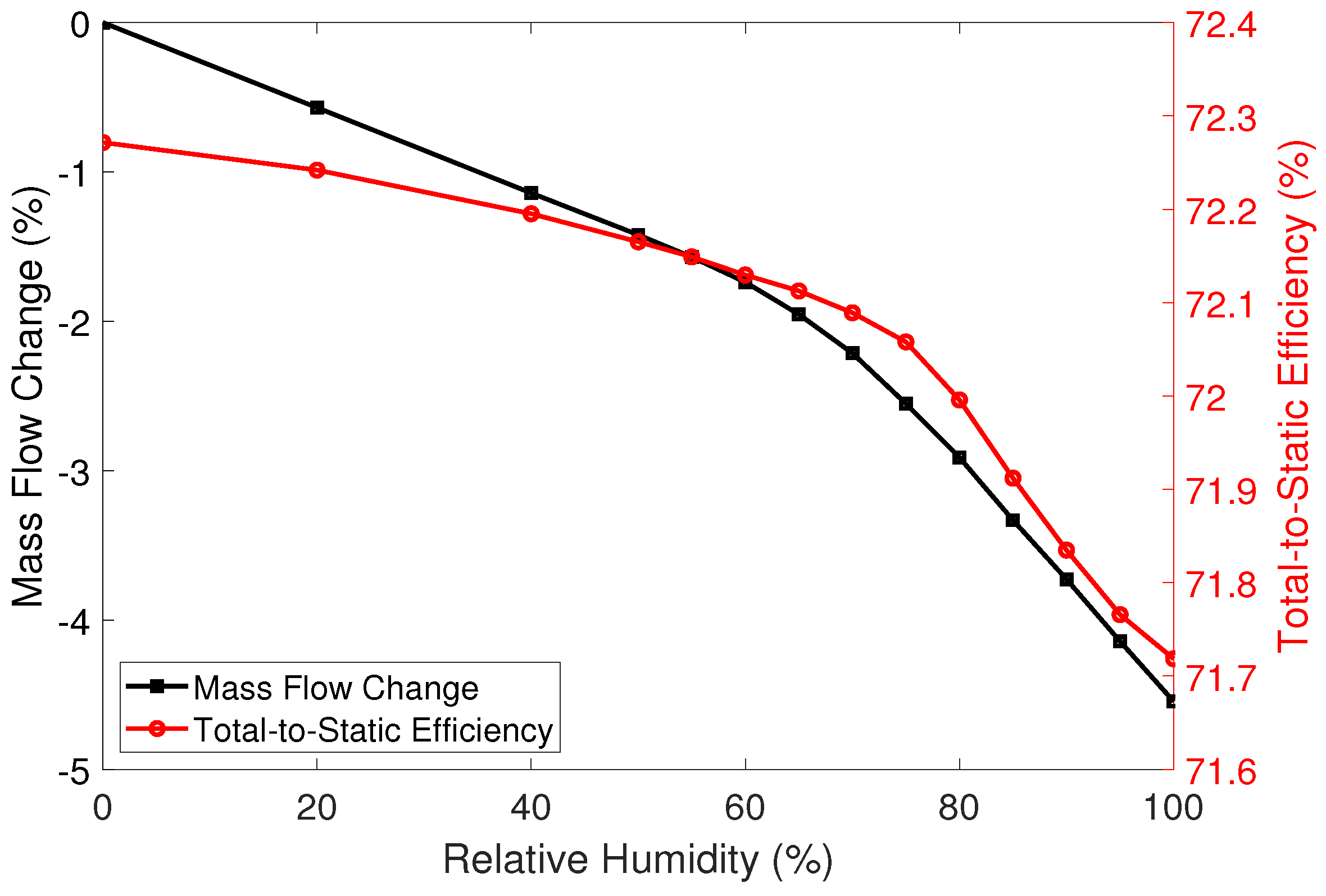
3.4. Efficiency Reduction
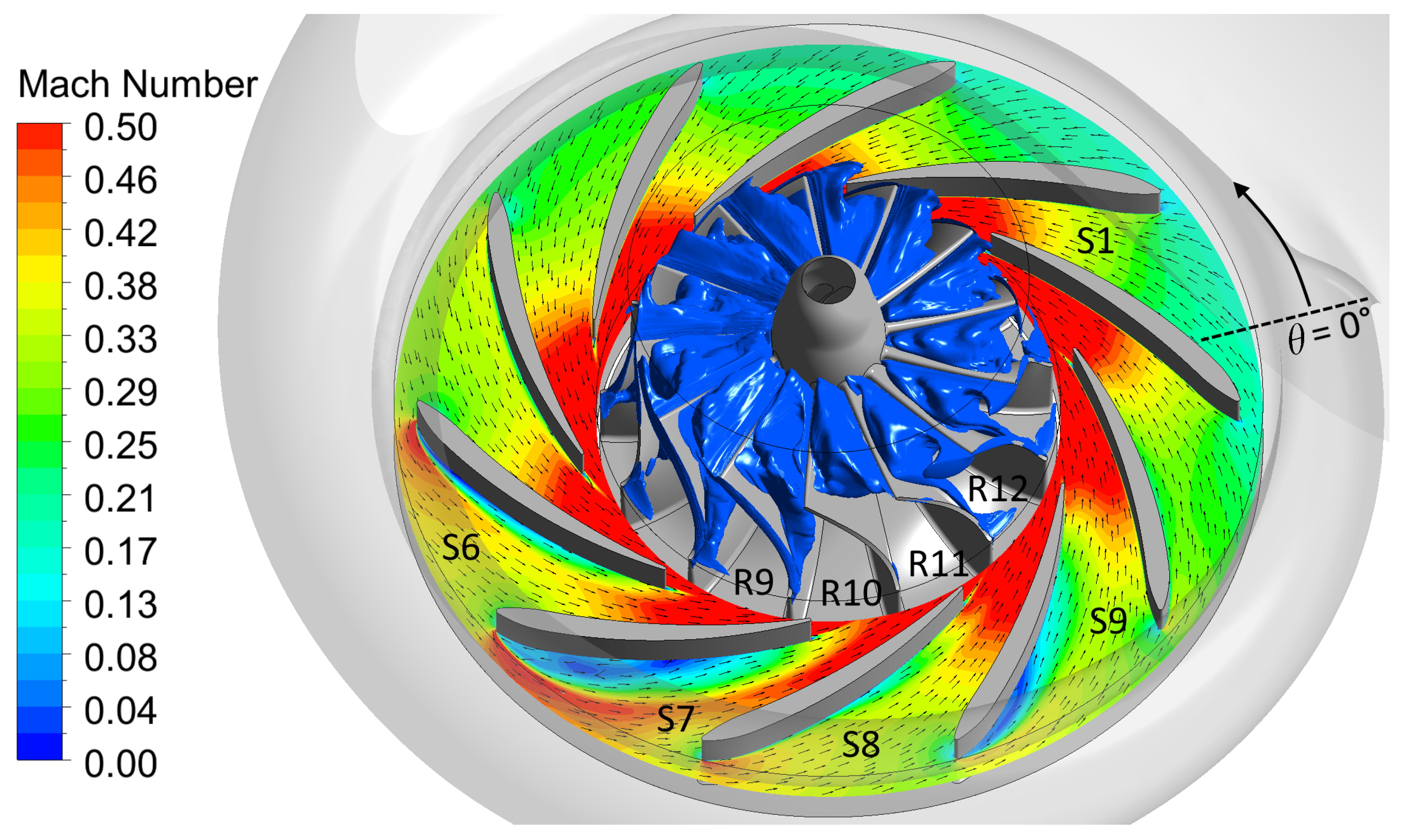
3.5. Circumferential Asymmetry of the Turbine Flow
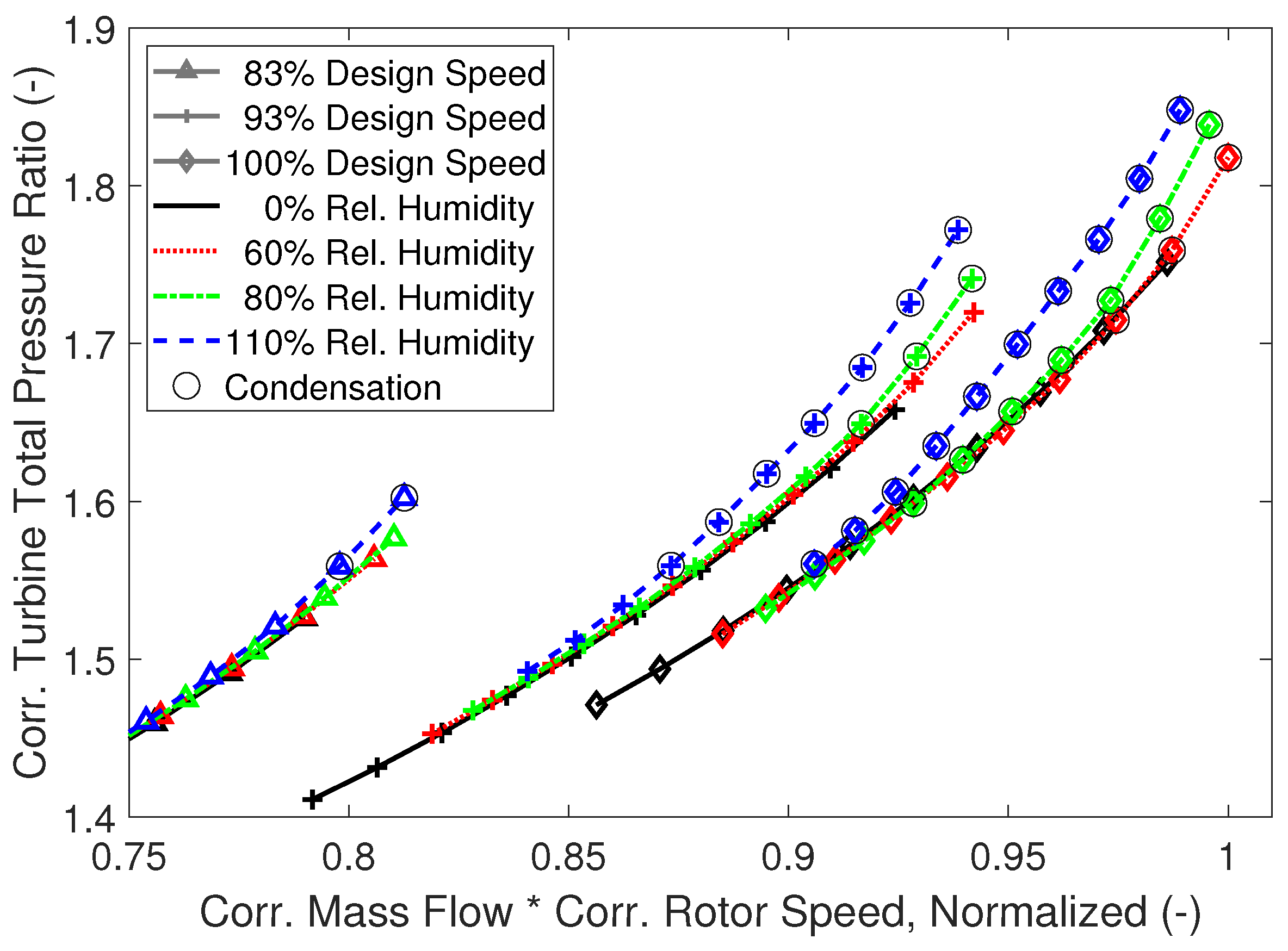
3.6. Effects on the Air-Management System as a Whole
3.7. Performance Increase for Multistage Turbines
3.8. Water Droplet Erosion
3.9. Corrosion
3.10. Water Induced Damage
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin characters | |
| c | Velocity |
| Specific heat capacity of the vapor | |
| h | Enthalpy |
| Latent heat | |
| Classical homogeneous nucleation rate | |
| Boltzmann constant | |
| Knudsen number | |
| Mass flow | |
| Molecule mass | |
| N | Rotational speed |
| P | Power |
| p | Pressure |
| Prandtl number | |
| Condensation coefficient | |
| R | Gas constant |
| r | Droplet radius |
| Critical droplet radius | |
| S | Supersaturation ratio |
| T | Temperature |
| Subcooling | |
| Greek characters | |
| Total-to-static efficiency | |
| Modeling parameter of Young’s growth law | |
| Modeling parameter of Young’s growth law | |
| Heat capacity ratio | |
| Circumferential angle | |
| Thermal conductivity | |
| Young’s correction factor | |
| Density | |
| Surface tension | |
| Subscripts | |
| Isentropic | |
| 0 | Turbine inlet |
| 2 | Turbine outlet |
| Corrected | |
| Dry flow without water vapor | |
| f | Saturated liquid phase |
| g | Vapor phase |
| Isentropic | |
| l | Droplet |
| s | Static |
| t | Total |
| Abbreviations | |
| AGARD | Advisory Group for Aerospace Research and Development |
| ARIEL | Charging for Fuel Cell Systems by Interdisciplinary Electric Air Compressors |
| (translated from German) | |
| CFD | Computational fluid dynamics |
| DPM | Discrete phase model |
| FAC | Flow accelerated corrosion |
| GCI | Grid convergence index |
| IAPWS | International Association for the Properties of Water and Steam |
| IWSMP | International Wet Steam Modelling Project |
| NISO | Non-isothermal correction |
| PEMFC | Proton-exchange membrane fuel cell |
| RANS | Reynolds-averaged Navier–Stokes |
| WDE | Water droplet erosion |
References
- Venturi, M.; Sang, J.; Knoop, A.; Hornburg, G. Air Supply System for Automotive Fuel Cell Application. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2012. [Google Scholar] [CrossRef]
- Kerviel, A.; Pesyridis, A.; Mohammed, A.; Chalet, D. An Evaluation of Turbocharging and Supercharging Options for High-Efficiency Fuel Cell Electric Vehicles. Appl. Sci. 2018, 8, 2474. [Google Scholar] [CrossRef]
- Wittmann, T.; Lück, S.; Hertwig, T.; Friedrichs, J. On the Importance of Condensation for the Thermodynamic Cycle of Fuel Cell Turbochargers in Aviation. In Proceedings of the ISABE 2022 Conference (in Print), International Society of Air Breathing Engines, Ottawa, ON, Canada, 25–30 September 2022. [Google Scholar]
- Kulp, G.W.; Gurski, S.; Nelson, D.J. PEM Fuel Cell Air Management Efficiency at Part Load. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2002. [Google Scholar] [CrossRef]
- Bao, C.; Ouyang, M.; Yi, B. Modeling and optimization of the air system in polymer exchange membrane fuel cell systems. J. Power Sources 2006, 156, 232–243. [Google Scholar] [CrossRef]
- Blunier, B.; Miraoui, A. Proton Exchange Membrane Fuel Cell Air Management in Automotive Applications. J. Fuel Cell Sci. Technol. 2010, 7, 727. [Google Scholar] [CrossRef]
- Traverso, A.; Magistri, L.; Massardo, A.F. Turbomachinery for the air management and energy recovery in fuel cell gas turbine hybrid systems. Energy 2010, 35, 764–777. [Google Scholar] [CrossRef]
- German Federal Ministry of Transport and Digital Infrastructure. Project ARIEL: (Aufladung für Brennstoffzellensysteme Durch Interdisziplinär Entwickelte Elektrische Luftverdichter–Charging for Fuel Cell Systems by Interdisciplinarilly Developed Electric Air Compressors): Verbundvorhaben 01183541/1–NIP II-ARIEL. Grant Number 03B10105D2. Available online: https://www.enargus.de/pub/bscw.cgi/?op=enargus.eps2&q=%2201183541/1%22&v=10&s=11&id=989361 (accessed on 7 June 2022).
- Wittmann, T.; Lück, S.; Bode, C.; Friedrichs, J. Modelling the Condensation Phenomena within the Radial Turbine of a Fuel Cell Turbocharger. Int. J. Turbomach. Propuls. Power 2021, 6, 23. [Google Scholar] [CrossRef]
- Wittmann, T.; Lück, S.; Hertwig, T.; Bode, C.; Friedrichs, J. The Influence of Condensation on the Performance Map of a Fuel Cell Turbocharger Turbine. In Proceedings of the ASME Turbo Expo 2021, American Society of Mechanical Engineers, Online, 7–11 June 2021. [Google Scholar] [CrossRef]
- Wittmann, T.; Lück, S.; Bode, C.; Friedrichs, J. Investigation of Water Droplet Erosion in the Radial Turbine of a Fuel Cell Turbocharger. In Proceedings of the Global Power & Propulsion Society, Xi’an, China, 18–20 October 2021. [Google Scholar] [CrossRef]
- Wittmann, T.; Wiśniewski, P.; Lück, S.; Dykas, S.; Friedrichs, J. Analysis of the Condensation Phenomena within the Radial Turbine of a Fuel Cell Turbocharger. In Proceedings of the ASME Turbo Expo 2022, American Society of Mechanical Engineers, Rotterdam, The Netherlands, 13–17 June 2022. [Google Scholar]
- Lück, S.; Wittmann, T.; Göing, J.; Bode, C.; Friedrichs, J. Impact of Condensation on the System Performance of a Fuel Cell Turbocharger. Machines 2022, 10, 59. [Google Scholar] [CrossRef]
- Cunningham, J.M.; Hoffman, M.A.; Eggert, A.R.; Friedman, D.J. The Implications of Using an Expander (Turbine) in an Air System of a PEM Fuel Cell Engine. In Proceedings of the Electric Vehicle Symposium 17, Portland, OR, USA, 14–17 June 2000. [Google Scholar]
- Filsinger, D.; Kuwata, G.; Ikeya, N. Tailored Centrifugal Turbomachinery for Electric Fuel Cell Turbocharger. Int. J. Rotating Mach. 2021, 2021, 3972387. [Google Scholar] [CrossRef]
- Wang, C.; Xing, Z.; Sun, S.; Chen, W.; He, Z. Experimental study on the performance of oil-free twin-screw expanders for recovering energy in fuel cell systems. Appl. Therm. Eng. 2020, 165, 114613. [Google Scholar] [CrossRef]
- Yuanyang, Z.; Liansheng, L.; Pengcheng, S. Thermodynamic Simulation of Scroll Compressor/Expander Module in Automotive Fuel Cell Engine. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2006, 220, 571–577. [Google Scholar] [CrossRef]
- Schuster, S.; Brillert, D.; Benra, F.K. Condensation in Radial Turbines—Part II: Application of the Mathematical Model to a Radial Turbine Series. J. Turbomach. 2018, 140, 289. [Google Scholar] [CrossRef]
- Hesketh, J.A.; Walker, P.J. Effects of Wetness in Steam Turbines. Proc. IMechE Part C J. Mech. Eng. Sci. 2005, 219, 1301–1314. [Google Scholar] [CrossRef]
- Bakhtar, F. Special Issue on Wet Steam-Part 1. Proc. IMechE Part C J. Mech. Eng. Sci. 2004, 218, i–iii. [Google Scholar] [CrossRef]
- Bakhtar, F. Special Issue on Wet Steam-Part 2. Proc. IMechE Part C J. Mech. Eng. Sci. 2005, 219, i–iii. [Google Scholar] [CrossRef]
- Young, J.B.; White, A.J. Special Issue on the Baumann Wet Steam Conference. Proc. IMechE Part A J. Power Energy 2014, 228, 108–109. [Google Scholar] [CrossRef]
- Bartoš, O.; Kolovratník, M. Editorial for the special issue on wet steam. Proc. Inst. Mech. Eng. Part J. Power Energy 2018, 232, 451. [Google Scholar] [CrossRef]
- Lettieri, C.; Yang, D.; Spakovszky, Z. An Investigation of Condensation Effects in Supercritical Carbon Dioxide Compressors. J. Eng. Gas Turbines Power 2015, 137, 40. [Google Scholar] [CrossRef]
- Young, J.B. Condensation in Jet Engine Intake Ducts during Stationary Operation. J. Eng. Gas Turbines Power 1995, 117, 227–236. [Google Scholar] [CrossRef]
- Fröhlig, F.; Flohr, A.; Männle, T.; Kech, J. Future Fuels and Drive Concepts—A Challenge for Turbocharging on the Way to Net Zero. In Proceedings of the 26th Supercharging Conference, Dresden, Germany, 20–21 September 2022; Zellbeck, H., Ed.; Technische Universität Dresden: Dresden, Germany, 2022. [Google Scholar]
- Barchewitz, L.P.; Seume, J.R. Conceptual Analysis of Air Supply Systems For In-Flight PEM-FC. In Proceedings of the ASME Turbo Expo 2006, Barcelona, Spain, 6–11 May 2006; pp. 229–238. [Google Scholar] [CrossRef]
- Cruz Champion, H.; Kabelac, S. Multifunctional fuel cell system for civil aircraft: Study of the cathode exhaust gas dehumidification. Int. J. Hydrogen Energy 2017, 42, 29518–29531. [Google Scholar] [CrossRef]
- Starzmann, J.; Hughes, F.R.; Schuster, S.; White, A.J.; Halama, J.; Hric, V.; Kolovratník, M.; Lee, H.; Sova, L.; Št’astný, M.; et al. Results of the International Wet Steam Modeling Project. Proc. IMechE Part A J. Power Energy 2018, 232, 550–570. [Google Scholar] [CrossRef]
- Bakhtar, F.; Young, J.B.; White, A.J.; Simpson, D.A. Classical Nucleation Theory and Its Application to Condensing Steam Flow Calculations. Proc. IMechE Part C J. Mech. Eng. Sci. 2005, 219, 1315–1333. [Google Scholar] [CrossRef]
- Kantrowitz, A. Nucleation in Very Rapid Vapor Expansions. J. Chem. Phys. 1951, 19, 1097–1100. [Google Scholar] [CrossRef]
- Young, J.B. Spontaneous Condensation of Steam in Supersonic Nozzles: N81-13307; Whittle Laboratory, University of Cambridge: Cambridge, UK, 1980. [Google Scholar]
- Lamanna, G. On Nucleation and Droplet Growth in Condensing Nozzle Flows. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2000. [Google Scholar] [CrossRef]
- Wiśniewski, P.; Dykas, S.; Yamamoto, S. Importance of Air Humidity and Contaminations in the Internal and External Transonic Flows. Energies 2020, 13, 3153. [Google Scholar] [CrossRef]
- Wiśniewski, P.; Majkut, M.; Dykas, S.; Smołka, K.; Zhang, G.; Pritz, B. Selection of a steam condensation model for atmospheric air transonic flow prediction. Appl. Therm. Eng. 2022, 203, 117922. [Google Scholar] [CrossRef]
- Gyarmathy, G. Grundlagen Einer Theorie der Nassdampfturbine. Ph.D. Thesis, Eidgenössische Technische Hochschule Zürich, Zurich, Switzerland, 1962. [Google Scholar] [CrossRef]
- White, A.J. A comparison of modelling methods for polydispersed wet-steam flow. Int. J. Numer. Methods Eng. 2003, 57, 819–834. [Google Scholar] [CrossRef]
- Hughes, F.R.; Starzmann, J.; White, A.J.; Young, J.B. A Comparison of Modeling Techniques for Polydispersed Droplet Spectra in Steam Turbines. J. Eng. Gas Turbines Power 2016, 138, 143. [Google Scholar] [CrossRef]
- Young, J.B. Two-Dimensional, Nonequilibrium, Wet-Steam Calculations for Nozzles and Turbine Cascades. J. Turbomach. 1992, 114, 569–579. [Google Scholar] [CrossRef]
- Gerber, A.G. Two-Phase Eulerian/Lagrangian Model for Nucleating Steam Flow. J. Fluids Eng. 2002, 124, 465–475. [Google Scholar] [CrossRef]
- Fakhari, K. Development of a Two-Phase Eulerian/Lagrangian Algorithm for Condensing Steam Flow. In Proceedings of the 44th AIAA Aerospace Sciences Meeting, Reno, Nevada, 9–12 January 2006; p. 229. [Google Scholar] [CrossRef]
- Sasao, Y.; Miyake, S.; Okazaki, K.; Yamamoto, S.; Ooyama, H. Eulerian-Lagrangian Numerical Simulation of Wet Steam Flow Through Multi-Stage Steam Turbine. In Proceedings of the ASME Turbo Expo 2013, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar] [CrossRef]
- Schuster, S.; Brillert, D.; Benra, F.K. Condensation in Radial Turbines—Part I: Mathematical Modeling. J. Turbomach. 2018, 140, 768. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, A. A Drag Coefficient Correlation. Z. Des Vereins Dtsch. Ingenieure 1935, 77, 318–320. [Google Scholar]
- Cunningham, E. On the velocity of steady fall of spherical particles through fluid medium. Proc. R. Soc. London Ser. Math. Phys. Eng. Sci. 1910, 83, 357–365. [Google Scholar] [CrossRef]
- The International Association for the Properties of Water and Steam. Revised Release on the IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam. 2012. Available online: https://www.teos-10.org/pubs/IAPWS-08.pdf (accessed on 7 June 2022).
- Wittmann, T.; Lück, S.; Bode, C.; Friedrichs, J. Numerical Simulation of Nucleation and Condensation in Nozzles and Radial Turbines. In Proceedings of the CADFEM ANSYS Simulation Conference 2019, Kassel, Germany, 16–17 October 2019. [Google Scholar]
- Wittmann, T.; Bode, C.; Friedrichs, J. The Feasibility of an Euler–Lagrange Approach for the Modeling of Wet Steam. J. Eng. Gas Turbines Power 2021, 143, 1301. [Google Scholar] [CrossRef]
- Moses, C.A.; Stein, G.D. On the Growth of Steam Droplets Formed in a Laval Nozzle Using Both Static Pressure and Light Scattering Measurements. J. Fluids Eng. 1978, 100, 311. [Google Scholar] [CrossRef]
- Fakhari, K. On the Effects of Unsteadiness on the Condensation Process in Low-Pressure Steam Turbines. In Proceedings of the ASME Turbo Expo 2009, Orlando, FL, USA, 8–12 June 2009. [Google Scholar] [CrossRef]
- Hellstrom, F.; Fuchs, L. Effects of Inlet Conditions on the Turbine Performance of a Radial Turbine. In Proceedings of the ASME Turbo Expo 2008, Berlin, Germany, 9–13 June 2008. [Google Scholar] [CrossRef]
- AGARD. Recommended Practices for the Assessment of the Effects of Atmospheric Water Ingestion on the Performance and Operability of Gas Turbine Engines: AGARD ADVISORY REPORT NO. 332; AGARD: Neuilly-sur-Seine, France, 1995. [Google Scholar]
- Kawagishi, H.; Onoda, A.; Shibukawa, N.; Niizeki, Y. Development of moisture loss models in steam turbines. Heat Transf.-Asian Res. 2013, 42, 651–664. [Google Scholar] [CrossRef]
- Starzmann, J.; Casey, M.M.; Mayer, J.F.; Sieverding, F. Wetness loss prediction for a low pressure steam turbine using computational fluid dynamics. Proc. Inst. Mech. Eng. Part J. Power Energy 2014, 228, 216–231. [Google Scholar] [CrossRef]
- Roumeliotis, I.; Mathioudakis, K. Analysis of moisture condensation during air expansion in turbines. Int. J. Refrig. 2006, 29, 1092–1099. [Google Scholar] [CrossRef]
- Menze, M.; Schoedel, M.; Seume, J.R. Numerical investigation of a radial turbine with variable nozzle geometry for fuel cell systems in automotive applications. In Proceedings of the 14th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, European Turbomachinery Society, Online, 12–16 April 2021. [Google Scholar] [CrossRef]


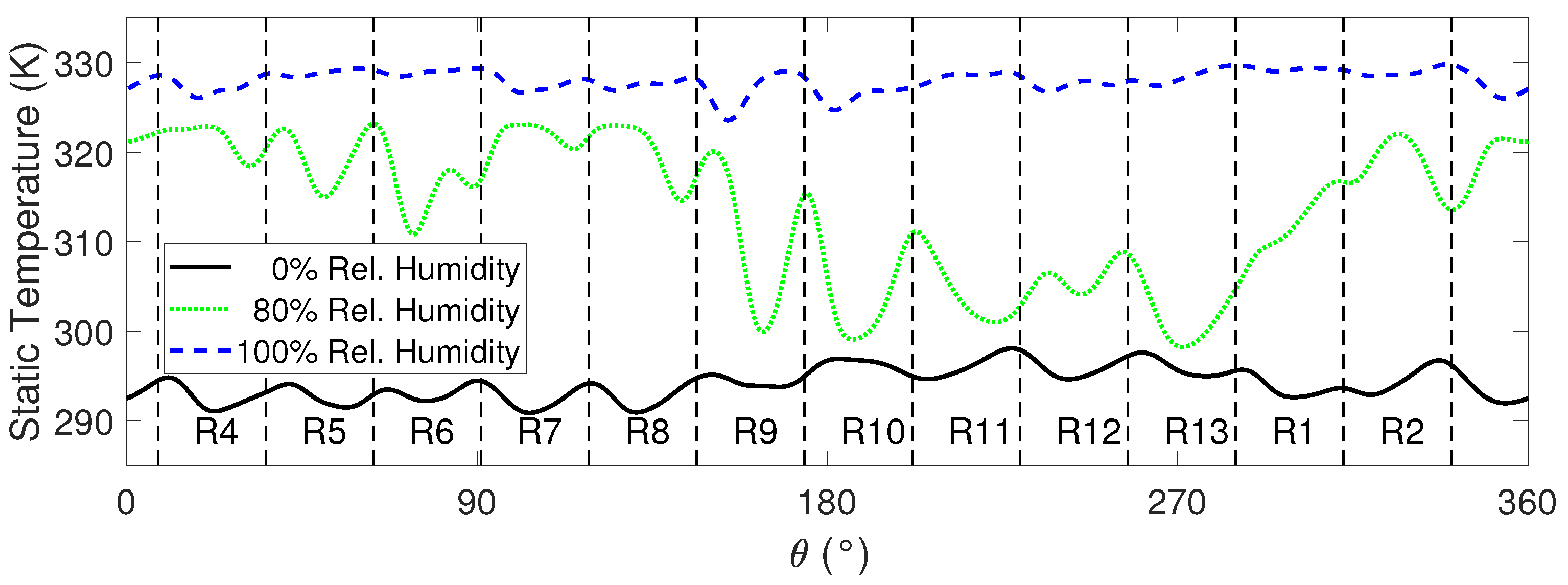

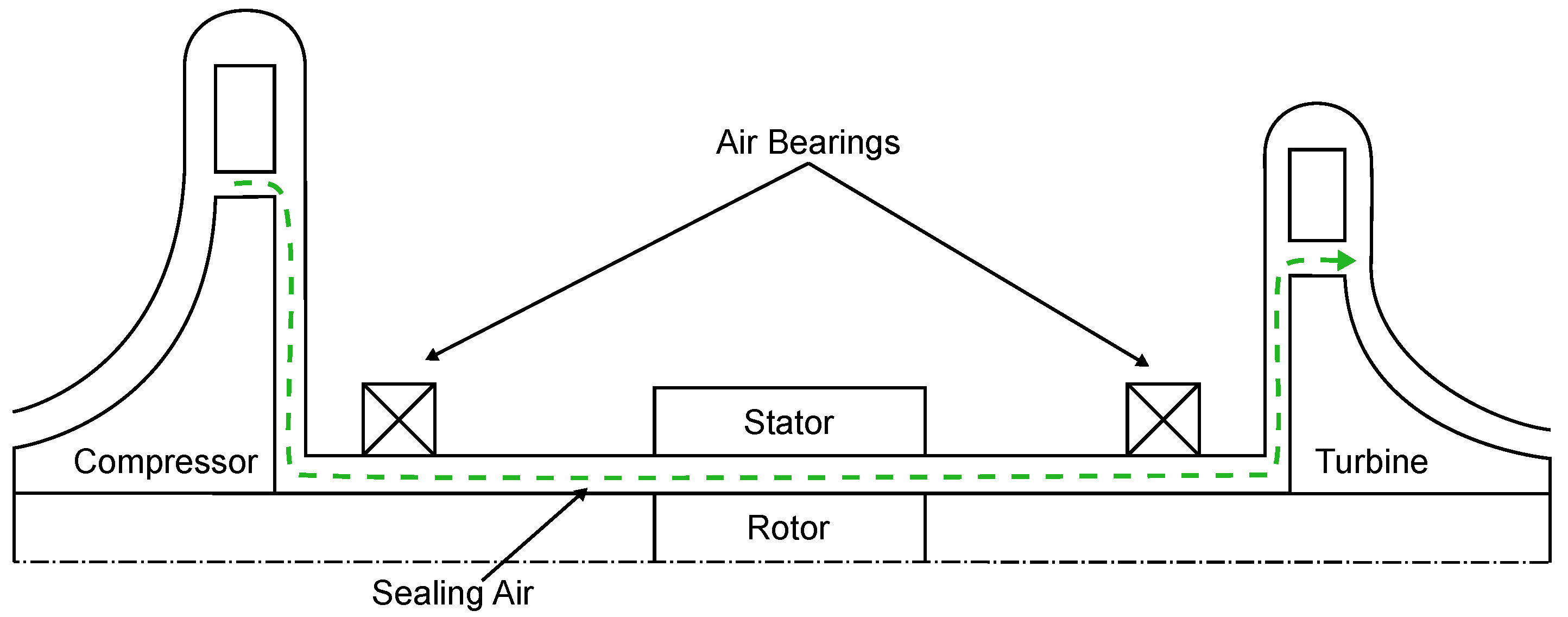
| Wet Case | Hypothetical Dry Case | |
|---|---|---|
| Inlet temperature stage 1 () | 353.15 | 353.15 |
| Outlet temperature stage 1 () | 325.7 | 269.8 |
| Outlet temperature stage 2 () | 301.5 | 205.4 |
| Inlet gas flow stage 1 (g s−1) | 110.8 | 110.8 |
| Outlet gas flow stage 1 (g s−1) | 106.6 | 110.8 |
| Outlet gas flow stage 2 (g s−1) | 103.2 | 110.8 |
| Power stage 1 () | 10.0 | 9.2 |
| Power stage 2 () | 8.7 | 5.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wittmann, T.; Lück, S.; Bode, C.; Friedrichs, J. On the Impact of Condensation and Liquid Water on the Radial Turbine of a Fuel Cell Turbocharger. Machines 2022, 10, 1053. https://doi.org/10.3390/machines10111053
Wittmann T, Lück S, Bode C, Friedrichs J. On the Impact of Condensation and Liquid Water on the Radial Turbine of a Fuel Cell Turbocharger. Machines. 2022; 10(11):1053. https://doi.org/10.3390/machines10111053
Chicago/Turabian StyleWittmann, Tim, Sebastian Lück, Christoph Bode, and Jens Friedrichs. 2022. "On the Impact of Condensation and Liquid Water on the Radial Turbine of a Fuel Cell Turbocharger" Machines 10, no. 11: 1053. https://doi.org/10.3390/machines10111053
APA StyleWittmann, T., Lück, S., Bode, C., & Friedrichs, J. (2022). On the Impact of Condensation and Liquid Water on the Radial Turbine of a Fuel Cell Turbocharger. Machines, 10(11), 1053. https://doi.org/10.3390/machines10111053








