Development and Experimental Verification of a High-Temperature and In-Plane Biaxial Testing Apparatus
Abstract
1. Introduction
1.1. Test Methods of Biaxial Stress
- (1)
- Biaxial stresses can be induced by bending through beams and thin plates [6,7]. An aluminum alloy was tested by Hazell using a diamond-shaped composite plate made of glass fiber honeycomb structures sandwiched between two thin aluminum plates, which allowed for examination of the material mechanical properties in two-dimensional stress spaces in the second and fourth quadrants [8].
- (2)
- (3)
- Biaxial stress states can be generated by tensile, compressive, or torsional loads applied to thin-walled tubes [12]. Despite the flexibility of this test, as it allows any continuous stress or strain ratio to be used, achieving any stress or strain path for a principal stress direction is impossible.
- (4)
1.2. In-Plane Biaxial Test Apparatus
1.2.1. Horizontal Structure
1.2.2. Vertical Structure
1.3. High-Temperature In-Plane Biaxial Apparatus
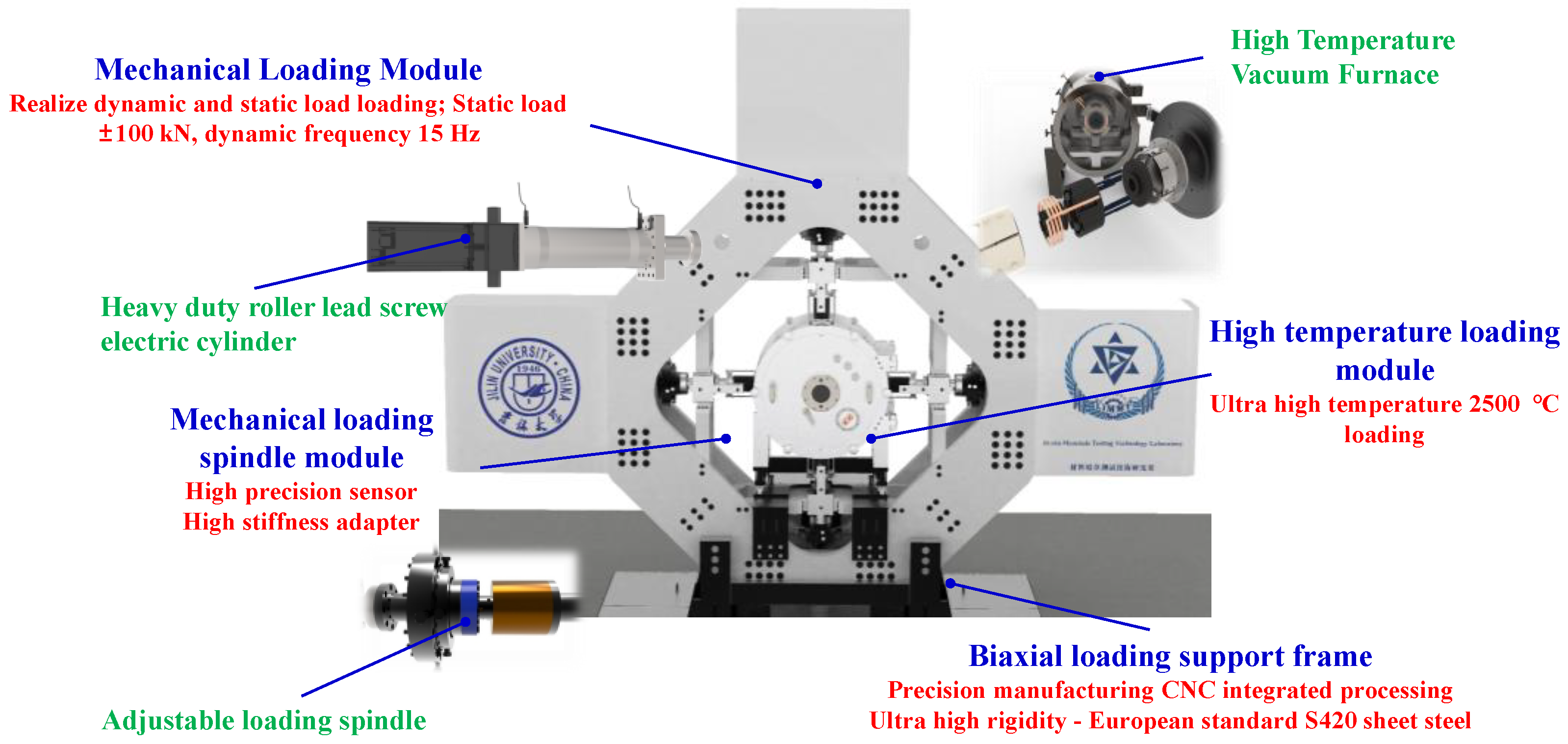
2. Development of the HTIPTA
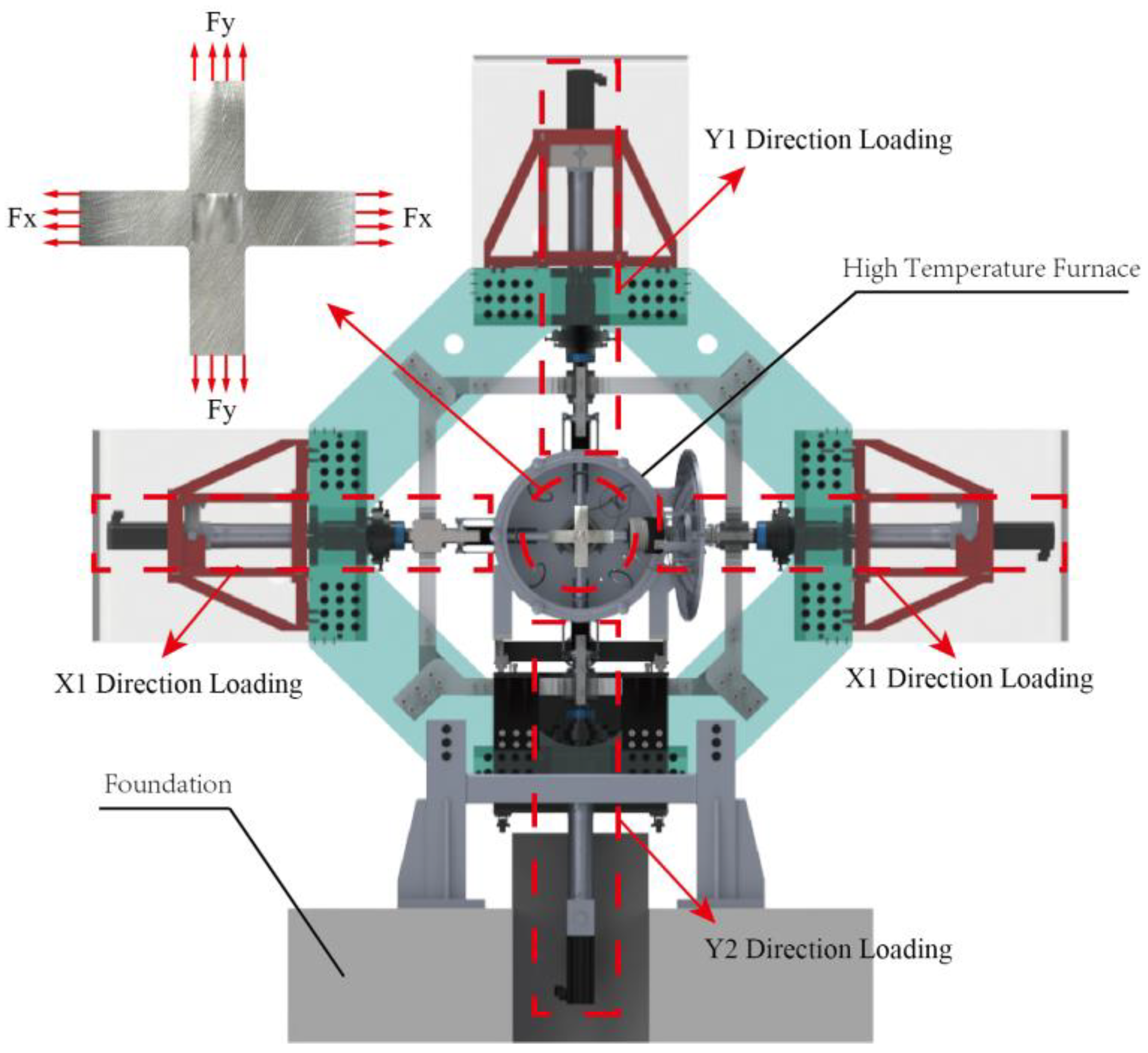
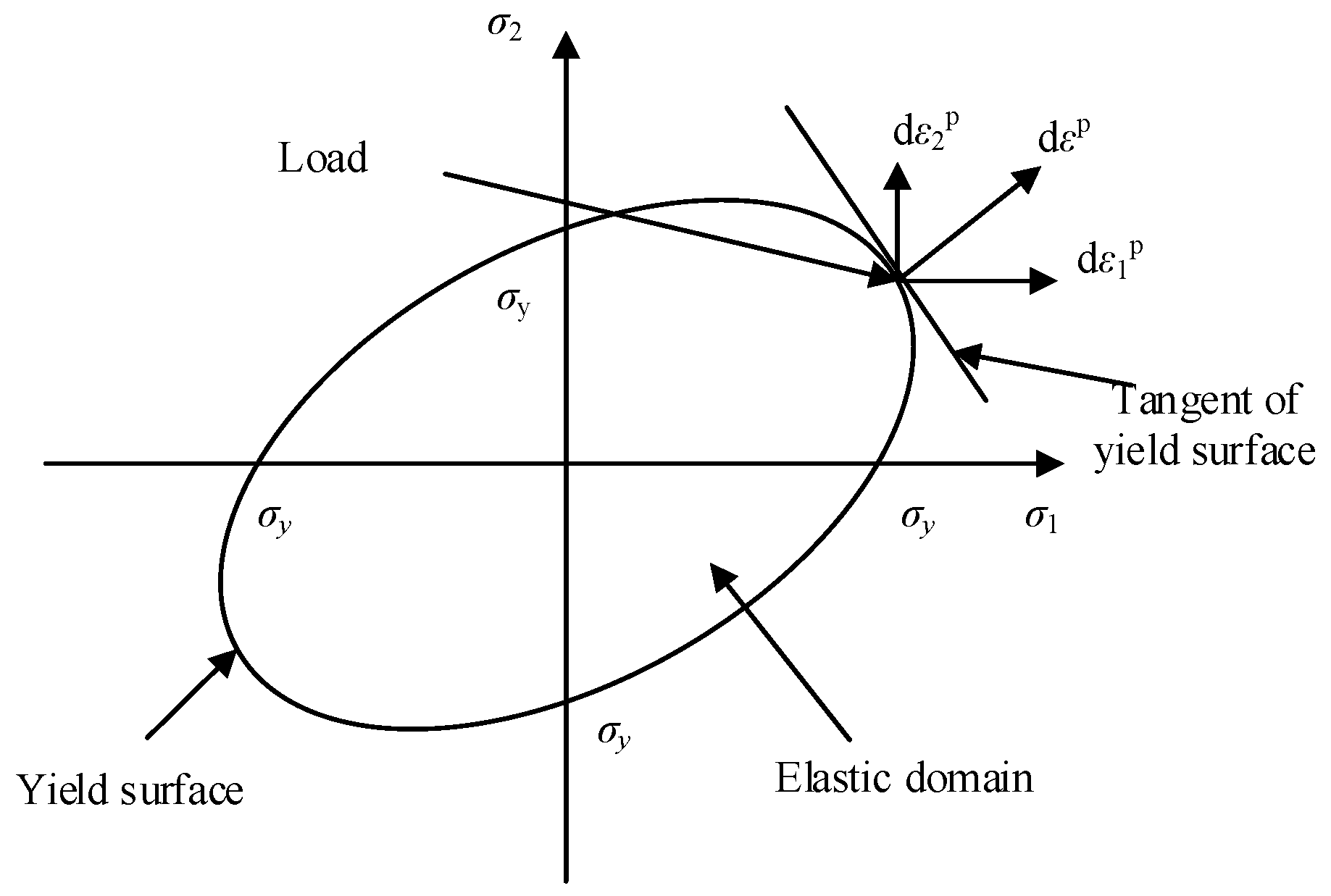
2.1. General Principle
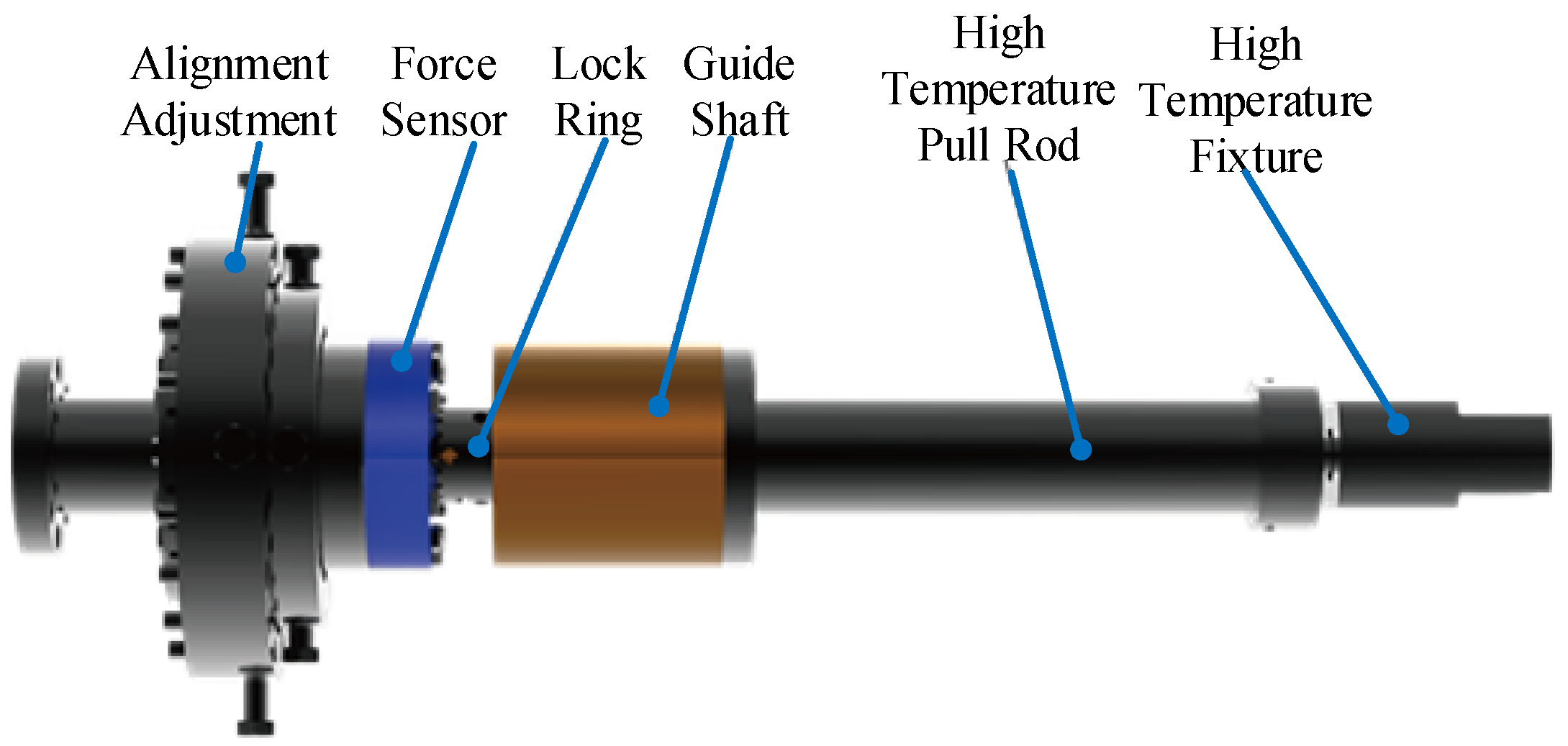
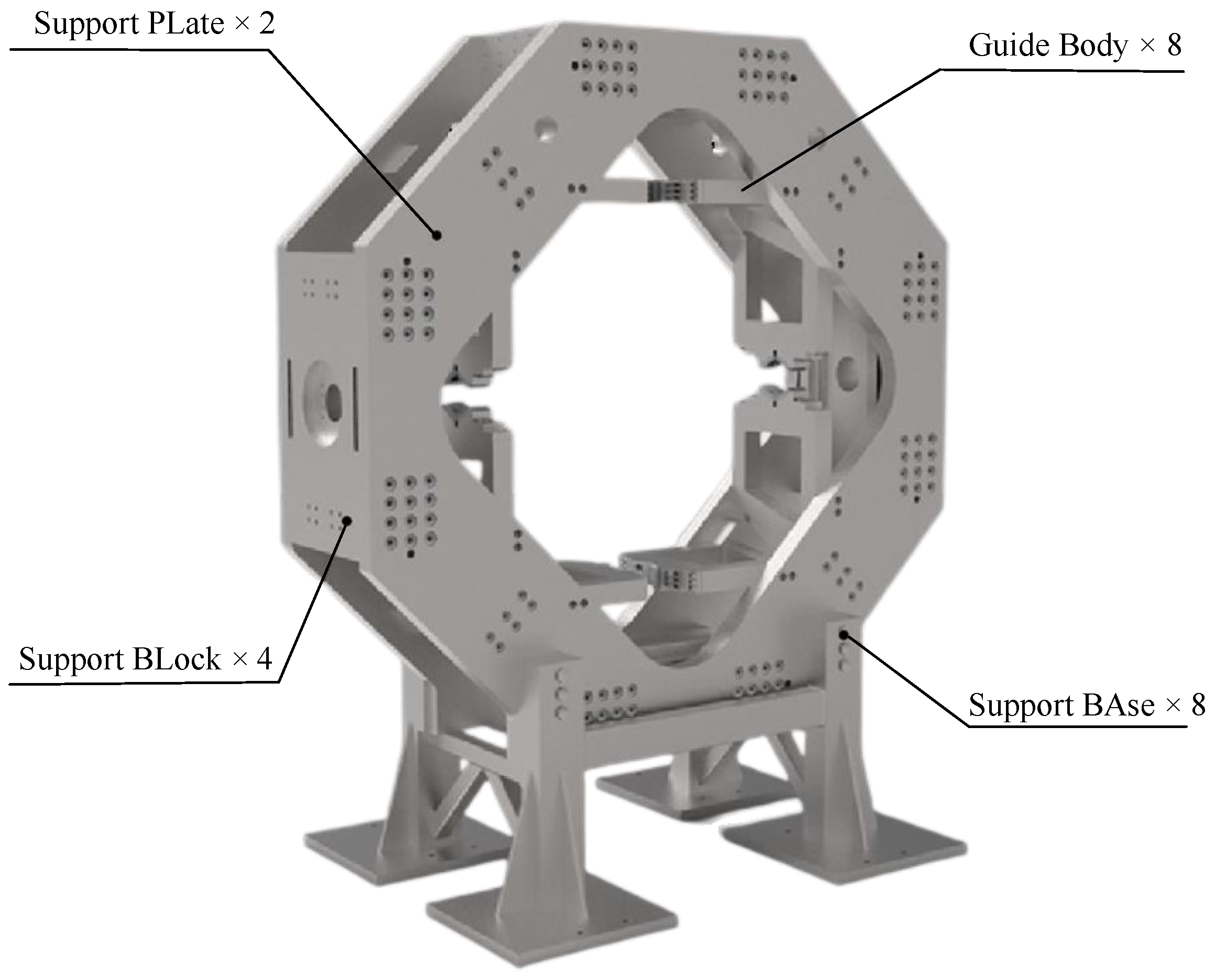
2.2. In-Plane Biaxial Loading Mold
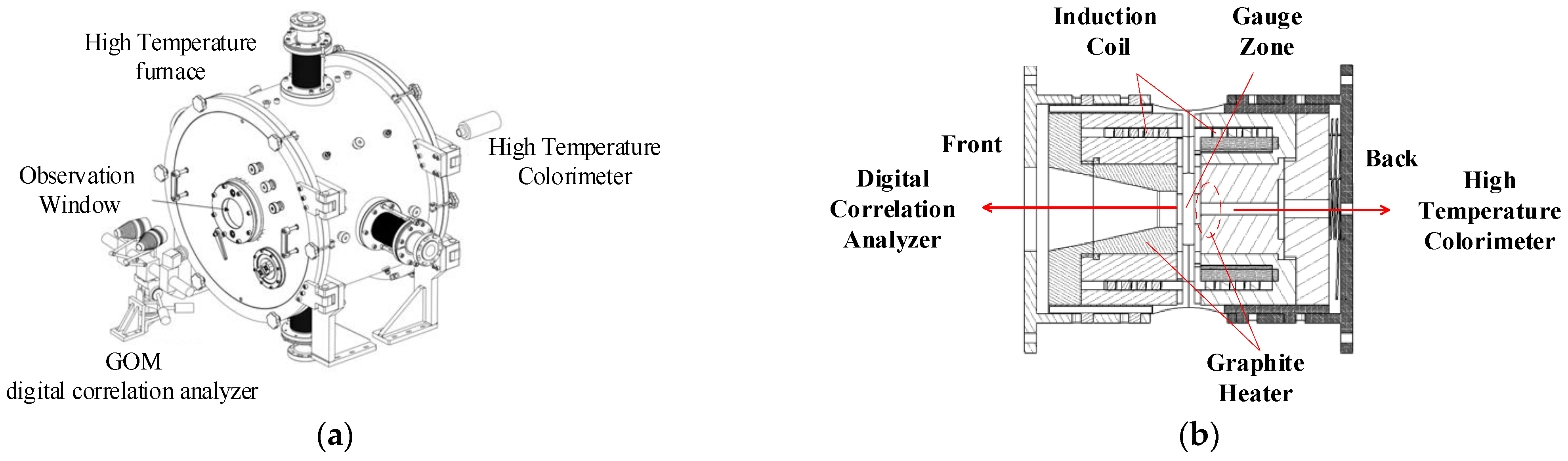
2.3. High-Temperature Loading Mold
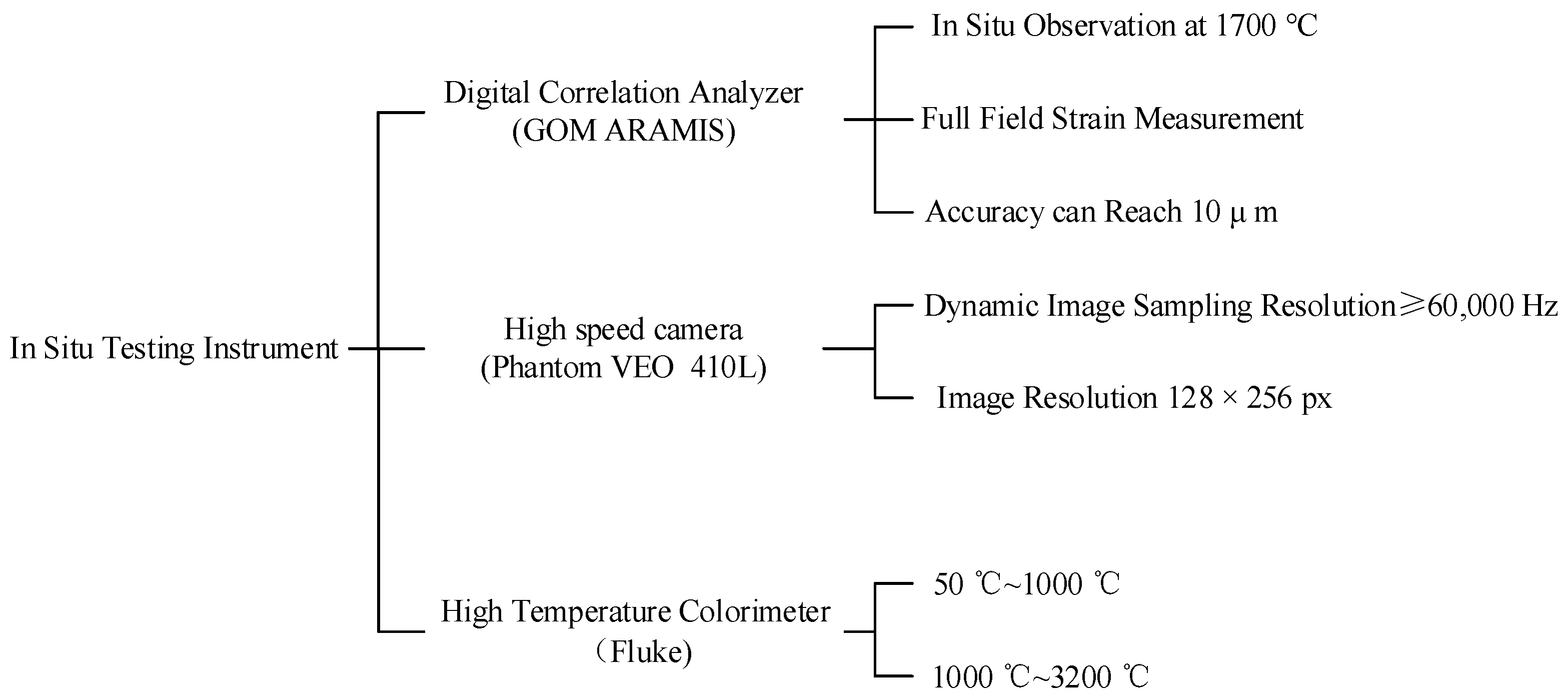
2.4. In Situ Detection Module
2.5. Calibrations and Corrections of the HTIPTA
2.5.1. Force Calibration of the Force Sensors
2.5.2. Strain Calibration of the Digital Correlation Apparatus
2.5.3. Calibration of the High-Temperature Colorimeter
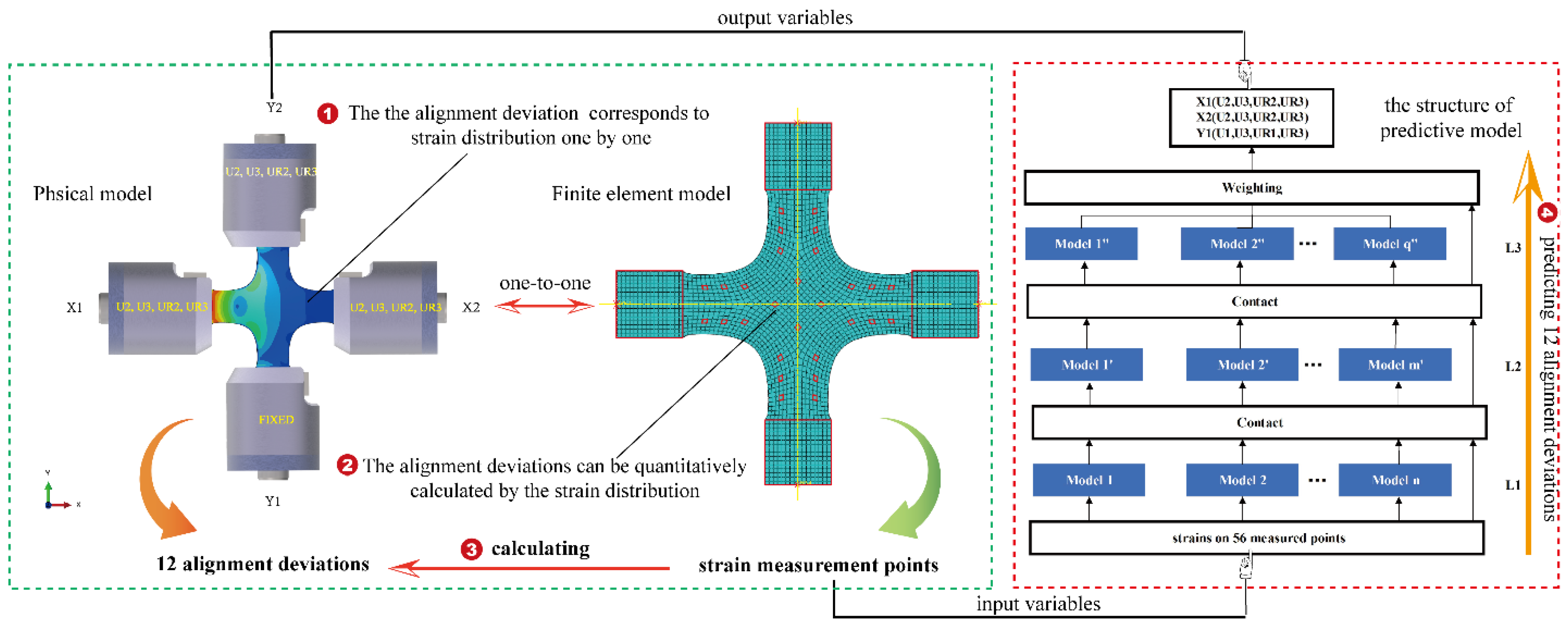
2.5.4. Alignment Deviation Calibration
3. Test Procedure of the HTIPTA
3.1. Specimen Clamping
3.2. High-Temperature Field Building
3.3. In-Plane Biaxial Loading
3.4. In Situ Monitoring
4. Experimental Results
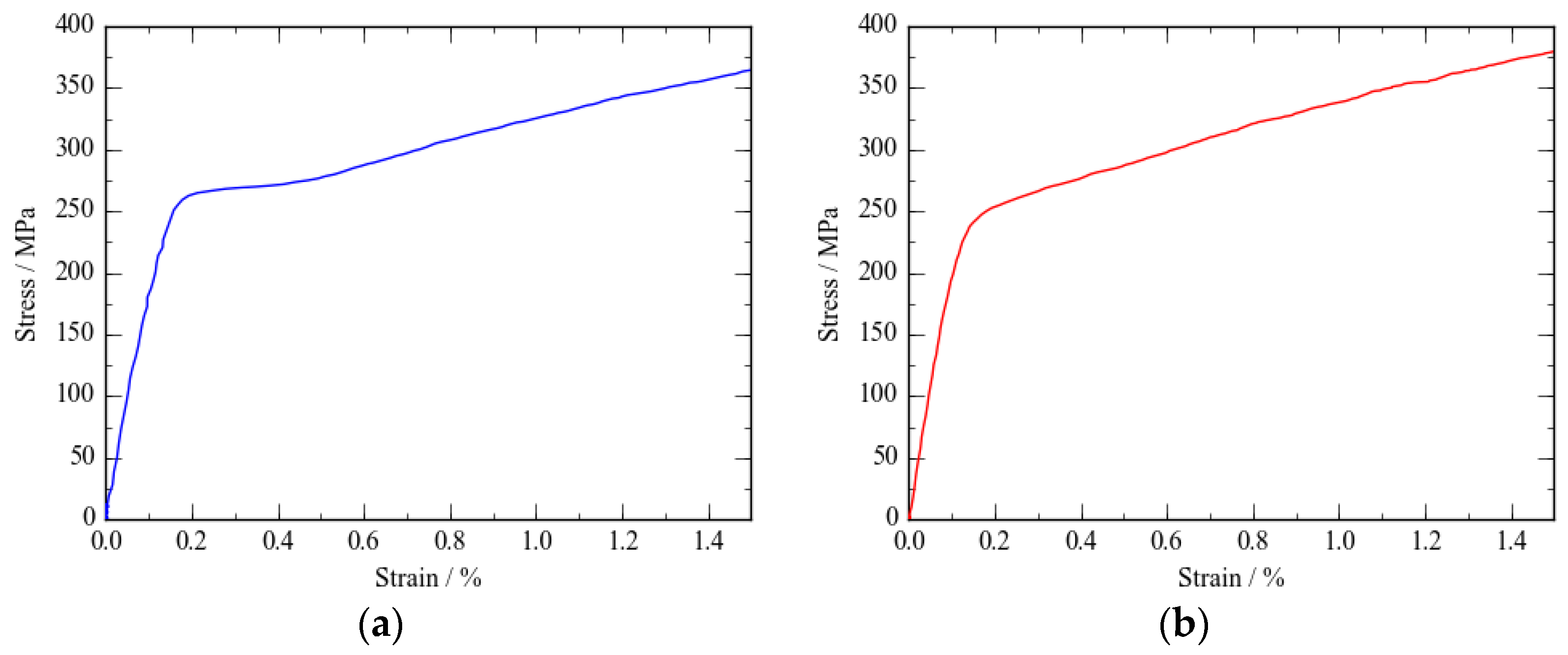
4.1. In Situ Tests under Combined In-Plane Tension Loads
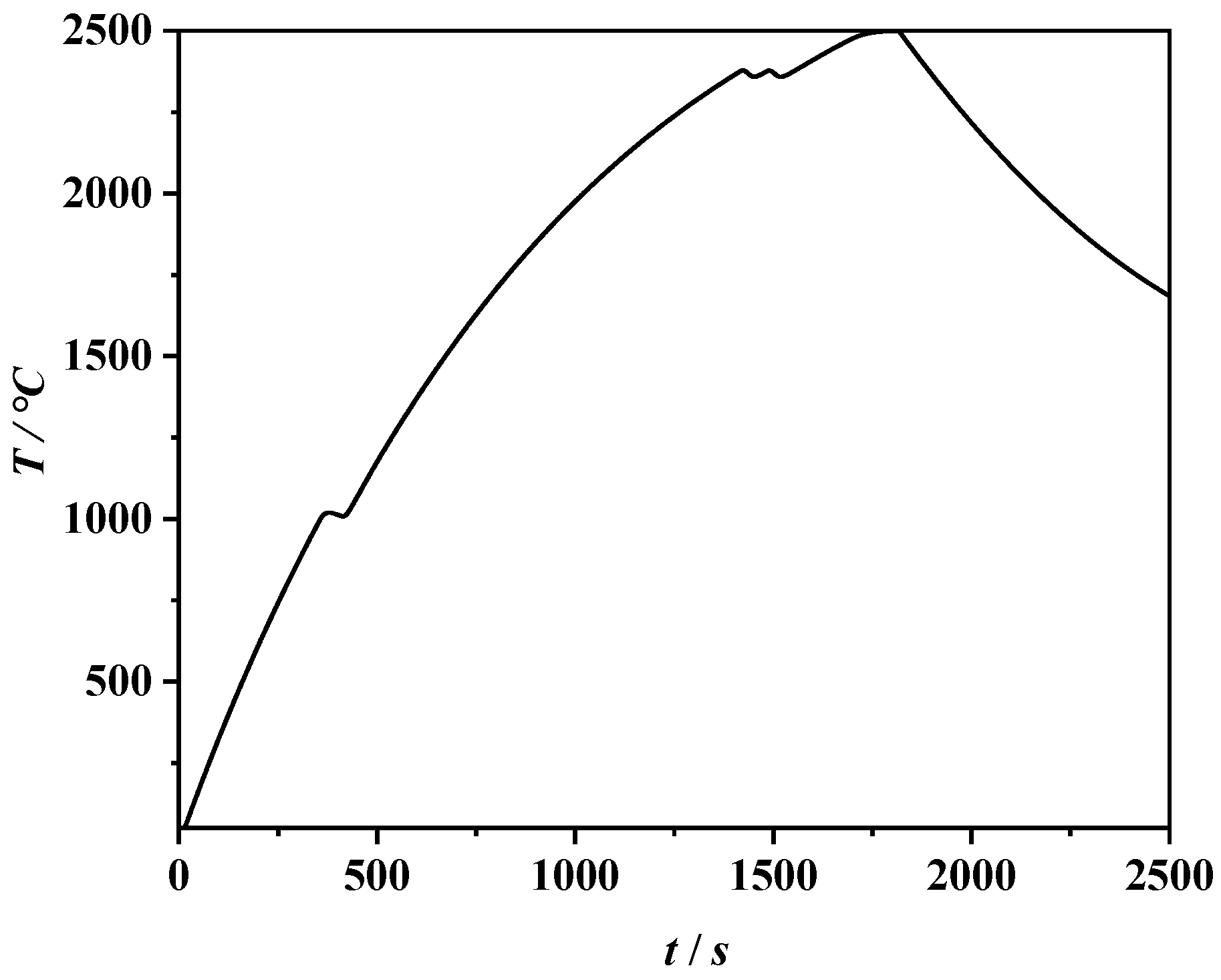
4.2. Impact Test of a Graphite Cruciform Specimen at 2500 °C
4.3. In Situ Tests under Combined Tension–Compression Loads at 1700 °C
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, W.-P.; Hu, H.-T. Parametric Study on the Failure of Fiber-Reinforced Composite Laminates under Biaxial Tensile Load. J. Compos. Mater. 2002, 36, 1481–1503. [Google Scholar] [CrossRef]
- Boehler, J.P.; Demmerle, S.; Koss, S. A new direct biaxial testing machine for anisotropic materials. Exp. Mech. 1994, 34, 1–9. [Google Scholar] [CrossRef]
- Blümel, K.W.; Gerlach, J. Biaxial Experimental Approach to Characterize Formability of Steel Sheet Metals; SAE International: Warrendale, PA, USA, 1998. [Google Scholar] [CrossRef]
- Green, D.E.; Neale, K.W.; MacEwen, S.R.; Makinde, A.; Perrin, R. Experimental investigation of the biaxial behaviour of an aluminum sheet. Int. J. Plast. 2004, 20, 1677–1706. [Google Scholar] [CrossRef]
- Jones, C. Biaxial testing of polymer composites. Mater. World 2001, 9, 19–21. [Google Scholar]
- McDiarmid, D. A new analysis of fatigue under combined bending and twisting. Aeronaut. J. 1974, 78, 325–329. [Google Scholar] [CrossRef]
- Quaresimin, M.; Susmel, L.; Talreja, R. Fatigue behaviour and life assessment of composite laminates under multiaxial loadings. Int. J. Fatigue 2010, 32, 2–16. [Google Scholar] [CrossRef]
- Hazell, C.R.; Marin, J. A possible specimen for the study of biaxial yielding of materials. Int. J. Mech. Sci. 1967, 9, 57–63. [Google Scholar] [CrossRef]
- Bird, J.E.; Duncan, J.L. Strain hardening at high strain in aluminum alloys and its effect on strain localization. Metall. Trans. A 1981, 12, 235–241. [Google Scholar] [CrossRef]
- Luk’Yanov, V.F.; Lyudmirskij, Y.G.; Naprasnikov, V.V. Testing components of shell structures in the biaxial stressed state; Pruefung der Komponenten von Kesselmantelstrukturen im biaxialen Spannungszustand. Zavod. Lab 1986, 52, 63–65. [Google Scholar]
- Dudderar, T.D.; Koch, F.B.; Doerries, E.M. Measurement of the shapes of foil bulge-test samples. Exp. Mech. 1977, 17, 133–140. [Google Scholar] [CrossRef]
- Yu, Y.; Wan, M. Design of a cruciform biaxial tensile specimen for limit strain analysis by FEM. J. Mater. Process. Technol. 2002, 123, 67–70. [Google Scholar] [CrossRef]
- Makinde, A.; Thibodeau, L.; Neale, K.W. Development of an apparatus for biaxial testing using cruciform specimens. Exp. Mech. 1992, 32, 138–144. [Google Scholar] [CrossRef]
- Welsh, J.S.; Adams, D.F. Development of a True Triaxial Testing Facility for Composite Materials. In Proceedings of the Symposium on Multiaxial Fatigue and Deformation, Seattle, WA, USA, 19–20 May 1999; American Society Testing and Materials: Seattle, WA, USA, 2000; pp. 423–437. [Google Scholar] [CrossRef]
- Welsh, J.S.; Adams, D.F. Development of an electromechanical triaxial test facility for composite materials. Exp. Mech. 2000, 40, 312–320. [Google Scholar] [CrossRef]
- Zouani, A.; Bui-Quoc, T.; Bernard, M. A Proposed Biaxial-Tensile Device for Fatigue Testing; American Society of Mechanical Engineers: New York, NY, USA, 1996. [Google Scholar]
- Hayhurst, D. A biaxial-tension creep-rupture testing machine. J. Strain Anal. 1973, 8, 119–123. [Google Scholar] [CrossRef]
- Fessler, H.; Musson, J. A 30 ton biaxial tensile testing machine. J. Strain Anal. 1969, 4, 22–26. [Google Scholar] [CrossRef]
- Shiratori, E.; Ikegami, K. A new biaxial tensile testing machine with flat specimen. Bull. Tokyo Inst. Technol. 1967, 82, 5–18. [Google Scholar]
- Smits, A.; Van Hemelrijck, D.; Philippidis, T.P.; Cardon, A. Design of a cruciform specimen for biaxial testing of fibre reinforced composite laminates. Compos. Sci. Technol. 2006, 66, 964–975. [Google Scholar] [CrossRef]
- Williamson, C.; Cook, J.; Clarke, A. Investigation into the Failure of Ppen and Filled Holes in CFRP Laminates under Biaxial Loading Conditions; QinetiQ Ltd.: Farmbrough, UK, 2004; Available online: http://www.escm.eu.org/docs/eccm/C209.pdf (accessed on 29 September 2022).
- Liu, W.; Guines, D.; Leotoing, L.; Ragneau, E. Identification of strain rate-dependent mechanical behaviour of DP600 under in-plane biaxial loadings. Mater. Sci. Eng. A 2016, 676, 366–376. [Google Scholar] [CrossRef]
- Güler, B.; Efe, M. Forming and fracture limits of sheet metals deforming without a local neck. J. Mater. Process. Technol. 2018, 252, 477–484. [Google Scholar] [CrossRef]
- Kuwabara, T.; Ikeda, S.; Kuroda, K. Measurement and analysis of differential work hardening in cold-rolled steel sheet under biaxial tension. J. Mater. Process. Technol. 1998, 80–81, 517–523. [Google Scholar] [CrossRef]
- Lin, S.B.; Ding, J.L. Experimental study of the plastic yielding of rolled sheet metals with the cruciform plate specimen. Int. J. Plast. 1995, 11, 583–604. [Google Scholar] [CrossRef]
- Kulawinski, D.; Ackermann, S.; Seupel, A.; Lippmann, T.; Henkel, S.; Kuna, M.; Weidner, A.; Biermann, H. Deformation and strain hardening behavior of powder metallurgical TRIP steel under quasi-static biaxial-planar loading. Mater. Sci. Eng. A. Mater. Prop. Microstruct. Process. 2015, 642, 317–329. [Google Scholar] [CrossRef]
- Lamkanfi, E.; Van Paepegem, W.; Degrieck, J. Shape optimization of a cruciform geometry for biaxial testing of polymers. Polym. Test. 2015, 41, 7–16. [Google Scholar] [CrossRef]
- Tierriault, P.; Settouane, K.; Brailovski, V. Biaxial Testing at Different Temperatures of Cruciform Ti-Ni Samples. In Proceedings of the International Conference on Shape Memory and Superplastic Technologies; SMST Society Inc.: Menlo Park, CA, USA, 2003; pp. 247–257. [Google Scholar] [CrossRef]
- Bruschi, S.; Altan, T.; Banabic, D.; Bariani, P.F.; Brosius, A.; Cao, J.; Ghiotti, A.; Khraisheh, M.; Merklein, M.; Tekkaya, A.E. Testing and modelling of material behaviour and formability in sheet metal forming. CIRP Ann. 2014, 63, 727–749. [Google Scholar] [CrossRef]
- Geiger, M.; van der Heyd, G.; Merklein, M.; Hussnaetter, W. Novel Concept of Experimental Setup for Characterization of Plastic Yielding of Sheet Metal at Elevated Temperatures. In Sheet Metal 2005; Geiger, M., Duflou, J., Kals, H.J.J., Shirvani, B., Singh, U.P., Eds.; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2005; Volume 6–8, pp. 657–664. [Google Scholar] [CrossRef]
- Chevalier, L.; Marco, Y. Identification of a strain induced crystallization model for PET under uni- and bi-axial loading: Influence of temperature dispersion. Mech. Mater. 2007, 39, 596–609. [Google Scholar] [CrossRef]
- Abu-Farha, F.; Hector, L.G.; Khraisheh, M. Cruciform-Shaped Specimens for Elevated Temperature Biaxial Testing of Lightweight Materials. Jom 2009, 61, 48–56. [Google Scholar] [CrossRef]
- Kulawinski, D.; Henkel, S.; Holländer, D.; Thiele, M.; Gampe, U.; Biermann, H. Fatigue behavior of the nickel-base superalloy Waspaloy™ under proportional biaxial-planar loading at high temperature. Int. J. Fatigue 2014, 67, 212–219. [Google Scholar] [CrossRef]
- Xiao, R.; Li, X.X.; Lang, L.H.; Chen, Y.K.; Yang, Y.F. Biaxial tensile testing of cruciform slim superalloy at elevated temperatures. Mater. Des. 2016, 94, 286–294. [Google Scholar] [CrossRef]
- Shao, Z.; Li, N.; Lin, J.; Dean, T.A. Development of a New Biaxial Testing System for Generating Forming Limit Diagrams for Sheet Metals Under Hot Stamping Conditions. Exp. Mech. 2016, 56, 1489–1500. [Google Scholar] [CrossRef]
- Le Cam, J.-B.; Robin, E.; Leotoing, L.; Guines, D. Calorimetric analysis of Portevin-Le Chatelier bands under equibiaxial loading conditions in Al–Mg alloys: Kinematics and mechanical dissipation. Mech. Mater. 2017, 105, 80–88. [Google Scholar] [CrossRef]
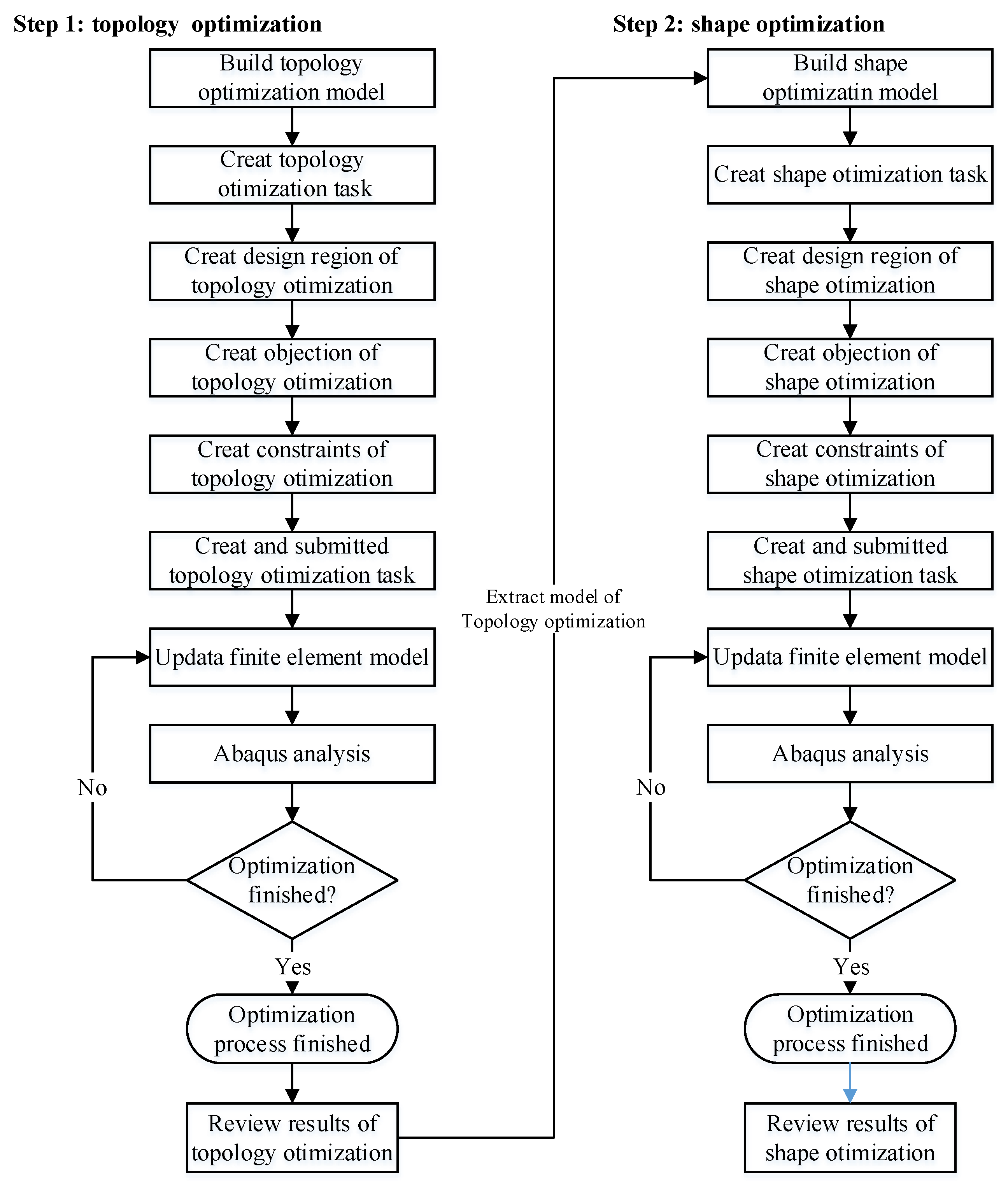
- Chen, J.; Zhang, J.; Zhao, H. Designing a Cruciform Specimen via Topology and Shape Optimizations under Equal Biaxial Tension Using Elastic Simulations. Materials 2022, 15, 5001. [Google Scholar] [CrossRef] [PubMed]
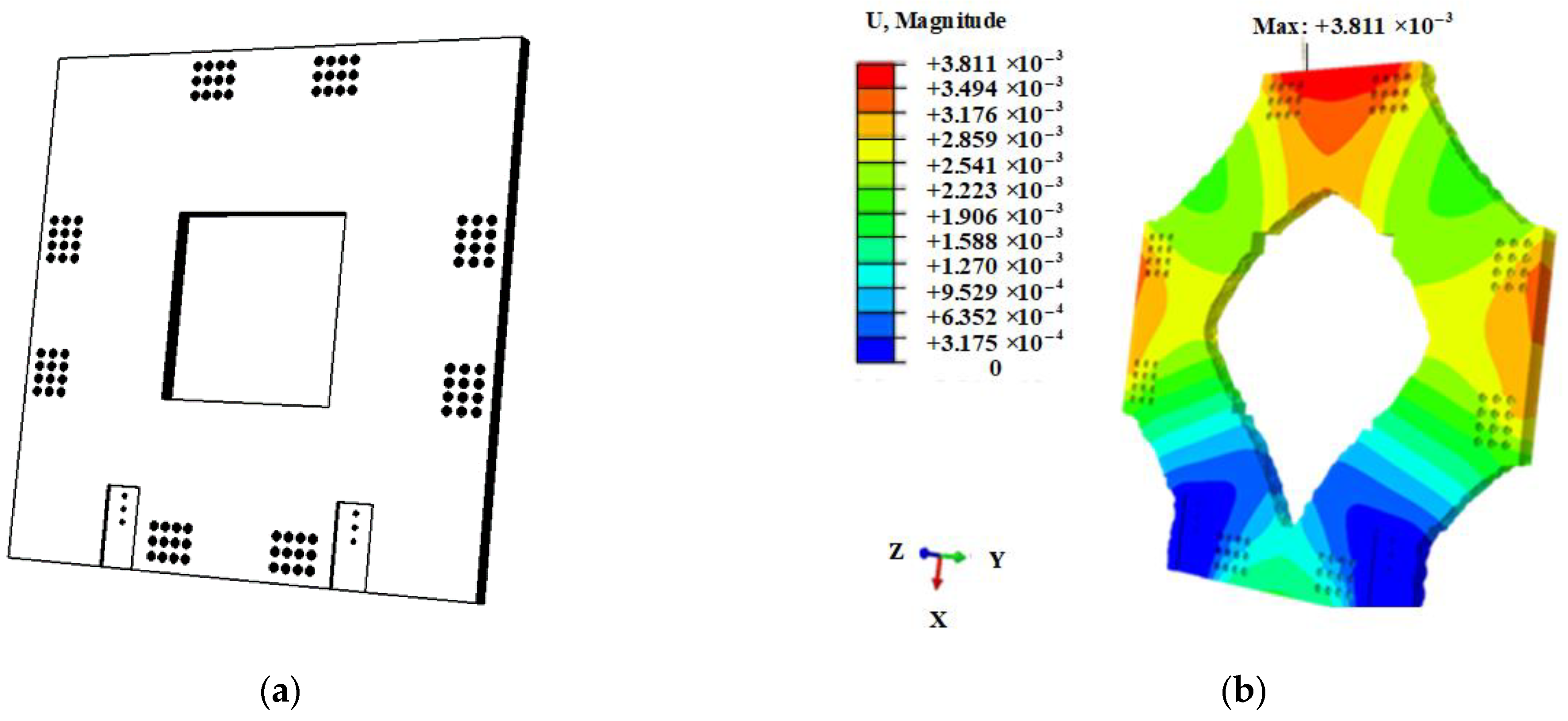
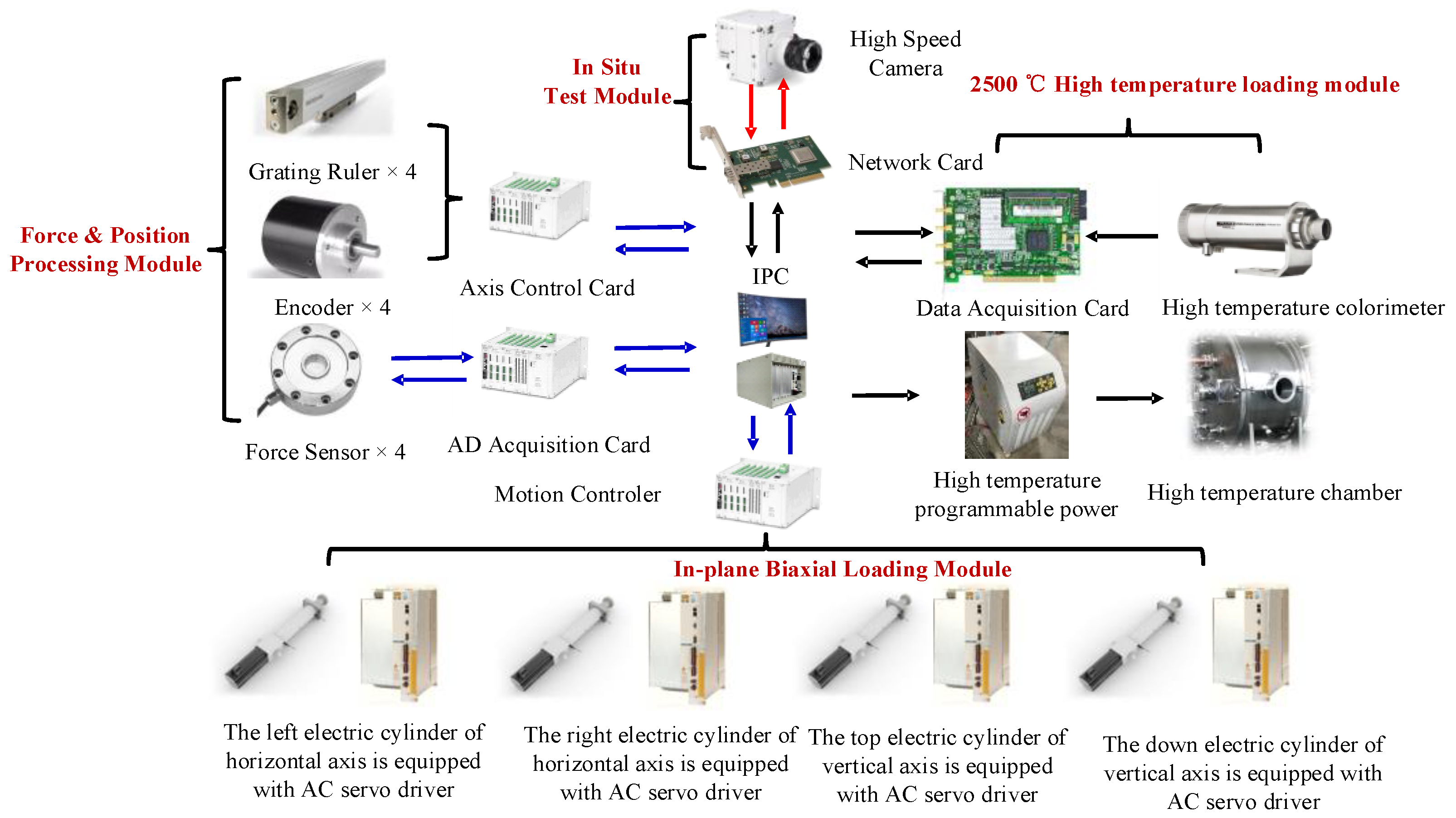

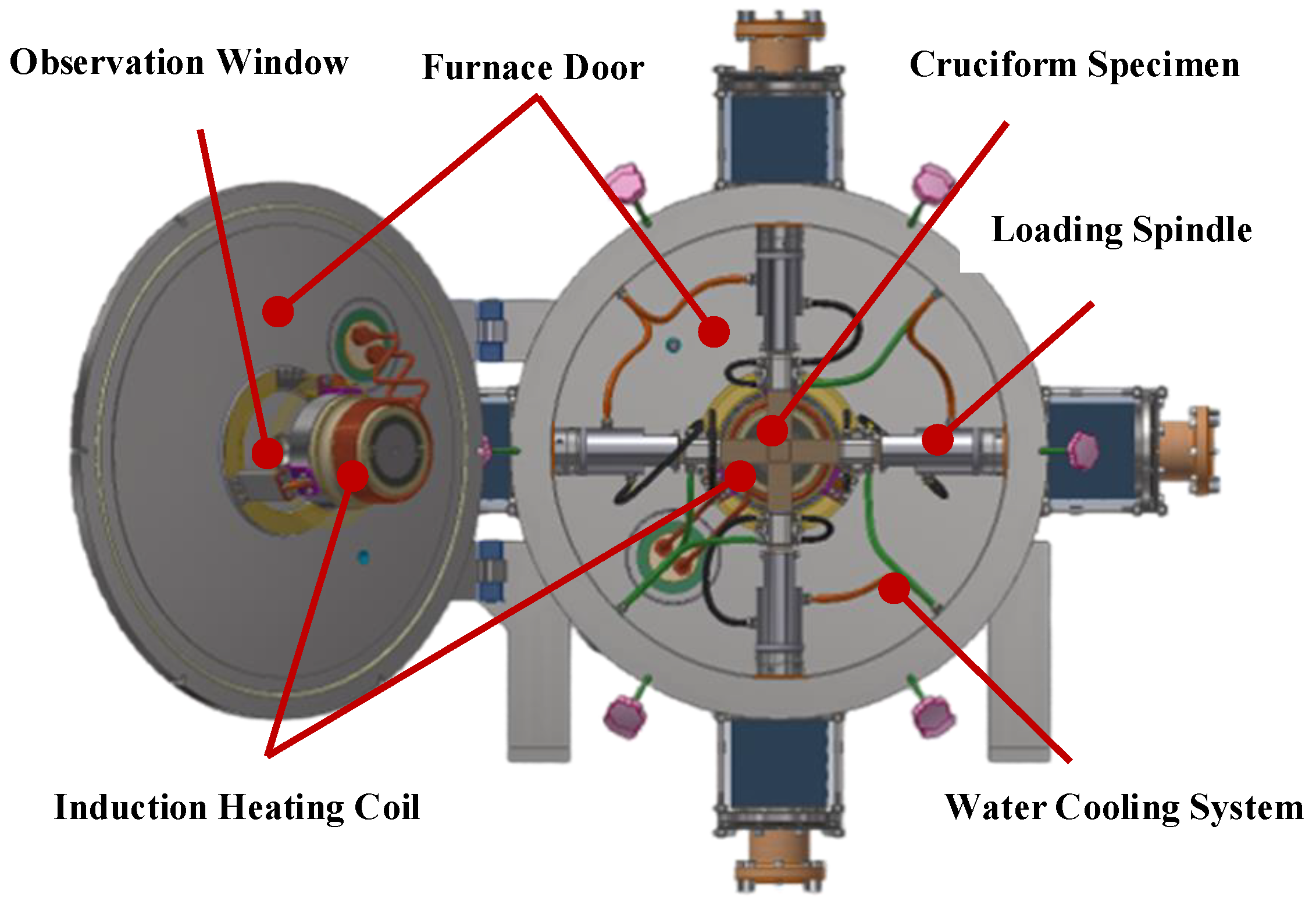
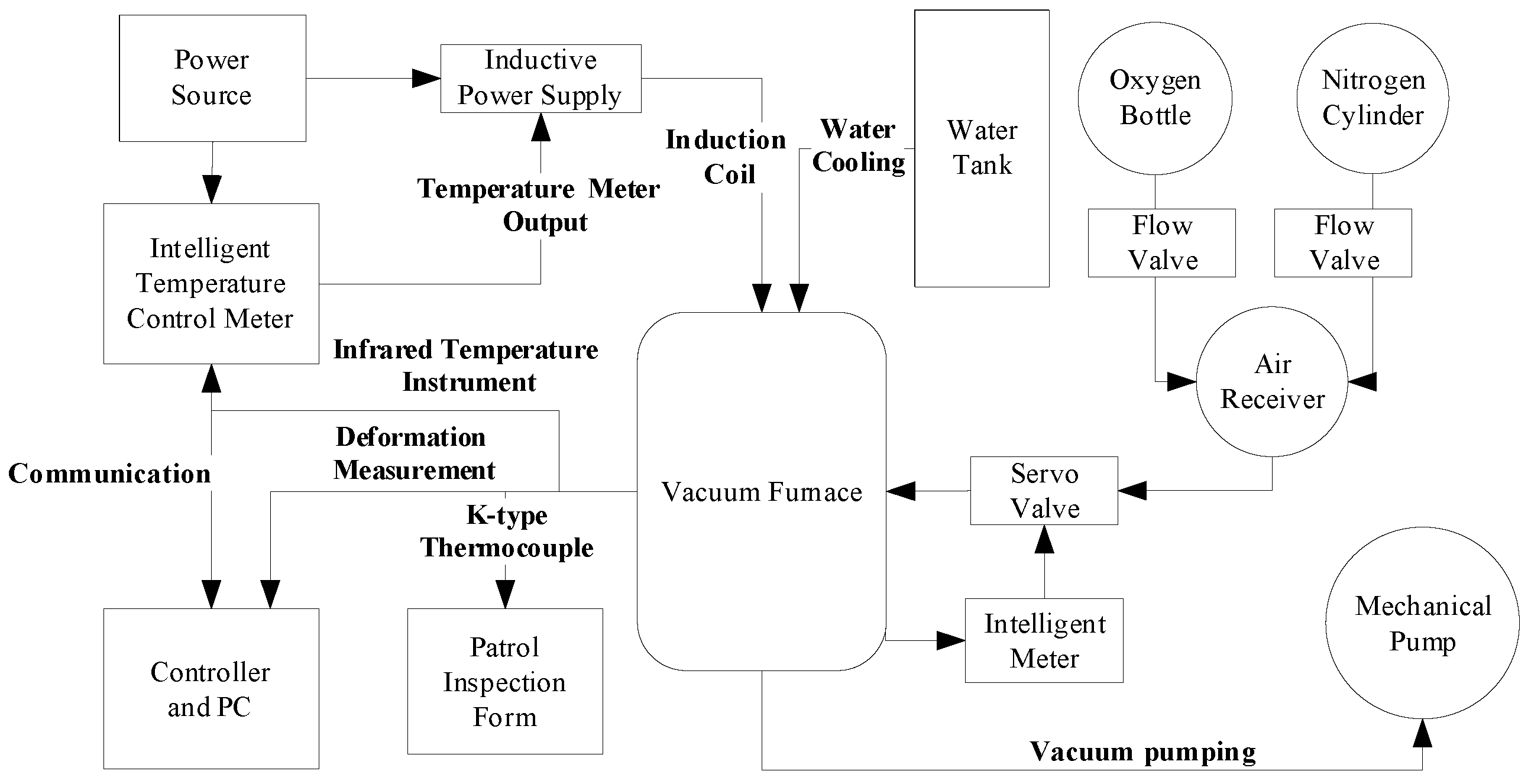






| Method | Advantages | Shortcomings |
|---|---|---|
| Induced bending of beams and plates |
|
|
| Bulging test |
|
|
| Thin-walled tubes subjected to tensile or compressive and torsion stress |
|
|
| In-plane biaxial tension/compression test |
|
|
| Structure of Plane Biaxial Test Equipment | Advantages | Shortcomings |
|---|---|---|
| Horizontal structure |
|
|
| Vertical structure |
|
|
| Heating Mode | Advantages | Shortcomings |
|---|---|---|
| Laser, halogen lamp, and hot air directly applied to the heat the gauge zone |
|
|
| Induction heating |
|
|
| Non-vacuum, high-temperature environment chamber |
|
|
| Heat conduction |
|
|
| Force Value (kN) | Force Sensor-1 Forward | Force Sensor-1 Backward | Force Sensor-2 Forward | Force Sensor-2 Backward | Force Sensor-3 Forward | Force Sensor-3 Backward | Force Sensor-4 Forward | Force Sensor-4 Backward |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.00002 | 0 | 0.00001 | 0 | 0.00002 | 0 | 0.00002 |
| 12 | 0.19536 | 0.19530 | 0.20505 | 0.20432 | 0.19329 | 0.19370 | 0.19726 | 0.19841 |
| 20 | 0.32583 | 0.32630 | 0.33986 | 0.33911 | 0.32249 | 0.32367 | 0.32898 | 0.32935 |
| 30 | 0.48985 | 0.49086 | 0.50768 | 0.50665 | 0.48527 | 0.48772 | 0.49114 | 0.49263 |
| 40 | 0.65488 | 0.65619 | 0.67493 | 0.67352 | 0.64999 | 0.65309 | 0.65682 | 0.65824 |
| 60 | 0.98604 | 0.98730 | 1.00863 | 1.00690 | 0.98113 | 0.98450 | 0.98698 | 0.98785 |
| 80 | 1.31769 | 1.31838 | 1.34215 | 1.34129 | 1.31306 | 1.31459 | 1.31721 | 1.31711 |
| 100 | 1.64946 | 1.64990 | 1.67556 | 1.67529 | 1.64524 | 1.64571 | 1.64783 | 1.64728 |
| 125 | 2.06440 | / | 2.09254 | / | 2.06079 | / | 2.06106 | / |
| Initial zero (mV/V): 0.02217, 0.02790, 0.02790, 0.01987 | ||||||||
| Repeatability: R1 (%) = 0.10, R2 (%) = 0.05, R3 (%) = 0.06, R4 (%) = 0.14 | ||||||||
| Relative tolerance between forward and backward: v1 (%) = 0.21, v2 (%) = −0.36, v3 (%) = 0.51, v4 (%) = 0.58 | ||||||||
| Measurement uncertainty: U1 = 2.0 × 10−4 (k = 2), U2 = 1.8 × 10−4 (k = 2), U3 = 1.8 × 10−4 (k = 2), U4 = 2.3 × 10−4 (k = 2) | ||||||||
| Number | Standard Value/με | Measured Value/με | Indication Error/με |
|---|---|---|---|
| 1 | 30,026 | 30,035 | 9 |
| 2 | 60,021 | 60,030 | 9 |
| 3 | 90,040 | 90,048 | 8 |
| 4 | 120,041 | 120,049 | 8 |
| 5 | 150,285 | 150,293 | 8 |
| 6 | 180,226 | 180,235 | 9 |
| 7 | 210,630 | 210,638 | 8 |
| 8 | 240,209 | 240,219 | 10 |
| 9 | 270,322 | 270,332 | 10 |
| 10 | 300,072 | 300,082 | 10 |
| Blackbody Temperature °C/°F | Test Temperature °C/°F | Blackbody Temperature °C/°F | Test Temperature °C/°F |
|---|---|---|---|
| 69.7 °C/157.5 °F | 69.9 °C/157.8 °F | 900.1 °C/1652.2 °F | 900.0 °C/1652.1 °F |
| 99.9 °C/211.8 °F | 99.8 °C/211.7 °F | 1000.0 °C/1832.0 °F | 999.9 °C/1831.8 °F |
| 148.9 °C/300.0 °F | 148.8 °C/299.9 °F | 1100.0 °C/2012.0 °F | 1099.9 °C/2011.9 °F |
| 200.0 °C/392.0 °F | 200.1 °C/392.1 °F | 1200.1 °C/2192.2 °F | 1200.1 °C/2192.1 °F |
| 300.1 °C/572.2 °F | 300.0 °C/572.1 °F | 1300.1 °C/2372.2 °F | 1300.0 °C/2372.0 °F |
| 500.0 °C/932.0 °F | 500.0 °C/932.0 °F | 1500.0 °C/2732.0 °F | 1500.0 °C/2732.1 °F |
| 600.0 °C/1112 °F | 600.0 °C/1112.1 °F | 1600.1 °C/2912.0 °F | 1600.0 °C/2912.0 °F |
| 700.0 °C/1292 °F | 700.0 °C/1292.1 °F | 1700.0 °C/3092.0 °F | 1700.1 °C/3092.0 °F |
| 792.0 °C/1457.6 °F | 791.9 °C/1457.4 °F | 1800.0 °C/3272.1 °F | 1800.0 °C/3272.0 °F |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Zhang, J.; Zhao, H. Development and Experimental Verification of a High-Temperature and In-Plane Biaxial Testing Apparatus. Machines 2022, 10, 1054. https://doi.org/10.3390/machines10111054
Chen J, Zhang J, Zhao H. Development and Experimental Verification of a High-Temperature and In-Plane Biaxial Testing Apparatus. Machines. 2022; 10(11):1054. https://doi.org/10.3390/machines10111054
Chicago/Turabian StyleChen, Junxian, Jianhai Zhang, and Hongwei Zhao. 2022. "Development and Experimental Verification of a High-Temperature and In-Plane Biaxial Testing Apparatus" Machines 10, no. 11: 1054. https://doi.org/10.3390/machines10111054
APA StyleChen, J., Zhang, J., & Zhao, H. (2022). Development and Experimental Verification of a High-Temperature and In-Plane Biaxial Testing Apparatus. Machines, 10(11), 1054. https://doi.org/10.3390/machines10111054







