CNC Machines for Rehabilitation: Ankle and Shoulder
Abstract
1. Introduction
| Reference/Year | DOF | Movements | Actuator | Control | Mechanism | Rehabilitation Type | Sensor |
|---|---|---|---|---|---|---|---|
| [17]/2021 | 1 | PF/DF | NS 1 | PID type controller | Parallel | Passive | NS |
| [18]/2020 | 4 | PF/DF, E/I, RI/RE | NS | NE | Series-parallel | Static/dynamic rehabilitation | NS |
| [19]/2020 | 3 | PF/DF, E/I, AB/AD 2 | Linear and stepping motor | PD controller | Parallel | Passive/active | Tension/pressure sensors, torque sensor and encoders |
| [20,21]/2020, 2012 | 3 | PF/DF, E/I | Direct drive ball screw actuator- brushless DC servomotor | PD with gravity compensation, Controller based on the sliding mode theory | Parallel | Passive/active | Force |
| [22]/2019 | 1 | DF/PF | Linear actuator | PID controller | Serial | Passive | Hall sensor |
| [23], 2019 | 2 | PF/DF, Varus/valgus | Electric motor | NS | Parallel | Passive | IMU 3 |
| [24], 2017 | 3 | PF/DF, E/I, AB/AD | Pneumatic actuator, Festo Fluidic muscles (FFMs) | PID controller | Parallel | Passive | magnetic rotary encoders |
| [25,26]/2017, 2017 | 2 | PF/DF, E/I | DC servomotor | PD and PID type controllers | Parallel | Active/Passive | Encoders and force sensors |
| [27]/2015 | 3 | PF/DF, E/I, AB/AD | Brushless motors | PID controller, Position and force control | Serial | Passive/active | Force sensors and position sensors |
| [28]/2014 | 3 | PF/DF, E/I, AB/AD | Pneumatic muscle actuators | Adaptive Fuzzy Logic Controller | Parallel | Passive/resistive | Linear potentiometers, pressure and force sensors |
| [29]/2009 | 3 | PF/DF, E/I, AB/AD | DC motor driven linear actuators | Impedance control | Parallel | Passive/resistive | Linear potentiometers, inclinometers and force/torque sensors |
2. Materials and Methods
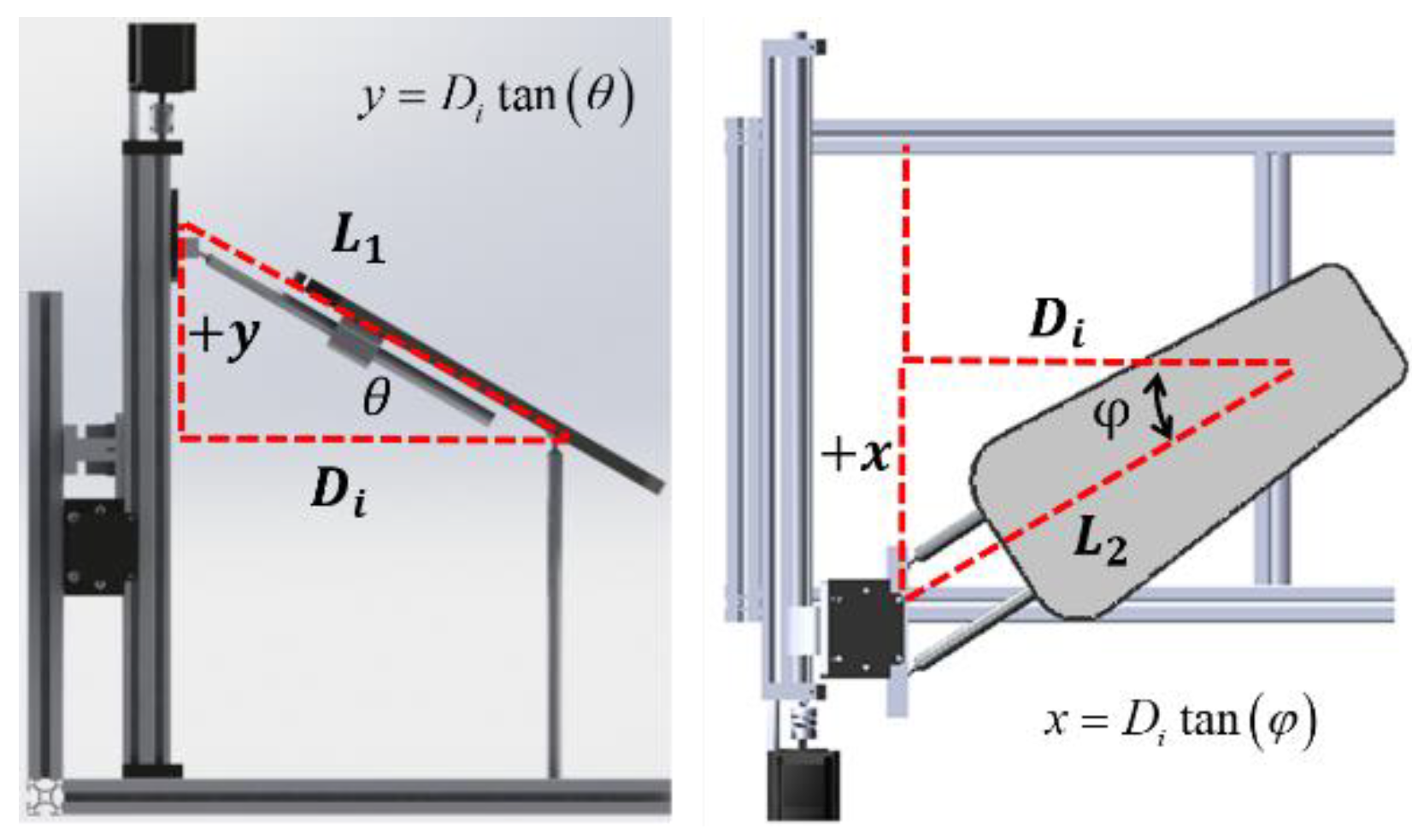
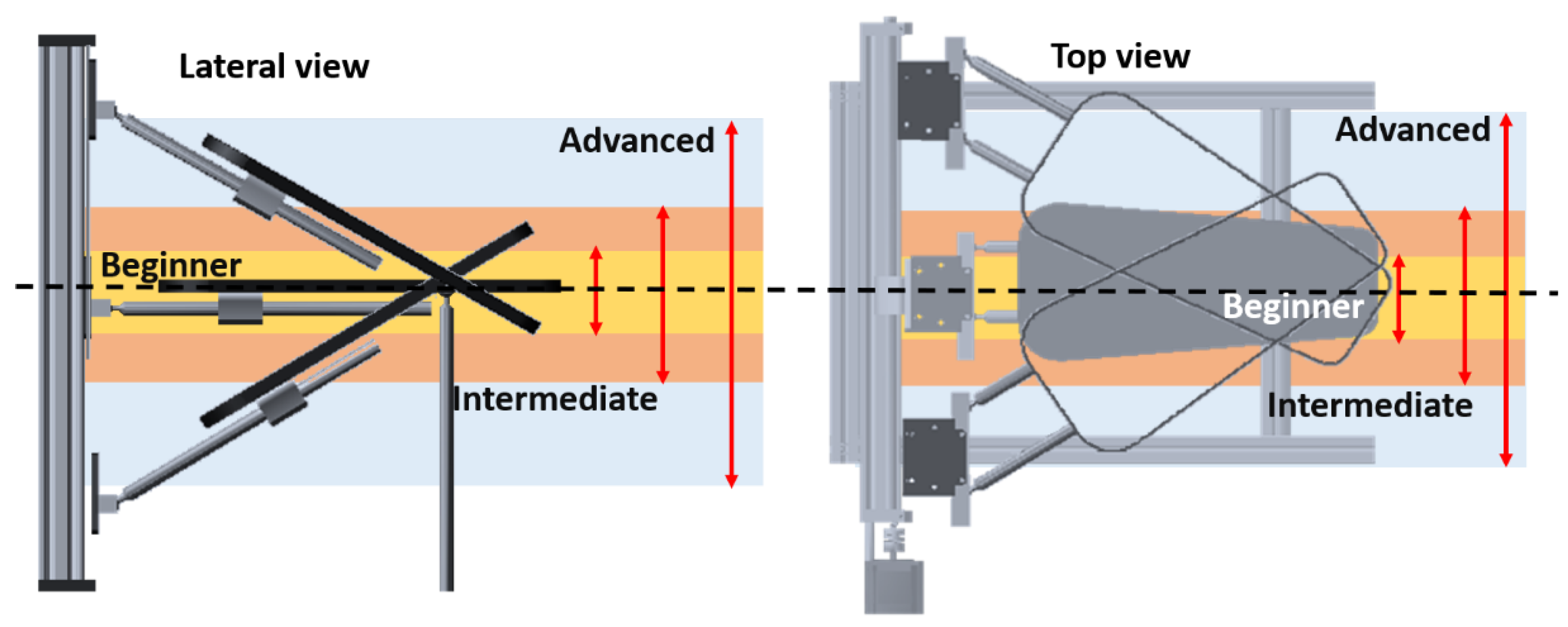
2.1. Ankle Rehabilitation Machine
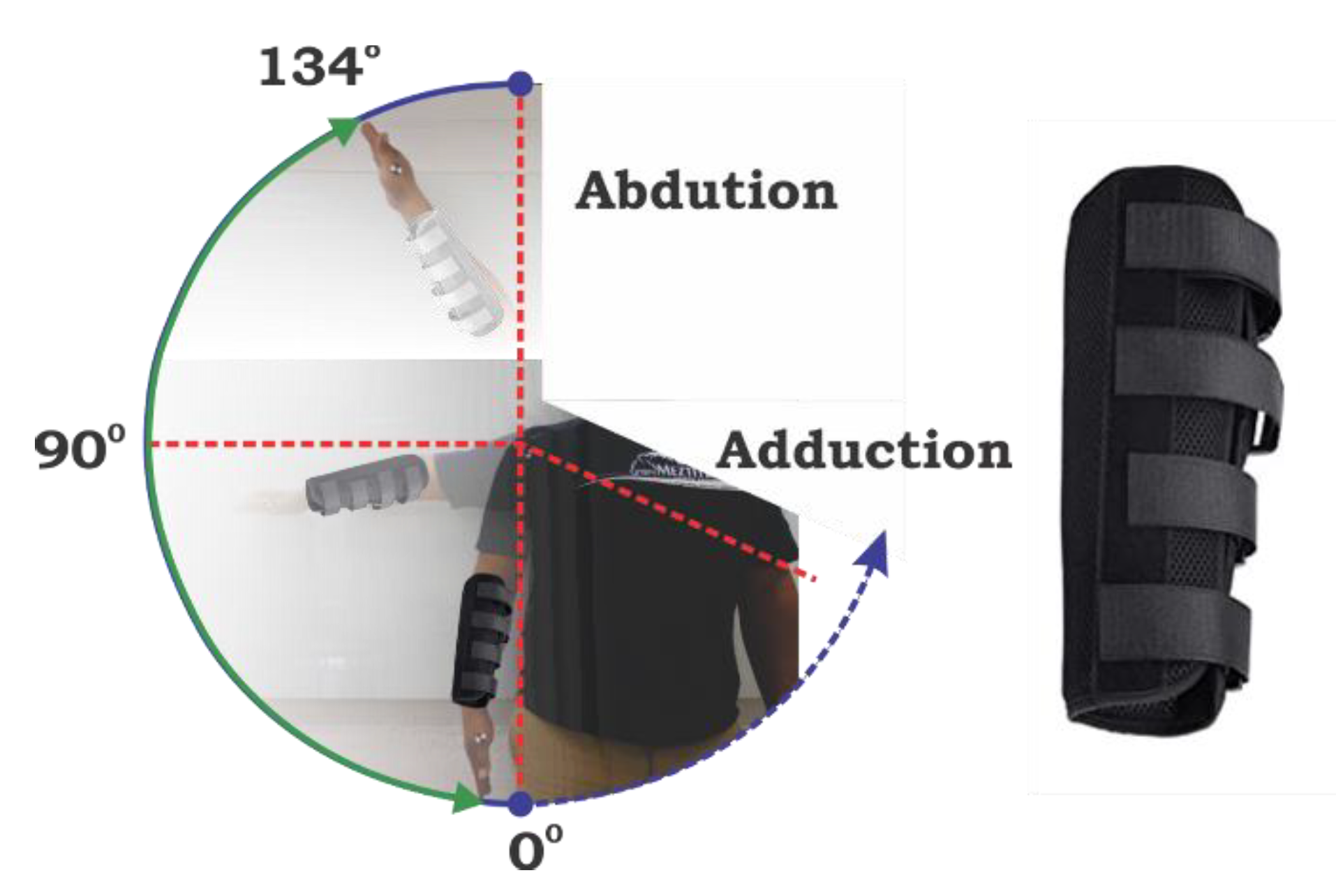
2.2. Shoulder Rehabilitation Machine
2.3. Computer Numerical Control
- Automation of machine movements.
- Flexible automation: it is based on a program that can be easily changed.
- Possibility of leaving the machine working unattended.
- Increase productivity.
- The influence of the “operator skill” in handling the machine is reduced, programming machining of complex curves.
- Improvement of precision and speed in movements.
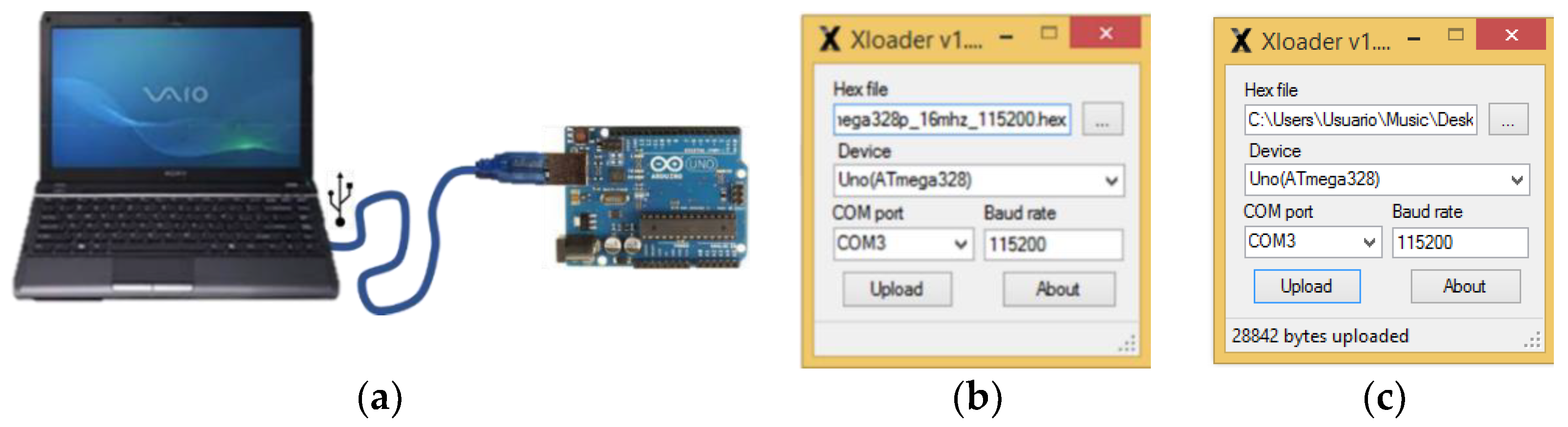
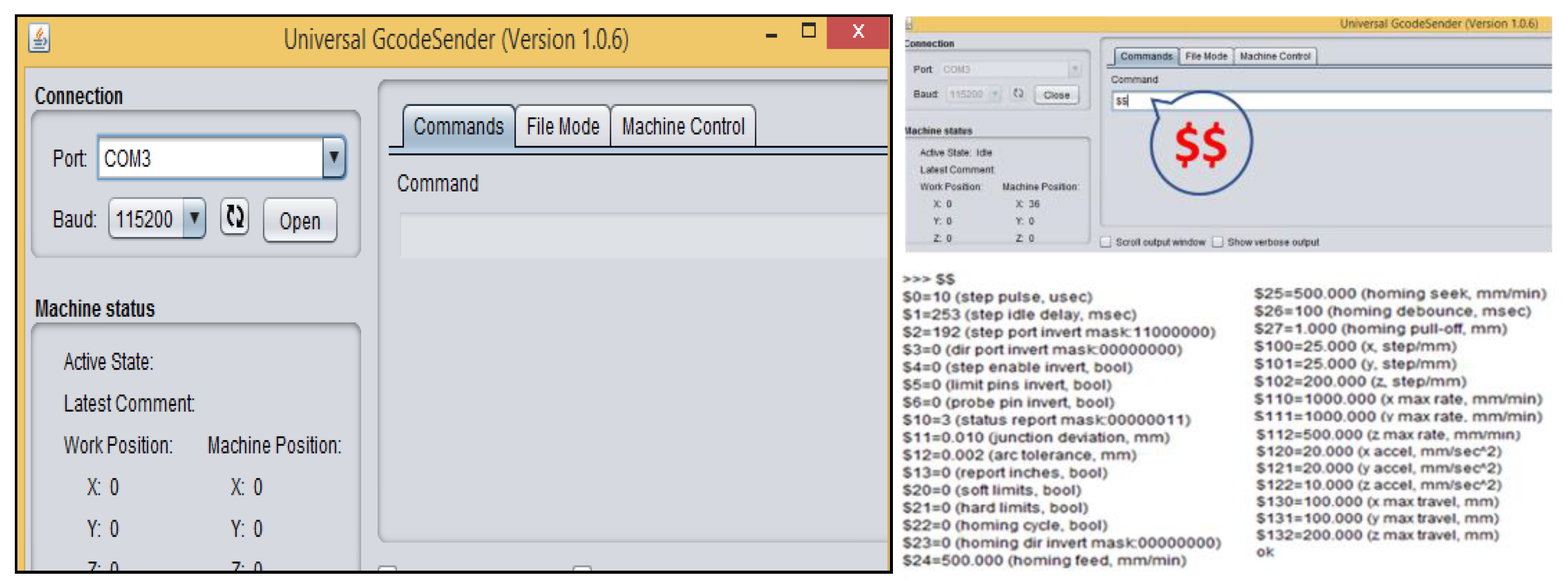
- Connect the Arduino UNO to the personal computer.
- Run XLoader.exe.
- In XLoader:
- Select the HEX file that contains the GRBL.
- Select the correct Arduino board.
- Select the COM port connected to the Arduino.
- Select the appropriate baud rate.
- Select Upload to send the HEX file to Arduino.
- 4.
- The indicator LEDs on the Arduino will start to blink and when finished XLoader will have been loaded on the Arduino UNO. Close the XLoader Window.
2.4. Hardware Configuration
2.5. Robust GPI Control
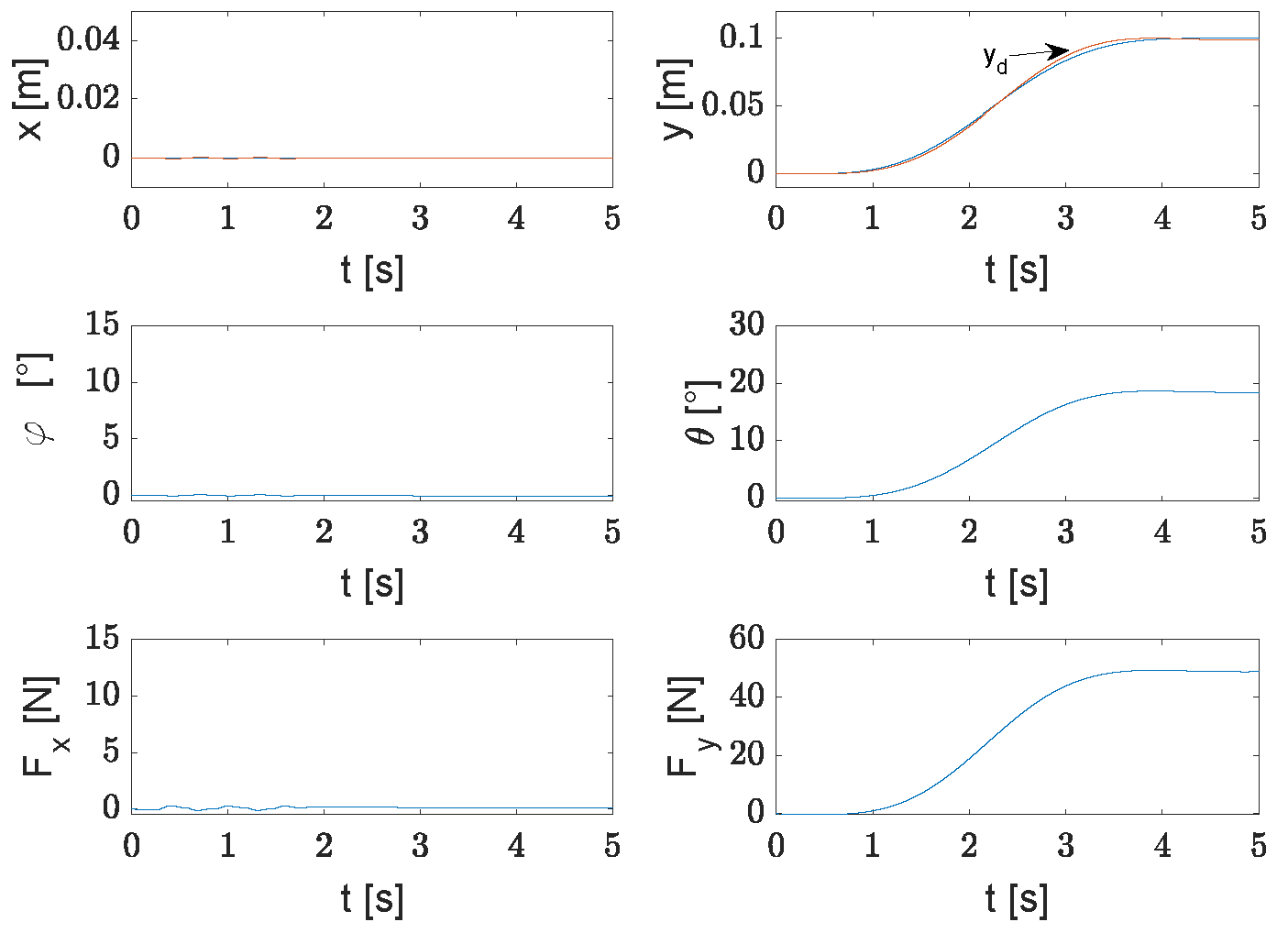
3. Results
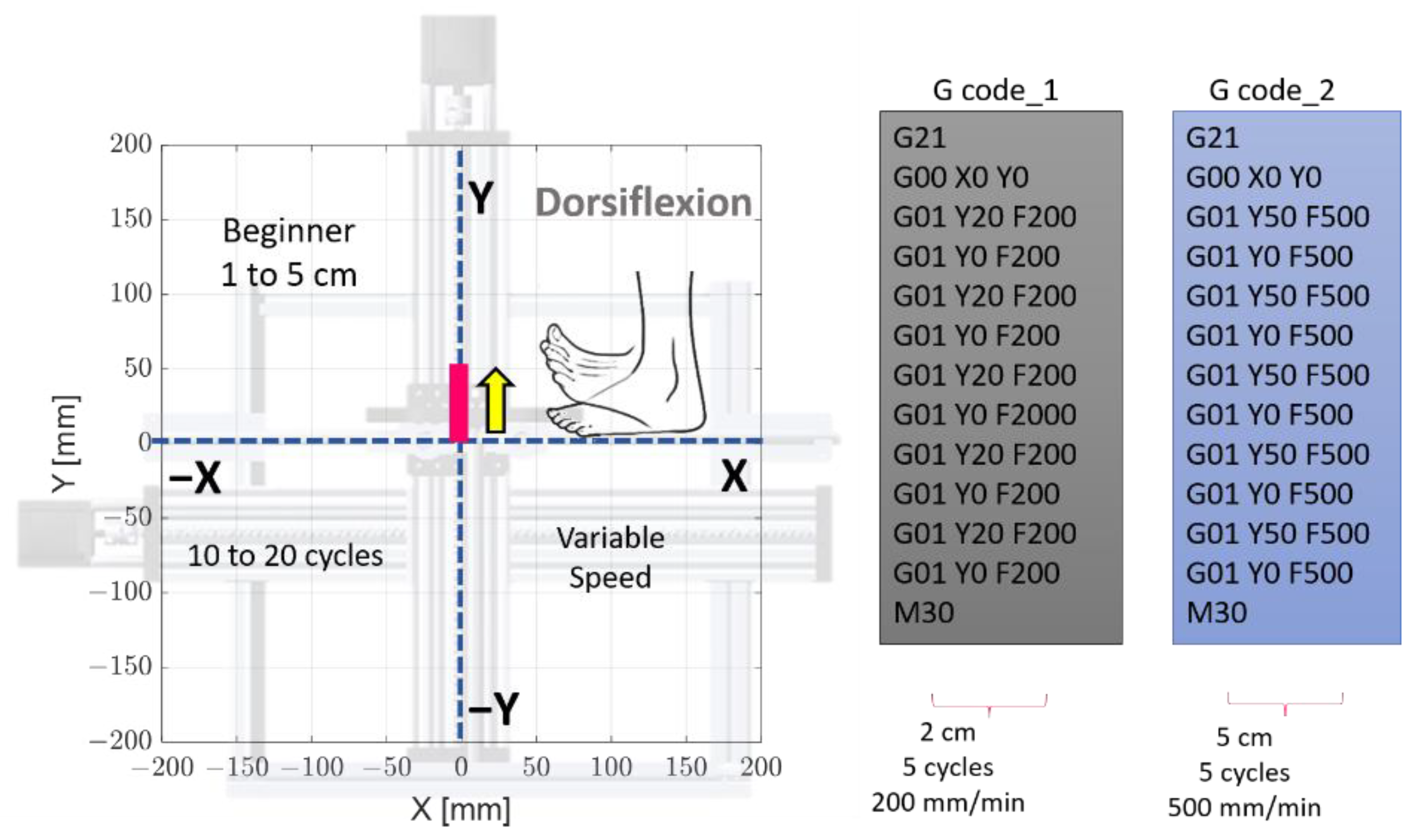
3.1. Rehabilitation Exercise Routine
3.2. Desired Reference Trajectory
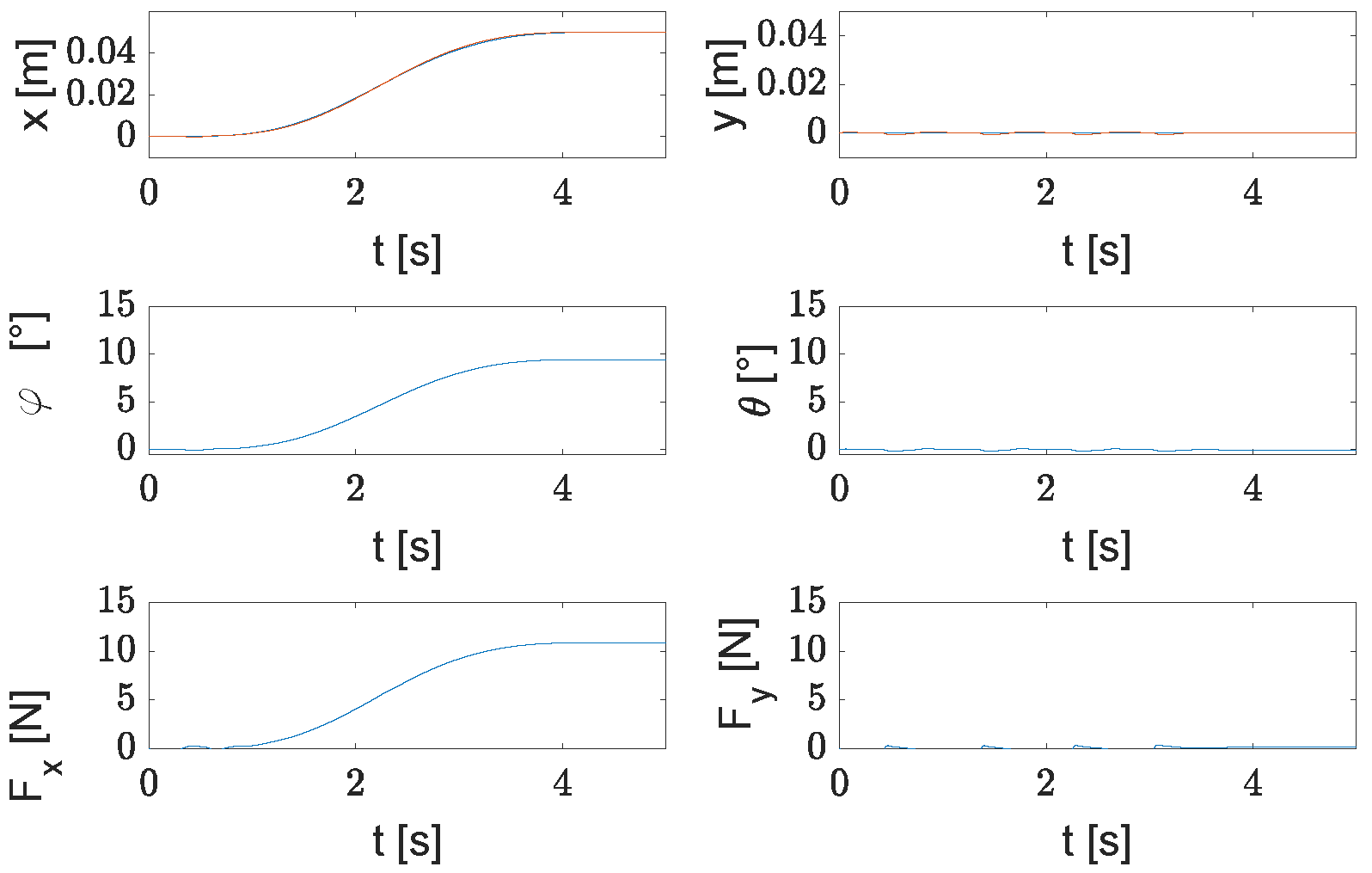
3.3. Robust Controller
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alvarez-Perez, M.G.; Garcia-Murillo, M.A.; Cervantes-Sánchez, J. Robot-assisted ankle rehabilitation: A review. Disabil. Rehabil. Assist. Technol. 2019, 15, 394–408. [Google Scholar] [CrossRef] [PubMed]
- Chee Chin, L.C.; Basah, S.N.; Affandi, M.; Shah, M.N.; Yaacob, S.; Ewe Juan, Y.; Din, M.Y. Home-based Ankle Rehabilitation System: Literature Review and Evaluation. J. Teknol. 2017, 79, 6. [Google Scholar] [CrossRef][Green Version]
- Demofonti, A.; Carpino, G.; Zollo, L.; Johnson, M.J. Affordable Robotics for Upper Limb Stroke Rehabilitation in Developing Countries: A Systematic Review. IEEE Trans. Med Robot. Bionics 2021, 3, 11–20. [Google Scholar] [CrossRef]
- Qassim, H.M.; Hasan, W.Z.W. A Review on Upper Limb Rehabilitation Robots. Appl. Sci. 2020, 10, 6976. [Google Scholar] [CrossRef]
- Alcocer, W.; Vela, L.; Blanco, A.; Gonzalez, J.; Oliver, M. Major Trends in the Development of Ankle Rehabilitation Devices. Dyna 2012, 79, 45–55. [Google Scholar]
- Hogan, N.; Krebs, H.I.; Charnnarong, J.; Srikrishna, P.; Sharon, A. MIT-MANUS: A workstation for manual therapy and training. In Proceedings of the IEEE International Workshop on Robot and Human Communication, Tokyo, Japan, 1–3 September 1992; pp. 161–165. [Google Scholar]
- Dehez, B.; Sapin, J. ShouldeRO, An alignment-free two-DOF rehabilitation robot for the shoulder complex. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–8. [Google Scholar]
- Ball, S.J.; Brown, I.E.; Scott, S.H. MEDARM: A rehabilitation robot with 5DOF at the shoulder complex. In Proceedings of the 2007 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Zurich, Switzerland, 4–7 September 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, S.-H.; Lien, W.-M.; Wang, W.-W.; Lee, G.-D.; Hsu, L.-C.; Lee, K.-W.; Lin, S.-Y.; Lin, C.-H.; Fu, L.-C.; Lai, J.-S.; et al. Assistive Control System for Upper Limb Rehabilitation Robot. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 1199–1209. [Google Scholar] [CrossRef] [PubMed]
- Zeiaee, A.; Soltani-Zarrin, R.; Langari, R.; Tafreshi, R. Design and kinematic analysis of a novel upper limb exoskeleton for rehabilitation of stroke patients. In Proceedings of the International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 759–764. [Google Scholar] [CrossRef]
- Niyetkaliyev, A.S.; Hussain, S.; Ghayesh, M.H.; Alici, G. Review on Design and Control Aspects of Robotic Shoulder Rehabilitation Orthoses. IEEE Trans. Hum. Mach. Syst. 2017, 47, 1134–1145. [Google Scholar] [CrossRef]
- Cornejo, J.; Huamanchahua, D.; Huaman-Vizconde, S.; Terrazas-Rodas, D.; Sierra-Huertas, J.; Janampa-Espinoza, A.; Gonzales, J.; Cardona, M. Mechatronic Exoskeleton Systems for Supporting the Biomechanics of Shoulder-Elbow-Wrist: An Innovative Review. In Proceedings of the 2021 IEEE International IOT, Electronics and Mechatronics Conference (IEMTRONICS), Toronto, ON, Canada, 21–24 April 2021; pp. 1–9. [Google Scholar] [CrossRef]
- Gull, M.A.; Bai, S.; Bak, T. A Review on Design of Upper Limb Exoskeletons. Robotics 2020, 9, 16. [Google Scholar] [CrossRef]
- Islam, R.; Spiewak, C.; Rahman, M.H.; Fareh, R. A Brief Review on Robotic Exoskeletons for Upper Extremity Rehabilitation to Find the Gap between Research Porotype and Commercial Type. Adv. Robot. Autom. 2017, 6, 177. [Google Scholar] [CrossRef]
- Hood-Daniel, P.; Floyd-Kelly, J. Build Your Own CNC Machine; Apress: Pune, India, 2009. [Google Scholar]
- Suk-hwan, S.; Seong-kyoon, K.; Dae-hyuk, C.; Stroud, I. Theory and Design of CNC Systems; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Guzmán-Valdivia, C.H.; Madrigal-López, O.; Désiga-Orenday, O.; Talavera-Otero, J.; Brizuela-Mendoza, J.A.; Chávez-Olivares, C.A.; Cruz-Domínguez, O.; Blanco-Ortega, A.; Berumen-Torres, J.A.; Gómez-Becerra, F.A. Design, Development and Control of a Therapeutic Robot Incorporating Aquatic Therapy for Ankle Rehabilitation. Machines 2021, 9, 254. [Google Scholar] [CrossRef]
- Zeng, D.; Wu, H.; Zhao, X.; Lu, W.; Luo, X. A New Type of Ankle-Foot Rehabilitation Robot Based on Muscle Motor Characteristics. IEEE Access 2020, 8, 215915–215927. [Google Scholar] [CrossRef]
- Li, J.; Fan, W.; Dong, M.; Rong, X. Research on control strategies for ankle rehabilitation using parallel mechanism. Cogn. Comput. Syst. 2020, 2, 105–111. [Google Scholar] [CrossRef]
- Abu-Dakka, F.J.; Valera, A.; Escalera, J.A.; Abderrahim, M.; Page, A.; Mata, V. Passive Exercise Adaptation for Ankle Rehabilitation Based on Learning Control Framework. Sensors 2020, 20, 6215. [Google Scholar] [CrossRef] [PubMed]
- Vallés, M.; Díaz-Rodríguez, M.; Valera, A.; Mata, V.; Page, A. Mechatronic Development and Dynamic Control of a 3-DOF Parallel Manipulator. Mech. Based Des. Struct. Mach. 2012, 40, 434–452. [Google Scholar] [CrossRef]
- Minh Duc, D.; Thuy Tram, L.T.; Dang Phuoc, P.; Xuan Tuy, T. Study on Ankle Rehabilitation Device Using Linear Motor. In Proceedings of the 2019 International Conference on System Science and Engineering (ICSSE), Dong Hoi, Vietnam, 20–21 July 2019; pp. 573–576. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Wang, T.; Li, H.; Du, W.; Meng, F.; Zhang, W. Research on an Ankle Joint Auxiliary Rehabilitation Robot with a Rigid-Flexible Hybrid Drive Based on a 2-S′′PS′′ Mechanism. Appl. Bionics Biomech. 2019, 2019, 7071064. [Google Scholar] [CrossRef]
- Zhang, M.; Cao, J.; Xie, S.Q.; Zhu, G.; Zeng, X.; Huang, X.; Xu, Q. A Preliminary Study on Robot-Assisted Ankle Rehabilitation for the Treatment of Drop Foot. J. Intell. Robot. Syst. 2017, 91, 207–215. [Google Scholar] [CrossRef]
- Alcocer-Rosado, W.; Vela-Valdés, L.; Blanco-Ortega, A.; Ruiz-Ascencio, J.; García-Beltrán, C.D. Passive Rehabilitation Exercises with an Ankle Rehabilitation Prototype Based in a Robot Parallel Structure. IEEE Lat. Am. Trans. 2017, 15, 48–56. [Google Scholar] [CrossRef]
- Rosado, W.M.A.; Ortega, A.B.; Valdes, L.G.V.; Ascencio, J.R.; Beltrán, C. Active Rehabilitation Exercises With a Parallel Structure Ankle Rehabilitation Prototype. IEEE Lat. Am. Trans. 2017, 15, 786–794. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Qin, J.; Wu, Z.; Duan, L.; Li, Z.; Cao, M.; Li, W.; Lu, Z.; Li, M.; et al. Development of an ankle rehabilitation robot for ankle training. In Proceedings of the Information and Automation, Lijiang, China, 8–10 August 2015; pp. 94–99. [Google Scholar] [CrossRef]
- Jamwal, P.K.; Xie, S.Q.; Hussain, S.; Parsons, J.G. An Adaptive Wearable Parallel Robot for the Treatment of Ankle Injuries. IEEE/ASME Trans. Mechatron. 2012, 19, 64–75. [Google Scholar] [CrossRef]
- Tsoi, Y.H.; Xie, S.Q.; Graham, A.E. Design, Modeling and Control of an Ankle Rehabilitation Robot. In Design and Control of Intelligent Robotic Systems; Liu, D., Wang, L., Tan, K.C., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2009; Volume 177. [Google Scholar] [CrossRef]
- Roy, A.; Krebs, H.I.; Bever, C.T.; Forrester, L.W.; Macko, R.F.; Hogan, N. Measurement of passive ankle stiffness in subjects with chronic hemiparesis using a novel ankle robot. J. Neurophysiol. 2011, 105, 2132–2149. [Google Scholar] [CrossRef]
- Blanco-Ortega, A.; Gómez-Becerra, F.A.; Vela-Valdés, L.G.; Delgado-Arcega, R.O. A Generalized Proportional Integral Controller for an Ankle Rehabilitation Machine Based on an XY Table. In Proceedings of the 2013 International Conference on Mechatronics, Electronics and Automotive Engineering, Morelos, Mexico, 19–22 November 2013; pp. 152–157. [Google Scholar] [CrossRef]
- Angulo Carrere, M.T.; Álvarez Méndez, A.; Fuentes Peñaranda, Y. Biomecánica clínica. Biomecánica de la Extremidad Superior. Exploración del Hombro. Reduca Enfermería Fisioter. Podol. 2011, 3, 104–123. [Google Scholar]
- Graham, S. CNC Machining Technology. Volume I. Design, Development and ClM Strategies; Springer-Verlag: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- GRBL CNC Controller. Popular Repositories. Available online: https://github.com/grbl/grbl (accessed on 28 April 2022).
- Sira-Ramírez, H.; Beltran-Carbajal, F.; Blanco-Ortega, A. A generalized proportional integral output feedback controller for the robust perturbation rejection in a mechanical system. e-STA 2008, 5, 24–32. [Google Scholar]
- Fliess, M.; Márquez, R.; Delaleau, E.; Sira-Ramírez, H. Correcteurs proportionnels-integraux Généralisés. ESAIM Control. Optim. Calc. Var. 2002, 7, 23–41. [Google Scholar] [CrossRef]
- Blanco-Ortega, A.; Vázquez-Sánchez, L.; Adam-Medina, M.; Colín-Ocampo, J.; Abúndez-Pliego, A.; Cortés-García, C.; García-Beltrán, C.D. A Robust Controller for Upper Limb Rehabilitation Exoskeleton. Appl. Sci. 2022, 12, 1178. [Google Scholar] [CrossRef]
- Magadán-Salazar, A.; Blanco-Ortega, A.; Gama-Velasco, A.K.; Abúndez-Pliego, A. Mechatronic Integral Ankle Rehabilitation System: Ankle Rehabilitation Robot, Serious Game, and Facial Expression Recognition System. In Advanced Topics on Computer Vision, Control and Robotics in Mechatronics; Vergara Villegas, O., Nandayapa, M., Soto, I., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 291–320. [Google Scholar]
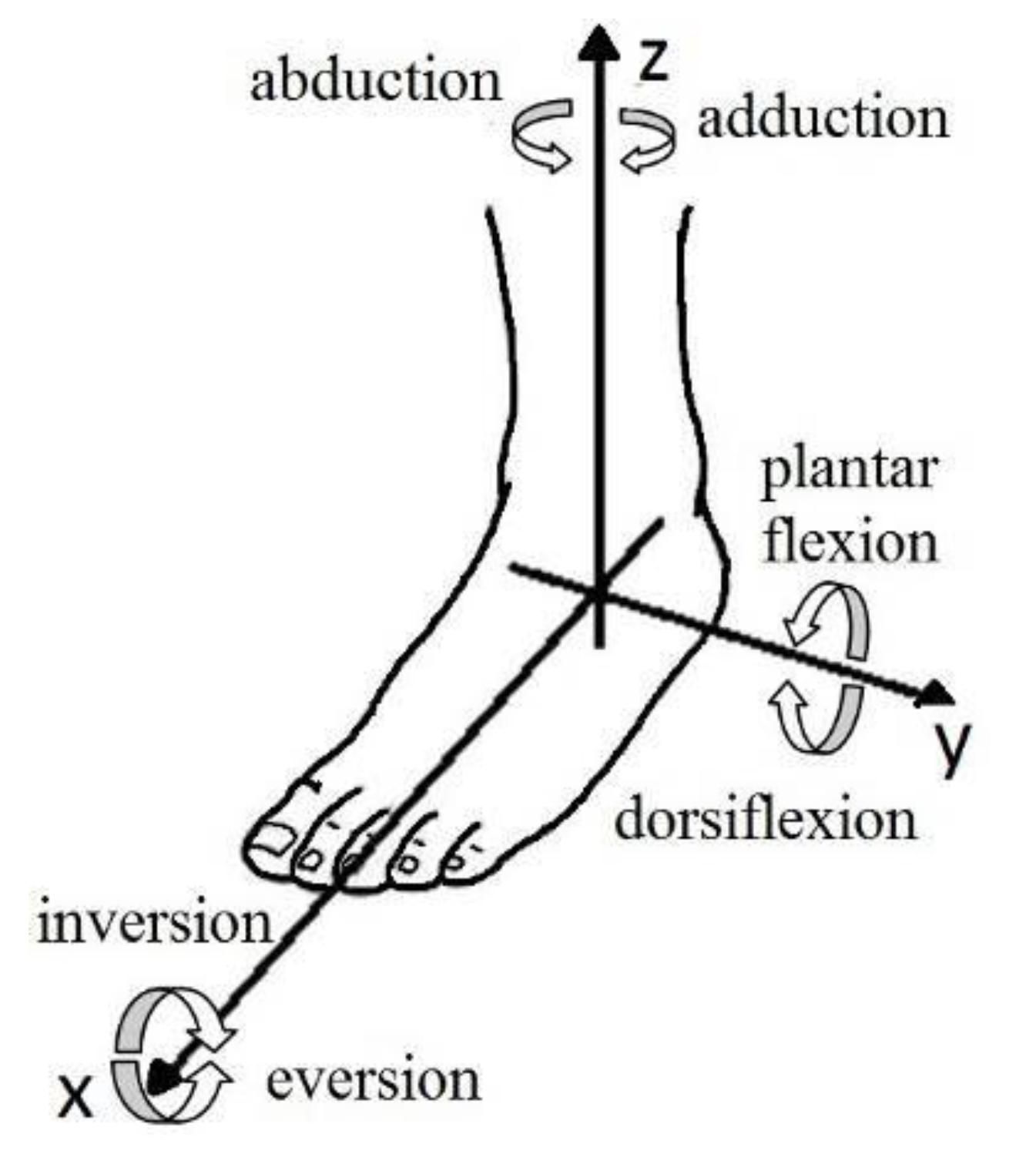

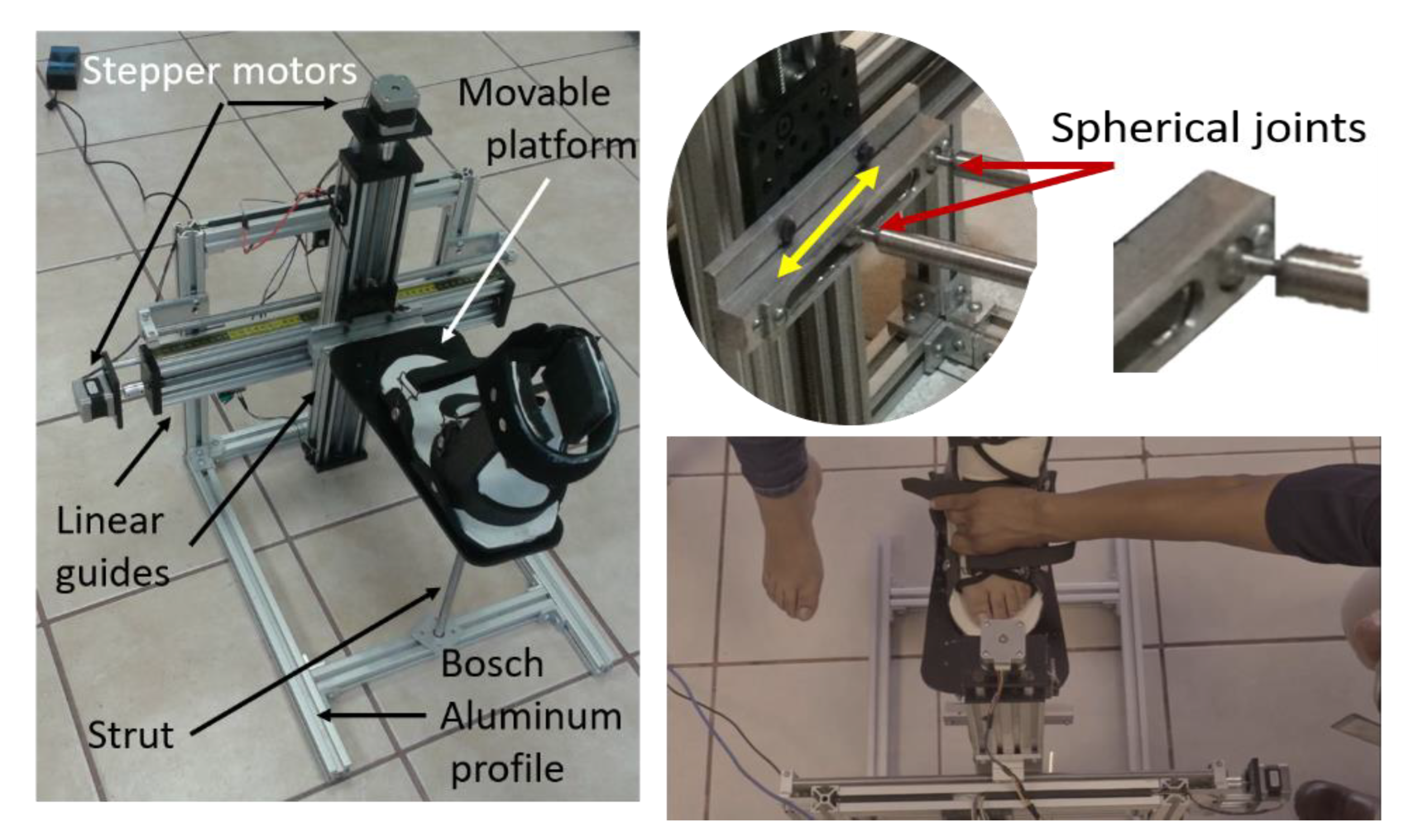


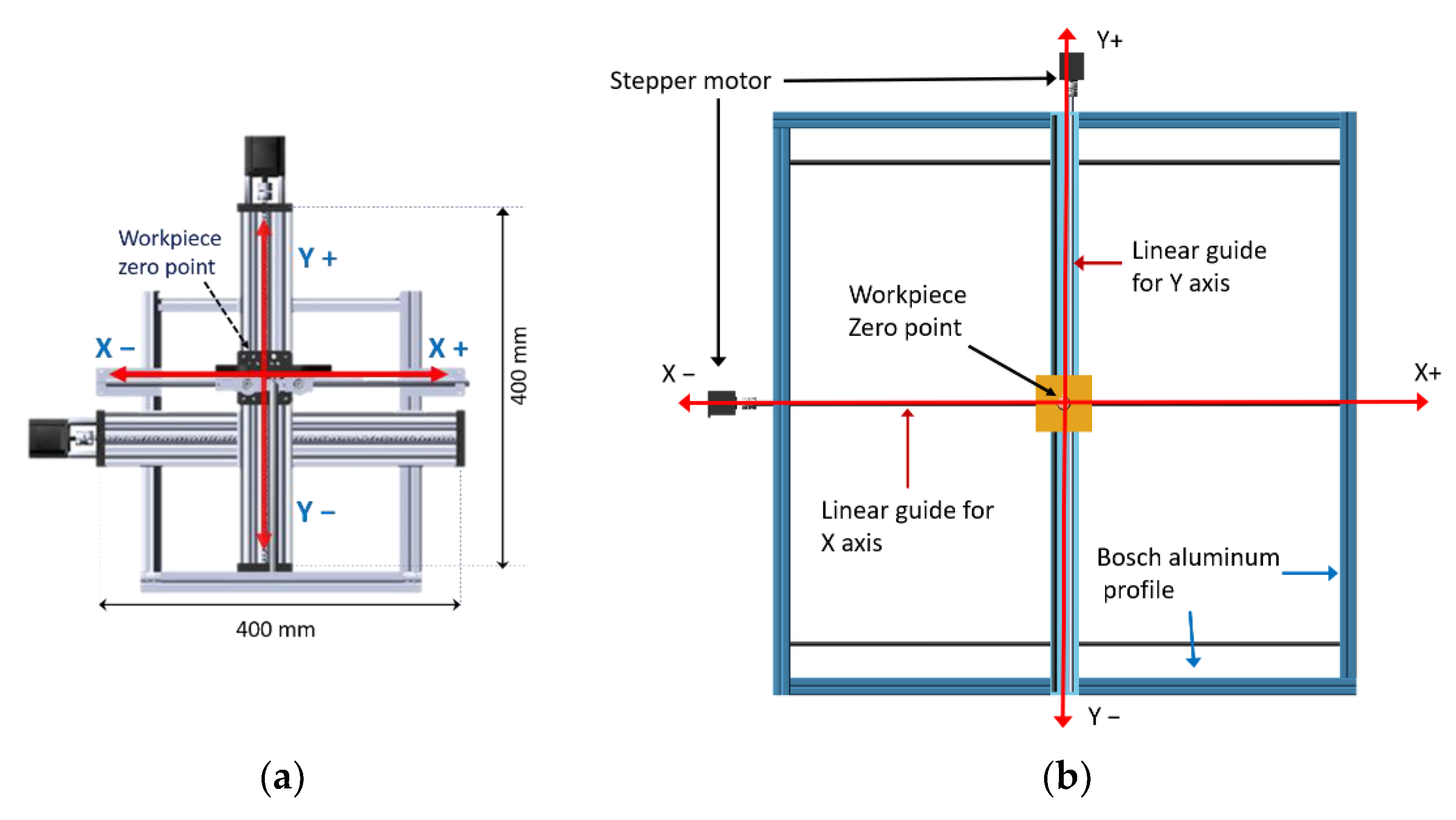









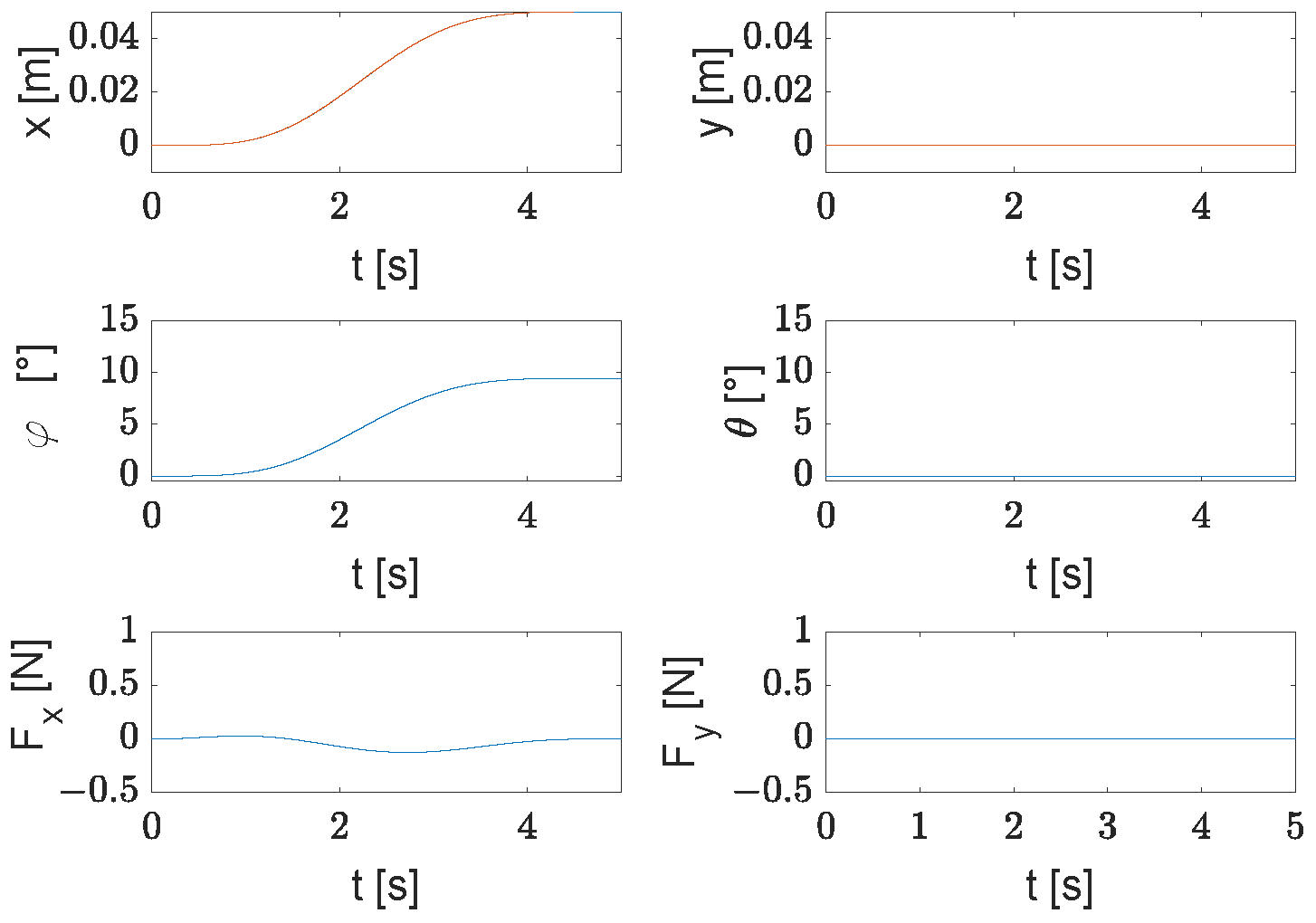

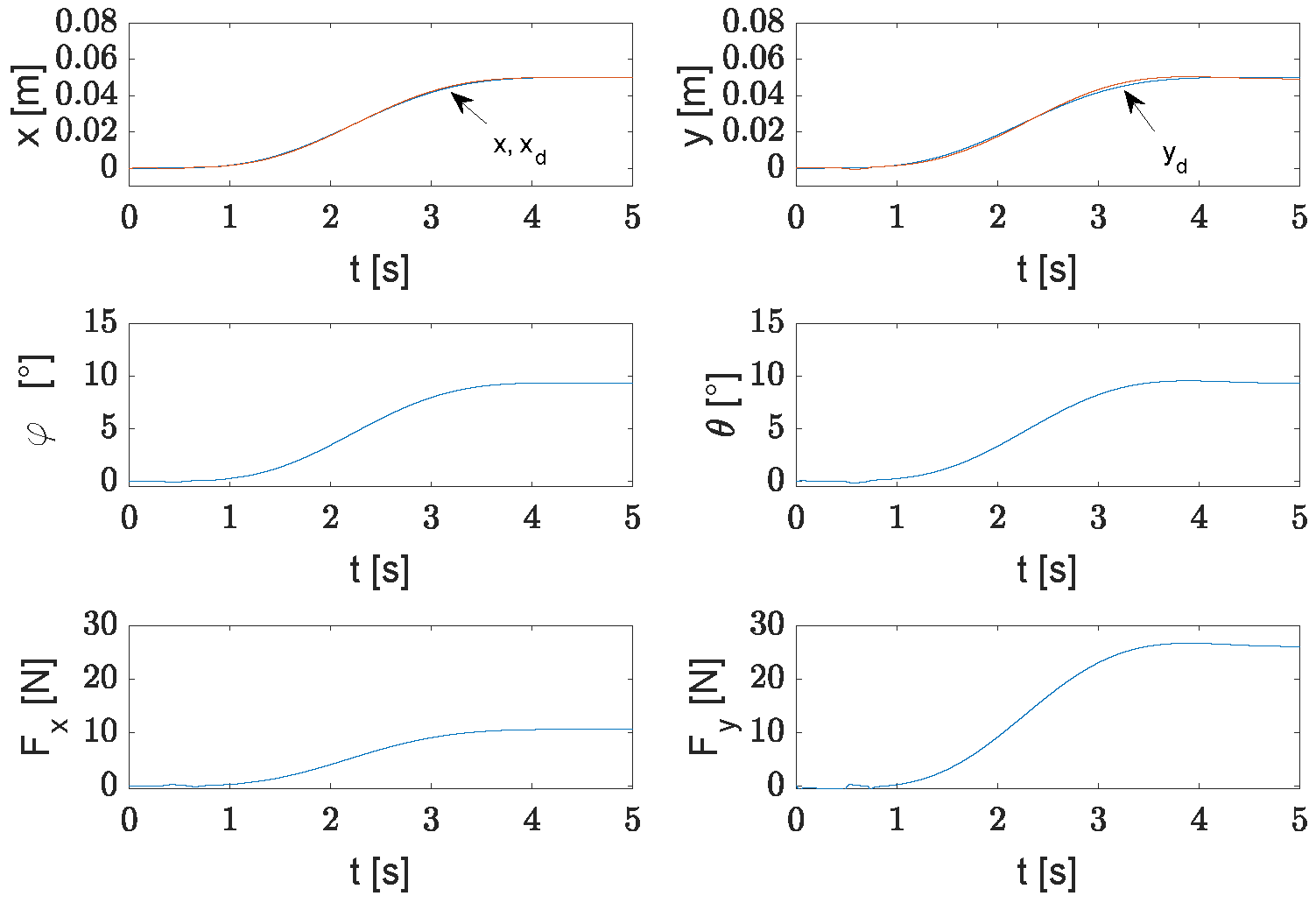
| Type of Motion | Max. Allowable Motion |
|---|---|
| Dorsiflexion | 20.3° a 29.8° |
| Plantarflexion | 37.6° a 45.8° |
| Inversion | 14.5° a 22.0° |
| Eversion | 10.0° a 17.0° |
| Abduction | 15.4° a 25.9° |
| Adduction | 22.0° a 36.0° |
| Type of Motion | Max. Allowable |
|---|---|
| Flexion | 180° |
| Extension | 50° |
| Adduction | 48° |
| Abduction | 134° |
| Internal rotation | 34° |
| External rotation | 142° |
| Circumduction | 360° |
| Code | Function | Code | Function |
|---|---|---|---|
| G00 | Positioning at rapid travel | G01 | Linear interpolation using a feed rate; |
| G02 | Circular interpolation clockwise | G03 | Circular interpolation, counterclockwise; |
| G17 | Select X-Y plane | G18 | Select Z-X plane; |
| G19 | Select Z-Y plane | G20 | Imperial units; |
| G21 | Metric units | G27 | Reference return check; |
| M00 | Automatic stop (CNC program end) | M02 | End of CNC program |
| M30 | End of tape (End of CNC program, with return to CNC program top) | ||
| R | It gives the radius of the arcs the machine makes | N | N gives the line number |
| P | To jump in time or a delayed time | ||
| X, Y, Z | These three values indicate the tools’ position in three dimensions—X and Y represent the horizontal and vertical dimensions, respectively, while Z represents the depth | F | To indicate how quickly the machine feeds the piece |
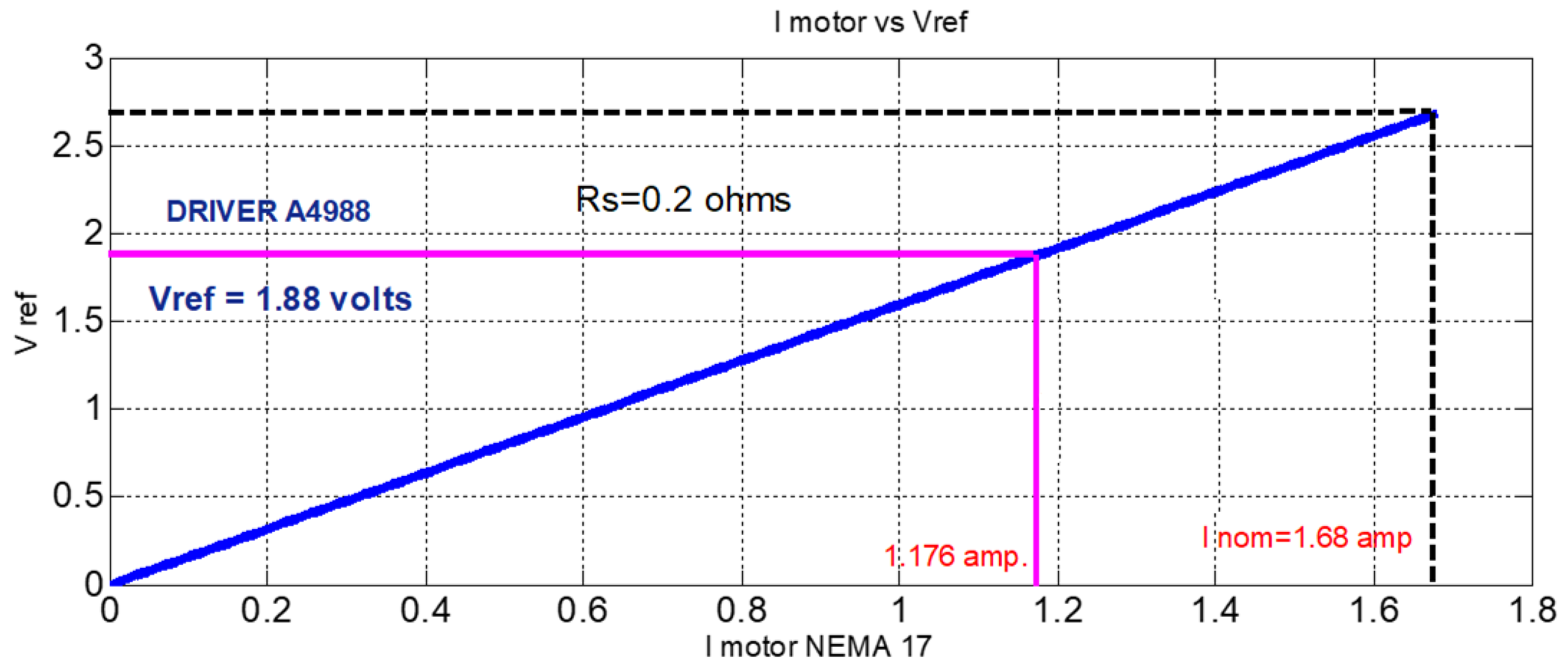
| Driver | |||
|---|---|---|---|
 | 0.1 Ω | 1.176 amp. | |
 | 0.2 Ω | 1.176 amp. |
| Dorsiflexion (DF) | Plantarflexion (PF) | Abduction (AB) | Adduction (AD) | ||||
|---|---|---|---|---|---|---|---|
| mm | Degrees | mm | Degrees | mm | Degrees | mm | Degrees |
| 10 | 2.2026 | −10 | −2.2026 | 10 | 2.2026 | −10 | −2.2026 |
| 20 | 4.3987 | −20 | −4.3987 | 20 | 4.3987 | −20 | −4.3987 |
| 30 | 6.5819 | −30 | −6.5819 | 30 | 6.5819 | −30 | −6.5819 |
| 40 | 8.7462 | −40 | −8.7462 | 40 | 8.7462 | −40 | −8.7462 |
| 50 | 10.886 | −50 | −10.886 | 50 | 10.886 | −50 | −10.886 |
| 60 | 12.995 | −60 | −12.995 | 60 | 12.995 | −60 | −12.995 |
| 70 | 15.068 | −70 | −15.068 | 70 | 15.068 | −70 | −15.068 |
| 80 | 17.103 | −80 | −17.103 | 80 | 17.103 | −80 | −17.103 |
| 90 | 19.093 | −90 | −19.093 | 90 | 19.093 | −90 | −19.093 |
| 100 | 21.038 | −100 | −21.038 | 100 | 21.038 | −100 | −21.038 |
| 110 | 22.932 | −110 | −22.932 | 110 | 22.932 | −110 | −22.932 |
| 120 | 24.775 | −120 | −24.775 | 120 | 24.775 | −120 | −24.775 |
| 130 | 26.565 | −130 | −26.565 | 130 | 26.565 | −130 | −26.565 |
| 140 | 28.301 | −140 | −28.301 | −140 | −28.301 | ||
| 150 | 29.982 | −150 | −29.982 | −150 | −29.982 | ||
| −160 | −31.608 | −160 | −31.608 | ||||
| −170 | −33.179 | −170 | −33.179 | ||||
| −180 | −34.695 | −180 | −34.695 | ||||
| −190 | −36.158 | −190 | −36.158 | ||||
| −200 | −37.569 | ||||||
| −210 | −38.928 | ||||||
| −220 | −40.236 | ||||||
| Letter | Trajectory | G Code |
|---|---|---|
 |  |  |
 | 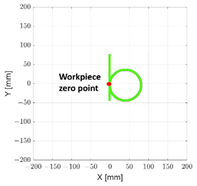 |  |
 | 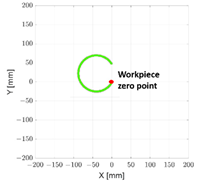 |  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blanco Ortega, A.; Magadán Salazar, A.; Guzmán Valdivia, C.H.; Gómez Becerra, F.A.; Palacios Gallegos, M.J.; García Velarde, M.A.; Santana Camilo, J.A. CNC Machines for Rehabilitation: Ankle and Shoulder. Machines 2022, 10, 1055. https://doi.org/10.3390/machines10111055
Blanco Ortega A, Magadán Salazar A, Guzmán Valdivia CH, Gómez Becerra FA, Palacios Gallegos MJ, García Velarde MA, Santana Camilo JA. CNC Machines for Rehabilitation: Ankle and Shoulder. Machines. 2022; 10(11):1055. https://doi.org/10.3390/machines10111055
Chicago/Turabian StyleBlanco Ortega, Andrés, Andrea Magadán Salazar, César. H. Guzmán Valdivia, Fabio Abel Gómez Becerra, Manuel J. Palacios Gallegos, Miguel A. García Velarde, and José Alfonso Santana Camilo. 2022. "CNC Machines for Rehabilitation: Ankle and Shoulder" Machines 10, no. 11: 1055. https://doi.org/10.3390/machines10111055
APA StyleBlanco Ortega, A., Magadán Salazar, A., Guzmán Valdivia, C. H., Gómez Becerra, F. A., Palacios Gallegos, M. J., García Velarde, M. A., & Santana Camilo, J. A. (2022). CNC Machines for Rehabilitation: Ankle and Shoulder. Machines, 10(11), 1055. https://doi.org/10.3390/machines10111055







