Abstract
The cosmic censorship hypothesis is regarded as one of the most important unsolved problems in classical general relativity; viz., will generic gravitational collapse of a star after it has exhausted its nuclear fuel lead to black holes only, under reasonable physical conditions. We discuss the collapse of a fluid with nonzero radial pressure within the context of the Vaidya spacetime considering a decaying cosmological parameter as well as nonzero charge. Previously, a similar analysis was done, but without considering charge. A decaying cosmological parameter may also be associated with dark energy. We found that both black holes and naked singularities can form, depending upon the initial conditions. Hence, charge does not restore the validity of the hypothesis. This provides another example of the violation of the cosmic censorship hypothesis. We also discuss some radiating rotating solutions, arriving at the same conclusion.
1. Introduction
The cosmic censorship hypothesis (CCH) [1] is regarded as one of the most important unsolved problems in classical general relativity theory. If we look at a typical star and ask what happens after it has exhausted its nuclear fuel, there are three possibilities, depending upon the mass of the star. The first two possibilities are, in order of increasing starting mass, a white dwarf or a neutron star. However, if the star is massive enough (typically in the order of about 10 solar masses or so, depending upon whether it rotates or not), after it has exhausted its nuclear fuel, there is nothing to halt the collapse process.
According to the Hawking–Penrose singularity theorems [2], it will end up in a singularity. However, these theorems do not provide information about the nature of this singularity itself. The cosmic censorship hypothesis says that the singularity will be a black hole, covered by an event horizon. Despite much investigation, as of yet, there is no proof of the hypothesis. However, there is another possibility, and that is that naked singularities can form, which can in principle, be observed by a distant observer. Nowadays, there are numerous examples in which the hypothesis is violated, although there is still no agreement as to whether these are physically realistic or not ([3,4] and references therein). One of the first examples thought to exhibit a naked singularity is the Vaidya solution [5], which represents a spherically symmetric body consisting of null dust that is radiating (or collapsing). The metric is given by
where v is the advanced ingoing time coordinate, r is the usual radial coordinate and represents the metric of the unit two-sphere. Dwivedi and Joshi [6] have given good treatment to the occurrence of the naked singularity for this spacetime.
One of the criticisms that has been levelled against the Vaidya metric is that it consists of null dust, which has no pressure. In a realistic gravitational collapse scenario, we expect there to be pressure. The question that arises is whether the introduction of pressure can help to avoid the naked singularity and hence restore the validity of the cosmic censorship hypothesis. Recently, an interesting generalization of the Vaidya spacetime has been given [7] which incorporates nonzero radial pressure:
where is the cosmological parameter—the considered variable—which represents the nonzero radial pressure. Some of the properties of this spacetime were studied in [7].
There are nowadays many reasons for considering a nonzero cosmological constant. With the recent discovery [8,9] of the accelerated expansion of the universe, the cosmological constant has made a massive comeback in the currently accepted ΛCDM concordance model of cosmology. Wagh and Maharaj [10] studied gravitational collapse in the Vaidya spacetime with a cosmological constant, and they found that the introduction of the cosmological constant did not make any difference to the situation. Apart from this, there are now strong reasons to consider a decaying cosmological parameter, since this can solve the cosmological constant problem, and it is claimed that this can give a better fit to cosmological observations than the usual concordance model [11,12]. We studied the collapse of this spacetime and found that naked singularities or black holes could form, depending upon the initial conditions [13].
In this work, the gravitational collapse of the Vaidya model is studied with a variable cosmological parameter and nonzero charge, to see whether the hypothesis is still violated. Of course, one can ask the obvious question as to whether charged stars exist in nature, since we expect stars to be electrically neutral. This question goes back to about a century ago [14], and Neslusan [15] has provided a nice treatment of the history of charged Newtonian stars in equilibrium. Essentially, the charge in stars arises from the fact that lighter electrons tend to move to the surface of a star, in contrast to the heavier ions. Some electrons escape from the surface, giving the nearby interstellar gas or accretion disc a net negative charge. What is left behind is a net positive charge of approximately 100 C per solar mass for such a star in equilibrium. However, in cases of compact stars or collapsing stars, as in the situation envisaged in this work, general relativity is required, and the very large gravitational force can allow the star to carry huge amounts of charge [16].
Hence, it is worthwhile to study the effect of charge on collapse. We find that the introduction of charge cannot restore the validity of the hypothesis. Again, in a physically realistic star, we expect rotation, and we investigate some rotating stars to see whether charge can affect the outcome of the collapse.
2. Nonzero Charge in Vaidya
To incorporate charge into the metric (2), we include an additional term as follows:
where Q is the charge. The nonzero components of the Einstein tensor for the metric (3) are
Here, an overdot represents a derivative with respect to v.
Let us now look at the energy momentum tensor for the problem under discussion. For the metric (3), the complex null vectors may be taken as follows:
where . Here and are real null vectors, and is complex. They satisfy the usual normalization conditions , with the other products of the null vectors being zero. From Einstein’s field equations , we find that the energy momentum tensor describing the matter content for the spacetime (3) is given by
where the coefficients , p and are the density, pressure and null density, respectively. These quantities are given by:
The component represents the matter field that moves along the null hypersurfaces , whereas represents the matter moving along the time-like trajectories. When , we get back the original Vaidya solution ([5]).
We now let be the tangent vector to a null geodesic, where k is an affine parameter. Now radial null geodesics satisfy the equation
Using this null condition, the goedesic equations take the form
For the singularity to be naked, there must be a light ray that emerges from the singularity. We will investigate the behavior of the radial null geodesics near the singularity to determine whether outgoing geodesics meet the singularity in the past. Then, from Equations (3) and (10), we get
We now make some reasonable assumptions for the mass, cosmological and charge parameters in Equation (13). For the mass function, we choose the form used in [6]:
The reason for the choice of a linear function for m is that a strongly curved singularity only occurs with a function that is linear [17]. For the cosmological parameter, we take the form which we used earlier [13]:
This choice is motivated by cosmological considerations in which it has been shown that the form (15) fits observations well with [18], which we will adopt. Finally, for the charge function, we adopt the form [19]
Lake and Zannias [19] have pointed out that the choices (14) and (16) allow the geodesic Equation (13) (without charge) to be homogeneous and thus to be solvable in terms of elementary functions. Further, this simplification has an invariant geometrical meaning related to the occurrence of a singularity with strong curvature.
To check whether there is a singularity as , we calculate the Kretchmann scalar:
and note that it diverges as , indicating a singularity. We now let be the tangent to a possible ougoing geodesic. In order to determine the nature of the limiting value of X at on a singular geodesic, we let
If Equation (19) exhibits at least one positive root, then this will indicate that there is at least one outgoing geodesic which terminates at the singularity in the past; i.e., a naked singularity. The absence of positive roots indicates that the singularity is a black hole. Thus the occurrence of positive roots implies that the strong CCH is violated, though not necessarily the weak CCH. It can easily be verified that Equation (19) has positive roots depending upon the parameters. We indicate a few positive roots for some values of the parameters in the Table 1 below.

Table 1.
Positive roots for some values of parameters.
In the Figure 1 below, we plot in 3-dimensions the allowable values of and , keeping fixed at 2.5. There do not appear to be any constraints on these parameters from observations as yet.
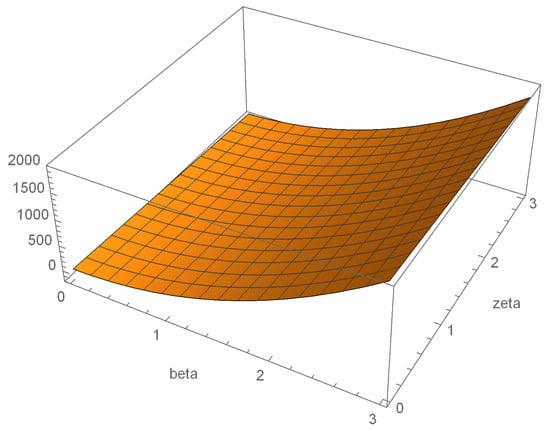
Figure 1.
Plot of beta against zeta.
3. Radiating Rotating Stars
Since the Vaidya metric does not describe a rotating star, it may be regarded as not very physical. So let us now look at the effect of rotation. The original Kerr solution is [20]:
Event horizons occur at [21]:
It can readily be seen from this equation that no event horizons occur when , corresponding to naked singularities. However, in this situation, the mass m is constant, and there is no charge or variable cosmological parameter. Let us now look at some radiating rotating stars taking into account, firstly, constant mass, charge and cosmological parameters. The Kerr–Newman–de Sitter metric [22] is:
where:
and . The equations for the event horizons are given in [23]. Due to the complicated expressions for the horizons, we do not repeat them here, but note that one of the conditions for event horizons to occur is that:
Hence, naked singularities will occur when
Let us now look at the situation with varable mass, charge and cosmological parameters (using the functional forms we used previously) considering the same rotating metric (22). We end up with the same condition as in (28). Noting Equation (15), and taking the , we find that the inequality (28) is satisfied, meaning a naked singularity. In any event, one can always find reasonable forms for the cosmological parameter for which we get naked singularities. Hence, the situation with rotation is actually worse than the initial Vaidya example that we analysed earlier, in the sense that a naked singularity appears to be favoured.
4. Discussion
Mkenyeleye et al. [24] have also analysed a generalised Vaidya spacetime and found that both black holes and naked singularities can form, depending upon the initial conditions. Their discussion was fairly general, whereas ours is more specific, showing clearly the effects of charge and the cosmological parameter. Brassel et al. [25] have studied the effects of different equations of state within a similar context, and arrived at the same conclusion.
Our metric (2) includes the following cases:
- Vaidya collapse with nonzero pressure when [13];
- Vaidya–de Sitter when , [10];
- Charged Vaidya–de Sitter collapse when [26];
- Vaidya collapse when and [5];
- Schwarschild–de Sitter when [27];
- The de Sitter when [28].
Thus, our work may be regarded as a generalization of the above works.
Is it possible in some way to detect naked singularities, if they really do physically exist? The detection of the shadow by the event horizon telescope team [29] is compatible with a Kerr black hole, but it is also compatible with a naked singularity [30], and future observations will be required to distinguish between the two. Apart from this, various other ways have been proposed to detect naked singularities, if they do exist. Chakraborty et al. [31] have proposed using the spin precession of a test gyroscope due to frame dragging; Shahidi et al. [32] suggested using the properties of thin accretion discs around these exotic objects; and Bhattacharya [33] suggested lensing. However, it seems that it will be some time before we can observationally distinguish between a black hole and a naked singularity.
5. Conclusions
In this work we first investigated the collapse of modified Vaidya spacetime with nonzero pressure (represented by a variable cosmological parameter) as well as charge. We found that the introduction of charge was not sufficient to halt the occurrence of naked singularities in the Vaidya spacetime with nonzero pressure. This provides yet another example of the violation of the CCH. This work bears similarity to the methods used in [34] in which the thermodynamic aspects of gravity were discussed, albeit with a completely different approach. We hope to investigate this comparison further in future. Secondly, we also looked at some rotating solutions, and found that naked singularities still occur.
Funding
This research received no external funding.
Acknowledgments
The author would like to thank the referees for constructive comments which led to a marked improvement in the article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Penrose, R. Gravitational collapse: The role of general relativity. Riv. Nuovo Cim. 1965, 1, 252–276. [Google Scholar]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Spacetime; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Hamid, A.I.M.; Goswami, R.; Maharaj, S.D. Cosmic censorship conjecture revisited: Covariantly. Class. Quantum Gravity 2014, 31, 135010. [Google Scholar] [CrossRef]
- Hamid, A.I.M.; Goswami, R.; Maharaj, S.D. Notes on cosmic censorship conjecture revisited: Covariantly. arXiv 2016, arXiv:1604.01157v1. [Google Scholar]
- Vaidya, P.C. The external field of a radiating star in general relativity. Curr. Sci. 1943, 12, 183. [Google Scholar] [CrossRef]
- Dwivedi, I.H.; Joshi, P.S. On the nature of naked singularities in Vaidya spacetimes. Class. Quantum Gravity 1989, 6, 1599–1606. [Google Scholar] [CrossRef]
- Ishwarchandra, N.; Singh, K.Y. Vaidya Solution in Non-Stationary de Sitter Background: Hawking’s Temperature. Int. J. Astron. Astrophys. 2013, 3, 494–499. [Google Scholar] [CrossRef][Green Version]
- Reiss, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.B.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Della Valle, M.; Deustua, S.; Ellis, R.S.; Fabbro, S.; Fruchter, A.; Goldhaber, G.; Groom, D.E.; Hook, I.M.; et al. Discovery of a supernova explosion at half the age of the Universe. Nature 1998, 391, 51–54. [Google Scholar] [CrossRef]
- Wagh, S.M.; Maharaj, S.D. Naked Singularity of the Vaidya-deSitter Spacetime and Cosmic Censorship Conjecture. Gen. Relat. Gravit. 1999, 31, 975–979. [Google Scholar] [CrossRef]
- Sola, J. Towards the first compelling signs of vacuum dynamics in modern cosmological observations. Mon. Not. R. Astron. Soc. 2018, 478, 435–437. [Google Scholar]
- Basilakos, S.; Mavromatos, N.E.; Peracaula, J.S. Scalar field theory description of the running vacuum model: The vacuumon. J. Cosm. Astron. Phys. 2019, 12, 025. [Google Scholar] [CrossRef]
- Beesham, A.; Ghosh, S.G. Vaidya collapse with nonzero radial pressure. J. Phys. Conf. Ser. 2018, 1051, 012005. [Google Scholar] [CrossRef]
- Pannekoek, A. Ionization in stellar atmospheres. Bull. Astr. Inst. Neth. 1922, 1, 107. [Google Scholar]
- Neslusan, L. On the global electrostatic charge of stars. Astron. Astrophys. 2001, 372, 913. [Google Scholar] [CrossRef]
- Ray, S.; Espindola, A.L.; Malheiro, M.; Lemos, J.P.S.; Yanchin, V.T. Electrically charged compact stars and formation of charged black holes. Phys. Rev. D 2003, 68, 084004. [Google Scholar] [CrossRef]
- Rajagopal, K.; Lake, K. Strengths of singularities in Vaidya spacetimes. Phys. Rev. D 1987, 35, 1531–1532. [Google Scholar] [CrossRef]
- Szydlowski, M.; Stachowski, A.; Urbanowski, K. The evolution of the FRW universe with decaying metastable darkenergy—A dynamical system analysis. arXiv 2002, arXiv:1812.00616. [Google Scholar]
- Lake, K.; Zannias, T. Structure of singularities in the spherical gravitational collapse of a charged null fluid. Phys. Rev. D 1991, 43, 1798–1802. [Google Scholar] [CrossRef]
- Kerr, R. Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 1963, 11, 237–238. [Google Scholar] [CrossRef]
- Visser, M. The Kerr spacetime: A brief introduction. arXiv 2007, arXiv:0706.0622. [Google Scholar]
- Xu, D.-Y. Radiating charged rotating metric in de Sitter space in retarded time coordinates and the energy–momentum tensor. Class. Quantum Gravity 1998, 15, 153–165. [Google Scholar] [CrossRef]
- Xu, D.-Y. Timelike limit surfaces, apparent horizons and event horizons of radiating Kerr–Newman–de Sitter black holes, inflation and cosmic censorship. Class. Quantum Gravity 1999, 16, 343–350. [Google Scholar] [CrossRef]
- Mkenyeleye, M.D.; Goswami, R.; Maharaj, S.D. Gravitational collapse of generalized Vaidya spacetime. Phys. Rev. D 2014, 90, 064034. [Google Scholar] [CrossRef]
- Brassel, B.P.; Goswami, R.; Maharaj, S.D. Collapsing radiating stars with various equations of state. Phys. Rev. D 2017, 95, 124051. [Google Scholar] [CrossRef]
- Beesham, A.; Ghosh, S.G. Naked singularities in the charged Vaidya-deSitter spacetime. Int. J. Mod. Phys. D 2003, 12, 801–809. [Google Scholar] [CrossRef]
- Tangherlini, F.R. Schwarzschild Field in n Dimensions and the Dimensionality of Space Problem. Nuovo Cimento 1963, 27, 636–651. [Google Scholar] [CrossRef]
- De Sitter, W. On Einstein’s Theory of Gravitation and its Astronomical Consequences. Mon. Not. R. Astron. Soc. 1917, 78, 3–28. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Balokovic, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar]
- Dey, D.; Joshi, P.S.; Joshi, A.; Bambhaniya, P. Towards an observational test of black hole versus naked singularity at the galactic center. Int. J. Mod. Phys. D 2019, 29, 1930024. [Google Scholar] [CrossRef]
- Chakraborty, C.; Kocherlakota, P.; Joshi, P.S. Spin precession in a black hole and naked singularity spacetimes. Phys. Rev. D 2017, 95, 04406. [Google Scholar] [CrossRef]
- Shahidi, S.; Harko, T.; Kovacs, Z. Distinguishing Brans–Dicke–Kerr type naked singularities and black holes with their thin disk electromagnetic radiation properties. Eur. Phys. J. C 2020, 80, 162. [Google Scholar] [CrossRef]
- Bhattacharya, K.; Dey, D.; Mazumdar, A.; Sarkar, T. New class of naked singularities and their observational signatures. Phys. Rev. D 2020, 101, 043005. [Google Scholar] [CrossRef]
- Padmanabhan, T. Thermodynamical aspects of gravity: New insights. Rep. Prog. Phys. 2010, 73, 046901. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).