Abstract
We compute the quasinormal frequencies for scalar perturbations of charged black holes in five-dimensional Einstein-power-Maxwell theory. The impact on the spectrum of the electric charge of the black holes, of the angular degree, of the overtone number, and of the mass of the test scalar field is investigated in detail. The quasinormal spectra in the eikonal limit are computed as well for several different space-time dimensionalities.
1. Introduction
In all metric theories of gravity black holes (BHs) generically are predicted to exist. Despite their simplicity are without a doubt fascinating objects both for classical and quantum gravity. Although they are characterized by a handful of parameters, such as mass, spin, and charges (even if one includes BHs with a scalar hair [1]), black holes link together several research areas, from gravitation and statistical physics to quantum mechanics and Astrophysics. By now their existence has been established in a two-fold way, namely first by the numerous direct detections of gravitational waves from black hole mergers [2,3,4,5,6], and then thanks to the first image of the supermassive black hole [7,8,9,10,11,12] located at the centre of the giant elliptical galaxy Messier 87 by the Event Horizon Telescope project [13] precisely one year ago.
Isolated black holes are in fact ideal objects. It turns out that realistic black holes in Nature are never isolated. Instead, they are constantly affected by their environment. Upon external perturbations black holes respond by emitting gravitational waves. Quasinormal modes (QNMs) are characteristic frequencies that depend on the details of the geometry and on the type of the perturbation (scalar, Dirac, vector or tensor), but not on the initial conditions. The information on how BHs relax after the perturbation has been applied is encoded into the non-vanishing imaginary part of the QN frequencies. Black hole perturbation theory [14,15,16,17,18,19] and QNMs become relevant during the ring down phase of a black hole merger, the stage where a single distorted object is formed, and where the geometry of space time undergoes dumped oscillations due to the emission of gravitational waves. Taking advantage of gravitational wave Astronomy we have now a powerful tool at our disposal that allows us to test gravitation under extreme conditions, such as BH mimickers, modifications of gravity, the Kerr paradigm of GR etc. For excellent reviews on the topic see [20,21,22], and also the Chandrasekhar’s monograph [23], which is the standard textbook on the mathematical aspects of black holes.
Another issue regarding BH QNMs is the so-called “Bohr-like approach to black hole quantum physics”. As the name suggests, that approach is somewhat similar to the historical semi-classical model of the structure of a hydrogen atom introduced by Bohr in 1913 [24,25]. In that approach, which has been published in [26,27] and then reviewed in [28], in a certain sense, the QNMs “triggered” by the emissions of Hawking quanta and by the absorption of external particles represent the “electron” which jumps from one level to another, and the absolute values of the quasi-normal frequencies represent the energy “shells”. Finally, it is worth mentioning here that the aforementioned approach proposes also an interesting solution to the BH information paradox [29].
A special attention has been devoted to non-linear electrodynamics (NLE) for several decades now, which has a long history and it has been studied over the years in several different contexts. To begin with, it is known that classical electrodynamics is based on a system of linear equations. However, when quantum effects are taken into account, the effective equations become non-linear. The first models go many decades back, when Euler and Heisenberg calculated QED corrections [30], while Born and Infeld managed to obtain a finite self-energy of point-like charges [31] in the 30’s. Moreover, assuming appropriate non-linear electromagnetic sources, which in the weak field limit are reduced to the usual Maxwell’s linear theory, one can generate a new class of Bardeen-like [32,33] BH solutions [34,35,36,37,38,39,40,41]. Those solutions on the one hand do have a horizon, and on the other hand their curvature invariants, such as the Ricci scalar R, are regular everywhere, contrary to the standard Reissner-Nordström solution [42].
Finally, a simple model that generalizes Maxwell’s linear theory in a straightforward manner leads to the so called Einstein-power-Maxwell (EpM) theory [43,44,45,46,47,48,49,50,51], described by a Lagrangian density of the form , where F is the Maxwell invariant, and k is an arbitrary rational number. Although our observable Universe is clearly four-dimensional, the question “How many dimensions are there?” is one of the fundamental questions that modern High Energy Physics tries to answer. Kaluza-Klein theories [52,53], Supergravity [54] and Superstring/M-Theory [55,56] have pushed forward the idea that extra spatial dimensions may exist. The advantage of the EpM theory is that it preserves the nice conformal properties of the four-dimensional Maxwell’s theory in any number of space-time dimensionality D, provided that the power k is chosen to be , as it is easy to verify that for this particular value the electromagnetic stress-energy tensor becomes traceless.
What is more, over the years the computation of QNMs of higher-dimensional BHs has attracted a lot of attention for several reasons, such as (i) the study of features of higher-dimensional GR [57,58], (ii) the analysis of the physical implications of the brane-world scenario [59], and (iii) the understanding of thermodynamic properties of BHs in Loop Quantum Gravity [60,61], to mention just a few. Given the interest in Gravitational Wave Astronomy and in QNMs of black holes, it would be interesting to see what kind of QN spectra are expected from higher-dimensional black holes in EpM theory. In this work we propose to compute the QN spectrum for scalar perturbations of charged BHs in EpM theory in higher dimensions, extending two previous similar works of ours [48,51] in .
Our work in the present article is organized as follows: In the next section we briefly review charged BH solutions in EpM theory, and we also very briefly discuss the wave equation with the corresponding effective potential barrier for the scalar perturbations. In the third section we compute the quasinormal frequencies adopting the WKB approximation of 6th order, and we discuss our results. There we also compute the QNMs in the eikonal regime for several different values of space-time dimensionality. Finally, in section four we summarize our work with some concluding remarks. We adopt the mostly positive metric signature , and we work in geometrical units where the universal constants are set to unity, .
2. The Black Hole Gravitational Background and Scalar Perturbations
2.1. Charged Black Hole Solutions in EpM Theory
We are interested in a D-dimensional theory described by the action
where R is the Ricci scalar, g the determinant of the metric tensor , is the Maxwell potential, k is an arbitrary rational number, and the Maxwell invariant with being the electromagnetic field strength defined by
where the indices run from 0 to .
Varying the action with respect to the metric tensor one obtains Einstein’s field equations sourced by the electromagnetic energy-momentum tensor [43]
with being the Einstein tensor. Next, varying the action with respect to the Maxwell potential one obtains the generalized Maxwell equations [43]
We seek static, spherically symmetric solutions making as usual for the metric tensor the Ansätz
with r being the radial coordinate, and with being the line element of the unit (D-2)-dimensional sphere. In the case , for instance, it is given by [62,63]
The electric field is found to be [43]
where C is a constant of integration, and the power is given by [43]
while the metric function is computed to be [43]
where are two constants related to the mass M and the electric charge Q of the BH, respectively. The constant q and the constant of integration C in five dimensions are related via [43]
Furthermore, we shall consider the case in which the power . In order to have real roots for the metric function , the constants must satisfy the conditions and [43]
where the upper bound corresponds to extremal BHs, and it is given by
Clearly, setting we recover the well-known case of the higher-dimensional version of the Reissner-Nordström BH [42] of Maxwell’s linear electrodynamics. Furthermore, setting the solution for the higher-dimensional version of the Schwarzschild geometry [64] is recovered.
2.2. Wave Equation for Scalar Perturbations
Here we very briefly review the necessary ingredients to deal with the computation of the QN frequencies for scalar perturbations. To that end, let us consider the propagation of a test scalar field, , which is assumed to be real, massive, electrically neutral, and canonically coupled to gravity, in a fixed gravitational background. Its wave equation is given by the usual Klein-Gordon equation, see e.g., [65,66,67,68]
with m being the mass of the test scalar field.
In order to solve the Klein-Gordon equation, we apply as usual the separation of variables making the following Ansätz:
where is the frequency to be determined, while is the higher-dimensional generalization of the usual spherical harmonics, and they depend on the angular coordinates [69]. Making the previous Ansätz it is straightforward to obtain for the radial part a Schrödinger-like equation
with x being the tortoise coordinate, i.e.,
Finally, the effective potential barrier for scalar perturbations in any number of dimensions D is given by [70]
where the prime denotes differentiation with respect to r, and is the angular degree.
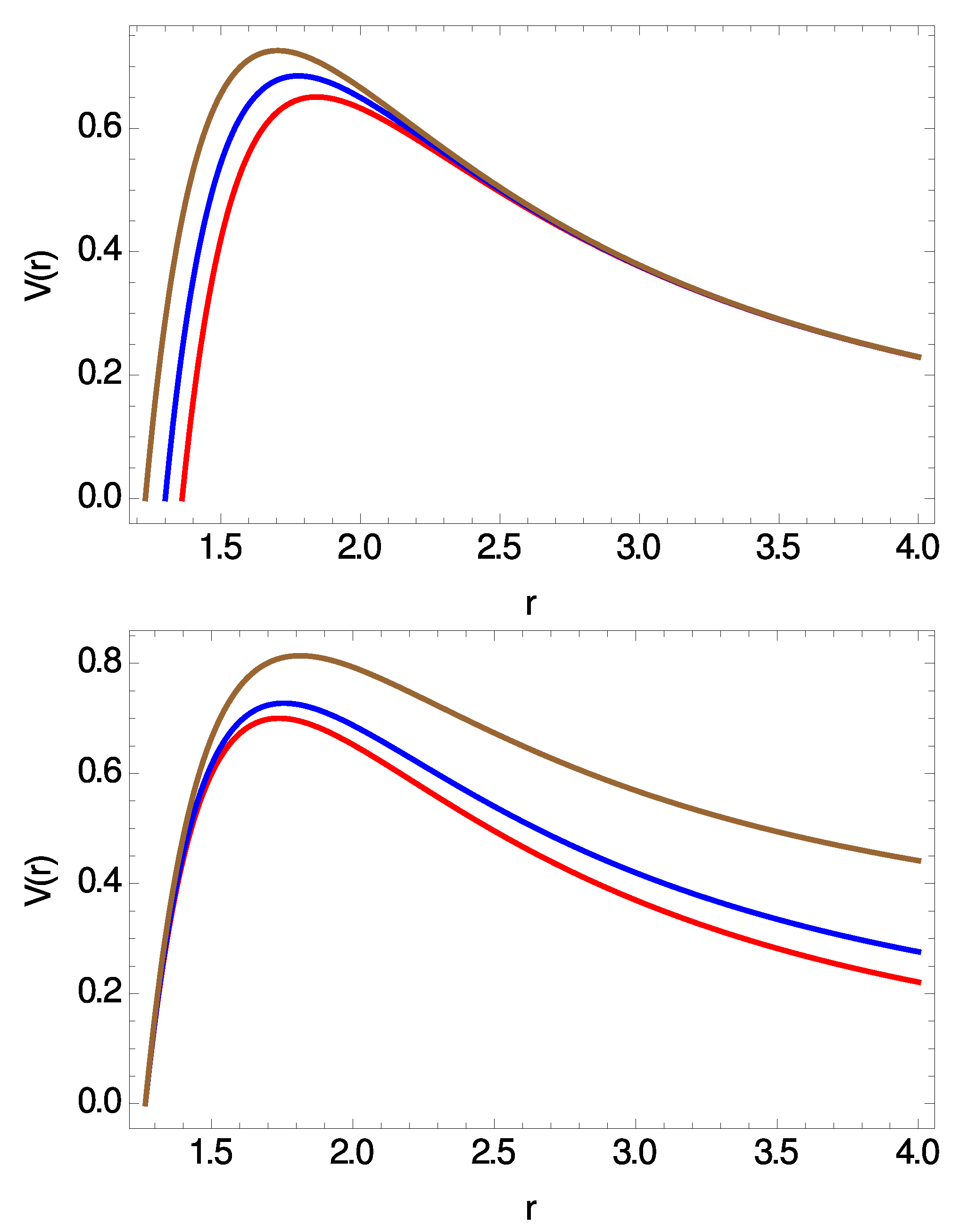
The effective potential barrier for and is shown in Figure 1 for three different values of q (top panel) and three different values of m (bottom panel) for fixed .
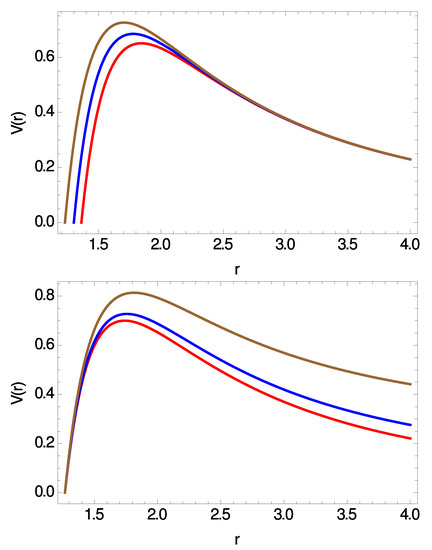
Figure 1.
Effective potential barrier for scalar perturbations vs. radial coordinate for , , and . (Top panel) From bottom to top (red), (blue) and (brown). (Bottom panel) From bottom to top (red), (blue) and (brown).
3. Quasinormal Frequencies
In the discussion to follow, we shall fix the mass parameter of the BHs , and for concreteness we shall consider the five-dimensional case
since as already mentioned in the introduction this is precisely the value of the power k for which the electromagnetic stress-energy tensor becomes traceless. Then the allowed range for q becomes, . In the next subsection we shall compare the QN spectra in the eikonal limit for several different space-time dimensionalities.
Exact analytical calculations for QN spectra of black holes may be performed in some special cases, e.g., either when the effective potential barrier takes the form of the Pöschl-Teller potential [71,72,73,74,75,76], or when the differential equation for the radial part of the wave function may be recast into the Gauss’ hypergeometric function [77,78,79,80,81,82]. More generically, however, due to the complexity of the problem, some numerical method is employed. Over the years several different methods to compute the QNMs of black holes have been developed, such as the Frobenius method, generalization of the Frobenius series, fit and interpolation approach, method of continued fraction etc. For more details the interested reader may consult e.g., [22]. In particular, semi-analytical methods based on the Wentzel-Kramers-Brillouin (WKB) approximation (familiar from non-relativistic quantum mechanics) [83,84,85] are among the most popular ones, and they have been extensively applied to several cases. For a partial list see for instance [86,87,88,89,90,91], and for more recent works [48,49,92,93,94], and references therein.
Applying the WKB method, the QN spectra may be computed making use of the following expression
where is the overtone number, , is the maximum of the effective potential barrier, is the second derivative of the potential evaluated at the maximum, while are complicated expressions of and higher derivatives of the potential evaluated at the maximum, and they can be found e.g., in [87,92]. Here we have used the Wolfram Mathematica [95] code with WKB at any order from one to six presented in [96]. For a given angular degree l we have considered values only, since this is the case for which the best results are obtained, see e.g., Tables II, III, IV and V of [97]. For higher order WKB corrections, and recipes for simple, quick, efficient and accurate computations see [97,98,99].
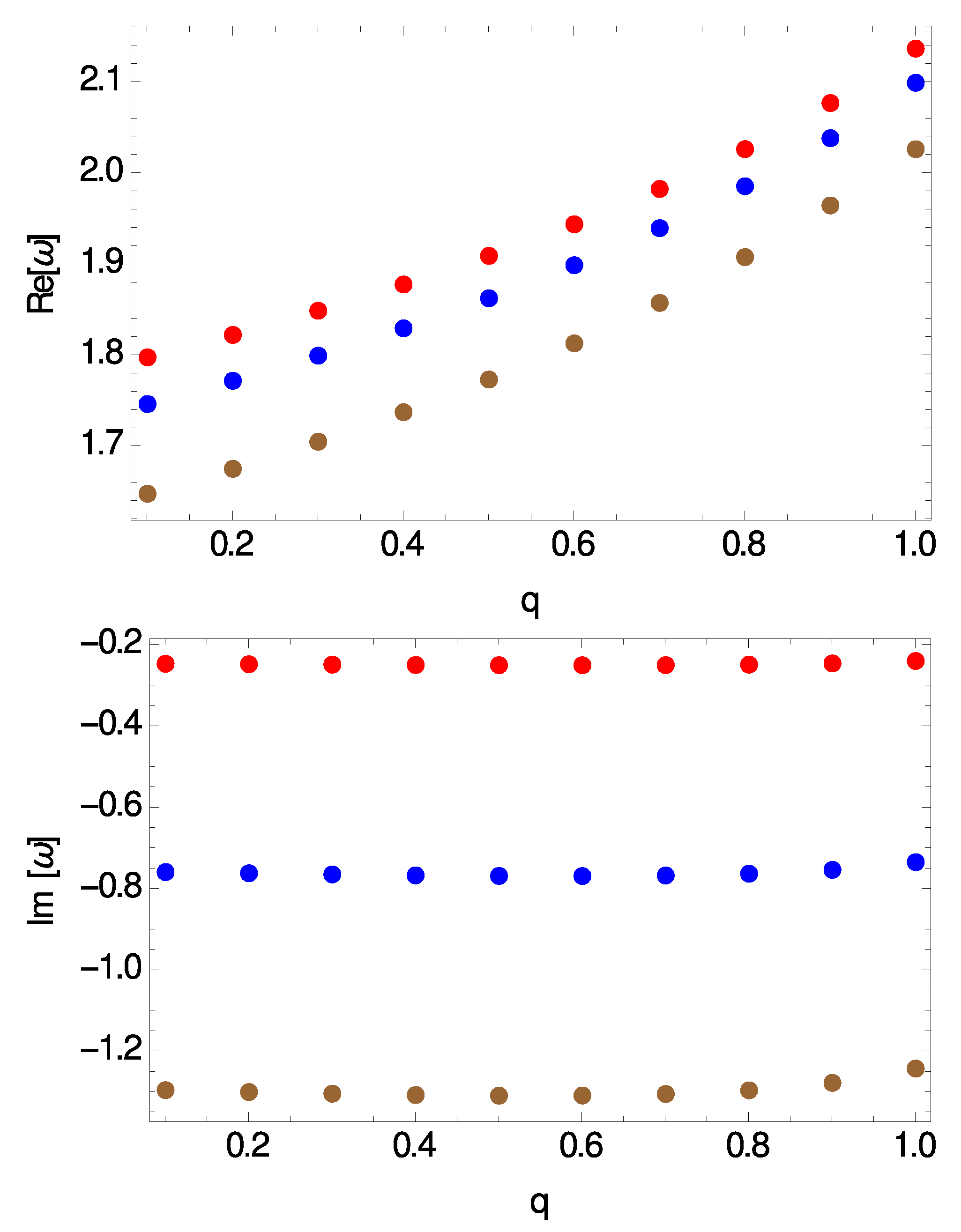
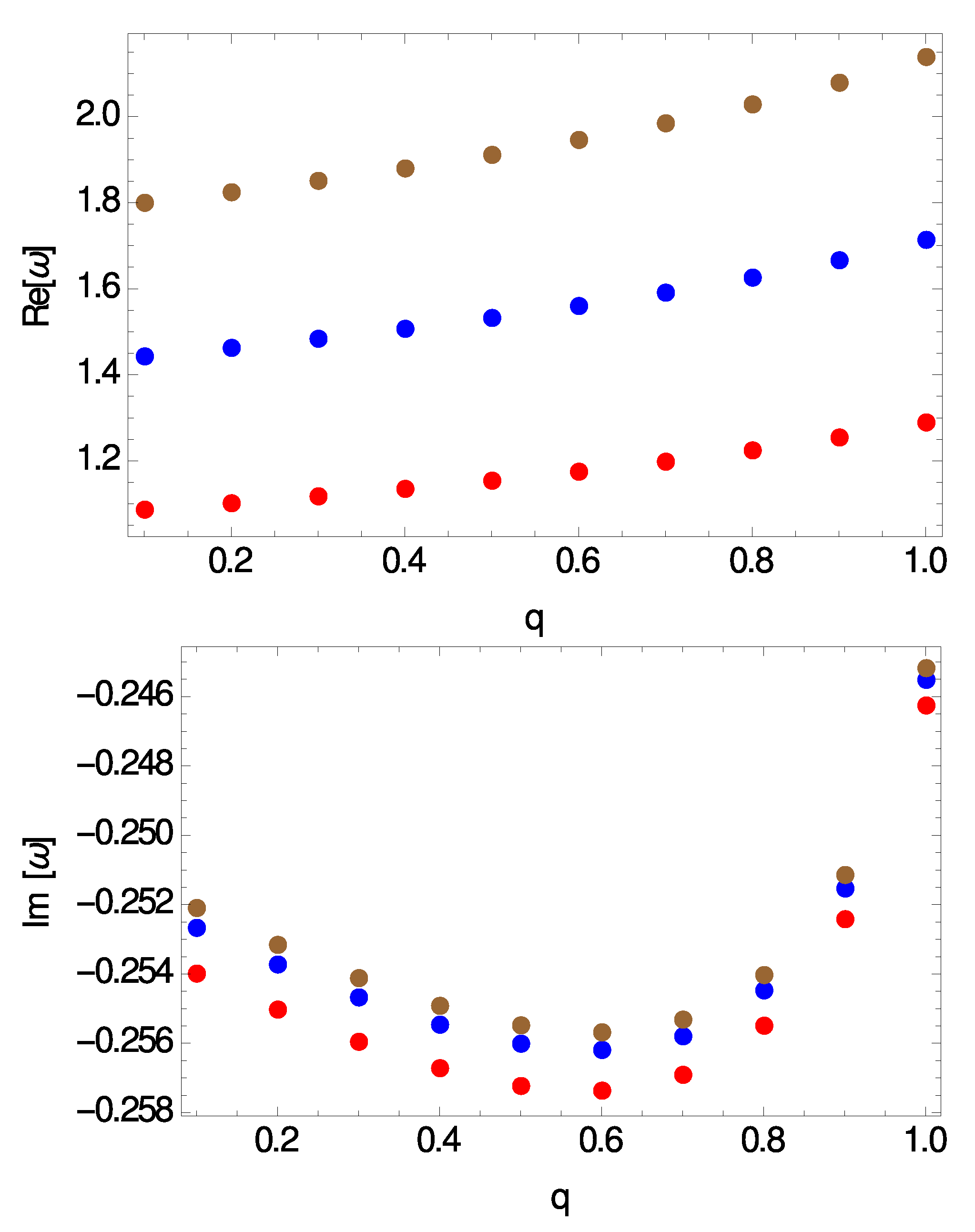
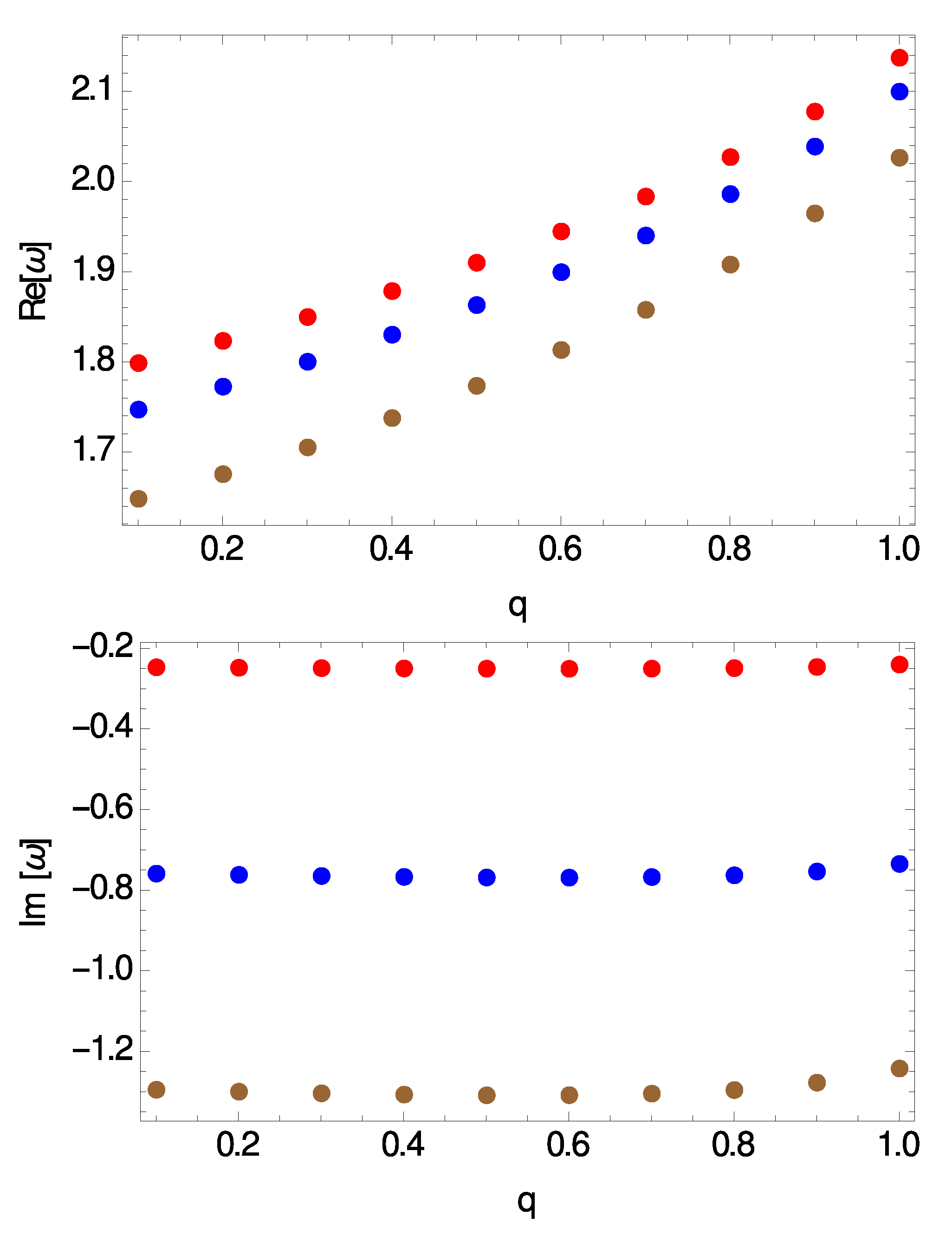
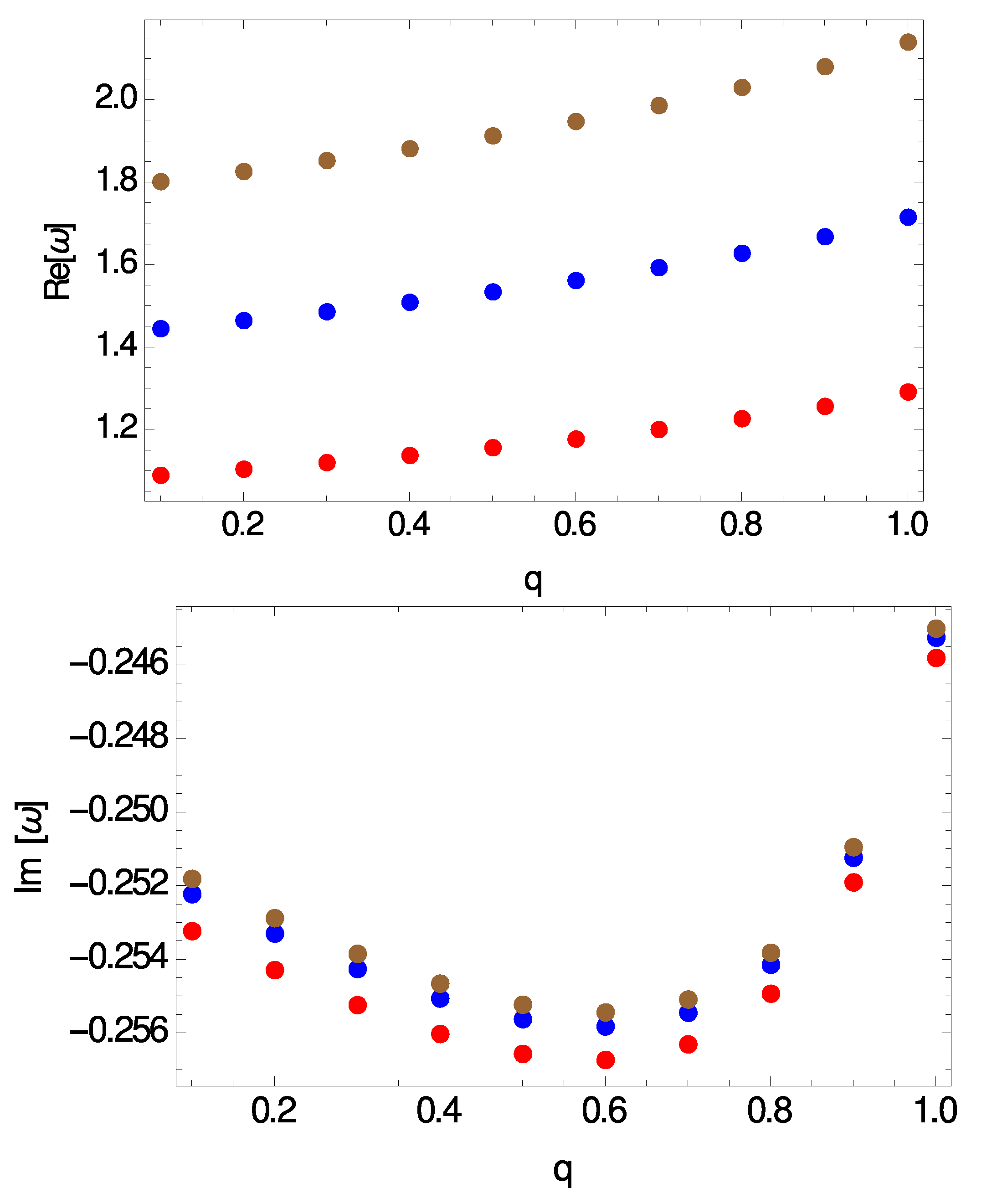
Our main numerical results are summarized in Figure 2, Figure 3, Figure 4 and Figure 5. In particular, in Figure 2 we show the real and the imaginary part of the frequencies vs. the electric charge of the BHs, q, for and three different values of the overtone number, . In Figure 3 we show the real and the imaginary part of the modes vs. the electric charge of the BHs for and three different values of the angular degree, . In the other two plots we have considered a heavier test scalar field with a mass . Although it is not visible in the plots shown here, there is a small difference in the values between the and the case. This is demonstrated in Table 1 for the case . Overall we can say that the spectrum obtained here exhibits the following features: (i) the real part of the frequencies, , is positive while the imaginary part, , is negative, and therefore all modes are found to be stable, (ii) the real part increases with and decreases with n, (iii) the absolute value of the imaginary part increases with n, decreases with , while itself as a function of q acquires a minimum value around .
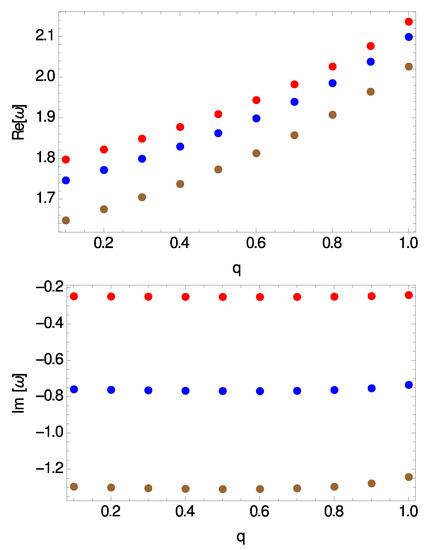
Figure 2.
Real part (top panel) and imaginary part (bottom panel) of the modes vs. electric charge for . From top to down .
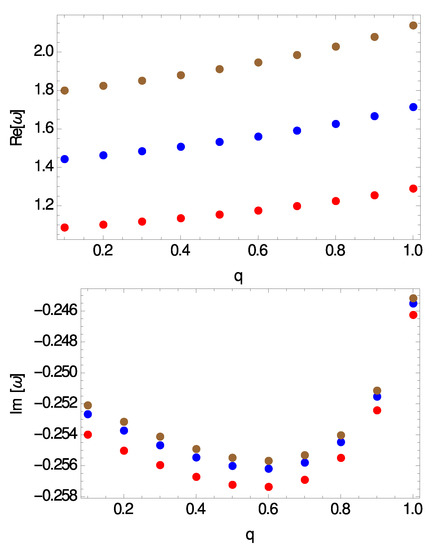
Figure 3.
Real part (top panel) and imaginary part (bottom panel) of the modes vs. electric charge for . From bottom to top .
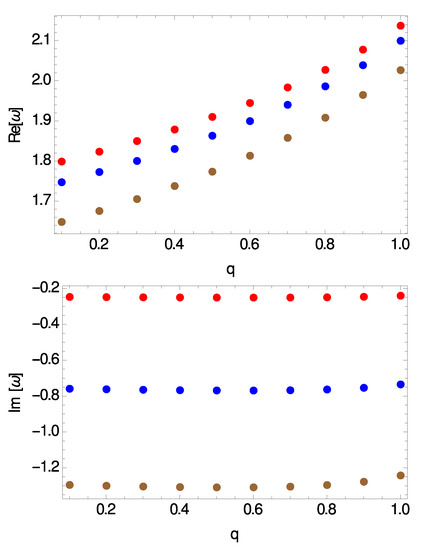
Figure 4.
Same as Figure 2, but for .
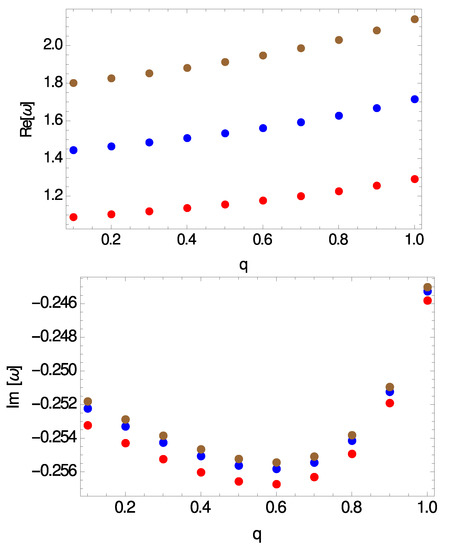
Figure 5.
Same as Figure 3, but for .

Table 1.
QN frequencies of EpM black holes for and two different masses of the test scalar field.
Quasinormal Spectrum in the Eikonal Limit
In the eikonal regime, , the WKB approximation becomes infinitely accurate, and therefore one can compute the QN spectrum within the first-order WKB semi-analytical approach. In this limit the angular momentum term is the dominant one in the effective potential barrier irrespectively of the dimensionality of space-time
where we introduce a new function . It is easy to verify that the maximum of the potential is located at that is computed solving the following algebraic equation
Then the spectrum may be computed using the first-order formula [83,84]
where the new function is defined to be . If the real part of the frequencies is much larger than the imaginary part, , then it is not difficult to obtain the following expression for the QNMs in the eikonal limit
where the Lyapunov exponent, , as well as the frequency of the null geodesics, , are computed to be
It is worth noticing that the real part of the modes is proportional to the angular degree, while the imaginary part depends on the overtone only.
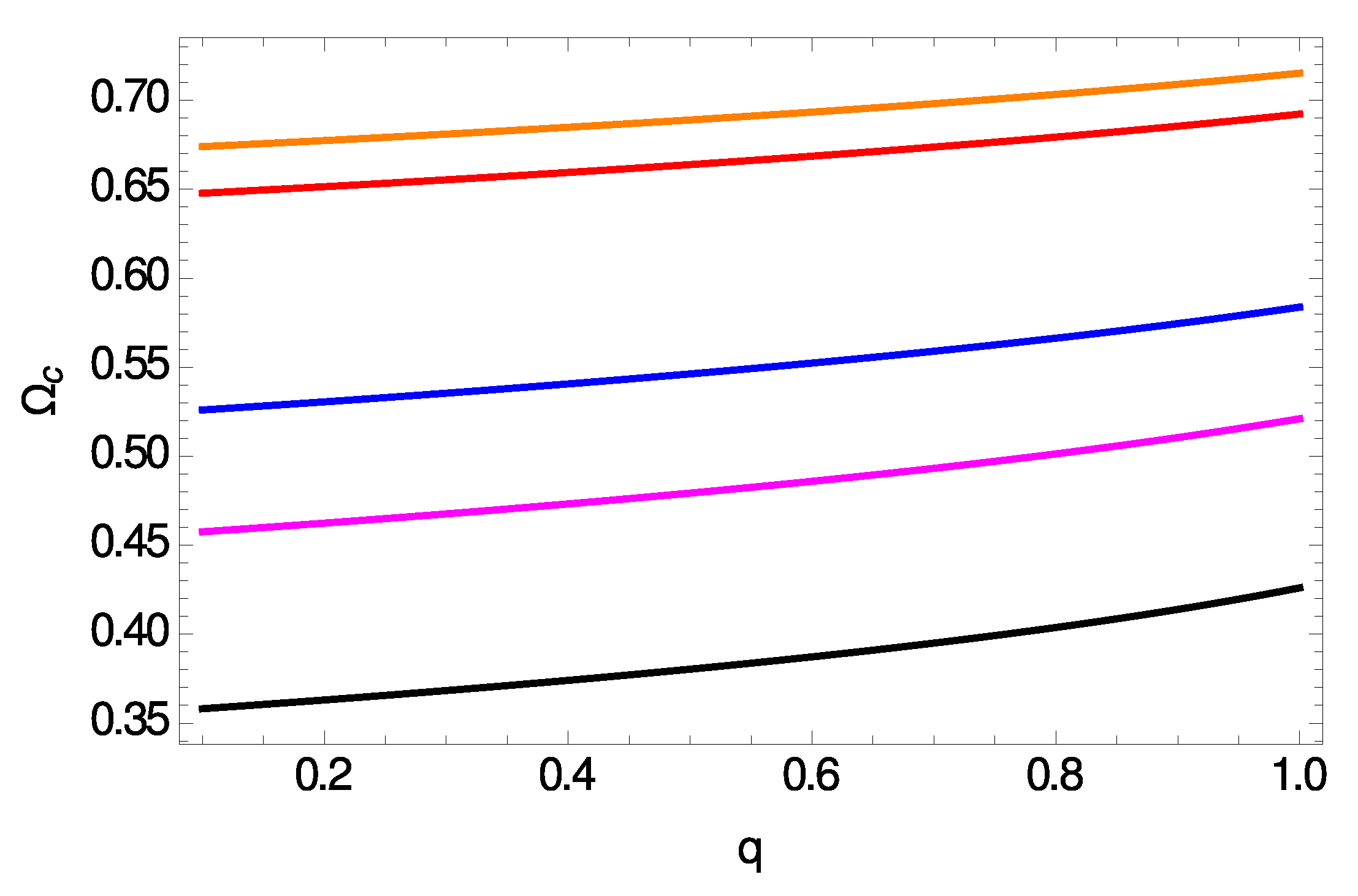
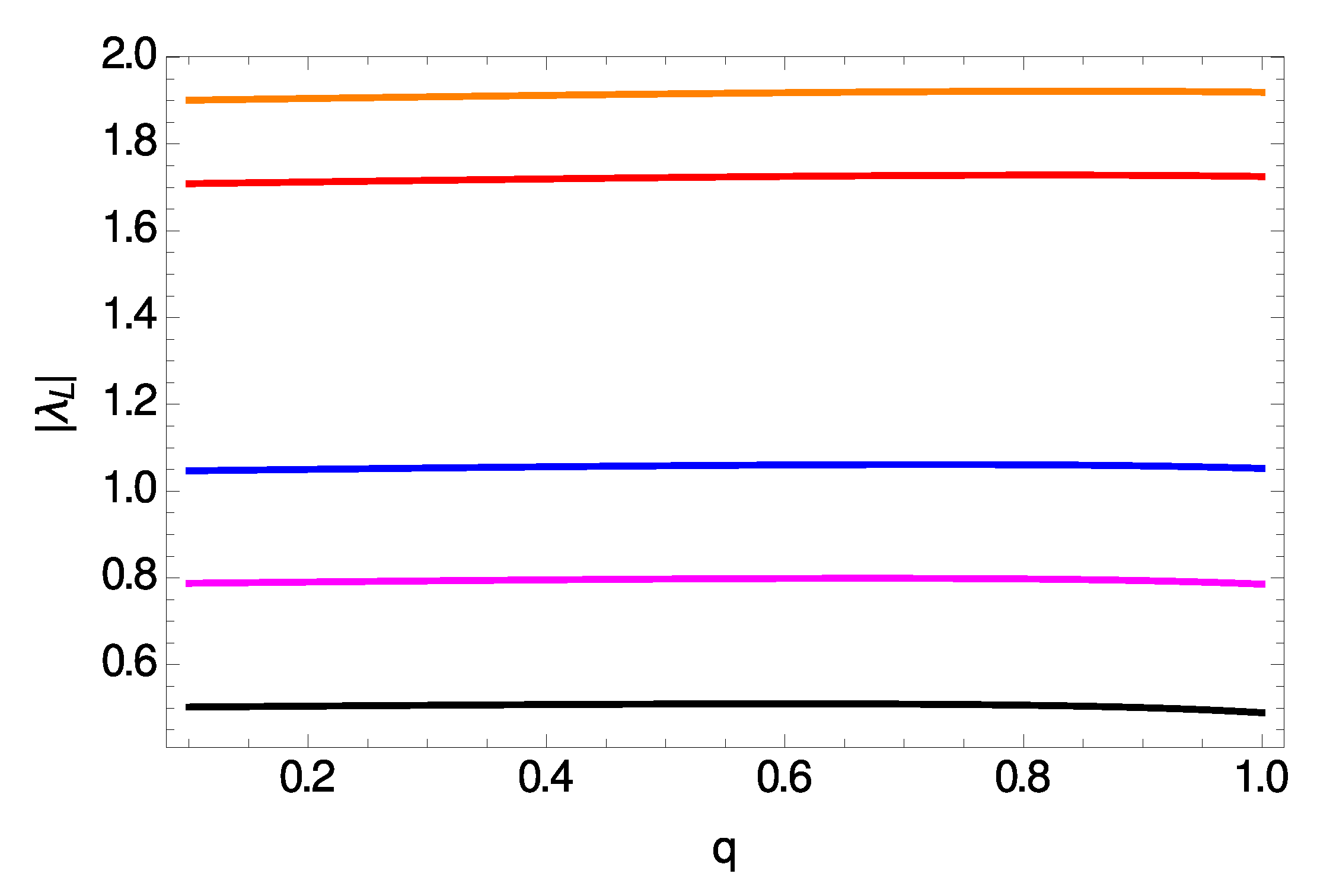
In Figure 6 we show both and vs. the electric charge of the BH for several different dimensionalities of space-time, namely for and , which is the maximum number of dimensions according to M-theory. According to our results, is an increasing function of q, and as D increases the curves are shifted upwards. Moreover, exhibits a maximum value at a certain value of that depends on the dimensionality of space-time (although this feature is hardly seen in the bottom panel of Figure 6), and the curves are again shifted upwards as D increases.
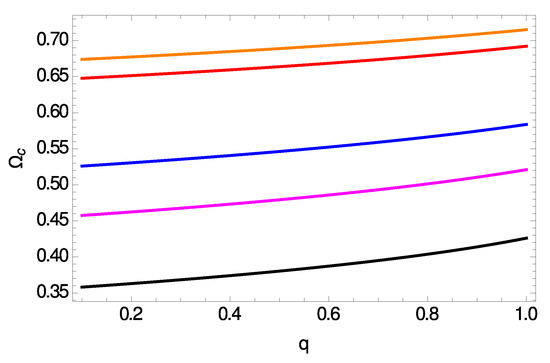
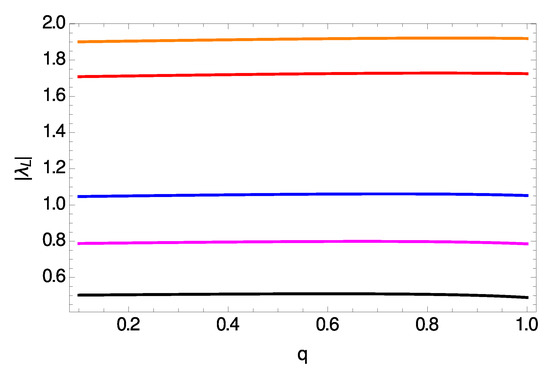
Figure 6.
Eikonal regime : Frequency of null geodesics (top panel) and Lyapunov exponent (bottom panel) vs. electric charge for . In both panels shown are from bottom to top (black), (magenta), (blue), (red) and (orange).
Regarding future work, there are still a couple of things to be done. For instance, one may compute the quasinormal frequencies for charged scalar fields, and also the quasinormal spectra for other types of fields, such as Dirac or electromagnetic and gravitational perturbations. We hope to be able to address those interesting issues in forthcoming works.
4. Conclusions
In summary, in this work we have computed the quasinormal spectrum for scalar perturbations of charged five-dimensional black holes in the Einstein-power-Maxwell non-linear electrodynamics. The test field that perturbs the gravitational background is taken to be a real, massive, electrically neutral canonical scalar field, and we have adopted the popular and widely used WKB semi-analytical method. All modes are found to be stable. The mass parameter of the black hole is set to two, , and we have considered two distinct values of the mass of the test scalar field (). We have shown graphically both the real and the imaginary part of the frequencies vs. the electric charge of the black hole for several different values of the angular degree l as well as the overtone number n. Finally, the QN spectrum in the eikonal regime for several different space-time dimensionalities has been computed as well.
Funding
This research was funded by FCT, Portugal, grant number UIDB/00099/2020.
Acknowledgments
The author thanks the Fundação para a Ciência e Tecnologia (FCT), Portugal, for the financial support to the Center for Astrophysics and Gravitation-CENTRA, Instituto Superior Técnico, Universidade de Lisboa, through the Grant No. UIDB/00099/2020.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Herdeiro, C.A.R.; Radu, E. Asymptotically flat black holes with scalar hair: A review. Int. J. Mod. Phys. D 2015, 24, 1542014. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170608: Observation of a 19-solar-mass Binary Black Hole Coalescence. Astrophys. J. 2017, 851, L35. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Azulay, R.; Baczko, A.-K.; Baloković, M.; Barrett, J.; Blackburn, L.; Bouman, K.L.; Bower, G.C.; Brinkerink, C.D.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. 2019, 875, L1. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. II. Array and Instrumentation. Astrophys. J. 2019, 875, L2. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. III. Data Processing and Calibration. Astrophys. J. 2019, 875, L3. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. Astrophys. J. 2019, 875, L4. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. Astrophys. J. 2019, 875, L5. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. 2019, 875, L6. [Google Scholar]
- Event Horizon Telescope web page. Available online: https://eventhorizontelescope.org (accessed on 23 March 2020).
- Regge, T.; Wheeler, J.A. Stability of a Schwarzschild singularity. Phys. Rev. 1957, 108, 1063. [Google Scholar] [CrossRef]
- Zerilli, F.J. Effective potential for even parity Regge-Wheeler gravitational perturbation equations. Phys. Rev. Lett. 1970, 24, 737. [Google Scholar] [CrossRef]
- Zerilli, F.J. Gravitational field of a particle falling in a schwarzschild geometry analyzed in tensor harmonics. Phys. Rev. D 1970, 2, 2141. [Google Scholar] [CrossRef]
- Zerilli, F.J. Perturbation analysis for gravitational and electromagnetic radiation in a reissner-nordstroem geometry. Phys. Rev. D 1974, 9, 860. [Google Scholar] [CrossRef]
- Moncrief, V. Gauge-invariant perturbations of Reissner-Nordstrom black holes. Phys. Rev. D 1975, 12, 1526. [Google Scholar] [CrossRef]
- Teukolsky, S.A. Rotating black holes—Separable wave equations for gravitational and electromagnetic perturbations. Phys. Rev. Lett. 1972, 29, 1114. [Google Scholar] [CrossRef]
- Kokkotas, K.D.; Schmidt, B.G. Quasinormal modes of stars and black holes. Living Rev. Rel. 1999, 2, 2. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal modes of black holes and black branes. Class. Quant. Grav. 2009, 26, 163001. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Quasinormal modes of black holes: From astrophysics to string theory. Rev. Mod. Phys. 2011, 83, 793. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Clarendon: Oxford, UK, 1985; 646p. [Google Scholar]
- Bohr, N. On the Constitution of Atoms and Molecules. 2. Systems containing only a Single Nucleus. Phil. Mag. Ser. 6 1913, 26, 476. [Google Scholar] [CrossRef]
- Bohr, N. On the Constitution of Atoms and Molecules. Phil. Mag. Ser. 6 1913, 26, 1. [Google Scholar] [CrossRef]
- Corda, C.; Hendi, S.H.; Katebi, R.; Schmidt, N.O. Effective state, Hawking radiation and quasi-normal modes for Kerr black holes. JHEP 2013, 1306, 008. [Google Scholar] [CrossRef]
- Corda, C. Precise model of Hawking radiation from the tunnelling mechanism. Class. Quant. Grav. 2015, 32, 195007. [Google Scholar] [CrossRef]
- Corda, C. Quasi-Normal Modes: The ‘Electrons’ of Black Holes as ‘Gravitational Atoms’? Implications for the Black Hole Information Puzzle. Adv. High Energy Phys. 2015, 2015, 867601. [Google Scholar] [CrossRef]
- Corda, C. Time dependent Schrödinger equation for black hole evaporation: No information loss. Ann. Phys. 2015, 353, 71. [Google Scholar] [CrossRef]
- Heisenberg, W.; Euler, H. Folgerungen aus der Diracschen Theorie des Positrons. Z. Phys. 1936, 98, 714. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the new field theory. Proc. Roy. Soc. Lond. A 1934, 144, 425. [Google Scholar] [CrossRef]
- Bardeen, J.M. Non-singular general-relativistic gravitational collapse. In Proceedings of the International Conference GR5, USSR, Tbilisi, Georgia, 1968; p. 174. [Google Scholar]
- Borde, A. Regular black holes and topology change. Phys. Rev. D 1997, 55, 7615. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garcia, A. Regular black hole in general relativity coupled to nonlinear electrodynamics. Phys. Rev. Lett. 1998, 80, 5056. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garcia, A. Nonsingular charged black hole solution for nonlinear source. Gen. Rel. Grav. 1999, 31, 629. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garcia, A. New regular black hole solution from nonlinear electrodynamics. Phys. Lett. B 1999, 464, 25. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Regular magnetic black holes and monopoles from nonlinear electrodynamics. Phys. Rev. D 2001, 63, 044005. [Google Scholar] [CrossRef]
- Dymnikova, I. Regular electrically charged structures in nonlinear electrodynamics coupled to general relativity. Class. Quant. Grav. 2004, 21, 4417. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and evaporation of regular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef]
- Balart, L.; Vagenas, E.C. Regular black hole metrics and the weak energy condition. Phys. Lett. B 2014, 730, 14. [Google Scholar] [CrossRef]
- Balart, L.; Vagenas, E.C. Regular black holes with a nonlinear electrodynamics source. Phys. Rev. D 2014, 90, 124045. [Google Scholar] [CrossRef]
- Reissner, H. Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie (in German). Ann. Phys. 1916, 355, 106–120. [Google Scholar] [CrossRef]
- Hassaine, M.; Martinez, C. Higher-dimensional charged black holes solutions with a nonlinear electrodynamics source. Class. Quant. Grav. 2008, 25, 195023. [Google Scholar] [CrossRef]
- Gurtug, O.; Mazharimousavi, S.H.; Halilsoy, M. 2+1-dimensional electrically charged black holes in Einstein - power Maxwell Theory. Phys. Rev. D 2012, 85, 104004. [Google Scholar] [CrossRef]
- Mazharimousavi, S.H.; Gurtug, O.; Halilsoy, M.; Unver, O. 2+1 dimensional magnetically charged solutions in Einstein - Power - Maxwell theory. Phys. Rev. D 2011, 84, 124021. [Google Scholar] [CrossRef]
- Xu, W.; Zou, D.C. (2+1) -Dimensional charged black holes with scalar hair in Einstein–Power–Maxwell Theory. Gen. Rel. Grav. 2017, 49, 73. [Google Scholar] [CrossRef]
- Rincón, Á.; Contreras, E.; Bargueño, P.; Koch, B.; Panotopoulos, G.; Hernández-Arboleda, A. Scale dependent three-dimensional charged black holes in linear and non-linear electrodynamics. Eur. Phys. J. C 2017, 77, 494. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, Á. Quasinormal modes of black holes in Einstein-power-Maxwell theory. Int. J. Mod. Phys. D 2017, 27, 1850034. [Google Scholar] [CrossRef]
- Rincón, Á.; Panotopoulos, G. Quasinormal modes of scale dependent black holes in (1+2)-dimensional Einstein-power-Maxwell theory. Phys. Rev. D 2018, 97, 024027. [Google Scholar] [CrossRef]
- Rincón, Á.; Contreras, E.; Bargueño, P.; Koch, B.; Panotopoulos, G. Scale-dependent (2+1)-dimensional electrically charged black holes in Einstein-power-Maxwell theory. Eur. Phys. J. C 2018, 78, 641. [Google Scholar] [CrossRef]
- Panotopoulos, G. Charged scalar fields around Einstein-power-Maxwell black holes. Gen. Rel. Grav. 2019, 51, 76. [Google Scholar] [CrossRef]
- Kaluza, T. On the Problem of Unity in Physics. Sitzungsber. Preuss. Akad. Wiss. Berl. (Math. Phys.) 1921, 1921, 966. [Google Scholar]
- Klein, O. Quantum Theory and Five-Dimensional Theory of Relativity. Z. Phys. 1926, 37, 895, (In German and English). [Google Scholar] [CrossRef]
- Nilles, H.P. Supersymmetry, Supergravity and Particle Physics. Phys. Rep. 1984, 110, 1. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory, Vol. 1 & 2; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Polchinski, J. String Theory, Vol. 1 & 2; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Bizon, P.; Chmaj, T.; Schmidt, B.G. Critical behavior in vacuum gravitational collapse in 4+1 dimensions. Phys. Rev. Lett. 2005, 95, 071102. [Google Scholar] [CrossRef] [PubMed]
- Bizon, P.; Chmaj, T.; Rostworowski, A.; Schmidt, B.G.; Tabor, Z. On vacuum gravitational collapse in nine dimensions. Phys. Rev. D 2005, 72, 121502. [Google Scholar] [CrossRef]
- Kanti, P. Black holes in theories with large extra dimensions: A Review. Int. J. Mod. Phys. A 2004, 19, 4899. [Google Scholar] [CrossRef]
- Hod, S. Bohr’s correspondence principle and the area spectrum of quantum black holes. Phys. Rev. Lett. 1998, 81, 4293. [Google Scholar] [CrossRef]
- Kunstatter, G. d-dimensional black hole entropy spectrum from quasinormal modes. Phys. Rev. Lett. 2003, 90, 161301. [Google Scholar] [CrossRef]
- Zhou, K.; Yang, Z.Y.; Zou, D.C.; Yue, R.H. Static spherically symmetric star in Gauss-Bonnet gravity. Chin. Phys. B 2012, 21, 020401. [Google Scholar] [CrossRef]
- Hansraj, S.; Chilambwe, B.; Maharaj, S.D. Exact EGB models for spherical static perfect fluids. Eur. Phys. J. C 2015, 75, 277. [Google Scholar] [CrossRef]
- Tangherlini, F.R. Schwarzschild field in n dimensions and the dimensionality of space problem. Nuovo Cim. 1963, 27, 636. [Google Scholar] [CrossRef]
- Crispino, L.C.B.; Higuchi, A.; Oliveira, E.S.; Rocha, J.V. Greybody factors for nonminimally coupled scalar fields in Schwarzschild–de Sitter spacetime. Phys. Rev. D 2013, 87, 104034. [Google Scholar] [CrossRef]
- Kanti, P.; Pappas, T.; Pappas, N. Greybody factors for scalar fields emitted by a higher-dimensional Schwarzschild–de Sitter black hole. Phys. Rev. D 2014, 90, 124077. [Google Scholar] [CrossRef]
- Pappas, T.; Kanti, P.; Pappas, N. Hawking radiation spectra for scalar fields by a higher-dimensional Schwarzschild–de Sitter black hole. Phys. Rev. D 2016, 94, 024035. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, Á. Quasinormal modes of five-dimensional black holes in non-commutative geometry. Eur. Phys. J. Plus 2020, 135, 33. [Google Scholar] [CrossRef]
- Muller, C. Lecture Notes in Mathematics: Spherical Harmonics; Springer: Berlin/Heidelberg, Germany, 1966. [Google Scholar]
- Harmark, T.; Natario, J.; Schiappa, R. Greybody Factors for d-Dimensional Black Holes. Adv. Theor. Math. Phys. 2010, 14, 727. [Google Scholar] [CrossRef]
- Poschl, G.; Teller, E. Bemerkungen zur Quantenmechanik des anharmonischen Oszillators. Z. Phys. 1933, 83, 143. [Google Scholar] [CrossRef]
- Ferrari, V.; Mashhoon, B. New approach to the quasinormal modes of a black hole. Phys. Rev. D 1984, 30, 295. [Google Scholar] [CrossRef]
- Cardoso, V.; Lemos, J.P.S. Scalar, electromagnetic and Weyl perturbations of BTZ black holes: Quasinormal modes. Phys. Rev. D 2001, 63, 124015. [Google Scholar] [CrossRef]
- Cardoso, V.; Lemos, J.P.S. Quasinormal modes of the near extremal Schwarzschild-de Sitter black hole. Phys. Rev. D 2003, 67, 084020. [Google Scholar] [CrossRef]
- Molina, C. Quasinormal modes of d-dimensional spherical black holes with near extreme cosmological constant. Phys. Rev. D 2003, 68, 064007. [Google Scholar] [CrossRef]
- Panotopoulos, G. Electromagnetic quasinormal modes of the nearly-extremal higher-dimensional Schwarzschild–de Sitter black hole. Mod. Phys. Lett. A 2018, 33, 1850130. [Google Scholar] [CrossRef]
- Birmingham, D. Choptuik scaling and quasinormal modes in the AdS / CFT correspondence. Phys. Rev. D 2001, 64, 064024. [Google Scholar] [CrossRef]
- Fernando, S. Quasinormal modes of charged dilaton black holes in (2+1)-dimensions. Gen. Rel. Grav. 2004, 36, 71. [Google Scholar] [CrossRef]
- Fernando, S. Quasinormal modes of charged scalars around dilaton black holes in 2+1 dimensions: Exact frequencies. Phys. Rev. D 2008, 77, 124005. [Google Scholar] [CrossRef]
- Destounis, K.; Panotopoulos, G.; Rincón, Á. Stability under scalar perturbations and quasinormal modes of 4D Einstein–Born–Infeld dilaton spacetime: Exact spectrum. Eur. Phys. J. C 2018, 78, 139. [Google Scholar] [CrossRef]
- Ovgün, A.; Jusufi, K. Quasinormal Modes and Greybody Factors of f(R) gravity minimally coupled to a cloud of strings in 2+1 Dimensions. Ann. Phys. 2018, 395, 138. [Google Scholar] [CrossRef]
- Rincón, Á.; Panotopoulos, G. Greybody factors and quasinormal modes for a nonminimally coupled scalar field in a cloud of strings in (2+1)-dimensional background. Eur. Phys. J. C 2018, 78, 858. [Google Scholar] [CrossRef]
- Schutz, B.F.; Will, C.M. Black Hole Normal Modes: A Semianalytic Approach. Astrophys. J. 1985, 291, L33. [Google Scholar] [CrossRef]
- Iyer, S.; Will, C.M. Black Hole Normal Modes: A WKB Approach. 1. Foundations and Application of a Higher Order WKB Analysis of Potential Barrier Scattering. Phys. Rev. D 1987, 35, 3621. [Google Scholar] [CrossRef]
- Konoplya, R.A. Quasinormal behavior of the d-dimensional Schwarzschild black hole and higher order WKB approach. Phys. Rev. D 2003, 68, 024018. [Google Scholar] [CrossRef]
- Iyer, S. Black Hole Normal Modes: A Wkb Approach. 2. Schwarzschild Black Holes. Phys. Rev. D 1987, 35, 3632. [Google Scholar] [CrossRef]
- Kokkotas, K.D.; Schutz, B.F. Black Hole Normal Modes: A WKB Approach. 3. The Reissner-Nordstrom Black Hole. Phys. Rev. D 1988, 37, 3378. [Google Scholar] [CrossRef]
- Seidel, E.; Iyer, S. Black Hole Normal Modes: A Wkb Approach. 4. Kerr Black Holes. Phys. Rev. D 1990, 41, 374. [Google Scholar] [CrossRef]
- Konoplya, R. Quasinormal modes of the charged black hole in Gauss-Bonnet gravity. Phys. Rev. D 2005, 71, 024038. [Google Scholar] [CrossRef]
- Fernando, S.; Holbrook, C. Stability and quasi normal modes of charged black holes in Born-Infeld gravity. Int. J. Theor. Phys. 2006, 45, 1630. [Google Scholar] [CrossRef][Green Version]
- Chakrabarti, S.K. Quasinormal modes of tensor and vector type perturbation of Gauss Bonnet black hole using third order WKB approach. Gen. Rel. Grav. 2007, 39, 567. [Google Scholar] [CrossRef][Green Version]
- Fernando, S.; Correa, J. Quasinormal Modes of Bardeen Black Hole: Scalar Perturbations. Phys. Rev. D 2012, 86, 064039. [Google Scholar] [CrossRef]
- Santos, V.; Maluf, R.V.; Almeida, C.A.S. Quasinormal frequencies of self-dual black holes. Phys. Rev. D 2016, 93, 084047. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Khoo, F.S.; Kunz, J. Quasinormal modes of Einstein-Gauss-Bonnet-dilaton black holes. Phys. Rev. D 2017, 96, 064008. [Google Scholar] [CrossRef]
- Wolfram Mathematica web page. Available online: http://www.wolfram.com (accessed on 23 March 2020).
- Konoplya, R.A.; Zhidenko, A. Passage of radiation through wormholes of arbitrary shape. Phys. Rev. D 2010, 81, 124036. [Google Scholar] [CrossRef]
- Matyjasek, J.; Opala, M. Quasinormal modes of black holes. The improved semianalytic approach. Phys. Rev. D 2017, 96, 024011. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A.; Zinhailo, A.F. Higher order WKB formula for quasinormal modes and grey-body factors: Recipes for quick and accurate calculations. Class. Quant. Grav. 2019, 36, 155002. [Google Scholar] [CrossRef]
- Hatsuda, Y. Quasinormal modes of black holes and Borel summation. Phys. Rev. D 2020, 101, 024008. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).