An Evaluation of ARFIMA (Autoregressive Fractional Integral Moving Average) Programs †
Abstract
:1. Introduction
2. LRD and ARFIMA Model
2.1. Autoregressive (AR) Model
2.2. Moving Average (MA) Model
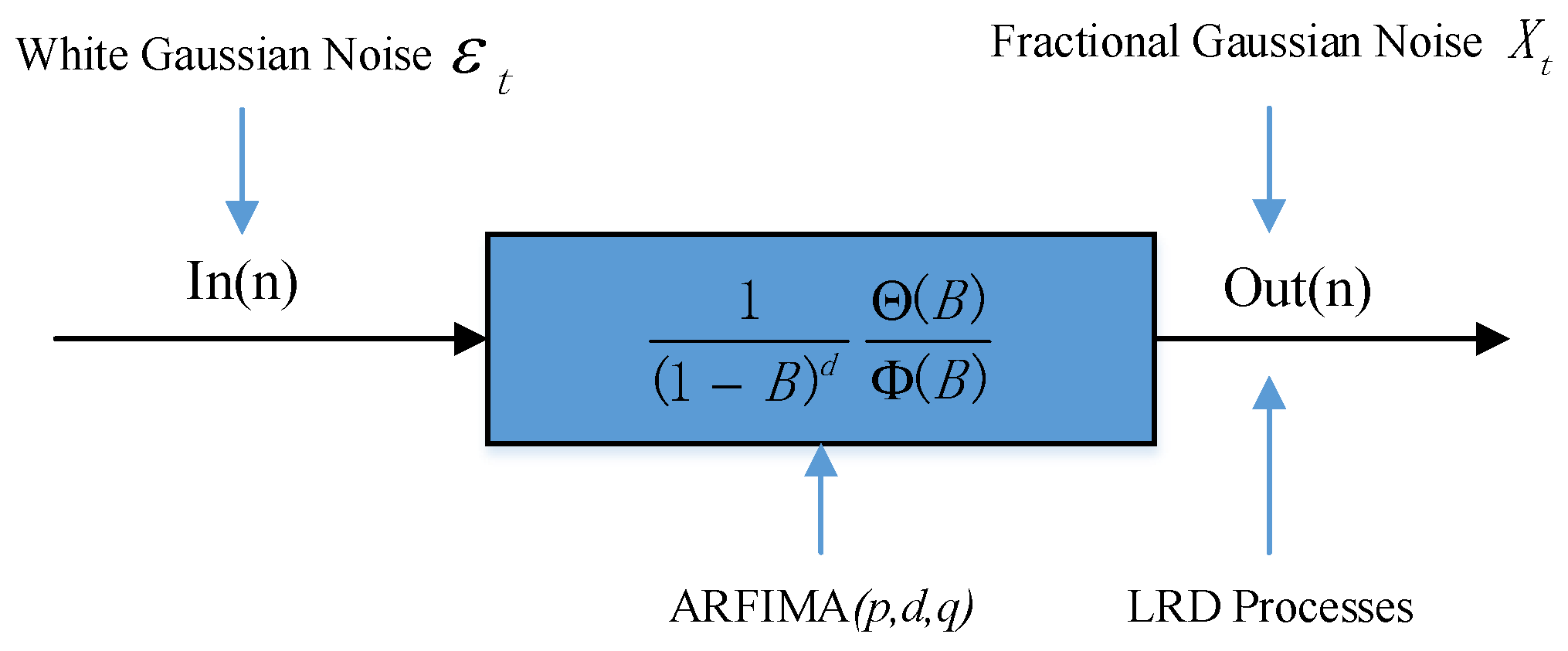
2.3. ARIMA and ARFIMA Model
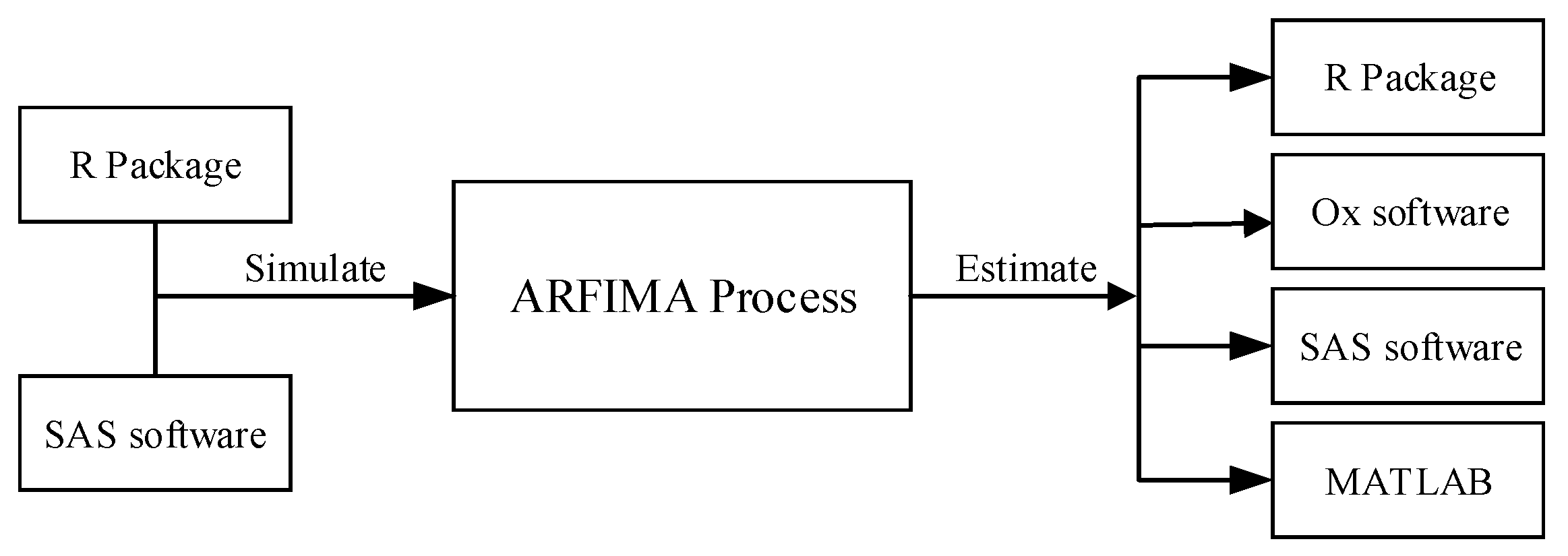
3. Review and Evaluation
- MATLAB applicationsMATLAB® (Matrix Laboratory) is a multi-paradigm numerical computing environment and fourth-generation programming language developed by MathWorks (Natick, MA 01760-2098, USA). The MATLAB applications are interactive applications written to perform technical computing tasks with the MATLAB scripting language from MATLAB File Exchange, through additional MATLAB products, and by users.
- SAS softwareSAS (Statistical Analysis System) is a software suite developed by SAS Institute (Cary, NC 27513-2414, USA) for advanced analytics, multivariate analyses, business intelligence, data management, and predictive analytics.
- R packagesR packages and projects are contributed by RStudio (Boston, MA 02210, USA) team on CRAN (Comprehensive R Archive Network). R users are doing some of the most innovative and important work in science, education, and industry. It is a daily inspiration and challenge to keep up with the community and all it is accomplishing.
- OxMetricsOxTM is an object-oriented matrix language with a comprehensive mathematical and statistical function library developed by Timberlake Consultants Limited (Richmond, Surrey TW9 3GA, UK). Many packages were written for Ox including software mainly for econometric modelling. The Ox packages for time series analysis and forecasting.
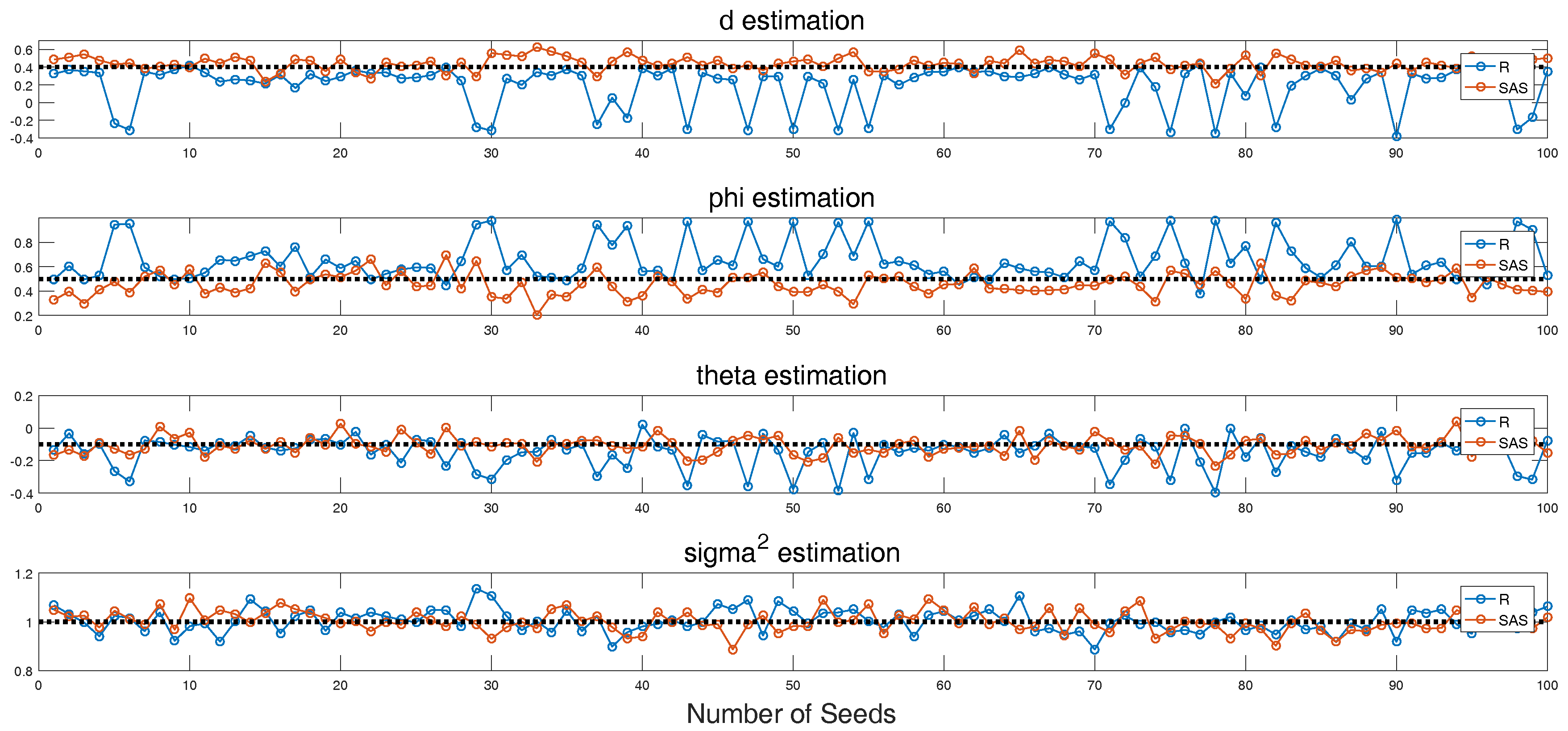
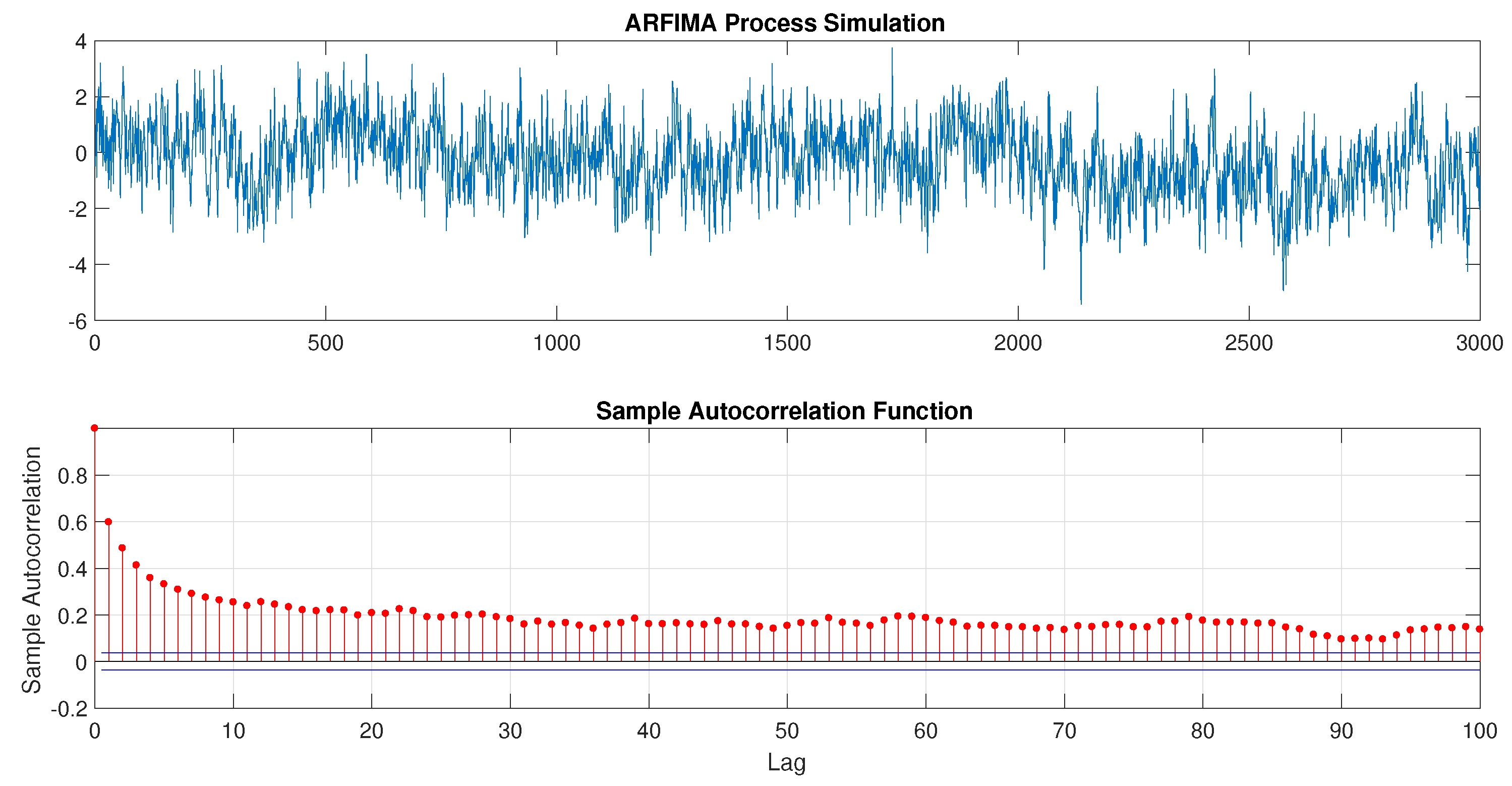
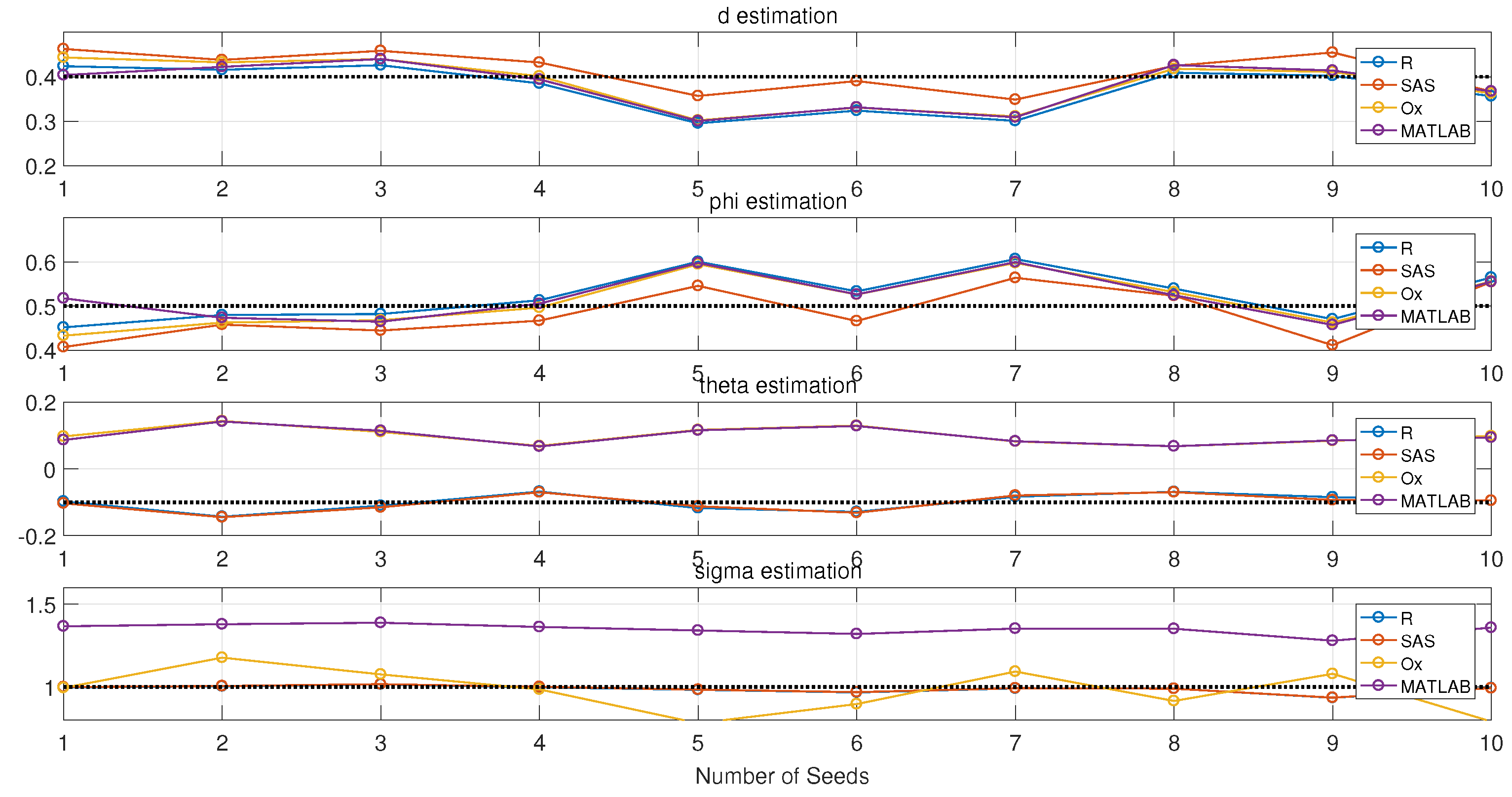
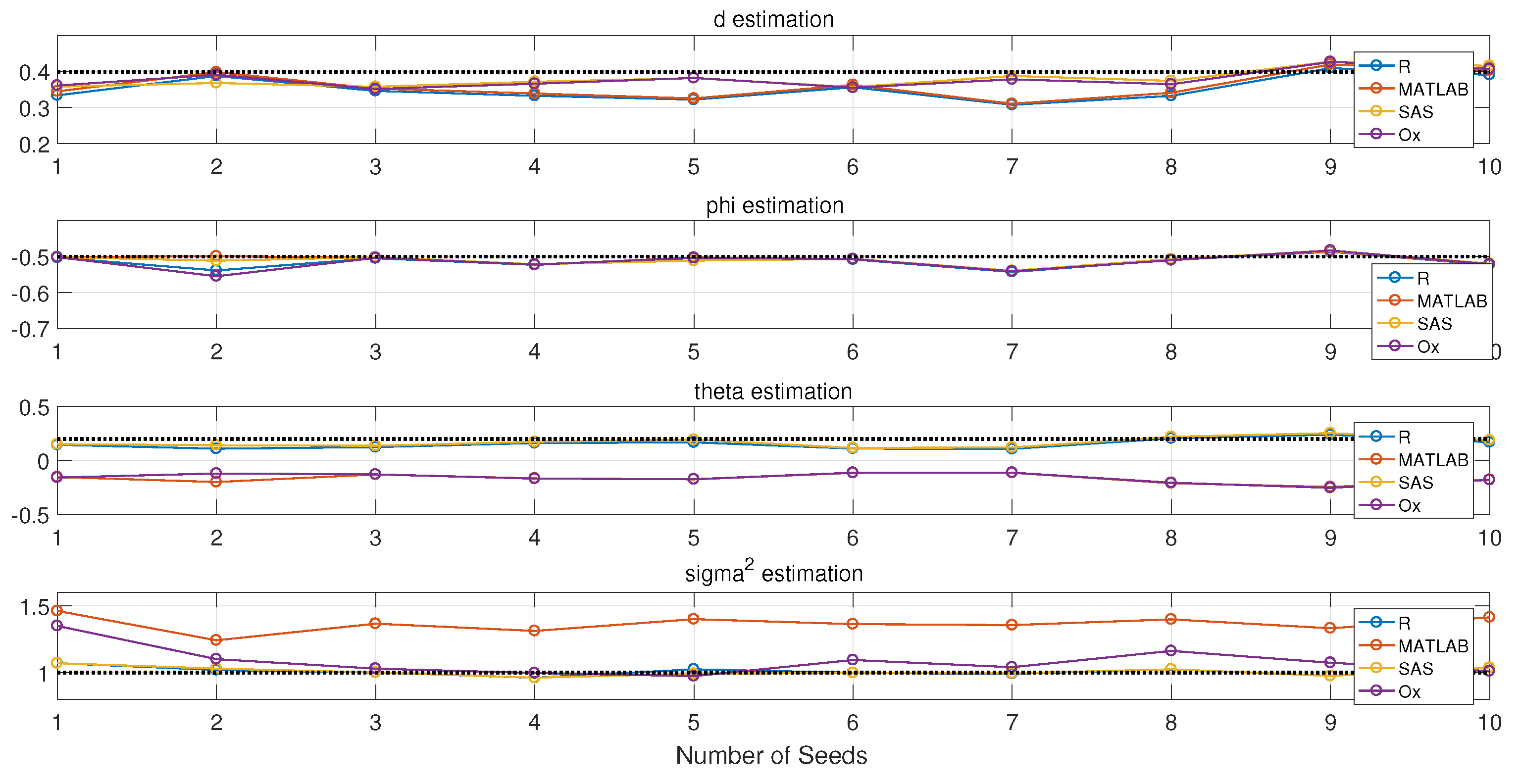
3.1. Simulation
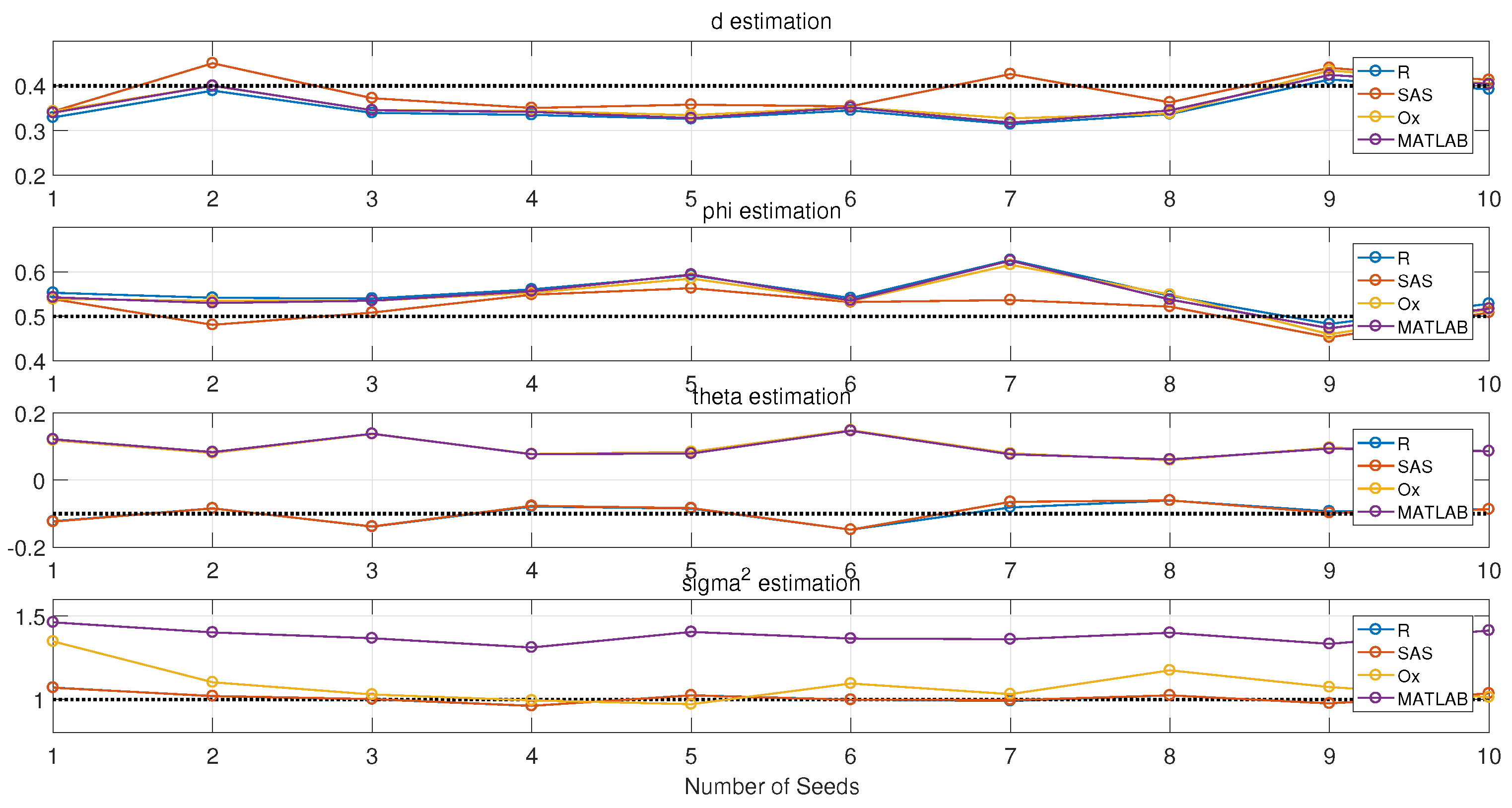
- Estimation results also depend on the initial random seeds, even the series that are from their own simulations.
- The test results may be different if not enough points/observations are generated. More than 300 points are preferred.
- Estimation results may not be accurate if they only use one method. R should be more desirable to try first.
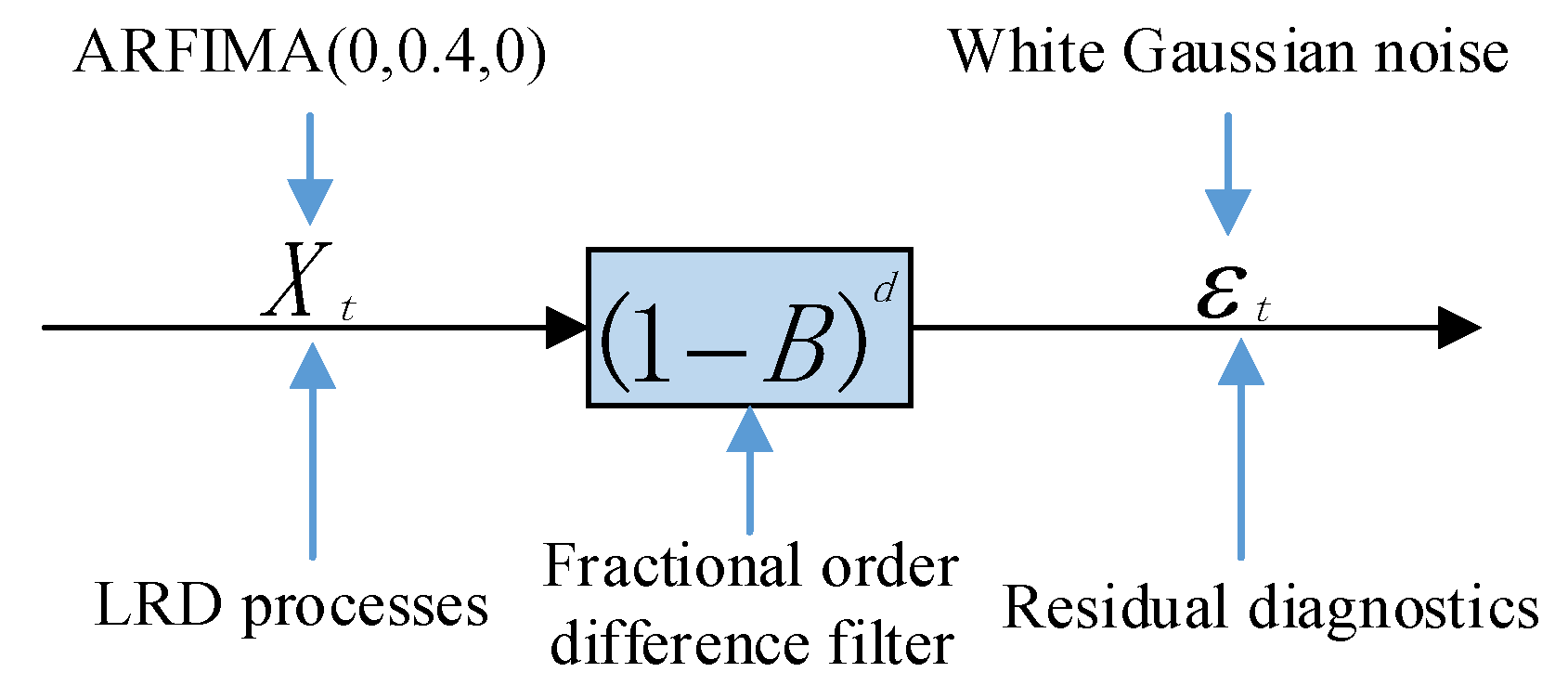
3.2. Fractional Order Difference Filter
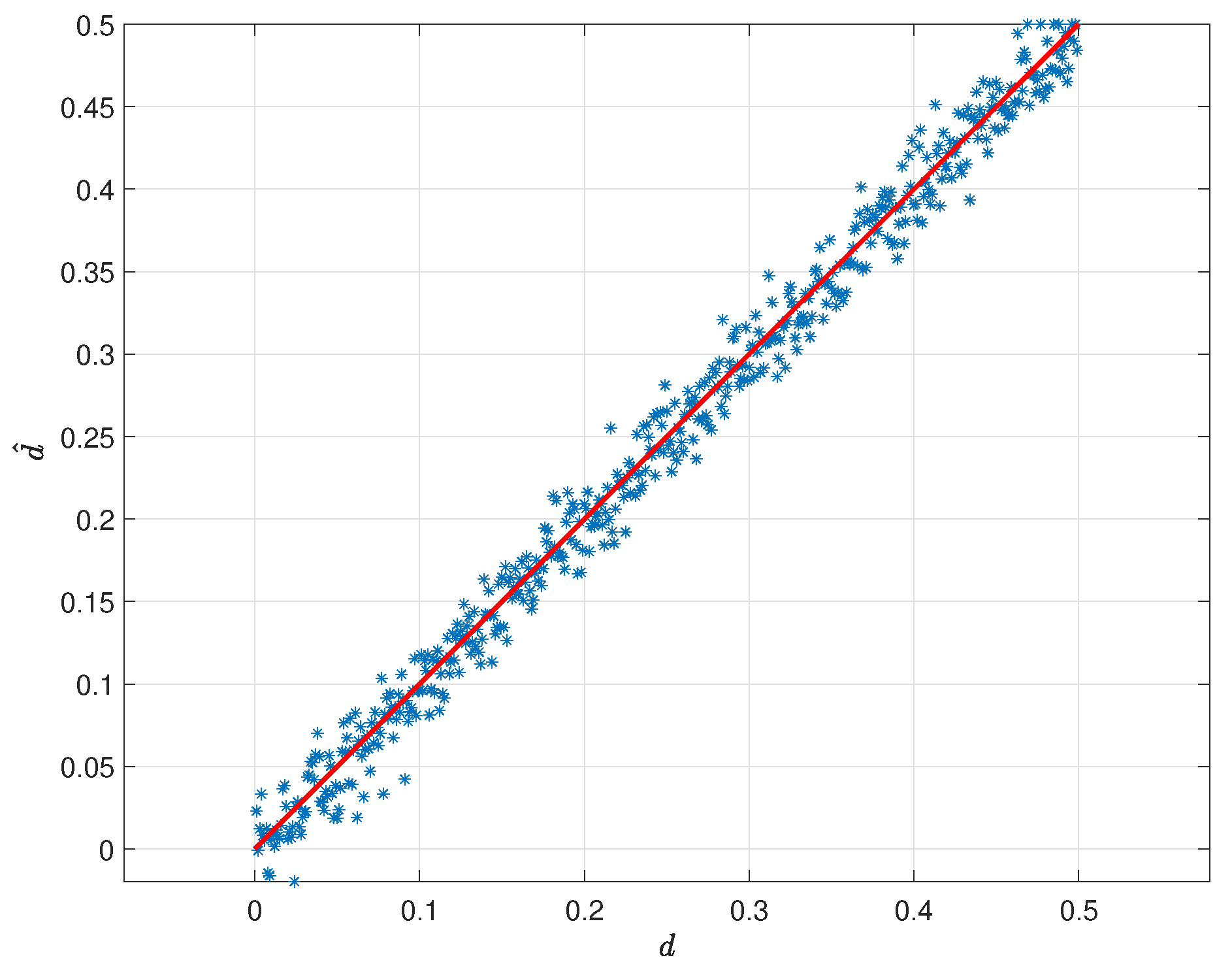
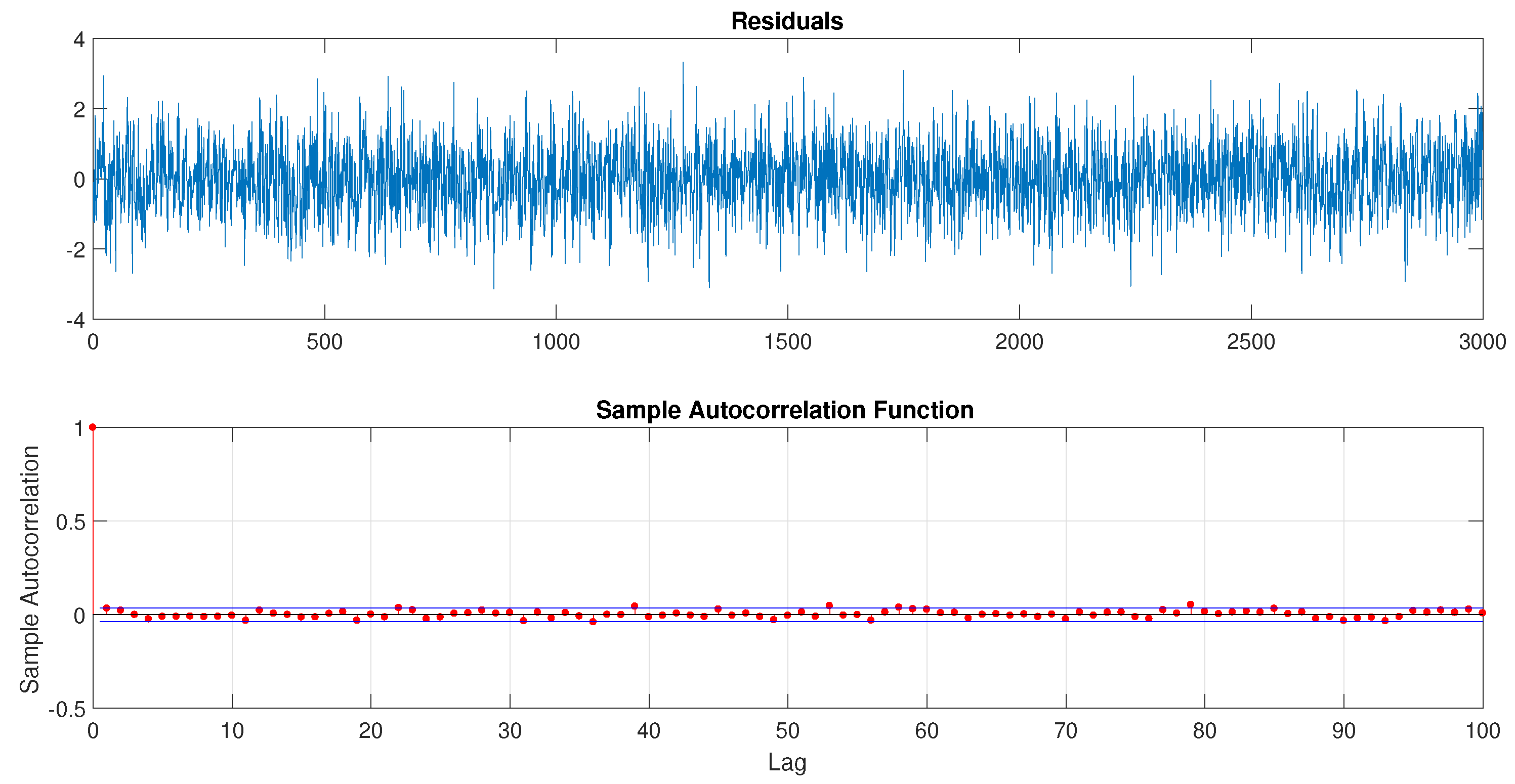
3.3. Parameter Estimation
3.4. Forecast
- d is the parameter to be estimated first when doing ARFIMA model fitting. Therefore, if the estimation of d is different for a certain time series, the following estimations for AR() and MA() will be different.
- The ideal length (horizon) of predictions is within 30 steps. With the increasing steps of forecast, prediction errors are adding up. If a long range prediction series is required, R and MATLAB should be priorities for their smaller prediction errors.
- Compared with other forecast results with true values in Table 4, R produces the minimum prediction errors and MAPE.
4. Summary of Selection Guidelines
- R and SAS software are priorities for the simulation of ARFIMA process, since they could define the initial seeds. R is one of the desirable tools for the estimation of ARFIMA process, since it has more than five packages including Hurst estimators, ACF plot, Quantile-Quantile (QQ) plot, white noise test and some LRD examples.
- Estimation results of the ARFIMA process may be different if the number of observations is not large enough. Therefore, more than one estimation method should be used in order to guarantee the accuracy.
- d is the parameter to be estimated first. All of this software could use fractional difference functions to filter the trend and thereafter stationarize time series data.
- The ideal length (horizon) of predictions is within 30 steps. If a long range prediction series is required, R and MATLAB are the priorities for their smaller prediction errors.
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Box, G.E.; Hunter, W.G.; Hunter, J.S. Statistics for Experimenters: An Introduction to Design, Data Analysis, and Model Building; John Wiley & Sons: Hoboken, NJ, USA, 1978; Volume 1. [Google Scholar]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Sheng, H.; Chen, Y.; Qiu, T. Fractional Processes and Fractional-Order Signal Processing: Techniques and Applications; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Mathai, A.M.; Saxena, R.K. The H-Function with Applications in Statistics and Other Disciplines; John Wiley & Sons: Hoboken, NJ, USA, 1978. [Google Scholar]
- Saxena, R.; Mathai, A.; Haubold, H. On fractional kinetic equations. Astrophys. Space Sci. 2002, 282, 281–287. [Google Scholar] [CrossRef]
- Saxena, R.; Mathai, A.; Haubold, H. On generalized fractional kinetic equations. Phys. A Stat. Mech. Its Appl. 2004, 344, 657–664. [Google Scholar] [CrossRef]
- Sun, R.; Chen, Y.; Li, Q. Modeling and prediction of Great Salt Lake elevation time series based on ARFIMA. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Las Vegas, NV, USA, 4–7 September 2007; American Society of Mechanical Engineers: New York, NY, USA, 2007; pp. 1349–1359. [Google Scholar]
- Li, Q.; Tricaud, C.; Sun, R.; Chen, Y. Great Salt Lake surface level forecasting using FIGARCH model. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Las Vegas, NV, USA, 4–7 September 2007; American Society of Mechanical Engineers: New York, NY, USA, 2007; pp. 1361–1370. [Google Scholar]
- Sheng, H.; Chen, Y. The modeling of Great Salt Lake elevation time series based on ARFIMA with stable innovations. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, CA, USA, 30 August–2 September 2009; American Society of Mechanical Engineers: New York, NY, USA, 2009; pp. 1137–1145. [Google Scholar]
- Contreras-Reyes, J.E.; Palma, W. Statistical analysis of autoregressive fractionally integrated moving average models in R. Comput. Stat. 2013, 28, 2309–2331. [Google Scholar] [CrossRef]
- Baillie, R.T.; Chung, S. Modeling and forecasting from trend-stationary long memory models with applications to climatology. Int. J. Forecast. 2002, 18, 215–226. [Google Scholar] [CrossRef]
- Doornik, J.A.; Ooms, M. Computational aspects of maximum likelihood estimation of autoregressive fractionally integrated moving average models. Comput. Stat. Data Anal. 2003, 42, 333–348. [Google Scholar] [CrossRef]
- Doornik, J.A.; Ooms, M. A package for estimating, forecasting and simulating ARFIMA models: Arfima package 1.0 for Ox; Erasmus University: Rotterdam, The Netherlands, 1999. [Google Scholar]
- Doornik, J.A.; Ooms, M. Inference and forecasting for ARFIMA models with an application to US and UK inflation. Stud. Nonlinear Dyn. Econ. 2004, 8, 1208–1218. [Google Scholar] [CrossRef]
- Burnecki, K. Identification, Validation and Prediction of Fractional Dynamical Systems; Oficyna Wydawnicza Politechniki Wrocławskiej: Wroclaw, Poland, 2012. [Google Scholar]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar]
- Ye, X.; Xia, X.; Zhang, J.; Chen, Y. Effects of trends and seasonalities on robustness of the Hurst parameter estimators. IET Signal Process. 2012, 6, 849–856. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance; CRC Press: Boca Raton, FL, USA, 1994; Volume 1. [Google Scholar]
- Woodward, W.A.; Gray, H.L.; Elliott, A.C. Applied Time Series Analysis with R, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Kale, M.; Butar, F.B. Fractal analysis of time series and distribution properties of Hurst exponent. J. Math. Sci. Math. Educ. 2011, 5, 8–19. [Google Scholar]
- Karasaridis, A.; Hatzinakos, D. Network heavy traffic modeling using α-stable self-similar processes. IEEE Trans. Commun. 2001, 49, 1203–1214. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, Y. FARIMA with stable innovations model of Great Salt Lake elevation time series. Signal Process. 2011, 91, 553–561. [Google Scholar] [CrossRef]
- Granger, C.W.; Joyeux, R. An introduction to long-memory time series models and fractional differencing. J. Time Ser. Anal. 1980, 1, 15–29. [Google Scholar] [CrossRef]
- Hosking, J.R. Fractional differencing. Biometrika 1981, 68, 165–176. [Google Scholar] [CrossRef]
- Brockwell, P.J.; Davis, R.A. Time Series: Theory and Methods; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Reisen, V.; Abraham, B.; Lopes, S. Estimation of parameters in ARFIMA processes: A simulation study. Commun. Stat.-Simul. Comput. 2001, 30, 787–803. [Google Scholar] [CrossRef]
- Reisen, V.A. Estimation of the fractional difference parameter in the ARIMA (p, d, q) model using the smoothed periodogram. J. Time Ser. Anal. 1994, 15, 335–350. [Google Scholar] [CrossRef]
- Fatichi, S. ARFIMA Simulations. Available online: https://www.mathworks.com/matlabcentral/fileexchange/25611-arfima-simulations/content/ARFIMASIM.m (accessed on 15 June 2017).
- Caballero, C.V.R. ARFIMA(p, d, q). Available online: https://www.mathworks.com/matlabcentral/fileexchange/53301-arfima-p-d-q-/content/dgparfima.m (accessed on 15 June 2017).
- Inzelt, G. ARFIMA(p, d, q) Estimator. Available online: https://www.mathworks.com/matlabcentral/fileexchange/30238-arfima-p-d-q--estimator (accessed on 15 June 2017).
- Constantine, W.; Percival, D.; Constantine, M.W.; Percival, D.B. The Fractal Package for R. Available online: https://cran.r-project.org/web/packages/fractal/fractal.pdf (accessed on 15 June 2017).
- Maechler, M.; Fraley, C.; Leisch, F. The Fracdiff Package for R. Available online: https://cran.r-project.org/web/packages/fracdiff/fracdiff.pdf (accessed on 15 June 2017).
- Contreras-Reyes, J.E.; Goerg, G.M.; Palma, W. The Afmtools Package for R. Available online: http://www2.uaem.mx/r-mirror/web/packages/afmtools/afmtools.pdf (accessed on 15 June 2017).
- Kraft, P.; Weber, C.; Lebo, M. The ArfimaMLM Package for R. Available online: https://cran.r-project.org/web/packages/ArfimaMLM/ArfimaMLM.pdf (accessed on 15 June 2017).
- Veenstra, J.Q.; McLeod, A. The Arfima Package for R. Available online: https://cran.r-project.org/web/packages/arfima/arfima.pdf (accessed on 15 June 2017).
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications: With R Examples; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Jensen, A.N.; Nielsen, M.Ø. A fast fractional difference algorithm. J. Time Ser. Anal. 2014, 35, 428–436. [Google Scholar] [CrossRef]
- Ljung, G.M.; Box, G.E. On a measure of lack of fit in time series models. Biometrika 1978, 65, 297–303. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, Y.; Qiu, T. On the robustness of Hurst estimators. IET Signal Process. 2011, 5, 209–225. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, R.; Zhou, A. An improved Hurst parameter estimator based on fractional Fourier transform. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Las Vegas, NV, USA, 4–7 September 2007; American Society of Mechanical Engineers: New York, NY, USA, 2007; pp. 1223–1233. [Google Scholar]
- Palma, W. Long-Memory Time Series: Theory and Methods; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 662. [Google Scholar]
- Palma, W.; Olea, R. An efficient estimator for locally stationary Gaussian long-memory processes. Ann. Stat. 2010, 38, 2958–2997. [Google Scholar] [CrossRef]

| Procedures | MATLAB | R | SAS | OxMetrics |
|---|---|---|---|---|
| Simulation | ✔ | ✔ | ✔ | ✗ |
| Fractional Difference | ✔ | ✔ | ✔ | ✔ |
| Parameter Estimation | ✔ | ✔ | ✔ | ✔ |
| Forecast | ✔ | ✔ | ✗ | ✔ |
| Package | Author | Release Date | Typical Functions | Requirements |
|---|---|---|---|---|
| fractal | William Constantine et al. [31] | 2016-05-21 | hurstSpec | R (≥ 3.0.2) |
| fracdiff | Martin Maechler et al. [32] | 2012-12-02 | fracdiff | longmemo, urca |
| afmtools | Javier E. Contreras-Reyes et al. [33] | 2012-12-28 | arfima.whittle | R (≥ 2.6.0), polynom fracdiff, hypergeo, sandwich, longmemo |
| ArfimaMLM | Patrick Kraft et al. [34] | 2015-01-21 | arfimaMLM | R (≥ 3.0.0), fractal |
| arfima | Justin Q. Veenstra et al. [35] | 2015-12-31 | arfima | R (≥ 2.14.0), ltsa |
| Software | MATLAB | R | SAS | Ox |
|---|---|---|---|---|
| Function | d_filter | diffseries | fdif | fracdiff |
| p-values with 1,5,10,15 lags | 0.0710 | 0.09998 | 0.1062 | 0.0862 |
| 0.2253 | 0.2395 | 0.2414 | 0.2114 | |
| 0.5850 | 0.5320 | 0.5198 | 0.5898 | |
| 0.5330 | 0.4571 | 0.4473 | 0.5473 |
| Number | Parameters | R | SAS | OxMetrices | MATLAB |
|---|---|---|---|---|---|
| 1 | mu | 0.9833 | N/A (Not Applicable) | 0.98799 | 0.9878 |
| 2 | d | 0.1670 | 0.1479624 | 0.282087 | 0.2313 |
| 3 | ar | 0.9070119 | 0.8939677 | −0.254265 | 0.6473 |
| 4 | ma | 0.8603811 | 0.8318787 | 0.18698 | 0.6393 |
| 5 | sigma | 0.1078173 | 0.1073417 | 0.1246 | 0.1163 |
| 6 | p value Lag1 | 0.9195 | N/A | 0.7709458 | 0.9101 |
| 7 | p value Lag5 | 0.6369 | N/A | 0.341324 | 0.6959 |
| 8 | p value Lag10 | 0.8659 | N/A | 0.4367925 | 0.9037 |
| 9 | p value Lag15 | 0.6491 | N/A | 0.6229542 | 0.6776 |
| 10 | LogLikelihood | 2117.224 | 1851.5512 | −570.599 | 1162.527 |
| 11 | MAPE | 28.95 | N/A | 29.36 | 29.02 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Chen, Y.; Zhang, X. An Evaluation of ARFIMA (Autoregressive Fractional Integral Moving Average) Programs. Axioms 2017, 6, 16. https://doi.org/10.3390/axioms6020016
Liu K, Chen Y, Zhang X. An Evaluation of ARFIMA (Autoregressive Fractional Integral Moving Average) Programs. Axioms. 2017; 6(2):16. https://doi.org/10.3390/axioms6020016
Chicago/Turabian StyleLiu, Kai, YangQuan Chen, and Xi Zhang. 2017. "An Evaluation of ARFIMA (Autoregressive Fractional Integral Moving Average) Programs" Axioms 6, no. 2: 16. https://doi.org/10.3390/axioms6020016
APA StyleLiu, K., Chen, Y., & Zhang, X. (2017). An Evaluation of ARFIMA (Autoregressive Fractional Integral Moving Average) Programs. Axioms, 6(2), 16. https://doi.org/10.3390/axioms6020016







