Multivariate Extended Gamma Distribution

Abstract

In this paper, I consider multivariate analogues of the extended gamma density, which will provide multivariate extensions to Tsallis statistics and superstatistics. By making use of the pathway parameter $\beta$, multivariate generalized gamma density can be obtained from the model considered here. Some of its special cases and limiting cases are also mentioned. Conditional density, best predictor function, regression theory, etc., connected with this model are also introduced.

1. Introduction

Consider the generalized gamma density of the form

$$g\left(x\right)=c_1{x}^{\gamma }{\mathrm{e}}^{-a{x}^{\delta }},x\ge 0,a>0,\delta >0,\gamma +1>0,$$

(1)

where $c_1=\frac{\delta a^{\frac{\gamma +1}{\delta }}}{\Gamma \left(\frac{\gamma +1}{\delta }\right)},$ is the normalizing constant. Note that this is the generalization of some standard statistical densities such as gamma, Weibull, exponential, Maxwell-Boltzmann, Rayleigh and many more. We will extend the generalized gamma density by using pathway model of [1] and we get the extended function as

$$g_1\left(x\right)=c_2{x}^{\gamma }{[1+a(\beta -1)x^{\delta }]}^{-\frac{1}{\beta -1}},x\ge 0,\beta >1,a>0,\delta >0$$

(2)

where $c_2=\frac{\delta {\left(a(\beta -1)\right)}^{\frac{\gamma +1}{\delta }}\Gamma \left(\frac{1}{\beta -1}\right)}{\Gamma \left(\frac{\gamma +1}{\delta }\right)\Gamma (\frac{1}{\beta -1}-\frac{\gamma +1}{\delta })},$ is the normalizing constant.

Note that $g_1\left(x\right)$ is a generalized type-2 beta model. Also ${\displaystyle \underset{\beta \to 1}{lim}{g}_1\left(x\right)=g\left(x\right),}$ so that it can be considered to be an extended form of $g\left(x\right)$. For various values of the pathway parameter $\beta$ a path is created so that one can see the movement of the function denoted by $g_1\left(x\right)$ above towards a generalized gamma density. From the Figure 1 we can see that, as $\beta$ moves away from 1 the function $g_1\left(x\right)$ moves away from the origin and it becomes thicker tailed and less peaked. From the path created by $\beta$ we note that we obtain densities with thicker or thinner tail compared to generalized gamma density. Observe that for $\beta <1$, writing $\beta -1=-(1-\beta )$ in Equation (2) produce generalized type-1 beta form, which is given by

$$g_2\left(x\right)=c_3{x}^{\gamma }{[1-a(1-\beta )x^{\delta }]}^{\frac{1}{1-\beta }},1-a(1-\beta )x^{\delta }\ge 0,\beta <1,a>0,\delta >0$$

where $c_3=\frac{\delta {\left(a(1-\beta )\right)}^{\frac{\gamma +1}{\delta }}\Gamma (\frac{1}{1-\beta }+1+\frac{\gamma +1}{\delta })}{\Gamma \left(\frac{\gamma +1}{\delta }\right)\Gamma (\frac{1}{1-\beta }+1)},$ is the normalizing constant (see [2]).

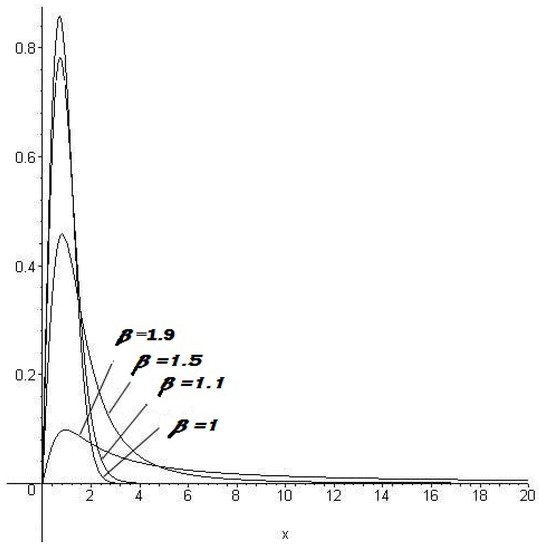
Figure 1. The graph of $g_1\left(x\right)$, for $\gamma =1,$$a=1,\delta =2,\eta =1$ and for various values of $\beta$.

From the above graph, one can see the movement of the extended gamma density denoted by $g_1\left(x\right)$ towards the generalized gamma density, for various values of the pathway parameter $\beta$. Beck and Cohen’s superstatistics belong to the case (2) [3,4]. For $\gamma =1,a=1,\delta =1$ we have Tsallis statistics [5,6] for $\beta >1$ from (2).

Several multivariate extensions of the univariate gamma distributions exist in the literature [7,8,9]. In this paper we consider a multivariate analogue of the extended gamma density (2) and some of its properties.

2. Multivariate Extended Gamma

Various multivarite generalizatons of pathway model are discussed in the papers of Mathai [10,11]. Here we consider the multivariate case of the extended gamma density of the form (2). For $X_i\ge 0,i=1,2,\dots ,n,$ let

$$\begin{array}{cc}\hfill f_{\beta }(x_1,x_2,\dots ,x_n)=& k_{\beta }{x}_1^{{\gamma }_1}{x}_2^{{\gamma }_2}\dots x_n^{{\gamma }_n}{[1+(\beta -1)(a_1{x}_1^{{\delta }_1}+a_2{x}_2^{{\delta }_2}+\dots +a_n{x}_n^{{\delta }_n})]}^{-\frac{\eta }{\beta -1}},\hfill \\ \hfill & \beta >1,\eta >0,{\delta }_i>0,a_i>0,i=1,2,\dots ,n,\hfill \end{array}$$

(3)

where $k_{\beta }$ is the normalizing constant, which will be given later. This multivariate analogue can also produce multivariate extensions to Tsallis statistics [5,12] and superstatistics [3]. Here the variables are not independently distributed, but when $\beta \to 1$ we have a result that $X_1,X_2,\dots ,X_n$ will become independently distributed generalized gamma variables. That is,

$$\begin{array}{ccc}\hfill {\displaystyle \underset{\beta \to 1}{lim}{f}_{\beta }(x_1,x_2,\dots ,x_n)}& =& f(x_1,x_2,\dots ,x_n)\hfill \\ & =& k{x}_1^{{\gamma }_1}{x}_2^{{\gamma }_2}\dots x_n^{{\gamma }_n}{\mathrm{e}}^{-b_1{x}_1^{{\delta }_1}-\dots -b_n{x}_n^{{\delta }_n}},\hfill \\ & & x_i\ge 0,b_i=\eta a_i>0,{\delta }_i>0,i=1,2,\dots ,n,\hfill \end{array}$$

(4)

where ${\displaystyle k=\prod _{i=1}^n\frac{{\delta }_i{b}_i^{\frac{{\gamma }_i+1}{{\delta }_i}}}{\Gamma \left(\frac{{\gamma }_i+1}{{\delta }_i}\right)},{\gamma }_i+1>0,i=1,2,\dots ,n.}$

The following are the graphs of 2-variate extended gamma with ${\gamma }_1=1,{\gamma }_2=1,a_1=1,a_2=1,$ ${\delta }_1=2,{\delta }_2=2$ and for various values of the pathway parameter $\beta .$ From the Figure 2, Figure 3 and Figure 4, we can see the effect of the pathway parameter $\beta$ in the model.

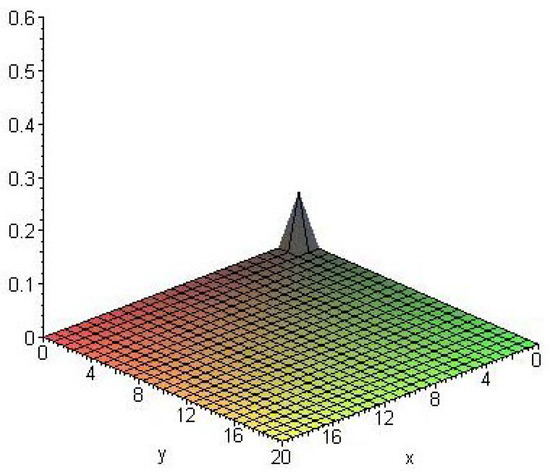
Figure 2. $\beta =1.2$.

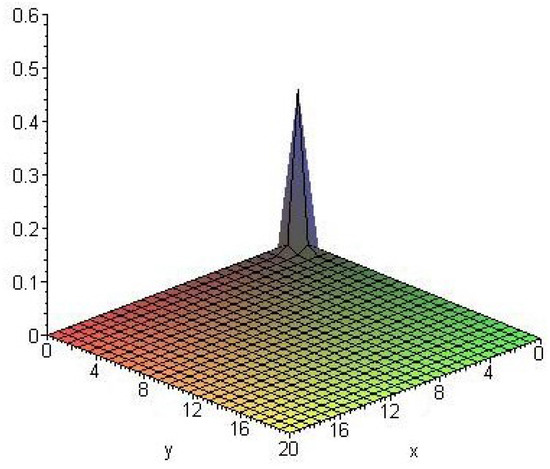
Figure 3. $\beta =1.5$.

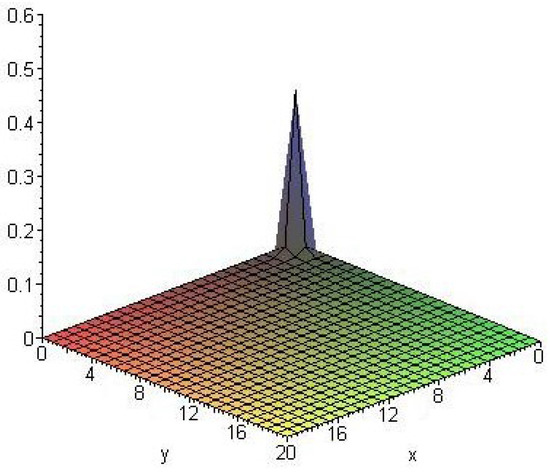
Figure 4. $\beta =2$.

Special Cases and Limiting Cases

• When $\beta$ → 1, (3) will become independently distributed generalized gamma variables. This includes multivariate analogue of gamma, exponential, chisquare, Weibull, Maxwell- Boltzmann, Rayleigh, and related models.
• If $n=1,a_1=1,{\delta }_1=1,\beta =2$, (3) is identical with type-2 beta density.
• If $\beta =2,a_1=a_2=\dots =a_n=1,{\delta }_1={\delta }_2=\dots ={\delta }_n=1$ in (3), then (3) becomes the type-2 Dirichlet density,

  $$D(x_1,x_2,\dots ,x_n)=d{x}_1^{{\nu }_1-1}{x}_2^{{\nu }_2-1}\dots x_n^{{\nu }_n-1}{[1+x_1+x_2+\dots +x_n]}^{-({\nu }_1+\dots +{\nu }_{n+1})},x_i\ge 0,$$

  (5)

  where ${\nu }_i={\gamma }_i+1,i=1,2,\dots ,n,{\nu }_{n+1}=\eta -({\nu }_1+\dots +{\nu }_n)$ and d is the normalizing constant (see [13,14]).

A sample of the surface for $n=2$ is given in the Figure 5.

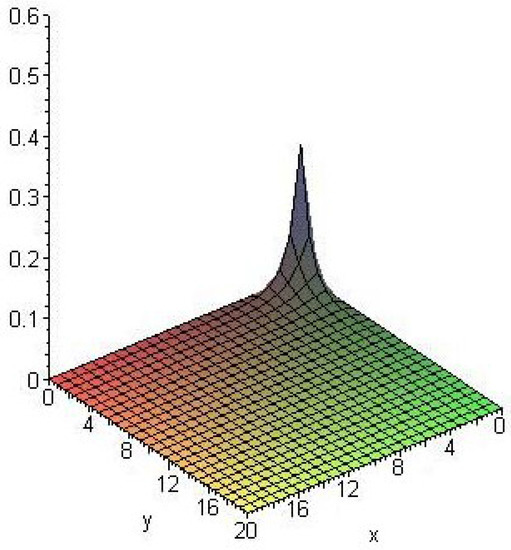
Figure 5. The graph of bivariate type-2 Dirichlet with ${\gamma }_1={\gamma }_2=1,\eta =6.$

3. Marginal Density

We can find the marginal density of $X_i$, by integrating out $X_1,X_2,\dots ,X_{i-1},X_{i+1},\dots ,$$X_{n-1},X_n$. First let us integrate out $X_n,$ then the joint density of $X_1,X_2,\dots ,X_{n-1}$ denoted by $f_1$ is given by

$$\begin{array}{ccc}\hfill f_1(x_1,x_2,\dots ,x_{n-1})& =& {\int }_{x_n>0}{f}_{\beta }(x_1,x_2,\dots ,x_n)\mathrm{d}{x}_n\hfill \\ & =& k_{\beta }{x}_1^{{\gamma }_1}{x}_2^{{\gamma }_2}\dots x_{n-1}^{{\gamma }_{n-1}}{[1+(\beta -1)(a_1{x}_1^{{\delta }_1}+\dots +a_{n-1}{x}_{n-1}^{{\delta }_{n-1}})]}^{-\frac{\eta }{\beta -1}}\hfill \\ & & \times {\int }_{x_n}{x}_n^{{\gamma }_n}{[1+C{x}_n^{{\delta }_n}]}^{-\frac{\eta }{\beta -1}}\mathrm{d}{x}_n,\hfill \end{array}$$

(6)

where $C=\frac{(\beta -1)a_n}{[1+(\beta -1)(a_1{x}_1^{{\delta }_1}+\dots +a_{n-1}{x}_{n-1}^{{\delta }_{n-1}})]}.$ By putting $y=C{x}_n^{{\delta }_n}$ and integrating we get

$$\begin{array}{cc}\hfill f_1(x_1,x_2,\dots ,x_{n-1})=& \frac{k_{\beta }\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_n+1}{{\delta }_n})\Gamma \left(\frac{{\gamma }_n+1}{{\delta }_n}\right)}{{\delta }_n{\left[a_n(\beta -1)\right]}^{\frac{{\gamma }_n+1}{{\delta }_n}}\Gamma \left(\frac{\eta }{\beta -1}\right)}{x}_1^{{\gamma }_1}{x}_2^{{\gamma }_2}\dots x_{n-1}^{{\gamma }_{n-1}}\hfill \\ \hfill & \times {[1+(\beta -1)(a_1{x}_1^{{\delta }_1}+a_2{x}_2^{{\delta }_2}+\dots +a_{n-1}{x}_{n-1}^{{\delta }_{n-1}})]}^{-\left[\frac{\eta }{\beta -1}-\frac{{\gamma }_n+1}{{\delta }_n}\right]},\hfill \end{array}$$

(7)

$x_i\ge 0,i=1,2,\dots ,n-1,a_i>0,{\delta }_i>0,i=1,2,\dots ,n,\beta >1,\eta >0,\frac{\eta }{\beta -1}-\frac{{\gamma }_n+1}{{\delta }_n}>0,{\gamma }_n+1>0.$

In a similar way we can integrate out $X_1,X_2,\dots ,X_{i-1},X_{i+1},\dots ,X_{n-1}$. Then the marginal density of $X_i$ is denoted by $f_2$ and is given by

$$f_2\left(x_i\right)=k_2{x}_i^{{\gamma }_i}{[1+(\beta -1)a_i{x}_i^{{\delta }_i}]}^{-\left[\frac{\eta }{\beta -1}-\frac{{\gamma }_n+1}{{\delta }_n}-\dots -\frac{{\gamma }_{i-1}+1}{{\delta }_{i-1}}-\frac{{\gamma }_{i+1}+1}{{\delta }_{i+1}}-\dots \frac{{\gamma }_1+1}{{\delta }_1}\right]},$$

(8)

where $x_i\ge 0,\beta >1,{\delta }_i>0,\eta >0,$

$$k_2=\frac{{\delta }_i{(a_i(\beta -1))}^{\frac{{\gamma }_i+1}{{\delta }_i}}\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_n+1}{{\delta }_n}-\dots -\frac{{\gamma }_{i-1}+1}{{\delta }_{i-1}}-\frac{{\gamma }_{i+1}+1}{{\delta }_{i+1}}-\dots -\frac{{\gamma }_1+1}{{\delta }_1})}{\Gamma (\frac{{\gamma }_i+1}{{\delta }_i})\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+1}{{\delta }_n})},$$

$${\gamma }_i+1>0,\frac{\eta }{\beta -1}-\frac{{\gamma }_n+1}{{\delta }_n}-\dots -\frac{{\gamma }_{i-1}+1}{{\delta }_{i-1}}-\frac{{\gamma }_{i+1}+1}{{\delta }_{i+1}}-\dots -\frac{{\gamma }_1+1}{{\delta }_1}>0,\frac{\eta }{\beta -1}-\frac{{\gamma }_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+1}{{\delta }_n}>0.$$

If we take any subset of $(X_1,\dots ,X_n),$ the marginal densities belong to the same family. In the limiting case they will also become independently distributed generalized gamma variables.

Normalizing Constant

Integrating out $X_i$ from (8) and equating to 1, we will get the normalizing constant $k_{\beta }$ as

$$k_{\beta }=\frac{{\delta }_1{\delta }_2\dots {\delta }_n{\left(a_1(\beta -1)\right)}^{\frac{{\gamma }_1+1}{{\delta }_1}}{\left(a_2(\beta -1)\right)}^{\frac{{\gamma }_2+1}{{\delta }_2}}\dots {\left(a_n(\beta -1)\right)}^{\frac{{\gamma }_n+1}{{\delta }_n}}\Gamma \left(\frac{\eta }{\beta -1}\right)}{\Gamma \left(\frac{{\gamma }_1+1}{{\delta }_1}\right)\Gamma \left(\frac{{\gamma }_2+1}{{\delta }_2}\right)\dots \Gamma \left(\frac{{\gamma }_n+1}{{\delta }_n}\right)\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+1}{{\delta }_n})},$$

(9)

$${\delta }_i>0,a_i>0,{\gamma }_i+1>0,i=1,2,\dots ,n,\beta >1,\eta >0,\frac{\eta }{\beta -1}-\frac{{\gamma }_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+1}{{\delta }_n}>0.$$

4. Joint Product Moment and Structural Representations

Let $(X_1,\dots ,X_n)$ have a multivariate extended gamma density (23). By observing the normalizing constant in (9), we can easily obtained the joint product moment for some arbitrary $(h_1,\dots ,h_n)$,

$$\begin{array}{cc}\hfill E(x_1^{h_1}{x}_2^{h_2}\dots x_n^{h_n})& =k_{\beta }\frac{\Gamma \left(\frac{{\gamma }_1+h_1+1}{{\delta }_1}\right)\dots \Gamma \left(\frac{{\gamma }_n+h_n+1}{{\delta }_n}\right)\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_1+h_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+h_n+1}{{\delta }_n})}{{\delta }_1{\delta }_2\dots {\delta }_n{\left(a_1(\beta -1)\right)}^{\frac{{\gamma }_1+h_1+1}{{\delta }_1}}\dots {\left(a_n(\beta -1)\right)}^{\frac{{\gamma }_n+h_n+1}{{\delta }_n}}\Gamma \left(\frac{\eta }{\beta -1}\right)}\hfill \\ & =\frac{{\displaystyle \Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_1+h_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+h_n+1}{{\delta }_n})\prod _{i=1}^n\Gamma \left(\frac{{\gamma }_i+h_i+1}{{\delta }_i}\right)}}{{\displaystyle \Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+1}{{\delta }_n})\prod _{i=1}^n{\left[a_i(\beta -1)\right]}^{\frac{h_i}{{\delta }_i}}\Gamma \left(\frac{{\gamma }_i+1}{{\delta }_i}\right)}},\hfill \end{array}$$

(10)

$$\frac{\eta }{\beta -1}-\sum _{i=1}^n\frac{{\gamma }_i+h_i+1}{{\delta }_i}>0,{\gamma }_i+h_i+1>0,\frac{\eta }{\beta -1}-\sum _{i=1}^n\frac{{\gamma }_i+1}{{\delta }_i}>0,{\gamma }_i+1>0,a_i>0,\beta >1,{\delta }_i>0,i=1,2,\dots ,n.$$

Property 1.

The joint product moment of the multivariate extended gamma density can be written as

$$E(x_1^{h_1}{x}_2^{h_2}\dots x_n^{h_n})=\frac{{\displaystyle \Gamma \left(\frac{\eta }{\beta -1}-\sum _{i=1}^n\frac{{\gamma }_i+h_i+1}{{\delta }_i}\right)}}{{\displaystyle \Gamma \left(\frac{\eta }{\beta -1}-\sum _{i=1}^n\frac{{\gamma }_i+1}{{\delta }_i}\right)}}{\displaystyle \prod _{i=1}^{n}E\left(y_i^{h_i}\right)},$$

(11)

where $Y_i$’ s are generalized gamma random variables having density function

$$f_y\left(y_i\right)=c_i{y}_i^{{\gamma }_i}{\mathrm{e}}^{-{\left[a_i(\beta -1)y_i\right]}^{{\delta }_i}},y_i\ge 0,\beta >1,a_i>0,{\delta }_i>0,$$

(12)

where $c_i=\frac{{\delta }_i{\left[a_i(\beta -1)\right]}^{\frac{{\gamma }_i+1}{{\delta }_i}}}{\Gamma \left(\frac{{\gamma }_i+1}{{\delta }_i}\right)},{\gamma }_i+1>0,i=1,2,\dots ,n,$ is the normalizing constant.

Property 2.

Letting $h_2=\dots =h_n=0,$ in (10), we get

$$E\left(x_1^{h_1}\right)=\frac{\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_1+h_1+1}{{\delta }_1}-\frac{{\gamma }_2+1}{{\delta }_2}-\dots -\frac{{\gamma }_n+1}{{\delta }_n})\Gamma \left(\frac{{\gamma }_1+h_1+1}{{\delta }_1}\right)}{\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+1}{{\delta }_n}){\left[a_1(\beta -1)\right]}^{\frac{h_1}{{\delta }_1}}\Gamma \left(\frac{{\gamma }_1+1}{{\delta }_1}\right)},$$

(13)

${\displaystyle \frac{\eta }{\beta -1}-\frac{{\gamma }_1+h_1+1}{{\delta }_1}-\sum _{i=2}^n\frac{{\gamma }_i+1}{{\delta }_i}>0,\frac{{\gamma }_1+h_1+1}{{\delta }_1}>0,\frac{\eta }{\beta -1}-\sum _{i=1}^n\frac{{\gamma }_i+1}{{\delta }_i}>0,{\gamma }_1+1>0,a_1>0,}$ $\beta >1,$ ${\delta }_1>0.$ (13) is the $h_1^{th}$ moment of a random variable with density function of the the form (8),

$$f_3\left(x_1\right)=k_3{x}_1^{{\gamma }_1}{[1+(\beta -1)a_1{x}_1^{{\delta }_1}]}^{-\left[\frac{\eta }{\beta -1}-\frac{{\gamma }_2+1}{{\delta }_2}-\dots -\frac{{\gamma }_n+1}{{\delta }_n}\right]},$$

(14)

where $k_3$ is the normalizing constant. Then

$$E\left(x_1^{h_1}\right)=k_3{\int }_0^{\infty }{x}_1^{{\gamma }_1}{[1+a_1(\beta -1)x_1^{{\delta }_1}]}^{-[\frac{\eta }{\beta -1}-\frac{{\gamma }_2+1}{{\delta }_2}-\dots -\frac{{\gamma }_n+1}{{\delta }_n}]}\mathrm{d}{x}_1$$

(15)

Making the substitution $y=a_1(\beta -1)x_1^{{\delta }_1}$, then it will be in the form of a type-2 beta density and we can easily obtained the $h_1^{th}$ moment as in (13).

Property 3.

Letting $h_3=\dots =h_n=0,$ in (10), we get

$$E\left(x_1^{h_1}{x}_2^{h_2}\right)=\frac{\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_1+h_1+1}{{\delta }_1}-\frac{{\gamma }_2+h_2+1}{{\delta }_2}-\dots -\frac{{\gamma }_n+1}{{\delta }_n})\Gamma \left(\frac{{\gamma }_1+h_1+1}{{\delta }_1}\right)\Gamma \left(\frac{{\gamma }_2+h_2+1}{{\delta }_2}\right)}{\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+1}{{\delta }_n}){\left[a_1(\beta -1)\right]}^{\frac{h_1}{{\delta }_1}}{\left[a_2(\beta -1)\right]}^{\frac{h_2}{{\delta }_2}}\Gamma \left(\frac{{\gamma }_1+1}{{\delta }_1}\right)\Gamma \left(\frac{{\gamma }_2+1}{{\delta }_2}\right)},$$

(16)

${\displaystyle \frac{\eta }{\beta -1}-\frac{{\gamma }_1+h_1+1}{{\delta }_1}-\frac{{\gamma }_2+h_2+1}{{\delta }_2}-\sum _{i=3}^n\frac{{\gamma }_i+1}{{\delta }_i}>0,\frac{\eta }{\beta -1}-\sum _{i=1}^n\frac{{\gamma }_i+1}{{\delta }_i}>0,\beta >1,{\gamma }_i+h_i+1>0,}$ ${\gamma }_i+1>0,$ $a_i>0,{\delta }_i>0,i=1,2,$ which is the joint product moment of a bivariate extended gamma density is denoted by $f_4$ and is given by

$$f_4\left(x_1{x}_2\right)=k_4{x}_1^{{\gamma }_1}{x}_2^{{\gamma }_2}{[1+(\beta -1)(a_1{x}_1^{{\delta }_1}+a_2{x}_2^{{\delta }_2})]}^{-\left[\frac{\eta }{\beta -1}-\frac{{\gamma }_3+1}{{\delta }_3}-\dots -\frac{{\gamma }_n+1}{{\delta }_n}\right]},$$

(17)

where $k_4$ is the normalizing constant. (17) is obtained by integrating out $X_3,\dots ,X_n$ from (3). By putting $h_4=\dots =h_n=0,$ in (10), we get the joint product moment of trivariate extended gamma density and so on.

Theorem 1.

When $X_1,\dots ,X_n$ has density in (3), then

$$\begin{array}{cc}\hfill & E\{x_1^{h_1}\dots x_n^{h_n}{[1+(\beta -1)(a_1{x}_1^{{\delta }_1}+\dots +a_n{x}_n^{{\delta }_n})]}^{h^{\prime }}\}\hfill \\ \hfill =& k_{\beta }\frac{\Gamma \left(\frac{{\gamma }_1+h_1+1}{{\delta }_1}\right)\dots \Gamma \left(\frac{{\gamma }_n+h_n+1}{{\delta }_n}\right)\Gamma (\frac{\eta }{\beta -1}-h^{\prime }-\frac{{\gamma }_1+h_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+h_n+1}{{\delta }_n})}{{\delta }_1{\delta }_2\dots {\delta }_n{\left(a_1(\beta -1)\right)}^{\frac{{\gamma }_1+h_1+1}{{\delta }_1}}\dots {\left(a_n(\beta -1)\right)}^{\frac{{\gamma }_n+h_n+1}{{\delta }_n}}\Gamma (\frac{\eta }{\beta -1}-h^{\prime })}\hfill \\ \hfill =& \frac{{\displaystyle \Gamma \left(\frac{\eta }{\beta -1}\right)\Gamma (\frac{\eta }{\beta -1}-h^{\prime }-\frac{{\gamma }_1+h_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+h_n+1}{{\delta }_n})\prod _{i=1}^n\Gamma \left(\frac{{\gamma }_i+h_i+1}{{\delta }_i}\right)}}{{\displaystyle \Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+1}{{\delta }_n})\Gamma (\frac{\eta }{\beta -1}-h^{\prime })\prod _{i=1}^n\left\{{\left[a_i(\beta -1)\right]}^{\frac{h_i}{{\delta }_i}}\Gamma \left(\frac{{\gamma }_i+1}{{\delta }_i}\right)\right\}}},\hfill \end{array}$$

(18)

${\displaystyle \frac{\eta }{\beta -1}-h^{\prime }-\sum _{i=1}^n\frac{{\gamma }_i+h_i+1}{{\delta }_i}>0,{\gamma }_i+h_i+1>0,\frac{\eta }{\beta -1}-\sum _{i=1}^n\frac{{\gamma }_i+1}{{\delta }_i}>0,{\gamma }_i+1>0,a_i>0,\beta >1,}$$\eta >0,$${\delta }_i>0,$$i=1,2,\dots ,n.$

Corollary 1.

When $X_1,\dots ,X_n$ has density in (3), then

$$E\left\{{[1+(\beta -1)(a_1{x}_1^{{\delta }_1}+\dots +a_n{x}_n^{{\delta }_n})]}^{h^{\prime }}\right\}=\frac{\Gamma \left(\frac{\eta }{\beta -1}\right)\Gamma (\frac{\eta }{\beta -1}-h^{\prime }-\frac{{\gamma }_1+h_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+h_n+1}{{\delta }_n})}{\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_1+1}{{\delta }_1}-\dots -\frac{{\gamma }_n+1}{{\delta }_n})\Gamma (\frac{\eta }{\beta -1}-h^{\prime })},$$

(19)

$$\frac{\eta }{\beta -1}-h^{\prime }-\sum _{i=1}^n\frac{{\gamma }_i+h_i+1}{{\delta }_i}>0,\frac{\eta }{\beta -1}-h^{\prime }>0,\frac{\eta }{\beta -1}-\sum _{i=1}^n\frac{{\gamma }_i+1}{{\delta }_i}>0,a_i>0,\beta >1,\eta >0,{\delta }_i>0,i=1,2,\dots ,n.$$

4.1. Variance-Covariance Matrix

Let X be a $n\times 1$ vector. Variance-covariance matrix is obtained by taking $E\left[(X-E\left(X\right)){(X-E\left(X\right))}^{\prime }\right]$. Then the elements will be of the form

$$E\left[(X-E\left(X\right)){(X-E\left(X\right))}^{\prime }\right]=\left[\begin{array}{cccc}\mathrm{Var}\left(x_1\right)\hfill & \mathrm{Cov}({\mathrm{x}}_1,{\mathrm{x}}_2)\hfill & \dots \hfill & \mathrm{Cov}({\mathrm{x}}_1,{\mathrm{x}}_{\mathrm{n}})\hfill \\ \mathrm{Cov}({\mathrm{x}}_2,{\mathrm{x}}_1)\hfill & \mathrm{Var}\left(x_2\right)\hfill & \dots \hfill & \mathrm{Cov}({\mathrm{x}}_2,{\mathrm{x}}_{\mathrm{n}})\hfill \\ ⋮\hfill & \hfill & \ddots \hfill & \hfill \\ \mathrm{Cov}({\mathrm{x}}_{\mathrm{n}},{\mathrm{x}}_1)\hfill & \mathrm{Cov}({\mathrm{x}}_{\mathrm{n}},{\mathrm{x}}_2)\hfill & \dots \hfill & \mathrm{Var}\left(x_n\right)\hfill \end{array}\right]$$

where

$$\mathrm{Cov}(x_i,x_j)=E\left(x_i{x}_j\right)-E\left(x_i\right)E\left(x_j\right),i,j=1,2,\dots ,n,i\ne j$$

(20)

and

$$\mathrm{Var}\left(x_i\right)=E\left(x_i^2\right)-{\left[E\left(x_i\right)\right]}^2,i=1,2,\dots ,n.$$

(21)

$E\left(x_i{x}_j\right)$’s are obtained from (10) by putting $h_i=h_j=1$ and all other $h_k=0,k=1,2,\dots ,n,$ $k\ne i,j$. $E\left(x_i\right)$’s and $E\left(x_i^2\right)$’s are respectively obtained from (10) by putting $h_i=1$ and $h_i=2$ and all other $h_k=0,k=1,2,\dots ,n,k\ne i.$ Where

$$E\left(x_1{x}_2\right)={\int }_0^{\infty }{\int }_0^{\infty }{x}_1{x}_2{f}_2(x_1,x_2)\mathrm{d}{x}_1\mathrm{d}{x}_2.$$

(22)

4.2. Normalizing Constant

Integrate out $x_i$ from (8) and equate with 1, we will get the normalizing constant $K_{\alpha }$ as

$$K_{\alpha }=\frac{{\delta }_1{\delta }_2\cdots {\delta }_n{\left(a_1(\alpha -1)\right)}^{\frac{{\gamma }_1+1}{{\delta }_1}}{\left(a_2(\alpha -1)\right)}^{\frac{{\gamma }_2+1}{{\delta }_2}}\cdots {\left(a_n(\alpha -1)\right)}^{\frac{{\gamma }_n+1}{{\delta }_n}}\Gamma \left(\frac{\eta }{\alpha -1}\right)}{\Gamma \left(\frac{{\gamma }_1+1}{{\delta }_1}\right)\Gamma \left(\frac{{\gamma }_2+1}{{\delta }_2}\right)\cdots \Gamma \left(\frac{{\gamma }_n+1}{{\delta }_n}\right)\Gamma (\frac{\eta }{\alpha -1}-\frac{{\gamma }_1+1}{{\delta }_1}-\cdots -\frac{{\gamma }_n+1}{{\delta }_n})}.$$

(23)

5. Regression Type Models and Limiting Approaches

The conditional density of $X_i$ given $X_1,X_2,\dots ,X_{i-1},X_{i+1},\dots ,X_n$ is denoted by $f_5$ and is given by

$$\begin{array}{cc}\hfill & f_5\left(x_i\right|x_1,x_2,\dots ,x_{i-1},x_{i+1},\dots ,x_n)=\frac{f_{\beta }(x_1,x_2,\dots ,x_n)}{f_6(x_1,x_2,\dots ,x_{i-1},x_{i+1},\dots ,x_n)}\hfill \\ \hfill =& \frac{{\delta }_i{\left[a_i(\beta -1)\right]}^{\frac{{\gamma }_i+1}{{\delta }_i}}\Gamma \left(\frac{\eta }{\beta -1}\right)}{\Gamma \left(\frac{{\gamma }_i+1}{{\delta }_i}\right)\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_i+1}{{\delta }_i})}{x}_i^{{\gamma }_i}\hfill \\ & \times {[1+\frac{(\beta -1)a_i{x}_i^{{\delta }_i}}{1+(\beta -1)(a_1{x}_1^{{\delta }_1}+a_2{x}_2^{{\delta }_2}+\dots +a_{i-1}{x}_{i-1}^{{\delta }_{i-1}}+a_{i+1}{x}_{i+1}^{{\delta }_{i+1}}+\dots +a_n{x}_n^{{\delta }_n})}]}^{-\frac{\eta }{\beta -1}}\hfill \\ & \times {[1+(\beta -1)(a_1{x}_1^{{\delta }_1}+a_2{x}_2^{{\delta }_2}+\dots +a_{i-1}{x}_{i-1}^{{\delta }_{i-1}}+a_{i+1}{x}_{i+1}^{{\delta }_{i+1}}+\dots +a_n{x}_n^{{\delta }_n})]}^{-\frac{{\gamma }_i+1}{{\delta }_i}},\hfill \end{array}$$

(24)

where $f_6$ is the joint density of $X_1,X_2,\dots ,X_{i-1},X_{i+1},\dots ,X_n$. When we take the limit as $\beta \to 1$ in Equation (24), we can see that the conditional density will be in the form of a generalized gamma density and is given by

$$\begin{array}{c}\hfill {\displaystyle \underset{\beta \to 1}{lim}{f}_5\left(x_i\right|x_1,x_2,\dots ,,x_{i-1},x_{i+1},\dots ,x_n)=\frac{{\delta }_i{\left(\eta a_i\right)}^{\frac{{\gamma }_i+1}{{\delta }_i}}}{\Gamma \left(\frac{{\gamma }_i+1}{{\delta }_i}\right)}{x}_i^{{\gamma }_i}{\mathrm{e}}^{-a_i{x}_i^{{\delta }_i}},}\end{array}$$

(25)

$$x_i\ge 0,{\delta }_i>0,\eta >0,{\gamma }_i+1>0.$$

Theorem 2.

Let $(X_1,X_2,\dots ,X_n)$ have a multivariate extended gamma density (3), then the limiting case of the conditional density $f_{\beta }\left(x_i\right|x_1,x_2,\dots ,,x_{i-1},x_{i+1},\dots ,x_n)$ will be a generalized gamma density (25).

Best Predictor

The conditional expectation, $E\left(x_n\right|x_1,\dots ,x_{n-1})$, is the best predictor, best in the sense of minimizing the expected squared error. Variables which are preassigned are usually called independent variables and the others are called dependent variables. In this context, $X_n$ is the dependent variable or being predicted and $X_1,\dots ,X_{n-1}$ are the preassigned variables or independent variables. This ‘best’ predictor is defined as the regression function of $X_n$ on $X_1,\dots ,X_{n-1}$.

$$\begin{array}{cc}\hfill & E\left(x_n\right|x_1,\dots ,x_{n-1})={\int }_{x_n=0}^{\infty }{x}_n{f}_7\left(x_n\right|x_1,\dots ,x_{n-1})\mathrm{d}{x}_n\hfill \\ \hfill =& \frac{{\delta }_n{\left[a_n(\beta -1)\right]}^{\frac{{\gamma }_n+1}{{\delta }_n}}\Gamma \left(\frac{\eta }{\beta -1}\right)}{\Gamma \left(\frac{{\gamma }_n+1}{{\delta }_n}\right)\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_n+1}{{\delta }_n})}{[1+(\beta -1)(a_1{x}_1^{{\delta }_1}+a_2{x}_2^{{\delta }_2}+\dots +a_{n-1}{x}_{n-1}^{{\delta }_{n-1}})]}^{-\frac{{\gamma }_n+1}{{\delta }_n}+\frac{\eta }{\beta -1}}\hfill \\ & \times {\int }_{x_n=0}^{\infty }{x}_n^{{\gamma }_n+1}{[1+(\beta -1)(a_1{x}_1^{{\delta }_1}+a_2{x}_2^{{\delta }_2}+\dots +a_n{x}_n^{{\delta }_n})]}^{-\frac{\eta }{\beta -1}}\mathrm{d}{x}_n.\hfill \end{array}$$

(26)

We can integrate the above integral as in the case of Equation (6). Then after simplification we will get the best predictor of $X_n$ at preassigned values of $X_1,\dots ,X_{n-1}$ which is given by

$$\begin{array}{cc}\hfill E\left(x_n\right|x_1,\dots ,x_{n-1})=& \frac{{\delta }_n{\left[a_n(\beta -1)\right]}^{-\frac{1}{{\delta }_n}}\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_n+2}{{\delta }_n})\Gamma \left(\frac{{\gamma }_n+2}{{\delta }_n}\right)}{\Gamma \left(\frac{{\gamma }_n+1}{{\delta }_n}\right)\Gamma (\frac{\eta }{\beta -1}-\frac{{\gamma }_n+1}{{\delta }_n})}\hfill \\ & \times {[1+(\beta -1)(a_1{x}_1^{{\delta }_1}+a_2{x}_2^{{\delta }_2}+\dots +a_{n-1}{x}_{n-1}^{{\delta }_{n-1}})]}^{-\frac{1}{{\delta }_n}},\hfill \end{array}$$

(27)

${\delta }_n>0,a_n>0,\beta >1,x_i>0,i=1,2,\dots ,n-1,\frac{\eta }{\beta -1}-\frac{{\gamma }_n+2}{{\delta }_n}>0,{\gamma }_n+1>0.$ We can take the limit $\beta \to 1$ in (27). For taking limit, let us apply Stirling’s approximations for gamma functions, see for example [15]

$$\Gamma (z+a)\to {\left(2\pi \right)}^{\frac{1}{2}}{z}^{z+a-\frac{1}{2}}{\mathrm{e}}^{-z},\mathrm{for}\left|z\right|\to \infty \mathrm{and}a\mathrm{is}\mathrm{bounded}$$

(28)

to the gamma’s in (27). Then we will get

$$\begin{array}{ccc}\hfill \underset{\beta \to 1}{lim}E\left(x_n\right|x_1,\dots ,x_{n-1})& =& \frac{{\delta }_n\Gamma \left(\frac{{\gamma }_n+2}{{\delta }_n}\right)}{{\left(a_n\eta \right)}^{\frac{1}{{\delta }_n}}\Gamma \left(\frac{{\gamma }_n+1}{{\delta }_n}\right)}\hfill \end{array}$$

(29)

which is the moment of a generalized gamma density as given in (25).

6. Multivariate Extended Gamma When $\mathit{\beta }<\mathbf{1}$

Consider the case when the pathway parameter $\beta$ is less than 1, then the pathway model has the form

$$g\left(x\right)=K{x}^{\gamma }{[1-a(1-\beta )x^{\delta }]}^{\frac{\eta }{1-\beta }},\beta <1,a>0,\delta >0,\eta >0,$$

(30)

$1-a(1-\beta )x^{\delta }\ge 0,$ and K is the normalizing constant. $g\left(x\right)$ is the generalized type-1 beta model. Let us consider a multivariate case of the above model as

$$\begin{array}{cc}\hfill g_{\beta }(x_1,x_2,\dots ,x_n)=& K_{\beta }{x}_1^{{\gamma }_1}{x}_2^{{\gamma }_2}\dots x_n^{{\gamma }_n}{[1-(1-\beta )(a_1{x}_1^{{\delta }_1}+a_2{x}_2^{{\delta }_2}+\dots +a_n{x}_n^{{\delta }_n})]}^{\frac{\eta }{1-\beta }},\hfill \\ & \beta <1,\eta >0,{\delta }_i>0,a_i>0,i=1,2,\dots ,n,\hfill \\ & 1-(1-\beta )(a_1{x}_1^{{\delta }_1}+a_2{x}_2^{{\delta }_2}+\dots +a_n{x}_n^{{\delta }_n})\ge 0.\hfill \end{array}$$

(31)

where $K_{\beta }$ is the normalizing constant and it can be obtained by solving

$$\begin{array}{c}\hfill {\displaystyle K_{\beta }\int \dots {\int }_{}{x}_1^{{\gamma }_1}\dots x_n^{{\gamma }_n}{[1-(1-\beta )(a_1{x}_1^{{\delta }_1}+\dots +a_n{x}_n^{{\delta }_n})]}^{\frac{\eta }{1-\beta }}\mathrm{d}{x}_1\dots \mathrm{d}{x}_n=1}\end{array}$$

(32)

Integration over $x_n$ yields the following,

$$K_{\beta }{x}_1^{{\gamma }_1}{x}_2^{{\gamma }_2}\dots x_{n-1}^{{\gamma }_{n-1}}{[1-(1-\beta )(a_1{x}_1^{{\delta }_1}+\dots +a_{n-1}{x}_{n-1}^{{\delta }_{n-1}})]}^{\frac{\eta }{1-\beta }}{\int }_0^u{x}_n^{{\gamma }_n}{[1+C_1{x}_n^{{\delta }_n}]}^{-\frac{\eta }{\beta -1}}\mathrm{d}{x}_n,$$

(33)

where $u={\left[\frac{1-(1-\beta )(a_1{x}_1^{{\delta }_1}+\dots +a_{n-1}{x}_{n-1}^{{\delta }_{n-1}})}{a_n(1-\beta )}\right]}^{\frac{1}{\delta }}$ and $C_1=\frac{(1-\beta )a_n}{[1-(1-\beta )(a_1{x}_1^{{\delta }_1}+\dots +a_{n-1}{x}_{n-1}^{{\delta }_{n-1}})]}.$ Letting $y=C_1{x}_n^{{\delta }_n},$ then the above integral becomes a type-1 Dirichlet integral and the normalizing constant can be obtained as

$$\begin{array}{c}\hfill K_{\beta }=\frac{{\displaystyle \prod _{j=1}^n\left[{\delta }_j{\left((1-\beta )a_j\right)}^{\frac{{\gamma }_j+1}{{\delta }_j}}\right]\Gamma (1+\frac{\eta }{1-\beta }+\frac{{\gamma }_1+1}{{\delta }_1}+\dots +\frac{{\gamma }_n+1}{{\delta }_n})}}{\Gamma \left(\frac{{\gamma }_1+1}{{\delta }_1}\right)\dots \Gamma \left(\frac{{\gamma }_n+1}{{\delta }_n}\right)\Gamma (1+\frac{\eta }{1-\beta })}\end{array}$$

(34)

When $\beta \to 1$, (31) will become the density of independently distributed generalized gamma variables. By observing the normalizing constant in (34), we can easily obtaine the joint product moment for some arbitrary $(h_1,\dots ,h_n)$,

$$\begin{array}{c}\hfill E(x_1^{h_1}{x}_2^{h_2}\dots x_n^{h_n})=K_{\beta }\frac{\Gamma \left(\frac{{\gamma }_1+h_1+1}{{\delta }_1}\right)\dots \Gamma \left(\frac{{\gamma }_n+h_n+1}{{\delta }_n}\right)\Gamma (1+\frac{\eta }{1-\beta })}{{\displaystyle \prod _{j=1}^n\left[{\delta }_j{\left((1-\beta )a_j\right)}^{\frac{{\gamma }_j+h_j+1}{{\delta }_j}}\right]\Gamma (1+\frac{\eta }{1-\beta }+\frac{{\gamma }_1+h_1+1}{{\delta }_1}+\dots +\frac{{\gamma }_n+h_n+1}{{\delta }_n})}}\\ \hfill =\frac{\Gamma (1+\frac{\eta }{1-\beta }+\frac{{\gamma }_1+1}{{\delta }_1}+\dots +\frac{{\gamma }_n+1}{{\delta }_n})\Gamma \left(\frac{{\gamma }_1+h_1+1}{{\delta }_1}\right)\dots \Gamma \left(\frac{{\gamma }_n+h_n+1}{{\delta }_n}\right)}{{\displaystyle \prod _{j=1}^n\left[{\left((1-\beta )a_j\right)}^{\frac{h_j}{{\delta }_j}}\right]\Gamma (1+\frac{\eta }{1-\beta }+\frac{{\gamma }_1+h_1+1}{{\delta }_1}+\dots +\frac{{\gamma }_n+h_n+1}{{\delta }_n})\Gamma \left(\frac{{\gamma }_1+1}{{\delta }_1}\right)\dots \Gamma \left(\frac{{\gamma }_n+1}{{\delta }_n}\right)}},\end{array}$$

(35)

$${\gamma }_i+h_j+1>0,{\gamma }_j+1>0,a_j>0,\beta <1,{\delta }_j>0,j=1,2,\dots ,n.$$

Letting $h_2=\dots =h_n=0,$ in (35), we get

$$E\left(x_1^{h_1}\right)=\frac{\Gamma (1+\frac{\eta }{1-\beta }+\frac{{\gamma }_1+1}{{\delta }_1}+\dots +\frac{{\gamma }_n+1}{{\delta }_n})\Gamma \left(\frac{{\gamma }_1+h_1+1}{{\delta }_1}\right)}{{\left[(1-\beta )a_1\right]}^{\frac{h_1}{{\delta }_1}}]\Gamma (1+\frac{\eta }{1-\beta }+\frac{{\gamma }_1+h_1+1}{{\delta }_1}+\frac{{\gamma }_2+1}{{\delta }_2}\dots +\frac{{\gamma }_n+1}{{\delta }_n})\Gamma \left(\frac{{\gamma }_1+1}{{\delta }_1}\right)},$$

(36)

$${\gamma }_1+h_1+1>0,{\gamma }_j+1>0,a_1>0,\beta <1,{\delta }_j>0,\eta >0,j=1,2,\dots ,n.$$

(13) is the $h_1^{\mathrm{th}}$ moment of a random variable with density function,

$$g_1\left(x_1\right)=K_1{x}_1^{{\gamma }_1}{[1-(1-\beta )a_1{x}_1^{{\delta }_1}]}^{\frac{\eta }{1-\beta }+\frac{{\gamma }_2+1}{{\delta }_2}+\dots +\frac{{\gamma }_n+1}{{\delta }_n}},$$

(37)

where $K_1$ is the normalizing constant.

Letting $h_3=\dots =h_n=0,$ in (35), we get

$$\begin{array}{cc}\hfill & E\left(x_1^{h_1}{x}_2^{h_2}\right)\hfill \\ \hfill =& \frac{\Gamma (1+\frac{\eta }{1-\beta }+\frac{{\gamma }_1+1}{{\delta }_1}+\dots +\frac{{\gamma }_n+1}{{\delta }_n})\Gamma \left(\frac{{\gamma }_1+h_1+1}{{\delta }_1}\right)\Gamma \left(\frac{{\gamma }_2+h_2+1}{{\delta }_2}\right)}{{\displaystyle \prod _{j=1}^2\left[{\left((1-\beta )a_j\right)}^{\frac{h_j}{{\delta }_j}}\right]\Gamma \left(1+\frac{\eta }{1-\beta }+\sum _{i=1}^2\frac{{\gamma }_i+h_i+1}{{\delta }_i}+\sum _{j=3}^n\frac{{\gamma }_j+1}{{\delta }_j}\right)\Gamma \left(\frac{{\gamma }_1+1}{{\delta }_1}\right)\Gamma \left(\frac{{\gamma }_2+1}{{\delta }_2}\right)}},\hfill \end{array}$$

(38)

$${\gamma }_1+h_1+1)>0,({\gamma }_2+h_2+1>0,{\gamma }_j+1>0,a_1>0,a_2>0\beta <1,{\delta }_j>0,{\gamma }_j+1>0,j=1,2,\dots ,n.$$

If we proceed in the similar way as in Section 4.1, here we can deduce the variance-covariance matrix of multivariate extended gamma for $\beta <1$.

7. Conclusions

Multivariate counterparts of the extended generalized gamma density is considered and some properties are discussed. Here we considered the variables as not independently distributed, but when the pathway parameter $\beta \to 1$ we can see that $X_1,X_2,\dots ,X_n$ will become independently distributed generalized gamma variables. Joint product moment of the multivariate extended gamma is obtained and some of its properties are discussed. We can see that the limiting case of the conditional density of this multivariate extended gamma is a generalized gamma density. A graphical representation of the pathway is given in Figure 1, Figure 2, Figure 3 and Figure 4.