Extended Parametric Family of Two-Step Methods with Applications for Solving Nonlinear Equations or Systems

Abstract

The parametric family of two-step methods, with its special cases, has been introduced in various papers. However, in most cases, the local convergence analysis relies on the existence of derivatives of orders that the method does not require. Moreover, the more challenging semi-local convergence analysis was not introduced for this class of methods. These drawbacks are considered in this paper. We determine the radius of convergence and the uniqueness of the solution based on generalized continuity conditions. We also present the semi-local convergence analysis for this family of methods, which has not been studied before, using majorizing sequences. Numerical experiments and basins of attraction are included to validate the theoretical conditions and demonstrate the stability of the methods.

1. Introduction

Mathematical modeling is mostly used to convert problems from diverse disciplines to equations like

$$F\left(x\right)=0,$$

(1)

where for $X,Y$ denoting Banach spaces and $D\subset B_1$ an open convex subset, $F:D\to Y$ is a continuously differentiable operator in the Fréchet sense. Then, mostly iterative methods are developed to approximate a solution $x^{\ast }\in D$ of the equation $F\left(x\right)=0$. This is the case since a closed-form solution can be obtained only in special cases.

Newton’s method defined for $x_0\in D$ and each $n=0,1,2,\dots$ by

$$x_{n+1}=x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)$$

(2)

is without a doubt the most popular iterative method [1,2,3,4,5]. Here, the operator $F^{\prime }\left(x\right)\in \mathcal{L}(X,Y)$, which is the space of bounded linear operators mapping X into Y. Newton’s method is of convergence order provided that the initial point $x_0$ is close enough to $x^{\ast }$ and the operator $F^{\prime }\left(x\right)$ is invertible about in a neighborhood about the solution. There is extensive literature on multi-point methods generated to increase the convergence order of an iterative method [6,7,8,9,10,11,12,13,14].

In the present paper, we study the convergence of the family of two-step methods with parameters defined for $x_0\in D$ and each $n=0,1,2,\dots$ by

$$\begin{array}{cc}\hfill y_n& =x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)\hfill \\ \hfill x_{n+1}& =x_n-p_n{F}^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)-q_n{F}^{\prime }{\left(x_n\right)}^{-1}F\left(y_n\right)\hfill \end{array}$$

(3)

or

$$\begin{array}{cc}\hfill y_n& =x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)\hfill \\ \hfill x_{n+1}& =y_n-{\overline{p}}_n{F}^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)-{\overline{q}}_n{F}^{\prime }{\left(x_n\right)}^{-1}F\left(y_n\right),\hfill \end{array}$$

(4)

where $\left\{p_n\right\},\left\{q_n\right\},\left\{{\overline{q}}_n\right\}\in \mathcal{L}(X,Y)$ are sequences depending on $F,F^{\prime }$ and information from previous iterates. Notice that if ${\overline{p}}_n=p_n-I$, then the method (4) reduces to (3). So, it suffices to study only the convergence of the method (3). A plethora of choices exists for the sequences $\left\{p_n\right\}$ and $\left\{q_n\right\}$. As an example, choose $p_n=q_n=I$. Then, method (3) reduces to

$$\begin{array}{cc}\hfill y_n& =x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)\hfill \\ \hfill x_{n+1}& =y_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(y_n\right),\hfill \end{array}$$

(5)

which is a two-step Newton’s method of convergence order three using two function evaluations and one inverse per complete step [2]. Methods of convergence order four with particular interest when $X=Y={\mathbb{R}}^{\alpha }$, where $\alpha$ is a natural number, and the sequences $\left\{p_n\right\},\left\{q_n\right\}$ depend on previous iterates that have already been studied by A. Cordero et al. [15], and J.R. Sharma et al. [16] and are given, respectively, by

$$\begin{array}{cc}\hfill y_n& =x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right),\hfill \\ \hfill x_{n+1}& =y_n-{\displaystyle \frac{2b_n}{1+\lambda b_n}}{F}^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)-{\displaystyle \frac{1}{1+\lambda b_n}}{F}^{\prime }{\left(x_n\right)}^{-1}F\left(y_n\right),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill y_n& =x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)\hfill \\ \hfill x_{n+1}& =x_n-{\gamma }_1\Psi \left(b_n\right)F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)-{\gamma }_2\Psi \left(b_n\right)F^{\prime }{\left(x_n\right)}^{-1}F\left(y_n\right),\hfill \end{array}$$

(7)

where $\lambda$, ${\gamma }_1,{\gamma }_2\in \mathbb{R}$, $b_n={\displaystyle \frac{F{\left(y_n\right)}^{T}F\left(y_n\right)}{F{\left(x_n\right)}^{T}F\left(x_n\right)}}={\displaystyle \frac{\left|\right|F\left(y_n\right){\left|\right|}^2}{\left|\right|F\left(x_n\right){\left|\right|}^2}}$; function $\Psi :{\mathbb{R}}^{\alpha }\to \mathbb{R}$ satisfies $\Psi \left(0\right)={\displaystyle \frac{1}{{\gamma }_1}}={\displaystyle \frac{1}{{\gamma }_2}}$, ${\Psi }^{\prime }\left(0\right)=2\Psi \left(0\right)$ and the superscript T denotes the transpose of the vector function. If we select ${\overline{p}}_n={\displaystyle \frac{2b_n}{1+\lambda b_n}}$ and ${\overline{q}}_n={\displaystyle \frac{1}{1+\lambda b_n}}$, the method (4) specializes to (6). Moreover, if ${\overline{p}}_n={\gamma }_1\psi \left(b_n\right)$ and ${\overline{q}}_n={\gamma }_2\psi \left(b_n\right)$, then method (4) reduces to (7). Notice that the local convergence of methods (6) and (7) has been shown using Taylor series expansions, requiring the existence of derivatives which are not in these methods. As an example, we can choose the following function:

Let $D=[-2,2]$. Define function f on D by

$$f\left(t\right)=\left\{\begin{array}{cc}{\theta }_1^{4}logt+{\theta }_2{t}^5+{\theta }_3{t}^6,\hfill & t\ne 0\hfill \\ 0,\hfill & t=0,\hfill \end{array}\right.$$

where ${\theta }_1\ne 0$ and ${\theta }_1+{\theta }_2=0$. Notice that $f^{\left(4\right)}\left(0\right)$ does not exist, and $x^{\ast }=1\in D$ solves the equation $f\left(x^{\ast }\right)=0$. So, the results in [15,16] cannot guarantee convergence.

Other limitations of this approach have been reported in [16]. The new local convergence is shown using only the operators on the method (3). Moreover, the more important and challenging semi-local convergence of method (3) (i.e., of methods (6) and (7) too) not previously studied is presented using majorizing sequences in a Banach space setting. Moreover, generalized continuity is used to control the derivative and sharpen the error bounds $\left|\right|x_{n+1}-x_n\left|\right|$, $\left|\right|x^{\ast }-x_n\left|\right|$. This way, the applicability of these methods is extended. The same technique can be used on other methods and for the same reasons [1,2,3,4,6,7,8,9,10,11,12,13,14,15,16,17,18,19].

The rest of the paper is structured as follows. Section 2 and Section 3 contain the local and semi-local convergence of method (3), respectively. The numerical experiments appear in Section 4. Final concluding remarks appear in Section 5.

2. Local Convergence Analysis

Let $T=[0,+\infty )$. The analysis relies on some real functions with domain T or a subset of it. It is convenient to introduce the following abbreviations:

(FCND)

For a function which is continuous as well as nondecreasing on the interval T or a subset of it.

(SSE)

For the smallest solution of an equation.

Suppose the following:

(H₁)

There exists FCND $g_0:T\to T$ such that the equation $g_0\left(t\right)-1=0$ has SSE in $T-\left\{0\right\}$, which shall be denoted by $s_0$. Define the set $T_0=[0,s_0)$.

(H₂)

There exists FCND $g:T_0\to T$ such that for function $h_1:T_0\to T$ defined by

$$h_1\left(t\right)={\displaystyle \frac{{\int }_0^{1}g\left((1-\theta )t\right)d\theta }{1-g_0\left(t\right)}}.$$

The equation $h_1\left(t\right)-1=0$ has SSE in $T_0-\left\{0\right\}$, which shall be denoted by $s_1$.

(H₃)

Let $p\ge 0$ and $q\ge 0$ be given constants. The function $h_2:T_0\to T$ defined by

$$h_2\left(t\right)={\displaystyle \frac{{\int }_0^{1}g\left((1-\theta )t\right)d\theta +p(1+{\int }_0^1{g}_0\left(\theta t\right)d\theta )+q(1+{\int }_0^1{g}_0\left(\theta h_1\left(t\right)t\right)d\theta )h_1\left(t\right)}{1-g_0\left(t\right)}}$$

is such that the equation $h_2\left(t\right)-1=0$ has SSE in $T_0-\left\{0\right\}$, which shall be denoted by $s_2$.

Define the parameter s and the interval $T_1$, respectively, by

$$s=min\left\{s_j\right\},j=1,2$$

(8)

and

$$T_1=[0,s).$$

(9)

The parameter s is shown to be a convergence radius for method (3) in Theorem 1. Then, by the definition of functions $h_1,h_2,s$ and $T_1$, we deduce that for each $t\in T_1$

$$0\le g_0\left(t\right)<1$$

(10)

and

$$0\le h_j\left(t\right)<1.$$

(11)

Next, we connect functions $h_1,h_2$ and radius s to the mappings on the method (3).

(H₄)

There exists a solution $x^{\ast }\in D$ and an invertible operator $A\in \mathcal{L}(B_1,B_2)$ such that for each $u\in D$

$$\left|\right|A^{-1}(F^{\prime }\left(u\right)-A)\left|\right|\le g_0\left(\right||u-x^{\ast }\left|\right|).$$

Define the set $D_0=U(x^{\ast },s_0)\cap D$.

(H₅)

$\left|\right|A^{-1}(F^{\prime }\left(u_2\right)-F^{\prime }\left(u_1\right))\left|\right|\le g\left(\right||u_2-u_1\left|\right|)$ for each $u_2,u_1\in D_0$.

(H₆)

There exist parameters $p\ge 0$ and $q\ge 0$ such that for each $n=0,1,2,\dots$

$$\left|\right|I-p_n\left|\right|\le p\mathrm{and}\left|\right|q_n\left|\right|\le q,$$

and

(H₇)

$\mathcal{U}[x^{\ast },s]\subset D$.

Remark 1. 

The linear operator A can be chosen to be $A=I$ (the identity operator) or $A=F^{\prime }\left(\tilde{x}\right)$ for some $\tilde{x}\in D$ other than $x^{\ast }$ or $A=F^{\prime }\left(x^{\ast }\right)$. In the latter case, $x^{\ast }$ is a simple solution of the equation $F\left(x\right)=0$. Other selections are also possible. It is worth noting that conditions $\left(H_4\right)$ and $\left(H_5\right)$ do not necessarily imply that the linear operator $F^{\prime }\left(x^{\ast }\right)$ is invertible.

Next, the main result follows for the local convergence analysis of the method (3). Define the set $U_0=U(x^{\ast },s)-\left\{x^{\ast }\right\}$.

Theorem 1. 

Suppose that the conditions $\left(H_1\right)$–$\left(H_7\right)$ hold. Then, the sequence $\left\{x_n\right\}$ starting from $x_0\in U_0$ and generated by the method (3) converges to the solution $x^{\ast }\in D$ of the equation $F\left(x\right)=0$. Moreover, the following assertions hold for each $n=0,1,2,\dots$

$$\left|\right|y_n-x^{\ast }\left|\right|\le h_1\left(\right||x_n-x^{\ast }\left|\right|\left)\right||x_n-x^{\ast }\left|\right|\le \left|\right|x_n-x^{\ast }\left|\right|<s$$

(12)

and

$$\left|\right|x_{n+1}-x^{\ast }\left|\right|\le h_2\left(\right||x_n-x^{\ast }\left|\right|\left)\right||x_n-x^{\ast }\left|\right|\le \left|\right|x_n-x^{\ast }\left|\right|.$$

(13)

Proof. 

Mathematical induction shall be used to establish the existence of the iterates $\left\{x_n\right\},\left\{y_n\right\}$ as well as the assertions (12) and (13). Let $w\in U_0$. Using the conditions (H₁), (H₄) and (10), we have, in turn, that

$$\left|\right|A^{-1}(F^{\prime }\left(w\right)-A)\left|\right|\le g_0\left(\right||w-x^{\ast }\left|\right|)\le g_0\left(s\right)<1.$$

(14)

Then, it follows by estimate (14) and the Banach lemma on invertible operators [1,3,4,5] that $F^{\prime }\left(w\right)$ is an invertible linear operator and

$$\left|\right|F^{\prime }{\left(w\right)}^{-1}A\left|\right|\le {\displaystyle \frac{1}{1-g_0\left(\right||w-x^{\ast }\left|\right|)}}.$$

(15)

Notice that estimate (15) holds if $w=x_0$, since $x_0\in U_0$. Consequently, the iterate $y_0$ is well defined by the first substep of the method (3), and we can write

$$\begin{array}{cc}\hfill y_0-x^{\ast }& =x_0-x^{\ast }-F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right)\hfill \\ \hfill & =\left[F^{\prime }{\left(x_0\right)}^{-1}A\right]\left[{\int }_0^1{A}^{-1}(F^{\prime }(x^{\ast }+\theta (x_0-x^{\ast }))-F^{\prime }\left(x_0\right))d\theta \right](x_0-x^{\ast }).\hfill \end{array}$$

(16)

By (8), (H₅), (11) (for $j=1$), (15) and (16), we in turn obtain that

$$\begin{array}{cc}\hfill \left|\right|y_0-x^{\ast }\left|\right|& \le {\displaystyle \frac{{\int }_0^{1}g\left((1-\theta )\right||x_0-x^{\ast }\left|\right|\left)d\theta \right||x_0-x^{\ast }\left|\right|}{1-g_0\left(\right||x_0-x^{\ast }\left|\right|)}}\hfill \\ \hfill & \le h_1\left(\right||x_0-x^{\ast }\left|\right|\left)\right||x_0-x^{\ast }\left|\right|\le \left|\right|x_0-x^{\ast }\left|\right|<s,\hfill \end{array}$$

(17)

which shows the assertion (12) if $n=0$ and that the iterate $y_0\in U(x^{\ast },s)$. We need the following estimates:

$$\begin{array}{cc}\hfill F\left(y_0\right)& =F\left(y_0\right)-F\left(x^{\ast }\right)={\int }_0^1{F}^{\prime }(x^{\ast }+\theta (y_0-x^{\ast }))d\theta (y_0-x^{\ast })\hfill \\ \hfill & ={\int }_0^1\left[(F^{\prime }(x^{\ast }+\theta (y_0-x^{\ast }))-A+A)d\theta \right](y_0-x^{\ast }).\hfill \end{array}$$

(18)

So, by (H₄) and (18), it follows that

$$\begin{array}{cc}\hfill \left|\right|A^{-1}F\left(y_0\right)\left|\right|& \le \left[{\int }_0^1{A}^{-1}(F^{\prime }(x^{\ast }+\theta (y_0-x^{\ast }))-A)d\theta +I\right](y_0-x^{\ast })\hfill \\ \hfill \mathrm{and}\\ \hfill \left|\right|A^{-1}F\left(y_0\right)\left|\right|& \le \left(1+{\int }_0^1{g}_0\left(\theta \right||y_0-x^{\ast }\left|\right|)d\theta \right)\left|\right|y_0-x^{\ast }\left|\right|.\hfill \end{array}$$

(19)

By switching $y_0$ by $x_0$ in (19), we also have

$$\left|\right|A^{-1}F\left(x_0\right)\left|\right|\le (1+{\int }_0^1{g}_0\left(\theta \right||x_0-x^{\ast }\left|\right|\left)d\theta \right)\left|\right|x_0-x^{\ast }\left|\right|.$$

(20)

Notice that the iterate $x_1$ is well defined by the second substep of the method (3) since the linear operator $F^{\prime }\left(x_0\right)$ is invertible, and we can write

$$\begin{array}{cc}\hfill x_1-x^{\ast }& =x_0-x^{\ast }-F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right)+(I-p_0)F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right)\hfill \\ \hfill & -q_0{F}^{\prime }{\left(x_0\right)}^{-1}F\left(y_0\right).\hfill \end{array}$$

(21)

In view of (8), (11) (for $j=2$), (17), and (19)–(21), we obtain in turn that

$$\begin{array}{cc}\hfill \left|\right|x_1-x^{\ast }\left|\right|& \le {\displaystyle \frac{1}{1-g_0\left(\right||x_0-x^{\ast }\left|\right|)}}[{\int }_0^{1}g\left((1-\theta )\left|\right|x_0-x^{\ast }\left|\right|\right)d\theta \hfill \\ \hfill & +p(1+{\int }_0^1{g}_0\left(\theta \right||x_0-x^{\ast }\left|\right|\left)d\theta \right)\hfill \\ \hfill & +q(1+{\int }_0^1{g}_0(\theta h_1\left(\right||x_0-x^{\ast }\left|\right|\left)\right)\left|\right|x_0-x^{\ast }\left|\right|)d\theta ]\hfill \\ \hfill & \le h_2\left(\right||x_0-x^{\ast }\left|\right|\left)\right||x_0-x^{\ast }\left|\right|\le \left|\right|x_0-x^{\ast }\left|\right|.\hfill \end{array}$$

(22)

So, the assertion (13) holds if $n=0$ and the iterate $x_1\in U(x^{\ast },s)$. The induction can be completed if we just exchange $x_0,y_0,x_1$ by $x_m,y_m,x_{m+1}$, respectively, in the preceding calculations. Set $c=h_2\left(\right||x_0-x^{\ast }\left|\right|)$. Then, from (13) and since $c\in [0,1)$, we have

$$\left|\right|x_{m+1}-x^{\ast }\left|\right|\le c\left|\right|x_m-x^{\ast }\left|\right|\le c^{m+1}\left|\right|x_0-x^{\ast }\left|\right|<s.$$

(23)

Hence, by (23) ${lim}_{m\to +\infty }{x}_m=x^{\ast }$ and $x_{m+1}\in U(x^{\ast },s)$.    □

Next, a set is determined that contains $x^{\ast }$ as the only solution.

Proposition 1. 

Suppose that the condition $\left(H_4\right)$ holds in the ball $U(x^{\ast },s_3)$ for some $s_3>0$, and there exists $s_4\ge s_3$ such that

$${\int }_0^1{g}_0\left(\theta s_4\right)d\theta <1.$$

(24)

Define the set $D_1=U[x^{\ast },s_4]\cap D$. Then, the only solution of the equation $F\left(x\right)=0$ in the set $D_1$ is $x^{\ast }$.

Proof. 

(See [3])    □

Remark 2. 

Under all the conditions $\left(H_1\right)$–$\left(H_7\right)$, one can set $s_3=s$ in the Proposition 1.

3. Semi-Local Convergence Analysis

Majorizing sequences for $\left\{x_n\right\}$ shall be used to show its convergence to a solution $x^{\ast }\in D$ of the equation $F\left(x\right)=0$. The majorant functions $g_0,g$ are replaced by $v_0$, v, and $x^{\ast }$ by $x_0$, respectively. Moreover, the formulas are similar to the local analysis.

Suppose the following:

(C₁)

There exists FCND $v_0:T\to T$ such that the equation $v_0\left(t\right)-1=0$ has SSE in the interval $T-\left\{0\right\}$ which shall be denoted by $r_0$. Set $T_2=[0,r_0)$.

(C₂)

There exists FCND $v:T_2\to T$. Define the sequence $\left\{a_n\right\}$ for each $n=0,1,2,\dots$ by $a_0=0$, some $b_0\ge 0$, $p\ge 0$ and $q\ge 0$

$$c_n={\int }_0^{1}v\left((1-\theta )(b_n-a_n)\right)d\theta (b_n-a_n),$$

$$a_{n+1}=b_n+p(b_n-a_n)+{\displaystyle \frac{q{c}_n}{1-v_0\left(a_n\right)}}$$

(25)

$$d_{n+1}={\int }_0^{1}v\left((1-\theta )(a_{n+1}-a_n)\right)d\theta (a_{n+1}-a_n)+(1+v_0\left(a_n\right))(a_{n+1}-b_n)$$

and

$$b_{n+1}=a_{n+1}+{\displaystyle \frac{d_{n+1}}{1-v_0\left(a_{n+1}\right)}}.$$

It is shown in Theorem 1 that the sequence $\left\{a_n\right\}$ majorizes $\left\{x_n\right\}$. But first, let us provide a general convergence condition for it.

(C₃)

There exists $r\in [0,r_0)$ such that for each $n=0,1,2,\dots$ $v_0\left(a_n\right)<1$ and $a_n\le r$. These conditions, the definition of sequence $\left\{a_n\right\}$ and induction, show that for each $n=0,1,2,\dots$ $0\le a_n\le b_n\le a_{n+1}\le r$ and there exists $r^{\ast }\in [0,r]$ such that ${lim}_{n\to +\infty }{a}_n=r^{\ast }$. It is well known that the limit point $r^{\ast }$ is the (unique) least upper bound of the sequence $\left\{a_n\right\}$.

As in the local analysis, the functions $v_0$ and v relate to the operators on the method (3).

(C₄)

There exists $x_0\in D$ and an invertible operator $A\in \mathcal{L}(B_1,B_2)$ such that for each $u\in D$

$$\left|\right|A^{-1}(F^{\prime }\left(u\right)-A)\left|\right|\le v_0\left(\right||u-x_0\left|\right|).$$

If $u=x_0$, conditions (C₁) and (C₄) imply $\left|\right|A^{-1}(F^{\prime }\left(x_0\right)-A)\left|\right|<1$. Therefore, $F^{\prime }\left(x_0\right)$ is invertible. Thus, we can choose $b_0\ge \left|\right|F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right)\left|\right|$.

Define the set $D_2=U(x_0,r_0)\cap D$.

(C₅)

$\left|\right|A^{-1}(F^{\prime }\left(u_2\right)-F^{\prime }\left(u_1\right))\left|\right|\le v\left(\right||u_2-u_1\left|\right|)$ for each $u_2,u_1\in D_2$.

(C₆)

There exists $p\ge 0$ and $q\ge 0$ such that for each $n=0,1,2,\dots$

$$\left|\right|I-p_n\left|\right|\le p\mathrm{and}\left|\right|q_n\left|\right|\le q$$

and

(C₇)

$U[X_0,r^{\ast }]\subset D$.

Remark 3. 

The linear operator A can be chosen to be $A=I$ or $A=F^{\prime }\left(\tilde{x}\right)$ for some $\tilde{x}\in D$ or some other choice.

Next, the main semi-local convergence result follows for the method (3).

Theorem 2. 

Suppose that the conditions $\left(C_1\right)$–$\left(C_7\right)$ hold. Then, the sequence $\left\{x_n\right\}$ produced by (3) is well defined in the ball $U(x_0,r^{\ast })$ and stays in $U(x_0,r^{\ast })$ and there exists a solution $x^{\ast }\in U[x_0,r^{\ast }]$ of the equation $F\left(x\right)=0$ such that for each $n=0,1,2,\dots$

$$\left|\right|x^{\ast }-x_n\left|\right|\le r^{\ast }-a_n.$$

(26)

Proof. 

We shall establish the assertions

$$\left|\right|y_n-x_n\left|\right|\le b_n-a_n$$

(27)

and

$$\left|\right|x_{n+1}-y_n\left|\right|\le a_{n+1}-b_n$$

(28)

using induction. By the choice of $b_0$ in the condition (C₄) and the first substep of method (3), we have $\left|\right|y_0-x_0\left|\right|=\left|\right|F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right)\left|\right|\le b_0=b_0-a_0<r^{\ast }$. Thus, the estimate (27) holds if $n=0$ and the iterate $y_0\in U(x_0,r^{\ast })$. Let $u\in D$. Then, conditions (C₁) and (C₄) give $\left|\right|A^{-1}(F^{\prime }\left(u\right)-A)\left|\right|\le v_0\left(\right||u-x_0\left|\right|)<1$; thus, the linear operator $F^{\prime }\left(u\right)$ is invertible and

$$\left|\right|F^{\prime }{\left(u\right)}^{-1}A\left|\right|\le {\displaystyle \frac{1}{1-v_0\left(\right||u-x_0\left|\right|)}}.$$

(29)

Notice that for $u=x_m$, the iterate $x_{m+1}$ is well defined by the second substep of the method (3). Moreover, by subtracting the first from the second substep of the method (3), we can write in turn that

$$x_{m+1}-y_m=(I-p_m)F^{\prime }{\left(x_m\right)}^{-1}F\left(x_m\right)-q_m{F}^{\prime }{\left(x_m\right)}^{-1}F\left(y_m\right).$$

(30)

We need the following estimates:

$$\left|\right|F^{\prime }{\left(x_m\right)}^{-1}F\left(x_m\right)\left|\right|=\left|\right|y_m-x_m\left|\right|\le b_m-a_m,$$

(31)

$$\begin{array}{cc}\hfill F\left(y_m\right)& =F\left(y_m\right)-F\left(x_m\right)-F^{\prime }\left(x_m\right)(y_m-x_m)\hfill \\ \hfill & ={\int }_0^1(F^{\prime }(x_m+\theta (y_m-x_m))-F^{\prime }\left(x_m\right))d\theta (y_m-x_m).\hfill \end{array}$$

(32)

Hence, by the induction hypotheses and (C₅), we in turn have

$$\begin{array}{cc}\hfill \left|\right|A^{-1}F\left(y_m\right)\left|\right|& \le {\int }_0^{1}v\left((1-\theta )\left|\right|y_m-x_m\left|\right|\right)d\theta \left|\right|y_m-x_m\left|\right|\hfill \\ \hfill & \le {\int }_0^{1}v\left((1-\theta )(b_m-a_m)\right)d\theta (b_m-a_m)=c_m.\hfill \end{array}$$

(33)

Summing up (31), (33) and using the condition (C₆) in (30), we obtain by the following (25): and (29)

$$\begin{array}{cc}\hfill \left|\right|x_{m+1}-y_m\left|\right|& \le \left|\right|I-p_m\left|\right|(b_m-a_m)+{\displaystyle \frac{\left|\right|q_m\left|\right|c_m}{1-v_0\left(a_m\right)}}\hfill \\ \hfill & \le p(b_m-a_m)+{\displaystyle \frac{q{c}_m}{1-v_0\left(a_m\right)}}=a_{m+1}-b_m\hfill \end{array}$$

(34)

and

$$\begin{array}{cc}\hfill \left|\right|x_{m+1}-x_0\left|\right|& \le \left|\right|x_{m+1}-y_m\left|\right|+\left|\right|y_m-x_0\left|\right|\hfill \\ \hfill & \le a_{m+1}-b_m+b_m-a_0=a_{m+1}<r^{\ast }.\hfill \end{array}$$

So, the assertion (28) holds for $m=n$ and the iterate $x_{m+1}\in U(x_0,r^{\ast })$. In view of the first substep of the method (3), we can write in turn that

$$\begin{array}{cc}\hfill F\left(x_{m+1}\right)& =F\left(x_{m+1}\right)-F\left(x_m\right)-F^{\prime }\left(x_m\right)(y_m-x_m)\hfill \\ \hfill & =F\left(x_{m+1}\right)-F\left(x_m\right)-F^{\prime }\left(x_m\right)(x_{m+1}-x_m)\hfill \\ \hfill & +F^{\prime }\left(x_m\right)(x_{m+1}-y_m)\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}& ={\int }_0^1(F^{\prime }(x_m+\theta (x_{m+1}-x_m))-F^{\prime }\left(x_m\right))d\theta (x_{m+1}-x_m)\hfill \\ \hfill & +F^{\prime }\left(x_m\right)(x_{m+1}-y_m).\hfill \end{array}$$

(36)

As in (32) for $x_{m+1}=y_m$, we obtain

$$\begin{array}{cc}\hfill & \left|\right|{\int }_0^1{A}^{-1}(F^{\prime }(x_m+\theta (x_{m+1}-x_m))-F^{\prime }\left(x_m\right))d\theta (x_{m+1}-x_m)\left|\right|\hfill \\ \hfill & \le {\int }_0^{1}v\left((1-\theta )(a_{m+1}-a_m)\right)d\theta (a_{m+1}-a_m)\hfill \end{array}$$

(37)

and

$$\begin{array}{c}\hfill \left|\right|A^{-1}{F}^{\prime }\left(x_m\right)\left|\right|=\left|\right|A^{-1}(F^{\prime }\left(x_m\right)-A+A)\left|\right|\\ \hfill \le 1+v_0\left(\right||x_m-x_0\left|\right|)\le 1+v_0\left(a_m\right).\end{array}$$

(38)

Then, by (25) and (35)–(38), we obtain

$$\begin{array}{cc}\hfill \left|\right|A^{-1}F\left(x_{m+1}\right)\left|\right|& \le {\int }_0^{1}v\left((1-\theta )(a_{m+1}-a_m)\right)d\theta (a_{m+1}-a_m)\hfill \\ \hfill & +(1+v_0\left(a_m\right))(a_{m+1}-b_m)=d_{m+1}.\hfill \end{array}$$

(39)

Hence, by the first substep of the method (3) for $n=m+1$, we obtain

$$\begin{array}{cc}\hfill \left|\right|y_{m+1}-x_{m+1}\left|\right|& \le \left|\right|F^{\prime }{\left(x_{m+1}\right)}^{-1}A\left|\right|·\left|\right|A^{-1}F\left(x_{m+1}\right)\left|\right|\hfill \\ \hfill & \le {\displaystyle \frac{d_{m+1}}{1-v_0\left(a_{m+1}\right)}}=b_{m+1}-a_{m+1}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \left|\right|y_{m+1}-x_0\left|\right|& \le \left|\right|y_{m+1}-x_{m+1}\left|\right|+\left|\right|x_{m+1}-x_0\left|\right|\hfill \\ \hfill & \le b_{m+1}-a_{m+1}+a_{m+1}-a_0=b_{m+1}<r^{\ast }.\hfill \end{array}$$

The induction for the assertions (27) and (28) is completed and gives the iterates $\left\{x_m\right\}\in U(x_0,r^{\ast })$. By the triangle inequality, (27) and (28), we obtain

$$\left|\right|x_{m+1}-x_m\left|\right|\le a_{m+1}-a_m.$$

(40)

It follows that the sequence $\left\{x_m\right\}$ is Cauchy (since $\left\{a_m\right\}$ is Cauchy as convergent by the condition (C₃) in a Banach space $B_1$ and as such it converges to some $x^{\ast }\in U[x_0,r^{\ast }]$). By letting $m\to +\infty$ in (39), we deduce that $F\left(x^{\ast }\right)=0$. Furthermore, the triangle inequality and (40) show for $i=0,1,2,\dots$ that

$$\left|\right|x_{m+i}-x_m\left|\right|\le a_{m+i}-a_m.$$

(41)

Finally, by letting $i\to +\infty$ in (41), we show (26).    □

Next, a set is determined that contains only one solution of the equation $F\left(x\right)=0$.

Proposition 2. 

Suppose that there exists a solution $z_1\in U(x_0,r_1)$ for some $r_1>0$; condition $\left(C_4\right)$ holds in the ball $U(x_0,r_1)$, and there exists $r_2\ge r_1$ such that

$${\int }_0^1{v}_0\left((1-\theta )r_1+\theta r_2\right)d\theta <1.$$

(42)

Define the set $D_3=U[x_0,r_2]\cap D$. Then, $r_1$ is the only solution of the equation $F\left(x\right)=0$ in the set $D_3$.

Proof. 

(See [3])    □

Remark 4. 

(a) 

The limit point $r^{\ast }$ can be replaced by $r_0$ in $\left(C_7\right)$ (see $\left(C_1\right)$).

(b) 

If all the conditions $\left(C_1\right)$–$\left(C_7\right)$ hold, then we can set $r_1=r^{\ast }$ and $z_1=x^{\ast }$ in the Proposition 2.

4. Numerical Results

This section provides the evaluation of the efficiency and convergence behaviour of the analyzed extended parametric family of methods. To validate the theoretical results, the performance of the analyzed schemes is compared with several established iterative methods from the literature.

4.1. Experimental Setup

The numerical computations utilized high-precision arithmetic (specifically, 1000 digits of precision) to minimize round-off errors and verify the theoretical findings. The algorithms were implemented in Python (https://www.python.org/) using the python-flint library for high-precision calculations. Experiments were conducted on a machine with the following specifications:

• Processor: Intel(R) Core(TM) i7-10510U CPU @ 1.80 GHz
• RAM: 32 GB
• Operating System: Microsoft Windows 11 Pro (64-bit)

The iterative process for each method terminates when the following stopping criterion is satisfied:

$$\parallel F\left(x_k\right)\parallel +\parallel x_k-x_{k-1}\parallel <{10}^{-100}.$$

(43)

To verify the theoretical order of convergence, we compute the Computational Order of Convergence (COC) using the following formula:

$$\mathrm{COC}\approx {\displaystyle \frac{log(\parallel x_{k+1}-x_k\parallel /\parallel x_k-x_{k-1}\parallel )}{log(\parallel x_k-x_{k-1}\parallel /\parallel x_{k-1}-x_{k-2}\parallel )}}.$$

(44)

This metric yields a numerical approximation of the asymptotic convergence rate.

4.2. Numerical Experiments

We compare some famous methods of the parametric family (3) with known fourth-order algorithms. We consider special cases of (7) that achieve fourth-order convergence:

• Case 1. Linear Weight (LW) [16]. We utilize the linear weight function $\Psi \left(b_n\right)=1+2b_n$.

  $$\begin{array}{cc}\hfill y_k& =x_k-F^{\prime }{\left(x_k\right)}^{-1}F\left(x_k\right)\hfill \\ \hfill x_{k+1}& =x_k-\left(1+2b_n\right)F^{\prime }{\left(x_k\right)}^{-1}\left[F\left(x_k\right)+F\left(y_k\right)\right]\hfill \end{array}$$

  (45)
• Case 2. Rational Weight (RW) [16]. We utilize the rational weight function $\Phi \left(v_k\right)={\displaystyle \frac{1+\beta b_n}{1+(\beta -2)b_n}}$. For these experiments, we assume $\beta =1.5$.

  $$\begin{array}{cc}\hfill y_n& =x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)\hfill \\ \hfill x_{n+1}& =x_n-\left({\displaystyle \frac{1+1.5b_n}{1-0.5b_n}}\right)F^{\prime }{\left(x_n\right)}^{-1}\left[F\left(x_n\right)+F\left(y_n\right)\right]\hfill \end{array}$$

  (46)

Additionally, (6) is considered.

• Cordero’s Method (CM) [15]. This is investigated as a special case of the family with parameter $\lambda =-2$.

  $$\begin{array}{cc}\hfill y_n& =x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right),\hfill \end{array}$$

  (47)

  $$\begin{array}{cc}\hfill x_{n+1}& =y_n-{\displaystyle \frac{2b_n}{1-2b_n}}{F}^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)-{\displaystyle \frac{1}{1-2b_n}}{F}^{\prime }{\left(x_n\right)}^{-1}F\left(y_n\right),\hfill \end{array}$$

  (48)

These methods are compared to three fourth-order convergence methods.

• OM (Ostrowski’s Method) [17] is a classic optimal fourth-order multipoint method requiring two function evaluations and one Jacobian inversion per iteration.

  $$\begin{array}{cc}\hfill y_n& =x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right),\hfill \end{array}$$

  (49)

  $$\begin{array}{cc}\hfill x_{n+1}& =y_n-{\left[2[y_n,x_n;F]-F^{\prime }\left(x_n\right)\right]}^{-1}F\left(y_n\right)\hfill \end{array}$$

  (50)
• SNM (Singh’s Method) [18] is a three-step fourth-order method defined as follows:

  $$\begin{array}{cc}\hfill y_n& =x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)\hfill \\ \hfill z_n& =x_n-F^{\prime }{\left(x_n\right)}^{-1}(F\left(x_n\right)+F\left(y_n\right))\hfill \\ \hfill x_{n+1}& =z_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(z_n\right)\hfill \end{array}$$

  (51)
• SHM (Sharma’s Method) [19] is a fourth-order modified Newton approach:

  $$\begin{array}{cc}\hfill y_n& =x_n-{\displaystyle \frac{2}{3}}{F}^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)\hfill \\ \hfill x_{n+1}& =x_n-{\displaystyle \frac{1}{2}}\left[-I+{\displaystyle \frac{9}{4}}{F}^{\prime }{\left(y_n\right)}^{-1}{F}^{\prime }\left(x_n\right)+{\displaystyle \frac{3}{4}}{F}^{\prime }{\left(x_n\right)}^{-1}{F}^{\prime }\left(y_n\right)\right]F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)\hfill \end{array}$$

  (52)

To clarify the relationship between the analyzed schemes and the analyzed theoretical framework,

Table 1. Classification of all comparison methods against the analysed framework (4) defined by sequences ${\overline{p}}_n$ and ${\overline{q}}_n$.

Method	Belongs to (4)	Sequences $({\overline{\mathit{p}}}_{\mathit{n}},{\overline{\mathit{q}}}_{\mathit{n}})$
Linear Weight (LW)	Yes	${\overline{p}}_n=2b_n,{\overline{q}}_n=1+2b_n$
Rational Weight (RW)	Yes	${\overline{p}}_n={\displaystyle \frac{2b_n}{1-0.5b_n}},{\overline{q}}_n={\displaystyle \frac{1+1.5b_n}{1-0.5b_n}}$
Cordero’s Method (CM)	Yes	${\overline{p}}_n={\displaystyle \frac{2b_n}{1-2b_n}},{\overline{q}}_n={\displaystyle \frac{1}{1-2b_n}}$
Ostrowski’s Method (OM)	No	–
Singh’s Method (SNM)	No	–
Sharma’s Method (SHM)	No	–

classifies each method based on its adherence to the structure defined in (4) and provides the specific defining sequences ${\overline{p}}_n$ and ${\overline{q}}_n$ where applicable.

4.3. Computational Efficiency

To objectively compare the performance of the analyzed methods against existing schemes, we utilize the Computational Efficiency Index, denoted $CE$. Unlike the order of convergence, which solely measures error decay, the Computational Efficiency Index acts as a general normalized metric for processing time, allowing for comparisons that are unaffected by the specific machine architecture used. Similar analysis was also provided in [16] for parametric families (6) and (7).

According to the methodology for high-precision arithmetic contexts, the computational efficiency is defined as follows:

$$CE={\displaystyle \frac{1}{D}}{\displaystyle \frac{logp}{C_{total}}}$$

(53)

where p is the order of convergence of the method, and $C_{total}$ is the total computational cost per iteration. D acts as a normalization factor for the arithmetic cost; for our analysis, we set $D={10}^{-5}$

To compare the efficiency of the analyzed methods against existing schemes, we establish a computational cost function $C_{total}$ for a system of nonlinear equations of dimension m. This function accounts for evaluations of elementary functions, linear algebra operations, and elementary vector operations.

The total computational cost is expressed as a weighted sum of function evaluations and algebraic operations, normalized to the cost of a single multiplication product. The cost function is defined as follows:

$$C_{total}=m{\sigma }_f+m^2{\sigma }_d+G(m,\gamma )+E(m,\gamma )$$

where the parameters are defined as follows:

• ${\sigma }_f$ is the computational cost of evaluating a single component of $F\left(x\right)$.
• ${\sigma }_d$ is the computational cost of evaluating a single component of the Jacobian $F^{\prime }\left(x\right)$.
• $G(m,\gamma )$ is the aggregated cost of solving linear systems, where $\gamma$ is the cost ratio of a division relative to a multiplication.
• $E(m,\gamma )$ is the cost of elementary operations, including scalar–vector, vector–vector, and matrix–vector multiplications.

The algebraic cost $G(m,\gamma )$ depends on the matrix factorization technique. We assume an LU decomposition strategy. Based on standard linear algebra complexities, the cost of one LU decomposition ($C_{LU}$) and the resolution of the necessary triangular systems ($C_{TS}$) for a system of size m are given by

$$\begin{array}{cc}\hfill C_{LU}(m,\gamma )& ={\displaystyle \frac{m(m-1)(2m-1)}{6}}+\gamma {\displaystyle \frac{m(m-1)}{2}},\hfill \\ \hfill C_{TS}(m,\gamma )& =m(m-1)+\gamma m.\hfill \end{array}$$

Additionally, we explicitly account for the cost of auxiliary operations ($E\left(m\right)$). The costs for scalar–vector ($C_{sv}$), vector–vector inner product ($C_{vv}$), and matrix–vector ($C_{mv}$) multiplications are defined as follows:

$$C_{sv}=m,C_{vv}=m,C_{mv}=m^2.$$

By substituting the expressions for $C_{LU}$ and $C_{TS}$ into the method-specific operation counts, we derive the final polynomial cost formulas for the analyzed family (LW, RW, CM) and the comparison methods (SM, SHM, OM).

1. LW and RW

LW and RW require two function evaluations and one Jacobian evaluation. Algebraically, they perform one LU decomposition and two triangular system solutions. The update step involves two vector–vector products and one scalar–vector multiplication ($E\left(m\right)=2C_{vv}+1C_{sv}=3m$).

$$\begin{array}{cc}\hfill C_{LW}=C_{RW}& =2m{\sigma }_f+m^2{\sigma }_d+C_{LU}(m,\gamma )+2C_{TS}(m,\gamma )+3m\hfill \\ \hfill & =2m{\sigma }_f+m^2{\sigma }_d+{\displaystyle \frac{m}{6}}\left(2m^2+9m+7+3\gamma (m+3)\right),\hfill \\ \hfill C{E}_{LW}=C{E}_{RW}& ={\displaystyle \frac{1}{D}}{\displaystyle \frac{log4}{C_{RW}}}.\hfill \end{array}$$

2. Cordero’s Method (CM)

Similar to the previous approaches, this method requires two function evaluations, one Jacobian evaluation, one LU decomposition, and two triangular solutions. However, the update formula applies distinct weights to the function vectors, requiring an additional scalar–vector multiplication ($E\left(m\right)=4m$).

$$\begin{array}{cc}\hfill C_{CM}& =2m{\sigma }_f+m^2{\sigma }_d+C_{LU}(m,\gamma )+2C_{TS}(m,\gamma )+4m\hfill \\ \hfill & =2m{\sigma }_f+m^2{\sigma }_d+{\displaystyle \frac{m}{6}}\left(2m^2+9m+13+3\gamma (m+3)\right),\hfill \\ \hfill C{E}_{CM}& ={\displaystyle \frac{1}{D}}{\displaystyle \frac{log4}{C_{CM}}}.\hfill \end{array}$$

3. Singh’s Method (SM)

This method requires three function evaluations and one Jacobian evaluation. It performs one LU decomposition and three triangular system solutions.

$$\begin{array}{cc}\hfill C_{SM}& =3m{\sigma }_f+m^2{\sigma }_d+C_{LU}(m,\gamma )+3C_{TS}(m,\gamma )\hfill \\ \hfill & =3m{\sigma }_f+m^2{\sigma }_d+{\displaystyle \frac{m}{6}}\left(2m^2+15m-17+3\gamma (m+5)\right),\hfill \\ \hfill C{E}_{SM}& ={\displaystyle \frac{1}{D}}{\displaystyle \frac{log4}{C_{SM}}}.\hfill \end{array}$$

4. Sharma’s Method (SHM)

Sharma’s Method evaluates the Jacobian at two points and performs one function evaluation. It requires two LU decompositions and three triangular solutions. The method also involves matrix–algebraic approximations requiring two matrix–vector multiplications and four scalar–vector multiplications ($E\left(m\right)=2m^2+4m$).

$$\begin{array}{cc}\hfill C_{SHM}& =m{\sigma }_f+2m^2{\sigma }_d+2C_{LU}(m,\gamma )+3C_{TS}(m,\gamma )+2m^2+4m\hfill \\ \hfill & =m{\sigma }_f+2m^2{\sigma }_d+{\displaystyle \frac{m}{3}}\left(2m^2+12m+4+3\gamma (m+2)\right),\hfill \\ \hfill C{E}_{SHM}& ={\displaystyle \frac{1}{D}}{\displaystyle \frac{log4}{C_{SHM}}}.\hfill \end{array}$$

5. Ostrowski’s Method (OM)

Ostrowski’s method requires two function evaluations and one Jacobian. It also involves a divided difference that contains m(m − 1) additional function evaluations.

$$\begin{array}{cc}\hfill C_{OM}& =m(m+1){\sigma }_f+m^2{\sigma }_d+2C_{LU}(m,\gamma )+2C_{TS}(m,\gamma )\hfill \\ \hfill & =2m{\sigma }_f+m^2{\sigma }_d+{\displaystyle \frac{m}{3}}\left(2m^2+6m-5+3\gamma (1+2m)\right),\hfill \\ \hfill C{E}_{OM}& ={\displaystyle \frac{1}{D}}{\displaystyle \frac{log4}{C_{OM}}}.\hfill \end{array}$$

To accurately assess the efficiency of the analyzed iterative methods, we evaluated the computational cost of elementary functions using arbitrary-precision arithmetic. Unlike standard floating-point arithmetic, which is heavily optimized by hardware, arbitrary-precision calculations provide a hardware-independent benchmark that reflects the algorithmic complexity of the operations.

The costs were estimated using the python-flint library with a precision of 1000 decimal digits. The computational cost C of each function is defined relative to the time required for a single multiplication operation ($xy$):

$$C\left(f\right)={\displaystyle \frac{T\left(f\right)}{T_{mul}}}$$

(54)

where $T\left(f\right)$ is the average execution time of the function f and $T_{mul}$ is the average execution time of one multiplication.

Table 2. Estimation of computational costs of elementary functions using arbitrary-precision arithmetic (1000 decimal digits).

Functions	$\mathbf{xy}$	$\mathit{x}/\mathit{y}$	$\sqrt{\mathit{x}}$	${\mathit{e}}^{\mathit{x}}$	$cos\left(\mathit{x}\right)$	$sin\left(\mathit{x}\right)$
$C\left(f\right)$	1.00	1.26	1.19	22.23	27.99	29.05

presents the estimated costs used in this study.

As shown in the table, the cost of transcendental functions (e.g., $sin\left(x\right)$, $e^x$) increases significantly at high precision compared to basic arithmetic operations. This weighting is crucial for calculating $CE$, as it accounts for the heavy penalty of evaluating complex nonlinear functions in high-precision environments.

To test the applicability and robustness of the analyzed iterative methods, we have prepared a diverse set of numerical examples spanning low- to high-dimensional systems. The first two examples are selected from [16] to benchmark the implementation of the method against existing schemes in the article.

4.3.1. Example 1: Exponential Trigonometric System [16]

We consider the following system of nonlinear equations of dimension two:

$$F\left(x\right)=\left\{\begin{array}{c}{e}^{-x_1^2}-sin\left(x_2\right)=0\hfill \\ -sin\left(x_1\right)+e^{-x_2^2}=0\hfill \end{array}\right.$$

(55)

For this problem, the initial estimate $x_0={(-2,-2)}^T$ is used. The approximate solution for this system is $x^{\ast }\approx {(-3.14164,-3.14164)}^T$, and the cost parameters are $({\sigma }_f,{\sigma }_d)=(52.28,26.11)$.

The results are presented in

Table 3. Comparison of the methods’ performance for Example 1 ($m=2$).

Method	k	$\parallel {\mathit{x}}_{\mathit{k}-1}-{\mathit{x}}_{\mathit{k}-2}\parallel$	$\parallel {\mathit{x}}_{\mathit{k}}-{\mathit{x}}_{\mathit{k}-1}\parallel$	$\parallel \mathit{F}\left({\mathit{x}}_{\mathit{k}}\right)\parallel$	COC	CPU Time (s)	CE
OM	6	8.54 × 10−23	1.89 × 10−112	1.89 × 10−112	4	8.68 × 10−3	3.146 × 102
SM	6	3.31 × 10−93	0.00	0.00	4	9.20 × 10−3	3.195 × 102
SHM	6	1.32 × 10−67	4.55 × 10−272	4.55 × 10−272	4	1.06 × 10−2	3.989 × 102
CM	6	1.28 × 10−62	1.59 × 10−252	1.59 × 10−252	4	7.44 × 10−3	4.165 × 102
LW	5	3.89 × 10−29	1.33 × 10−118	1.33 × 10−118	4	5.94 × 10−3	4.190 × 102
RW	5	1.93 × 10−29	8.11 × 10−120	8.11 × 10−120	4	7.62 × 10−3	4.190 × 102

. The columns report the number of iterations (k) required to meet the stopping criterion, the difference between two last iteratates ($\parallel x_k-x_{k-1}\parallel$), the residual norm ($\parallel F\left(x_k\right)\parallel$), the Computational Order of Convergence (COC), computational efficiency (CE), and the CPU time. For all examples, we set $\gamma =1.26$ (see Table 2).

The analyzed methods (RW and LW) demonstrate superior efficiency, converging in only five iterations compared to six for all other methods. This faster convergence is reflected in the CPU time, with LW being the fastest (0.00594 s). The computational efficiency analysis reveals that the analyzed methods, LW and RW, achieve the highest efficiency index. Although SHM and CM achieve extremely small residual norms (e.g., ${10}^{-272}$), this level of precision required an additional iteration, whereas the analyzed methods achieved sufficient accuracy (${10}^{-118}$) one step earlier, satisfying the ${10}^{-100}$ tolerance more quickly. CM requires six iterations but remains relatively fast. All methods exhibit a COC of approximately 4, confirming their theoretical fourth-order convergence.

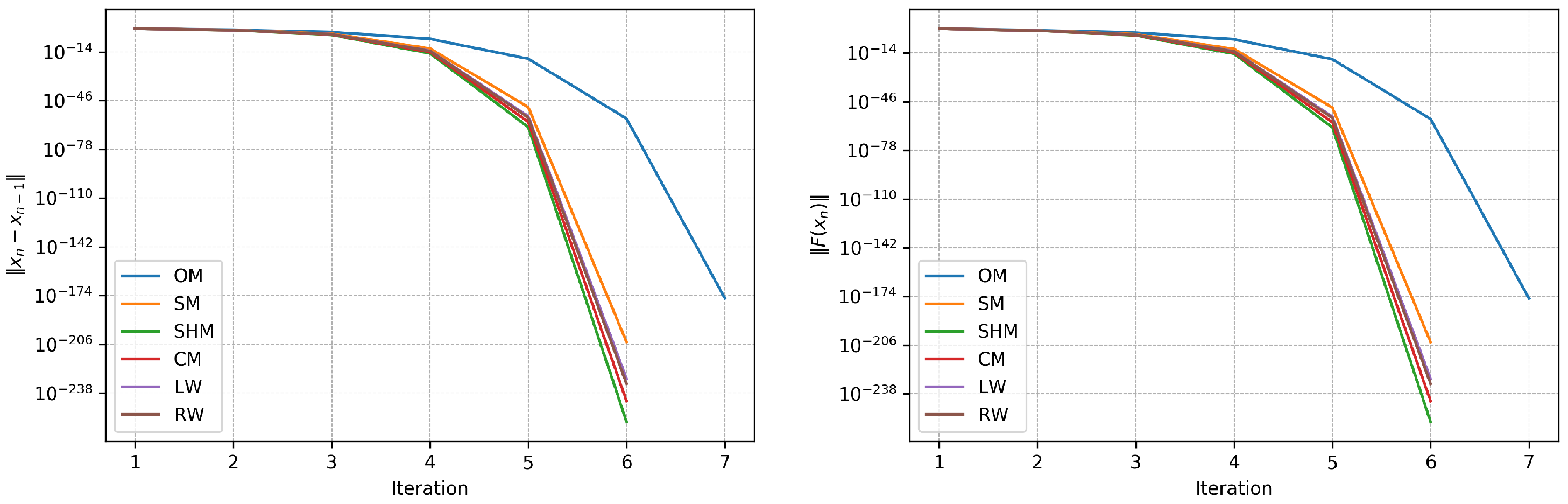
Figure 1 illustrates the convergence behaviour of the iterative methods for Example 1 by plotting the error norms versus the iteration number k. The plots display the logarithm of the step norm, ${log}_{10}\parallel x_n-x_{n-1}\parallel$, and the logarithm of the residual norm, ${log}_{10}\parallel F\left(x_n\right)\parallel$, against the iteration number. It is evident that the analyzed methods, LW (purple) and RW (brown), exhibit the fastest rate of decay (they coincide) and reach the required machine precision levels by the fifth iteration. In contrast, other algorithms require six iterations to converge, but all of them, except OM, achieve quite high precision. Overall, both plots corroborate the numerical results in Table 3, validating the enhanced performance of the analyzed methods.

4.3.2. Example 2: Trigonometric System [16]

The following system of nonlinear equations is considered:

$$cos\left(x_i-\sum _{j\ne i}{x}_j\right)-x_i=0,i=1,\dots ,m.$$

(56)

For this experiment, $m=10$ is selected, and the initial estimate $x_0={(1.5,\dots ,1.5)}^T$ is used. The parameters needed for cost evaluation are $({\sigma }_f,{\sigma }_d)=(27.99,29.05)$. Different algorithms yield different solutions.

Table 4. Comparison of performance for Example 2 ($m=10$).

Method	k	$\parallel {\mathit{x}}_{\mathit{k}-1}-{\mathit{x}}_{\mathit{k}-2}\parallel$	$\parallel {\mathit{x}}_{\mathit{k}}-{\mathit{x}}_{\mathit{k}-1}\parallel$	$\parallel \mathit{F}\left({\mathit{x}}_{\mathit{k}}\right)\parallel$	COC	CPU Time (s)	CE
OM	31	3.92 × 10−86	4.77 × 10−258	4.24 × 10−257	4	1.12 × 10−1	19.53
SM	47	1.22 × 10−62	3.29 × 10−249	2.24 × 10−248	4	1.83 × 10−1	31.55
SHM	9	9.68 × 10−29	7.49 × 10−112	3.63 × 10−111	4	7.95 × 10−2	18.94
CM	14	6.50 × 10−40	2.75 × 10−157	2.15 × 10−156	4	6.51 × 10−2	34.22
LW	12	5.89 × 10−33	1.27 × 10−128	6.13 × 10−128	4	5.57 × 10−2	34.30
RW	7	5.53 × 10−47	1.44 × 10−185	1.13 × 10−184	4	2.81 × 10−2	34.30

summarizes the performance of several iterative methods for Example 2. The Rational Weight (RW) method demonstrates the highest efficiency, converging in seven iterations with the lowest CPU time of 0.0281 seconds. The Sharma et al. Method (SHM) requires nine iterations and a longer CPU time (0.0795 s) than RW. The Linear Weight (LW) and Cordero’s Method (CM) converge in 12 and 14 iterations, respectively, with moderate CPU times. Ostrowski’s Method (OM) and Sharma’s Method (SM) are notably slower, requiring 31 and 47 iterations, respectively, and significantly more computational time. For this medium-sized system ($m=10$), CM, LW, and RW achieve efficiency scores nearly double that of Sharma’s Method and significantly exceeding Ostrowski’s Method. All methods achieve a computational order of convergence (COC) of 4.0000, consistent with their theoretical fourth-order convergence.

Figure 2 presents the overall convergence rate for all methods in Example 2. The RW method exhibits the fastest decay, confirming its rapid convergence. SHM demonstrates a similar process, while OM and SM display significantly slower convergence.

4.3.3. Example 3: High-Dimensional Cyclic System [9]

To evaluate the method on large-scale problems, the following cyclic system is considered:

$$x_i^2{x}_{i+1}-1=0,i=1,\dots ,m-1,\mathrm{and}{x}_m^2{x}_1-1=0.$$

(57)

A dimension of $m=300$ is selected, with the initial approximation $x_0={(1.8,\dots ,1.8)}^T$ and cost parameters $({\sigma }_f,{\sigma }_d)=(2,0.003)$.

The numerical results for Example 3, presented in

Table 5. Comparison of performance for Example 3 ($m=300$).

Method	k	$\parallel {\mathit{x}}_{\mathit{k}-1}-{\mathit{x}}_{\mathit{k}-2}\parallel$	$\parallel {\mathit{x}}_{\mathit{k}}-{\mathit{x}}_{\mathit{k}-1}\parallel$	$\parallel \mathit{F}\left({\mathit{x}}_{\mathit{k}}\right)\parallel$	COC	CPU Time (s)	CE
OM	7	1.34 × 10−58	1.62 × 10−176	4.86 × 10−176	4	5.59 × 10−1	7.422 × 10−3
SM	6	4.50 × 10−51	3.15 × 10−205	9.46 × 10−205	4	8.43 × 10−1	1.479 × 10−2
SHM	6	4.24 × 10−64	1.24 × 10−257	3.73 × 10−257	4	1.49 × 101	7.431 × 10−3
CM	6	1.02 × 10−60	5.64 × 10−244	1.69 × 10−243	4	4.59 × 10−1	1.493 × 10−2
LW	6	4.54 × 10−57	2.18 × 10−229	6.55 × 10−229	4	8.02 × 10−1	1.493 × 10−2
RW	6	7.10 × 10−58	1.30 × 10−232	3.90 × 10−232	4	4.68 × 10−1	1.493 × 10−2

, indicate that most methods (SM, SHM, CM, LW, RW) converge in six iterations, while Ostrowski’s Method (OM) requires seven. Cordero’s Method (CM) and the Rational Weight (RW) method are the most efficient in terms of CPU time, taking approximately 0.46 seconds, whereas SHM is significantly slower at 14.9 seconds. In the high-dimensional case, the efficiency gap widens drastically; the analyzed methods exhibit efficiency indices approximately twice as large as those of Ostrowski’s and Sharma’s Methods ($1.49\times {10}^{-2}$ vs $0.74\times {10}^{-2}$), highlighting the critical benefit of minimizing matrix factorizations in large-scale problems. All methods exhibit a computational order of convergence of 4.0000, validating their theoretical properties on this large-scale problem. In Figure 3, most methods follow a similar rapid decay trajectory, with OM lagging slightly behind by requiring an additional step to reach the same precision.

4.4. Calculating Radius of Convergence

To show how the convergence radius can be calculated, we consider the following problem:

• Example 4: The motion of a certain object is governed by the initial value problem

  $$\begin{array}{cc}\hfill f_1^{\prime }\left(t\right)& =e^t,\hfill \\ \hfill f_2^{\prime }\left(t\right)& =1\hfill \\ \hfill \mathrm{and}{f}_3^{\prime }\left(t\right)& =(e-1)t+1\hfill \end{array}$$

  with $f_1\left(0\right)=f_2\left(0\right)=f_3\left(0\right)=0$. Define the mapping $F:D\subset {\mathbb{R}}^3\to {\mathbb{R}}^3$ where $D=\mathcal{U}[0,1]$ for $\overline{t}={(t_1,t_2,t_3)}^T$ by

  $$F\left(\overline{s}\right)={(f_1\left(t_1\right),f_2\left(t_2\right),f_3\left(t_3\right))}^T.$$

  Notice that

  $$f_1\left(t_1\right)=e^{t_1}-1,f_2\left(t_2\right)=t_2\mathrm{and}{f}_3\left(t_3\right)={\displaystyle \frac{1}{2}}(e-1)t_3^2+t_3$$

  solve the boundary problem. According to these definitions, the Fréchet derivative $F^{\prime }$ of the operator F is given by

  $$F^{\prime }\left(\overline{t}\right)=\left[\begin{array}{ccc}{e}^{t_1}& 0& 0\\ 0& 1& 0\\ 0& 0& (e-1)t_3+1\end{array}\right].$$

The vector $x^{\ast }={(0,0,0)}^T$ solves the equation $F\left(\overline{t}\right)=0$ and $F^{\prime }\left(\overline{t}\right)=I$. Then, for $A=F^{\prime }\left(x^{\ast }\right)$, the conditions $\left(H_1\right),\left(H_4\right)$ and $\left(H_5\right)$ are satisfied if

$$s_0={\displaystyle \frac{1}{e-1}},g_0\left(t\right)=(e-1)t\mathrm{and}g\left(t\right)=e^{{\displaystyle \frac{1}{e-1}}}t.$$

We shall calculate the radius of convergence for (6). After defining these functions and SSE, we can calculate $h_1\left(t\right)$ and $h_2\left(t\right)$ using formulas from (H₁) and (H₂). We set parameters $p=0$ and $q=1$ as they satisfy (H₆). After this, we find $s_1$ and $s_2$ as the SSE of equations $h_1\left(t\right)-1$ and $h_2\left(t\right)-1$ in $T_0-\left\{0\right\}$, respectively. In this case, $s_1=0.5494$ and $s_2=0.428$, so the radius of convergence will be $s=min\{s_1,s_2\}=s_2=0.428$

4.5. Example 5: Nonlinear Integral Equation [20]

To evaluate the robustness of the analyzed methods on high-dimensional problems derived from real-world applications, we consider the following integral equation on the interval $[0,1]$:

$$u\left(t\right)={\displaystyle \frac{t}{\mathrm{e}}}+{\int }_0^{1}2t\sigma exp\left(-u{\left(\sigma \right)}^2\right)d\sigma .$$

(58)

The equation is discretized using a uniform grid with m subintervals and step size $h=1/m$, with nodes defined as $t_i=ih$ for $i=1,\dots ,m$. The integral is approximated using the trapezoidal rule with weights $w_1=w_m=h/2$, and $w_j=h$ for $j=2,\dots ,m-1$. This discretization results in a system of nonlinear equations given by

$$F_i\left(u\right)=u_i-{\displaystyle \frac{t_i}{\mathrm{e}}}-2t_i\sum _{j=1}^m{w}_j{t}_{j}exp\left(-u_j^2\right)=0,i=1,\dots ,m.$$

(59)

For this numerical test, we select a large-scale dimension of $m=1000$ and use the initial guess $u_0={(-0.1,\dots ,-0.1)}^{\top }$. The convergence behavior is compared against the reference solution $u^{★}$. The numerical results, including error norms at each iteration and total CPU time, are summarized in

Table 6. Errors $\parallel x_n-x^{\ast }{\parallel }_{\infty }$ and CPU time (s) for the integral equation ($m=1000$).

k	LW	RW	SM	SHM	OM	CM
1	6.39 × 10−2	1.38 × 10−1	2.98 × 10−1	2.39 × 10−1	2.14	8.52 × 10−1
2	9.17 × 10−7	6.85 × 10−6	1.84 × 10−5	3.73 × 10−6	4.56	5.48 × 10−3
3	4.44 × 10−16	3.33 × 10−16	3.33 × 10−16	3.33 × 10−16	3.01 × 10−1	1.72 × 10−9
4	–	–	–	–	4.21 × 10−4	3.33 × 10−16
5	–	–	–	–	2.08 × 10−13	–
6	–	–	–	–	2.22 × 10−16	–
CPU (s)	3.17 × 10−1	3.06 × 10−1	4.17 × 10−1	1.35	8.98 × 10−1	7.13 × 10−1

. This experiment shows how many iterations each method requires to achieve accuracy ${10}^{-15}$.

The results presented in Table 6 demonstrate the distinct advantages of the analyzed parametric family methods (LW and RW) in solving high-dimensional systems ($m=1000$). Both LW and RW converge rapidly, satisfying the stopping criterion within only three iterations. In contrast, Cordero’s Method (CM) requires four iterations, while Ostrowski’s Method (OM) exhibits instability in the early stages, indicated by an increase in error at the second iteration, and requires six iterations to converge.

In terms of CPU time, the Rational Weight (RW) and Linear Weight (LW) methods are the fastest, with execution times of approximately $0.306$ s and $0.317$ s, respectively. While Sharma’s Method (SHM) also converges in three iterations, it is computationally expensive, requiring $1.35$ s, which is more than four times the cost of the RW method. This confirms that the analyzed family offers an optimal balance between low iteration count and low computational cost per step for large-scale integral equations.

4.6. Basins of Attraction Analysis

The dynamical behavior of the iterative methods (3) is analyzed by generating basins of attraction. This visualization technique enables assessment of the method’s stability and sensitivity to the choice of initial guess. The basin of attraction of a root $x^{\ast }$ is defined as the set of all initial points $x_0$ in a domain D that converge to $x^{\ast }$ under the iterative mapping. If an initial point fails to converge to any root within a specified maximum number of iterations, it is considered divergent.

To generate these basins, we define a mesh of $201\times 201$ points within a rectangular domain $D=[-2,2]\times [-2,2]\subset {\mathbb{R}}^2$. Each point $z\in D$ is used as an initial guess $x_0$. If the sequence generated by the iterative method converges to a root $x^{\ast }$, the starting point is colored according to that specific root. To provide further insight into the computational cost, the color intensity is scaled based on the number of iterations required: brighter colors indicate faster convergence (fewer iterations). Black regions indicate points that diverge or fail to converge within the maximum iteration limit.

For these visual simulations, the stopping criterion is set to $\parallel F\left(x_k\right)\parallel +\parallel x_k-x_{k-1}\parallel <{10}^{-3}$ or a maximum of 50 iterations. The basins are examined for three nonlinear systems:

1.

System A: $\left\{\begin{array}{c}{x}_1^2+4x_2^2-4=0\hfill \\ 4x_1^2+x_2^2-4=0\hfill \end{array}\right.$

2.

System B: $\left\{\begin{array}{c}{x}_1^3-x_2-1=0\hfill \\ x_2^3-x_1+1=0\hfill \end{array}\right.$

3.

System C: $\left\{\begin{array}{c}{x}_1^2+2x_2^2-4=0\hfill \\ x_1^2-x_2-1=0\hfill \end{array}\right.$

To provide a theoretical verification of the stability regions observed in the basins of attraction, we calculated the precise radii of convergence for Systems A, B, and C. For the methods LW, RW, and CM, the parameters p and q utilized in the local convergence analysis (Condition (H₆)) are determined by the limit behavior of the weight functions at the solution, resulting in $p=0$ and $q=1$.

The bounding functions $g_0\left(t\right)$ and $g\left(t\right)$ were determined as linear functions $Lt$ satisfying the generalized continuity conditions $\left(H_4\right)$ and $\left(H_5\right)$. In our analysis, we selected $g_0\left(t\right)=g\left(t\right)=Lt$, where L is the constant. A is selected as $F^{\prime }\left(x^{\ast }\right)$. While it is theoretically possible to find a smaller $L_0$ for $g_0\left(t\right)$ (since it is restricted to paths originating from $x^{\ast }$), using the global constant L provides a rigorous sufficient condition for convergence that holds throughout the entire domain.

The calculated radii are summarized in Table 7. A key observation is the distinction between the polynomial systems:

• Systems A and C. These systems consist of quadratic equations where the second Fréchet derivative is constant. Due to the geometric symmetry of the roots, the norm of the inverse Jacobian $\parallel A^{-1}\parallel$ is identical for all solutions. Consequently, the constant L and the resulting convergence radius s are the same for every root.
• System B. This system involves cubic equations, meaning the second derivative changes with x. Furthermore, the roots are not symmetrically distributed. For instance, at the integer root $(1,0)$, the Jacobian matrix contains a zero on the diagonal, leading to a larger norm $\parallel A^{-1}\parallel$ compared to other roots. This increases the constant L and results in a significantly smaller theoretical radius ($s\approx 0.011$) compared to the more stable roots ($s\approx 0.020$).

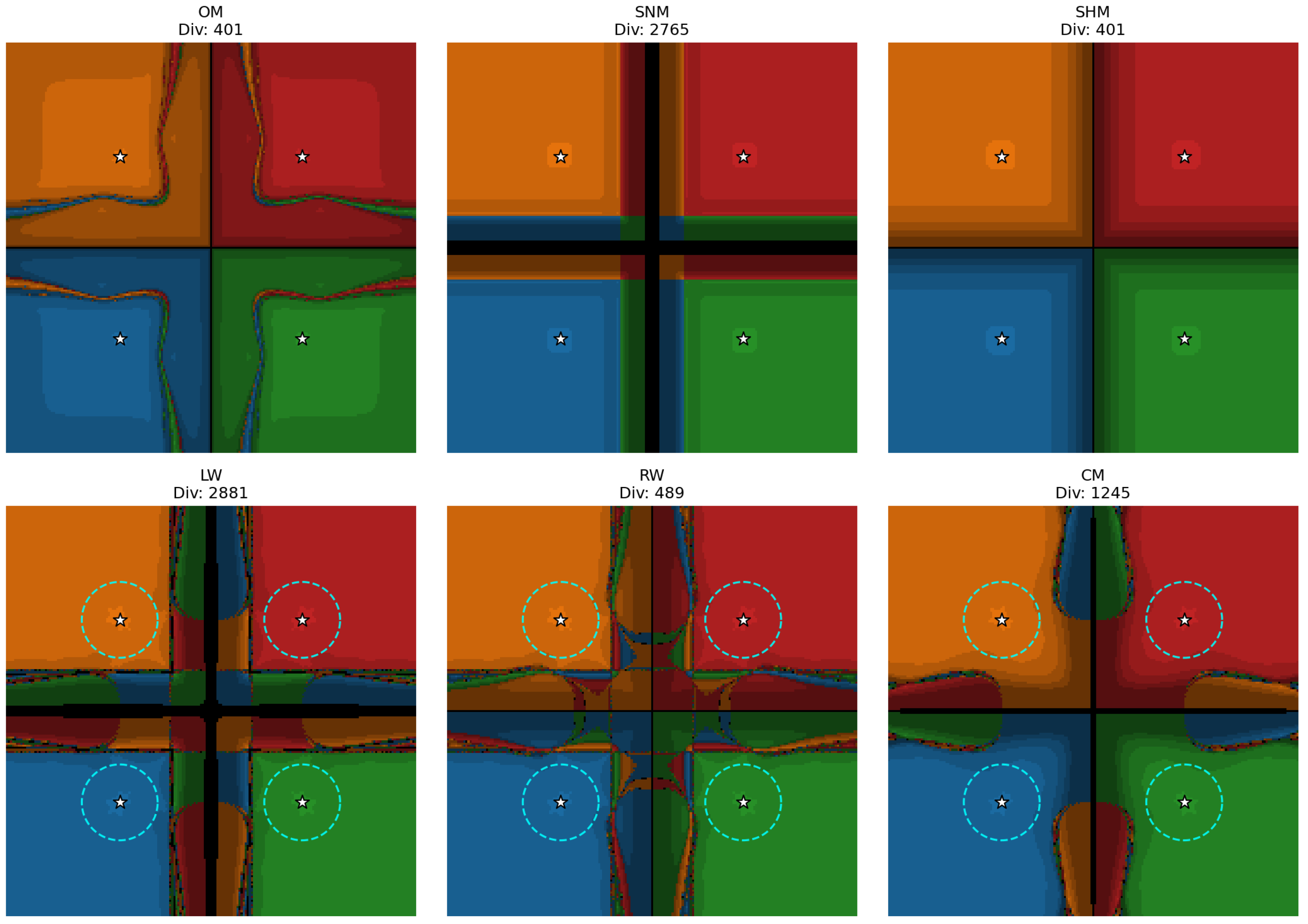
Figure 4 shows the basins for System A. In this visualization, the theoretical radius of convergence ($s\approx 0.37$), marked by cyan dashed circles for the analyzed family, is clearly visible and fully contained within the stable regions. The stability is quantitatively confirmed by the low divergence counts (Div). The Rational Weight (RW) method exhibits excellent stability with only $\mathrm{Div}=489$ divergent points (out of 40,401), which is comparable to Ostrowski’s Method ($\mathrm{Div}=401$) and significantly better than the Linear Weight (LW) method ($\mathrm{Div}=2881$). While both RW and OM are stable, RW displays larger bright areas, indicating a faster rate of convergence. The analyzed methods (LW, RW, CM) exhibit similar morphological shapes, suggesting consistent dynamical behavior across the parametric family.

Table 7. Convergence bounding functions and calculated radii for Systems A, B, and C (Methods: LW, RW, CM with $p=0,q=1$).

Problem	Solution Vector ${\mathit{x}}^{\ast }$	${\mathit{g}}_0\left(\mathit{t}\right)=\mathit{g}\left(\mathit{t}\right)$	${\mathit{s}}_1$	${\mathit{s}}_2$	Radius s
System A	All 4 roots $(\pm 0.89,\pm 0.89)$	$1.118t$	0.5963	0.3703	0.3703
System B	Root 1 $(-0.54,-1.15)$	$20.26t$	0.0329	0.0204	0.0204
	Root 2 $(0.00,-1.00)$	$37.95t$	0.0176	0.0109	0.0109
	Root 3 $(0.68,-0.68)$	$21.68t$	0.0307	0.0191	0.0191
	Root 4 $(1.00,0.00)$	$37.77t$	0.0177	0.0110	0.0110
	Root 5 $(1.15,0.54)$	$20.17t$	0.0331	0.0205	0.0205
System C	All 2 roots $(\pm 1.41,1.00)$	$0.85t$	0.7858	0.4879	0.4879

Table 7. Convergence bounding functions and calculated radii for Systems A, B, and C (Methods: LW, RW, CM with $p=0,q=1$).

Problem	Solution Vector ${\mathit{x}}^{\ast }$	${\mathit{g}}_0\left(\mathit{t}\right)=\mathit{g}\left(\mathit{t}\right)$	${\mathit{s}}_1$	${\mathit{s}}_2$	Radius s
System A	All 4 roots $(\pm 0.89,\pm 0.89)$	$1.118t$	0.5963	0.3703	0.3703
System B	Root 1 $(-0.54,-1.15)$	$20.26t$	0.0329	0.0204	0.0204
	Root 2 $(0.00,-1.00)$	$37.95t$	0.0176	0.0109	0.0109
	Root 3 $(0.68,-0.68)$	$21.68t$	0.0307	0.0191	0.0191
	Root 4 $(1.00,0.00)$	$37.77t$	0.0177	0.0110	0.0110
	Root 5 $(1.15,0.54)$	$20.17t$	0.0331	0.0205	0.0205
System C	All 2 roots $(\pm 1.41,1.00)$	$0.85t$	0.7858	0.4879	0.4879

Figure 5 presents the results for System B. This system poses a unique challenge with fivw roots and the high constant L, resulting in a very small theoretical radius of convergence ($s\approx 0.02$). Consequently, the cyan radius circles are not visible at this scale. Despite this, the actual basins are extensive. The RW method demonstrates superior stability among the analyzed schemes, significantly reducing the divergence area ($\mathrm{Div}=1971$) compared to Singh’s Method ($\mathrm{Div}=9640$) and Cordero’s Method ($\mathrm{Div}=5164$). Although OM achieves the lowest divergence ($\mathrm{Div}=38$), the analyzed RW method exhibits larger areas of high brightness, implying faster convergence speed. This highlights a trade-off where RW offers competitive stability with enhanced speed.

Figure 6 illustrates the basins for System C, which is computationally the most difficult due to the presence of extensive divergent regions across all methods. OM and SNM exhibit narrow corridors of convergence surrounded by significant chaotic boundaries. In contrast, the analyzed methods LW and RW display wider, more uniform basins around the roots, with minimal chaotic interference. The theoretical stability circles ($s\approx 0.4879$) are clearly distinguishable and verify that the immediate neighborhood of the roots is safe. Numerical metrics confirm that the divergence count is lower for the Rational Weight method (Div = 17,631) compared to LW (Div = 20,753) and SNM (Div = 19,767). The analyzed methods (LW, RW, and CM) also appear slightly brighter and maintain similar basin shapes, whereas the comparison methods do not exhibit this common topology.

To complement the visual analysis of the basins of attraction, we computed numerical stability metrics over a $201\times 201$ grid ($40,401$ total points). Table 8 reports the Stability Index ($S_{ind}$), defined as the percentage of initial guesses that successfully converged to any root, the average number of iterations ($I_{avg}$) for these converged points, and the total count of divergent points ($N_{div}$).

The results indicate clear distinctions in robustness across the systems:

• System A. This system is well behaved for most methods. Ostrowski’s Method (OM) and Sharma’s Method (SHM) exhibit the highest stability ($S_{ind}\approx 99\%$) with minimal divergence ($N_{div}=401$). Among the analyzed family, the Rational Weight (RW) method performs best, achieving $98.79\%$ stability, which is comparable to the optimal methods and significantly more robust than Linear Weight (LW) at $92.87\%$.
• System B. This system presents a greater challenge due to its cubic nonlinearity. While OM achieves near-perfect stability ($99.91\%$), the analyzed RW method demonstrates strong performance with $95.12\%$ stability, significantly outperforming Singh’s Method (SNM) which drops to $76.14\%$. The LW method shows moderate instability here ($N_{div}=7511$), confirming the theoretical sensitivity observed in the radius of convergence analysis.
• System C. This system proves to be the most difficult for all iterative schemes, likely due to the geometry of the solution space causing the Jacobian to become singular near the coordinate axes. All methods struggle to exceed $60\%$ stability. However, the RW method again proves to be the most robust of the analyzed family, achieving the highest stability index ($56.36\%$) of all tested methods, effectively minimizing the chaotic regions compared to LW ($48.63\%$).

Overall, the Rational Weight (RW) method consistently provides the best trade-off between stability and convergence speed within the analyzed parametric family, often rivaling established methods like OM and SHM.

Figure 6. Basins of attraction for System C. The roots are marked with white stars. Starting the iterative process from a point within a region of a specific color leads to convergence to the corresponding root. The cyan dashed circles indicate the theoretical radius of convergence $s\approx 0.4879$. Black regions indicate divergence (Div).

Figure 6. Basins of attraction for System C. The roots are marked with white stars. Starting the iterative process from a point within a region of a specific color leads to convergence to the corresponding root. The cyan dashed circles indicate the theoretical radius of convergence $s\approx 0.4879$. Black regions indicate divergence (Div).

Table 8. Numerical stability metrics for Systems A, B, and C. $S_{ind}$: Stability Index (percentage of converged points); $I_{avg}$: Average iterations per converged point; $N_{div}$: Number of divergent points (out of 40,401 total grid points).

System	Method	${\mathit{S}}_{\mathit{ind}}$ (%)	${\mathit{I}}_{\mathit{avg}}$	${\mathit{N}}_{\mathit{div}}$
System A	OM	99.01	3.39	401
	SNM	93.16	3.39	2765
	SHM	99.01	2.94	401
	LW	92.87	4.19	2881
	RW	98.79	4.06	489
	CM	96.92	3.79	1245
System B	OM	99.91	5.53	38
	SNM	76.14	5.31	9640
	SHM	97.44	5.59	1034
	LW	81.41	6.19	7511
	RW	95.12	7.17	1971
	CM	87.22	6.67	5164
System C	OM	55.64	3.57	17,921
	SNM	51.07	4.22	19,767
	SHM	55.90	3.43	17,817
	LW	48.63	5.19	20,753
	RW	56.36	4.74	17,631
	CM	55.20	5.82	18,099

Table 8. Numerical stability metrics for Systems A, B, and C. $S_{ind}$: Stability Index (percentage of converged points); $I_{avg}$: Average iterations per converged point; $N_{div}$: Number of divergent points (out of 40,401 total grid points).

System	Method	${\mathit{S}}_{\mathit{ind}}$ (%)	${\mathit{I}}_{\mathit{avg}}$	${\mathit{N}}_{\mathit{div}}$
System A	OM	99.01	3.39	401
	SNM	93.16	3.39	2765
	SHM	99.01	2.94	401
	LW	92.87	4.19	2881
	RW	98.79	4.06	489
	CM	96.92	3.79	1245
System B	OM	99.91	5.53	38
	SNM	76.14	5.31	9640
	SHM	97.44	5.59	1034
	LW	81.41	6.19	7511
	RW	95.12	7.17	1971
	CM	87.22	6.67	5164
System C	OM	55.64	3.57	17,921
	SNM	51.07	4.22	19,767
	SHM	55.90	3.43	17,817
	LW	48.63	5.19	20,753
	RW	56.36	4.74	17,631
	CM	55.20	5.82	18,099

Across all three examples, OM is the most stable method, but it has fewer bright areas than the parametric family, indicating slightly slower convergence. The RW method exhibits larger bright areas and fewer divergent points, representing the best trade-off between speed and stability. Additionally, the methods RW, LW, and CM display similar shapes across all examples.

5. Conclusions

We devised an extended parametric family of two-step iterative methods for solving nonlinear equations in Banach space. The main theoretical contribution of this work is the formulation of local and semi-local convergence analyses that do not require the existence of high-order derivatives, unlike standard approaches relying on Taylor series expansions. We obtained accurate error estimates, the radius of convergence, and the uniqueness of solutions by applying generalized continuity conditions to the first Fréchet derivative. The semi-local convergence was efficiently validated using the method of majorizing sequences, with only the initial data as the criterion of convergence. This greatly enhances the method’s applicability to equations where the operator lacks a derivative of the required order to satisfy Taylor-based conditions. Theoretical fourth-order convergence was verified through numerical experiments based on high-precision arithmetic. Comparative analysis revealed that certain members of the analyzed family, especially the Linear Weight (LW) variation, exhibit better performance in CPU time, Computational Efficiency Index, and iteration count than existing strategies such as Ostrowski’s and Singh’s.

The dynamical analysis further validated these theoretical results by superimposing calculated convergence radii onto basin plots, confirming that the theoretical bounds are strictly contained within stable regions. Notably, among the proposed variations, the Rational Weight (RW) method demonstrated superior global stability, minimizing the number of divergent points even in the most challenging test problems.

Future work on the direction of extensions of this analytical framework using majorizing sequences and generalized continuity for Banach spaces will also be very interesting for other classes of higher-order iterative schemes. The implementation of this tight approach with existing and future methods, which mainly rely on restrictive Taylor series assumptions, will help to characterize convergence domains and error estimates in their weak settings and thereby extend the practical applicability of these methods. The technique presented in this paper is very general. This is why it can be used to extend the usage of other methods [1,2,6,7,8,9,10,11,12,13,15,16,17,18,19,21] analogously. This shall be the focus of future research.