Structural Results on the HMLasso

Abstract

HMLasso (Lasso with High Missing Rate) is a useful technique for sparse regression when a high-dimensional design matrix contains a large number of missing data. To solve HMLasso, an appropriate positive semidefinite symmetric matrix must be obtained. In this paper, we present two structural results on the HMLasso problem. These results allow existing acceleration algorithms for strongly convex functions to be applied to solve the HMLasso problem.

1. Introduction

Let X be an $n\times p$ design matrix and let $\mathit{y}$ be an n-dimensional response. Consider the following standard linear regression model:

$$\mathit{y}=X\mathit{\beta }+\mathit{ϵ},$$

(1)

where $\mathit{ϵ}$ is a noise term. The popular model focuses on the sparsity assumption of the regression vector. The Lasso [1] (Least absolute shrinkage and selection operator) is among the most popular procedures for estimating the unknown sparse regression vector in a high-dimensional linear model. Lasso is formulated as an ${\ell }^1$-penalized regression problem as follows:

$$\underset{\mathit{\beta }}{min}{\displaystyle \frac{1}{2n}}{\parallel \mathit{y}-X\mathit{\beta }\parallel }_2^2+\alpha {\parallel \mathit{\beta }\parallel }_1$$

(2)

where $\alpha >0$ is a regularization parameter and ${\parallel ·\parallel }_1$ (resp. ${\parallel ·\parallel }_2$) is the ${\ell }^1$ (resp. ${\ell }^2$) norm. Here, we consider the case where the design matrix X contains missing data. Missing data is prevalent and inevitable, which affects not only the representativeness and quality of data but also the results of Lasso regression. Therefore, it is crucial to develop a method applicable to process missing data. HMLasso [2] was proposed to effectively address this issue and is formulated as follows:

$$\begin{array}{cc}\hfill & \underset{\Sigma }{min}{\displaystyle \frac{1}{2}}{\parallel W\odot (\Sigma -S^{\mathrm{pair}})\parallel }_{\mathrm{F}}^2\mathrm{s}.\mathrm{t}.\Sigma ⪰0\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & \underset{\mathit{\beta }}{min}{\displaystyle \frac{1}{2}}{\mathit{\beta }}^{\top }\widehat{\Sigma }\mathit{\beta }-{\mathit{\rho }}^{\mathrm{pair}\top }\mathit{\beta }+\alpha {\parallel \mathit{\beta }\parallel }_1,\hfill \end{array}$$

(4)

where ⊙ is the Hadamard product, ${\parallel ·\parallel }_{\mathrm{F}}$ is the Frobenius norm, $S^{\mathrm{pair}},W\in {\mathbb{R}}^{p\times p},{\mathit{\rho }}^{\mathrm{pair}}\in {\mathbb{R}}^p$ is defined using X (see Section 2 for details), and $\widehat{\Sigma }=\underset{\Sigma ⪰0}{\mathrm{argmin}}{\displaystyle \frac{1}{2}}{\parallel W\odot (\Sigma -S^{\mathrm{pair}})\parallel }_{\mathrm{F}}^2$ (i.e., $\widehat{\Sigma }$ is the solution to problem (3)). It is known that problem (4) can be equivalently written as Lasso (2), and in the literature dedicated to sparse regression, the most encountered algorithm is the proximal gradient method when dealing with a sum of two convex functions. Therefore, the key to solving HMLasso is to consider how fast and accurately problem (3) can be solved.

To deal with this challenge, we consider two structural results on the HMlasso problem. In the first, we show that the gradient of the objective function of (3) is Lipschitz continuous; in the second, we show that the objective function of (3) is strongly convex. These results guarantee that accelerated algorithms for strongly convex functions can be applied to solve (3). Finally, we conduct numerical experiments on the real data considered in [2]. The numerical results show that the accelerated algorithm for strongly convex functions is effective for solving problem (3).

2. Preliminaries

This section reviews basic definitions, facts, and notation that will be used throughout the paper.

Let $A,B\in {\mathbb{R}}^{n\times p}$. ${\mathbb{S}}_{+}^p$ denote the set of positive semidefinite matrices. Let $\mathcal{D}\subset {\mathbb{R}}^{p\times p}$. The indicator function $i_{\mathcal{D}}:{\mathbb{R}}^{p\times p}\to (-\infty ,\infty ]$ of $\mathcal{D}$ is defined by

$$i_{\mathcal{D}}\left(B\right):=\left\{\begin{array}{cc}0\hfill & (B\in \mathcal{D});\hfill \\ \infty \hfill & \left(\mathrm{otherwise}\right).\hfill \end{array}\right.$$

Let $f:{\mathbb{R}}^{p\times p}\to (-\infty ,\infty ]$ be a proper and convex function. The proximal mapping ${\mathrm{prox}}_{\gamma f}\left(x\right)$ of f is defined by

$${\mathrm{prox}}_f(\Sigma ):=\underset{W\in {\mathbb{R}}^{p\times p}}{\mathrm{argmin}}\left\{f\left(W\right)+{\displaystyle \frac{1}{2}}{\parallel W-\Sigma \parallel }_{\mathrm{F}}^2\right\}.$$

Let $\Sigma \in {\mathbb{S}}^p$. Then, there exist a diagonal matrix $\Lambda \in {\mathbb{R}}^{p\times p}$ and a $p\times p$ orthogonal matrix U such that $\Sigma =U\Lambda U^{\top }$. Let $P_{{\mathbb{S}}_{+}^p}$ be the matrix projection from ${\mathbb{S}}^p$ onto ${\mathbb{S}}_{+}^p$. Then, the following holds (see, for example, [3] (Example 29.31), [4] (Theorem 6.3)):

$$P_{{\mathbb{S}}_{+}^p}(\Sigma )=U{\Lambda }_{+}{U}^{\top },$$

(5)

where ${\Lambda }_{+}$ is the diagonal matrix obtained from $\Lambda$ by setting the negative entries to 0.

Let $X\in {\mathbb{R}}^{n\times p}$ be a design matrix. Set

$$I_{jk}:=\{i:X_{ij}\mathrm{and}{X}_{ik}\mathrm{are}\mathrm{observed}\}$$

and let $n_{jk}$ be the number of elements of $I_{jk}$. We define matrices $S^{\mathrm{pair}}$ and W as follows:

$$\begin{array}{c}\hfill {\left(S^{\mathrm{pair}}\right)}_{jk}:=\left\{\begin{array}{cc}{\displaystyle \frac{1}{n_{jk}}}\sum _{i\in I_{jk}}{x}_{ij}{x}_{ik}\hfill & (I_{jk}\ne ⌀)\hfill \\ 0\hfill & (I_{jk}=⌀)\hfill \end{array}\right.,{\left(W\right)}_{jk}:={\displaystyle \frac{n_{jk}}{n}}.\end{array}$$

(6)

We also define a vector ${\mathit{\rho }}^{\mathrm{pair}}$ as follows:

$$\begin{array}{c}\hfill {\left({\mathit{\rho }}^{\mathrm{pair}}\right)}_j:=\left\{\begin{array}{cc}{\displaystyle \frac{1}{n_{jj}}}\sum _{i\in I_{jj}}{x}_{ij}{y}_i\hfill & (I_{jj}\ne ⌀)\hfill \\ 0\hfill & (I_{jj}=⌀)\hfill \end{array}\right.\end{array}$$

(7)

Let $L\in [0,\infty )$ and let $h:{\mathbb{R}}^{p\times p}\to \mathbb{R}\cup \{\infty \}$ be a differentiable function. The gradient $\nabla h$ of h is said to be L-Lipschitz continuous if

$$\parallel \nabla h\left({\Sigma }_1\right)-\nabla h\left({\Sigma }_2\right){\parallel }_{\mathrm{F}}\le L{\parallel {\Sigma }_1-{\Sigma }_2\parallel }_{\mathrm{F}}(\forall {\Sigma }_1,{\Sigma }_2\in {\mathbb{R}}^{p\times p}).$$

(8)

This condition is often called L-smoothness in the literature. Let $h:{\mathbb{R}}^{p\times p}\to \mathbb{R}$ be L-smooth on ${\mathbb{R}}^{p\times p}$. Then, we can upper bound the function h as

$$h\left({\Sigma }_1\right)\le h\left({\Sigma }_2\right)+〈\nabla h\left({\Sigma }_2\right),{\Sigma }_1-{\Sigma }_2〉+{\displaystyle \frac{L}{2}}{\parallel {\Sigma }_1-{\Sigma }_2\parallel }_{\mathrm{F}}^2(\forall {\Sigma }_1,{\Sigma }_2\in {\mathbb{R}}^{p\times p})$$

(9)

(see, for example, [5] (Theorem 5.8), [6] (Theorem A.1)).

Let $\mu \in (0,\infty )$ and let $g:{\mathbb{R}}^{p\times p}\to \mathbb{R}\cup \{+\infty \}$. g is said to be $\mu$-strongly convex if for each ${\Sigma }_1,{\Sigma }_2\in {\mathbb{R}}^{p\times p}$ and $\lambda \in (0,1)$, we have

$$g(\lambda {\Sigma }_1+(1-\lambda ){\Sigma }_2)\le \lambda g\left({\Sigma }_1\right)+(1-\lambda )g\left({\Sigma }_2\right)-{\displaystyle \frac{\mu }{2}}\lambda (1-\lambda ){\parallel {\Sigma }_1-{\Sigma }_2\parallel }_{\mathrm{F}}^2.$$

(10)

Suppose that g is $\mu$-strongly convex and differentiable. Then, (10) is equivalent to the following condition:

$$〈\nabla g\left({\Sigma }_1\right)-\nabla g\left({\Sigma }_2\right),{\Sigma }_1-{\Sigma }_2〉\ge \mu {\parallel {\Sigma }_1-{\Sigma }_2\parallel }_{\mathrm{F}}^2(\forall {\Sigma }_1,{\Sigma }_2\in {\mathbb{R}}^{p\times p}).$$

(11)

3. Main Results

In this section, we present two structural results on the HMlasso problem (3).

Define $f(\Sigma ):={\displaystyle \frac{1}{2}}{\parallel W\odot (\Sigma -S^{\mathrm{pair}})\parallel }_{\mathrm{F}}^2$. In this case, the gradient $\nabla f$ of f is described as the following:

$$\nabla f(\Sigma )=\nabla \left({\displaystyle \frac{1}{2}}{\parallel W\odot (\Sigma -S^{\mathrm{pair}})\parallel }_{\mathrm{F}}^2\right)=W\odot W\odot (\Sigma -S^{\mathrm{pair}})$$

(12)

see [2]).

3.1. Lipschitz Continuity

The first structural result deals with the gradient of the objective function in (3). We show the Lipschitz continuity of $\nabla f$.

Lemma 1.

The gradient $\nabla f$ of f is Lipschitz continuous and its Lipschitz constant is ${\parallel W\odot W\parallel }_{\mathrm{F}}$.

Proof. 

Let $\overline{\alpha }$ be defined by $\overline{\alpha }:={\sum }_{j=1}^p{\sum }_{k=1}^p{W}_{jk}^4$. By (12), we obtain

$$\begin{array}{cc}\hfill \parallel \nabla f\left({\Sigma }_1\right)-\nabla f\left({\Sigma }_2\right){\parallel }_{\mathrm{F}}^2& =\parallel W\odot W\odot ({\Sigma }_1-S^{\mathrm{pair}})-W\odot W\odot ({\Sigma }_2-S^{\mathrm{pair}}){\parallel }_{\mathrm{F}}^2\hfill \\ \hfill & =\parallel W\odot W\odot ({\Sigma }_1-{\Sigma }_2){\parallel }_{\mathrm{F}}^2\hfill \\ \hfill & =\sum _{j=1}^p\sum _{k=1}^p{\left(W_{jk}^2({\Sigma }_{1jk}-{\Sigma }_{2jk})\right)}^2.\hfill \end{array}$$

On the other hand,

$$\begin{array}{cc}\hfill {\parallel W\odot W\parallel }_{\mathrm{F}}^2{\parallel {\Sigma }_1-{\Sigma }_2\parallel }_{\mathrm{F}}^2& =\underset{\overline{\alpha }}{\underbrace{\sum _{j=1}^p\sum _{k=1}^p{W}_{jk}^4}}·\sum _{j=1}^p\sum _{k=1}^p{\left({\Sigma }_{1jk}-{\Sigma }_{2jk}\right)}^2.\hfill \end{array}$$

This implies

$$\begin{array}{cc}\hfill {\parallel W\odot W\parallel }_{\mathrm{F}}^2\parallel {\Sigma }_1-{\Sigma }_2{\parallel }_{\mathrm{F}}^2-{\parallel \nabla f\left({\Sigma }_1\right)-\nabla f\left({\Sigma }_2\right)\parallel }_{\mathrm{F}}^2& =\sum _{j=1}^p\sum _{k=1}^p\left(\overline{\alpha }-W_{jk}^4\right){\left({\Sigma }_{1jk}-{\Sigma }_{2jk}\right)}^2\hfill \\ \hfill & \ge 0,\hfill \end{array}$$

where the last inequality follows from $\overline{\alpha }-W_{jk}^4\ge 0$ for any j and k. Hence,

$$\begin{array}{c}\hfill \parallel \nabla f\left({\Sigma }_1\right)-\nabla f\left({\Sigma }_2\right){\parallel }_{\mathrm{F}}\le {\parallel W\odot W\parallel }_{\mathrm{F}}{\parallel {\Sigma }_1-{\Sigma }_2\parallel }_{\mathrm{F}}.\end{array}$$

   □

3.2. Strong Convexity

We next consider the strong convexity of f. This is our second result.

Lemma 2.

f is ${min}_{l,m}{(W\odot W)}_{l,m}$-strongly convex.

Proof. 

We show (11) with constant ${min}_{l,m}{(W\odot W)}_{l,m}$. Let ${\Sigma }_1,{\Sigma }_2\in {\mathbb{R}}^{p\times p}$.

$$\begin{array}{cc}\hfill 〈\nabla f\left({\Sigma }_1\right)-\nabla f\left({\Sigma }_2\right),{\Sigma }_1-{\Sigma }_2〉& =〈W\odot W\odot ({\Sigma }_1-{\Sigma }_2),{\Sigma }_1-{\Sigma }_2〉\hfill \\ \hfill & =\sum _{j=1}^p\sum _{k=1}^p{W}_{jk}^2{({\Sigma }_{1jk}-{\Sigma }_{2jk})}^2\hfill \\ \hfill & \ge \sum _{j=1}^p\sum _{k=1}^p\underset{j,k}{min}{(W\odot W)}_{j,k}{({\Sigma }_{1jk}-{\Sigma }_{2jk})}^2\hfill \\ \hfill & =\underset{l,m}{min}{(W\odot W)}_{l,m}{\parallel {\Sigma }_1-{\Sigma }_2\parallel }_{\mathrm{F}}^2,\hfill \end{array}$$

where the second-to-last inequality follows from $W_{jk}^2\ge {min}_{l,m}{(W\odot W)}_{l,m}$ for any j and k. This implies that f is ${min}_{l,m}{(W\odot W)}_{l,m}$-strongly convex.    □

Remark 1.

From Lemmas 1 and 2, the objective function of (3) is strongly convex and has a Lipschitz gradient. It should be noted that we can guarantee a faster convergence than just a regular convex function if we know the objective function is strongly convex and smooth (see, for example, [6]).

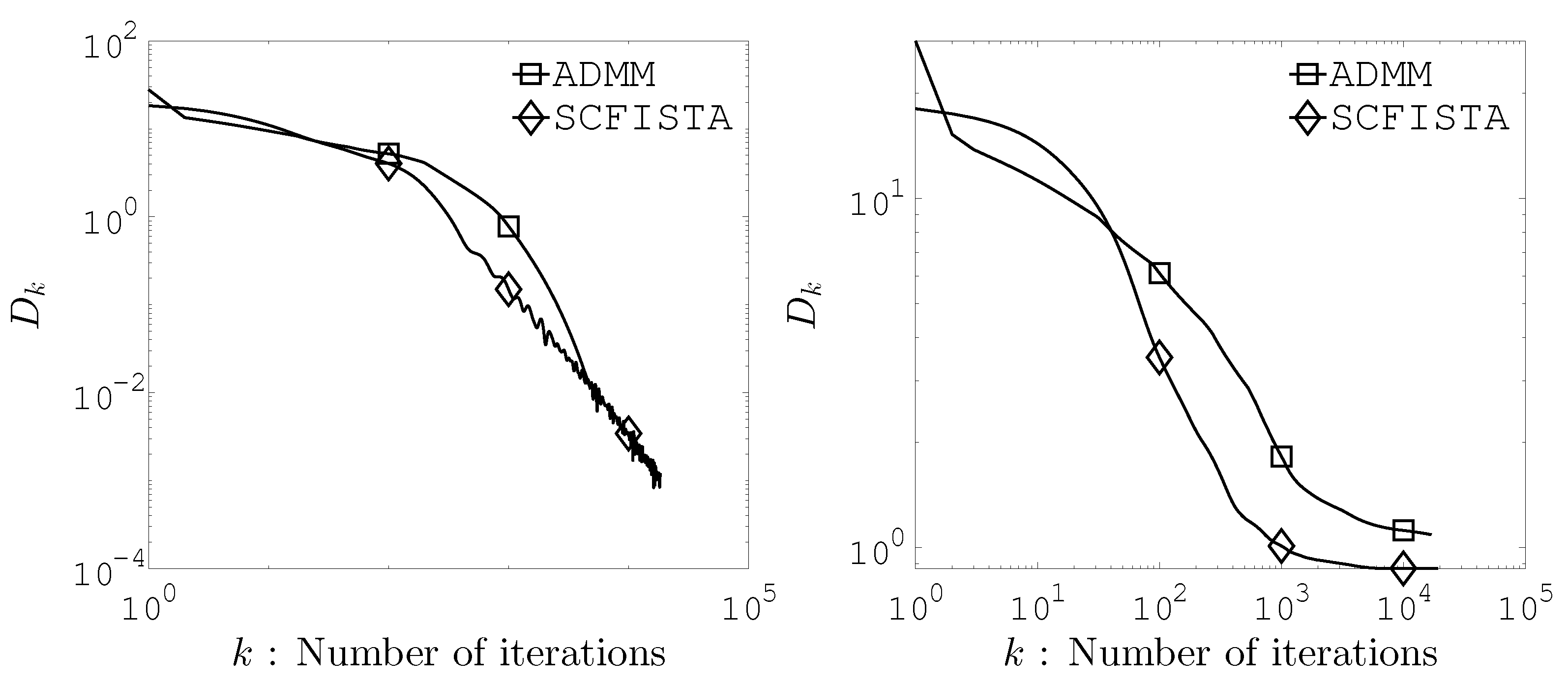
4. Numerical Experiments

In this section, we consider a strongly convex variant of FISTA [6] (Algorithm 1) to solve problem (3).

4.1. Strongly Convex FISTA

Let $f:{\mathbb{R}}^{p\times p}\to \mathbb{R}$ be an L-smooth and $\mu$-strongly convex function with $\mathrm{dom}\left(f\right)={\mathbb{R}}^{p\times p}$, and let $h:{\mathbb{R}}^{p\times p}\to \mathbb{R}\cup \{\infty \}$ be a convex function with $\{\Sigma :h(\Sigma )<\infty \}\ne \varnothing$. We consider the problem of minimizing the sum of f and h:

$$\underset{\Sigma \in {\mathbb{R}}^{p\times p}}{min}f(\Sigma )+h(\Sigma ).$$

(13)

In this setting, forward-backward splitting strategies were introduced as classical methods for solving (13). In the context of acceleration methods, the fast iterative shrinkage threshold algorithm (FISTA) was introduced by Beck and Teboulle [7] using the idea of forward-backward splitting. This topic is addressed in many references, and we refer to [3,5,6].

Here, we focus on the following strongly convex variant of FISTA involving backtracking investigated in [6].

Algorithm 1 Strongly convex FISTA [6]

Input:  An initial point ${\Sigma }_0\in {\mathbb{R}}^{p\times p}$, and initial estimate $L_0>\mu$. 1: Initialize ${\Phi }_0={\Sigma }_0$, $t_0=0$, and some $\alpha >1$. 2: for  $k=0,\dots$do 3:    $L_{k+1}=L_k$ 4:    while do 5:      $q_{k+1}=\mu /L_{k+1}$ 6:      $t_{k+1}={\displaystyle \frac{2t_k+1+\sqrt{4t_k+4q_{k+1}{t}_k^2+1}}{2(1-q_{k+1})}}$ 7:      set ${\tau }_k={\displaystyle \frac{(t_{k+1}-t_k)(1+q_{k+1}{t}_k)}{t_{k+1}+2q_{k+1}{t}_k{t}_{k+1}-q_k{t}_k^2}}$ and ${\delta }_k={\displaystyle \frac{t_{k+1}-t_k}{1+q_{k+1}{t}_{k+1}}}$ 8:      ${\Psi }_k={\Sigma }_k+{\tau }_k({\Phi }_k-{\Sigma }_k)$ 9:      ${\Sigma }_{k+1}={\mathrm{prox}}_{h/L_{k+1}}({\Psi }_k-{\displaystyle \frac{1}{L_{k+1}}}\nabla f\left({\Psi }_k\right))$ 10:      ${\Phi }_{k+1}=(1-q_{k+1}{\delta }_k){\Phi }_k+q_{k+1}{\delta }_k{\Psi }_k+{\delta }_k({\Sigma }_{k+1}-{\Psi }_k)$ 11:      if $f\left({\Sigma }_{k+1}\right)\le f\left({\Sigma }_k\right)+〈\nabla f\left({\Sigma }_k\right),{\Sigma }_{k+1}-{\Sigma }_k〉+{\displaystyle \frac{L_{k+1}}{2}}{\parallel {\Sigma }_{k+1}-{\Sigma }_k\parallel }_{\mathrm{F}}^2$ holds then 12:         $\mathbf{break}\{k\mathrm{will}\mathrm{be}\mathrm{incremented}.\}$ 13:      else 14:         $L_{k+1}=\alpha L_{k+1}\{\mathrm{Recompute}\mathrm{new}{L}_{k+1}.\}$ 15:      end if 16:    end while 17: end for Output:  An approximate solution ${\Sigma }_{k+1}$

Remark 2.

The Lipschitz and strongly convex constants of the objective function affect the convergence of the algorithm (see [6]), but are highly dependent on the number of missing values in the data (see Lemmas 1 and 2 and (6)). The above algorithm includes a backtracking procedure with respect to the smoothness constant, which allows for robust solutions even when there are many missing values in the design matrix.

Remark 3.

We demonstrate how strongly convex FISTA can be applied to (3). Set

$$f(\Sigma ):={\displaystyle \frac{1}{2}}{\parallel W\odot (\Sigma -S^{\mathrm{pair}})\parallel }_{\mathrm{F}}^2\mathit{and}h(\Sigma ):=i_{{\mathbb{S}}_{+}^p}(\Sigma ).$$

In this case, problem (3) is the special instance of problem (12). The gradient $\nabla f$ can be computed by (12). Moreover, the proximal mapping ${\mathrm{prox}}_h$ is $P_{{\mathbb{S}}_{+}^p}$ (see, for example, [3] (Example 12.25)) and hence the computation in the algorithm is simple.

4.2. Residential Building Dataset

We compared the performance of HMLasso (3) with the strongly convex FISTA (SCFISTA) and the alternating direction multiplier method (ADMM) used in [6]. All experiments are conducted on a PC with an Apple M1 Max CPU and 32 GB RAM. Methods are implemented with MATLAB (R2025a).

The numerical experiment uses an actual residential building dataset from the UCI Data Repository https://archive.ics.uci.edu/ml/datasets/Residential+Building+Data+Set (accessed on 20 May 2024). The data consisted of $n=300$ samples and $p=27$ variables. We set the average missing rates to $20\%$, $40\%$, $60\%$, and $80\%$. As choices for $L_0$, $\alpha$, and $\mu$ occurring in an algorithm, we let $L_0:=1$, $\alpha :=1.1$, and $\mu :={min}_{l,m}{(W\odot W)}_{l,m}$. We chose 10 random initial points ${\Sigma }_0^{\left(i\right)}\in {\mathbb{R}}^{p\times p}$ ($i=1,2,\dots ,10$), and all entries at the initial point are defined from a standard normal distribution. Figures demonstrate the following function:

$$D_k^{\left(i\right)}:={\parallel {\Sigma }_k^{\left(i\right)}-{\Sigma }_{\mathrm{cvx}}\parallel }_{\mathrm{F}}\mathrm{and}{D}_k:=(1/10)\sum _{i=1}^{10}{D}_k^{\left(i\right)},$$

(14)

where ${\Sigma }_{\mathrm{cvx}}$ denotes the solution obtained by cvx and $\left\{{\Sigma }_k^{\left(i\right)}\right\}$ is the sequence generated by ${\Sigma }_0^{\left(i\right)}$ and each of SCFISTA and ADMM.

Figure 1 and Figure 2 show the computation results of the relation between the distance to a solution and iteration number. As we can see from these figures, SCFISTA and ADMM converge to the solution as the number of iterations increases. Furthermore, we found it more effective to solve the HMLasso problem using the acceleration algorithm for strongly convex functions.

5. Conclusions

In this paper, we present two structural results on the HMlasso problem, covering Lipschitz continuity of the gradient of the objective function and strong convexity of the objective function. These results allow existing acceleration algorithms for strongly convex functions to be applied to solve the HMLasso problem. Our numerical experiments suggest that accelerated algorithms for strongly convex functions are computationally attractive.