Extended Expressive Intonation: An Application of the Convergents and Semiconvergents in Pythagorean Tuning

Abstract

Cyclic scales are associated with convergents and semiconvergents of the continued fraction expansions of the generator tone. After each convergent, a scale lineage ends and another begins. Along a lineage, a constant number of generic accidentals are successively added to its first scale, becoming regularly interspersed. In this way, it is easier to know where each note is to go. This process, applied to the lineage of the 7-, 12-, and 17-tone scales, is related to expressive intonation. Such a concept is extended to larger scales with added microtones and it is described how they can be chosen in terms of the starting index of the scale. An automorphism in terms of the step and co-step indices associated with the two elementary intervals provides a two-dimensional representation that shares some common features with the musical staff.

1. Introduction

The cellist Pau Casals is often credited with the coining of the term expressive intonation. A former pupil of Casals [1] explains that “when asked what was the secret of his playing, he would say: It is my intonation: I know where each note is to go”.

This paper extends [2] where a lineage of cyclic scales is defined by studying an application of the convergents and semiconvergents of the continuous fraction expansions generating a cyclic scale, i.e., a generalized non-degenerate Pythagorean scale. From a mathematical viewpoint, it is explained how they can be used to obtain a scale with specific regular microtonal subdivisions, i.e., of less than a semitone of the usual 12-tone scale.

After each convergent, a lineage ends and another begins, meaning that in each successive scale of the chain of cyclic scales, the same number of new tones (generic accidentals) are incorporated to the tones of the previous scale (generic diatones). Along a lineage, the new tones become regularly interspersed between the tones of the first scale of the lineage, making it easy for a music player (using a fretless instrument) to know where each note is to go.

Based on the algebraic structure of cyclic scales, Hellegouarch [3] gave a mathematical interpretation of expressive intonation. Here, an alternative interpretation based on the elementary interval distribution is proposed. It has three novelties. First, it generalizes the concept of expressive intonation to scales of $n>12$ tones, which is referred to as extended expressive intonation. Second, in the current approach, it is possible to choose where to place the enharmonics, that is, to choose which notes are we interested in allowing a microtonal variation. Third, along a lineage, the step and co-step indices associated with both elementary intervals become a coordinate system to refer the scale tones. The generic diatones remain fixed to one coordinate; likewise, they have a fixed position on the staff, and the generic accidentals share one coordinate with the diatones and differ in the other, like the accidental symbols that modify the diatones in the staff.

Section 2, Section 3 and Section 4 are necessary to introduce and review some basic concepts. A new degree of freedom, the starting index, has been introduced in the definition of a concrete scale. This is a key concept that allows to select specific microtones. Section 5 explains how expressive intonation is understood in music. Section 6 proposes several measures accounting for the degree of expressivity and transportability of the scale. Section 7 and Section 8 determine how, along a lineage, the step and co-step indices (accounting for the cyclic order of the scale tones) are related to the number of iterates of the generator, and vice versa. Such relationships relay on the starting index of the concrete scale and are used to represent the scale tones in a two-dimensional graph to describe their evolution along a lineage, as well as the position of the new accidentals. Section 9 provides examples for lineages $7\prec 12\prec 17$ and $17\prec 29\prec 41\prec 53$, depending on the selection of the microtones. The last section summarizes the main results.

2. Preliminaries

2.1. Frequency and Pitch

In music, two frequencies (or tones) $\nu \in \mathsf{\Omega }=(0,\infty )$ and $2\nu$ are identified in one category, although saying that the latter is one octave higher than the former. This implies an equivalence relation between frequencies by considering all the frequencies $2^k\nu$, $k\in \mathbb{Z}$ as one equivalence class. Since $\mathsf{\Omega }$ with the product in $\mathbb{R}$ is a commutative group, by assuming the fundamental frequency as ${\nu }_0=1$, the set of all its octaves, denoted as ${\mathsf{\Omega }}^2=\{2^k,k\in \mathbb{Z}\}$, is a cyclic subgroup of $\mathsf{\Omega }$ of infinite cardinal. The frequency classes (FCs) are the elements of the factor group ${\mathsf{\Omega }}_0=\mathsf{\Omega }/{\mathsf{\Omega }}^2$, also commutative for multiplication. Thus, each frequency $\nu$ has its FC $\overline{\nu }$ in ${\mathsf{\Omega }}_0$.

By taking the binary logarithm of $\nu$, we obtain its pitch (or note) $x={log}_2\nu \in \mathbb{R}$. This is what the ear hears, since the sense of hearing detects relative variations of frequency. The corresponding pitch class (PC) is noted as $\overline{x}\in \mathbb{R}/\mathbb{Z}\equiv S_0$. $S_0$ is the octave, usually represented as a circle of unit length. Distances between two FCs, $\overline{{\nu }_1}<\overline{{\nu }_2}$, are measured according to the metric given by the circle distance in terms of their PCs, $d_0(\overline{{\nu }_1},\overline{{\nu }_2})=min\left({log}_2{\displaystyle \frac{\overline{{\nu }_2}}{\overline{{\nu }_1}}},1-{log}_2{\displaystyle \frac{\overline{{\nu }_2}}{\overline{{\nu }_1}}}\right)$.

2.2. Abstract Scale

A cyclic scale (also known as a well-formed scale of one generator) is a scale generated by a single tone g other than a power of 2. In Pythagorean tuning, the generator is the third harmonic, $g=3$ (or equivalently, its PC, the fifth $g={\displaystyle \frac{3}{2}}$). The infinitely many tones generated by g can be described as follows.

Given $g\in \mathsf{\Omega }$, a g-projection function [4] is defined as

$${\pi }_g:\mathsf{\Omega }\to {\mathsf{\Omega }}_0,{\pi }_g\nu =\overline{g\nu }\equiv {\pi }_{g\nu }$$

This family of projection functions is an Abelian group for composition, which is isomorphic to ${\mathsf{\Omega }}_0$. We say that $\alpha$ and $\beta$ belong to complementary FCs if they satisfy ${\pi }_{\alpha }{\pi }_{\beta }={\pi }_1$, i.e., ${\pi }_{\beta }={\pi }_{\alpha }^{-1}={\pi }_{{\alpha }^{-1}}$. For $n\in \mathbb{Z}$, it holds that ${\pi }_{\alpha }^n={\pi }_{{\alpha }^n}$.

The family ${\mathsf{\Omega }}^g=\{g^k,k\in \mathbb{Z}\}$ is an infinite cyclic subgroup of $\mathsf{\Omega }$ and its FCs are the elements of the factor group $E^g\equiv {\mathsf{\Omega }}^g/{\mathsf{\Omega }}^2$, therefore isomorphic to the family of projection functions generated by ${\pi }_g$. Thus, we write $E^g=\{{\pi }_g^k,k\in \mathbb{Z}\}$.

In general, subfamilies of $E^g$, which are referred to a set of indices A, namely $E_A^g=\{{\pi }_g^k,k\in A\}$, are not a subgroup of $E^g$, unless A is a subgroup of $\mathbb{Z}$, i.e., $A=n\mathbb{Z}$ with $n\in \mathbb{N}$, in which cases $E_A^g$ is of infinite cardinal. The only case where $E^g$ is a finite cyclic group is for $g=2^{{\displaystyle \frac{1}{n}}}$. This corresponds to an n-tone equal temperament (n-TET) scale, which is considered as a degenerate cyclic scale.

In order to obtain a finite and closed set of FCs ${\pi }_g^k$, we should consider that a particular FC ${\pi }_g^n$ plays the same role as the fundamental (for instance, when hearing is not able to differentiate both tones). This can be achieved if the iterates ${\pi }_g^0,\dots ,{\pi }_g^n$ are chosen so that in $S_0$ the interval between ${\pi }_g^0=1$ and the last iterate ${\pi }_g^n$ contains no previous iterates. This is known as the closure condition [5,6,7]. Then, we may assume $d_0({\pi }_g^n,1)\to 0$. Therefore, in the family of projection functions $E^g$, an equivalence relation identifying two projection functions ${\pi }_g^p,{\pi }_g^q$ can be defined if there exists an integer r such that ${\pi }_g^p={\pi }_g^q{\pi }_g^{rn}$. Given the subgroup $E^{g^n}=\{{\pi }_g^{kn},k\in \mathbb{Z}\}\subset E^g$, the factor group

$${\overline{E}}_n^g\equiv E^g/E^{g^n}=\left\{\overline{{\pi }_g^k},k\in {\mathbb{Z}}_n\right\}$$

determines an n-tone abstract scale.

2.3. Concrete Scale

The abstract scale ${\overline{E}}_n^g$ is a finite cyclic group of classes of projection functions. For each class $\overline{{\pi }_g^k}$, we choose a representative in ${\mathsf{\Omega }}_0$. In order to include the fundamental ${\pi }_g^0=1$, the representatives must satisfy the condition of being n consecutive iterates ${\pi }_g^k$ with $-(n-1)\le k<n$. Any set of n consecutive tones within the above set is a concrete scale.

The obvious case is to choose the representatives from the fundamental onward, $k=0,\dots ,n-1$ (forward iterates). This forms a musical section [3]. Another musical section is formed by the representatives $k=-1,\dots ,-n$ (backward iterates). The equivalent representatives of both sections differ in the factor system ${\pi }_g^n$. Therefore, by choosing the starting index $-\alpha$, with $0\le \alpha <n$, it is possible to select FCs of a unique section ($\alpha =0$), or FCs belonging to both sections, allowing to choose tones differing in a small quantity corresponding to the factor system, which in music is referred to as comma. Thus, depending on the starting index, a concrete scale is formed by the FCs (referred to as scale tones),

$$E_{n\left(\alpha \right)}^g=\left\{{\pi }_g^k,-\alpha \le k<n-\alpha \right\}$$

For example, in the case of the 7-tone Pythagorean scale, by assuming the fundamental as the note C, the iterates $k=0,\dots ,6$ would generate the FCs of $E_{7\left(0\right)}^3=\left\{\mathbf{1},{\displaystyle \frac{3}{2}},\dots ,{\displaystyle \frac{3^6}{2^9}}\right\}$, which correspond to the notes C-G-D-A-E-B-F^♯. Instead, the iterates $k=-1,\dots ,5$ would generate the FCs of $E_{7(-1)}^3=\left\{{\displaystyle \frac{2^2}{3}},\mathbf{1},{\displaystyle \frac{3}{2}},\dots ,{\displaystyle \frac{3^5}{2^7}}\right\}$, with notes F-C-G-D-A-E-B. The ratio between the two differing tones, ${\displaystyle \frac{3^6}{2^9}}$ (F^♯) in the former case and ${\displaystyle \frac{2^2}{3}}$ (F) in the latter, is ${\pi }_3^7={\displaystyle \frac{3^7}{2^{11}}}$, which generates the factor group.

Several criteria to select the starting index of a concrete scale are discussed in [3,8,9,10,11].

3. Properties of the Cyclic Scales

3.1. Parameters Determining the Scale

Among those studied in [2], to follow the current paper, some important properties need to be pointed out. According to the notation in [4,12], the scale tones ${\pi }_g^k$ are written as ${\nu }_k={\displaystyle \frac{g^k}{2^{〚k〛}}}$, with $〚k〛\equiv \left[k{log}_{2}g\right]$ ($[·]$ meaning the integer part, i.e., the floor function $\lfloor a\rfloor$ if $a\ge 0$ and the ceiling function $\lceil a\rceil$ if $a<0$).

Forward iterations ordered from lowest to highest pitch (in cyclic order, or by ordinal) have two extreme tones, the minimum tone ${\nu }_m$ and the maximum tone ${\nu }_M$, which determine the two elementary factors in the multiplicative space of frequencies, namely $U\equiv {\nu }_m={\displaystyle \frac{g^m}{2^{〚m〛}}}$ (up the fundamental) and $D\equiv {\displaystyle \frac{2}{{\nu }_M}}={\displaystyle \frac{2^{〚M〛+1}}{g^M}}$ (down the fundamental), so that $U^M{D}^m=2$. For $n\ge 2$, the indices satisfy $n=m+M$, all of them coprime. These factors have the corresponding elementary intervals in the additive logarithmic space of notes, $u={log}_{2}U$ and $d={log}_{2}D$, with $Mu+md=1$. The value ${\varphi }_n=u-d$ is the interval closure.

The tone ${\nu }_n={\displaystyle \frac{g^n}{2^{〚n〛}}}$, which does not belong to the scale $E_n^g$, provides the closure condition, either ${\nu }_n\to 1^{+}$, above the fundamental, or ${\nu }_n\to 2^{-}$, below the fundamental.

Two parameters inform us whether ${\nu }_n$ closes above or below the fundamental. For $m,M\ne 0$, and by using the index $N=〚m〛+〚M〛+1$ (also $N=[n{log}_{2}g+{\displaystyle \frac{1}{2}}]$), one parameter is the scale closure ${\gamma }_n={\displaystyle \frac{g^n}{2^N}}$, which is a value close to 1 (${\gamma }_n={\displaystyle \frac{U}{D}}$).

The distance from the fundamental to the frequency class of ${\nu }_n$ is known as the (Pythagorean) comma ${\kappa }_n$. Then, either ${\gamma }_n>1\iff$${\kappa }_n={\nu }_n={\gamma }_n$ or ${\gamma }_n<1\iff$${\kappa }_n={\displaystyle \frac{2}{{\nu }_n}}={\gamma }_n^{-1}$. That is, ${log}_2{\kappa }_n=\left|{log}_2{\gamma }_n\right|$. Then, the perfect closure of the scale would take place for ${\gamma }_n=1$ or, by taking logarithms, for ${log}_2{\gamma }_n=n{log}_{2}g-N=0$. Therefore, as we explain in the following section, the best closures can be determined from the best approximations $|n{log}_{2}g-N|\to 0$, which connects the current geometrical approach with the theory of continued fractions and best rational approximations of an irrational number.

The other parameter is the scale digit $\delta =N-〚n〛$, which takes values 0 or 1. Thus, $\delta =0\iff {\gamma }_n>1$ (${\nu }_n\to 1^{+}$) and $\delta =1\iff {\gamma }_n<1$ (${\nu }_n\to 2^{-}$). The index N is known as chromatic length of the generator.

3.2. Pythagorean Tuning

In Pythagorean tuning, the PCs corresponding to the n scale tones can be written as $x_k=k{log}_{2}3-\left[k{log}_{2}3\right]$ (the iterate minus its integer part), with $-\alpha \le k<n-\alpha$. In the circle of the octave $S_0$, they can be placed clockwise, with 0 representing the fundamental. Multiplied by 1200, we obtain the value of the PC in cents ($¢$).

Figure 1 provides an example of how the 12-tone Pythagorean scale generated by the fifth (the class of the third harmonic) is formed. The fifths iterates of indices $m=7$ and $M=5$ are the extreme tones, while $n=12$ provides the closure, since there is no other tone with a frequency that is between ${\nu }_{12}$ and the fundamental. The ratio between consecutive iterates is either ${\displaystyle \frac{3}{2}}$ or ${\displaystyle \frac{3}{4}}$, except for the last iterate (the wolf fifth), which compensates for the comma. When the scale tones are arranged in pitch order, i.e., by ordinals, their ratios are either $U={\displaystyle \frac{3^7}{2^{11}}}$ (the corresponding interval is $u=113.7¢$) or $D={\displaystyle \frac{2^8}{3^5}}$ (the corresponding interval is $d=90.2¢$).

In terms of the kth iteration (fifth), the notation generally used for these notes is as follows (the diatones, i.e., the notes of the heptatonic Pythagorean scale, are in boldface):

…

B♭♭♭

F𝄫

C𝄫

…

B𝄫

F♭

C♭

…

B♭

F

C

G

D

A

E

B

F♯

C♯

…

B♯

F𝄪

C𝄪

…

B𝄪

F𝄪♯

C𝄪♯

…

…

−16

−15

−14

…

−9

−8

−7

…

−2

−1

0

1

2

3

4

5

6

7

…

12

13

14

…

19

20

21

…

The accidentals added to a note X mean the following: X^♯ is X plus $113.7¢$, X^♭ is X plus $90.2¢$, and X^𝄪 is equivalent to X^♯♯.

3.3. Convergents and Semiconvergents

Determining a cyclic scale from the closure condition is equivalent to ${\displaystyle \frac{N}{n}}$ being a convergent or semiconvergent of the canonic continued fraction expansions of ${log}_{2}g$.

The scales corresponding to the best rational approximations (best approximation of the second kind [13,14]) ${\displaystyle \frac{N}{n}}$ of ${log}_{2}g$ are the convergents of its canonic continued fraction expansions (Best Approximation Theorem, e.g, [15]). However, while the convergents are the best double-sided approximations, the semiconvergents are only best one-sided approximations.

Appendix A provides extensive information about the theory of continued fractions and its relation with one-sided best approximations, as well as the main properties of convergents and semiconvergents.

The convergents are associated with the best closure ${\gamma }_n\approx 1$. They provide optimal scales. Then, by considering the interval closure ${\varphi }_n={log}_2{\gamma }_n$ in $S_0$, $E_n^g$ is optimal $\iff |{\varphi }_n|<|{\varphi }_k|$ for $0<k<n$.

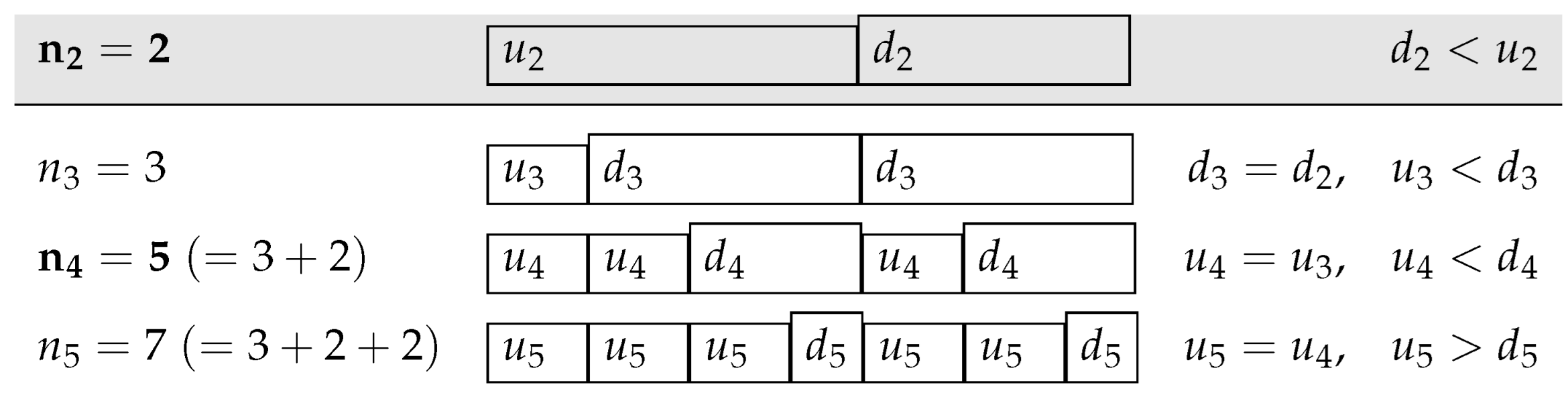
3.4. Chain of Cyclic Scales

Cyclic scales (whether optimal or not) form a chain, $\dots \subset E_n^g\subset E_{n^{+}}^g\subset \dots$ We are assuming the same starting index for all of them. In each link, the scale $E_{n^{+}}^g$ is composed of the tones of $E_n^g$, the generic diatones, in addition to the new non-adjacent tones, the generic accidentals [12].

Cyclic scales can be obtained from the following iterative process. Starting from the indices of the extreme tones m and M of $E_n^g$, with $n=m+M$ ($n\ge 2$), for the next cyclic scale in the chain $E_{n^{+}}^g$, these values are obtained as

$$\begin{array}{ccccc}\left(\mathrm{i}\right)& m^{+}=m+M,& M^{+}=M,& n^{+}=n+M\hfill & \iff \delta =0\hfill \\ \left(\mathrm{ii}\right)& m^{+}=m,& M^{+}=m+M,& n^{+}=n+m\hfill & \iff \delta =1\hfill \end{array}$$

(1)

which, in matrix form, can be written as

$$\left(\begin{array}{cc}{m}^{+}& M^{+}\\ 〚m^{+}〛& 〚M^{+}〛+1\end{array}\right)=\left(\begin{array}{cc}m& M\\ 〚m〛& 〚M〛+1\end{array}\right)\left(\begin{array}{cc}1& \delta \\ 1-\delta & 1\end{array}\right)$$

(2)

Therefore, according to (1), one of the indices of the extreme tones always repeats. This happens while approximations are improving by one side until reaching an optimal scale. Then, the approximations begin to improve by the other side.

3.5. Similar Algorithms

In addition to the approaches described above to build cyclic scales, there are other equivalent and related algorithms.

For the cyclic scale $E_n^h$, with extreme tones of indices m and M, the value n provides a convergent or semiconvergent ${\displaystyle \frac{N}{n}}$ of ${log}_{2}g$ according to one of these cases: $\frac{〚m〛}{m}<\frac{N}{n}<{log}_{2}h<\frac{〚M〛+1}{M}$ or ${\displaystyle \frac{〚m〛}{m}}<{log}_{2}h<{\displaystyle \frac{N}{n}}<{\displaystyle \frac{〚M〛+1}{M}}$, depending on whether ${\gamma }_n>1$ or ${\gamma }_n<1$. Then, we meet a situation such as ${\displaystyle \frac{a^{\prime }}{a}}<{log}_{2}h<{\displaystyle \frac{b^{\prime }}{b}}$, together with the Bézout’s identity corresponding to pairs of coprime numbers, $a{b}^{\prime }-b{a}^{\prime }=1$, which leads to a new improvement ${\displaystyle \frac{a^{\prime }+b^{\prime }}{a+b}}$ of the approximation. This situation is common to the continued fractions approach, the Farey sums, the structure of the Stern–Brocot tree, and its dual, the Raney tree [16,17,18], also known as Calkin–Wilf tree [19,20], where for two consecutive approximations, by using the extended Euclidean algorithm, it is possible from one to determine the other.

In the case of the Farey sums [21], if two rational approximations satisfy ${log}_{2}g\in ({\displaystyle \frac{a^{\prime }}{a}},{\displaystyle \frac{b^{\prime }}{b}})$ then we can lessen the size of the interval from a new approximation ${\displaystyle \frac{a^{\prime }+b^{\prime }}{a+b}}$ that substitutes the appropriate extreme. This algorithm basically reproduces the Stern–Brocot tree.

The Stern–Brocot tree is a full binary tree where the nodes are labeled in such a way that each positive rational number occurs exactly once. Vertically, it provides the usual ordering of the rationals. For ${\displaystyle \frac{p_1}{q_1}}$ and ${\displaystyle \frac{p_2}{q_2}}$, the median is the fraction ${\displaystyle \frac{p_1+p_2}{q_1+q_2}}$ of which they are the parents. Every row consists of the fractions that are medians of elements of previous rows. Positive irrational numbers can be associated with a unique infinite pathway down the tree and the nodes which are passed by on such a finite or infinite path are the semiconvergents of the corresponding rational or irrational number.

Depending on the value of $\delta$ in (2), the matrix $\left(\begin{array}{cc}1& \delta \\ 1-\delta & 1\end{array}\right)$ is equivalent to the $2\times 2$ matrix representing one branche of the Stern–Brocot tree [22,23,24,25] that encode the subsequent nodes of the fractions ${\displaystyle \frac{N}{n}}$. If $\delta =0$, the subsequent indices in the tree are obtained by multiplying by $L=\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)$. If $\delta =1$, the subsequent indices are obtained by multiplying by $R=\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)$.

4. Regular Subdivisions

4.1. Lineages

If R is the index of one of the extreme tones, all the scales where this index is repeated form the R-lineage (or simply lineage). Each scale represents an stage of the lineage. From the first repetition of R (second stage of a lineage) until the end of the lineage, R is the ruling index.

Table 1. Values are referred to the ith Pythagorean scale ($g=3$): $n_i$ (number of tones); $m_i,M_i$ (indices of the minimum and maximum tones); ${\delta }_i$ (0 or 1, depending on whether the closure is just below or above the fundamental). $R_i$ indicates the ruling index (marked with gray/white bands). The symbols ♀ and ♂ denote lineages of minimum or maximum tone, respectively. The beginning of a lineage is in bold. The symbol ↷ indicates an optimal scale (the digit ${\delta }_i$ changes).

i	${\mathit{n}}_{\mathit{i}}$		${\mathit{m}}_{\mathit{i}}$	$⋚$	${\mathit{M}}_{\mathit{i}}$		${\mathit{\delta }}_{\mathit{i}}$	${\mathit{R}}_{\mathit{i}}$
2	2		1	=	1	♀	0 ↷	1
3	3	♂	2	>	1	♀	1	1
4	5	♂	2	<	3		1 ↷	2
5	7	♂	2	<	5	♀	0	2
6	12		7	>	5	♀	0 ↷	5
7	17	♂	12	>	5	♀	1	5
8	29	♂	12	<	17		1	12
9	41	♂	12	<	29		1 ↷	12
10	53	♂	12	<	41	♀	0 ↷	12
11	94	♂	53	>	41	♀	1	41
12	147	♂	53	<	94		1	53
13	200	♂	53	<	147		1	53
14	253	♂	53	<	200		1	53
15	306	♂	53	<	253		1 ↷	53
16	359	♂	53	<	306	♀	0	53
17	665		359	>	306	♀	0 ↷	306
18	971	♂	665	>	306	♀	1	306
19	1636	♂	665	<	971		1	665
20	2301	♂	665	<	1636		1	665
21	2966	♂	665	<	2301		1	665
22	3631	♂	665	<	2966		1	665
23	4296	♂	665	<	3631		1	665
24	4961	♂	665	<	4296		1	665
25	5626	♂	665	<	4961		1	665
26	6291	♂	665	<	5626		1	665
27	6956	♂	665	<	6291		1	665
28	7621	♂	665	<	6956		1	665
29	8286	♂	665	<	7621		1	665
30	8951	♂	665	<	8286		1	665
31	9616	♂	665	<	8951		1	665
32	10,281	♂	665	<	9616		1	665
33	10,946	♂	665	<	10,281		1	665
34	11,611	♂	665	<	10,946		1	665
35	12,276	♂	665	<	11,611		1	665
36	12,941	♂	665	<	12,276		1	665
37	13,606	♂	665	<	12,941		1	665
38	14,271	♂	665	<	13,606		1	665
39	14,936	♂	665	<	14,271		1	665
40	15,601	♂	665	<	14,936		1 ↷	665
41	16,266	♂	665	<	15,601	♀	0	665
42	31,867		16,266	>	15,601	♀	0 ↷	15,601
43	47,468	♂	31,867	>	15,601	♀	1	15,601
44	79,335	♂	31,867	<	47,468		1 ↷	31,867
45	111,202	♂	31,867	<	79,335	♀	0 ↷	31,867
46	190,537	♂	111,202	>	79,335	♀	1 ↷	79,335
47	301,739	♂	111,202	<	190,537	♀	0	111,202
48	492,276		301,739	>	190,537	♀	0	190,537
49	682,813		492,276	>	190,537	♀	0	190,537
50	873,350		682,813	>	190,537	♀	0	190,537
51	1,063,887		873,350	>	190,537	♀	0	190,537

of [2] is reproduced here to facilitate understanding the process. It displays the lineages for Pythagorean scales ($n\ge 2$) in terms of their ith ordinal in the chain (indicated by the subindex of $n_i$). The beginning (and end) of a lineage is marked with a bold symbol. The symbol ↷ indicates an optimal scale, i.e., when the number of tones is the denominator of a continued fraction convergent, while the others are semiconvergents. The first lineages are $3\prec 5\prec 7$, $7\prec 12\prec 17$, $17\prec 29\prec 41\prec 53$, etc. Some facts to remark:

• In $E_{n_k}^g$ ends and starts, a lineage ⇔$E_{n_{k-1}}^g$ is optimal.
• The ruling index of a lineage is the number of tones of the optimal scale just before the first scale of the lineage.
• The scale digit $\delta$ is the same along a lineage, except in the last stage, where a new lineage begins.
• If the first scale of the lineage is optimal, it is also its penultimate. Then, the lineage is short.

Extended expressive intonation refers to the regular subdivision of the scales within a lineage. A lineage includes a series of consecutive semiconvergents and ends after the next convergent. During a lineage, the generator ${log}_{2}g$ is approximated by one side by a convergent, say ${\displaystyle \frac{N_i}{n_i}}$, and by the other side by a series of semiconvergents ${\displaystyle \frac{N_j}{n_j}}$, $j>i$, which do not improve the approximation of the convergent. Just after reaching a new convergent (on the opposite side of ${\displaystyle \frac{N_i}{n_i}}$), the lineage ends and a new one begins. In the next sections, we see that what happens during this process is that one of the elementary intervals remains constant, the one corresponding to the ruling index, and the other becomes successively subdivided in a regular manner. This facilitates a precise tuning while using scales with extended tones.

4.2. Mechanical Words

Cyclic scales can also be built from mechanical words [12,26,27,28]. It can be defined as a Christoffel word of the alphabet $\{U,D\}$, associated with both elementary factors, with slope ${\displaystyle \frac{m}{M}}$ and length n. The full octave is then represented by a word with M letters U and m letters D, since $U^M{D}^m=2$. For forward iterates starting at the fundamental, from left to right, the first step must be U and the last step of the octave must be D. For backward iterates starting at the fundamental, the sequence is symmetric. Each value n is associated with one word $w_n$, for instance, $w_2=UD$, $w_7=UUUDUUD$, $w_{12}=UDUDUDDUDUDD$.

Depending on the relative size of the elementary factors, the scale $E_n^g$ can be refined to form the next cyclic scale $E_{n^{+}}^g$ in the following way. Using forward iterates, if $U<D$, by factorizing $D=U{D}^{+}$, otherwise by factorizing $U=U^{+}D$, and so on.

For instance, for the successive cyclic scales $E_7^3\subset E_{12}^3$ (with starting index 0), the word associated with $E_7^3$ is $w_7=UUUDUUD$, where ${\displaystyle \frac{U}{D}}>1$. In the next cyclic scale, $n^{+}=12$, the smallest factor D is maintained (and so is the index M of the maximum tone). Therefore, in the 7-tone scale, the interval factorized is the one associated with the minimum tone, $U=U^{+}D$. Then, the generic accidentals of the 12-tone scale come just at the end of a factor $U^{+}$ (which come alone), and the generic diatones (the tones belonging to $E_7^3$) come at the end of a factor D. Thus, $w_{12}=\left(U^{+}D\right)\left(U^{+}D\right)\left(U^{+}D\right)D\left(U^{+}D\right)\left(U^{+}D\right)D$. Since the 7-tone scale is not optimal, in the next 12-tone scale, the relationship ${\displaystyle \frac{U}{D^{+}}}>1$ is still maintained. Hence, the next letter to be split is also U.

4.3. Scale Partition

The partition of the octave induced by the generator iterates has exactly two sizes of scale steps, and each number of generic intervals occurs in two different sizes (Myhill’s property) [29,30,31]. Both elementary intervals are associated with the two families of tones, the generic diatones and accidentals [12].

The semiconvergents of the canonic continued fraction expansions of the generator, although they do not provide optimal scales, induce a regular subdivision of one of the elementary intervals until reaching a convergent, which marks the scale lineages along the chain of cyclic scales.

The general properties of the scale lineages were studied in [2] and are not reproduced here. Instead, we focus on the subdivisions within a lineage, which follow the same procedure as mechanical words. It is illustrated in the scheme of Figure 2, corresponding to the lineage $3\prec 5\prec 7$.

The scale $n_2=2$ is optimal (in boldface). Subindex 2 indicates that this is the second scale in the chain (the first only contains the fundamental, and the second contains the fundamental and the class of the generator). The next scale, $n_3=3$, is the beginning of the lineage (and the end of the previous lineage). The scale $n_4=5$ is optimal. Therefore, the next scale, $n_5=7$, is the end of the lineage (and the beginning of the next lineage). In each stage of the lineage $3\prec 5\prec 7$, the greatest interval of the scale $n_2=2$ ($u_2$) is subdivided into two intervals, one with the same size as the smaller interval ($d_2$) and the other with the remaining size ($u_i$ on the left and $d_i$ on the right) until the size of the remaining interval becomes the smallest one.

In each stage, 2 tones (the ruling index), as many as the tones of the previous optimal scale, are added. The old notes are the generic diatones, and the new ones are the generic accidentals. Along the lineage, one interval is maintained (which becomes the diatonic interval in the next scale) by producing a regular subdivision of the intervals of the previous optimal scale $n_2=2$.

The generic diatones of the first scale of the lineage are the subdiatones of the lineage, i.e., the tones of the previous optimal scale. The generic diatones of the last scale of the lineage are the superdiatones of the lineage. The sum of the number of subdiatones and superdiatones matches the number of tones of the last scale of the lineage.

5. Extended Expressive Intonation

We pay attention to the lineage $7\prec 12\prec 17$, with ruling index $R=5$. In each stage, 5 new tones are regularly added. In the last 17-tone scale, the elementary interval $u_5$ of the 7-tone scale is split twice into 2 intervals, one of them with the same size as $d_5$.

In music, this lineage has the following interpretation. First, we may have the freedom of choosing a set of notes to which refer the added ones (it is not necessary to choose the first scale of the lineage). Traditionally, it has been the heptatonic scale C, D, E, F, G, A, B, corresponding to the iterates $k=-1,\dots ,6$. We call them structural diatones of the lineage. Choosing the starting index $-\alpha =-6$, for $k=-6\dots ,-2$ we obtain five new tones, namely D♭, E♭, G♭, A♭, and B♭, which are added to the left of some structural diatones. For $k=7,\dots ,11$, we obtain another set of five accidentals, namely C♯, D♯, F♯, G♯, and A♯, which are added to the other side.

Usually, expressive intonation is understood [32] as that sharps are played slightly higher and flats slightly flatter than they are on a keyboard tuned in equal temperament, that is, played as in Pythagorean tuning [3]. Such pairs of notes that in the Pythagorean tuning do not produce an identical pitch, but are still called enharmonic, providing a (fretless) string player with more degrees of freedom in order to tune specific frequency ratios, such as closer to just intonation, to meantone temperament or to equal temperament [11].

For example, in the 12-tone cyclic scale, seven fifth iterations forward starting at the note X lead to the note X^♯ = X$+u$ (modulo one octave), where $u=113.69¢$ is the chromatic semitone. Seven fifth iterations backward yield X^♭ = X$-u$. The chromatic semitone is the interval between a diatone X and its homonymous accidentals X^♭ and X^♯. Instead, the semitone between a diatone and its enharmonic equivalent accidentals is the diatonic semitone $d=90.22¢$, e.g., D and E♭ (instead of D♯), and D and C♯ (instead of D♭).

Notice that d is the smallest semitone of the heptatonic scale, e.g., the interval B-C. Their difference, ${\varphi }_n=u-d=23.46¢$, is the interval closure (the interval closure is related to the Pythagorean comma ${\kappa }_n$ as ${log}_2{\kappa }_n=\left|{\varphi }_n\right|$), resulting from 12 consecutive fifth iterations. Similarly, the interval between 7 iterations forward and 5 iterations backward (e.g., D^♭←C→C^♯) is $23.46¢$. Therefore, in expressive intonation, it is possible to apply microtonal corrections of $\pm 23.46¢$.

Between the tones of the 7-tone cyclic scale one tone apart (the intervals E-F and B-C are distant one diatonic semitone d) we can have the following accidentals: on the one hand, C^♯ = C$+u$ = D$-d$, D^♯ = D$+u$ = E$-d$, F^♯ = F$+u$ = G$-d$, G^♯ = G$+u$ = A$-d$, and A^♯ = A$+u$ = B$-d$, which form the typical 12-tone Pythagorean scale, and on the other hand, D^♭ = C$+d$ = D$-u$, E^♭ = D$+d$ = E$-u$, G^♭ = F$+d$ = G$-u$, A^♭ = G$+d$ = A$-u$, and B^♭ = A$+d$ = B$-u$, which complete a 17-tone cyclic scale. That is, each accidental is a structural diatone $\pm d$.

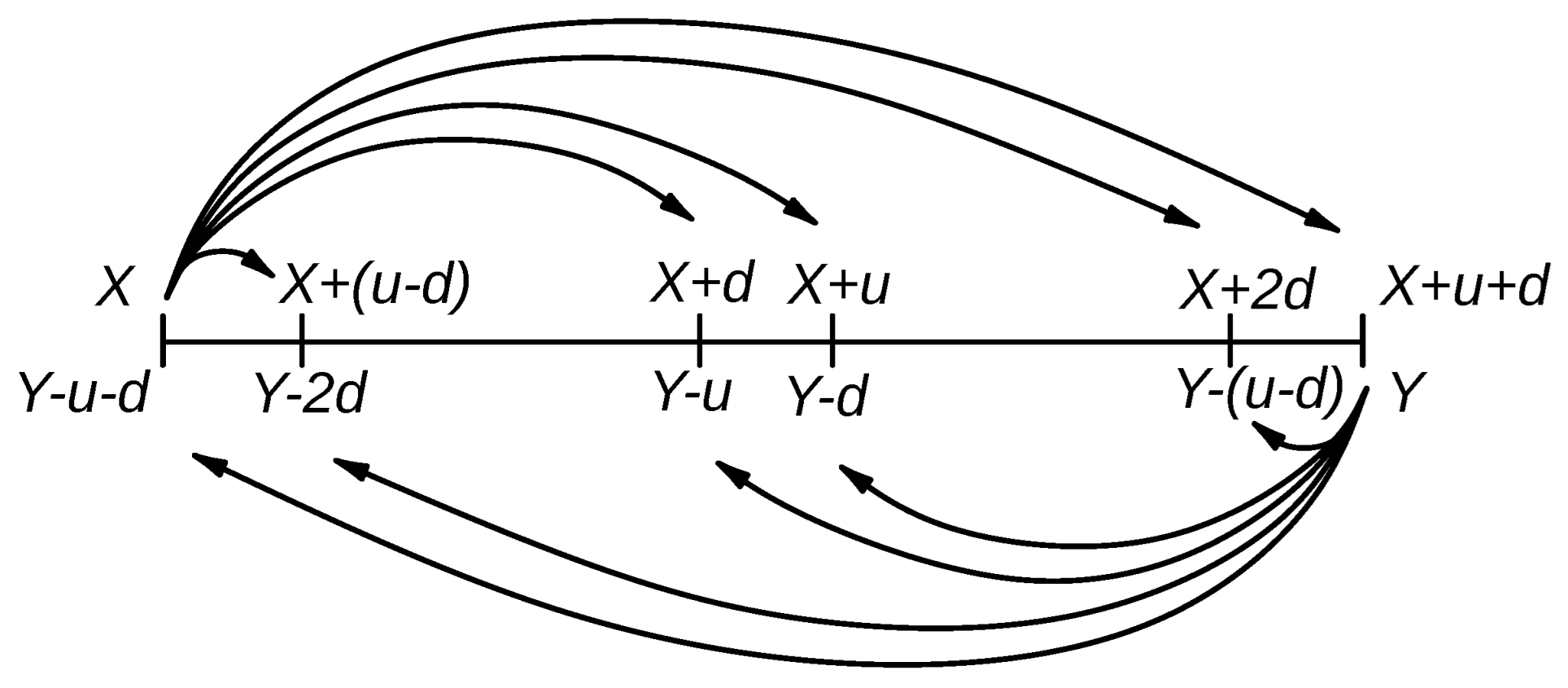
Figure 3 shows how the elementary intervals can be subdivided, including forward and backward iterates. Notice that the notation generally used in Pythagorean tuning is $X^{♯}=X+u$ and $Y^{♭}=Y-u$, which are two different tones. But $X+(u-d)=Y-2d$ and $X+2d=Y-(u-d)$ have no specific symbol referred either to X or Y. They are usually referred to the tone before X or to the tone after Y, respectively. For instance, if $X=C$, then $X+(u-d)=Y-2d=B^{♯}$; if $Y=D$, then $X+2d=Y-(u-d)=E^{𝄫}$. Instead, the Turkish notation (p. 46 in [33]) has specific symbols for all of them, although it is not consistent with the Pythagorean convention, since it actually assumes equal temperament and considers that the flat and sharp match.

Such a relationship between the 7-, 12-, and 17-tone consecutive cyclic scales in which expressive intonation is based (the lineage $7\prec 12\prec 17$) can be reproduced for other lineages. The tones of the first scale of the lineage are the tones to which the successively added accidentals can be referred with precision. In this way, in non-fretted instruments, such as stringed instruments and some brass instruments (natural horn, trombone, etc.), it is possible to know with precision “where each note is to go”.

For families beyond the lineage $17\prec 29\prec 41\prec 53$, extended expressive intonation may seem of difficult application. Nevertheless, the current work is also useful to highlight some important properties of cyclic scales and may help to understand their structure.

Some Middle-East music systems, such as the Ottoman, use a similar approach [34], where a selected row of tones out of 53 are allowed to vary one Pythagorean comma up or down to producing melodies with emotional intent or to tuning to precise frequency ratios. As mentioned in [2], according to [34] (and references therein), Al-Kindi (ca. 800–873) was the first to make use of the Abjad (Arabic shorthand for “ABCD”) pitch notation to denote finger positions on the ud for his 12-note approach, which was purely Pythagorean. It was the precursor to Urmavi’s 17-tone scale (1216–1294), which added five additional fifth iterations. The resulting scale was formed according to a starting index $-12$. This is an example of the lineage $7\prec 12\prec 17$.

On the other hand, several extensions of the 17-tone scale, by adding fifths backward and forward, generate the 24-tone Arel–Ezgi–Uzdilek and Yekta variants, with starting index −12 for the former and −14 for the latter.

By completing the above scales, the 53-tone Pythagorean scale is reached. This is an example of the lineage $17\prec 29\prec 41\prec 53$. It embodies Urmavi, Arel–Ezgi–Uzdilek, and Yekta-24 systems.

The 53-tone Pythagorean is very close to the 53-TET scale. We see in Section 9.2 that the difference between the two elementary intervals is only $3.62¢$. For this reason, in practice, the 53-TET scale has replaced the Pythagorean (similarly to what happened with the usual 12-tone scale), although the procedure of adding generic accidentals to a set of generic diatones is governed by the Pythagorean approach. In the end, the 53-TET scale has 9 commas per whole tone and 53 commas per octave. This comma is Holdrian, i.e., $22.64¢$ wide, which is less than one cent error to the Pythagorean comma.

6. Expressivity and Transportability

In addition to the greater flexibility gained with expressive intonation to approximate simple frequency ratios, it also increases the possibilities of interval translations to match an existing scale note. We give an estimation of how transportable the intervals ranging from the fundamental to each note of an n-tone cyclic scale are.

Once the iterates of the scale are ordered by pitch along the octave, from C onward and according to the cardinal index $j=0,\dots ,n-1$, their elementary factors U and D form a word with two letters, such as $w_{12}=UDUDDUDUDUDD$ (for the starting index $-1$). In addition, this word can be broken into syllables, so that each syllable is the interval between two consecutive generic diatones, such as $UD·UD·D·UD·UD·UD·D$, or, in general, between two structural diatones. The syllabicated word of the scale intervals is noted as $W_n$.

Given $W_n$, we select an interval $I\left(W_n\right)$ composed of the first I elementary intervals. Then, we check whether this interval translated to the jth tone ($1\le j\le n-1$) ends matching any note of the scale. If yes, it is transportable or transferable. The number of transportable intervals (labeled according to the starting note) is noted as $N_T$ (the first interval, starting at the fundamental $j=0$, is not included). This is performed for all possible intervals from $I=1$ to $n-1$ (the full octave P8 is not included). For an equal temperament scale, all the intervals are transferable, so that the number of matches is ${(n-1)}^2$. Hence, the ratio

$$t\left(W_n\right)={\displaystyle \frac{1}{{(n-1)}^2}}\sum _I{N}_T\left(I\left(W_n\right)\right)$$

estimates the transportability of the intervals relative to an equal temperament scale.

Nevertheless, from a tonal perspective, what is more important is whether the intervals can be translated matching any diatone of the scale, since this can be used as a measure of how expressive the intonation is. In such a case, we let $n^{\prime }$ be the number of diatones and $N_D$ be the number of transferable intervals to the diatones. Since for an equal temperament scale the number of matches is $(n-1)(n^{\prime }-1)$, the transportability over the diatones relative to an equal temperament scale is given through

$$e\left(W_n\right)={\displaystyle \frac{1}{(n-1)(n^{\prime }-1)}}\sum _I{N}_D\left(I\left(W_n\right)\right)$$

which we call expressivity. Hence, the following ratio expresses the contribution of the diatones to the overall transportability:

$${\displaystyle r\left(W_n\right)=\frac{{\displaystyle \sum _I{N}_D\left(I\left(W_n\right)\right)}}{{\displaystyle \sum _I{N}_T\left(I\left(W_n\right)\right)}}=\frac{n^{\prime }-1}{n-1}\frac{e\left(W_n\right)}{t\left(W_n\right)}}$$

Table 2. For 12-tone scale, the tables display: Interval name (P = perfect, M = major, m = minor, d = diminished, a = augmented, number indicates the generic interval or diatonic number); (I) number of elementary intervals referred to the syllabicated word $W_n$, notes where these intervals are transferable, ($N_T$) number of translations, and ($N_D$) number of translations to a diatone. The full octave P8 (gray) is listed only to show the whole set of notes.

Interval	I	(${\mathit{W}}_{12}=\mathbf{UD}·\mathbf{UD}·\mathit{D}·\mathbf{UD}·\mathbf{UD}·\mathbf{UD}·\mathit{D}$)	${\mathit{N}}_{\mathit{T}}$	${\mathit{N}}_{\mathit{D}}$
a1	1	C D F G A	4	4
M2	2	C C♯ D E F F♯ G G♯ A B	9	6
a2	3	C F G	2	2
M3	4	C D E F F♯ G A B	7	6
P4	5	C C♯ D D♯ E F G G♯ A A♯ B	10	5
a4	6	C D E F G A	5	5
P5	7	C C♯ D D♯ E F F♯ G G♯ A B	10	6
a5	8	C D F G	3	3
M6	9	C C♯ D E F F♯ G A B	8	6
a6	10	C F	1	1
M7	11	C D E F G A B	6	6
P8	12	C C♯ D D♯ E F F♯ G G♯ A A♯ B	11	6

illustrates these qualities for the 12-tone scale, referred to the structural diatones of the 7-tone scale with starting index −1, notes C, D, E, F, G, A, B. For the 12-tone scale, we obtain the following values: $t\left(W_{12}\right)=0.54$, $e\left(W_{12}\right)=0.76$, $r\left(W_{12}\right)=0.77$. It is worth remarking that the transportability of the diatonic intervals (i.e., M2, M3, P4, P5, M6, and M7) over the diatones is nearly full, with the exception of P4 that is not transferable to F. Thus, a high value of r indicates that most transportability is due to the diatones; in other words, there is low transportability to non-diatones.

Table 3. For 17-tone scale, the tables display: Interval name (P = perfect, M = major, m = minor, d = diminished, a = augmented, number indicates the generic interval or diatonic number); (I) number of elementary intervals referred to the syllabicated word $W_n$, notes where these intervals are transferable, ($N_T$) number of translations, and ($N_D$) number of translations to a diatone. The full octave P8 (gray) is listed only to show the whole set of notes.

Interval	I	(${\mathit{W}}_{17}=\mathbf{UDD}·\mathbf{UDD}·\mathit{D}·\mathbf{UDD}·\mathbf{UDD}·\mathbf{UDD}·\mathit{D}$)	${\mathit{N}}_{\mathit{t}}$	${\mathit{N}}_{\mathit{D}}$
m2	1	C C♯ D D♯ E F F♯ G G♯ A A♯ B	11	6
a1	2	C D♭ D E♭ F G♭ G A♭ A♭ B	9	4
M2	3	C D♭ C♯ D E♭ E F G♭ F♯ G A♭ G♯ A B♭ B	14	6
m3	4	C C♯ D E♭ D♯ E F F♯ G G♯ A B♭ A♯ B	13	6
a2	5	C D♭ E♭ F G♭ G A♭ B♭	7	2
M3	6	C D♭ D E E♭ F G♭ F♯ G A♭ A B♭ B	12	6
P4	7	C D♭ C♯ D E♭ D♯ E F F♯ G A♭ G♯ A B♭ A♯ B	15	6
d5	8	C C♯ D D♯ E F♯ G G♯ A A♯ B	10	5
a4	9	C D♭ D E♭ E F G♭ G A♭ A B♭	10	5
P5	10	C D♭ C♯ D E♭ D♯ E F G♭ F♯ G A♭ G♯ A B♭ B	15	6
m6	11	C C♯ D D♯ E F F♯ G G♯ A B♭ A♯ B	12	6
a5	12	C D♭ D E♭ F G♭ G A♭ B♭	8	3
M6	13	C D♭ C♯ D E♭ E F G♭ F♯ G A♭ A B♭ B	13	6
d7	14	C C♯ D E♭ D♯ E F F♯ G A♭ G♯ A B♭ A♯ B	14	6
a6	15	C D♭ E♭ F G♭ A♭ B♭	6	1
M7	16	C D♭ D E♭ E F G♭ G A♭ A B♭ B	11	6
P8	17	C D♭ C♯ D E♭ D♯ E F G♭ F♯ G A♭ G♯ A B♭ A♯ B	16	6

displays the same values for the 17-tone scale, with starting index −6 and the same structural diatones as before. We obtain $t\left(W_{17}\right)=0.70$, $e\left(W_{17}\right)=0.83$, $r\left(W_{12}\right)=0.44$. Therefore, the scale has gained transportability and expressivity relatively to the 12-tone scale, mostly for non-diatonic intervals.

7. Step and Co-Step Indices

The ratios corresponding to the tones of the scale $E_n^g$ in ${\mathsf{\Omega }}_0$ can be expressed in terms of the elementary factors $U={\nu }_m={\displaystyle \frac{g^m}{2^{〚m〛}}}$ and $D={\displaystyle \frac{2}{{\nu }_M}}={\displaystyle \frac{2^{〚M〛+1}}{g^M}}$ from the following relationship:

$${\nu }_k\equiv \Phi (p,q)\equiv {\nu }_m^p{\left({\displaystyle \frac{2}{{\nu }_M}}\right)}^q$$

for $0\le k\le n$, $0\le p\le M$, $0\le q\le m$. Then, it is straightforward to obtain

$$\left(\begin{array}{c}k\\ 〚k〛\end{array}\right)=\left(\begin{array}{cc}m& -M\\ 〚m〛& -(〚M〛+1)\end{array}\right)\left(\begin{array}{c}p\\ q\end{array}\right)$$

(3)

Since ${\nu }_m^M{\left({\displaystyle \frac{2}{{\nu }_M}}\right)}^m=2$ [4], then $(〚M〛+1)m-〚m〛M=1$, so that the determinant of the foregoing matrix is $-1$. Hence, there is an isomorphism between the two pairs of indices describing the scale. Therefore, the two elementary factors generate the scale tones and introduce the non-equal temperament.

Now, we translate this relationship to the logarithmic space of notes in terms of the elementary intervals and refer to the ith cyclic scale of the chain.

In a cyclic scale of $n_i$ tones, after $n_i-1$ iterations of the generator, the octave remains composed of $n_i$ intervals, which are a combination of the two elementary intervals of different sizes, $u_i$ and $d_i$, so that $M_i{u}_i+m_i{d}_i=1$. The scale tones can be expressed in terms of the step and co-step indices as ${\nu }_k=\Phi (p_i,q_i)$, so that the note with cardinal $j_i=p_i+q_i$ is given by ${log}_2\Phi (p_i,q_i)=p_i{u}_i+q_i{d}_i$.

As mentioned before, the next cyclic scale to $n_i$, with $n_{i+1}$ tones, is obtained by dividing the greatest of both intervals $u_i,d_i$ into two intervals, one with the same size as the smaller interval and the other with the remaining size.

The scale tone corresponding to the kth iterate (fifth, in Pythagorean scales) and $j_i$ th cardinal have a unique interval decomposition [12] (for $0\le k<n_i$, it holds that $0<p_i\le M_i$, $0\le q_i<m_i$, for other values of k these values can also be negative) in terms of $u_i$ and $d_i$, so that, by inverting (3), we obtain

$$\left(\begin{array}{c}{p}_i\left(k\right)\\ q_i\left(k\right)\end{array}\right)={\mathsf{\Lambda }}_i\left(\begin{array}{c}k\\ 〚k〛\end{array}\right),0\le k<n_i;{\mathsf{\Lambda }}_i=\left(\begin{array}{cc}〚M_i〛+1& -M_i\\ 〚m_i〛& -m_i\end{array}\right),det{\mathsf{\Lambda }}_i=-1$$

(4)

$$j_i\left(k\right)=p_i\left(k\right)+q_i\left(k\right)=N_{i}k-n_i〚k〛;0\le j_i<n_i$$

(5)

where $N_i=〚M_i〛+〚m_i〛+1$ and $0<p_i\le M_i,0\le q_i<m_i$. Equation (5) describes an automorphism of ${\mathbb{Z}}_{n_i}$.

Depending on the scale digit ${\delta }_i=N_i-〚n_i〛$, we distinguish two cases. To a lineage, one of them applies.

(i)

If ${\delta }_i=0$ ($u_i>d_i$), then $m_{i+1}=n_i$, $M_{i+1}=M_i$, $N_i=〚n_i〛$.

Since $m_{i+1}>M_{i+1}$, $d_{i+1}$ (with the same size as $d_i$) is the diatonic elementary factor.

According to (4), since $M_i$ is maintained,

$$\begin{array}{c}{p}_{i+1}\left(k\right)=p_i\left(k\right);0\le k<n_{i+1}\hfill \\ q_{i+1}\left(k\right)=N_{i}k-n_i〚k〛=j_i\left(k\right)=p_i\left(k\right)+q_i\left(k\right)\hfill \\ j_{i+1}\left(k\right)=2p_i\left(k\right)+q_i\left(k\right)(0\le j_{i+1}<n_{i+1})\hfill \end{array}$$

Then, $q_{i+1}\left(k\right)=j_i\left(k\right)$ for $0\le j_i\left(k\right)<n_{i+1}$. Therefore, the isomorphism

$$\left(\begin{array}{c}{p}_{i+1}\left(k\right)\\ q_{i+1}\left(k\right)\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)\left(\begin{array}{c}{p}_i\left(k\right)\\ q_i\left(k\right)\end{array}\right)$$

(6)

redistributes the $n_{i+1}$ tones along the octave, so that $p_i$ is maintained (while $u_i>d_i$, the size of the $u_i$-intervals becomes smaller as i increases) and the number $q_i$ of $d_i$-intervals increases progressively (their size is maintained). In each step, the new accidentals associated with the $d_i$-interval generate a family of microtones with a regular intervalic space between them.

For all indices such that $R_{i+l}=M_i$, with $l\ge 0$, since $q_{i+l}\left(k\right)=l{p}_i\left(k\right)+q_i\left(k\right)$, the $n_{i+l}$-tone scales in the lineage of $n_i$ can be represented as a lattice in the coordinate system with axes accounting for the u- and d-intervals, according to

$$\left(p_{i+l}\left(k\right),q_{i+l}\left(k\right)\right)=\left(p_i\left(k\right),l{p}_i\left(k\right)+q_i\left(k\right)\right);0\le k<n_{i+l}$$

(7)

The number of steps, either horizontally or vertically, between notes is the note cardinal.

The generic diatones are determined by the index $q_{i+l}$ associated with the interval $d_i$. In the last scale of the lineage, say of $n_{\omega }$ tones, the elementary intervals satisfy $u_{\omega }<d_i$. The last added accidentals share their coordinate $q_{\omega }$ with a diatone and are at this smaller distance $u_{\omega }$ from it. Therefore, they play the role of the enharmonics.

(ii)

If ${\delta }_i=1$ ($d_i>u_i$), then $M_{i+1}=n_i$, $m_{i+1}=m_i$, $N_i=〚n_i〛+1$.

Since $M_{i+1}>m_{i+1}$, $u_{i+1}$ (with the same size as $u_i$) is the diatonic elementary factor.

According to (4), as $m_i$ is maintained,

$$\begin{array}{c}{p}_{i+1}\left(k\right)=N_{i}k-n_i〚k〛=j_i\left(k\right)=p_i\left(k\right)+q_i\left(k\right);0\le k<n_{i+1}\hfill \\ q_{i+1}\left(k\right)=q_i\left(k\right)\hfill \\ j_{i+1}\left(k\right)=p_i\left(k\right)+2q_i\left(k\right)(0\le j_{i+1}<n_{i+1})\hfill \end{array}$$

Then, $p_{i+1}\left(k\right)=j_i\left(k\right)$ for $0\le j_i\left(k\right)<n_{i+1}$. Hence,

$$\left(\begin{array}{c}{p}_{i+1}\left(k\right)\\ q_{i+1}\left(k\right)\end{array}\right)=\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)\left(\begin{array}{c}{p}_i\left(k\right)\\ q_i\left(k\right)\end{array}\right)$$

(8)

In this case, $q_i$ is maintained while the size of the $d_i$-intervals becomes smaller as i increases (on condition that $d_i>u_i$), and the number $p_i$ of $u_i$-intervals progressively increases while their size is maintained. The new accidentals associated with the $u_i$-interval generate a family of regular microtones.

For all the indices such that $R_{i+l}=M_i$ for $l\ge 0$, since $p_{i+1}\left(k\right)=p_i\left(k\right)+l{q}_i\left(k\right)$, the $n_{i+l}$-tone scales in the lineage of $n_i$ have coordinates

$$\left(p_{i+l}\left(k\right),q_{i+l}\left(k\right)\right)=\left(p_i\left(k\right)+l{q}_i\left(k\right),q_i\left(k\right)\right);0\le k<n_{i+l}$$

(9)

The generic diatones are determined by the index $p_{i+l}$ associated with the interval $u_i$. In the last scale of the lineage, say of $n_{\omega }$ tones, the last added accidentals share the coordinate $p_{\omega }$ with a diatone and are separated by the elementary interval $d_{\omega }<u_i$.

The matrices in (6) and (8) are equivalent to the matrix $\left(\begin{array}{cc}1& \delta \\ 1-\delta & 1\end{array}\right)$ of (2), representing the branches of the Stern–Brocot tree. Therefore, from this viewpoint, a lineage is composed of consecutive cyclic scales in the same branche, which are connected by the same matrix.

8. Step Intervals

Let us modify (Equation (38) in [12]) in order to work explicitly in terms of the starting index, i.e., with tone iterates satisfying $-\alpha \le k<n_i-\alpha$, for $\alpha$ such that $0\le \alpha <n_i$. The kth fifth iterate, with cardinal $j_i$, is the tone notated as ${\nu }_k=\Phi (p_i,q_i)$. The tone with cardinal cardinal $j_i+1$ is given by

$${\Phi }^{+}(p_i,q_i)=\left\{\begin{array}{c}\Phi (p_i,q_i+1)={\nu }_{k-M_i},\mathrm{if}k-M_i\ge -\alpha \hfill \\ \Phi (p_i+1,q_i)={\nu }_{k+m_i},\mathrm{if}k-M_i<-\alpha \hfill \end{array}\right.$$

(10)

In other words, we may think of backward and forward iterates from $k=0$ to gain such a degree of freedom.

The inversion of (5) yields

$$k=p_i{m}_i-q_i{M}_i;0<p_i\le M_i,0\le q_i<m_i$$

(11)

or, alternatively,

$$k=j_i{m}_i-q_i{n}_i=j_i{m}_{i}mod{n}_i,0\le j_i<n_i$$

In the former equality, each iterate of the $n_i$-tone scale is described from a direct product ${\mathbb{Z}}_{M_i}\times {\mathbb{Z}}_{m_i}$ and, in the latter equality, as an automorphism of ${\mathbb{Z}}_{n_i}$.

In this way, from the values $p_i,q_i$, Equation (11) determines k. According to (10), depending on the value $k-M_i$, we know which interval, either u or d, leads to the following tone.

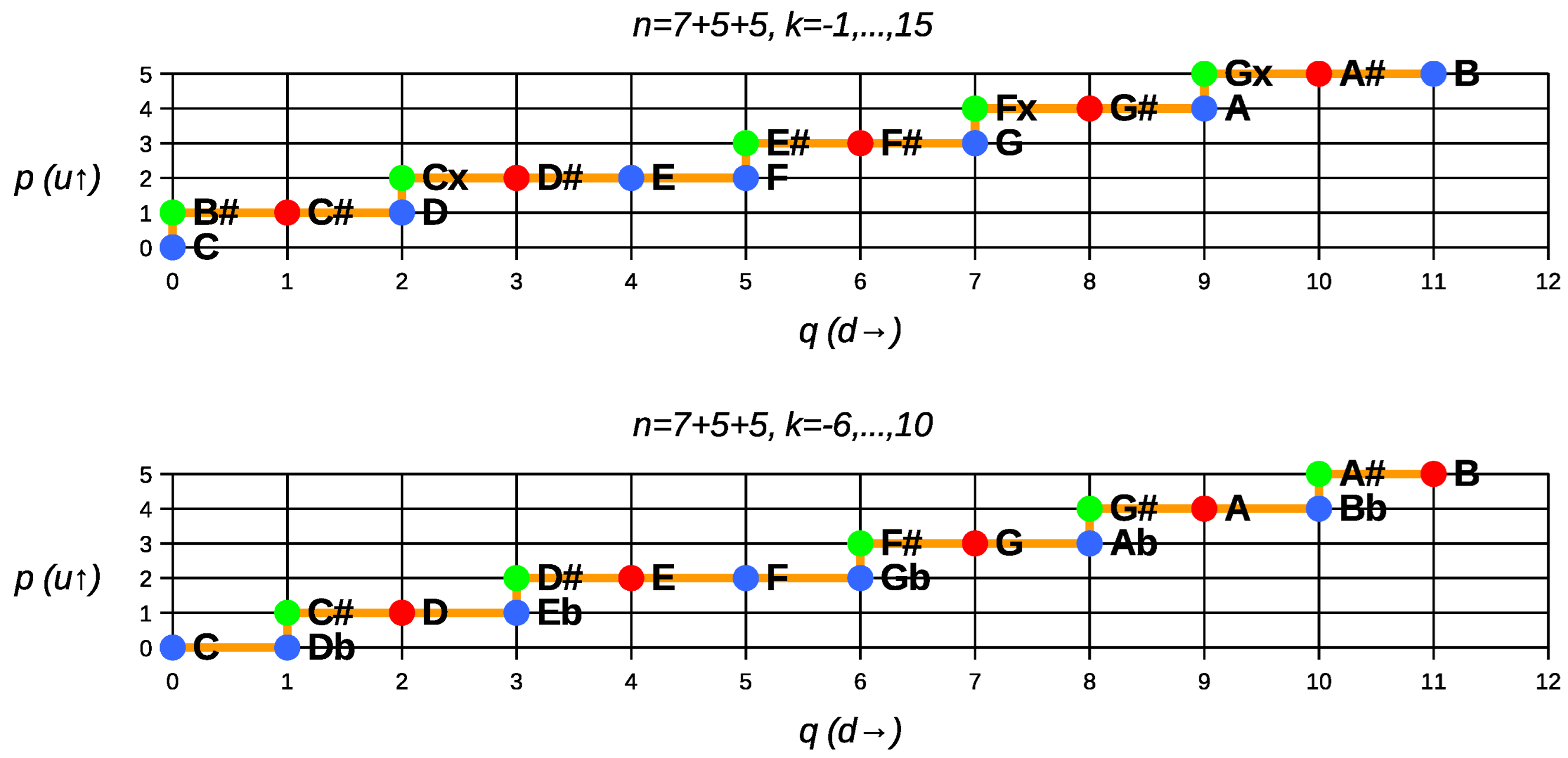
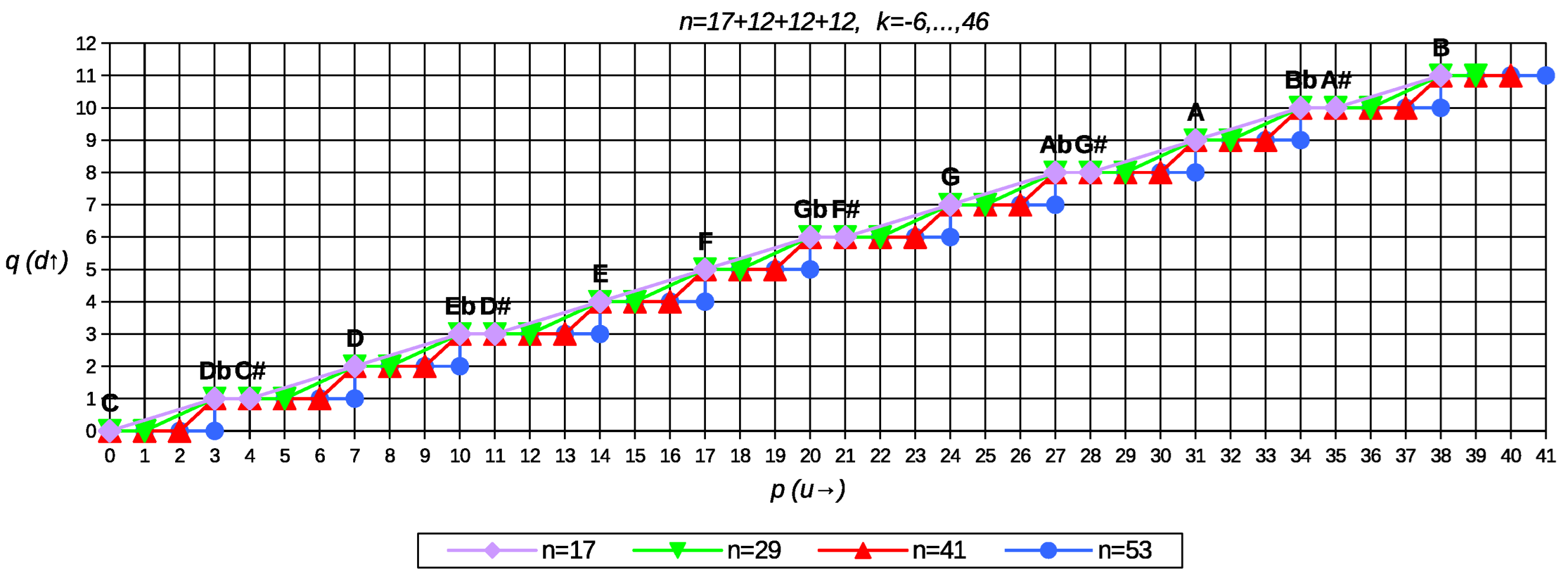
Figure 4 shows two examples, corresponding to the case (i) of the previous section, for the scales $E_{12}^3$ and $E_{17}^3$ in relation to the structural diatones of $E_7^3$, with iterates $k=-1,\dots ,6$ (F, C, G, D, A, E, B, blue dots).

Tonal Western music has a diatonic structure, which is reflected on the musical staff and key signature. Its historical evolution until serial dodecaphonism could be viewed as a process of gaining resources and flexibility about this diatonic skeleton.

On the top of Figure 4, such a diatonic structure for the 12-tone scale becomes clear. The diatones, which in the pentagram occupy a precise position, either in a ledger line or in a space, in the above graph are assigned to a unique q value (since d is the interval associated with the diatones). The accidentals, which in the staff need to be notated with an accidental symbol since they occupy the position of a diatone, in the graph have the same coordinate q as a diatone but a different coordinate p.

In the next cyclic scale, on the bottom of Figure 4, the 17-tone scale, the previous accidentals now occupy an exclusive coordinate q, i.e., all the tones of the 12-tone scale are now the generic diatones of the 17-tone scale, each one in a different q position. The new generic accidentals share their q coordinate with a generic diatone, although with a different coordinate p.

9. Choosing the Microtones

9.1. Lineage 7 ≺ 12 ≺ 17

First, we discuss the lineage $7\prec 12\prec 17$ that begins with $n_5=7$ and ${\delta }_5=0$ (Table 1). In the last stage, for the 17-tone Pythagorean scale ($n_7=17$), the actual interval sizes are $u_7=23.46¢$ and $d_7=90.22¢$. Since $d_7$ is nearly four times greater than $u_7$, it may be useful to choose where we want to intersperse the microtonal intervals. Depending on the starting index, either $k=-1$ (F) or $k=-6$ (G^♭), the scale tones are those on the top or bottom of

Table 4. (Top) Iterates starting with F ($k=-1,\dots ,15$) that successively generate Pythagorean scales of 7, 12, and 17 tones. (Bottom) Iterates starting with G^♭ ($k=-6,\dots ,10$). Second and third rows contain the generic accidentals added to the previous row.

F	C	G	D	A	E	B
F♯	C♯	G♯	D♯	A♯
E♯	B♯	F𝄪	C𝄪	G𝄪
G♭	D♭	A♭	E♭	B♭	F	C
G	D	A	E	B
F♯	C♯	G♯	D♯	A♯

. The first row contains the five generic diatones of $E_7^3$ and the two generic accidentals. The former, the subdiatones of the lineage, is refined to produce the new accidentals of the rows below.

Graphically, Figure 5 displays the intervals by keeping the actual proportions, where we are able to see that such a difference matters.

On the top panel, a row contains the accidentals added to the first scale of the lineage until reaching the next diatone. However, the enharmonic intervals become alternative tones to the diatones of the 7-tone scale, which is not useful, since these diatones are used as structural notes.

On the bottom panel, beginning the iterates with $k=-6$, the 17-tone scale corresponds to the expressive tuning of the 12-tone scale, where the notes G, D, A, E, B are equidistant to their respective flats and sharps. That is, the enharmonic intervals correspond to the same coordinate q, not matching that of the structural diatone of the 7-tone scale, so that it is possible to have two alternative accidentals to these diatones.

Therefore, a scale lineage describes an orderly refinement process that, depending on the starting index $-\alpha$, is able to introduce a desirable set of microtones.

9.2. Lineage 17 ≺ 29 ≺ 41 ≺ 53

We now discuss the lineage $17\prec 29\prec 41\prec 53$. In the link involving the scales of $n_7=17$ and $n_8=29$ tones, the digit of scale changes its value to ${\delta }_7=1$. Hence, a new lineage starts. Since $u_7<d_7$, from this point onward the interval $d_7$ is the one to be subdivided in terms of the interval $u_7$ by adding 12 tones and intervals in each stage, ending in the 53-tone scale, where the intervals $u_{10}=u_7=23.46¢$ and $d_{10}=19.84¢$ are of a similar size ($u_{10}-d_{10}=3.62¢$). Therefore, in this case, the added accidentals remain well distributed, regardless of the starting iteration.

By starting the iterates with $k=-6$ (as in the previous 17-tone scale), this lineage is represented in Figure 6, where only the tones of the 17-tone scale are labeled. In this way, the successive accidentals remain regularly distributed, since the difference of $3.62¢$ between intervals is, in practice, inaudible. The color lines between consecutive tones of the respective scales allow us to visualize how each interval step of a scale is formed in terms of the elementary intervals of the 53-tone scale.

Figure 7 displays the process of subdivision along this lineage. Notice that this scale would become of equal temperament if both intervals were approximated by $1200{log}_2{2}^{{\displaystyle \frac{1}{53}}}=22.64¢$ (the Holdrian or Arabian comma). Such an approximation would modify $d_7$ in $2.8¢$ and $u_7$ in $0.8¢$, quantities almost imperceptible. Therefore, the 53-TET scale is like a wild card, with many good properties [35] that can be used either as a generalized Pythagorean scale (containing those of less tones) or for approximating scales based on just intonation.

10. Conclusions

A non-degenerate cyclic scale is a well-formed scale of one generator, other than a rational power of two. It excludes equal temperament scales and is formed by a set of notes that fulfills the closure condition. The notes divide the octave into the same number of intervals of exactly two different sizes.

Its algebraic structure is given by the abstract scale, which is a quotient group of classes of projection functions. However, such an approach does not account for the size of the intervals between notes. For this purpose, it is necessary to choose a representative of each class in order to define a concrete scale. The n tones $\{{\alpha }_1,\dots ,{\alpha }_n\}$ of a concrete scale must meet two basic conditions. First, the set must include the fundamental. Second, the scale tones in the octave $S_0$ must fulfill ${\alpha }_i={\pi }_g^i{\alpha }_1$, for $i=2,\dots ,n$. Therefore, there are n different ways to choose the scale.

From a mathematical viewpoint, this means either to fix a tone as the origin of the iterations or to choose which tone takes the role of fundamental. From a musical viewpoint, this is important for two reasons. One is that depending on the chosen origin, the tones are more or less close to specific frequency ratios, such as ${\displaystyle \frac{5}{4}}$, ${\displaystyle \frac{6}{5}}$, ${\displaystyle \frac{5}{3}}$, etc., which is of interest in order to approximate just intonation scales [11]. The other reason, which is a main point in the present article, is that depending on where the series of iterates starts, it is possible to select the microtones generated along a lineage.

Scale lineages are associated with the convergents and semiconvergents of the continued fraction expansions of the generator. According to [2], after a scale corresponding to a convergent, a lineage of scales begins and the previous one ends. A lineage includes a series of consecutive semiconvergents and ends after the next convergent. During a lineage, one of the elementary intervals remains constant, and the other is successively subdivided in a regular manner. At each stage, the intervals that are subdivided are those of generalized diatones. In addition, it is possible to select a set of structural diatones to which the accidentals are referred.

Western musical notation follows such a similar process, and it is this process that the current work has tried to reproduce. The seven notes of the diatonic scale occupy a precise position in the pentagram, either in a ledger line or in a space. Over the centuries, the set of scale notes has become larger, by gaining in harmonic and melodic resources. For instance, old pentatonic and heptatonic scales have been extended with scales such as the usual 12-tone chromatic scale, scales based on quarter-tone temperament such as Arabic 24-tone, Vicentino’s 31-tone system, Arabic 17- and 53-tone systems, or a manifold of just intonation microtonal scales [36].

New tones have been added to the heptatonic scale, which constitute the basic structure of the staff, although they need to be notated with an accidental symbol, since they occupy the same position of a diatone.

When the seven notes of the diatonic scale are notated with sharps and flats to modify their pitch, we speak of expressive intonation. This corresponds to the lineage $7\prec 12\prec 17$. If the same is performed in one of the following lineages, we are speaking of extended expressive intonation.

This way of considering the scale notes, as a set of structural diatones in addition to forward and backward accidentals, has a two-dimensional representation to which we also pay attention.

The way of describing the scale notes in cyclic order from the fundamental is by giving two coordinates indicating how many generic diatonic and accidental intervals there are between each note and the fundamental. This is the representation of the scale in terms of the step and co-step indices, which is given by an automorphism, either (7) or (9), depending on the lineage, i.e., depending on the side where the semiconvergents are improving the approximations of the generator tone.

When the notes are represented in a two-dimensional graph, the generic diatones are anchored to fixed values on one of the coordinate axes. In this axis, the generic diatones take consecutive values (just like in the position of a staff). The generic accidentals added to a diatone maintain the coordinate linked to the diatone, but vary in the other coordinate (also similar to the accidentals symbols added to the notes on the staff). By changing the starting index of the scale, the microtones that are generated vary and their distribution changes, so it is possible to choose the distribution that is most interesting from a musical point of view.