Modified Two-Parameter Ridge Estimators for Enhanced Regression Performance in the Presence of Multicollinearity: Simulations and Medical Data Applications

Abstract

Predictive regression models often face a common challenge known as multicollinearity. This phenomenon can distort the results, causing models to overfit and produce unreliable coefficient estimates. Ridge regression is a widely used approach that incorporates a regularization term to stabilize parameter estimates and improve the prediction accuracy. In this study, we introduce four newly modified ridge estimators, referred to as RIRE1, RIRE2, RIRE3, and RIRE4, that are aimed at tackling severe multicollinearity more effectively than ordinary least squares (OLS) and other existing estimators under both normal and non-normal error distributions. The ridge estimators are biased, so their efficiency cannot be judged by variance alone; instead, we use the mean squared error (MSE) to compare their performance. Each new estimator depends on two shrinkage parameters, $k$ and $d$, making the theoretical analysis complex. To address this, we employ Monte Carlo simulations to rigorously evaluate and compare these new estimators with OLS and other existing ridge estimators. Our simulations show that the proposed estimators consistently minimize the MSE better than OLS and other ridge estimators, particularly in datasets with strong multicollinearity and large error variances. We further validate their practical value through applications using two real-world datasets, demonstrating both their robustness and theoretical alignment.

1. Introduction

Multicollinearity is a prevalent challenge in predictive modeling, occurring when input features exhibit high correlation, which results in unstable model estimates and reduced prediction accuracy.

The multiple linear regression model is a widely used statistical tool across disciplines, including business, environmental studies, industry, medicine, and social sciences. A crucial assumption of this model is the independence of explanatory variables. However, in practice, explanatory variables often exhibit moderate to strong linear relationships, leading to multicollinearity. This instability makes the coefficients less reliable. In a basic regression model, we have

$$y=X\alpha +ϵ.$$

(1)

In Equation (1), $y\in R^{n\times 1}$ denotes the vector of observed responses, $X\in R^{n\times p}$ represents the design matrix comprising the predictor variables, $\alpha \in R^{p\times 1}$ is the vector of unknown regression coefficients, and $\epsilon \in R^{n\times 1}$ is the vector of random errors.

The typical method for estimating these coefficients is the OLS method, which is represented in Equation (2) as follows:

$${\widehat{\alpha }}_{OLS}={\left(X^{\prime }X\right)}^{-1}{X}^{\prime }y and Cov\left({\widehat{\alpha }}_{OLS}\right)={\sigma }^2{\left(X^{\prime }X\right)}^{-1}.$$

(2)

A key measure for detecting multicollinearity is the Condition Number (CN), which compares the largest (${\lambda }_{max}$) and smallest (${\lambda }_{min}$) eigenvalues of the matrix ${\mathrm{X}}^{\prime }\mathrm{X}$:

$$\mathrm{C}\mathrm{N}\left(X\right)={\displaystyle \frac{{\lambda }_{max}}{{\lambda }_{min}}}.$$

(3)

A high CN (e.g., greater than 30) suggests severe multicollinearity, which leads to unstable estimates of the regression coefficients. Another common diagnostic tool is the Variance Inflation Factor (VIF), which measures how much the variance of a regression coefficient is inflated due to multicollinearity. It is calculated for each predictor as in Equation (4).

$${VIF}_i={\displaystyle \frac{1}{1-R_i^2}},$$

(4)

where $R_i^2$ is the coefficient of determination when the $i^{th}$ predictor is regressed on all the others. A VIF greater than 10 indicates sever multicollinearity in the data. When multicollinearity exists, the matrix $X^{\prime }X$ becomes close to singular, which makes OLS estimates less reliable. One effective solution is the ridge regression, a regularization technique that introduces a penalty term to mitigate overfitting [1]. In ref. [2], the authors modified new ridge estimator for severe multicollinear datasets. The shrinkage parameter, which controls the strength of regularization, was tuned simultaneously to find optimize the regression coefficients. The shrinkage parameter adjustment takes place during both the tuning and validation phases to achieve a balance between fitting the data well and avoiding overfitting.

• A ridge estimator is defined as follows:

$${\widehat{\alpha }}_{ridge}={\left(X^{\prime }X+kI\right)}^{-1}{X}^{\prime }y.$$

(5)

The $k$ term, a small positive value known as the shrinkage or ridge parameter, is used to improve the numerical stability of the regression model. Additionally, $I$ is the identity matrix, which is controlled by the ridge parameter k. This technique effectively shrinks the coefficients, which, in turn, helps reduce the variance or minimize the MSE. A key strength of the ridge parameter k is its simplicity and computational efficiency, especially when the model includes fewer independent variables. However, the performance of ridge estimators is highly influenced by the choice of k, which is typically determined through cross-validation. There are scenarios where a single regularization parameter may not be sufficient, especially in complex models. This is where two-parameter ridge estimators come into play, offering advantages over the traditional ridge estimator is widely used to handle multicollinearity. For example, ref. [3] examined coefficient testing under ridge models, while ref. [4] proposed a new ridge-type estimator with improved performance.

However, ref. [5] introduced the two-parameter ridge or shrinkage estimator, which adds another scale parameter, $d,$ to adjust the penalty term, as in Equation (6).

$${\widehat{\alpha }}_{(d,k)}={d\left(X^{\prime }X+kI\right)}^{-1}{X}^{\prime }y,$$

(6)

where

$$\widehat{d}={\displaystyle \frac{{\left(X^{\prime }y\right)}^{\prime }{\left(X^{\prime }X+kI\right)}^{-1}{X}^{\prime }y}{{\left(X^{\prime }y\right)}^{\prime }{\left(X^{\prime }X+kI\right)}^{-1}{X}^{\prime }X{\left(X^{\prime }X+kI\right)}^{-1}{X}^{\prime }y}}.$$

(7)

This approach allows for more flexibility, making it better suited for handling multicollinearity in complex cases. If $\mathrm{d}=1 \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{k}=0$, Equation (6) reverts to the standard OLS estimator. The authors in [6] improved the two-parameter ridge regression estimator for the multicollinearity dataset and compared their estimators with others based on the MSE.

While ref. [7] introduced a generalized ridge estimator as a comprehensive solution for handling severe multicollinearity, ref. [8] introduced three shrinkage estimators based on averages for severe multicollinear data. Ref. [9] developed the bias–variance trade-off by incorporating data-specific tuning parameters, offering a more tailored approach to ridge regression.

Theoretical improvements have focused on utilizing higher-order eigenvalue terms to improve ridge regression techniques. Ref. [10] developed new ridge estimators to effectively reduce the effect of multicollinearity from the data. Ref. [11] further highlighted and improved the shrinkage parameters in practical applications of ridge regression to address multicollinearity, making it an essential tool in regression analysis. While refs. [12,13] expanded the scope of ridge estimators to handle severe multicollinearity datasets in fields such as genetics, environmental studies, and econometrics, ref. [14] proposed ridge estimators based on rank, a method particularly useful for analyzing complex multicollinearity genetic data.

Extensive research has been conducted on estimating the ridge or shrinkage parameters in linear regression models. Ref. [15] innovated two-parameter estimators of complex multicollinear data to improve the accuracy of the Almon distributed-lag model. Ref. [16] developed ridge estimators to enhance the accuracy of linear regression models and compared these estimators with OLS and other established estimators based on the MSE. More recently, ref. [17] used bootstrap–quantile and improved ridge estimators for linear regression, while ref. [18] introduced six new two-parameter ridge estimators to address multicollinearity challenges and compared these modified estimators with other established estimators based on the MSE. The authors in both [19,20] further introduced two-parameter ridge estimators to more effectively handle data with high multicollinearity, compared to other existing estimators.

The literature clearly shows that no single ridge estimator performs well across all multicollinearity scenarios. To deal with this issue, many researchers have proposed modifications to improve the estimator performance under severe multicollinearity. In this study, we propose four new ridge-type estimators, denoted as RIRE1, RIRE2, RIRE3, and RIRE4, that demonstrate better performance in simulation studies across different conditions such as sample sizes, number of predictors, error variances, and correlation structures. These estimators outperform the OLS and other existing shrinkage methods, maintaining robust efficiency under both normal and non-normal distributions, particularly when datasets have severe multicollinearity. The remainder of the paper is organized as follows: Section 2 presents the statistical methodology for ridge estimators, including a review of existing estimators and the introduction of our four newly modified estimators. Section 3 describes the Monte Carlo simulations conducted to assess the performance of these estimators under various conditions. In Section 4, the proposed estimators are applied to the analysis of two real-world datasets to demonstrate their practical utility. Finally, Section 5 offers concluding remarks and summarizes the key findings of the study.

2. Methodology

Ridge regression is a supervised learning method that adds a penalty term to the regression equation in order to reduce multicollinearity. This section provides the mathematical foundation for existing ridge estimators and the newly proposed modified estimator for ridge regression models.

To simplify the regression model in Equation (1), we can reformulate it into its canonical form as

$$y=U\beta +ϵ,$$

(8)

where $U=XQ$ is the transformed design matrix, $\beta$ is the parameter vector in the canonical space, and $ϵ$ represents the noise, as before. The matrix $Q$ is orthogonal, derived from the eigenvectors of $X^{\prime }X,$ and satisfies $Q^{\prime }Q=I_p$. This transformation aligns the design matrix $U$ with the principal components of $X$, simplifying the regression problem.

Additionally, we define

$$\Lambda =Q^{\prime }{X}^{\prime }XQ,$$

(9)

where $\Lambda$ is a diagonal matrix containing the eigenvalues ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_p$ arranged in ascending order. The relationship between the original parameters and the canonical parameters is expressed as $\beta =Q^{\prime }\alpha ,$ which enables the model to operate in the canonical space.

In this form, the OLS estimator becomes

$$\widehat{\beta }={\Lambda }^{-1}{U}^{\prime }y,$$

(10)

where ${\Lambda }^{-1}$ scales $U^{\prime }y$ by the inverse eigenvalues. However, small eigenvalues can cause instability in the OLS solution. Ridge regression mitigates this by introducing a regularization parameter $k>0$, modifying the estimator to be

$${\widehat{\beta }}_k={\left(\Lambda +k{I}_p\right)}^{-1}{U}^{\prime }y,$$

(11)

which adds $k$ to the diagonal elements of Λ, stabilizing the solution by reducing the influence of small eigenvalues.

A generalized two-parameter ridge regression estimator extends this idea, taking the form

$${\widehat{\beta }}_{(d,k)}={d\left(\Lambda +k{I}_p\right)}^{-1}{U}^{\prime }y,$$

(12)

where $d$ adjusts the intensity of shrinkage. This added flexibility allows for better control over the trade-off between bias and variance, catering to various modeling requirements.

2.1. Existing Ridge-Type Estimators

In this part, some existing estimators are discussed and reviewed. Hoerl and Kennard in [1] developed the first ridge estimator, commonly known as the HK estimator, and its mathematical formulation is given as

$${\widehat{k}}_{HK}={\displaystyle \frac{{\widehat{\sigma }}^2}{{\widehat{\beta }}_{Max}^2}}\hspace{1em}\hspace{1em} \mathrm{with}\hspace{1em}\hspace{1em} {\beta }_{Max}=\mathrm{m}\mathrm{a}\mathrm{x}({\beta }_1, {\beta }_2, \dots ,{\beta }_p).$$

(13)

The authors in [8] explored three ridge estimators designed to address multicollinearity in data using averaging techniques. These are the Arithmetic Mean (KAM), the Geometric Mean (KGM), and the Median (KMed). They are mathematically expressed as

$$\begin{array}{c}{\widehat{k}}_{AM}={\displaystyle \frac{1}{p}}{\sum }_{i=1}^p{\displaystyle \frac{{\widehat{\sigma }}^2}{{\widehat{\beta }}_i^2}},\\ {\widehat{k}}_{GM}={\displaystyle \frac{{\widehat{\sigma }}^2}{{\left({\prod }_{i=1}^p{\widehat{\beta }}_i^2\right)}^{\frac{1}{p}}}},\\ {\widehat{k}}_{Med}=\mathrm{M}\mathrm{e}\mathrm{d}\left({\displaystyle \frac{{\widehat{\sigma }}^2}{{\widehat{\beta }}_i^2}}\right).\end{array}$$

(14)

Ref. [21] introduced an eigenvalue-based estimator, known as the KMS estimator, to effectively handle multicollinearity. Its mathematical expression is given as

$${\widehat{k}}_{KMS}={\mathsf{\lambda }}_{\max }{\displaystyle \frac{{\sum }_{i=1}^p\left|{\widehat{\beta }}_i\right|}{\left\{\frac{{\widehat{\sigma }}^2}{{\widehat{\beta }}_{Max}^2}\right\}}}.$$

(15)

Similarly, a two-parameter ridge estimator, referred to as the TK estimator, was established by [6], with the optimal values for ${\widehat{d}}_{opt}$ and ${\widehat{k}}_{opt}$ derived as follows:

$${\widehat{d}}_{opt}={\displaystyle \frac{{\sum }_{i=1}^p{\widehat{\beta }}_i^2\frac{{\lambda }_i}{{\lambda }_i+k}}{{\sum }_{i=1}^p\frac{{\widehat{\beta }}^2{\lambda }_i+{\widehat{\gamma }}_i^2{\lambda }_i^2}{{\left({\lambda }_i+k\right)}^2}}},$$

(16)

$${\widehat{k}}_{opt}={\displaystyle \frac{{\widehat{d}}_{opt}{\sum }_{i=1}^p\frac{{\widehat{\sigma }}^2}{{\lambda }_i}+\left({\widehat{d}}_{opt}-1\right) {\sum }_{i=1}^p{\widehat{\beta }}_i^2{\lambda }_i^2}{{\sum }_{i=1}^p{\widehat{\beta }}_i^2{\lambda }_i}}.$$

(17)

Ref. [22] developed three estimators for multicollinearity data, denoted as MPR1, MPR2, and MPR3. Their mathematical expressions are given below:

$$\begin{array}{c}{\widehat{k}}_{MPR1}^{*}={\displaystyle \frac{\sum _{i=1}^p{k}_i^{*}}{p}} ,\\ {\widehat{k}}_{MPR2}^{*}={\left(\prod _{i=1}^p{k}_i^{*}\right)}^{{\displaystyle \frac{1}{p}}} ,\\ {\widehat{k}}_{MPR3}^{*}={\displaystyle \frac{p}{\sum _{i=1}^p\frac{1}{k_i^{*}}}} .\end{array}$$

(18)

In these formulations, the adjusted ridge parameter for the $i^{th}$ predictor is computed as

$$k_i^{*}={\omega }_i{\widehat{k}}_{opt},$$

where ${\beta }_i$ is a weight defined by the ratio of the eigenvalue ${\lambda }_i$ to the absolute value of the corresponding coefficient estimate ${\beta }_i$:

$${\omega }_i={\displaystyle \frac{{\mathit{\lambda }}_{\mathit{i}}}{\left|{\beta }_i\right|}}.$$

From the well-established ridge-type estimators available, we selected the estimators HK, KAM, KGM, KMed, KMS, TK, MPR1, MPR2, MPR3, and OLS to be compared with our four modified estimators using Monte Carlo simulations based on the MSE.

2.2. New Ridge-Type Estimators

The newly proposed estimators, referred to as RIRE1, RIRE2, RIRE3, and RIRE4, effectively address various multicollinearity conditions. For these estimators, the ${\widehat{k}}_i-$values $(i=1,2,3,4$) are presented below:

$${\widehat{k}}_1=\mathit{log}\left(1+{\displaystyle \frac{{\sum }_{i=1}^p{\lambda }_i\cdot \left|{\widehat{\beta }}_i\right|}{{\widehat{\sigma }}^2}}\right),$$

(19)

In this estimator, the logarithmic function imposes a nonlinear growth constraint on the penalization term. By summing ${\lambda }_{\mathit{i}}\left|{\widehat{\beta }}_i\right|$ over $p$, this estimator accumulates the contribution of each variable to multicollinearity.

$${\widehat{k}}_2={\displaystyle \frac{{\sum }_{i=1}^p\left({\lambda }_i^2\cdot \left|{\widehat{\beta }}_i\right|\right)}{p\cdot \mathit{max}\left(\left|{\widehat{\beta }}_i\right|\right)}},$$

(20)

Squaring the eigenvalues in this estimator increases the weight of highly collinear directions. Normalizing by the maximum coefficient ensures that the penalty strength does not disproportionately increase due to one dominant variable. Thus, RIRE2 enforces balanced shrinkage that is tailored to both the multicollinearity severity and the variable scale.

$${\widehat{k}}_3={\displaystyle \frac{{\left({\sum }_{i=1}^p\left({\lambda }_i\cdot \left|{\widehat{\beta }}_i\right|\right)\right)}^2}{p\cdot {\widehat{\sigma }}^2}},$$

(21)

The RIRE3 estimator captures the squared contribution of eigenvalue-weighted coefficients, scaled by residual variance, effectively linking penalization strength to the overall signal-to-noise ratio in the presence of multicollinearity.

$${\widehat{k}}_4={\displaystyle \frac{{\sum }_{i=1}^p\left({\lambda }_i^3\cdot {\left|{\widehat{\beta }}_i\right|}^2\right)}{p\cdot \sqrt{{\sum }_{i=1}^p{\left({\lambda }_i\cdot \left|{\widehat{\beta }}_i\right|\right)}^2}}}.$$

(22)

RIRE4 introduces higher-order penalization sensitivity by cubing the eigenvalues and squaring the coefficients, allowing it to react more forcefully to severe collinearity. The denominator acts as a normalization factor, stabilizing the shrinkage magnitude. This estimator is particularly effective when a subset of predictors exhibits extremely high multicollinearity.

Equations (19)–(22) are used to optimize the $\widehat{k}$-values, while Equation (7) is utilized to compute $\widehat{d}$.

2.3. The Performance of Estimators Based on the MSE Criterion

We assessed and compared the performance of our proposed modified estimators with OLS and other existing estimators based on the MSE criterion. The MSE has been applied in various studies such as in [23,24,25,26,27,28] to evaluate the accuracy of estimators. The MSE can be calculated as

$$MSE\left(\widehat{\beta }\right)=E(\widehat{\beta }-\beta {)}^{\prime }\left(\widehat{\beta }-\beta \right)$$

(23)

$$\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle \frac{1}{p}}{\sum }_{i=1}^p(\widehat{\beta }-\beta {)}^2.$$

(24)

Since it is challenging to compare Equations (23) and (24) theoretically, we will, instead, analyze their performance through Monte Carlo simulations in the next section.

3. Computational Analysis Using Monte Carlo Simulation

Equation (25) is used for generating predictors as seen in previous research studies [26,27,28].

$$x_{ij}=\sqrt{1-{\rho }^2}\cdot U_{ji}+\mathsf{\rho }\cdot U_{j,p+1}, i=\mathrm{1,2},\dots ,p; j=\mathrm{1,2},\dots ,n.$$

(25)

The correlation ($\mathsf{\rho }$) between predictors was varied across values of 0.50, 0.70, $0.88, 0.94, 0.98, \mathrm{and} 0.999$ to examine different multicollinearity scenarios. Independent samples ($U_{ji}$) were drawn from a standard normal distribution, with sample sizes $(n=20, 50, 100)$ and predictor counts $(p=4, 10)$ used to evaluate model robustness. The response variable ($y_i$) was generated using the following model:

$$y_i={\beta }_0+{\sum }_{i=1}^p{\sum }_{j=1}^n{\beta }_i{x}_{ij}+{ϵ}_j,$$

(26)

where ${\beta }_0$ is the intercept (set to zero), ${\beta }_i$ is the regression coefficient, and ${ϵ}_j$ is the error term with variance $\left({\sigma }^2\right)$ analyzed at levels 0. 4, 1, 4, and 8. Furthermore, to examine the impact of non-normal errors, we generated error terms from a t-distribution with 2 degrees of freedom ($t_{(v=2)})$ and an F-distribution with 6 and 12 degrees of freedom (F (6,12)).

To calculate the MSE of the estimators, Algorithm 1 was used, as detailed below.

Algorithm 1 Step-By-Step Procedure for MSE

Standardize the matrix of independent variables using Equation (25), then compute eigenvalues $\left({\lambda }_1,\dots ,{\lambda }_p\right)$ and eigenvectors $\left(e_1,\dots ,e_p\right)$ of X′X. Determine regression coefficients $\beta$ in canonical form as $\beta$ $=e_{max} P,$ where $P=\left[e_1,\dots ,e_p\right]$ and $e_{max}$ corresponds to the maximum eigenvalue. Generate random error terms from $N\left(0,{\sigma }^2\right),$ ($t_{(v=2)})$ and F (6,12). Compute dependent variable values using Equation (12). Calculate OLS and ridge regression estimates using their expressions. Repeat for ($N$ ) Monte Carlo iterations and calculate the MSE for all estimators using Equation (27):

$$MSE\left(\widehat{\beta }\right)={\displaystyle \frac{1}{N}}{\sum }_j^N{\sum }_{i=1}^p({\widehat{\beta }}_{ji}-\beta {)}^2.$$ (27)

Simulations with N = 10,000 were performed in R to evaluate the MSE across varying values of $\rho$, $n,$ and $p$.

Table A1. MSE of the estimators when the error term is from $N(0,{\sigma }^2)$ with p = 4.

${\mathit{\sigma }}^2$	$\mathit{\rho }$	OLS	HK	KAM	KGM	KMed	KMS	TK	MPR1	MPR2	MPR3	RIRE1	RIRE2	RIRE3	RIRE4
$\mathit{n}\mathbf{=}\mathbf{20}\mathbf{,}\mathit{p}\mathbf{=}\mathbf{4}$
0.4	0.50	0.073951	0.07009	0.06501	0.05002	0.06010	0.06724	0.527504	0.004045	0.00574	0.00379	0.023472	0.862165	0.004671	0.004882
	0.70	0.154764	0.16805	0.11201	0.09301	0.10013	0.12441	0.449249	0.036702	0.006398	0.04313	0.018951	0.885575	0.003202	0.003262
	0.88	0.41983	0.29878	0.39401	0.10233	0.13921	0.26419	1.05164	0.00346	0.0052	0.21013	0.02708	0.8835	0.0036	0.00367
	0.94	0.93178	0.51971	0.8543	0.17675	0.17751	0.52554	0.55939	0.00322	0.00437	0.23803	0.02105	0.88549	0.00313	0.00317
	0.98	4.02085	0.92407	3.48983	0.62666	0.60485	2.3352	0.02093	0.00389	0.0067	0.88691	0.0117	0.84329	0.00379	0.0038
	0.999	30.2152	10.1044	24.69695	3.06734	2.85568	20.74441	0.01463	0.00361	0.34109	26.5806	0.00455	0.68418	0.00368	0.00357
1	0.50	0.471081	0.35637	0.42891	0.31090	0.33221	0.34011	1.87709	0.03430	0.04377	0.06904	0.21630	0.86290	0.02847	0.02900
	0.70	0.906126	0.41437	0.68088	0.50104	0.52109	0.50549	1.15681	0.02818	0.03685	0.13420	0.20738	0.87964	0.01873	0.01876
	0.88	1.5296	0.63508	1.34282	0.27129	0.29164	0.82298	0.66456	0.01627	0.026	0.2546	0.19215	0.86637	0.01668	0.01665
	0.94	3.75033	1.44066	3.2434	0.42648	0.61069	2.1537	0.69443	0.0311	0.0457	1.27068	0.17073	0.84	0.01125	0.01128
	0.98	13.28834	4.1721	11.1909	1.72149	1.30542	8.84601	0.2275	0.01257	0.10896	7.74713	0.08601	0.76634	0.01261	0.01268
	0.999	189.2337	82.4359	163.1312	6.42991	5.33438	162.615	0.02605	0.01701	1.26916	223.494	0.02545	0.45848	0.01701	0.01702
4	0.50	7.66693	3.27760	5.18011	4.70111	5.10070	5.47787	4.927237	1.258017	1.608114	2.415233	7.255416	0.803279	3.935243	1.03045
	0.70	14.1184	4.89515	10.8011	9.0008	9.84210	9.99855	5.10435	1.025688	1.647636	3.716123	12.29468	0.766644	3.679225	0.63616
	0.88	29.52701	10.03968	23.13117	2.38363	2.40419	19.80498	6.95945	1.17032	3.15291	11.0893	25.0997	0.6716	9.18939	0.36537
	0.94	76.75983	13.81462	64.48364	5.59462	5.19788	61.20032	7.00312	0.88386	4.16774	18.2229	57.6472	0.7166	13.9633	1.03077
	0.98	344.9427	43.67665	289.2984	17.26461	25.82321	298.8172	8.01124	4.2132	14.43937	74.6336	165.193	2.23344	56.1680	9.12821
	0.999	3578.164	1203.462	2954.479	65.70776	155.6806	3370.649	6.15416	0.30664	288.5284	2395.80	384.486	0.4254	174.338	0.26710
8	0.50	27.97977	9.89430	19.0783	14.00230	17.85421	22.13756	15.9351	7.43566	9.03079	12.10400	27.8370	0.92590	24.0870	6.7705
	0.70	60.32027	21.0721	32.0455	22.98620	25.67423	48.50253	19.5939	5.218080	10.3561	21.19716	59.5323	0.90563	43.8843	4.6457
	0.88	210.4346	76.48462	180.3505	12.73913	10.45576	184.3273	33.04655	10.77392	23.0375	74.9708	205.608	3.44496	127.525	12.7075
	0.94	231.1361	68.63926	181.6852	7.8081	7.81836	188.0916	17.50542	3.96455	14.84129	77.9513	222.079	1.10124	123.890	5.5442
	0.98	1542.333	469.0137	1269.645	33.61444	62.11816	1424.113	17.18871	1.67272	85.44791	658.256	1361.53	1.66598	568.515	1.81108
	0.999	15504.66	4212.58	13184.39	206.2171	701.1982	15073.13	4.66529	1.51772	1871.055	9753.54	8562.20	2.68289	2898.11	1.49617
$\mathit{n}\mathbf{=}\mathbf{50}\mathbf{,}\mathit{p}\mathbf{=}\mathbf{4}$
0.4	0.50	0.017404	0.01723	0.016908	0.0139834	0.015700	0.01716	0.01818	0.00344	0.00449	0.00271	0.01309	0.9194	0.00386	0.00397
	0.70	0.02869	0.02808	0.2500951	0.195321	0.210555	0.02750	0.04384	0.00177	0.00218	0.001628	0.01451	0.94051	0.00193	0.00197
	0.88	0.23197	0.19757	0.22532	0.07225	0.07847	0.17125	0.30953	0.00212	0.00225	0.00214	0.02357	0.95685	0.0021	0.00216
	0.94	0.84732	0.5221	0.79101	0.21142	0.24082	0.50658	0.68423	0.00544	0.00624	0.01007	0.15065	0.95395	0.00556	0.00558
	0.98	0.42179	0.19338	0.39884	0.08805	0.10905	0.24954	1.23522	0.0032	0.00695	0.01633	0.02258	0.95823	0.00149	0.00144
	0.999	1.36534	0.54322	1.20202	0.16416	0.18689	0.59781	0.15934	0.00424	0.00457	0.00648	0.08871	0.95223	0.00422	0.00424
1	0.50	0.11088	0.10410	0.108673	0.101089	0.10749	0.10322	0.13656	0.02282	0.02640	0.02134	0.09272	0.92224	0.02483	0.02514
	0.70	0.17920	0.15735	0.154310	0.12018	0.139901	0.14848	1.34616	0.01144	0.01297	0.01095	0.11383	0.94123	0.01223	0.01230
	0.88	2.04337	0.99133	1.84145	0.31533	0.39598	1.15175	0.00349	0.00149	0.00183	0.0283	0.00742	0.94877	0.0014	0.00149
	0.94	7.10821	2.86307	6.03619	0.89092	0.83422	4.2161	0.02795	0.00469	0.01112	0.15894	0.05114	0.91936	0.00461	0.00463
	0.98	20.37455	6.40403	17.34736	2.28811	2.17237	14.0285	0.00122	0.00115	0.00267	0.27476	0.00203	0.87	0.00105	0.00115
	0.999	80.18668	26.44708	68.06002	5.30821	5.06567	63.5989	0.00496	0.00435	0.04677	31.5392	0.0122	0.7702	0.00436	0.00435
4	0.50	1.661129	0.972841	1.40678	1.13095	1.30045	1.22904	1.54590	0.54382	0.57918	0.57665	1.63800	0.92136	1.08122	0.52991
	0.70	2.646676	1.182489	1.80271	1.17033	1.6037	1.69987	2.63450	0.28781	0.32620	0.39972	2.52816	0.92458	0.85142	0.21585
	0.88	19.399	6.73939	16.55286	2.16792	1.84785	13.60881	3.31542	0.11534	0.38781	2.79094	16.76723	0.86899	1.26829	0.10624
	0.94	82.83129	23.92996	71.55387	6.72950	6.7874	68.0975	8.13257	1.12523	2.97176	9.69059	82.08457	0.86907	52.8097	1.29353
	0.98	39.58026	17.67036	33.80071	2.32531	1.57101	29.99145	4.86613	0.0976	0.43331	11.79607	29.23133	0.83111	1.12204	0.0957
	0.999	158.2587	47.6339	134.3208	11.6048	13.15687	131.382	15.66578	0.56629	8.79829	32.24649	155.7649	0.76783	83.1196	0.44195
8	0.50	6.431320	2.78396	5.49099	5.02120	5.45151	4.88902	5.12529	3.09498	3.21145	3.26344	6.42498	0.91765	6.04074	3.09070
	0.70	11.25657	4.11070	9.3910	7.10526	7.62710	8.24032	6.332224	1.76984	2.05548	2.48279	11.2133	0.89576	9.10518	1.76110
	0.88	221.061	72.05232	190.549	8.10785	7.35947	190.3216	0.6669	0.10307	1.434	56.70598	78.55509	0.68304	1.589	0.10312
	0.94	892.8785	290.3552	765.0705	37.74841	56.05124	817.7414	3.46528	0.47735	14.98799	271.4889	804.4739	0.56682	168.134	0.47433
	0.98	2321.362	925.6411	1957.959	32.91	106.8443	2173.832	0.24129	0.09809	44.17089	1694.655	69.54608	0.36351	0.17039	0.09802
	0.999	10742.45	4226.892	9433.356	139.9765	526.9947	10459.59	1.69789	0.36952	618.6483	6623.015	4847.395	0.83904	1037.22	0.64117
$\mathit{n}\mathbf{=}\mathbf{100}\mathbf{,}\mathit{p}\mathbf{=}\mathbf{4}$
0.4	0.50	0.06173	0.05959	0.05701	0.50002	0.05481	0.058708	0.076784	0.00980	0.01055	0.00954	0.05404	0.063417	0.01021	0.01025
	0.70	0.09466	0.22017	0.08621	0.06591	0.69083	0.084509	0.046697	0.00636	0.00695	0.00856	0.07057	0.17112	0.00564	0.0056
	0.88	0.07901	0.07328	0.07768	0.03446	0.03028	0.06659	1.9179	0.00093	0.00097	0.00091	0.02064	0.97767	0.00095	0.00099
	0.94	0.15327	0.13382	0.14895	0.04526	0.04914	0.11512	0.01158	0.00068	0.0007	0.00066	0.02211	0.97884	0.00068	0.00069
	0.98	0.63589	0.38543	0.5845	0.12206	0.13129	0.31773	0.0018	0.00062	0.00064	0.00123	0.01086	0.97919	0.0006	0.00062
	0.999	6.75286	2.24917	5.75308	0.87664	0.87186	3.87702	0.15289	0.00106	0.16738	0.35255	0.00235	0.9608	0.00071	0.00079
1	0.50	0.00887	0.00881	0.00789	0.007009	0.007441	0.00878	0.00921	0.00127	0.001530	0.001096	0.00715	0.06267	0.00137	0.00138
	0.70	0.01399	0.17528	0.01135	0.01080	0.01114	0.01359	0.005802	0.000845	0.000869	0.000915	0.00889	0.07110	0.00080	0.00081
	0.88	0.30495	0.23596	0.29084	0.08413	0.09767	0.19944	0.49857	0.00219	0.00223	0.00199	0.11169	0.97772	0.0021	0.00215
	0.94	0.55703	0.34937	0.51474	0.09489	0.10705	0.28484	0.01983	0.00266	0.00276	0.00299	0.10489	0.97831	0.00267	0.00266
	0.98	3.73614	1.51349	3.32496	0.41897	0.53884	2.18233	0.17225	0.00191	0.00215	0.09621	0.08357	0.96829	0.00191	0.00191
	0.999	25.79758	7.93808	21.2882	2.33726	2.1845	17.34861	0.00297	0.00244	0.00632	0.63923	0.01573	0.92516	0.00242	0.0024
4	0.50	3.76212	1.85054	3.36201	2.41430	3.01890	2.74141	3.12299	1.05907	1.11897	1.12864	3.75703	0.95612	3.27879	1.03474
	0.70	5.97052	2.19765	4.79011	3.00501	4.22532	4.11125	3.39824	0.61205	0.66287	0.75801	5.94999	0.95167	4.32545	0.54348
	0.88	8.20008	3.72389	7.09282	0.79415	0.70616	5.39433	2.17817	0.08282	0.11944	0.37173	7.30579	0.95178	0.31515	0.066
	0.94	12.89088	3.83781	10.76851	1.85071	1.83411	8.19489	2.62793	0.0673	0.25753	1.12289	10.16395	0.94389	0.22097	0.05526
	0.98	80.00399	24.34528	68.09791	5.55944	5.94392	64.35405	1.15865	0.07679	0.62793	32.93304	33.10672	0.88355	0.14131	0.07653
	0.999	790.2309	356.1047	670.3665	29.19727	52.97386	714.206	8.01852	0.05022	9.02564	362.4368	35.00289	0.698	0.05678	0.04996
8	0.88	34.96333	12.10528	30.15691	3.2319	2.81566	26.85708	4.57652	0.67641	0.60442	1.66179	34.69934	0.91594	19.18435	0.58735
	0.50	17.0934	4.8921	4.7821	5.3018	4.0415	6.3420	3.4201	0.30148	0.15271	1.19653	3.89901	0.9701	3.6012	0.18001
	0.70	21.5632	6.003	5.9083	4.1420	3.7821	10.3024	3.70130	0.32098	0.33013	2.0531	5.0314	0.95310	4.2190	0.21782
	0.94	48.57863	13.47561	38.68585	2.64434	2.00231	33.85232	3.99476	0.28518	0.44851	3.91056	47.7088	0.90318	18.11658	0.27043
	0.98	296.01	90.36443	246.6287	14.02309	16.02278	252.4491	1.66377	0.29794	1.93885	37.04322	268.4781	0.79677	29.10229	0.36641
	0.999	2950.282	1023.924	2492.777	55.83524	234.5598	2790.654	81.1498	11.69118	190.2149	1258.198	1733.336	5.17676	232.1123	81.34243

Note: Bold values represent minimum MSE of the estimator(s).

,

Table A2. MSE of the estimators when the error term is from $N(0,{\sigma }^2)$ with p = 10.

${\mathit{\sigma }}^2$	$\mathit{\rho }$	OLS	HK	KAM	KGM	KMEd	KMS	TK	MPR1	MPR2	MPR3	RIRE1	RIRE2	RIRE3	RIRE4
$\mathit{n}\mathbf{=}\mathbf{20}\mathbf{,}\mathit{p}\mathbf{=}\mathbf{10}$
0.4	0.50	0.273204	0.23689	0.27030	0.09301	0.1058	0.22138	1.21060	0.00623	0.00691	0.00858	0.04717	0.76775	0.00643	0.00743
	0.70	0.458580	0.35384	0.43672	0.10194	0.1138	0.303620	0.997411	0.00306	0.00348	0.01454	0.04138	0.82309	0.00316	0.00346
	0.88	3.91246	1.36519	3.5875	0.12144	0.1305	1.51764	0.72913	0.00214	0.0041	1.9033	0.04262	0.82751	0.00193	0.00196
	0.94	9.01626	3.5988	8.24395	0.21865	0.26862	4.1422	0.09993	0.00118	0.00225	4.61485	0.03454	0.7826	0.00117	0.00119
	0.98	59.30098	25.34738	54.54498	1.28987	1.37766	39.31198	0.01301	0.0016	0.02208	265.392	0.01397	0.61544	0.00158	0.00159
	0.999	680.4489	126.4956	630.2829	9.71346	8.09246	572.3732	0.00374	0.00114	0.66127	614.4841	0.00238	0.3317	0.00113	0.00113
1	0.50	1.74943	1.07480	1.61742	0.40711	0.21529	1.20087	1.82160	0.03907	0.05165	0.16147	0.44905	0.75502	0.04480	0.04965
	0.70	2.89447	1.43638	14.3201	0.54385	0.78421	1.73350	1.47249	0.02311	0.0300	0.31078	0.41370	0.78228	0.02182	0.02270
	0.88	19.8859	6.15931	18.48695	0.84597	1.02599	12.15691	0.737	0.00701	0.02141	3.33025	0.41692	0.70585	0.00798	0.00709
	0.94	43.57093	12.18268	40.41556	1.12514	1.35883	29.81562	1.83399	0.01001	0.05797	22.00458	0.28482	0.64404	0.00815	0.00824
	0.98	275.9795	86.99909	255.6994	4.61141	4.25305	217.8209	0.01443	0.00539	0.11984	108.1642	0.11081	0.40246	0.00543	0.0054
	0.999	3573.643	1198.085	3345.453	34.09147	36.9116	3297.919	0.14138	0.00602	14.41213	4598.09	0.01738	0.17447	0.00588	0.00582
4	0.50	28.70702	12.9907	28.2015	6.0189	7.4012	23.6601	11.8093	1.9568	3.2443	7.70907	20.7392	0.63872	6.10429	1.90838
	0.70	48.73058	18.7559	47.9501	7.5271	8.4201	38.6589	11.5886	1.04562	2.50860	10.8107	27.9943	0.57537	5.31472	0.74434
	0.88	370.8789	80.98412	336.1424	8.76102	9.22541	293.1163	10.19119	0.2626	6.89437	153.2982	88.53049	0.44571	14.46624	0.23389
	0.94	1235.223	371.662	1150.184	18.21878	18.98581	1100.431	9.19108	0.23617	18.732	478.3979	141.9199	0.32627	11.72474	0.14734
	0.98	5478.044	1884.823	5096.395	72.03096	97.45278	5099.33	6.00552	0.10324	178.5535	4008.61	261.8155	0.20441	9.33502	0.08747
	0.999	58825.48	13630.44	53884.44	478.8809	844.9028	57028.34	1.40252	0.08314	2767.719	43493.05	245.8212	0.12506	1.65141	0.08009
8	0.5	115.782	49.381071	110.3289	15.0222	18.010	103.4455	39.3918	11.87321	17.2509	35.8517	109.3970	1.19516	60.54285	11.9859
	0.70	194.0101	76.588817	184.030	22.6751	29.1452	169.4795	44.5398	9.66185	20.6959	64.2878	171.2270	1.23940	73.1614	9.11843
	0.88	1771.582	657.6508	1629.759	36.17003	46.28355	1579.484	126.5747	10.71246	128.505	659.9068	1156.344	2.48156	335.0989	9.38348
	0.94	4185.055	971.2387	3838.037	67.45471	94.33316	3823.446	70.88444	9.33719	157.4286	1279.797	1996.782	14.87611	501.5169	27.59571
	0.98	19589.31	7385.396	17720.12	283.1349	437.0629	18483.08	15.86521	0.54089	1191.74	12749.92	3888.588	1.7194	960.6192	0.5007
	0.999	321702.9	128034.1	299937.4	1532.046	2985.823	317632.6	67.50312	0.51262	14602.36	242456.4	21222.9	181.6545	7286.865	174.3037
$\mathit{n}\mathbf{=}\mathbf{50}\mathbf{,}\mathit{p}\mathbf{=}\mathbf{10}$
0.4	0.50	0.05642	0.05544	0.53160	0.04183	0.05231	0.054396	0.58694	0.00276	0.00291	0.00260	0.03095	0.89180	0.00281	0.00298
	0.70	0.09005	0.08698	0.08931	0.06903	0.07301	0.081610	1.44763	0.00120	0.00126	0.00113	0.03275	0.92651	0.00122	0.00126
	0.88	0.76504	0.59944	0.7525	0.07716	0.08316	0.44464	0.0027	0.00052	0.00054	0.00059	0.05661	0.95458	0.0005	0.00052
	0.94	1.17129	0.78819	1.14328	0.11719	0.15143	0.5893	0.23592	0.00066	0.00074	0.02611	0.04361	0.95638	0.0006	0.00067
	0.98	6.67922	3.48764	6.42183	0.4317	0.64383	3.45506	1.02487	0.00073	0.01487	32.6338	0.01451	0.93169	0.00066	0.00069
	0.999	85.60993	39.0467	82.49322	3.42557	4.52126	67.03686	0.00065	0.00058	0.01178	14.6095	0.00213	0.79042	0.00058	0.00058
1	0.50	0.37074	0.33347	0.36198	0.12974	0.20781	0.32268	1.52673	0.01831	0.0196	0.01758	0.24710	0.89531	0.01924	0.0199
	0.70	0.60348	0.49302	0.57023	0.19781	0.24111	0.43609	0.951456	0.00757	0.00792	0.00707	0.28526	0.92689	0.00788	0.00791
	0.88	2.51231	1.32617	2.42996	0.24148	0.33357	1.19205	0.03302	0.00169	0.00196	0.00305	0.3184	0.94754	0.00173	0.00179
	0.94	5.99643	3.08027	5.79862	0.53567	0.69578	3.23425	0.0097	0.00277	0.00313	0.00738	0.31451	0.93244	0.0027	0.00273
	0.98	28.22377	13.11499	27.07277	1.60607	2.3963	18.44751	0.07059	0.00274	0.07806	0.27128	0.11427	0.86674	0.00206	0.00266
	0.999	284.4602	114.7574	273.4414	13.83428	17.88907	240.382	0.00197	0.00149	0.24323	62.4939	0.01557	0.67481	0.00144	0.00139
4	0.50	5.86187	3.03065	5.65201	0.93198	1.8015	4.50601	4.8863	0.44253	0.61138	0.70836	5.55190	0.86506	1.8182	0.4457
	0.70	9.27568	4.39199	9.00210	1.98032	2.0015	6.63299	4.05055	0.20488	0.27721	0.42819	8.05068	0.8693	1.0222	0.1352
	0.88	59.09221	22.74984	56.54517	3.15782	4.51955	42.64532	0.94742	0.06055	0.13444	1.02745	39.48437	0.80911	1.74163	0.06136
	0.94	148.3422	76.98177	142.2942	7.41513	9.84157	119.161	1.2478	0.04512	0.49566	11.86129	69.30609	0.73421	0.87809	0.04476
	0.98	703.4064	287.881	671.2525	27.77957	40.09705	613.6097	0.5709	0.0455	5.39058	49.45997	119.1378	0.54885	0.24292	0.04502
	0.999	7397.197	2817.599	7106.537	270.3228	549.9711	7106.359	0.06214	0.04756	118.0473	2342.599	45.67117	0.26099	0.07347	0.04752
8	0.50	22.9576	11.0157	20.0018	8.84912	10.4201	19.4740	15.7162	4.17936	5.0543	5.62259	22.819	0.84320	17.8121	4.46197
	0.70	36.7418	17.515	35.2789	12.4520	18.4621	29.8219	18.2198	1.59043	3.03735	5.40666	36.136	0.81366	21.3810	1.61219
	0.88	308.3659	139.2778	296.4588	16.86977	21.7048	265.9689	30.0717	0.28013	16.58609	59.97508	288.7624	0.65323	94.19413	0.24905
	0.94	565.616	248.2435	544.0324	30.05951	46.43855	501.6179	28.75879	1.79963	32.92276	129.4953	510.6058	0.77639	159.1103	11.98808
	0.98	2599.358	1024.884	2489.276	103.9563	202.3081	2414.816	40.88745	0.22908	271.7408	964.3896	1882.989	0.44482	342.5718	0.21802
	0.999	36102.18	13834.66	34829.84	938.2313	2044.239	35488.04	4.40322	0.20329	4695.001	24473.3	9634.414	0.31432	1152.142	0.20097
$\mathit{n}\mathbf{=}\mathbf{100}\mathbf{,}\mathit{p}\mathbf{=}\mathbf{10}$
0.4	0.50	0.03296	0.03260	0.31990	0.02098	0.02899	0.031832	1.67970	0.00076	0.000794	0.000741	0.02069	0.95848	0.00077	0.00078
	0.70	0.05942	0.05796	0.05712	0.02371	0.02810	0.05397	2.60014	0.00035	0.000367	0.00054	0.02579	0.97024	0.00036	0.00036
	0.88	0.23635	0.21109	0.23424	0.02992	0.0294	0.16508	0.00339	0.00026	0.00028	0.00022	0.0534	0.97684	0.00026	0.00023
	0.94	0.55087	0.43598	0.54206	0.05132	0.06122	0.31131	0.00106	0.0003	0.00029	0.00025	0.0546	0.97816	0.00026	0.00027
	0.98	2.48105	1.3243	2.40698	0.23425	0.28624	1.21976	0.0005	0.00037	0.00037	0.0005	0.0306	0.97547	0.0003	0.00036
	0.999	23.77011	10.55223	22.77502	1.56801	1.91868	15.32827	0.0032	0.00028	0.01742	1.40894	0.00418	0.93757	0.00026	0.00029
1	0.50	0.20253	0.189616	0.19111	0.09807	0.10420	0.17662	1.80561	0.00453	0.00462	0.00445	0.14804	0.95892	0.00464	0.00467
	0.70	0.37609	0.325973	0.36134	0.90100	0.1010	0.2728	0.14007	0.00243	0.002481	0.00236	0.20155	0.97027	0.00247	0.00247
	0.88	0.90712	0.63313	0.88719	0.1038	0.1119	0.47234	0.00736	0.0001	0.001	0.00091	0.28031	0.97664	0.00096	0.00098
	0.94	1.96243	1.19667	1.90475	0.17864	0.21449	0.95831	0.01026	0.00112	0.00114	0.00124	0.2873	0.97462	0.00111	0.00111
	0.98	10.22892	4.22658	9.79098	0.6076	0.89193	5.65182	0.0221	0.00085	0.00137	0.03063	0.18248	0.95493	0.00081	0.00088
	0.999	79.71708	32.88264	76.17164	4.60908	5.49288	58.5886	0.00143	0.00124	0.00445	0.2138	0.03222	0.88761	0.00119	0.00114
4	0.50	3.2632	1.85317	3.11541	1.9852	2.1980	2.1717	2.02774	0.07574	0.0858	0.07736	3.05031	0.95095	0.35868	0.08013
	0.70	5.9610	2.84233	5.4501	1.7111	2.31782	3.71976	1.27220	0.03744	0.04411	0.04642	4.97659	0.95187	0.15462	0.03836
	0.88	26.06792	9.66087	25.09101	1.6031	2.50049	18.0479	0.99261	0.23071	0.44533	0.53398	18.71074	0.92255	0.25751	0.05104
	0.94	48.38914	20.69259	46.40617	3.55596	3.92733	35.02906	3.11772	0.10595	0.57049	3.15518	28.02816	0.90435	0.16159	0.03622
	0.98	250.8261	105.3578	239.7195	9.42762	12.97427	206.261	5.58563	0.01688	0.71079	27.10727	55.02553	0.81625	0.035	0.01644
	0.999	2085.657	932.4161	1977.85	60.19291	116.2668	1890.64	4.372	0.02271	22.28176	129.0323	32.52502	0.59655	0.02543	0.02256
8	0.50	12.9120	6.17682	12.0008	3.8961	4.9076	9.70529	9.07368	0.55585	0.75265	0.88159	12.8071	0.92106	7.77087	0.43839
	0.70	22.8643	10.3404	21.8923	3.0050	5.6712	16.5975	6.69110	0.25248	0.43656	0.76105	22.3076	0.91482	8.0065	0.19589
	0.88	96.93491	42.52122	92.90326	4.87156	6.95118	76.4377	17.23618	0.1113	0.77682	6.83051	93.21028	0.86177	27.23843	0.10798
	0.94	181.9405	62.04075	173.4768	6.64691	11.95612	147.608	23.11019	0.15778	6.8171	23.235	167.8899	0.82901	32.79634	0.13676
	0.98	804.9048	327.2723	768.1898	30.55916	54.76135	705.519	2.39289	0.07454	7.90943	119.4294	620.6272	0.71712	42.76083	0.07447
	0.999	10802.7	3996.385	10360.59	413.653	768.4276	10418.3	0.19403	0.10283	208.4076	2035.334	3091.883	0.39164	77.54405	0.10286

Note: Bold values represent minimum MSE of the estimator(s).

,

Table A3. MSE of the estimators when the error term is from ${\mathrm{t}}_{(v=2)}$.

$\mathit{\rho }$	OLS	HK	KMS	TK	MPR1	MPR2	MPR3	RIRE1	RIRE2	RIRE3	RIRE4
$\mathit{n}\mathbf{=}\mathbf{20}\mathbf{,}\mathit{p}\mathbf{=}\mathbf{4}$
0.88	63.094	20.09475	51.85141	4.51163	0.284677	6.834314	28.72313	33.2805	0.711249	16.86015	0.50633
0.94	132.6891	40.28189	112.8726	5.927243	1.664969	28.84621	94.85829	65.30242	0.696981	39.90088	1.325321
0.98	1323.112	396.0936	1274.718	4.375214	0.651577	235.274	971.919	1061.917	0.809809	990.8622	0.291227
0.999	6449.162	1756.255	6141.707	25.03019	3.79357	441.6999	5366.095	533.3464	0.178592	326.1639	0.097045
$\mathit{n}\mathbf{=}\mathbf{50}\mathbf{,}\mathit{p}\mathbf{=}\mathbf{10}$
0.88	23.11455	8.503365	18.78098	2.130157	0.124277	0.753228	3.557725	18.06554	0.902441	12.31618	0.074406
0.94	39.56925	13.58678	30.42002	2.065381	0.074773	1.182624	5.998539	26.79607	0.87603	13.12567	0.067348
0.98	9731.731	8851.649	9712.209	2404.488	1523.007	7235.084	9511.747	9680.697	18.41281	9524.838	9.204994
0.999	1595.967	664.388	1452.635	0.481238	0.021368	35.67525	680.1679	94.82878	0.500373	8.671352	0.021041
$\mathit{n}\mathbf{=}\mathbf{100}\mathbf{,}\mathit{p}\mathbf{=}\mathbf{10}$
0.88	79.83463	41.55167	65.29664	1.923576	0.008424	3.15922	13.86453	38.60891	0.912422	5.218145	0.008244
0.94	153.0814	63.64022	124.6087	0.672073	0.092515	1.882767	18.1359	45.80898	0.879268	9.558875	0.092366
0.98	21490.34	10845.46	21416.09	8425.539	41.25538	15455.22	20064.12	21101.81	109.3775	20978.06	1512.231
0.999	15832.93	7298.516	15423.05	3.752223	0.007309	2854.99	10934.56	6682.372	0.475797	2302.599	0.006042

Note: Bold values represent minimum MSE of the estimator(s).

and

Table A4. MSE of the the estimators when the error term is from F(6, 12).

$\mathit{\rho }$	OLS	HK	KMS	TK	MPR1	MPR2	MPR3	RIRE1	RIRE2	RIRE3	RIRE4
$\mathit{n}\mathbf{=}\mathbf{20}\mathbf{,}\mathit{p}\mathbf{=}\mathbf{4}$
0.88	42.83498612	14.38657	32.57022	5.448872	0.630816	2.924573	12.99575	28.79053	0.664105	4.562588	0.398823
0.94	89.08179498	28.50359	71.30223	4.882363	0.567054	5.641914	30.3766	42.70028	0.611152	4.401421	0.637798
0.98	299.0766636	95.76162	261.2717	5.536498	1.154745	20.8279	145.268	56.4244	0.418381	3.901233	0.297482
0.999	5942.03108	1898.832	5702.601	12.02855	0.697762	529.1481	4380.076	70.04776	0.517433	38.04217	2.08129
$\mathit{n}\mathbf{=}\mathbf{50}\mathbf{,}\mathit{p}\mathbf{=}\mathbf{10}$
0.88	7.283743	2.40194	4.589703	2.888377	0.175844	0.289982	0.91278	5.994432	0.906881	0.579107	0.110145
0.94	14.55647	4.711843	9.758353	3.715249	0.162381	0.467226	2.892056	9.738257	0.882802	0.360097	0.093259
0.98	44.84228	14.17757	33.70746	2.573353	0.126402	0.929532	9.750726	17.04606	0.821318	0.207079	0.080929
0.999	844.7873	253.141	760.2289	0.693394	0.079684	19.68093	456.0247	11.2576	0.512522	0.088484	0.079398
$\mathit{n}\mathbf{=}\mathbf{100}\mathbf{,}\mathit{p}\mathbf{=}\mathbf{10}$
0.88	14.60447576	5.821267	9.27512	0.810738	0.02467	0.03155	0.095169	7.909013	0.936877	0.06709	0.024492
0.94	28.9890857	11.13188	19.02777	0.679624	0.022362	0.045524	0.378438	11.32097	0.920774	0.037245	0.018435
0.98	89.6509455	33.30197	66.20271	0.601292	0.027136	0.157153	2.26947	17.98866	0.876012	0.02242	0.016455
0.999	1845.212998	666.0107	1672.256	0.127585	0.016499	3.489829	220.4394	8.331964	0.611101	0.016812	0.016495

Note: The bold values in the tables represent the lowest MSEs among the estimators.

in Appendix A present the MSEs for the proposed and existing estimators under these conditions. All analyses were conducted using R version 4.1.0. Detailed analysis follows in the next section.

Discussion and Analysis

The comparison of estimators in Table A1 and Table A2 illustrates how their performance, as measured by the MSE criterion, varies under different conditions, including variations in the sample size $\left(n\right)$, number of predictors (p), predictor correlations $\left(\rho \right)$, and error variance $\left({\sigma }^2\right)$ generated from $N\left(0,{\sigma }^2\right)$. Table A3 and Table A4 present the MSEs of different estimators when the error term is generated from a standardized t-distribution with 2 degrees of freedom (t₂) and an F-distribution with 6 and 12 degrees of freedom. This heavy-tailed error distribution introduces significant deviations from normality, challenging the robustness of classical estimators.

Here are some resulting remarks from the analysis:

i.

Effect of Sample Size ($\mathit{n}$): A small sample size $(n=20)$ exacerbated the limitations of the OLS and some classical ridge estimators, particularly under high correlations $(\rho >0.9)$ and large predictor counts $(p=10)$. For instance, OLS demonstrated very high MSEs in these cases, reflecting its instability in multicollinearity. Conversely, as the sample size increased $(n=50 or n=100)$, the MSE of all the estimators decreased, with the HK estimator showing improved performance. The KAM, KGM, and KMed estimators improved their performance in large sample sizes. For $n=20$, OLS showed significant variability in the error variance, especially as the correlation increased from $0.50 \mathrm{t}\mathrm{o} 0.70$. As the sample size increased ($n=50$ and $n=100$), the estimates stabilized, with OLS providing more consistent results. Higher error variances (σ² = $0.98)$ exacerbated this sensitivity, particularly in smaller samples. Estimators such as MPRs and RIREs showed less variability and became more reliable as the sample size increased. Notably, RIRE2, RIRE4, and MTPR estimators maintained low MSEs even in small-sample scenarios, suggesting their robustness to sample size variations.

ii.

Effect of Predictors ($\mathit{p}$): The number of predictors significantly affected the estimators’ performance. When $p$ is small $(p=4)$, classical ridge estimators such as HK, KAM, KGM, and KMed estimators performed relatively well under moderate multicollinearity $(\rho =0.88 \mathrm{o}\mathrm{r} 0.94)$. However, as $p$ increased to $10$, their MSE increased substantially, especially in high multicollinearity settings. This trend was more pronounced in OLS, which struggled to accommodate a higher predictor count. By contrast, RIRE2, RIRE4, and MPR variants exhibited remarkable scalability, maintaining low MSEs regardless of the predictor count.

iii.

Effect of Correlations ($\mathit{\rho }$): High correlations among the predictors $(\rho =0.98 \mathrm{o}\mathrm{r} 0.999)$ dramatically increased the MSE for OLS and classical ridge estimators. For example, the MSE of HK escalated in these conditions, particularly in small sample sizes and larger predictor settings. RIRE estimators and MTPR variants, however, showed resilience to extreme correlations, consistently achieving the lowest MSE across all scenarios.

iv.

Effect of Error Variance $\left({\sigma }^2\right)$: The ridge estimators (e.g., HK and KMS) were particularly sensitive to a high error variance (${\sigma }^2$), with their performance deteriorating in settings where both $\rho$ and $p$ were high. Our RIRE estimators demonstrated relative stability, maintaining lower MSEs under increasing error variances. MPR estimators also performed well in managing the effects of a higher error variance, making them suitable for noisy data.

v.

To assess the effect of non-normal error terms, errors were simulated from a heavy-tailed t-distribution with 2 degrees of freedom, which introduces significant departures from normality by allowing extreme values or outliers. Under these challenging conditions, classical estimators such as the OLS and conventional ridge-based methods (HK, KAM, KGM, KMed, KMS, TK, MPR1–MPR3) exhibited notably high mean squared errors (MSEs), especially at high correlation levels ($\rho$ close to 1). In contrast, the proposed modified ridge estimators (RIRE1 to RIRE4) showed marked resilience to the heavy-tailed noise structure. Their MSEs remained consistently low across different sample sizes and predictor dimensions, indicating enhanced robustness against outliers and extreme error values inherent to t₂-distributed noise. The robustness is particularly important in practical scenarios where normality assumptions are violated and error distributions have heavy tails. Among the RIRE estimators, some estimators (RIRE2 and RIRE4) performed better, suggesting that their specific modifications effectively mitigate the influence of large error fluctuations. These results highlight the advantage of the new estimators in maintaining accuracy and stability in regression models affected by non-normal, heavy-tailed error distributions.

vi.

The findings from Table A3 indicate that the new RIRE estimators provide improved accuracy and stability compared with classical and existing methods in regression models with t₂-distributed errors.

vii.

Table A4 show the MSEs when error terms follow a standardized F-distribution with (6, 12) degrees of freedom, representing heavy-tailed, non-normal errors. The modified ridge estimators (RIRE1–RIRE4) consistently outperformed OLS and other existing methods (HK, KAM, KGM, KMed, KMS, TK, MPR1–MPR3), especially at high correlations ($\rho$). Among them, RIRE3 and RIRE4 achieved the lowest MSEs, demonstrating superior robustness and accuracy under this complex error structure. This highlights the advantage of RIRE estimators in handling heavy-tailed, asymmetric noise effectively.

These results highlight that no single estimator performs optimally under all conditions. However, our modified estimators RIRE2 and RIRE4 consistently outperformed others when compared with OLS and other existing estimators in scenarios involving small samples, large predictors, high correlations, and high error variances. The other ridge estimators, such as HK, were effective under moderate conditions; however, they failed to handle extreme multicollinearity or challenging settings involving many predictors and small samples. OLS remained unsuitable for multicollinearity, especially when $\rho >0.90$.

The summary table (

Table 1. Recommended estimators under specific conditions.

$\mathit{n}$ $\downarrow$	${\mathit{\sigma }}^2\downarrow \mathit{\rho }\to$			$\mathit{p}=4$				$\mathit{p}=10$
		0.50	0.70	0.88	0.94	0.98	0.999	0.88	0.94	0.98	0.999
20	0.4	MPR3	RIRE3	MPR1	RIRE3	RIRE3	RIRE4	RIRE3	RIRE3	RIRE3	RIRE3
	1	RIRE3	RIRE3	MPR1	RIRE3	RIRE2	RIRE3	MPR1	RIRE4	RIRE4	RIRE4
	4	RIRE4	RIRE4	RIRE2	RIRE2	RIRE2	RIRE4	RIRE4	RIRE4	RIRE4	RIRE4
	8	RIRE3	RIRE3	RIRE2	RIRE2	RIRE2	RIRE4	RIRE2	MPTR1	RIRE4	MPTR1
50	0.4	MPR3	MPR3	RIRE3	MPR1	RIRE3	RIRE3	RIRE4	RIRE4	RIRE3	RIRE4
	1	MPR3	MPR3	MPR1	RIRE4	RIRE4	RIRE4	RIRE3	RIRE3	RIRE4	RIRE4
	4	RIRE3	RIRE3	RIRE4	RIPR2	RIRE4	RIRE4	MPR1	RIRE4	RIRE4	RIRE4
	8	RIRE4	RIRE4	MPR1	RIRE4	RIRE4	RIRE4	RIRE4	RIRE2	RIRE4	RIRE4
100	0.4	MPR3	RIRE4	MPR1	MTPR3	RIRE3	RIRE4	RIRE3	TK	RIRE4	RIRE4
	1	MPR3	RIRE3	MPR1	RIRE4	RIRE3	RIRE4	RIRE4	RIRE4	RIRE3	RIRE4
	4	RIRE4	RIRE4	RIRE4	RIRE4	RIRE4	RIRE4	RIRE4	RIRE4	RIRE4	RIRE4
	8	RIRE4	RIRE4	RIRE4	RIRE4	MPR1	MPR1	RIRE4	RIRE4	RIRE4	RIRE4

) was created based on the simulation results from Table A1, Table A2, Table A3 and Table A4. The proposed RIRE estimators demonstrated strong performance across a wide range of conditions, consistently outperforming other methods. In particular, RIRE3 and RIRE4 performed the best in 88 out of 120 cases, excelling in scenarios with varying sample sizes, error variances, and dimensions. RIRE2 also showed strength in nine scenarios, particularly at high error variances. Overall, our RIREs were the top choice in 97 out of 120 situations, proving their reliability and adaptability compared with alternatives such as MPR1 and MPR3, which performed well only in specific contexts.

4. Real-Life Applications

In this section, we utilize the newly modified proposed and competing estimators on three real-life applications. The first dataset is the Updated Longley (1959–2005), sourced from the Department of Labor, the Bureau of Statistics, and the Defense Manpower Data Center, Gujrati’s Basic Econometrics [29], and Mental Health and Digital Behavior (2020–2024). The second set of data is the Hospital Manpower dataset used in [17]. The third dataset is the Body Fat Dataset [30], which contains body composition measurements and is publicly available online. These datasets exhibit high multicollinearity and are recognized benchmarks for ridge regression analysis.

4.1. Practical Application of the Longley Dataset

The dataset consists of 47 observations spanning from 1959 to 2005, with a total of six variables: $\mathrm{y},{\mathrm{X}}_1,{\mathrm{X}}_2,{\mathrm{X}}_3,{\mathrm{X}}_4,\mathrm{and} {\mathrm{X}}_5$. Thus, the regression model can be written as

$$\mathrm{y}={\beta }_0+{\beta }_1{\mathrm{X}}_1+{\beta }_2{\mathrm{X}}_2+{\beta }_3{\mathrm{X}}_3+{\beta }_4{\mathrm{X}}_4+{\beta }_5{\mathrm{X}}_5+\mathsf{ϵ},$$

(28)

where $\mathrm{y}$ is the dependent variable, ${\mathrm{X}}_1 \mathrm{to} {\mathrm{X}}_5$ are the independent variables, ${\beta }_0$ is the intercept, ${\beta }_1 \mathrm{to} {\beta }_5$ are the coefficients for each independent variable, and $\mathsf{ϵ}$ is the error term.

To check for multicollinearity in the dataset, we looked at key indicators: eigenvalues, the CN, the VIF, and the heatmap display. These help in understanding how much the independent variables are related to each other and whether that could cause issues in our analysis. The eigenvalues of the dataset are: ${\lambda }_1\approx 4.278,{\lambda }_2\approx 0.714,{\lambda }_3\approx 0.113,{\lambda }_4\approx 0.00831,\mathrm{and} {\lambda }_5\approx 0.00832$.

We used Equation (3) to calculate the CN as follows:

$$\mathrm{C}\mathrm{N}={\displaystyle \frac{{\lambda }_{max}}{{\lambda }_{min}}}={\displaystyle \frac{4.278}{0.00831}}\approx 514.94$$

The CN for the dataset is about 514.94, which points to a significant amount of multicollinearity. Such a high CN suggests that the independent variables are strongly correlated to each other.

Equation (4) was utilized to calculate the VIFs for each predictor $X_i$.$R_i^2$ is the R-squared value from regressing $X_i$ on all the other predictors in the model. However, $R_i^2$ can be approximated using the inverse of the correlation matrix of the dataset. The diagonal elements of the inverse of the correlation matrix represent ${\displaystyle \frac{1}{(1-R_i^2)}}$ for each predictor. Therefore, the VIFs for the variables are as follows: ${\mathrm{X}}_1$ (52.90), ${\mathrm{X}}_2$ (79.94), ${\mathrm{X}}_3$ (35.94), ${\mathrm{X}}_4$ (4.18), and ${\mathrm{X}}_5$ (4.81). High VIF values indicate multicollinearity, with a VIF greater than 10 suggesting significant correlation among the predictors. In this analysis, $X_1$, $X_2,$ and $X_3$ showed high multicollinearity, while $X_4$ and $X_5$ had lower VIFs, indicating that they are less correlated with the other predictors.

Furthermore, in Figure 1, the heatmap shows that ${\mathrm{X}}_1$, ${\mathrm{X}}_2,$ and ${\mathrm{X}}_5$ are strongly related, meaning that they share a lot of the same information. In particular, ${\mathrm{X}}_1$ is highly correlated with ${\mathrm{X}}_2$ (0.97) and ${\mathrm{X}}_5$ (0.99), which suggests that these variables move together. On the other hand, ${\mathrm{X}}_4$ has a strong negative relationship with ${\mathrm{X}}_1$ (−0.87) and ${\mathrm{X}}_5$ (−0.87), indicating that as one increases, the other tends to decrease. This level of correlation could cause issues in regression analysis by making it harder to determine the unique effect of each variable. To remove the effect of severe multicollinearity, we used ridge regression, both with our proposed newly modified estimators and existing estimators.

The analysis of this real dataset validates the simulation results, confirming that our modified estimators (RIREs) performed better than other existing estimators, as shown in

Table 2. MSE and regression coefficients of the estimators for the Longley Dataset.

Estimators	MSE	${\widehat{\mathit{\beta }}}_0$	${\widehat{\mathit{\beta }}}_1$	${\widehat{\mathit{\beta }}}_2$	${\widehat{\mathit{\beta }}}_3$	${\widehat{\mathit{\beta }}}_4$	${\widehat{\mathit{\beta }}}_5$
OLS	2.55386	−0.42988	−0.42988	−0.42988	−0.43065	−0.42989	−0.43059
HK	2.28357	0.16511	0.165109	0.165087	0.017818	0.165109	0.016446
KAM	2.26034	−0.4602	−0.49694	−0.48578	−0.02990	−0.48689	−0.027300
KGM	1.73089	0.275996	0.275932	0.274027	0.005831	0.275844	0.0533000
KMed	2.01039	−0.68684	−0.68413	−0.61219	−0.71320	−0.68040	−0.701890
KMS	2.32719	−0.42987	−0.42987	−0.43000	−0.43119	−0.43238	−0.43063
TK	1.72091	−0.20198	−0.20204	−0.20169	−0.01613	−0.06932	−0.00792
MPR1	1.70736	−0.48381	−0.48478	−0.47839	−0.00613	−0.03464	−0.00290
MPR2	1.70921	0.270831	0.272393	0.262130	0.001201	0.007056	0.000566
MPR3	1.77600	−0.51895	−0.56097	−0.36087	−0.00018	−0.00106	−0.00191
RIRE1	1.72307	0.165083	0.165067	0.097102	0.141304	0.01703	0.152613
RIRE2	1.70730 *	−0.20209	−0.20203	−0.06674	−0.13526	−0.00776	−0.16257
RIRE3	1.70724 **	−0.48558	−0.48474	−0.03285	−0.11092	−0.00284	−0.18175
RIRE4	1.70733	0.273698	0.272329	0.006675	0.025312	0.000554	0.046711

Note that the estimator with the minimum MSE in compared with the OLS and other existing estimators is marked with double asterisks (**), while the one with the second lowest MSE is indicated by a single asterisk (*). Also, bold values represent the minimum MSE.

. Figure 2 shows that MPR1, RIRE2, and RIRE3 had the lowest MSEs, indicating the best overall estimator performance.

Comparison of the Estimators Based on Confidence Interval

The 99% confidence interval (C.I.) for each coefficient is calculated using the following formula: For each coefficient ${\widehat{\beta }}_i$ (for $i=0,1,2,\dots ,5$), $C.I={\widehat{\beta }}_i\pm Z_{{\displaystyle \frac{\alpha }{2}}}\times SE$, where $Z_{{\displaystyle \frac{\alpha }{2}}}$ is the critical value for a 99% C.I (2.576), and ${SE(\widehat{\beta }}_i)$ is the standard error of the coefficients, which can be calculated from the MSE and the number of observations. For each estimator, we used the MSE provided to calculate the standard error for each coefficient.

The standard error can be computed using the formula

$SE={\displaystyle \frac{MSE}{\sqrt{n}}}$, where $n=47$ is the number of observations. We denoted L (${\beta }_i$) and U (${\beta }_i$) as the lower and upper bounds of the C.I, respectively.

From

Table 3. Confidence interval of the estimator coefficients for the Longley Dataset.

Method	$\mathbf{L} \left({\mathit{\beta }}_0\right)$	$\mathbf{U} \left({\mathit{\beta }}_0\right)$	$\mathbf{L} \left({\mathit{\beta }}_1\right)$	$\mathbf{U} \left({\mathit{\beta }}_1\right)$	$\mathbf{L} \left({\mathit{\beta }}_2\right)$	$\mathbf{L} \left({\mathit{\beta }}_2\right)$	$\mathbf{L} \left({\mathit{\beta }}_3\right)$	$\mathbf{U} \left({\mathit{\beta }}_3\right)$	$\mathbf{L} \left({\mathit{\beta }}_4\right)$	$\mathbf{U} \left({\mathit{\beta }}_4\right)$	$\mathbf{L} \left({\mathit{\beta }}_5\right)$	$\mathbf{U} \left({\mathit{\beta }}_5\right)$
OLS	−1.389	0.53	−1.389	0.53	−1.389	0.53	−1.39	0.529	−1.389	0.53	−1.39	0.529
HK	−0.693	1.023	−0.693	1.023	−0.693	1.023	−0.84	0.876	−0.693	1.023	−0.842	0.874
KAM	−1.0251	0.1047	−1.061	0.0680	−1.055	0.0791	−0.595	0.5350	−1.054	0.0780	−0.592	0.5376
KGM	−0.2184	0.7703	−0.218	0.7703	−0.220	0.7684	−0.488	0.5002	−0.218	0.7702	−0.441	0.5476
KMed	−1.2196	−0.154	−1.216	−0.151	−1.145	−0.079	−1.246	−0.180	−1.213	−0.147	−1.234	−0.169
KMS	−1.304	0.445	−1.304	0.445	−1.304	0.444	−1.306	0.443	−1.307	0.442	−1.305	0.444
TK	−0.849	0.445	−0.849	0.445	−0.848	0.445	−0.663	0.63	−0.716	0.577	−0.655	0.639
MPR1	−1.125	0.158	−1.126	0.157	−1.12	0.163	−0.648	0.635	−0.676	0.607	−0.644	0.639
MPR2	−0.371	0.913	−0.37	0.915	−0.38	0.904	−0.641	0.643	−0.635	0.649	−0.642	0.643
MPR3	−1.186	0.148	−1.228	0.106	−1.028	0.306	−0.668	0.667	−0.668	0.666	−0.669	0.665
RIRE1	−0.482	0.813	−0.482	0.813	−0.55	0.745	−0.506	0.789	−0.63	0.664	−0.495	0.8
RIRE2	−0.844	0.439	−0.844	0.439	−0.708	0.575	−0.777	0.506	−0.649	0.634	−0.804	0.479
RIRE3	−1.127	0.156	−1.126	0.157	−0.674	0.609	−0.752	0.531	−0.644	0.639	−0.823	0.46
RIRE4	−0.368	0.915	−0.369	0.914	−0.635	0.648	−0.616	0.667	−0.641	0.642	−0.595	0.688

and based on the provided confidence intervals, we see that RIRE4 had the narrowest intervals across most of the coefficients, particularly for ${\beta }_0, {\beta }_1, \mathrm{a}\mathrm{n}\mathrm{d} {\beta }_5$, suggesting it as the most precise estimator. RIRE1 and RIRE2 also showed relatively narrow intervals but not as consistently as RIRE4. Thus, RIRE4 appears to be the best estimator, as it had the smallest range between the lower and upper bounds for most of the coefficients.

4.2. Hospital Manpower Data

This dataset contains 17 observations with five predictors: $X_1$ (monthly man-hours; Load), $X_2$ (monthly X-ray exposures; Xray), $X_3$ (occupied bed days; BedDays), $X_4$ (population in thousands; AreaPop), and $X_5$ (average patient stay; Stay). The dependent variable y represents the average daily patient load (Hours). The linear model is given as

$$\mathrm{y}={\beta }_0+{\sum }_{i=1}^5{\beta }_{\mathrm{i}}{\mathrm{X}}_{\mathrm{i}}+\mathsf{ϵ}$$

(29)

To assess multicollinearity, the CN, VIF, and heatmap were used. The CN of about 278.87 far exceeds the common threshold of 30, indicating severe multicollinearity. The VIF values were ($X_1$ (8.189), $X_2$ (7929.5), $X_3$ (4.083), $X_4$ (8504.7), and $X_5$ (19.75). Since values above 5 (or sometimes 10) indicate problematic multicollinearity, several variables here exceed that threshold. This, along with the very high CN, suggests strong inter-variable dependencies that could significantly affect the analysis.

It is also clear from Figure 3 that strong positive correlations among most hospital manpower variables were observed, except for moderate correlations involving $X_3$, indicating potential multicollinearity issues in the dataset.

Table 4. MSE of the estimators for the Hospital Manpower data.

Method	MSE	${\widehat{\mathit{\beta }}}_1$	${\widehat{\mathit{\beta }}}_2$	${\widehat{\mathit{\beta }}}_3$	${\widehat{\mathit{\beta }}}_4$	${\widehat{\mathit{\beta }}}_5$
OLS	4.201927	−0.47925	−0.54294	0.11981	−4.6 × 10−5	0.001716
HK	2.281989	0.146531	−0.57516	0.022228	−0.47962	−0.00634
KAM	2.839242	−0.54385	0.144872	−0.00039	0.061828	−0.48026
KGM	2.419772	−1.30095	0.058787	−0.48135	−0.51012	0.023354
KMed	2.465291	−0.47522	−0.45787	0.078561	−0.02504	0.001436
KMS	2.506194	0.139116	−0.00912	0.00782	−0.4793	−0.00529
TK	2.201562	−0.29022	0.145804	−0.0001	0.063327	−0.48037
MPR1	2.192073	−0.00197	0.061378	−0.48033	−0.53958	0.026517
MPR2	2.196175	−0.47905	−0.50277	0.025407	−0.18276	0.001667
MPR3	2.475307	0.146158	−0.02077	0.001584	−0.48136	−0.00615
RIRE1	2.202072	−0.52202	0.146367	−1.9 × 10−5	0.008256	−0.48119
RIRE2	2.192351	−0.03997	0.063038	−0.48101	−0.03242	0.13538
RIRE3	2.19175	−0.47924	−0.53404	0.050479	−0.00011	0.037279
RIRE4	2.192247	0.146516	−0.08759	0.003821	−0.4804	−0.20413

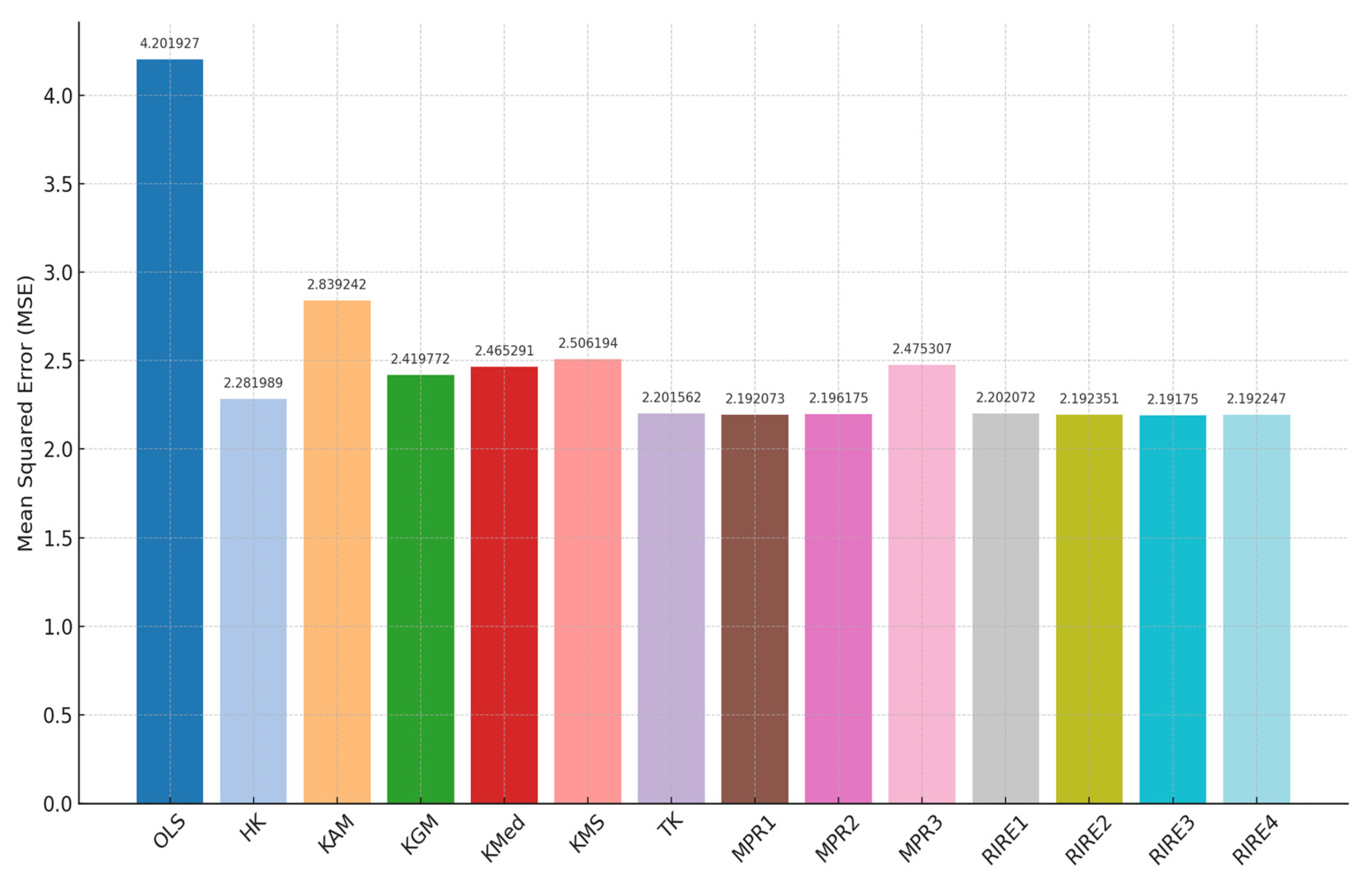
Note: Bold values represent minimum MSE.

shows that the newly proposed RIRE1–RIRE4 estimators consistently achieved the minimum MSE (2.19175–2.202072), outperforming OLS (4.201927) and the other existing methods. This indicates that the new proposed RIRE estimators provide better prediction accuracy on the Hospital Manpower data based on the MSE criterion. Figure 4 confirms that RIRE3, MPR1, and RIRE2 offer the most accurate estimates with minimal MSEs, while OLS demonstrates the least efficiency.

Comparisons of Estimator Coefficients Based on the 99% C.I for the Hospital Manpower Data

To calculate the 99% C.I. for the Hospital Manpower data regression model, we followed the same steps as above, ensuring correct application of formulas for the SE and the confidence intervals for $n=17$.

Table 5. Confidence intervals (99%) for the Hospital Manpower data.

Method	$\mathbf{L} \left({\mathit{\beta }}_1\right)$	$\mathbf{U} \left({\mathit{\beta }}_1\right)$	$\mathbf{L} \left({\mathit{\beta }}_2\right)$	$\mathbf{L} \left({\mathit{\beta }}_2\right)$	$\mathbf{L} \left({\mathit{\beta }}_3\right)$	$\mathbf{U} \left({\mathit{\beta }}_3\right)$	$\mathbf{L} \left({\mathit{\beta }}_4\right)$	$\mathbf{U} \left({\mathit{\beta }}_4\right)$	$\mathbf{L} \left({\mathit{\beta }}_5\right)$	$\mathbf{U} \left({\mathit{\beta }}_5\right)$
OLS	−3.104	2.146	−3.168	2.082	−2.505	2.745	−2.625	2.625	−2.624	2.627
HK	−1.279	1.572	−2.001	0.851	−1.403	1.448	−1.905	0.946	−1.432	1.419
KAM	−1.596	0.5089	−0.907	1.1976	−1.053	1.0524	−0.990	1.1146	−1.533	0.5725
KGM	−2.272	−0.329	−0.913	1.0307	−1.453	0.4905	−1.482	0.4618	−0.948	0.9952
KMed	−1.456	0.5057	−1.438	0.5231	−0.902	1.0595	−1.006	0.9559	−0.979	0.9824
KMS	−1.427	1.705	−1.575	1.557	−1.558	1.574	−2.045	1.086	−1.571	1.561
TK	−1.666	1.085	−1.23	1.521	−1.376	1.375	−1.312	1.439	−1.856	0.895
MPR1	−1.372	1.368	−1.308	1.431	−1.85	0.889	−1.909	0.83	−1.343	1.396
MPR2	−1.851	0.893	−1.875	0.869	−1.347	1.398	−1.555	1.189	−1.37	1.374
MPR3	−1.400	1.693	−1.567	1.526	−1.545	1.548	−2.028	1.065	−1.553	1.54
RIRE1	−1.898	0.854	−1.229	1.522	−1.376	1.376	−1.368	1.384	−1.857	0.895
RIRE2	−1.41	1.33	−1.307	1.433	−1.851	0.889	−1.402	1.337	−1.234	1.505
RIRE3	−1.849	0.89	−1.903	0.835	−1.319	1.42	−1.369	1.369	−1.332	1.407
RIRE4	−1.223	1.516	−1.457	1.282	−1.366	1.373	−1.85	0.889	−1.574	1.166

presents the confidence intervals (C.I.) for the coefficients of several estimators applied to the Hospital Manpower dataset. The RIRE estimators outperformed the existing methods in terms of providing more consistent and narrower confidence intervals, particularly for coefficients like ${\beta }_3$ and ${\beta }_4$. RIRE1 offered substantial improvements over OLS, with tighter intervals for most coefficients, especially ${\beta }_1$ and ${\beta }_4$. RIRE2 showed better precision for ${\beta }_3$, with narrower intervals than OLS, HK, and MPR1, although it still had wider intervals compared with KMS for certain coefficients. RIRE3 delivered significant improvements over OLS and TK, offering narrower and more stable intervals for several coefficients, especially for ${\beta }_3$ and ${\beta }_4$. RIRE4 provided the most balanced results, with narrower intervals for ${\beta }_1$, ${\beta }_3$, and ${\beta }_5$, outperforming traditional estimators (MPR2 and MPR3) in terms of precision. Overall, the RIREs produced more reliable and precise estimates compared with traditional methods, especially when dealing with multicollinearity issues in the dataset.

4.3. Body Fat Dataset

This dataset contains body composition and anthropometric data for 252 individuals, including variables like BODYFAT (y), DENSITY (X₁), AGE (X₂), WEIGHT (X₃), HEIGHT (X₄), ADIPOSITY (X₅), and various circumferences (e.g., NECK (X₆), CHEST (X₇), ABDOMEN (X₈), etc.). It is useful for analyzing the relationship between body fat and physical attributes. A regression model is given below:

$$\mathrm{y}={\beta }_0+\sum _{i=1}^{15}{\beta }_{\mathrm{i}}{\mathrm{X}}_{\mathrm{i}}+\mathsf{ϵ}$$

Multicollinearity was assessed using CN, eigenvalues, VIF, and heatmap display. The results indicated severe multicollinearity, with a CN of 1234.89 (well above the threshold of 30) and VIF values between 2.31 and 62.63. Figure 5 suggests potential multicollinearity, particularly between variables such as weight, adiposity, and abdominal circumference, which exhibit very high correlations and could lead to issues in predictive modeling or regression analysis.

To address the issue of multicollinearity, we use our proposed and existing estimators to enhance model stability and to reduce the multicollinearity effects.

Table 6. MSE of the estimators of body fat data.

Estimators	OLS	HK	KAM	KGM	KMed	KMS	TK
MSE	1.469843	1.181408	1.456093	1.058971	1.047234	1.107574	3.074038
Estimators	MPR1	MPR2	MPR3	RIRE1	RIRE2	RIRE3	RIRE4
MSE	0.908925	0.946894	1.000825	0.997009	1.2547	0.905712	0.927553

Note: Bold values represent minimum MSE of the estimator.

shows that the estimation in this third dataset aligns with the simulation results, where the proposed estimator RIRE3 achieved the minimum MSE compared with OLS and other existing ridge estimators.

5. Conclusions

This study presented four new modified ridge regression estimators, referred to as RIRE1, RIRE2, RIRE3, and RIRE4, which were designed to enhance precision in estimations when modeling multicollinear data. The adaptive characteristics of these estimators provided a versatile method for regularization, rendering them appropriate for contemporary predictive modeling challenges. The analysis highlighted the impressive performance of our newly modified RIRE estimators, especially RIRE2, RIRE3, and RIRE4, as they effectively handled challenging scenarios such as small sample sizes, severe multicollinearity, and large error variances compared with OLS and other existing estimators under both normal and non-normal error distributions. Our new estimators achieved the lowest MSE in both simulations and real-world dataset analyses, confirming their reliability and practical usefulness, which offer a clear advantage over other ridge regression estimators.

Future research could focus on adapting RIRE estimators for high-dimensional data and testing their effectiveness on a wider range of real-world datasets. This exploration would offer valuable insights into their potential for handling complex data structures.