Marginal Design of a Pneumatic Stage Position Using Filtered Right Coprime Factorization and PPC-SMC
Abstract
1. Introduction
- By applying filtered right coprime factorization, the plant structure is simplified, allowing for the application of strict PPC-SMC to pneumatic stage systems with complex nonlinearities. This enables a more precise configuration of PPC-SMC that incorporates the nonlinearities of the pneumatic stage, resulting in a smaller performance function. Thus, the maximum error can be reduced compared to previous methods, contributing to even more precise positioning of the pneumatic stage.
- Experimental comparisons with previous studies were conducted, confirming that the proposed method achieves the smallest steady-state error.
2. Preparations
2.1. Definition of Operator
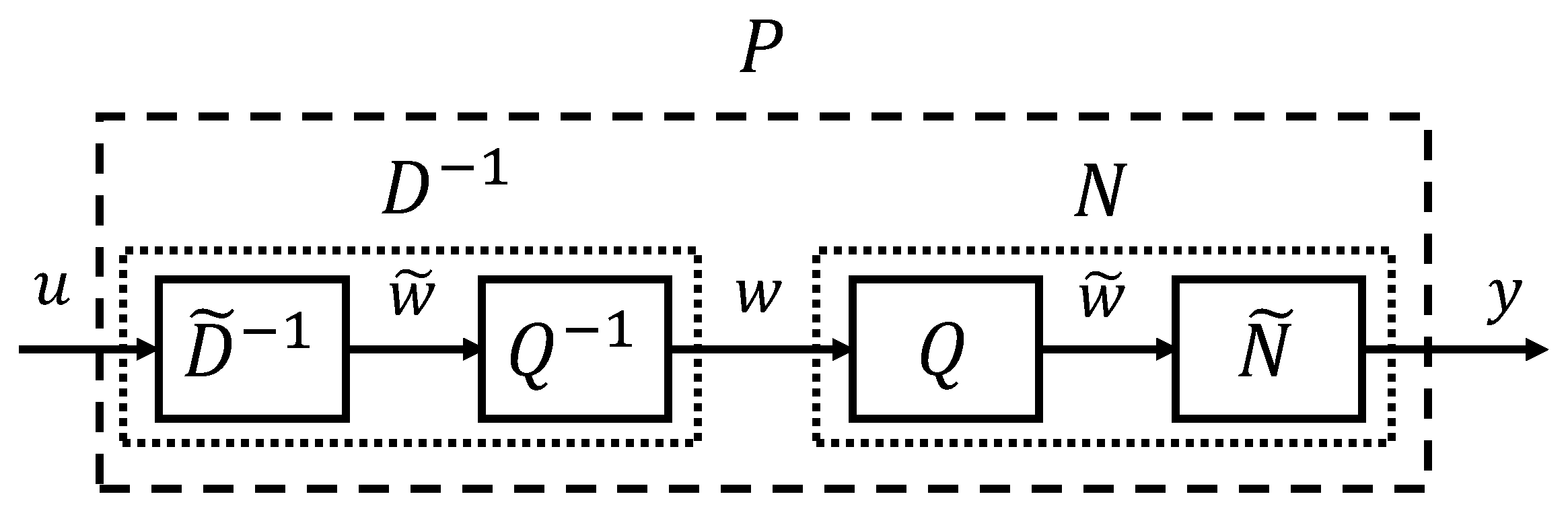
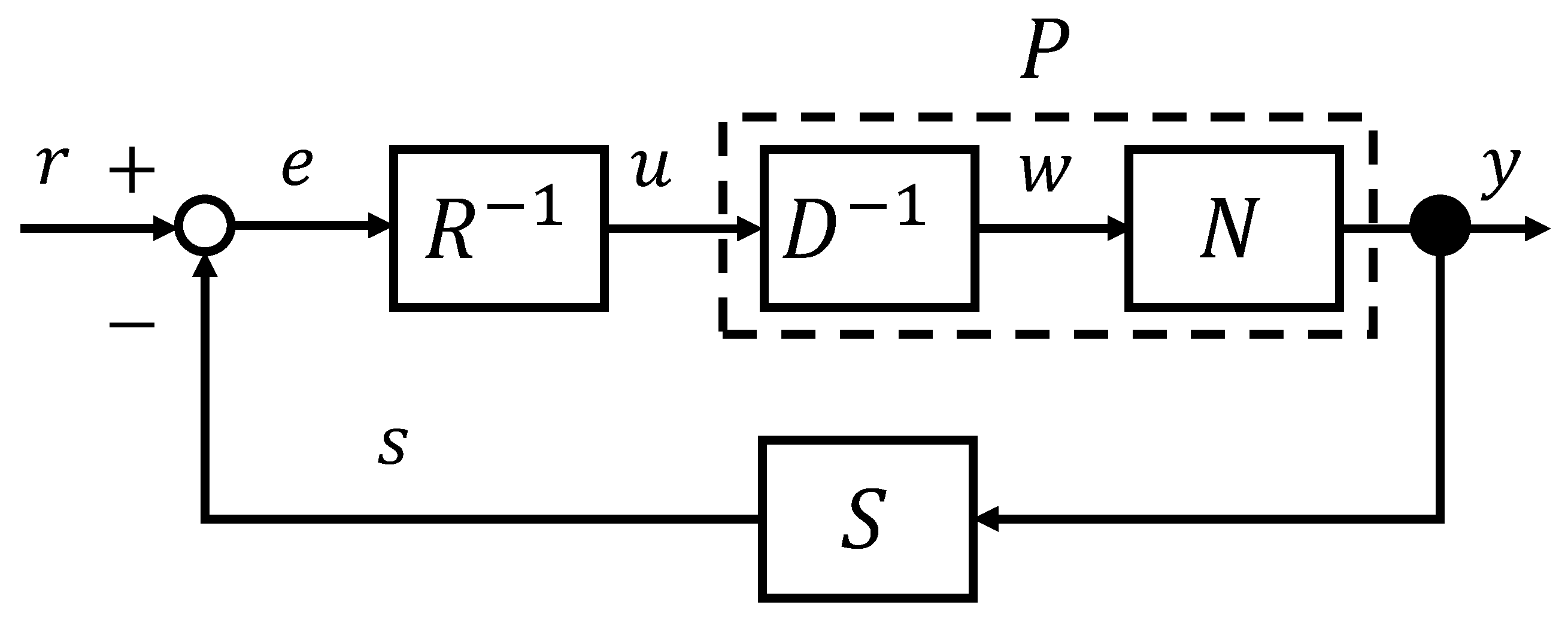
2.2. Filtered Right Comprime Factorization Based on Operator Theory
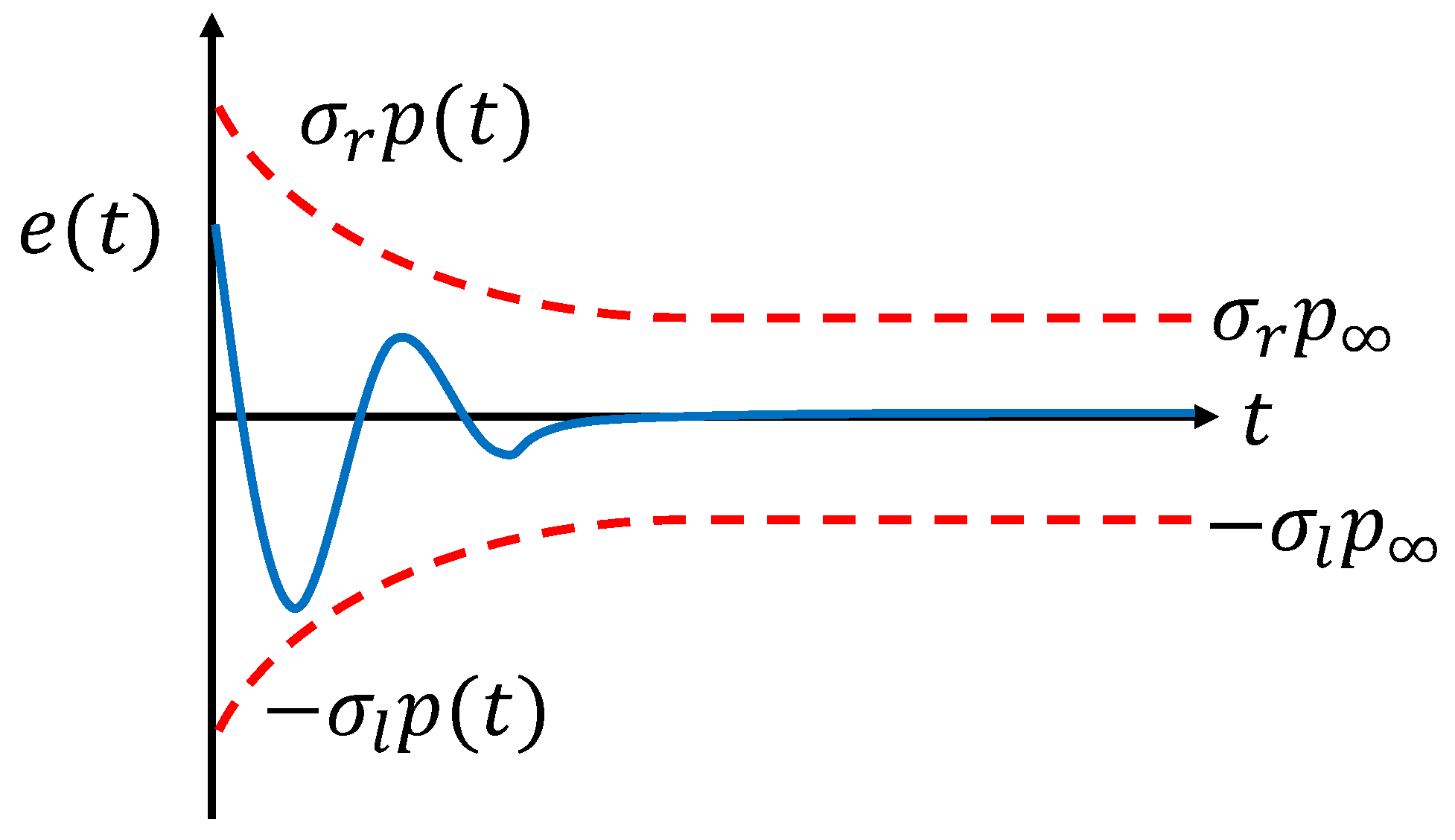
2.3. Prescribed Performance Control (PPC)
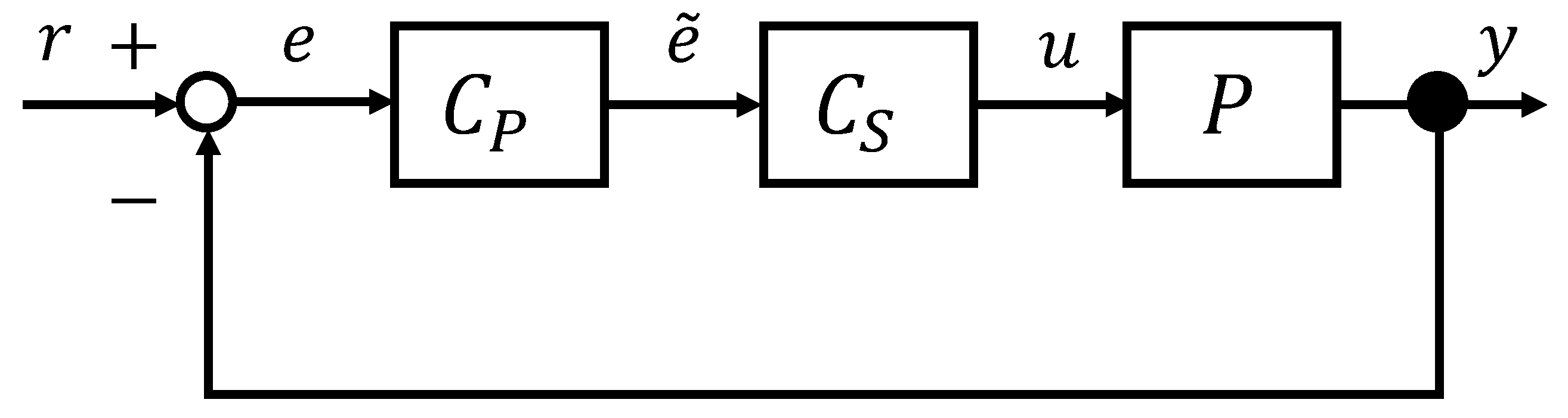
2.4. Prescribed Performance Control–Sliding Mode Control (PPC-SMC)
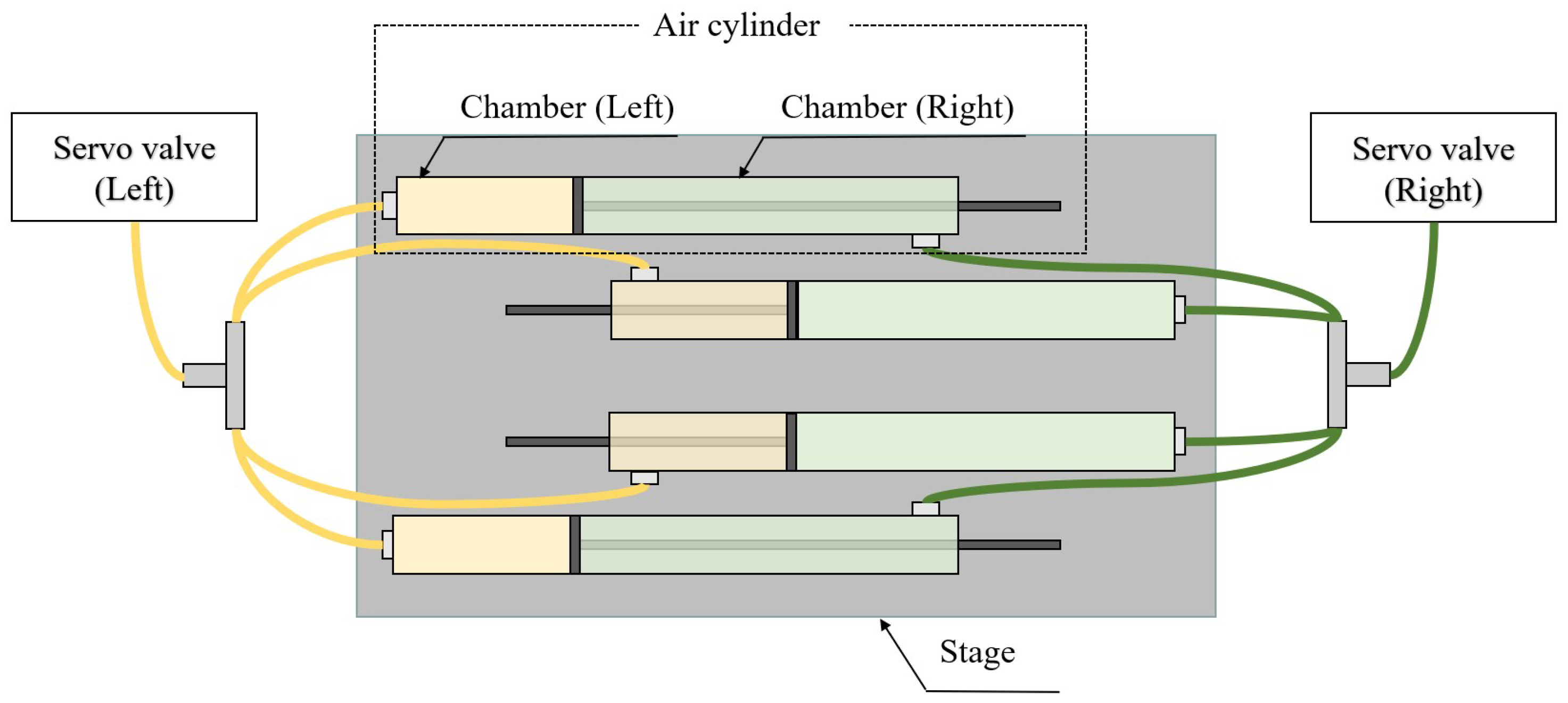
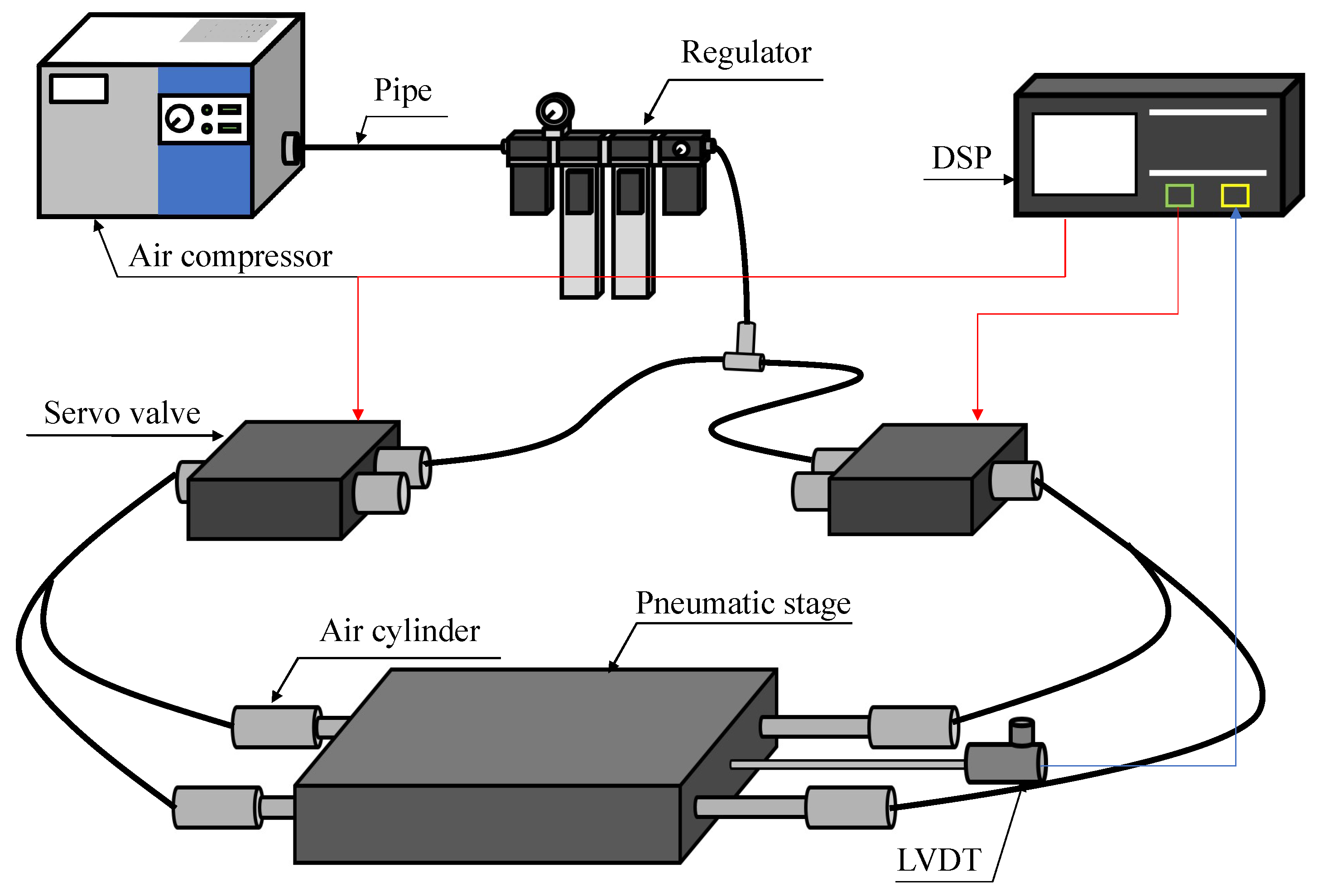
3. Pneumatic Stage and Problem Setting
3.1. Pneumatic Stage
3.2. Problem Setting
4. Control System Design
4.1. Filtered Right Coprime Factorization
4.2. PPC-SMC Controller
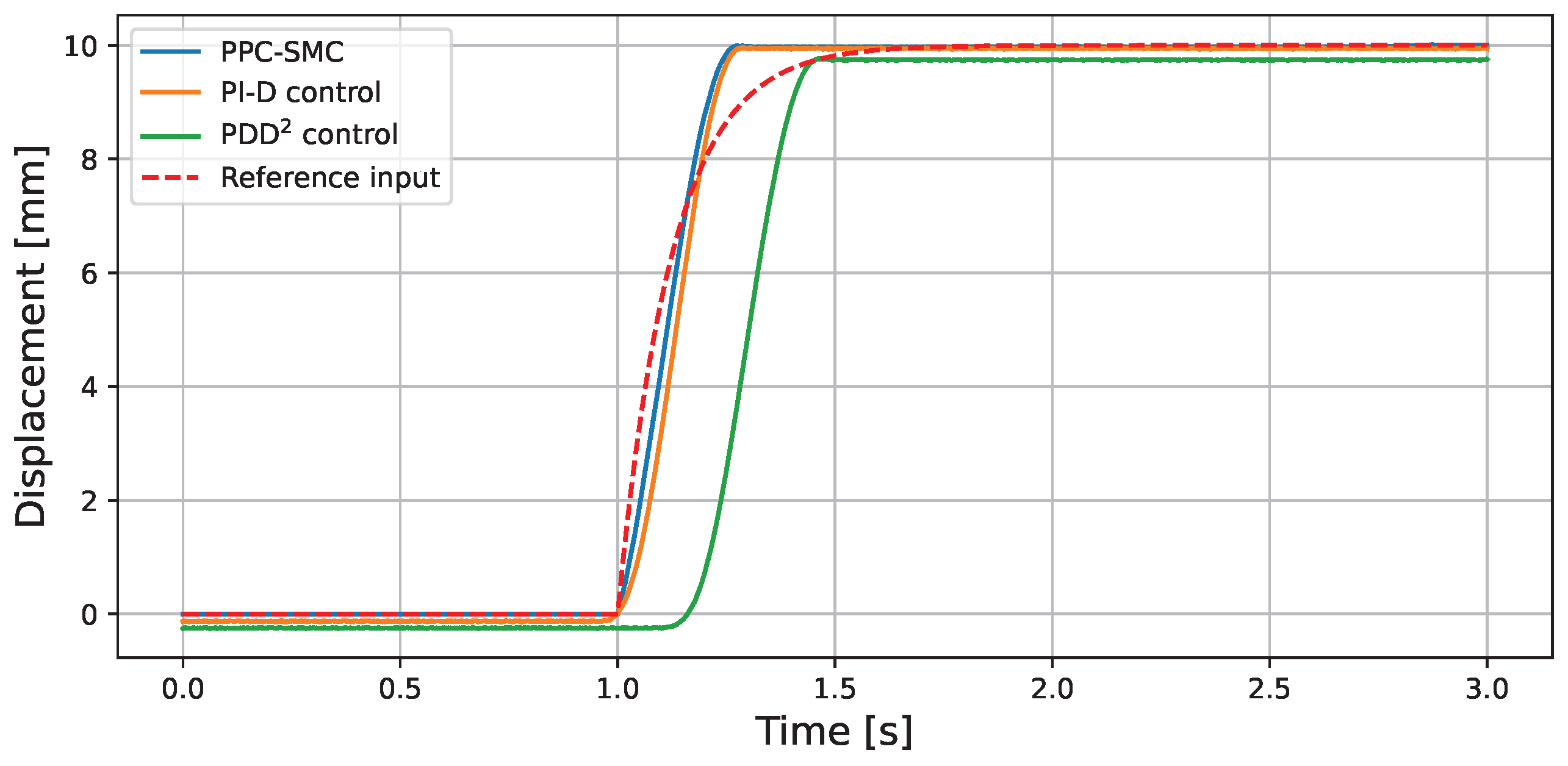
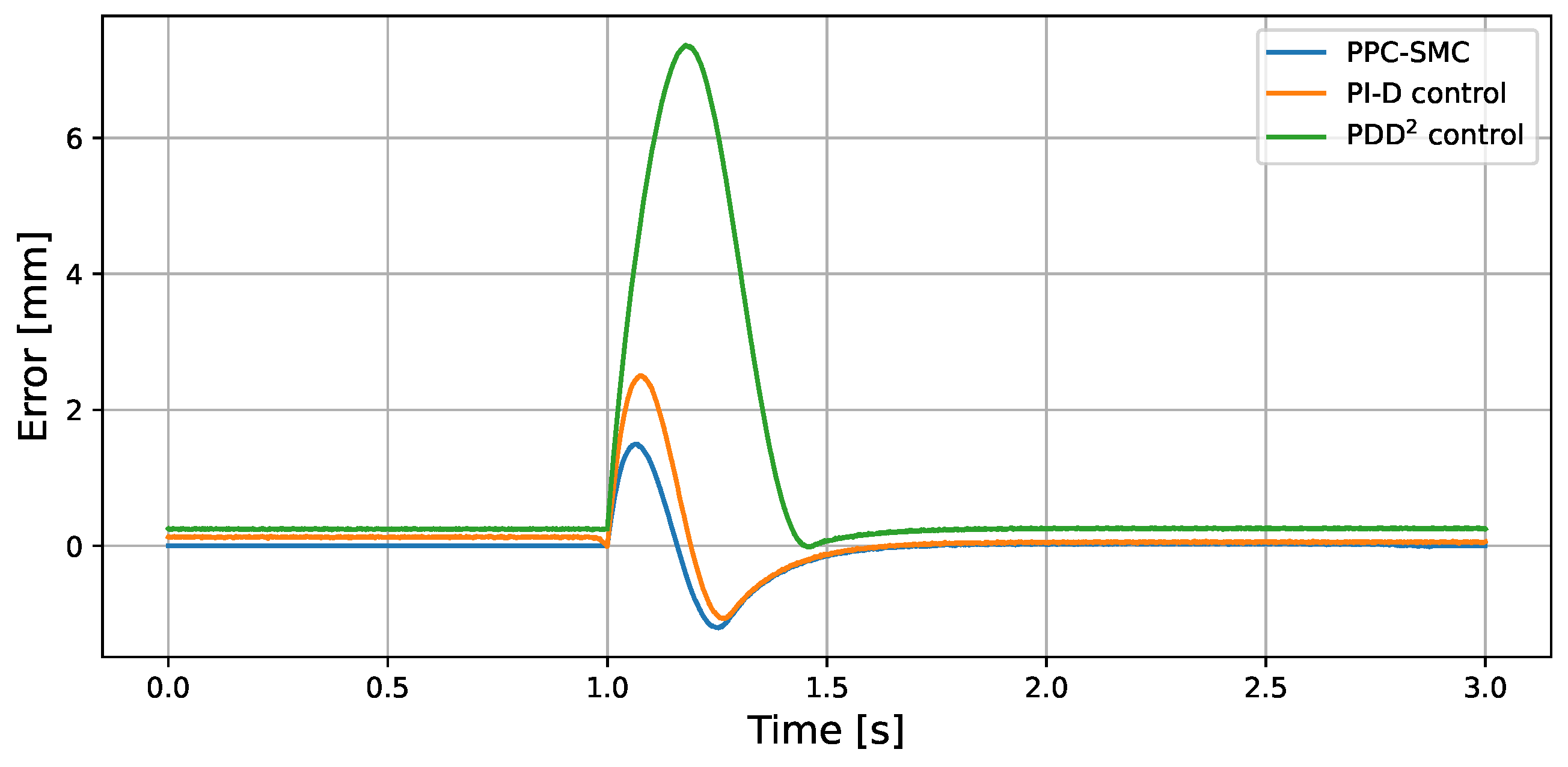
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Each Term in Equation (34)
- Derivation ofLet ; then,Here, are design parameters that satisfy . It becomes less than zero because , , and .
- Derivation ofLet ; then,
- Derivation ofLet ; then,
- Derivation ofLet ; then,
- Derivation ofLet ; then,
References
- Bohr, M. A 30 year retrospective on Dennard’s MOSFET scaling paper. IEEE Solid-State Circuits Soc. Newsl. 2009, 12, 11–13. [Google Scholar] [CrossRef]
- Wang, H.; Li, Q.; Zhou, F.; Zhang, J. High-Precision Positioning Stage Control Based on a Modified Disturbance Observer. Sensors 2024, 24, 591. [Google Scholar] [CrossRef] [PubMed]
- Kawashima, K.; Arai, T.; Tadano, K.; Fujita, T.; Kagawa, T. Development of coarse/fine dual stage using pneumatically driven bellows actuator and cylinder with air bearings. Precis. Eng. 2010, 34, 526–533. [Google Scholar] [CrossRef]
- Sato, K.; Sano, Y. Practical and intuitive controller design method for precision positioning of a pneumatic cylinder actuator stage. Precis. Eng. 2014, 38, 703–710. [Google Scholar] [CrossRef]
- De Wit, C.C.; Olsson, H.; Åstrom, K.J.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef]
- Yanada, H.; Sekikawa, Y. Modeling of dynamic behaviors of friction. Mechatronics 2008, 18, 330–339. [Google Scholar] [CrossRef]
- Tran, X.B.; Hafizah, N.; Yanada, H. Modeling of dynamic friction behaviors of hydraulic cylinders. Mechatronics 2012, 22, 65–75. [Google Scholar] [CrossRef]
- Xi, T.; Fujita, T.; Kehne, S.; Ikeda, R.; Fey, M.; Brecher, C. An extended LuGre model for estimating nonlinear frictions in feed drive systems of machine tools. Procedia CIRP 2022, 107, 452–457. [Google Scholar] [CrossRef]
- Johanastrom, K.; Canudas-De-Wit, C. Revisiting the LuGre friction model. IEEE Control Syst. Mag. 2008, 28, 101–114. [Google Scholar] [CrossRef]
- Freidovich, L.; Robertsson, A.; Shiriaev, A.; Johansson, R. LuGre-model-based friction compensation. IEEE Trans. Control Syst. Technol. 2009, 18, 194–200. [Google Scholar] [CrossRef]
- Tran, X.B.; Yanada, H. Dynamic friction behaviors of pneumatic cylinders. Intell. Control Autom. 2013, 4, 180–190. [Google Scholar] [CrossRef]
- Tran, X.B.; Dao, H.; Tran, K. A new mathematical model of friction for pneumatic cylinders. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 2399–2412. [Google Scholar] [CrossRef]
- Hildebrandt, A.; Neumann, R.; Sawodny, O. Optimal system design of siso-servopneumatic positioning drives. IEEE Trans. Control Syst. Technol. 2009, 18, 35–44. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, Y.; Xia, Y.; Liu, Z. Active disturbance rejection position control for a magnetic rodless pneumatic cylinder. IEEE Trans. Ind. Electron. 2015, 62, 5838–5846. [Google Scholar] [CrossRef]
- Saravanakumar, D.; Mohan, B.; Muthuramalingam, T. A review on recent research trends in servo pneumatic positioning systems. Precis. Eng. 2017, 49, 481–492. [Google Scholar] [CrossRef]
- Richer, E.; Hurmuzlu, Y. A high performance pneumatic force actuator system: Part I Nonlinear mathematical model. J. Dyn. Sys., Meas. Control 2000, 122, 416–425. [Google Scholar] [CrossRef]
- Richer, E.; Hurmuzlu, Y. A high performance pneumatic force actuator system: Part II nonlinear controller design. J. Dyn. Sys. Meas. Control 2000, 122, 426–434. [Google Scholar] [CrossRef]
- Ishii, H.; Wakui, S. Performance improvement of PDD 2 compensator embedded in position control for pneumatic stage. In Proceedings of the 2019 International Conference on Advanced Mechatronic Systems, Kusatsu, Japan, 26–28 August 2019; pp. 158–162. [Google Scholar]
- Ishii, H.; Wakui, S. Proposal of Speeding up Scheme for Pneumatic Stage. In Proceedings of the 2019 IEEE International Conference on Mechatronics, Ilmenau, Germany, 18–20 March 2019; Volume 1, pp. 79–84. [Google Scholar]
- Aoki, S.; Deng, M. Nonlinear position control of pneumatically driven stage considering friction characteristics of pneumatic cylinder. In Proceedings of the 2023 International Conference on Advanced Mechatronic Systems (ICAMechS), Melbourne, Australia, 4–7 September 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Tanabata, Y.; Deng, M. Filtered Right Coprime Factorization and Its Application to Control a Pneumatic Cylinder. Processes 2024, 12, 1475. [Google Scholar] [CrossRef]
- De Figueiredo, R.J.; Chen, G. Nonlinear Feedback Control Systems: An Operator Theory Approach; Academic Press Professional, Inc.: Cambridge, MA, USA, 1993. [Google Scholar]
- Deng, M. Operator-Based Nonlinear Control Systems: Design and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Bechlioulis, C.P.; Rovithakis, G.A. Prescribed performance adaptive control of SISO feedback linearizable systems with disturbances. In Proceedings of the 2008 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 1035–1040. [Google Scholar] [CrossRef]
- Bu, X. Prescribed performance control approaches, applications and challenges: A comprehensive survey. Asian J. Control 2021, 2020, 1–24. [Google Scholar] [CrossRef]
- Yao, Y.; Zhuang, Y.; Xie, Y.; Xu, P.; Wu, C. Prescribed Performance Global Non-Singular Fast Terminal Sliding Mode Control of PMSM Based on Linear Extended State Observer. Actuators 2025, 14, 65. [Google Scholar] [CrossRef]
- Nguyen, V.C.; Kim, S.H. A novel fixed-time prescribed performance sliding mode control for uncertain wheeled mobile robots. Sci. Rep. 2025, 15, 5340. [Google Scholar] [CrossRef]


| Symbol | Description |
|---|---|
| z | Average deflection of sliding surface |
| Bristle stiffness | |
| Microviscous friction coefficient | |
| Coefficient of viscous friction | |
| v | Relative velocity of piston and cylinder |
| Stribeck speed | |
| Maximum speed of lubrication film thickness change | |
| Non-dimensional non-stationary lubricant film thickness | |
| Non-dimensional steady-state lubricant film thickness | |
| T | Time constants for fluid friction dynamics |
| Frictional force | |
| Coulomb’s friction force | |
| Maximum static friction | |
| Time constant of lubricant film dynamics | |
| Proportionality constant of lubricant film thickness | |
| m | Mass of stage |
| Piston cross-sectional area | |
| k | Spring constant |
| Servo valve time constant | |
| Servo valve gain |
| Symbol | Value | Unit | Symbol | Value | Unit |
|---|---|---|---|---|---|
| m | 15 | ||||
| 198 | |||||
| 174 | k | ||||
| T | 0 | 100 | − | ||
| n | - | K | 20 | − | |
| f | 218 | ||||
| 99 | − | ||||
| − | |||||
| 5 | − | ||||
| 20 | 100 | − | |||
| 1 | − | ||||
| − | − | ||||
| Method | Settling Time | Steady-State Error | MAE | ITAE |
|---|---|---|---|---|
| PPC-SMC | ||||
| PI-D control | ||||
| PDD2 control |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoshina, T.; Tanabata, Y.; Deng, M. Marginal Design of a Pneumatic Stage Position Using Filtered Right Coprime Factorization and PPC-SMC. Axioms 2025, 14, 534. https://doi.org/10.3390/axioms14070534
Hoshina T, Tanabata Y, Deng M. Marginal Design of a Pneumatic Stage Position Using Filtered Right Coprime Factorization and PPC-SMC. Axioms. 2025; 14(7):534. https://doi.org/10.3390/axioms14070534
Chicago/Turabian StyleHoshina, Tomoya, Yusaku Tanabata, and Mingcong Deng. 2025. "Marginal Design of a Pneumatic Stage Position Using Filtered Right Coprime Factorization and PPC-SMC" Axioms 14, no. 7: 534. https://doi.org/10.3390/axioms14070534
APA StyleHoshina, T., Tanabata, Y., & Deng, M. (2025). Marginal Design of a Pneumatic Stage Position Using Filtered Right Coprime Factorization and PPC-SMC. Axioms, 14(7), 534. https://doi.org/10.3390/axioms14070534







