Dynamic Sliding Mode Control of Spherical Bubble for Cavitation Suppression
Abstract
1. Introduction
2. Bubble State Space Model
2.1. The Spherical Bubble Model
2.2. State Space Model of Bubble
3. Sliding Mode Controller (SMC) Design
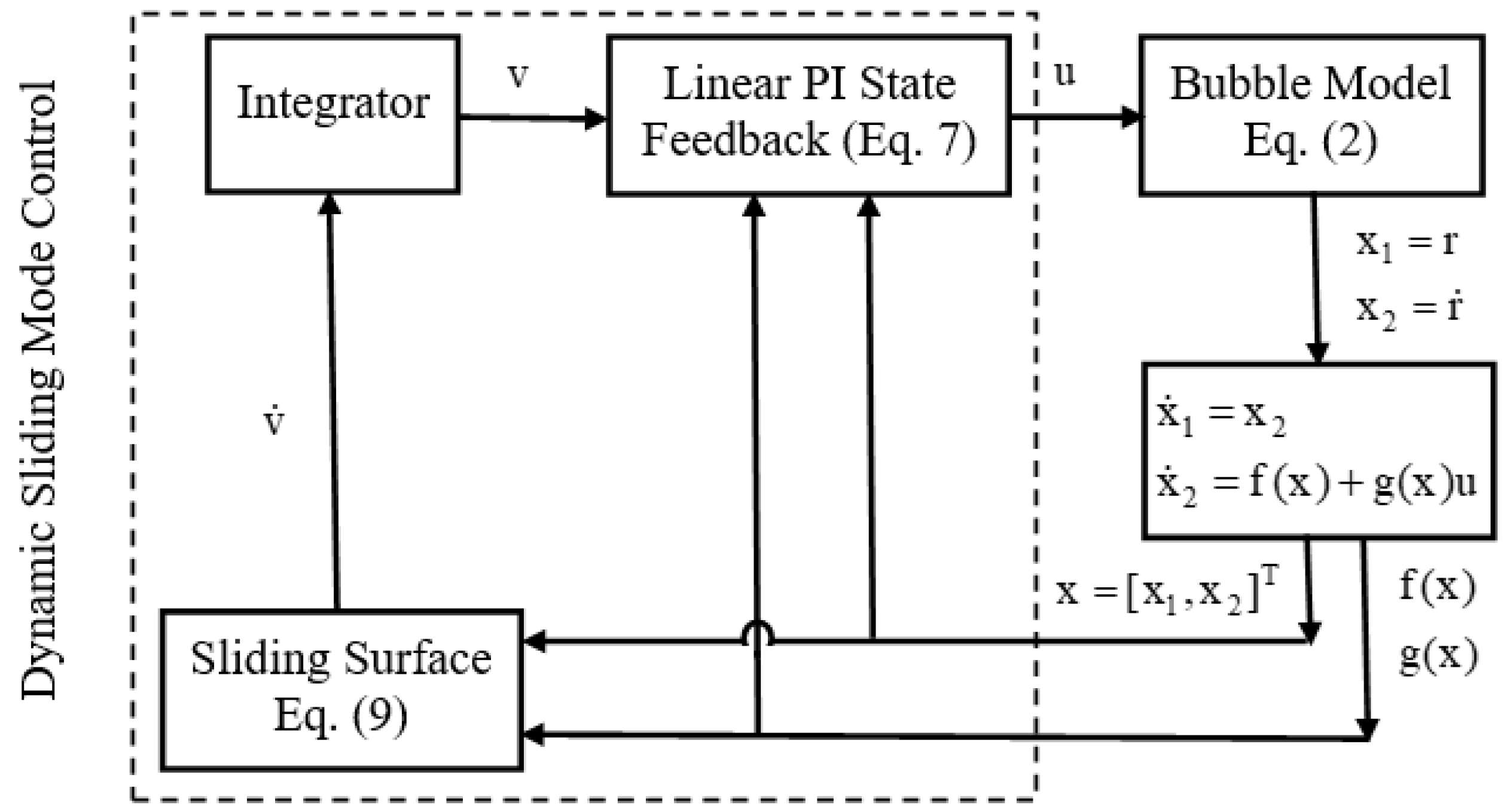
3.1. Dynamic Sliding Mode Control (DSMC)
- First case: If , then from Equation (13), one can write . By integrating this inequality between zero and , we have , and then, .
- Second case: If , then from Equation (13), one can write . By integrating this inequality between zero and , we have , and then, .
- Thus, we can conclude that , and the proof is completed. □
3.2. Traditional Sliding Mode Control (TSMC)
4. Simulations Section
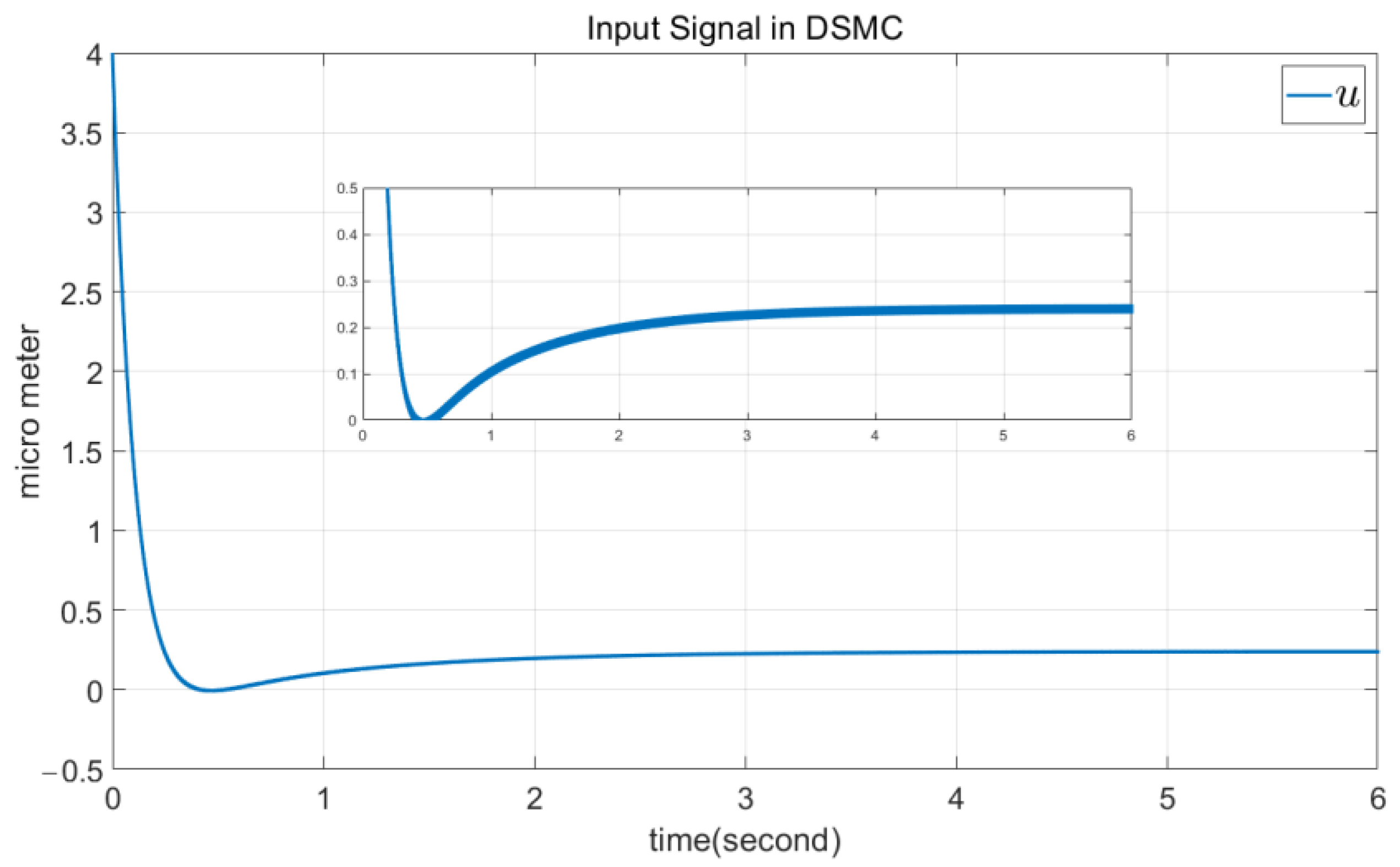
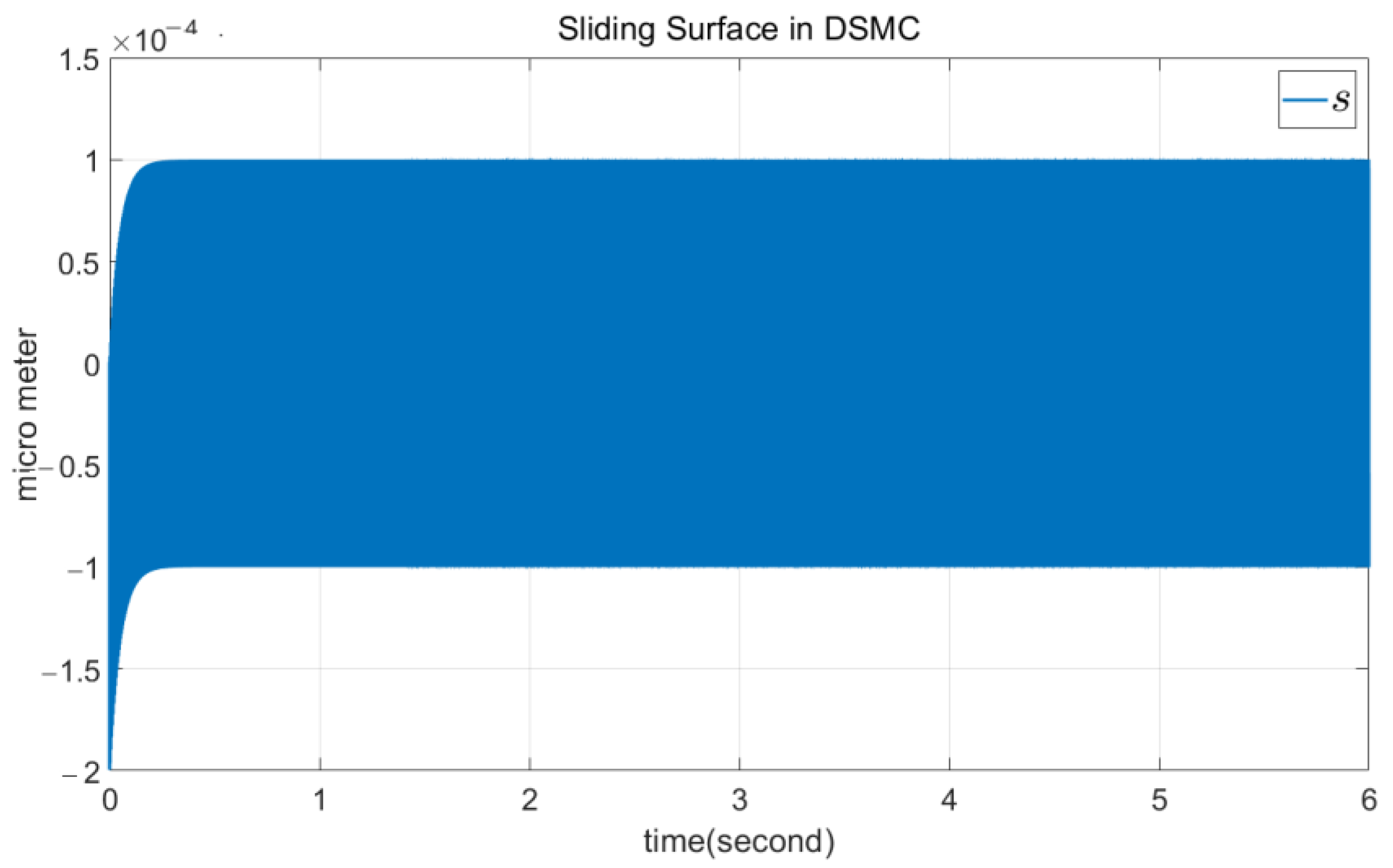
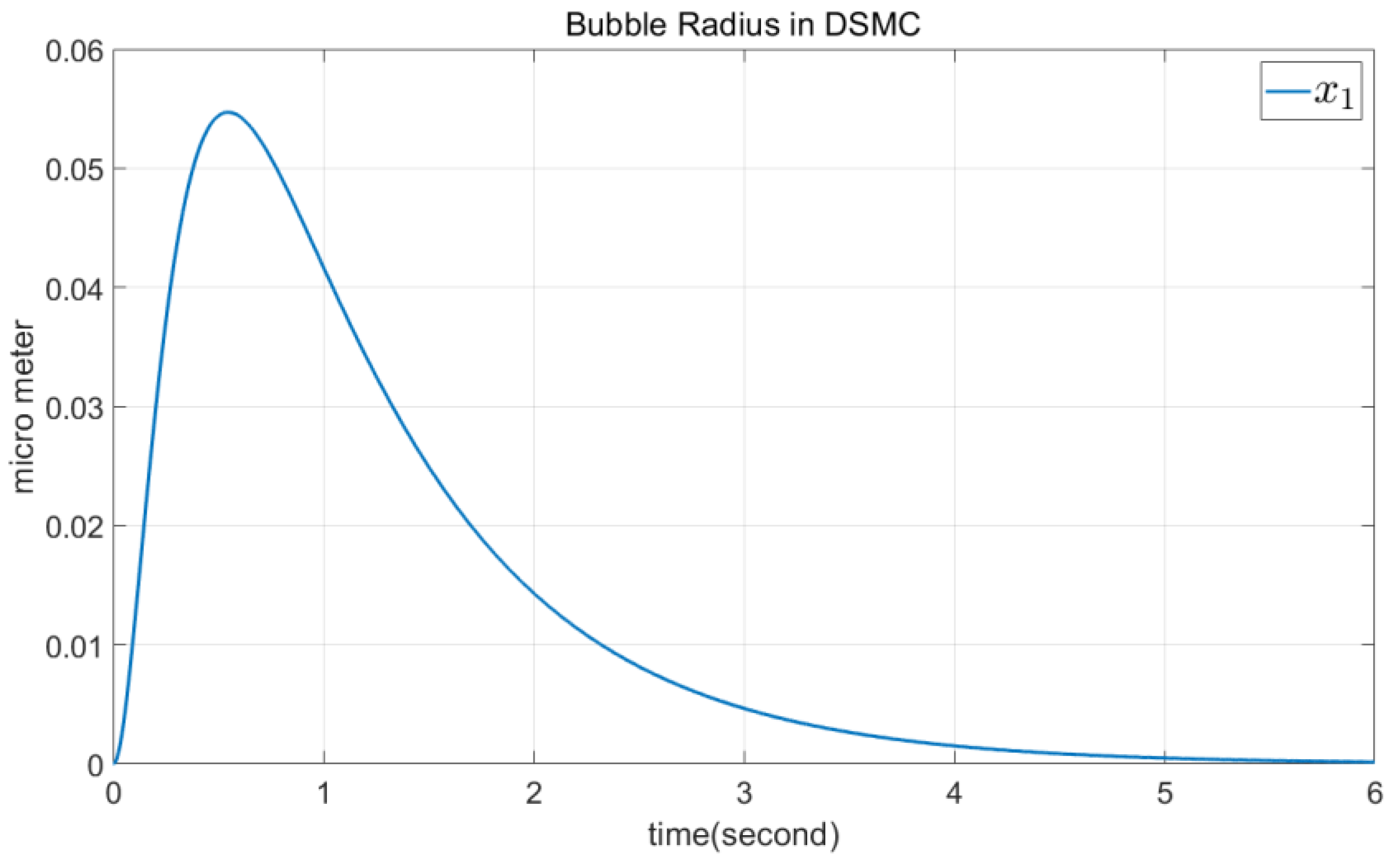
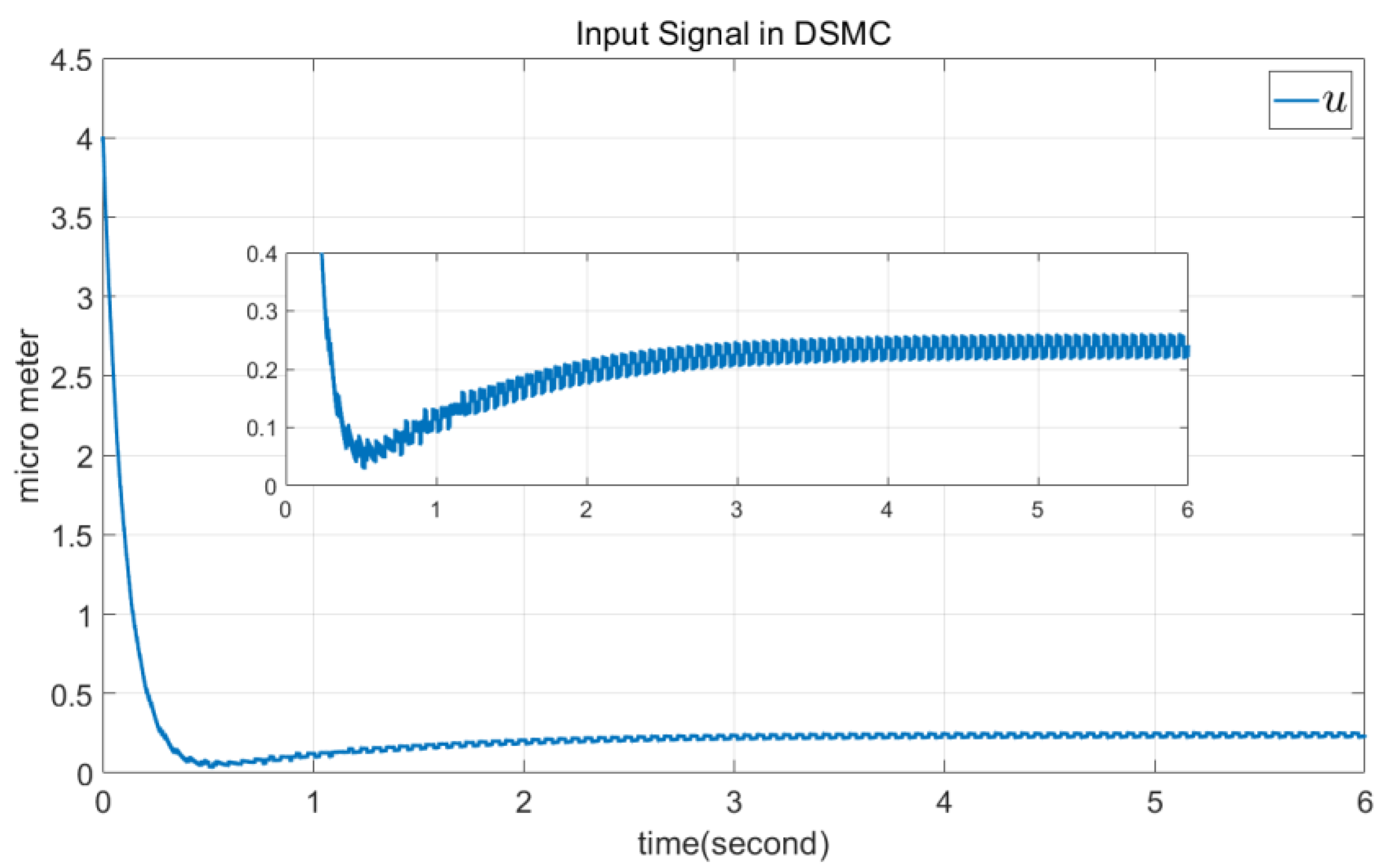
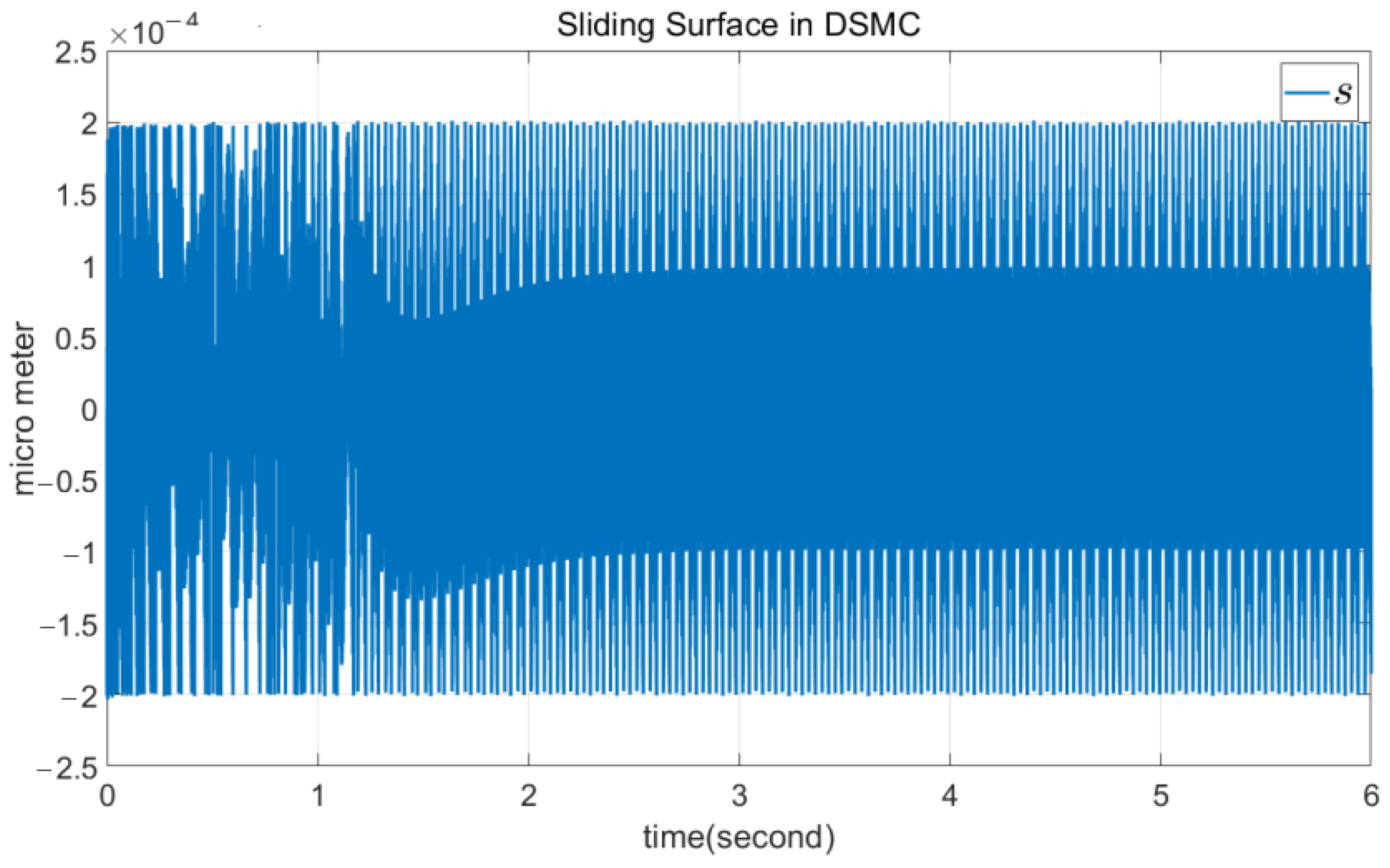
4.1. DSMC Simulation
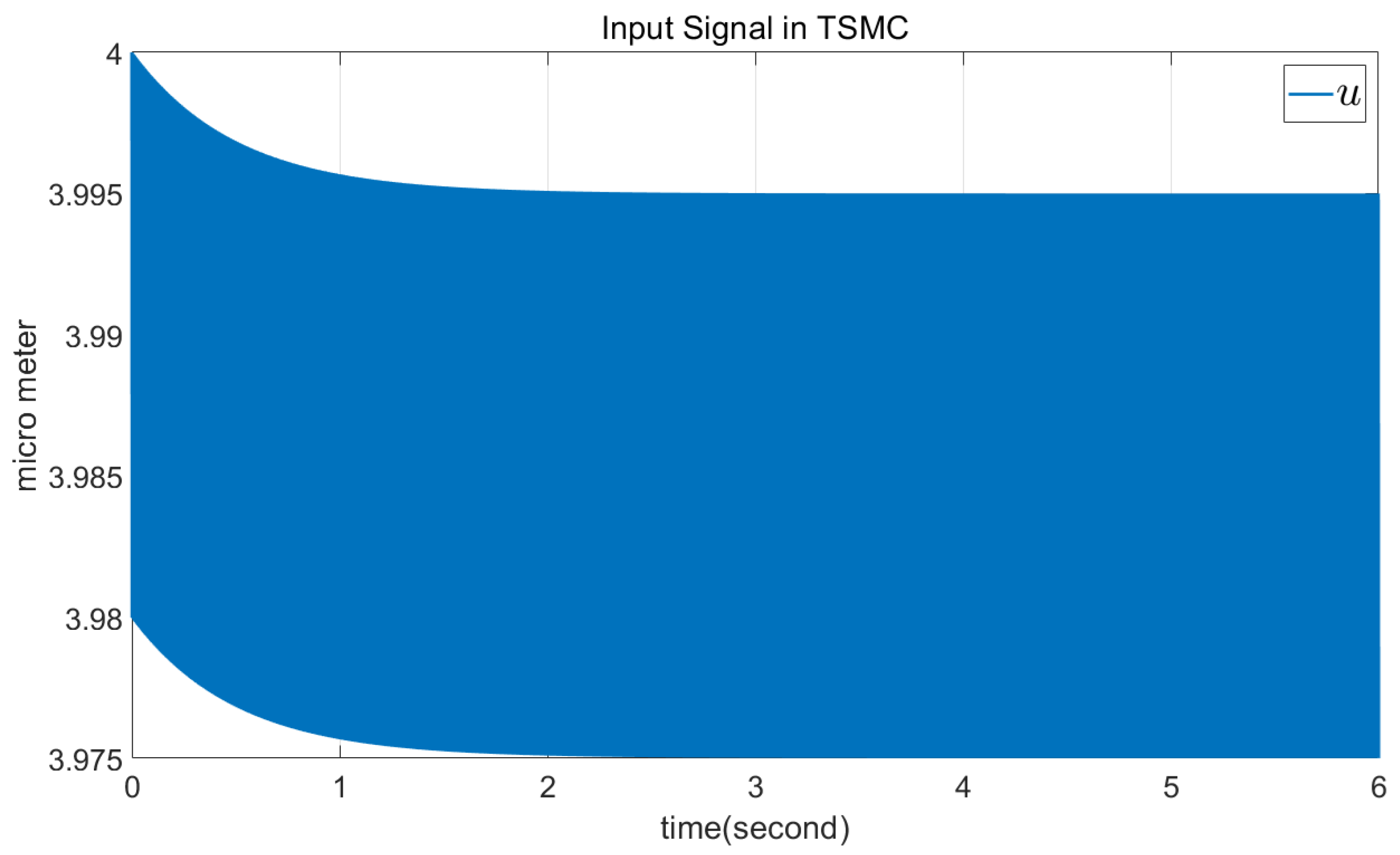
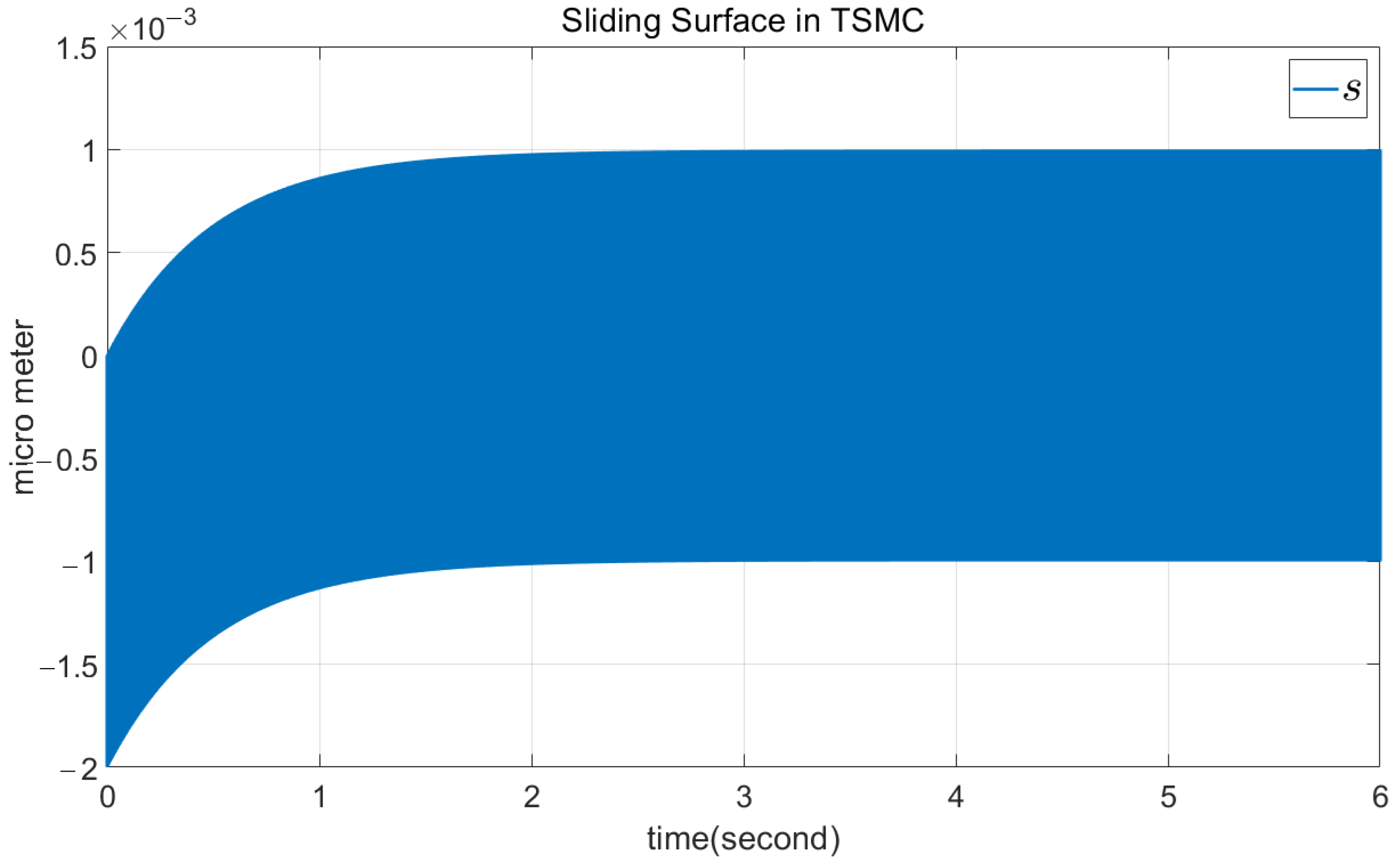
4.2. TSMC Simulation
4.3. Comparison of DSMC and TSMC
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, J.; Wesley, L. Ultrasound, cavitation bubbles and their interaction with cells. Adv. Drug Deliv. Rev. 2008, 60, 1103–1116. [Google Scholar] [CrossRef]
- Huang, S.; Mohamad, A.A. Modeling of cavitation bubble dynamics in multicomponent mixtures. J. Fluids Eng. 2009, 131, 031301. [Google Scholar] [CrossRef]
- Prosperetti, A.; Lezzi, A. Bubble dynamics in a compressible liquid. Part 1. First-order theory. J. Fluid Mech. 1986, 168, 457–478. [Google Scholar] [CrossRef]
- Haosheng, C.; Jiadao, W.; Darong, C. Cavitation damages on solid surfaces in suspensions containing spherical and irregular microparticles. Wear 2009, 266, 345–348. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Aired, L.; Bouakaz, A. Dynamics of a contrast agent microbubble attached to an elastic wall. IEEE Trans. Med. Imaging 2012, 31, 654–662. [Google Scholar] [CrossRef]
- Orlandi, F.; Montorsi, A.; Milani, M. Cavitation analysis through CFD in industrial pumps: A review. Int. J. Thermofluids 2023, 20, 100506. [Google Scholar] [CrossRef]
- Akhatov, S.; Konovalova, S. Regular and chaotic dynamics of a spherical bubble. J. Appl. Math. Mech. 2005, 69, 575–584. [Google Scholar] [CrossRef]
- Kannan, Y.S.; Karri, B.; Sahu, K.C. Entrapment and interaction of an air bubble with an oscillating cavitation bubble. Phys. Fluids 2018, 30, 041701. [Google Scholar] [CrossRef]
- Rahmatizadeh, B.; Hamidi Beheshti, M.T.; Azadegan, M.; Najafi, N. Stability analysis and sliding mode control of a single spherical bubble described by Keller–Miksis equation. Int. J. Dyn. Cont. 2021, 9, 1757–1764. [Google Scholar] [CrossRef]
- Kirschner, I.N.; Kring, D.C.; Stokes, A.W.; Fine, N.E.; Uhlman, J.S. Control strategies for supercavitating vehicles. J. Vib. Contr. 2002, 8, 219–242. [Google Scholar] [CrossRef]
- Dzielski, J.; Kurdila, A. A benchmark control problem for supercavitating vehicles and an initial investigation of solutions. J. Vib. Contr. 2003, 9, 791–804. [Google Scholar] [CrossRef]
- Lin, G.; Balachandran, B.; Abed, E.H. Nonlinear dynamics and bifurcations of a supercavitating vehicle. IEEE J. Ocean. Eng. 2008, 32, 753–761. [Google Scholar] [CrossRef]
- Mao, X.; Qian, W. Nonlinear control design for a supercavitating vehicle. IEEE Trans. Contr. Sys. Tech. 2009, 17, 816–832. [Google Scholar]
- Vanek, B.; Balas, G.J.; Arndt, R. Linear, parameter-varying control of a supercavitating vehicle. Contr. Eng. Pract. 2010, 18, 1003–1012. [Google Scholar] [CrossRef]
- Mao, X.; Wang, Q. Adaptive control design for a supercavitating vehicle model based on fin force parameter estimation. J. Vib. Contr. 2015, 21, 1220–1233. [Google Scholar] [CrossRef]
- Han, Y.; Xu, Z.; Guan, L. Predictive control of a supercavitating vehicle based on time-delay characteristics. IEEE Access 2020, 9, 13499–13512. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Cao, G.; Zhao, Y.; Zhang, J. Design of RBF adaptive sliding mode controller for a supercavitating vehicle. IEEE Access 2021, 9, 39873–39883. [Google Scholar]
- Badfar, E.; Alinaghizadeh Ardestani, M.; Azadegan, M.; Najafi, N. Utilizing sliding mode control for the cavitation phenomenon and using the obtaining result in modern medicine. SN Appl. Sci. 2019, 1, 1419. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Perruquetti, W.; Barbot, J.P. Sliding Mode Control in Engineering; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Karami-Mollaee, A.; Pariz, N.; Shanechi, H.M. Position control of servomotors using neural dynamic sliding mode. J. Dyn. Sys. Meas. Contr. 2011, 133, 141–150. [Google Scholar] [CrossRef]
- Karami-Mollaee, A.; Tirandaz, H.; Barambones, O. Dynamic sliding mode position control of induction motors based load torque compensation using adaptive state observer. Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 2249–2262. [Google Scholar] [CrossRef]
- Alsaadi, F.E.; Yasami, A.; Alsubaie, H.; Alotaibi, A.; Jahanshahi, H. Control of a hydraulic generator regulating system using Chebyshev-neural-network-based non-singular fast terminal sliding mode method. Mathematics 2023, 11, 168–186. [Google Scholar] [CrossRef]
- Zhu, Q. Model-free sliding mode enhanced proportional, integral, and derivative (SMPID) control. Axioms 2023, 12, 721. [Google Scholar] [CrossRef]
- Nie, J.; Hao, L.; Lu, X.; Wang, H.; Sheng, C. Global fixed-time sliding mode trajectory tracking control design for the saturated uncertain rigid manipulator. Axioms 2023, 12, 883. [Google Scholar] [CrossRef]
- Lee, H.; Utkin, V.I. Chattering suppression methods in sliding mode control systems. Annu. Rev. Control 2007, 31, 179–188. [Google Scholar] [CrossRef]
- Fuh, C.-C. Variable-thickness boundary layers for sliding mode control. J. Mar. Sci. Tech. 2008, 16, 288–294. [Google Scholar] [CrossRef]
- Chen, H.-M.; Renn, J.-C.; Su, J.-P. Sliding mode control with varying boundary layers for an electro-hydraulic position servo system. Int. J. Adv. Manuf. Tech. 2005, 26, 117–123. [Google Scholar] [CrossRef]
- Zhang, X. Sliding mode-like fuzzy logic control with adaptive boundary layer for multiple-variable discrete. J. Intell. Syst. 2016, 25, 209–220. [Google Scholar] [CrossRef]
- Gandikota, G.; Das, D.K. Disturbance observer–based adaptive boundary layer sliding mode controller for a type of nonlinear multiple-input multiple-output system. Int. J. Robust. Nonlinear Contr. 2019, 29, 5886–5912. [Google Scholar] [CrossRef]
- Cucuzzella, M.; Incremona, G.P.; Ferrara, A. Design of robust higher order sliding mode control for microgrids. IEEE J. Emerg. Sel. Top. Cir. Sys. 2015, 5, 393–401. [Google Scholar] [CrossRef]
- Karami-Mollaee, A. Design of dynamic sliding mode controller for active suspension system. Modares Mech. Eng. 2016, 16, 51–58. [Google Scholar]
- Levant, A. Homogeneity approach to high-order sliding mode design. Automatica 2005, 41, 823–830. [Google Scholar] [CrossRef]
- Plestan, F.; Glumineau, A.; Laghrouche, S. A new algorithm for high-order sliding mode control. Int. J. Robust. Non. Contr. 2008, 18, 441–453. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Robust. Non. Contr. 2010, 76, 924–941. [Google Scholar] [CrossRef]
- Kerboua, K.; Hamdaoui, O. Insights into numerical simulation of controlled ultrasonic waveforms driving single cavitation bubble activity. Ultrason.-Sonochemistry 2018, 43, 237–247. [Google Scholar] [CrossRef]
- Hilgenfeldt, S.; Lohse, D.; Brenner, M. Phase diagrams for sonoluminescing bubbles. Phys. Fluids 1996, 11, 2808–2826. [Google Scholar] [CrossRef]
- Grossmann, S.; Hilgenfeldt, S.; Lohse, D.; Zomack, M. Sound radiation of 3-MHz driven gas bubbles. J. Acoust. Soc. Am. 1997, 2, 1223–1230. [Google Scholar] [CrossRef]



| Value | Notation | Gas or Vapor |
|---|---|---|
| 1.40 | Air | |
| 1.40 | Oxygen | |
| 1.40 | Nitrogen | |
| 1.41 | Hydrogen | |
| 1.66 | Helium | |
| 1.66 | Argon |
| Unit | Value | Parameter |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karami-Mollaee, A.; Barambones, O. Dynamic Sliding Mode Control of Spherical Bubble for Cavitation Suppression. Axioms 2024, 13, 706. https://doi.org/10.3390/axioms13100706
Karami-Mollaee A, Barambones O. Dynamic Sliding Mode Control of Spherical Bubble for Cavitation Suppression. Axioms. 2024; 13(10):706. https://doi.org/10.3390/axioms13100706
Chicago/Turabian StyleKarami-Mollaee, Ali, and Oscar Barambones. 2024. "Dynamic Sliding Mode Control of Spherical Bubble for Cavitation Suppression" Axioms 13, no. 10: 706. https://doi.org/10.3390/axioms13100706
APA StyleKarami-Mollaee, A., & Barambones, O. (2024). Dynamic Sliding Mode Control of Spherical Bubble for Cavitation Suppression. Axioms, 13(10), 706. https://doi.org/10.3390/axioms13100706










