Clifford Distributions Revisited
Abstract
1. Introduction
2. Signumdistributions
3. Cartesian Operators
- (i)
- for arbitrary constants and and for any distribution such that , with ;
- (ii)
- for arbitrarily constant and for any distribution such that ;
- (iii)
- for arbitrary constants and and for any distribution such that .
4. Signum Pairs and Cross Pairs of Operators
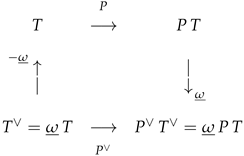

5. Spherical Operators
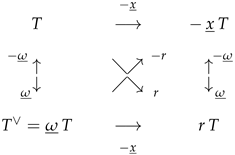
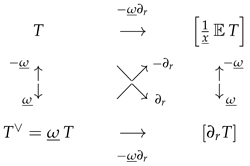

- (i)
- An alternative expression for isIndeed, it follows fromthatwhence we have the desired formula states for each of the components.
- (ii)
- For a general Clifford algebra-valued distribution, the action of the spherical derivative operator is defined through linearity with respect to the scalar components.
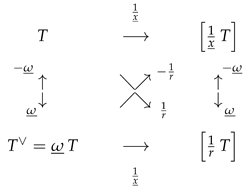

6. Action Uniqueness of Some Operators
- (i)
- If the distribution is radial, then the following actions are uniquely determined asand the actions of the corresponding signum partner operators on the signum-radial signumdistributionare also uniquely determined.
- (ii)
- If the distribution is homogeneous with homogeneity degree , then the following actions are uniquely determined:andAdditionally, the actions of the corresponding signum partner operators on the homogeneous signumdistribution , viz.,andare also uniquely determined.
- (iii)
- If the distribution is homogeneous with homogeneity degree , then the following actions are uniquely determined:and the actions of the corresponding signum partner operators on the homogeneous signumdistributionare uniquely determined as well.
- (iv)
- The conclusions contained in (iii) remain valid if the distribution and signumdistribution under consideration are both radial and signum-radial, respectively, and homogeneous with homogeneity degree .
- (v)
- The conclusions contained in (iii) remain valid if the distribution and signumdistribution under consideration are both signum-radial and radial, respectively, and homogeneous with homogeneity degree .
7. Cartesian Derivatives of Signumdistributions

8. Actions on and
8.1. The Operators , r, and
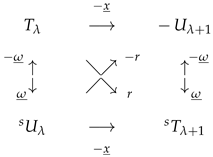
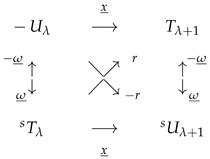
8.2. The Operators and
8.3. The Operators , , and
- ;
- ;
- .
- ;
- ;
- .
8.4. The Operators , , , and
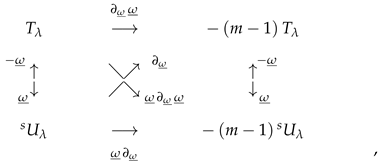
- ;
- .
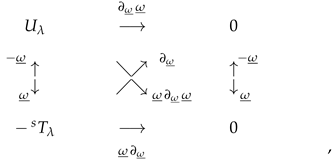
- ;
- .
8.5. The Operators , , and
8.6. The Operators
8.7. The Operators , , and
- ;
- ;
- .
- ;
- ;
- .
- ;
- ;
- .
- ;
- ;
- .
- For , we haveKeeping in mind that , it is confirmed that
- For , we haveconfirming that
- For , we haveandconfirming that
- For , we haveconfirming that
- For , we haveconfirming that
- For , we haveconfirming that
- ;
- ;
- .
- ;
- ;
- .
- ;
- ;
- .
- ;
- ;
- .
- ;
- ;
- .
- ;
- ;
- .
- .
- ;
- ;
- .
- ;
- ;
- .
8.8. The Operators and
8.9. The Operators , , , and
9. Cartesian Derivatives of and
9.1. The First-Order Partial Derivatives of
9.2. The First-Order Partial Derivatives of
9.3. Second-Order Partial Derivatives of
9.4. The Second-Order Partial Derivatives of
10. Powers of the Vector Variable
10.1. Integer Powers of as Regular Distributions and Signumdistributions
10.2. Integer Powers of as Finite Part Distributions and Signumdistributions
- ;
- ;
- .
10.3. Complex Powers of as Distributions
- For , we get
- For , we get
- is a meromorphic function of showing simple poles at ;
- is a meromorphic function of showing simple poles at .
- The case .We consider the distributionFor odd dimension m, we do not expect singularities to appear, and we indeed getwithwhenceFor even dimension m, we getwithwhence
- The case .We consider the distributionFor odd dimension m, we do not expect singularities to appear, and we indeed getwithwhenceFor even dimension m, we getwithwhence
- The case .We consider the distributionFor odd dimension m, we do not expect singularities to appear, and we indeed getwithwhenceFor even dimension m, we getwithwhence
- The case .We consider the distributionFor odd dimension m, we do not expect singularities to appear, and we indeed getwithwhenceFor even dimension m, we getwithwhence
- Consider the case . For odd dimension m, no singularities will appear, and we indeed find thatwhenceFor even dimension m, we findwhence
- Consider the case . For odd dimension m, no singularities will appear, and we indeed find thatwhenceFor even dimension m, we findwhence
- Consider the case . For odd dimension m, no singularities will appear, and we indeed find thatwhenceFor even dimension m, we findwhence
- Consider the case . For odd dimension m, no singularities will appear, and we indeed find thatwhenceFor even dimension m, we findwhence
10.4. Complex Powers of as Signumdistributions
- For ,
- For ,
- is a meromorphic function of showing simple poles at ;
- is a meromorphic function of showing simple poles at .
- Consider the case . For even dimension m, we do not expect singularities to appear, and indeed, we find thatwhenceFor odd dimension m, we findwhence
- Consider the case . For even dimension m, we do not expect singularities to appear, and indeed, we find thatwhenceFor odd dimension m, we findwhence
- Consider the case . For even dimension m, we do not expect singularities to appear, and indeed, we find thatwhenceFor odd dimension m, we findwhence
- Consider the case . For even dimension m, we do not expect singularities to appear, and indeed, we find thatwhenceFor odd dimension m, we findwhence
- Consider the case . For even dimension m, we do not expect singularities to appear, and we indeed find thatwhenceFor odd dimension m, we findwhence
- Consider the case . For even dimension m, we do not expect singularities to appear, and we indeed find thatwhenceFor odd dimension m, we findwhence
- Consider the case . For even dimension m, we do not expect singularities to appear, and we indeed find thatwhenceFor odd dimension m, we findwhence
- Consider the case . For even dimension m, we do not expect singularities to appear, and we indeed find thatwhenceFor odd dimension m, we findwhence
11. Physics in Three-Dimensional Euclidean Space
11.1. Gravitational Fields
11.2. Coulomb Potential of a Unit Point Charge
- (i)
- ;
- (ii)
- ;
- (iii)
- ;
- (iv)
- ;
- (v)
- ;
- (vi)
- .
11.3. A Novel Delta Function Identity
11.4. Electric and Magnetic Dipole Moment
11.5. Some More Delta Function Identities
11.6. Point Source Fields
12. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Distribution Fp on the Real Line
- ;
- ;
- .
- ;
- ;
- .
- ;
- .
Appendix B. The Distributions Tλ and Uλ in
- If or , then
- If or , then
- If or , then
- (i)
- ;
- (ii)
- ;
- (iii)
- ;
- (iv)
- ;
- (v)
- ;
- (vi)
- ; .
- (i)
- for all ;
- (ii)
- for all except for .
- (i)
- for all ;
- (ii)
- for all except for .
- (i)
- For , we have .
- (ii)
- (iii)
- For , we have .
- (iv)
- .
- (i)
- For , we haveand .
- (ii)
- For all , we haveand .
Appendix C. Spherical Means
Appendix D. Some Specific Distributions
- We havewhence is the regular distribution associated with constant function . Its properties are trivial.
- We havewhence is the regular distribution associated with function , which is the higher-dimensional counterpart to the signum distribution on the real line. Its properties are as follows:
- -
- ;
- -
- , which splits up into and ;
- -
- ;
- -
- ;
- -
- and ;
- -
- and ;
- -
- and ;
- -
- ;
- -
- ;
- -
- .
- We havewhence is the regular distribution associated with the locally integrable function in . Its properties are the following:
- -
- ;
- -
- , which splits up intoand ;
- -
- , which expresses the fact that is the fundamental solution of the Laplace operator
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- .
- We havewhence is the regular distribution associated with the locally integrable function in . Its properties are the following:
- -
- ;
- -
- , which splits up into and ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- .
- We havewhence is the regular distribution associated with the locally integrable function in . Its properties are the following:
- -
- ;
- -
- , which splits up intoand and expresses the fact that is the fundamental solution of the Dirac operator ;
- -
- ;
- -
- ;
- -
- ;
- -
- and ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- .
- We haveIts properties are the following:
- -
- ;
- -
- , which splits up intoand ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- .
- We havewhencewhich is the higher-dimensional analogue of the principal value distribution Pv on the real line. It is, up to a constant, the convolution kernel of the Hilbert transform, given, for a suitable function or distribution f, byIts properties are the following:
- -
- or ;
- -
- , which splits up into and;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- .
- We haveThe scalar distribution is, up to a constant, the convolution kernel for the so-called square root of the negative Laplacian, which, for an appropriate function or distribution f, is defined byIts properties are the following:
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- ;
- -
- .
As it holds that , orit becomes clear that the convolution kernel of the operator is precisely the convolution kernel of the so-called Hilbert-Dirac operator , whence
Appendix E. Clifford Algebra and Clifford Analysis
References
- Brackx, F.; De Knock, B.; De Schepper, H.; Eelbode, D. A Calculus scheme for Clifford Distributions. Tokyo J. Math. 2006, 29, 495–513. [Google Scholar] [CrossRef]
- Schwartz, L. Théorie des Distributions; Hermann: Paris, France, 1966. [Google Scholar]
- Brackx, F.; Sommen, F.; Vindas, J. On the radial derivative of the delta distribution. Complex Anal. Oper. Theory 2017, 11, 1035–1057. [Google Scholar] [CrossRef]
- Brackx, F. Calculus for the Delta Distribution. Contemp. Math. 2024, 5, 5238–5327. [Google Scholar] [CrossRef]
- Brackx, F. Radial and Angular Derivatives of Distributions. In Topics in Clifford Analysis. Trends in Mathematics; Bernstein, S., Ed.; Birkhäuser: Cham, Switzerland, 2019; pp. 141–171. [Google Scholar]
- Brackx, F. Distributions: A spherical co-ordinates approach. arXiv 2018, arXiv:1801.07393. [Google Scholar]
- Adkins, G.S. Three-dimensional Fourier transforms, integrals of spherical Bessel functions, and novel delta function identities. Bull. Allahabad Math. Soc. 2008, 31, 215–246. [Google Scholar]
- Frahm, C.P. Some novel delta-function identities. Am. J. Phys. 1983, 51, 826–829. [Google Scholar] [CrossRef]
- Hnidzo, V. Generalized second-order partial derivatives of 1/r. Eur. J. Phys. 2011, 32, 287–297. [Google Scholar]
- Franklin, J. Comment on “Some novel delta-function identities”. Am. J. Phys. 2010, 78, 1225–1226. [Google Scholar] [CrossRef]
- Bowen, J.M. Delta function terms arising from classical point-source fields. Am. J. Phys. 1994, 62, 511–515. [Google Scholar]
- Estrada, R.; Kanwal, R.P. The appearance of nonclassical terms in the analysis of point-source fields. Am. J. Phys. 1995, 63, 278. [Google Scholar] [CrossRef]
- Kanwal, R.P. Generalized Functions: Theory and Applications, 3rd ed.; Springer Science + Business Media: New York, NY, USA, 2004. [Google Scholar]
- Brackx, F.; De Schepper, H. On The Fourier Transform of Distributions and Differential Operators in Clifford Analysis. Complex Var. Theory Appl. 2004, 49, 1079–1091. [Google Scholar] [CrossRef]
- Brackx, F.; Delanghe, R.; Sommen, F. Clifford Analysis; Pitman Publishers: Boston, MA, USA; London, UK; Melbourne, Australia, 1982. [Google Scholar]
- Porteous, I. Clifford Algebras and the Classical Groups; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Stein, E.M.; Weiss, G. Generalization of the Cauchy-Riemann equations and representations of the rotation group. Amer. J. Math. 1968, 90, 163–196. [Google Scholar] [CrossRef]
- Delanghe, R.; Sommen, F.; Souček, V. Clifford Algebra and Spinor-Valued Functions: A Function Theory for the Dirac Operator; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Gürlebeck, K.; Habetha, K.; Sprössig, W. Holomorphic Functions in the Plane and n-Dimensional Space; Translated from the 2006 German Original; Birkhäuser Verlag: Basel, Switzerland, 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brackx, F. Clifford Distributions Revisited. Axioms 2025, 14, 533. https://doi.org/10.3390/axioms14070533
Brackx F. Clifford Distributions Revisited. Axioms. 2025; 14(7):533. https://doi.org/10.3390/axioms14070533
Chicago/Turabian StyleBrackx, Fred. 2025. "Clifford Distributions Revisited" Axioms 14, no. 7: 533. https://doi.org/10.3390/axioms14070533
APA StyleBrackx, F. (2025). Clifford Distributions Revisited. Axioms, 14(7), 533. https://doi.org/10.3390/axioms14070533







