Relativistic Scalar Particle Systems in a Spacetime with a Spiral-like Dislocation
Abstract
1. Introduction
2. On a Scalar Particle Confined to an Elastic Cylindrical Shell
3. Klein–Gordon Oscillator Under Effect of a Spiral-like Dislocation
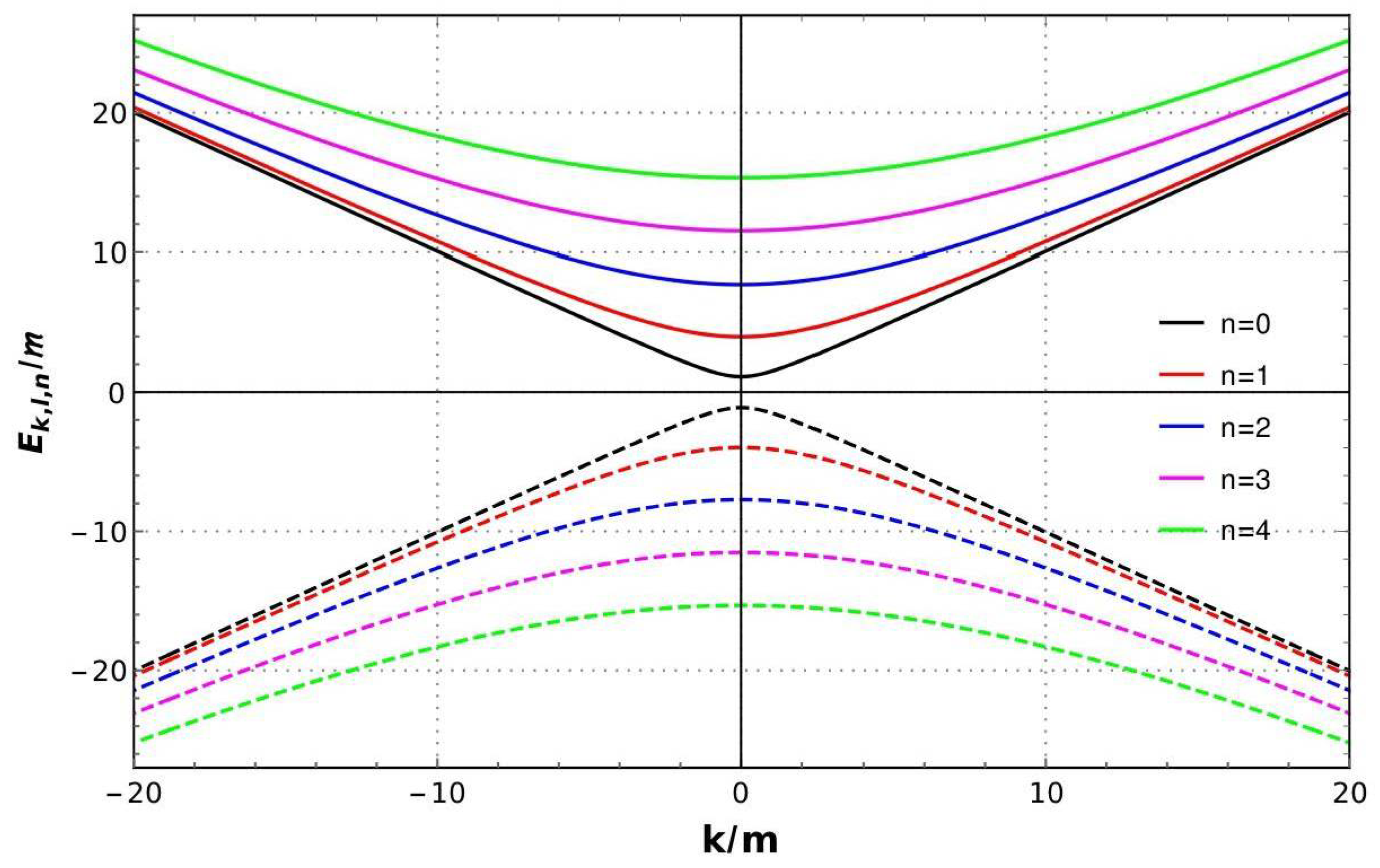
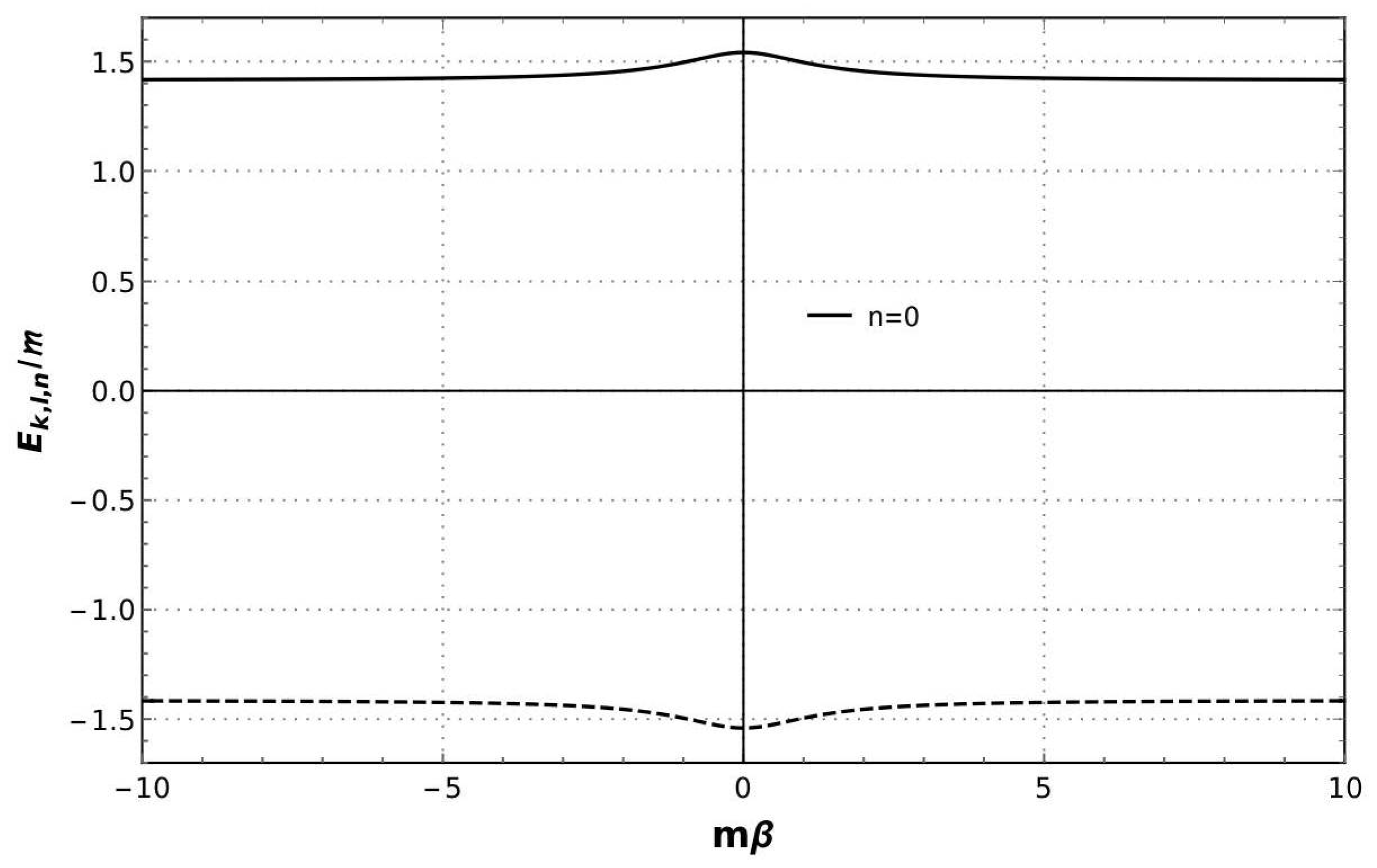
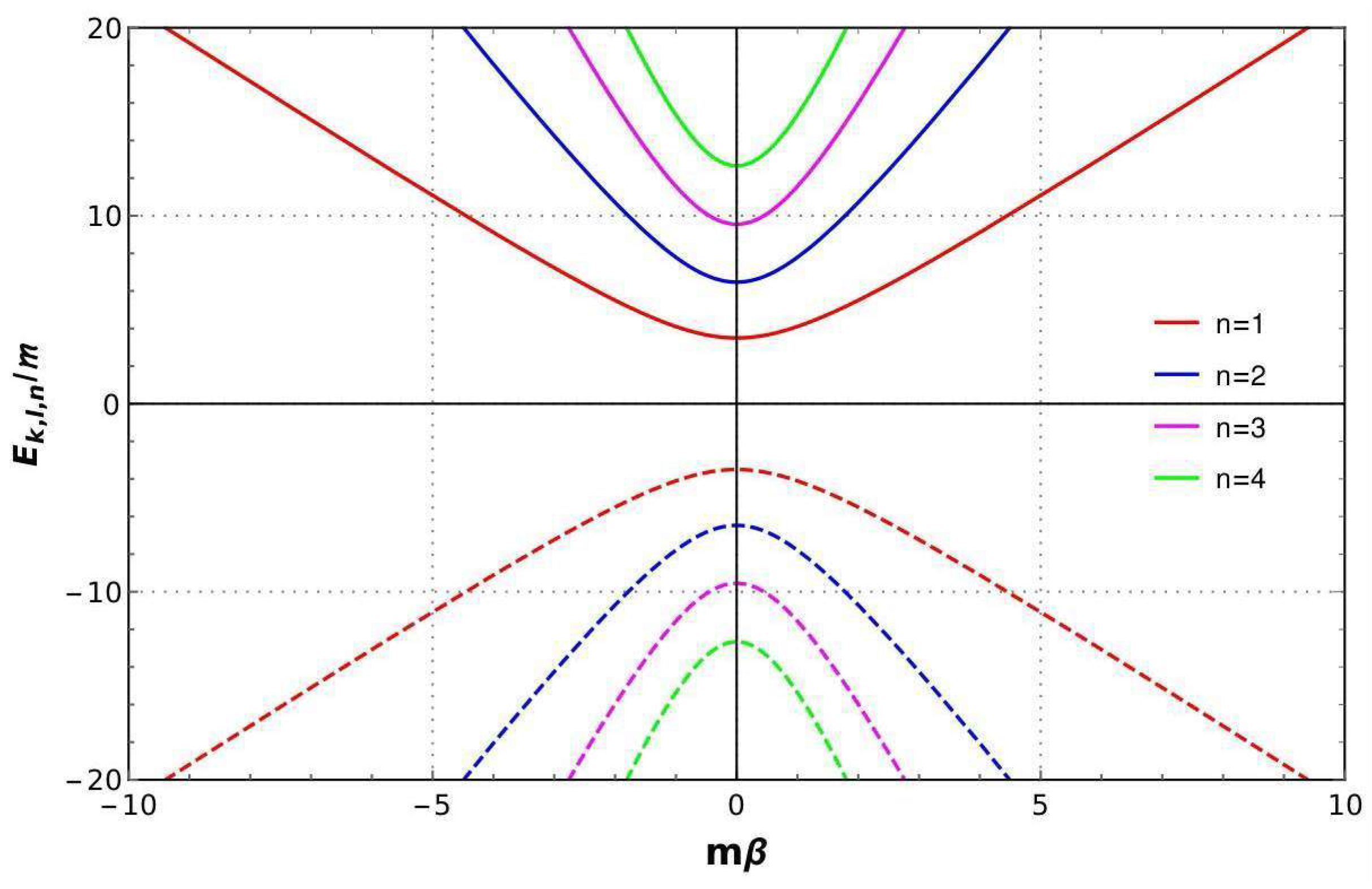
4. On the Klein–Gordon Oscillator Subjected to a Hard-Wall Potential in Spacetime with a Spiral-like Dislocation
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vilenkin, A.; Shellard, E.P.S. Strings and Other Topological Defects; Cambrigde University Press: Cambridge, UK, 1994. [Google Scholar]
- Vilenkin, A. Cosmic strings and domain walls. Phys. Rep. 1985, 121, 263. [Google Scholar] [CrossRef]
- Barriola, M.; Vilenkin, A. Gravitational field of a global monopole. Phys. Rev. Lett. 1989, 63, 341. [Google Scholar] [CrossRef]
- de Mello, E.R.B. Physics in the Global Monopole Spacetime. Braz. J. Phys. 2001, 31, 2. [Google Scholar]
- Vilenkin, A. Gravitational field of vacuum domain walls. Phys. Lett. B 1983, 133, 177. [Google Scholar] [CrossRef]
- Hiscock, W.A. Exact gravitational field of a string. Phys. Rev. D 1985, 31, 3288. [Google Scholar] [CrossRef] [PubMed]
- Linet, B. The static metrics with cylindrical symmetry describing a model of cosmic strings. Gen. Relativ. Gravit. 1985, 17, 1109. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Topology of cosmic domains and strings. J. Phys. A Math. Gen. 1976, 9, 1387. [Google Scholar] [CrossRef]
- Katanaev, M.O.; Volovich, I.V. Theory of defects in solids and three-dimensional gravity. Ann. Phys. 1992, 216, 1–28. [Google Scholar] [CrossRef]
- Valanis, K.C.; Panoskaltsis, V.P. Material metric, connectivity and dislocations in continua. Acta Mech. 2005, 175, 77. [Google Scholar] [CrossRef]
- Furtado, C.; Moraes, F. Landau levels in the presence of a screw dislocation. Europhys. Lett. 1999, 45, 279. [Google Scholar] [CrossRef]
- Marques, G.A.; Furtado, C.; Bezerra, V.B.; Moraes, F. Landau levels in the presence of topological defects. J. Phys. A Math. Gen. 2001, 34, 5945. [Google Scholar] [CrossRef]
- Furtado, C.; Moraes, F. Harmonic oscillator interacting with conical singularities. J. Phys. A Math. Gen. 2000, 33, 5513. [Google Scholar] [CrossRef]
- Bueno, M.J.; Furtado, C.; Bakke, K. On the effects of a screw dislocation and a linear potential on the harmonic oscillator. Phys. B 2016, 496, 45. [Google Scholar] [CrossRef]
- Bakke, K. Doubly anharmonic oscillator under the topological effects of a screw dislocation. Phys. B 2018, 537, 346. [Google Scholar] [CrossRef]
- Bakke, K. Torsion and noninertial effects on a nonrelativistic Dirac particle. Ann. Phys. 2014, 346, 51. [Google Scholar] [CrossRef]
- Maia, A.V.D.M.; Bakke, K. On an electron in an elastic medium with a spiral dislocation. Int. J. Mod. Phys. A 2019, 34, 1950153. [Google Scholar] [CrossRef]
- Maia, A.V.D.M.; Bakke, K. Harmonic oscillator in an elastic medium with a spiral dislocation. Phys. B 2018, 531, 213. [Google Scholar] [CrossRef]
- Langlois, P. Hawking radiation for Dirac spinors on the geon. Phys. Rev. D 2004, 70, 104008, Erratum in Phys. Rev. D 2005, 72, 129902. [Google Scholar] [CrossRef]
- Foo, J.; Arabaci, C.S.; Zych, M.; Mann, R.B. Quantum superpositions of Minkowski spacetime. Phys. Rev. D 2023, 107, 045014. [Google Scholar] [CrossRef]
- Volterra, V. Sur l’équilibre des corps élastiques multiplement connexes. Ann. Sci. Éc. Norm. Supér. 1907, 24, 401. [Google Scholar] [CrossRef]
- Puntigam, R.A.; Soleng, H.H. Volterra distortions, spinning strings, and cosmic defects. Class. Quantum Grav. 1997, 14, 1129. [Google Scholar] [CrossRef]
- Bezerra, V.B. Global effects due to a chiral cone. J. Math. Phys. 1997, 38, 5. [Google Scholar] [CrossRef]
- Cravalho, J.; Furtado, C.; Moraes, F. Dirac oscillator interacting with a topological defect. Phys. Rev. A 2011, 84, 032109. [Google Scholar] [CrossRef]
- Bakke, K.; Furtado, C. On the interaction of the Dirac oscillator with the Aharonov-Casher system in topological defect backgrounds. Ann. Phys. 2013, 336, 489. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Bakke, K. Torsion effects on a relativistic position-dependent mass system. Gen. Relativ. Gravit. 2016, 48, 161. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Bakke, K. Aharonov-Bohm effect for bound states in relativistic scalar particle systems in a spacetime with a spacelike dislocation. Int. J. Mod. Phys. D 2018, 27, 1850005. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Bakke, K. On the interaction of the scalar field with a Coulomb-type potential in a spacetime with a screw dislocation and the Aharonov-Bohm effect for bound states. Eur. Phys. J. Plus 2018, 133, 490. [Google Scholar] [CrossRef]
- Carvalho, J.; Carvalho, A.M.M.; Cavalcante, E.; Furtado, C. Klein-Gordon oscillator in Kaluza-Klein theory. Eur. Phys. J. C 2016, 76, 365. [Google Scholar] [CrossRef]
- Vitória, R.L.L. Noninertial effects on a scalar field in a spacetime with a magnetic screw dislocation. Eur. Phys. J. C 2019, 79, 844. [Google Scholar] [CrossRef]
- Ahmed, F. Klein-Gordon Oscillator in the Presence of External Fields in a Cosmic Space-Time with a Space-Like Dislocation and Aharonov-Bohm Effect. Adv. High Energy Phys. 2020, 2020, 691025. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Bakke, K. Rotating effects on the scalar field in the cosmic string spacetime, in the spacetime with space-like dislocation and in the spacetime with a spiral dislocation. Eur. Phys. J. C 2018, 78, 175. [Google Scholar] [CrossRef]
- Maia, A.V.D.M.; Bakke, K. Topological and rotating effects on the Dirac field in the spiral dislocation spacetime. Eur. Phys. J. C 2019, 79, 551. [Google Scholar] [CrossRef]
- Bruce, S.; Minning, P. The Klein-Gordon oscillator. Nuovo Cimento A 1993, 106, 711. [Google Scholar] [CrossRef]
- Arfken, G.B.; Weber, H.J. Mathematical Methods for Physicists, 6th ed.; Elsevier Academic Press: New York, NY, USA, 2005. [Google Scholar]
- Bezerra, V.B. Gravitational Aharonov-Bohm effect in a locally flat spacetime. Class. Quantum Grav. 1991, 8, 1939. [Google Scholar] [CrossRef]
- Bezerra, V.B.; dos Santos, I.B. Topological effects due to a cosmic string. Eur. J. Phys. 1992, 13, 122. [Google Scholar] [CrossRef]
- Furtado, C.; Bezerra, V.B.; Moraes, F. Quantum scattering by a magnetic flux screw dislocation. Phys. Lett. A 2001, 289, 160. [Google Scholar] [CrossRef]
- Bakke, K.; Furtado, C. Persistent currents for a moving neutral particle with no permanent electric dipole moment. Eur. Phys. J. B 2014, 87, 222. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegum, I.A. Handbook of Mathematical Functions; Dover Publications Inc.: New York, NY, USA, 1965. [Google Scholar]
- Moshinsky, M.; Szczepaniak, A. The Dirac oscillator. J. Phys. A Math. Gen. 1989, 22, L817. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Belich, H. On the Dirac oscillator subject to a Coulomb-type central potential induced by the Lorentz symmetry violation. Eur. Phys. J. Plus 2020, 135, 247. [Google Scholar] [CrossRef]
- Rao, N.A.; Kagali, B.A. Energy profile of the one-dimensional Klein-Gordon oscillator. Phys. Scr. 2008, 77, 015003. [Google Scholar] [CrossRef]
- Mirza, B.; Narimani, R.; Zare, S. Relativistic oscillators in a noncommutative space and in a magnetic field. Commun. Theor. Phys. 2011, 55, 405. [Google Scholar]
- Hamil, B.; Merad, M. Dirac and Klein-Gordon oscillators on anti-de Sitter space. Eur. Phys. J. Plus 2018, 133, 174. [Google Scholar] [CrossRef]
- Khosropour, B. Statistical aspects of the Klein-Gordon oscillator in the frame work of GUP. Indian J. Phys. 2018, 92, 43. [Google Scholar] [CrossRef]
- Santos, L.C.N.; Mota, C.E.; Barros, C.C., Jr. Klein-Gordon Oscillator in a Topologically Nontrivial Space-Time. Adv. High Energy Phys. 2019, 2019, 2729352. [Google Scholar] [CrossRef]
- Bakke, K.; Furtado, C. On the Klein-Gordon oscillator subject to a Coulomb-type potential. Ann. Phys. 2015, 355, 48. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Bakke, K. Relativistic quantum effects of confining potentials on the Klein-Gordon oscillator. Eur. Phys. J. Plus 2016, 131, 36. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Furtado, C.; Bakke, K. On a relativistic particle and a relativistic position-dependent mass particle subject to the Klein–Gordon oscillator and the Coulomb potential. Ann. Phys. 2016, 370, 128. [Google Scholar] [CrossRef]
- Deng, L.-F.; Long, C.-Y.; Long, Z.-W.; Xu, T. Generalized Dirac Oscillator in Cosmic String Space-Time. Adv. High Energy Phys. 2018, 2018, 2741694. [Google Scholar] [CrossRef]
- Wang, Z.; Longa, Z.; Long, C.; Wu, M. Relativistic quantum dynamics of a spinless particle in the Som-Raychaudhuri spacetime. Eur. Phys. J. Plus 2015, 130, 36. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Belich, H.; Bakke, K. A relativistic quantum oscillator subject to a Coulomb-type potential induced by effects of the violation of the Lorentz symmetry. Eur. Phys. J. Plus 2017, 132, 25. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Belich, H. Effects of a linear central potential induced by the Lorentz symmetry violation on the Klein-Gordon oscillator. Eur. Phys. J. C 2018, 78, 999. [Google Scholar] [CrossRef]
- Bragança, E.A.F.; Vitória, R.L.L.; Belich, H.; Bezerra de Mello, E.R. Relativistic quantum oscillators in the global monopole spacetime. Eur. Phys. J. C 2020, 80, 206. [Google Scholar] [CrossRef]
- Boumali, A.; Messai, N. Klein-Gordon oscillator under a uniform magnetic field in cosmic string space-time. Can. J. Phys. 2014, 92, 1. [Google Scholar] [CrossRef]
- Bakke, K. Noninertial effects on the Dirac oscillator in a topological defect spacetime. Eur. Phys. J. Plus 2012, 127, 82. [Google Scholar] [CrossRef]
- Bakke, K. Rotating effects on the Dirac oscillator in the cosmic string spacetime. Gen. Relat. Gravit. 2013, 45, 1847. [Google Scholar] [CrossRef]
- Castro, L.B. Noninertial effects on the quantum dynamics of scalar bosons. Eur. Phys. J. C 2016, 76, 61. [Google Scholar] [CrossRef]
- Santos, L.C.N.; Barros, C.C., Jr. Relativistic quantum motion of spin-0 particles under the influence of noninertial effects in the cosmic string spacetime. Eur. Phys. J. C 2018, 78, 13. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Belich, H. Effects of a Landau-Type Quantization Induced by the Lorentz Symmetry Violation on a Dirac Field. Adv. High Energy Phys. 2020, 2020, 4208161. [Google Scholar] [CrossRef]
- Bakke, K. On the rotating effects and the Landau-Aharonov-Casher system subject to a hard-wall confining potential in the cosmic string spacetime. Int. J. Theor. Phys. 2015, 54, 2119. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Belich, H. Harmonic oscillator in an environment with a pointlike defect. Phys. Scr. 2019, 94, 125301. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Belich, H. On a massive scalar field subject to the relativistic Landau quantization in an environment of aether-like Lorentz symmetry violation. Eur. Phys. J. Plus 2020, 135, 123. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Belich, H. A Central Potential with a Massive Scalar Field in a Lorentz Symmetry Violation Environment. Adv. High Energy Phys. 2019, 2019, 1248393. [Google Scholar] [CrossRef]
- Medeiros, E.R.F.; Bezerra de Mello, E.R. Relativistic quantum dynamics of a charged particle in cosmic string spacetime in the presence of magnetic field and scalar potential. Eur. Phys. J. C 2012, 72, 2051. [Google Scholar]
- Mustafa, O. KG-particles in a cosmic string rainbow gravity spacetime in mixed magnetic fields. Eur. Phys. J. C 2024, 84, 362. [Google Scholar] [CrossRef]
- Song, X.-Q.; Wang, C.-W.; Jia, C.-S. Thermodynamic properties for the sodium dimer. Chem. Phys. Lett. 2017, 673, 50. [Google Scholar] [CrossRef]
- Hassanabadi, H.; Hosseinpour, M. Thermodynamic properties of neutral particle in the presence of topological defects in magnetic cosmic string background. Eur. Phys. J. C 2016, 76, 553. [Google Scholar] [CrossRef]
- Eshghi, M.; Mehraban, H. Study of a 2D charged particle confined by a magnetic and AB flux fields under the radial scalar power potential. Eur. Phys. J. Plus 2017, 132, 121. [Google Scholar] [CrossRef]
- Ikot, A.N.; Lutfuoglu, B.C.; Ngwueke, M.I.; Udoh, M.E.; Zare, S.; Hassanabadi, H. Klein-Gordon equation particles in exponential-type molecule potentials and their thermodynamic properties in D dimensions. Eur. Phys. J. Plus 2016, 131, 419. [Google Scholar] [CrossRef]
- Hassanabadi, H.; Sargolzaeipor, S.; Yazarloo, B.H. Thermodynamic properties of the three-dimensional Dirac oscillator with Aharonov–Bohm field and magnetic monopole potential. Few-Body Syst. 2015, 56, 115. [Google Scholar] [CrossRef]
- Castellano, G. Thermodynamic potentials for simple magnetic systems. J. Magn. Magn. Mater. 2003, 260, 146. [Google Scholar] [CrossRef]
- Vitória, R.L.L.; Moy, T.; Belich, H. Thermodynamics Properties of a Quantum Particle Confined into Two Elastic Concentric Spheres. Few-Body Syst. 2022, 63, 51. [Google Scholar] [CrossRef]
- Nwabuzor, P.; Edet, C.; Ndem Ikot, A.; Okorie, U.; Ramantswana, M.; Horchani, R.; Abdel-Aty, A.-H.; Rampho, G. Analyzing the Effects of Topological Defect (TD) on the Energy Spectra and Thermal Properties of LiH, TiC and I2 Diatomic Molecules. Entropy 2021, 23, 1060. [Google Scholar] [CrossRef] [PubMed]
- Hassanabadi, H.; Hosseini, S.S.; Boumali, A.; Zarrinkamar, S. The statistical properties of Klein-Gordon oscillator in noncommutative space. J. Math. Phys. 2014, 55, 033502. [Google Scholar] [CrossRef]
- Hassanabadi, S.; říž, J.; Chung, W.S.; Lütfüoğlu, B.C.; Maghsoodi, E.; Hassanabadi, H. Thermodynamics of the Schwarzschild and Reissner-Nordström black holes under higher-order generalized uncertainty principle. Eur. Phys. J. Plus 2021, 136, 918. [Google Scholar] [CrossRef]
- Zhang, M.-Y.; Chen, H.; Hassanabadi, H.; Long, Z.-W.; Yang, H. Thermodynamic topology of Kerr-Sen black holes via Rényi statistics. Phys. Lett. B 2024, 856, 138885. [Google Scholar] [CrossRef]
- Martín-Martínez, E.; Smith, A.R.H.; Terno, D.R. Spacetime structure and vacuum entanglement. Phys. Rev. D 2016, 93, 044001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vitória, R.L.L. Relativistic Scalar Particle Systems in a Spacetime with a Spiral-like Dislocation. Axioms 2025, 14, 227. https://doi.org/10.3390/axioms14030227
Vitória RLL. Relativistic Scalar Particle Systems in a Spacetime with a Spiral-like Dislocation. Axioms. 2025; 14(3):227. https://doi.org/10.3390/axioms14030227
Chicago/Turabian StyleVitória, Ricardo L. L. 2025. "Relativistic Scalar Particle Systems in a Spacetime with a Spiral-like Dislocation" Axioms 14, no. 3: 227. https://doi.org/10.3390/axioms14030227
APA StyleVitória, R. L. L. (2025). Relativistic Scalar Particle Systems in a Spacetime with a Spiral-like Dislocation. Axioms, 14(3), 227. https://doi.org/10.3390/axioms14030227






