Abstract
We introduce a framework presenting the interaction between a four-level atom (F-LA) and a field mode that begins in a coherent state within the para-Bose field (P-BF). The F-LA is considered in a cascade configuration and initially prepared in the upper level. We display the system dynamics by solving the motion equation. We discuss various dynamical behaviors of fundamental quantum resources used in quantum optics and information tasks, including atomic population inversion, quantum entanglement (QE), and the statistical properties of the P-BF based on the parameters of the quantum model. In this context, we demonstrate the impact of various system parameters on these quantum resources. Finally, we illustrate the dynamic relationships among the quantum resources within the model.
MSC:
20-xx; 81-xx
1. Introduction
In recent decades, numerous studies have explored extensions and modifications of the bosonic Fock–Heisenberg algebra to enhance various aspects of quantum field theory. Researchers have introduced different q-deformations of the simple harmonic oscillator using Jackson’s q-calculus [1,2,3,4], leading to novel states associated with q-deformed Lie algebras, including q-coherent states, q-cat states, and q-squeezed states [4,5,6,7,8,9,10,11,12]. Another significant adaptation is the Wigner algebra, which integrates the reflection operator and the Wigner parameter into its structure. This formulation emerges within bosonic relationships and dynamics, yielding infinite-dimensional para-boson representations as well as finite-dimensional representations linked to parafermions [13]. These generalizations naturally lead to concepts involving para fields and para statistics [14,15].
The Jaynes–Cummings model (JCM) is widely utilized in quantum optics to depict the coupling between a two-level quantum system, such as an atom, and a single quantized mode of an electromagnetic field, adhering to the conditions of the rotating wave approximation [16]. This model has been expanded to encompass multi-photon transitions and various forms of fields, alongside an intensity-dependent coupling between the atom and the quantum field [17,18]. Extensions of the standard JCM have also explored additional levels, including three-level atomic systems [19,20,21,22,23]. In this context, many studies have examined the effects of the Kerr medium [24] and intensity-dependent coupling on the dynamics of three-level atomic systems. Furthermore, the interaction of two three-level atomic systems with a single-mode field, incorporating multi-photon transitions, has been examined in the presence of a Kerr nonlinear medium and detuning effects [25]. Recently, there has been growing interest in the quantum interaction between four-level atoms and cavity fields, with various configurations being explored [26,27].
Quantum entanglement is a fundamental feature of quantum theory, representing nonlocal correlations among composite quantum systems, where classical descriptions of correlations between subsystems are inadequate. It has been extensively studied in quantum information science [28,29,30,31,32] and is crucial for various applications, including quantum communication, teleportation, quantum entanglement swapping, cryptography, quantum computing, and dense coding [33,34,35,36,37,38,39]. The amount of entanglement can be quantified using measures such as von Neumann entropy, concurrence, linear entropy, and entanglement of formation [40,41]. Several methods have been proposed to quantify and identify quantum coherence within quantum systems [42]. Numerous studies have been undertaken to characterize and analyze quantum coherence, gaining significant attention through development and application of coherence quantification measures [43,44,45].
Beyond the specific domain of quantum optics, the mathematical methodologies and physical principles examined in this study have broader implications across multiple fields of physics. The deformed quantum algebras explored here, particularly para-Bose structures, have been extensively utilized in quantum gravity, where they play a crucial role in models of noncommutative space-time and extensions of the Heisenberg algebra [46,47,48,49]. Likewise, in condensed matter physics, these algebraic deformations have been instrumental in characterizing unconventional quantum phases, including topological insulators, superconductors, and quantum Hall systems, wherein fractional statistics arise as a consequence of strong electron correlations [50,51,52,53]. Specifically, para-statistics and deformed oscillator algebras provide a robust theoretical framework for investigating anionic excitations, which are fundamental to the description of fractional quantum Hall states and spin-liquid phases [54,55,56]. Furthermore, these mathematical structures contribute significantly to the theoretical modeling of correlated electron systems and quantum materials exhibiting nontrivial topological properties, where symmetry-protected quantum orders emerge [57,58,59]. In addition, the quantum resources analyzed in this work, such as entanglement and coherence, hold central importance in quantum information science, quantum computing, and quantum metrology. These properties are essential for advancing quantum cryptographic protocols, enhancing precision measurement techniques, and enabling the development of scalable quantum architectures [38,60,61,62,63]. By highlighting these interrelations, this study establishes a framework that extends beyond quantum optics and contributes to the broader landscape of modern physics. Moreover, our approach is closely aligned with recent experimental advances in superconducting qubit systems, engineered quantum states, and cavity quantum electrodynamics, further demonstrating the practical relevance of our findings beyond purely theoretical considerations [64,65,66].
Our manuscript focuses on examining the degree of entanglement, atomic coherence, and atomic inversion in a bipartite system where a four-level atom is coupled with a para-Bose field. We investigate how field deformation and photon transitions impact the dynamic behavior of quantifiers, particularly when the quantum field originates from a coherent state of the P-BF. The time evolution of entanglement between the four-level atom and para-Bose field is analyzed using quantum entropy, while atomic coherence is evaluated through the norm.
2. Mathematical Model and Dynamics
This section describing the Hamiltonian of the interaction between one-mode P-BF with an F-LA has a state upper to lower as
where represents the coupling constant between the F-LA and PB-field, denotes the number of photons exchanged in transitions between (F-LA) and (P-BF), and is the creation (annihilation) operator of the quantized field, respectively, acting on the Fock states as
Here, the is a positive function and is equal to , and is the P-BF deformed parameter.
The para-Bose field (P-BF) holds significance as it extends traditional bosonic field theory by introducing parastatistics, modifying the conventional commutation relations of annihilation and creation operators. These operators adhere to a parity-deformed oscillator algebra, where { and , with resulting in a more generalized Fock space representation. The operator R, known as the parity operator, is a Hermitian operator satisfying , meaning it has eigenvalues , which classify states into even and odd parity components. This extension enables the study of systems where particles exhibit characteristics that differ from purely bosonic or fermionic behavior, making it a fundamental concept in quantum optics and quantum field theory [67]. The coherent states in the P-BF are characterized as the eigenstates associated with the field’s annihilation operator. These states form an overcomplete and nonorthogonal basis, fulfilling the resolution of identity, akin to Glauber coherent states but with alterations due to parastatistical effects [67]. They exhibit notable quantum properties, such as photon antibunching, where the second-order intensity correlation function demonstrates a decreased probability of detecting two photons simultaneously. Additionally, they follow sub-Poissonian statistics, indicated by a negative Mandel parameter, signifying reduced photon number fluctuations compared to classical light sources [67]. Furthermore, these states show quadrature squeezing, where field quadratures x and p experience noise redistribution, confirming the presence of nonclassical effects [8]. Within the framework of JCM, extended to a single-mode P-BF, these states influence atomic inversion, modify Rabi oscillations, and enhance entanglement.
The final state of the (F-LA)–(P-BF) system at any time , where represents the scaled time, can be expressed as:
The amplitude can be obtained by solving the equation of motion of this system:
At the F-LA in the upper state and the field in the coherent state of the P-BF . So, the initial state is assumed to be
where are provided as [41]
Here, are the associated Laguerre polynomials.
The coefficients representing the probability amplitudes, are determined by solving the time-dependent Schrödinger Equation (4) with the initial condition . Consequently, these coefficients fulfill the following set of coupled differential equations:
In this paper, we focus on the effects of single- and double-photon transitions, corresponding to , respectively. We analyze the time-dependent features of various quantum quantifiers related to the quantum system under investigation using the wave function |ψ(τ)⟩ (see Appendix A).
The atomic population inversion, quantum entropy, and coherence are all linked to the components of the atomic density matrix , which is given by
The P-BF density matrix can be obtained as .
3. Quantum Quantifiers
To investigate the effect of the P-BF deformed parameter and single- and double-photon transition on the dynamics of quantum quantifiers, in Figure 1, Figure 2, Figure 3 and Figure 4 illustrate the time-dependent behavior of the atomic inversion, second-order correlation function (S-OCF), atomic entropy, and atomic coherence.
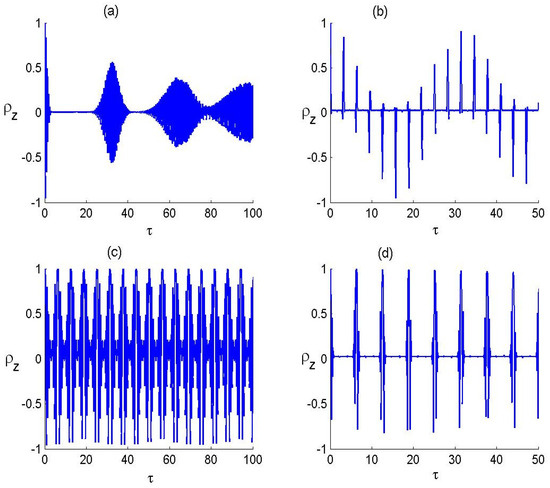
Figure 1.
Dynamics of the atomic inversion of F-LA with and for the parameter values of P-BF deformed parameter and number of photons transitioned as (a) , (b) , (c) and (d) .
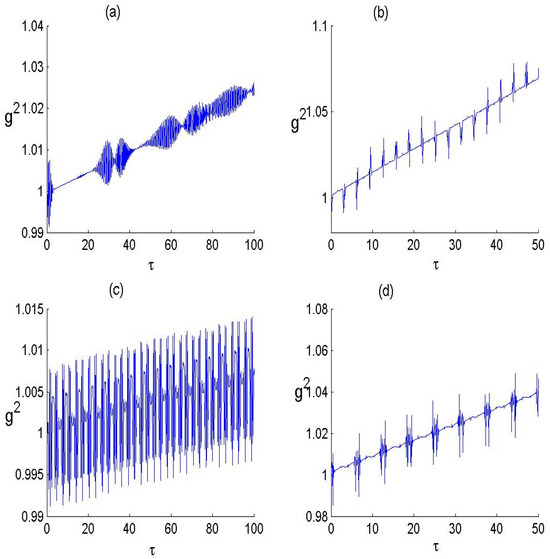
Figure 2.
Dynamics of the S-OCF with and for the parameter values of P-BF deformed parameter and number of photons transitioned as (a) , (b) , (c) and (d) .
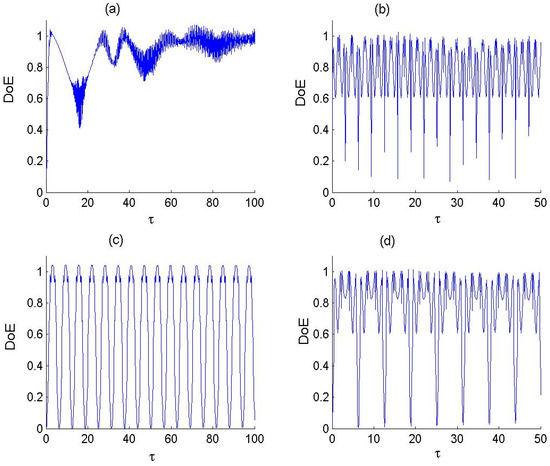
Figure 3.
Dynamics of the as a measure of QE between F-LA and P-BF with and for the parameter values of P-BF deformed parameter and number of photons transitioned as (a) , (b) , (c) and (d) .
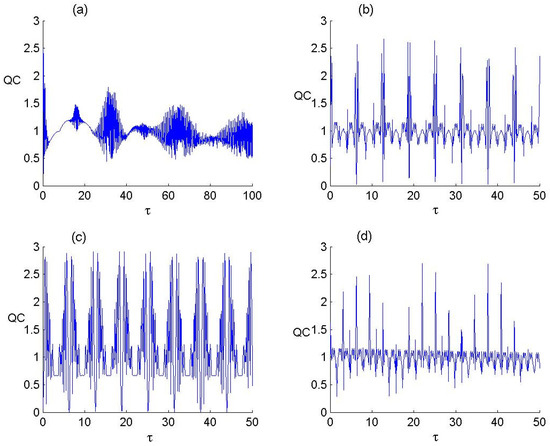
Figure 4.
Dynamics of the quantum coherence of F-LA with and for the parameter values of P-BF deformed parameter and number of photons transitioned as (a) , (b) , (c) and (d) .
3.1. Population Inversion Corresponding to the F-LA
Population inversion is one of the most significant quantities when considering quantum information. It can be applied to determine the collapse and revival times, which are crucial for characterizing the maximally entangled and separable state periods. We define the atomic population inversion through the diagonal elements of the atomic density matrix as
3.2. Nonclassical Effects
The S-OCF is widely employed to investigate the statistical characteristics of the field, as well as to assess photon bunching or antibunching phenomena. It is defined as:
We say that the quantized field is governed by super-Poissonian statistics if , Poissonian statistics if , and sub-Poissonian statistics if . The sub-Poissonian distribution of photons illustrates the quantum nature of the field.
3.3. Quantum Entanglement
The subsystem entropy, defined by the von Neumann entropy, can be used to determine the degree of entanglement (DoE) evolution of the (F-LA)–(P-BF) state. It is given by
where represents the F-LA density operator, as given by Equation (8). Based on refs. [40,41], the function takes the following form:
where is the jth eigenvalue of the state
3.4. Quantum Coherence
The diagonal components of the system’s density operator delineate the essential properties of coherence. The quantum coherence is determined by considering the absolute value of the non-diagonal elements and applying the norm. The coherence measure is the distance between the state in question and the nearest incoherent state from the point of view of the concept of entropy. To detect the amount of coherence, we consider the norm of coherence. This measure depends on off-diagonal elements for the density operator and it is defined by the formula [42]:
4. Numerical Results and Discussion
Figure 1 illustrates the dynamics of atomic population inversion in the F-LA system interacting with the P-BF under conditions of zero and non-zero deformation parameters, considering both single- and double-photon transitions. For a zero-deformation parameter, panels (a) and (b) depict the time evolution of atomic population for single- and double-photon excitations, respectively. In the single-photon excitation case, we observe distinct features of collapses and revivals in atomic population inversion. Initially, the collapses are well defined within the scaled time, but they become less distinct over time, with the revival amplitude gradually diminishing. In the double-photon excitation scenario, the atomic population exhibits brief revivals interspersed with adjacent collapses. These revivals are asymmetric around the zero-population inversion line, with fluctuations between positive and negative values of +1 and −1. The revival duration is notably shorter compared to the single-photon case. Panels (c) and (d) present the dynamics for a non-zero deformation parameter, set at 20 scaled units, for single- and double-photon transitions. In the single-photon case, we observe revivals in atomic population with very brief collapses, and the revival amplitude spans the entire range of population values. For the double-photon transition with a non-zero deformation parameter, the dynamics show collapses and revivals similar to the single-photon case, but with an increased collapse duration and a slightly reduced oscillation amplitude. Comparing the effects of varying photon transition numbers and deformation parameters, it is evident that these factors significantly influence the population inversion dynamics. For , increasing J from 1 to 2 leads to more frequent revivals and a reduction in their width. Conversely, for , increasing J does not increase the number of revivals but shortens the revival span. The collapse and revival phenomena observed in atom-field interactions indicate coherent quantum evolution, where revivals stem from constructive interference among atomic state amplitudes, while collapse periods reflect decoherence effects caused by transitions between energy levels. These results are consistent with previous research on Jaynes–Cummings models and intensity-dependent atom-field interactions, where nonlinearity and deformation significantly influence atomic transition dynamics. In particular, studies on q-deformed oscillators and para-Bose models reveal that deformation alters energy spectra and transition rates, leading to extended coherence times and modified revival patterns. The alignment of these findings with theoretical predictions in nonlinear optics and quantum field theories suggests that para-Bose field deformation serves as a controllable parameter for regulating atomic inversion dynamics.
Figure 2 shows the evolution of S-OCF for the F-LA system under conditions of zero and non-zero deformation parameters q, considering both single- and double-photon transitions respectively. For , we can observe that indicating sub-Poissonian statistics. As the time increases, the function becomes larger than , indicating super-Poissonian statistics. For , we can observe that the function exhibits an oscillatory behavior with values greater and smaller than one, indicating super- and sub-Poissonian statistics. In the case of we have at the beginning of interaction and as the time increases. The shift from sub- to super-Poissonian statistics suggests that interaction time significantly influences photon distribution. Studies on q-deformed oscillators and para-Bose fields demonstrate that deformation alters photon statistics by introducing nonlinear effects, leading to oscillatory behavior in for . Similar patterns have been observed in nonlinear quantum optics, such as Kerr media, where nonlinearity modulates photon distribution, indicating that para-Bose deformation introduces an additional degree of complexity to photon dynamics. The tunability of photon statistics enables the design of nonclassical light sources. Para-Bose deformation provides a useful method for controlling photon statistics, contributing to advancements in quantum optics applications.
Figure 3 displays the quantum entanglement (QE), as measured by the von Neumann entropy, for the F-LA–P-BF state under varying field deformation and photon transition numbers. For q = 0, panels (a) and (b) depict the dynamics for single-photon (J = 1) and double-photon (J = 2) transitions, respectively. In the single-photon case, rapid oscillations are observed in the entanglement measure, with the amplitude fluctuating around a steady-state value before eventually stabilizing. In contrast, for the double-photon transition (J = 2), the entanglement exhibits quasi-periodic behavior. Unlike the single-photon case, the entanglement measure does not settle into a steady state. Panels (c) and (d) show the time-dependent behavior of entanglement for a non-zero field deformation parameter q for both single- and double-photon transitions, respectively. For J = 1, the function exhibits consistent periodic behavior with a constant amplitude of oscillations throughout the dynamics. In the double-photon transition case (J = 2), the QE dynamics also display periodicity, but the amplitude of oscillations varies over time, introducing an additional layer of complexity to the system’s behavior. Thus, the consideration of field deformation and double-photon transitions enhances the periodic nature of the entanglement measure during the evolution. These observations align with established studies in quantum optics, particularly the JCM, where single-photon transitions typically lead to periodic entanglement oscillations, while multi-photon transitions introduce interactions that increase quantum correlations. The quasi-periodic behavior in the J = 2 case suggests an enhanced interaction mechanism, as multi-photon absorption–emission processes can induce more complex quantum correlations. Studies on q-deformed oscillators and para-Bose fields have shown that deformation modifies energy levels and transition dynamics, which explains the stable periodic behavior in the J = 1 case and the varying oscillation amplitude in the J = 2 case. Additionally, entanglement dynamics in nonlinear quantum optics, such as Kerr-type media, exhibit similar periodic structures, indicating that para-Bose deformation effectively introduces an adjustable nonlinearity that influences quantum correlations. The ability to control entanglement oscillations through deformation and photon transition tuning presents promising applications in different tasks in quantum information and optics.
Figure 4 displays the dynamics of QC for the F-LA system for both zero and non-zero deformation parameters q of the P-BF, considering single- and double-photon transitions. For the zero-deformation parameter case, the dynamics of QC for single- and double-photon transitions are shown in panels (a) and (b), respectively. In the single-photon case, the QC dynamics exhibit collapses and revivals, with the collapse line fluctuating around a value of 1. In contrast, for the double-photon transition (J = 2), periodic behavior is observed in the QC dynamics, characterized by increased amplitude fluctuations and a shorter revival width compared to the single-photon case. Notably, no collapses are present in this scenario. For the non-zero deformation parameter case, the QC dynamics for single-photon transitions show periodic behavior with an increased amplitude of oscillations compared to the zero-deformation case. In the double-photon transition case (J = 2), oscillations are observed in the QC dynamics, but the amplitude of these oscillations varies over time, indicating more complex dynamic behavior. In summary, the introduction of non-zero deformation parameters enhances the periodic nature of quantum coherence, with single-photon transitions leading to more pronounced oscillations, while double-photon transitions result in oscillations with varying amplitude.
5. Conclusions
In this study, we have explored the dynamics of atomic population inversion, S-OCF, degree of entanglement, and quantum coherence in the F-LA system interacting with the P-BF under both zero and non-zero deformation parameters. For zero deformation parameter values, the system exhibits characteristic collapses and revivals in atomic population inversion during single-photon transitions, while double-photon transitions lead to brief, asymmetric revivals. The S-OCF similarly shows collapses and revivals, with an increasing slope of the collapse line that remains constant across both single- and double-photon transitions. The entanglement dynamics under single-photon transitions oscillate rapidly, stabilizing around a steady state, whereas double-photon transitions induce periodicity without reaching a steady state. Quantum coherence dynamics for single-photon excitations display collapses and revivals, with a collapse line that fluctuates around a steady value. The introduction of non-zero deformation parameters adds additional complexity to the system. For atomic population inversion, the period of oscillation remains the same as in the single-photon transition case, but with an extended collapse duration. The S-OCF and quantum coherence exhibit periodic behaviors, with increased amplitude and variable oscillations, particularly in double-photon transitions. The entanglement dynamics also show enhanced periodicity under non-zero deformation, highlighting the effects of deformation parameter and photon transition numbers on the overall system behavior. Overall, this work highlights the significant impact of field deformation and photon transition numbers on the quantum dynamics of the F-LA system. It provides valuable insights into how these parameters can be effectively controlled to extract and optimize quantum resources from the system. Regarding the experimental feasibility of our findings, we highlight that our model, which considers the interaction between a four-level atom and a deformed para-Bose field, can be realized using trapped atoms or ions in cavity quantum electrodynamics setups, where four-level atomic structures naturally arise in alkali or alkaline-earth atoms through well-defined energy level configurations. Another promising platform is cold atoms in optical lattices, where multi-level atomic transitions can be engineered via laser coupling.
Author Contributions
M.A.: investigation (equal); methodology (equal); software (equal); writing—original draft (equal). S.A.-K.: investigation (equal); methodology (equal); writing—review and editing (equal). K.B.: investigation (equal); resources (equal); writing—original draft (equal). All authors have read and agreed to the published version of the manuscript.
Funding
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R225), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R225), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Detailed Calculation
The evolution of the quantum state of the system is governed by the time-dependent Schrödinger equation:
where represents the interaction Hamiltonian describing the coupling between the four-level atom and the para-Bose field. The objective is to express this equation in terms of a set of differential equations governing the probability amplitudes associated with the atomic and field states.
Given that the system comprises an atom possessing four distinct energy levels coupled to a quantized field mode, the wavefunction is articulated as a superposition of the atomic states and the field’s Fock states:
where represents the probability amplitude for the atom being in state with photons in the field. Substituting this expansion into the Schrödinger equation and differentiating,
Multiplying both sides by and utilizing the orthonormality of the basis states, we obtain
This equation provides a framework for obtaining the system of differential equations once we determine the Hamiltonian matrix elements. The interaction Hamiltonian for the quantum system is expressed as:
The operators and and govern the transitions between atomic levels, leading to the coupling terms in the equations of motion. Using the matrix elements obtained from the Hamiltonian action on the basis states, we obtain at the final system of coupled differential equations. The probability amplitudes evolve according to:
This system provides a full description of the time evolution of the probability amplitudes, incorporating the effects of multi-photon transitions and field deformation.
To determine the probability amplitudes , we solve the system of coupled differential equations. This system can be expressed in matrix form as
where is the column vector of probability amplitudes and is the coupling matrix. Since the matrix is time-independent, the formal solution can be obtained using matrix exponentiation:
If is diagonalizable, we write it as , leading to the solution:
where is the matrix whose columns are the eigenvectors of , and is a diagonal matrix with elements , where are the eigenvalues of . Alternatively, numerical-method techniques can be used. Once the amplitudes are determined, they allow analysis of quantum properties such as atomic population inversion, quantum coherence, and entanglement.
References
- Arik, M.; Coon, D.D. Hilbert spaces of analytic functions and generalized coherent states. J. Math. Phys. 1976, 17, 524. [Google Scholar] [CrossRef]
- Biedenharn, L.C. The quantum group SUq (2) and a q-analogue of the boson operators. J. Phys. A Math. Gen. 1989, 22, L873. [Google Scholar] [CrossRef]
- Macfarlane, A.J. On q-analogues of the quantum Harmonic oscillator and the quantum group SU (2). J. Phys. A Math. Gen. 1989, 22, 4581. [Google Scholar] [CrossRef]
- Fakhri, H.; Nouraddini, M. Right SUq (2)- and left SUq−1 (2)-invariances of the q-Hilbert–Schmidt scalar products for an adjoint representation of the quantum algebra Ŭq (su2). J. Geom. Phys. 2016, 110, 90. [Google Scholar] [CrossRef]
- Fakhri, H.; Hashemi, A. Nonclassical properties of the q-coherent and q-cat states of the Biedenharn–Macfarlane q oscillator with q > 1. Phys. Rev. A 2016, 93, 013802. [Google Scholar] [CrossRef]
- Fakhri, H.; Sayyah-Fard, M. Arik-Coon q-oscillator cat states on the noncommutative complex plane and their nonclassical properties. Int. J. Geom. Meth. Mod. Phys. 2017, 14, 1750060. [Google Scholar] [CrossRef]
- Fakhri, H.; Sayyah-Fard, M. Nonclassical properties of the Arik-Coon q−1-oscillator coherent states on the noncommutative complex plane Cq. Int. J. Geom. Meth. Mod. Phys. 2017, 14, 1750165. [Google Scholar] [CrossRef]
- Fakhri, H.; Sayyah-Fard, M. q-coherent states associated with the noncommutative complex plane C q2 for the Biedenharn–Mac-farlane q-oscillator. Ann. Phys. 2017, 387, 14. [Google Scholar] [CrossRef]
- Fakhri, H.; Sayyah-Fard, M. Triplet q-cat states of the Biedenharn–Macfarlane q-oscillator with q > 1. Quantum Inf. Process. 2020, 19, 19. [Google Scholar] [CrossRef]
- Fakhri, H.; Mousavi-Gharalari, S.E. Nonclassical properties of two families of q-coherent states in the Fock representation space of q-oscillator algebra. Eur. Phys. J. Plus 2020, 135, 253. [Google Scholar] [CrossRef]
- Fakhri, H.; Sayyah-Fard, M. Noncommutative photon-added squeezed vacuum states. Mod. Phys. Let. A 2020, 35, 2050167. [Google Scholar] [CrossRef]
- Sayyah-Fard, M. Nonclassicality of photon-added q-squeezed first excited states. Phys. A 2021, 567, 125636. [Google Scholar] [CrossRef]
- Plyushchay, M.S. Deformed Heisenberg algebra with reflection. Nucl. Phys. B 1997, 491, 619. [Google Scholar] [CrossRef]
- Wigner, E.P. Do the equations of motion determine the quantum mechanical commutation relations? Phys. Rev. 1950, 77, 711. [Google Scholar] [CrossRef]
- Green, H.S. A generalized method of field quantization. Phys. Rev. 1953, 90, 270. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Abdel-Aty, M. General formalism of interaction of a two-level atom with cavity field in arbitrary forms of nonlinearities. Phys. A 2002, 313, 471. [Google Scholar] [CrossRef]
- Baghshahi, H.R.; Tavassoly, M.K. Entanglement, quantum statistics and squeezing of two Ξ-type three-level atoms interacting nonlinearly with a single-mode field. Phys. Scr. 2014, 89, 075101. [Google Scholar] [CrossRef]
- Feneuile, S. Interaction of laser radiation with free atoms. Rep. Prog. Phys. 1977, 40, 1257. [Google Scholar] [CrossRef]
- Li, X.-S.; Lin, D.L.; Gong, C.D. Nonresonant interaction of a three-level atom with cavity fields. I. General formalism and level occupation probabilities. Phys. Rev. A 1987, 36, 5209. [Google Scholar] [CrossRef]
- Liu, Z.-D.; Li, X.-S.; Lin, D.L. Nonresonant interaction of a three-level atom with cavity fields. II. Coherent properties of the stimulated fields. Phys. Rev. A 1987, 36, 5220. [Google Scholar] [CrossRef]
- Abdel-Wahab, N.H. The general formalism for a three-level atom interacting with a two-mode cavity field. Phys. Scr. 2007, 76, 233. [Google Scholar] [CrossRef]
- Abdel-Wahab, N.H. A three-level atom interacting with a single mode cavity field: Different configurations. Phys. Scr. 2007, 76, 244. [Google Scholar] [CrossRef]
- Yurke, B.; Stoler, D. One-step synthesis of multiatom Greenberger-Horne-Zeilinger states. Phys. Rev. Lett. 1993, 57, 13. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Goorskey, D.; Xiao, M. Dependence of enhanced Kerr nonlinearity on coupling power in a three-level atomic system. Opt. Lett. 2002, 27, 258–260. [Google Scholar] [CrossRef]
- Baghshahi, H.R.; Tavassoly, M.K. Dynamics of different entanglement measures of two three-level atoms interacting nonlinearly with a single-mode field. Eur. Phys. J. Plus 2015, 130, 37. [Google Scholar] [CrossRef]
- Liu, Z.D.; Zhu, S.-Y.; Li, X.-S. The properties of a light field interacting with a four-level atom. J. Mod. Opt. 1988, 45, 833. [Google Scholar] [CrossRef]
- Vaglica, A.; Vetri, G. Irreversible decay of nonlocal entanglement via a reservoir of a single degree of freedom. Phys. Rev. A 2007, 75, 062120. [Google Scholar] [CrossRef]
- Ficek, Z.; Tanas, R. Dark periods and revivals of entanglement in a two-qubit system. Phys. Rev. A 2006, 74, 024304. [Google Scholar] [CrossRef]
- Vitali, D.; Gigan, S.; Ferreira, A.; Böhm, H.R.; Tombesi, P.; Guerreiro, A.; Vedral, V.; Zeilinger, A.; Aspelmeyer, M. Optomechanical entanglement between a movable mirror and a cavity field. Phys. Rev. Lett. 2007, 98, 030405. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, E.Y. Optimum parameters for biased two-state quantum key distribution protocol. Acta Phys. Sin. 2002, 51, 1684. [Google Scholar]
- Moller, C. Dissipative Rabi model in the dispersive regime. Phys. Rev. Res. 2020, 2, 033046. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Metwally, N.; Abdelaty, M.; Obada, A.-S.F. Quantum teleportation via entangled states generated by the Jaynes–Cummings model. Chaos Solitons Fractals 2004, 22, 529. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef]
- Bennett, C.H.; Wiesner, S.J. Communication via one-and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 1992, 69, 2881. [Google Scholar] [CrossRef]
- Yang, M.; Song, W.; Cao, Z.L. Entanglement swapping without joint measurement. Phys. Rev. A 2005, 71, 034312. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bennett, C.H.; Shor, P.W.; Smolin, J.A.; Thapliyal, A.V. Entanglement-assisted classical capacity of noisy quantum channels. Phys. Rev. Lett. 1999, 83, 3081. [Google Scholar] [CrossRef]
- Phoenix, S.J.D.; Knight, P.L. Establishment of an entangled atom-field state in the Jaynes-Cummings model. Phys. Rev. A 1991, 44, 6023. [Google Scholar] [CrossRef]
- Phoenix, S.J.D.; Knight, P. Comment on “Collapse and revival of the state vector in the Jaynes-Cummings model: An example of state preparation by a quantum apparatus”. Phys. Rev. Lett. 1991, 66, 2833. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef]
- Berrada, K.; Algarni, M.; Marin, M.; Abdel-Khalek, S. Effects of Dipole-Dipole Interaction and Time-Dependent Coupling on the Evolution of Entanglement and Quantum Coherence for Superconducting Qubits in a Nonlinear Field System. Symmetry 2023, 15, 732. [Google Scholar] [CrossRef]
- Algarni, M.; Berrada, K.; Abdel-Khalek, S. Quantum coherence and parameter estimation for mixed entangled coherent states. Mod. Phys. Lett. A 2022, 37, 2250159. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Algarni, M.; Marin, M.; Berrada, K. Entanglement, quantum coherence and quantum Fisher information of two qubit-field systems in the framework of photon-excited coherent states. Opt. Quant. Elect. 2023, 55, 1288. [Google Scholar] [CrossRef]
- Majid, S. Foundations of Quantum Group Theory; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Madore, J. Noncommutative Geometry for Pedestrians. Phys. Rep. 1997, 282, 1. [Google Scholar]
- Snyder, H.S. Quantized Space-Time. Phys. Rev. 1947, 71, 38. [Google Scholar] [CrossRef]
- Freidel, L.; Livine, E.R. Ponzano-Regge model revisited III: Feynman diagrams and effective field theory. Class. Quantum Grav. 2006, 23, 2021. [Google Scholar] [CrossRef]
- Wen, X.-G. Quantum Field Theory of Many-Body Systems; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083. [Google Scholar] [CrossRef]
- Das Sarma, S.; Freedman, M.; Nayak, C. Topologically protected qubits from a possible non-Abelian fractional quantum Hall state. Phys. Rev. Lett. 2005, 94, 166802. [Google Scholar] [CrossRef]
- Read, N.; Rezayi, E. Beyond paired quantum Hall states: Parafermions and incompressible states in the first excited Landau level. Phys. Rev. B 1999, 59, 8084. [Google Scholar] [CrossRef]
- Moore, G.; Read, N. Nonabelions in the fractional quantum Hall effect. Nucl. Phys. B 1991, 360, 362. [Google Scholar] [CrossRef]
- Kitaev, A. Fault-tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2. [Google Scholar] [CrossRef]
- Wen, X.-G. Topological orders and edge excitations in fractional quantum Hall states. Adv. Phys. 1995, 44, 405. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 2006, 314, 1757. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Kitaev, A. Periodic table for topological insulators and superconductors. AIP Conf. Proc. 2009, 1134, 22. [Google Scholar]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560 Pt 1, 7–11. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Caves, C.M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 1994, 72, 3439. [Google Scholar] [CrossRef]
- Dowling, J.P.; Milburn, G.J. Quantum technology: The second quantum revolution. Phil. Trans. R. Soc. A 2003, 361, 1655. [Google Scholar] [CrossRef]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023. [Google Scholar] [CrossRef]
- Clarke, J.; Wilhelm, F.K. Superconducting quantum bits. Nature 2008, 453, 1031. [Google Scholar] [CrossRef] [PubMed]
- Barends, R.; Kelly, J.; Megrant, A.; Veitia, A.; Sank, D.; Jeffrey, E.; White, T.C.; Mutus, J.; Fowler, A.G.; Campbell, B.; et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 2014, 508, 500. [Google Scholar] [CrossRef] [PubMed]
- Haroche, S.; Raimond, J.-M. Exploring the Quantum: Atoms, Cavities, and Photons; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Fakhri, H.; Sayyah-Fard, M. The Jaynes–Cummings model of a two-level atom in a single-mode para-Bose cavity field. Sci. Rep. 2021, 11, 22861. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).