Hammerstein Nonlinear Integral Equations and Iterative Methods for the Computation of Common Fixed Points
Abstract
1. Introduction
- is continuous in y for almost all x, and measurable in x for any fixed y,
- is nondecreasing for any fixed x,
- for any fixed y, and
- the linear integral operator associated with is bounded from into and positive,
2. Solution of a Type of Nonlinear Hammerstein Integral Equation
3. A Modified Algorithm for the Search of Common Fixed Points of Nearly Asymptotically Nonexpansive Mappings
- 1.
- the map N defined as is asymptotically regular, and,
- 2.
- if additionally is uniformly continuous, the sequence has the AF property with respect to .
4. An Iterative Method for the Search of Common Fixed Points of a Finite Number of Quasi-Nonexpansive Operators
- 1.
- The sequence has the CLE property for any
- 2.
- The sequence has the AF property with respect to for any
Strong Convergence of the m-Steps Common N-Iteration
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hammerstein, A. Nichtlineare integralgleichungen nebst anwendungen. Acta Math. 1930, 54, 117–176. [Google Scholar] [CrossRef]
- Brézis, H.; Browder, F.E. Nonlinear integral equations and systems of Hammerstein type. Adv. Math. 1975, 18, 115–147. [Google Scholar] [CrossRef]
- Baker, C.T.H. The Numerical Treatment of Integral Equations; Clarendon Press: Oxford, UK, 1977. [Google Scholar]
- Kumar, S.; Sloan, I.H. A new collocation type method for Hammerstein equations. Math. Comp. 1987, 48, 585–593. [Google Scholar] [CrossRef]
- Banaś, J.; Madej, J. Asymptotically stable solutions of infinite systems of quadratic Hammerstein integral equations. Symmetry 2024, 16, 107. [Google Scholar] [CrossRef]
- Micula, S. Iterative numerical methods for a Fredholm–Hammerstein integral equation with modified argument. Symmetry 2023, 15, 66. [Google Scholar] [CrossRef]
- Navascués, M.A. Approximation sequences for fixed points of non contractive operators. J. Nonl. Funct. Anal. 2024, 20, 1–13. [Google Scholar]
- Sahu, D.R. Fixed points of demicontinuous nearly Lipschitzian mappings in Banach spaces. Comment. Math. Univ. Carolin. 2005, 46, 652–666. [Google Scholar]
- Navascués, M.A. An iterative method for the approximation of common fixed points of two mappings: Application to fractal functions. Fractal Fract. 2024, 8, 745. [Google Scholar] [CrossRef]
- Hutson, V.; Pym, J.S. Applications of Functional Analysis and Operator Theory; Mathematics in Science and Engineering; Academic Press: Cambridge, MA, USA, 1980; Volume 146. [Google Scholar]
- Krasnoselskii, M.A. Two remarks on the method of successive approximations. (Russian) Uspehi Mat. Nauk. 1955, 10-1, 123–127. [Google Scholar]
- Mann, W.R. Mean value methods in iteration. Proc. Am. Math. Soc. 1953, 44, 506–510. [Google Scholar] [CrossRef]
- Petryshyn, W.V. Construction of fixed points of demicompact mappings in Hilbert space. J. Math. Analysis Appl. 1966, 14, 276–284. [Google Scholar] [CrossRef]
- Browder, F.E. Fixed-points theorems for non-compact mappings in Hilbert spaces. Proc. Natl. Acad. Sci. USA 1965, 53, 1272–1276. [Google Scholar] [CrossRef] [PubMed]
- Osilike, M.O.; Aniagsbosor, S.C. Weak and strong convergence theorems for fixed points of asymptotically nonexpansive mappings. Math. Comput. Model. 2000, 32, 1181–1191. [Google Scholar] [CrossRef]
- Schu, J. Weak and strong convergence of fixed points of asymptotically nonexpansive mappings. Bull. Aust. Math. Soc. 1991, 43, 153–159. [Google Scholar] [CrossRef]
- Navascués, M.A.; Massopust, P. Fractal convolution: A new operation between functions. Fract. Calc. Appl. Anal. 2019, 22, 619–643. [Google Scholar] [CrossRef]
- Combettes, P.L.; Pennanen, T. Generalized Mann iterates for constructing fixed points in Hilbert spaces. J. Math. Anal. Appl. 2002, 275, 521–536. [Google Scholar] [CrossRef]
- Goebel, K.; Kirk, W.A. Topics in Metric Fixed Point Theory; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Jerri, A.J. Introduction to Integral Equations with Applications, 2nd ed.; Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Bakoda, H.O.; Darwish, M.A. Solving Hammerstein type integral equations by new discrete Adomian decomposition methods. Math. Probl. Eng. 2013, 760515. [Google Scholar] [CrossRef]
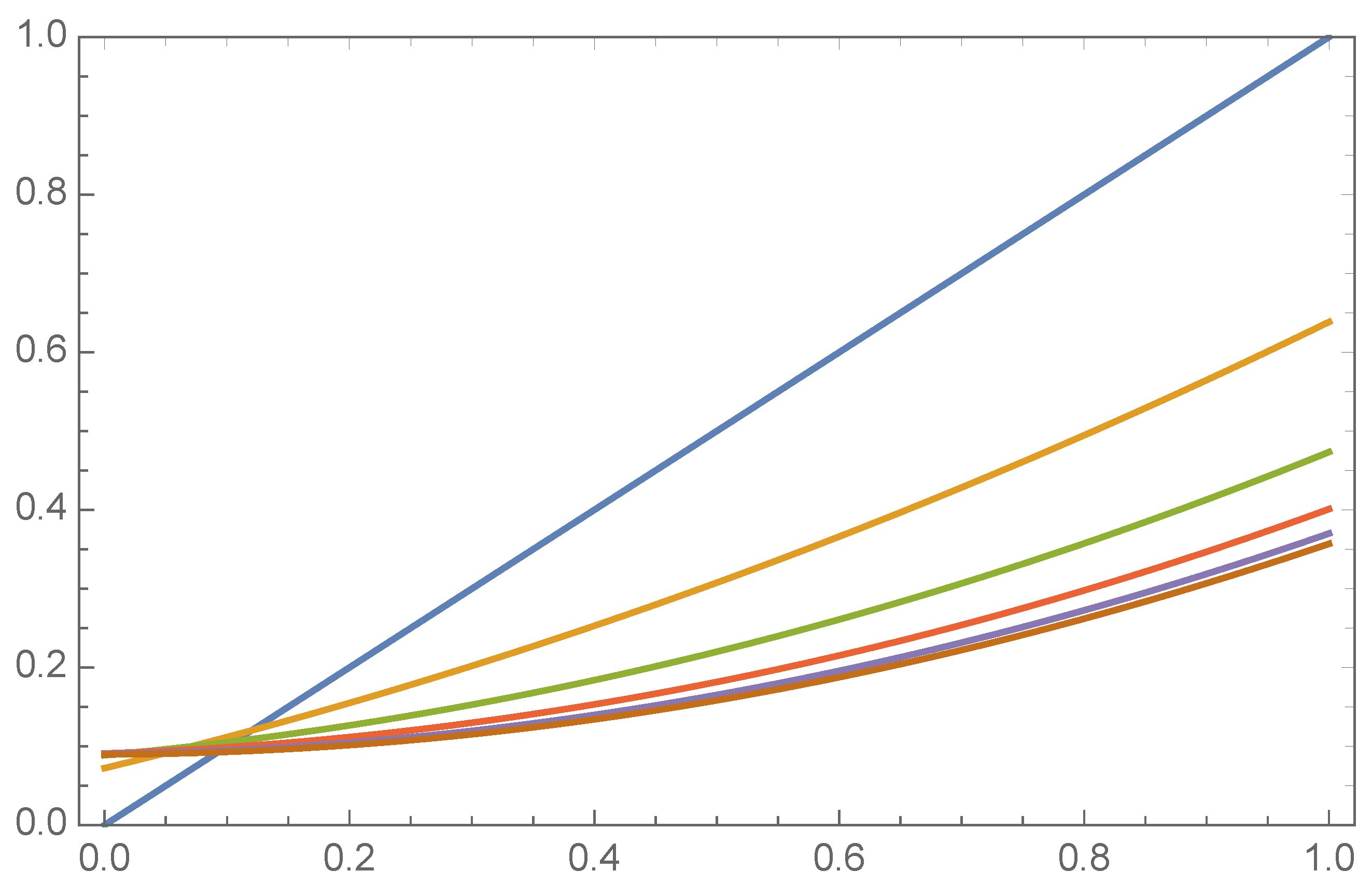
| Iteration (n) | |
|---|---|
| 1 | 0.216882 |
| 2 | 0.098364 |
| 3 | 0.043072 |
| 4 | 0.018419 |
| 5 | 0.007786 |
| 6 | 0.003275 |
| 7 | 0.001375 |
| 8 | 0.000577 |
| 9 | 0.000242 |
| 10 | 0.000103 |
| Iteration (n) | |
|---|---|
| 0 | 0.57735 |
| 1 | 0.056664 |
| 2 | 0.006714 |
| 3 | 0.000841 |
| 4 | 0.000108 |
| 5 | 0.000014 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navascués, M.A. Hammerstein Nonlinear Integral Equations and Iterative Methods for the Computation of Common Fixed Points. Axioms 2025, 14, 214. https://doi.org/10.3390/axioms14030214
Navascués MA. Hammerstein Nonlinear Integral Equations and Iterative Methods for the Computation of Common Fixed Points. Axioms. 2025; 14(3):214. https://doi.org/10.3390/axioms14030214
Chicago/Turabian StyleNavascués, María A. 2025. "Hammerstein Nonlinear Integral Equations and Iterative Methods for the Computation of Common Fixed Points" Axioms 14, no. 3: 214. https://doi.org/10.3390/axioms14030214
APA StyleNavascués, M. A. (2025). Hammerstein Nonlinear Integral Equations and Iterative Methods for the Computation of Common Fixed Points. Axioms, 14(3), 214. https://doi.org/10.3390/axioms14030214






