Characterization Results of Extremization Models with Interval Values

Abstract

The present paper investigates new connections and characterization results on interval-valued minimization models. Specifically, we describe the solution set of the considered control problem with mixed constraints by employing the solution set associated with a class of controlled split variational inequalities. These equivalence results are also accompanied by suitable numerical experiments.

1. Introduction

In their fundamental research paper, Hartman and Stampacchia [1] proved that variational inequalities are useful mathematical tools that can be used to study various variational optimization or control real-life problems. Based on this article, Giannessi has stated important results and theoretical developments in this direction in [2]. On the other hand, Moore [3,4] studied and developed interval analysis as an important mathematical object for studying various optimization problems generated by interval-valued objective/constraint functions or functionals. Stefanini and Bede [5] developed this point of view by considering the generalized Hukuhara-type differentiability for interval-valued functions. Later, many authors have considered this idea in their studies, and we enumerate some of them here: Jayswal et al. [6], Liu [7], Treanţă [8], Jayswal et al. [9], and Zhang et al. [10] (various theoretical results on vector variational problems and associated inequalities). Jha et al. [11] studied a family of interval-valued optimization problems by employing the associated modified models and saddle point optimality criteria. In addition, Treanţă [12,13] formulated conditions of optimality and efficiency in various interval-valued extremization models. Guo et al. [14], under generalized convexity, established new duality results and optimality conditions in interval-valued problems. For more information on this subject, we direct the reader to the following papers: Lodwick [15], Hanson [16], Antczak [17], Myskova [18], Wu [19], Zhang et al. [20,21], Alefeld and Mayer [22], Ishibuchi and Tanaka [23], and Wu [24]. Recently, Shang [25] considered the resilient interval consensus problems for continuous-time time-varying multi-agent systems when a normal agent is surrounded by no more than r misbehaving agents. Also, Shang [26] investigated on interval consensus of switched multiagent systems.

Over the years, the concept of convex function/set has been extended to various notions, such as harmonic convexity [27], quasi-convexity [28], strong convexity [29], p-convexity [30], or Schur-type convexity [31]. As applications, a lot of researchers have studied multiple equalities and/or inequalities, such as the Agliardo–Nirenberg inequality [32], Hardy-type inequality [33], Ostrowski-type inequality [34], and Olsen-type inequality [35,36,37].

Motivated by the research work outlined above, the present paper studies and formulates new characterization theorems associated with a particular class of interval-valued minimization models. Specifically, we describe the set of solutions of the considered optimization problem involving mixed constraints by considering the set of solutions associated with a special class of split variational inequalities. Also, suitable numerical experiments are provided. Performing a comparative analysis with the studies already carried out in this direction, we can say that the present work is a natural continuation of the investigations developed in Treanţă and Saeed’s article [38]. In their paper, the authors established certain relationships between the class of optimization problems considered here and a class of weak-type variational inequalities. In this study, we formulate new theorems to characterize the considered class of optimization problems (called $\left(Prob\right)$), using a new family of variational inequalities, namely the split variational inequalities (called $(Split-Ineq)$). More precisely, a first result establishes under which hypotheses a solution in $(Split-Ineq)$ also becomes an optimal solution of the $LU$ type of $\left(Prob\right)$. The second theorem is reciprocal to the previous result. Since the functionals used in this paper are of curvilinear-type integrals, real-world applications are not a problem. As we all know, by considering path-independent curvilinear-type integrals, we can compute the mechanical work developed by a variable force to move its application point along a given piecewise smooth curve.

This paper continues as follows. In Section 2, we present some ingredients on multi-dimensional variational control models that are useful for understanding the mathematical framework of this paper. Section 3 contains the preliminary tools, with the auxiliary results, and formulates the problem under study. Section 4 includes the principal results derived in this paper. Specifically, it provides some links and relations for the mentioned variational models, namely $\left(Prob\right)$ and $(Split-Ineq)$. Section 5 completes the theoretical developments with some numerical experiments. This paper ends with Section 6, where the conclusions associated with this paper are highlighted.

2. On Multi-Dimensional Variational Control Models

Let us start with two complete Riemann manifolds, denoted by ${\displaystyle (Q,\mathbf{g})}$ and ${\displaystyle (E,\mathbf{x})}$, having dimensions z and n, respectively. Denote by ${\displaystyle t=\left(t^{\iota }\right),\iota =\overline{1,z}}$, the local coordinates on ${\displaystyle (Q,\mathbf{g})}$, and by ${\displaystyle y=\left(y^{\sigma }\right),\sigma =\overline{1,n}}$, the local coordinates on ${\displaystyle (E,\mathbf{x})}$. By using the product order relation on ${\displaystyle R_{+}^z}$, the hyper-parallelepiped $W\subset R_{+}^z$, with the diagonally opposite points $t_0=\left(t_0^1,\dots ,t_0^z\right)$ and $t_1=\left(t_1^1,\dots ,t_1^z\right)$, can be written as the interval $\left[t_0;t_1\right]$. For ${\displaystyle \omega \ge 2}$, which is a fixed natural number, let $J^{\omega -1}(Q,E)$ be the $(\omega -1)$-th order jet bundle for ${\displaystyle Q}$ and E, and let ${\displaystyle {\Gamma }_{t_0,t_1}}$ be a $C^{\omega -1}$-class (piecewise) curve that links the points ${\displaystyle t_0}$ and ${\displaystyle t_1}$. Consider the following path-independent curvilinear integral functionals:

$${\displaystyle G^s\left(y(·)\right):={\int }_{{\Gamma }_{t_0,t_1}}{X}_{\iota }^s\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right)\right)d{t}^{\iota },s=\overline{1,l},\iota =\overline{1,z},}$$

determined by the (higher-order) closed Lagrange 1-form densities of ${\displaystyle C^{\infty }}$-class

$${\displaystyle X_{\iota }=\left(X_{\iota }^s\right):J^{\omega -1}(Q,E)\to R^l,s=\overline{1,l},\iota =\overline{1,z},}$$

with

$${\displaystyle {\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right):=\left(t,y\left(t\right),y_{{\theta }_1}\left(t\right),\dots ,y_{{\theta }_1{\theta }_2\dots {\theta }_{\omega -1}}\left(t\right)\right),t\in W,}$$

with ${\displaystyle y_{{\theta }_1}\left(t\right):=\frac{\partial y}{\partial t^{{\theta }_1}}\left(t\right),\dots ,}$${\displaystyle y_{{\theta }_1{\theta }_2\dots {\theta }_{\omega -1}}\left(t\right):=\frac{{\partial }^{\omega -1}y}{\partial t^{{\theta }_1}\partial t^{{\theta }_2}\dots \partial t^{{\theta }_{\omega -1}}}\left(t\right)}$, ${\displaystyle {\theta }_{\varsigma }\in \{1,2,\dots ,z\},\varsigma =\overline{1,\omega -1}}$, ${\displaystyle y=(y^1,\dots ,y^n)=\left(y^{\sigma }\right),\sigma =\overline{1,n}.}$ The complete conditions of integrability for ${\displaystyle \left(X_{\iota }^s\right)}$ are

$${\displaystyle D_{\eta }{X}_{\iota }^s=D_{\iota }{X}_{\eta }^s,\iota ,\eta =\overline{1,z},\iota \ne \eta ,s=\overline{1,l},}$$

where ${\displaystyle D_{\eta }:=\frac{\partial }{\partial t^{\eta }}}$ denotes the operator of total derivative.

Also, we consider the following PDI, respectively, which is the PDE of evolution

$${\displaystyle g\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right)\right)\le 0,V\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right)\right)=0,t\in W,}$$

determined by Lagrange-type matrix densities

$${\displaystyle g=\left(g_a^b\right):J^{\omega -1}(Q,E)\to R^{pq},a=\overline{1,q},b=\overline{1,p},p<n,}$$

$${\displaystyle V=\left(h_a^b\right):J^{\omega -1}(Q,E)\to R^{de},a=\overline{1,e},b=\overline{1,d},d<n.}$$

We point out that in $(*)$, we have used the following rules:

$${\displaystyle \sqcap =v\iff {\sqcap }_{\sigma }=v_{\sigma },\sqcap \le v\iff {\sqcap }_{\sigma }\le v_{\sigma },}$$

$${\displaystyle \sqcap <v\iff {\sqcap }_{\sigma }<v_{\sigma },\sqcap ⪯v\iff \sqcap \le v,\sqcap \ne v,\sigma =\overline{1,k},}$$

for any two vectors ${\displaystyle \sqcap =\left({\sqcap }_1,\dots ,{\sqcap }_k\right),v=\left(v_1,\dots ,v_k\right)}$ in ${\displaystyle R^k}$.

Using the space

$${\displaystyle C^{\infty }\left(W,E\right)=\left\{y:W\to E;yof{C}^{\infty }-class\right\},}$$

endowed with the distance

$${\displaystyle d\left(y,y^0\right)=d\left(y(·),y^0(·)\right)=\underset{t\in \Omega }{sup}{d}_{\mathbf{x}}\left(y\left(t\right),y^0\left(t\right)\right),}$$

where ${\displaystyle d_{\mathbf{x}}\left(y\left(t\right),y^0\left(t\right)\right)}$ is geodesic distance in ${\displaystyle (E,\mathbf{x})}$, we introduce the set ${\displaystyle G\left(W\right)}$ of all feasible solutions (domain)

$${\displaystyle y\in C^{\infty }\left(W,E\right),g\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right)\right)\le 0,V\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right)\right)=0,t\in W}$$

$${\displaystyle y\left(t_{\xi }\right)=y_{\xi },y_{{\theta }_1\dots {\theta }_{\varsigma }}\left(t_{\xi }\right)={\tilde{y}}_{{\theta }_1\dots {\theta }_{\varsigma }\xi },{\theta }_{\zeta }\in \{1,\dots ,z\},\zeta ,\varsigma =\overline{1,\omega -2},\xi \in \{0,1\},}$$

for the following multi-dimensional multiobjective variational problem:

$${\displaystyle (M.V.P)\underset{y\left(·\right)}{min}\left({\displaystyle G^1\left(y(·)\right),G^2\left(y(·)\right),\dots ,G^l\left(y(·)\right)}\right)}$$

$${\displaystyle \mathrm{subject}\mathrm{to}y\left(·\right)\in G\left(W\right).}$$

Note. Consider the constraints (or boundary conditions)

$${\displaystyle {y\left(t\right)|}_{\partial W}=given,y_{{\theta }_1}\left(t\right){{|}_{\partial W}=given,\dots ,y_{{\theta }_1\dots {\theta }_{\omega -2}}\left(t\right)|}_{\partial W}=given,}$$

instead of

$${\displaystyle y\left(t_{\xi }\right)=y_{\xi },y_{{\theta }_1\dots {\theta }_{\varsigma }}\left(t_{\xi }\right)={\tilde{y}}_{{\theta }_1\dots {\theta }_{\varsigma }\xi },{\theta }_{\zeta }\in \{1,\dots ,z\},\zeta ,\varsigma =\overline{1,\omega -2},\xi \in \{0,1\}.}$$

2.1. Necessary Optimality Conditions in Scalar Optimization Problems

We start by considering the following scalar optimization problem:

$${\displaystyle (S.P)\underset{y(·)}{min}{\int }_{{\Gamma }_{t_0,t_1}}{X}_{\iota }\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right)\right)d{t}^{\iota }}$$

$${\displaystyle \mathrm{subject}\mathrm{to}y\left(·\right)\in G\left(W\right).}$$

The necessary conditions for the optimality of ${\displaystyle y^0\in G\left(W\right)}$ in $(S.P)$ are

$${\displaystyle \frac{\partial L_{\iota }}{\partial y^{\sigma }}-D_{{\theta }_1}\frac{\partial L_{\iota }}{\partial y_{{\theta }_1}^{\sigma }}+\frac{1}{n({\theta }_1,{\theta }_2)}{D}_{{\theta }_1{\theta }_2}^2\frac{\partial L_{\iota }}{\partial y_{{\theta }_1{\theta }_2}^{\sigma }}-\frac{1}{n({\theta }_1,{\theta }_2,{\theta }_3)}{D}_{{\theta }_1{\theta }_2{\theta }_3}^3\frac{\partial L_{\iota }}{\partial y_{{\theta }_1{\theta }_2{\theta }_3}^{\sigma }}}$$

$${\displaystyle +\dots +{(-1)}^{\omega -1}\frac{1}{n({\theta }_1,{\theta }_2,\dots ,{\theta }_{\omega -1})}{D}_{{\theta }_1{\theta }_2\dots {\theta }_{\omega -1}}^{\omega -1}\frac{\partial L_{\iota }}{\partial y_{{\theta }_1{\theta }_2\dots {\theta }_{\omega -1}}^{\sigma }}=0,}$$

$${\displaystyle \sigma \in \left\{1,2,\dots ,n\right\},\iota \in \left\{1,2,\dots ,z\right\}(\mathrm{higher}\text{-}\mathrm{order}\mathrm{Euler}\text{-}\mathrm{Lagrange}\mathrm{PDE})}$$

$${\displaystyle {\varphi }_{\iota }\left(t\right)g\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)=0,{\varphi }_{\iota }\left(t\right)\ge 0,t\in W,}$$

where

∘

${\displaystyle D_{{\theta }_1\dots {\theta }_{\omega -1}}^{\omega -1}:=\frac{{\partial }^{\omega -1}}{\partial t^{{\theta }_1}\dots \partial t^{{\theta }_{\omega -1}}}}$ is the total derivative operator of order ${\displaystyle \omega -1;}$

∘

${\displaystyle L_{\iota }\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right),\alpha \left(t\right),\beta \left(t\right),\theta \right):=\theta X_{\iota }\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)+{\varphi }_{\iota }\left(t\right)g\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)+{\nu }_{\iota }\left(t\right)V\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right),\iota =\overline{1,z}}$, and

$${\displaystyle \alpha \left(t\right):=\left({\varphi }_{\iota }\left(t\right)\right)=\left({\varphi }_{\iota \lfloor }^{⊣}\left(t\right)\right),⊣=\overline{1,q},\lfloor =\overline{1,p},}$$

$${\displaystyle \beta \left(t\right):=\left({\nu }_{\iota }\left(t\right)\right)=\left({\nu }_{\iota \lfloor }^{⊣}\left(t\right)\right),⊣=\overline{1,e},\lfloor =\overline{1,d},}$$

which shows that the multipliers satisfy that ${\displaystyle L_{\iota }}$ is closed. Also, we accept the following notation:

∘

${\displaystyle {\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right):=\left(t,y^0\left(t\right),y_{{\theta }_1}^0\left(t\right),\dots ,y_{{\theta }_1{\theta }_2\dots {\theta }_{\omega -1}}^0\left(t\right)\right),t\in W;}$

∘

${\displaystyle n({\theta }_1,{\theta }_2,\dots ,{\theta }_k):=\frac{\mid 1_{{\theta }_1}+1_{{\theta }_2}+\dots +1_{{\theta }_k}\mid !}{(1_{{\theta }_1}+1_{{\theta }_2}+\dots +1_{{\theta }_k})!}}$ represents the Saunders number (see Saunders [39]).

Now, according to Valentine [40], we reformulate the necessary optimality conditions mentioned above in $(S.P)$ as follows:

Theorem 1.

Suppose that ${\displaystyle y^0\in G\left(W\right)}$ is an optimal solution and ${\displaystyle X=\left(X_{\iota }\right)}$, ${\displaystyle g,V}$ are of the ${\displaystyle C^{\infty }}$-class. In these conditions, there are ${\displaystyle \theta ,\alpha \left(t\right)}$ and ${\displaystyle \beta \left(t\right)}$, such that

$${\displaystyle \theta \frac{\partial X_{\iota }}{\partial y^{\sigma }}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)+{\varphi }_{\iota }\left(t\right)\frac{\partial g}{\partial y^{\sigma }}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)+{\nu }_{\iota }\left(t\right)\frac{\partial V}{\partial y^{\sigma }}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)}$$

$${\displaystyle -D_{{\theta }_1}\left\{\theta \frac{\partial X_{\iota }}{\partial y_{{\theta }_1}^{\sigma }}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)+{\varphi }_{\iota }\left(t\right)\frac{\partial g}{\partial y_{{\theta }_1}^{\sigma }}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle -D_{{\theta }_1}\left\{{\nu }_{\iota }\left(t\right)\frac{\partial V}{\partial y_{{\theta }_1}^{\sigma }}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}+\frac{1}{n({\theta }_1,{\theta }_2)}{D}_{{\theta }_1{\theta }_2}^2\left\{\theta \frac{\partial X_{\iota }}{\partial y_{{\theta }_1{\theta }_2}^{\sigma }}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle +\frac{1}{n({\theta }_1,{\theta }_2)}{D}_{{\theta }_1{\theta }_2}^2\left\{{\varphi }_{\iota }\left(t\right)\frac{\partial g}{\partial y_{{\theta }_1{\theta }_2}^{\sigma }}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)+{\nu }_{\iota }\left(t\right)\frac{\partial V}{\partial y_{{\theta }_1{\theta }_2}^{\sigma }}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle -\dots +{(-1)}^{\omega -1}\frac{1}{n({\theta }_1,\dots ,{\theta }_{\omega -1})}{D}_{{\theta }_1\dots {\theta }_{\omega -1}}^{\omega -1}\left\{\theta \frac{\partial X_{\iota }}{\partial y_{{\theta }_1{\theta }_2\dots {\theta }_{\omega -1}}^{\sigma }}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle +{(-1)}^{\omega -1}\frac{1}{n({\theta }_1,\dots ,{\theta }_{\omega -1})}{D}_{{\theta }_1\dots {\theta }_{\omega -1}}^{\omega -1}\left\{{\varphi }_{\iota }\left(t\right)\frac{\partial g}{\partial y_{{\theta }_1{\theta }_2\dots {\theta }_{\omega -1}}^{\sigma }}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle +{(-1)}^{\omega -1}\frac{1}{n({\theta }_1,\dots ,{\theta }_{\omega -1})}{D}_{{\theta }_1\dots {\theta }_{\omega -1}}^{\omega -1}\left\{{\nu }_{\iota }\left(t\right)\frac{\partial V}{\partial y_{{\theta }_1\dots {\theta }_{\omega -1}}^{\sigma }}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}=0}$$

$${\displaystyle \iota =\overline{1,z},\sigma =\overline{1,n}}$$

$${\displaystyle {\varphi }_{\iota }\left(t\right)g\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)=0,{\varphi }_{\iota }\left(t\right)\ge 0,t\in W.}$$

Definition 1

(Treanţă [8]). An optimal solution ${\displaystyle y^0(·)\in G\left(W\right)}$ in $(S.P)$ is called a normal optimal solution in $(S.P)$ if ${\displaystyle \theta \ne 0}$.

Definition 2

(Treanţă [8]). A point ${\displaystyle y^0(·)\in G\left(W\right)}$ in $(M.V.P)$ is called an efficient solution if there exists no ${\displaystyle y(·)\in G\left(W\right)}$ such that ${\displaystyle G\left(y(·)\right)⪯G\left(y^0(·)\right)}$, with

$${\displaystyle G\left(y(·)\right):=\left({\int }_{{\Gamma }_{t_0,t_1}}{X}_{\iota }^1\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right)\right)d{t}^{\iota },\dots ,{\int }_{{\Gamma }_{t_0,t_1}}{X}_{\iota }^l\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right)\right)d{t}^{\iota }\right).}$$

2.2. Necessary Efficiency Conditions in $(M.V.P)$

In order to develop an optimization theory on higher-order jet bundles, in accordance with Chankong and Haimes [41], let us establish the following results:

Lemma 1.

A feasible solution ${\displaystyle y^0}$ in $(M.V.P)$ is an efficient solution in $(M.V.P)$ if and only if ${\displaystyle y^0\in G\left(W\right)}$ is an optimal solution of ${\displaystyle P_s\left(y^0\right),s=\overline{1,l}}$,

$${\displaystyle \underset{y(·)}{min}{\int }_{{\Gamma }_{t_0,t_1}}{X}_{\iota }^s\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right)\right)d{t}^{\iota }}$$

$$subjectto$$

$${\displaystyle y\left(t_{\xi }\right)=y_{\xi },y_{{\theta }_1\dots {\theta }_{\varsigma }}\left(t_{\xi }\right)={\tilde{y}}_{{\theta }_1\dots {\theta }_{\varsigma }\xi },{\theta }_{\zeta }\in \{1,\dots ,z\},\zeta ,\varsigma =\overline{1,\omega -2},\xi \in \{0,1\}}$$

$${\displaystyle g\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right)\right)\le 0,V\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right)\right)=0,t\in W}$$

$${\displaystyle {\int }_{{\Gamma }_{t_0,t_1}}{X}_{\iota }^c\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left(t\right)\right)d{t}^{\iota }\le {\int }_{{\Gamma }_{t_0,t_1}}{X}_{\iota }^c\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)d{t}^{\iota },c=\overline{1,l},c\ne s.}$$

Lemma 2.

Let ${\displaystyle y^0\left(·\right)\in G\left(W\right)}$ be the optimal solution in ${\displaystyle P_s\left(y^0\right),s\in \{1,\dots ,l\}}$. Under these assumptions, there are ${\displaystyle {\theta }_{cl}\ge 0,c=\overline{1,l},{\varphi }_s\left(t\right)}$ and ${\displaystyle {\nu }_s\left(t\right)}$ satisfying

$${\displaystyle \sum _{c=1}^l{\theta }_{cl}\frac{\partial X_{\iota }^c}{\partial y}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)+{\varphi }_{s\iota }\left(t\right)\frac{\partial g}{\partial y}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)+{\nu }_{s\iota }\left(t\right)\frac{\partial V}{\partial y}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)}$$

$${\displaystyle -D_{{\theta }_1}\left\{\sum _{c=1}^l{\theta }_{cl}\frac{\partial X_{\iota }^c}{\partial y_{{\theta }_1}}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)+{\varphi }_{s\iota }\left(t\right)\frac{\partial g}{\partial y_{{\theta }_1}}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle -D_{{\theta }_1}\left\{{\nu }_{s\iota }\left(t\right)\frac{\partial V}{\partial y_{{\theta }_1}}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle +\dots +{(-1)}^{\omega -1}\frac{1}{n({\theta }_1,\dots ,{\theta }_{\omega -1})}{D}_{{\theta }_1\dots {\theta }_{\omega -1}}^{\omega -1}\left\{\sum _{c=1}^l{\theta }_{cl}\frac{\partial X_{\iota }^c}{\partial y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle +{(-1)}^{\omega -1}\frac{1}{n({\theta }_1,\dots ,{\theta }_{\omega -1})}{D}_{{\theta }_1\dots {\theta }_{\omega -1}}^{\omega -1}\left\{{\varphi }_{s\iota }\left(t\right)\frac{\partial g}{\partial y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle +{(-1)}^{\omega -1}\frac{1}{n({\theta }_1,\dots ,{\theta }_{\omega -1})}{D}_{{\theta }_1\dots {\theta }_{\omega -1}}^{\omega -1}\left\{{\nu }_{s\iota }\left(t\right)\frac{\partial V}{\partial y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}=0}$$

$${\displaystyle \iota =\overline{1,z}}$$

$${\displaystyle {\varphi }_{s\iota }\left(t\right)g\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)=0,{\varphi }_{s\iota }\left(t\right)\ge 0,t\in W.}$$

Definition 3.

The feasible solution ${\displaystyle y^0(·)\in G\left(W\right)}$ is called a normal efficient solution of the problem $(M.V.P)$ if it is a normal optimal solution for at least one of the scalar problems ${\displaystyle P_s\left(y^0\right),s=\overline{1,l}}$.

Now, we have all the necessary mathematical tools to establish the next result.

Theorem 2.

If ${\displaystyle y^0(·)\in G\left(W\right)}$ is a [normal] efficient solution in $(M.V.P)$, then there are ${\displaystyle \theta \in R^l,\alpha }$ and ${\displaystyle \beta }$, verifying

$${\displaystyle \sum _{c=1}^l{\theta }_c\frac{\partial X_{\iota }^c}{\partial y}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)+{\varphi }_{\iota }\left(t\right)\frac{\partial g}{\partial y}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)+{\nu }_{\iota }\left(t\right)\frac{\partial V}{\partial y}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)}$$

$${\displaystyle -D_{{\theta }_1}\left\{\sum _{c=1}^l{\theta }_c\frac{\partial X_{\iota }^c}{\partial y_{{\theta }_1}}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)+{\varphi }_{\iota }\left(t\right)\frac{\partial g}{\partial y_{{\theta }_1}}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle -D_{{\theta }_1}\left\{{\nu }_{\iota }\left(t\right)\frac{\partial V}{\partial y_{{\theta }_1}}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle +\dots +{(-1)}^{\omega -1}\frac{1}{n({\theta }_1,\dots ,{\theta }_{\omega -1})}{D}_{{\theta }_1\dots {\theta }_{\omega -1}}^{\omega -1}\left\{\sum _{c=1}^l{\theta }_c\frac{\partial X_{\iota }^c}{\partial y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle +{(-1)}^{\omega -1}\frac{1}{n({\theta }_1,\dots ,{\theta }_{\omega -1})}{D}_{{\theta }_1\dots {\theta }_{\omega -1}}^{\omega -1}\left\{{\varphi }_{\iota }\left(t\right)\frac{\partial g}{\partial y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}}$$

$${\displaystyle +{(-1)}^{\omega -1}\frac{1}{n({\theta }_1,\dots ,{\theta }_{\omega -1})}{D}_{{\theta }_1\dots {\theta }_{\omega -1}}^{\omega -1}\left\{{\nu }_{\iota }\left(t\right)\frac{\partial V}{\partial y_{{\theta }_1\dots {\theta }_{\omega -1}}}\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)\right\}=0}$$

$${\displaystyle \iota =\overline{1,z}}$$

$${\displaystyle {\varphi }_{\iota }\left(t\right)g\left({\pi }_{y_{{\theta }_1\dots {\theta }_{\omega -1}}^0}\left(t\right)\right)=0,{\varphi }_{\iota }\left(t\right)\ge 0,t\in W,\iota =\overline{1,z}}$$

$${\displaystyle \theta \ge 0,Z^t\theta =1,Z^t=\left(1,1,\dots ,1\right)\in R^l.}$$

3. Preliminaries

Consider ${\mathbb{R}}^m,{\mathbb{R}}^k$ and ${\mathbb{R}}^n$ to be the classical Euclidean spaces, and $\mathcal{M}\subset {\mathbb{R}}^m$ to be a compact set. Also, we consider $\Psi \subset \mathcal{M}$ as a piecewise curve that links the points $t_0=\left(t_0^{\gamma }\right)$, $t_1=\left(t_1^{\gamma }\right)$, $\gamma =\overline{1,m}$, and $t=\left(t^{\gamma }\right),\gamma =\overline{1,m}$ to be an arbitrary point in $\mathcal{M}$.

Denote $D_{\gamma }:={\displaystyle \frac{d}{d{t}^{\gamma }}}$, with $\gamma =\overline{1,m}$, and consider $\mathfrak{A}$ the class of differentiable functions (piecewise state functions) $a:\mathcal{M}\mapsto {\mathbb{R}}^n$, with ${\displaystyle \frac{\partial a}{\partial t^{\gamma }}}\left(t\right):=a_{\gamma }\left(t\right)$, $\mathfrak{R}$ being the class of continuous functions (piecewise control functions) $\varphi :\mathcal{M}\mapsto {\mathbb{R}}^k$, and by $\mathfrak{C}$ which is the family of all compact real intervals.

For $\mathfrak{X}=\left[{\mathfrak{x}}^L,{\mathfrak{x}}^U\right],\mathfrak{U}=\left[{\mathfrak{u}}^L,{\mathfrak{u}}^U\right]\in \mathfrak{C}$, the fololwing interval operations are considered:

• $\mathfrak{X}=\mathfrak{U}⟺{\mathfrak{x}}^L={\mathfrak{u}}^L,{\mathfrak{x}}^U={\mathfrak{u}}^U$
• if ${\mathfrak{x}}^L={\mathfrak{x}}^U=\mathfrak{x}$, then $\mathfrak{X}=[\mathfrak{x},\mathfrak{x}]=\mathfrak{x}$
• $\mathfrak{X}+\mathfrak{U}=\left[{\mathfrak{x}}^L+{\mathfrak{u}}^L,{\mathfrak{x}}^U+{\mathfrak{u}}^U\right]$
• $-\mathfrak{X}=-\left[{\mathfrak{x}}^L,{\mathfrak{x}}^U\right]=\left[-{\mathfrak{x}}^U,-{\mathfrak{x}}^L\right]$
• $\mathfrak{X}-\mathfrak{U}=\left[{\mathfrak{x}}^L-{\mathfrak{u}}^U,{\mathfrak{x}}^U-{\mathfrak{u}}^L\right]$
• $\lambda +\mathfrak{X}=\left[\lambda +{\mathfrak{x}}^L,\lambda +{\mathfrak{x}}^U\right],\lambda \in \mathbb{R}$
• $\lambda \mathfrak{X}=\left[\lambda {\mathfrak{x}}^L,\lambda {\mathfrak{x}}^U\right],\lambda \in \mathbb{R},\lambda \ge 0$
• $\lambda \mathfrak{X}=\left[\lambda {\mathfrak{x}}^U,\lambda {\mathfrak{x}}^L\right],\lambda \in \mathbb{R},\lambda <0$.

In addition, for $\mathfrak{X},\mathfrak{U}\in \mathfrak{C}$, we consider the $LU$-order, as follows:

• $\mathfrak{X}{⪯}_{LU}\mathfrak{U}⟺{\mathfrak{x}}^L\le {\mathfrak{u}}^L,{\mathfrak{x}}^U\le {\mathfrak{u}}^U$
• $\mathfrak{X}{\prec }_{LU}\mathfrak{U}⟺\mathfrak{X}{⪯}_{LU}\mathfrak{U},\mathfrak{X}\ne \mathfrak{U}$.

Next, following Treanţă [12], Ciontescu and Treanţă [42], Saeed and Treanţă [43], Treanţă and Saeed [38], and Jayswal et al. [44], we formulate the following auxiliary elements:

Definition 4.

The functional

$${\displaystyle P:\mathfrak{A}\times \mathfrak{R}\mapsto \mathfrak{C},P(a,\varphi )={\int }_{\Psi }{w}_{\nu }\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu }}$$

is named as the functional with interval values if it is written as follows:

$${\displaystyle P(a,\varphi )=\left[{\int }_{\Psi }{w}_{\nu }^L\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu },{\int }_{\Psi }{w}_{\nu }^U\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu }\right],}$$

with

$${\displaystyle P^L(a,\varphi ),P^U(a,\varphi ):\mathfrak{A}\times \mathfrak{R}\mapsto \mathbb{R},}$$

$${\displaystyle P^L(a,\varphi ):={\int }_{\Psi }{w}_{\nu }^L\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu },}$$

$${\displaystyle P^U(a,\varphi ):={\int }_{\Psi }{w}_{\nu }^U\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu },}$$

as functionals with real values, and $w_{\nu }:\mathcal{M}\times \mathfrak{A}\times \mathfrak{A}\times \mathfrak{R}\to \mathfrak{C},w_{\nu }=[w_{\nu }^L,w_{\nu }^U],\nu =\overline{1,m}$, satisfy the following inequality:

$${\displaystyle {\int }_{\Psi }{w}_{\nu }^L\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu }\le {\int }_{\Psi }{w}_{\nu }^U\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu }.}$$

Definition 5.

The functional P is called path-independent if the associated real-valued functionals $P^L$ and $P^U$ are path-independent, or equivalently, if the conditions

$$D_{\gamma }{w}_{\nu }^L=D_{\nu }{w}_{\gamma }^L$$

and

$$D_{\gamma }{w}_{\nu }^U=D_{\nu }{w}_{\gamma }^U,$$

are fulfilled, for $\nu \ne \gamma$.

Definition 6.

The real-valued functional

$${\displaystyle T:\mathfrak{A}\times \mathfrak{R}\mapsto \mathbb{R},T(a,\varphi )={\int }_{\Psi }{h}_{\nu }\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu }}$$

is said to be (strictly) convex at $(a^0,{\varphi }^0)\in \mathfrak{A}\times \mathfrak{R}$ if, for all $(a,\varphi )\in \mathfrak{A}\times \mathfrak{R}$, the relation

$${\displaystyle T(a,\varphi )-T(a^0,{\varphi }^0)\ge (>){\int }_{\Psi }\frac{\partial h_{\nu }}{\partial a}\left(t,a^0\left(t\right),a_{\gamma }^0\left(t\right),{\varphi }^0\left(t\right)\right)\left(a\left(t\right)-a^0\left(t\right)\right)d{t}^{\nu }}$$

$${\displaystyle +{\int }_{\Psi }\frac{\partial h_{\nu }}{\partial a_{\gamma }}\left(t,a^0\left(t\right),a_{\gamma }^0\left(t\right),{\varphi }^0\left(t\right)\right)D_{\gamma }\left(a\left(t\right)-a^0\left(t\right)\right)d{t}^{\nu }}$$

$${\displaystyle +{\int }_{\Psi }\frac{\partial h_{\nu }}{\partial \varphi }\left(t,a^0\left(t\right),a_{\gamma }^0\left(t\right),{\varphi }^0\left(t\right)\right)\left(\varphi \left(t\right)-{\varphi }^0\left(t\right)\right)d{t}^{\nu },}$$

is satisfied.

The functional $T:\mathfrak{A}\times \mathfrak{R}\mapsto \mathbb{R}$ is (strictly) convex on $\mathfrak{A}\times \mathfrak{R}$ if the definition given above is satisfied for each $(a^0,{\varphi }^0)$ in $\mathfrak{A}\times \mathfrak{R}$.

Definition 7.

The interval-valued functional

$$P:\mathfrak{A}\times \mathfrak{R}\mapsto \mathfrak{C},P(a,\varphi )={\int }_{\Psi }{w}_{\nu }\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu }=[P^L(a,\varphi ),P^U(a,\varphi )]$$

is called $LU$-convex at $(a^0,{\varphi }^0)\in \mathfrak{A}\times \mathfrak{R}$ if

$${\displaystyle P^L(a,\varphi )={\int }_{\Psi }{w}_{\nu }^L\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu }}$$

and

$${\displaystyle P^U(a,\varphi )={\int }_{\Psi }{w}_{\nu }^U\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu }}$$

are convex at $(a^0,{\varphi }^0)\in \mathfrak{A}\times \mathfrak{R}$.

Definition 8.

If ${\displaystyle P^L(a,\varphi )}$ and ${\displaystyle P^U(a,\varphi )}$ are convex at $(a^0,{\varphi }^0)\in \mathfrak{A}\times \mathfrak{R}$ and

$${\displaystyle P^L(a,\varphi )={\int }_{\Psi }{w}_{\nu }^L\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu }}$$

or

$${\displaystyle P^U(a,\varphi )={\int }_{\Psi }{w}_{\nu }^U\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu }}$$

is strictly convex at $(a^0,{\varphi }^0)\in \mathfrak{A}\times \mathfrak{R}$, then the interval-valued functional

$$P:\mathfrak{A}\times \mathfrak{R}\mapsto \mathfrak{C},P(a,\varphi )={\int }_{\Psi }{w}_{\nu }\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu }$$

is said to be strictly $LU$-convex at $(a^0,{\varphi }^0)\in \mathfrak{A}\times \mathfrak{R}$.

Next, we introduce and formulate the problem under study, as follows:

$$\begin{array}{c}\left(Prob\right){\displaystyle \underset{\left(a\right(·),\varphi (·\left)\right)}{min}}{\int }_{\Psi }{w}_{\nu }\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)d{t}^{\nu }\\ \mathit{subject}\mathit{to}\\ M_{\theta }\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)\le 0,\theta =\overline{1,s}\\ N_{\eta }\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right):={\displaystyle \frac{\partial a}{\partial t^{\gamma }}}\left(t\right)-Q_{\eta }\left(t,a\left(t\right),\varphi \left(t\right)\right)=0,\eta =\overline{1,l}\\ {a|}_{t=t_0,t_1}=\mathit{fixed},\end{array}$$

where $t\in \mathcal{M},w_{\nu }:\mathcal{M}\times \mathfrak{A}\times \mathfrak{A}\times \mathfrak{R}\mapsto \mathfrak{C},M_{\theta }:\mathcal{M}\times \mathfrak{A}\times \mathfrak{A}\times \mathfrak{R}\mapsto \mathbb{R}$ and $N_{\eta }:\mathcal{M}\times \mathfrak{A}\times \mathfrak{A}\times \mathfrak{R}\mapsto \mathbb{R}$ are functions of $C^1$-class.

The set of feasible solutions for $\left(Prob\right)$ is

$${\displaystyle \mathcal{O}=\{(a,\varphi )\in \mathfrak{A}\times \mathfrak{R}\mid M_{\theta }\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)\le 0,}$$

$${\displaystyle N_{\eta }\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)=0,a{|}_{t=t_0,t_1}=\mathit{fixed}\}}$$

and consider that it is a convex set of $\mathfrak{A}\times \mathfrak{R}$.

Further, we consider the following notation: $a=a\left(t\right),\varphi =\varphi \left(t\right),\zeta =\left(t,a\left(t\right),a_{\gamma }\left(t\right),\varphi \left(t\right)\right)$, ${\zeta }^0=\left(t,a^0\left(t\right),a_{\gamma }^0\left(t\right),{\varphi }^0\left(t\right)\right),w_{\nu ,a}={\displaystyle \frac{\partial w_{\nu }}{\partial a}},w_{\nu ,a_{\gamma }}={\displaystyle \frac{\partial w_{\nu }}{\partial a_{\gamma }}}$ and $w_{\nu ,\varphi }={\displaystyle \frac{\partial w_{\nu }}{\partial \varphi }}$.

Definition 9.

A pair $(a^0,{\varphi }^0)\in \mathcal{O}$ is named as a (strong) optimal solution of the $LU$ type of $\left(Prob\right)$ if, for all $(a,\varphi )\in \mathcal{O}$, inequality

$${\int }_{\Psi }{w}_{\nu }\left({\zeta }^0\right)d{t}^{\nu }{⪯}_{LU}\left({\prec }_{LU}\right){\int }_{\Psi }{w}_{\nu }\left(\zeta \right)d{t}^{\nu }$$

is satisfied.

In the following, we associate the next classes of controlled variational inequalities with $\left(Prob\right)$:

-

Find $(a^0,{\varphi }^0)\in \mathcal{O}$ for which there exists no other $(a,\varphi )\in \mathcal{O}$ satisfying

$${\displaystyle (Weak-Ineq){\int }_{\Psi }\left\{w_{\nu ,a}^L\left({\zeta }^0\right)+w_{\nu ,a}^U\left({\zeta }^0\right)\right\}\left(a-a^0\right)d{t}^{\nu }}$$

$${\displaystyle +{\int }_{\Psi }\left\{w_{\nu ,a_{\gamma }}^L\left({\zeta }^0\right)+w_{\nu ,a_{\gamma }}^U\left({\zeta }^0\right)\right\}{D}_{\gamma }\left(a-a^0\right)d{t}^{\nu }}$$

$${\displaystyle +{\int }_{\Psi }\left\{w_{\nu ,\varphi }^L\left({\zeta }^0\right)+w_{\nu ,\varphi }^U\left({\zeta }^0\right)\right\}\left(\varphi -{\varphi }^0\right)d{t}^{\nu }<0;}$$

-

Find $(a^0,{\varphi }^0)\in \mathcal{O}$ so that, for all feasible pairs $(a,\varphi )\in \mathcal{O}$, the following inequalities:

$${\displaystyle (Split-Ineq){\int }_{\Psi }\left\{w_{\nu ,a}^L\left({\zeta }^0\right)\right\}\left(a-a^0\right)d{t}^{\nu }+{\int }_{\Psi }\left\{w_{\nu ,a_{\gamma }}^L\left({\zeta }^0\right)\right\}{D}_{\gamma }\left(a-a^0\right)d{t}^{\nu }}$$

$${\displaystyle +{\int }_{\Psi }\left\{w_{\nu ,\varphi }^L\left({\zeta }^0\right)\right\}\left(\varphi -{\varphi }^0\right)d{t}^{\nu }>0}$$

and

$${\displaystyle {\int }_{\Psi }\left\{w_{\nu ,a}^U\left({\zeta }^0\right)\right\}\left(a-a^0\right)d{t}^{\nu }+{\int }_{\Psi }\left\{w_{\nu ,a_{\gamma }}^U\left({\zeta }^0\right)\right\}{D}_{\gamma }\left(a-a^0\right)d{t}^{\nu }}$$

$${\displaystyle +{\int }_{\Psi }\left\{w_{\nu ,\varphi }^U\left({\zeta }^0\right)\right\}\left(\varphi -{\varphi }^0\right)d{t}^{\nu }>0}$$

are satisfied.

Some relations between the class of the above-mentioned weak variational inequalities $(Weak-Ineq)$ and the associated optimization model $\left(Prob\right)$ are formulated and established in Treanţă and Saeed [38]. For completeness of the exposition, we will recall these results as follows:

Theorem 3

(Treanţă and Saeed [38]). Consider $(a^0,{\varphi }^0)\in \mathcal{O}$ to be an optimal solution of the $LU$ type to $\left(Prob\right)$ and ${\displaystyle {\int }_{\Psi }-w_{\nu }\left(\zeta \right)d{t}^{\nu }}$ to be $LU$-convex at $(a^0,{\varphi }^0)\in \mathcal{O}$. Then, $(a^0,{\varphi }^0)\in \mathcal{O}$ is a solution to $(Weak-Ineq)$.

Theorem 4

(Treanţă and Saeed [38]). Consider $(a^0,{\varphi }^0)\in \mathcal{O}$ to be a solution to $(Weak-Ineq)$ and ${\displaystyle {\int }_{\Psi }{w}_{\nu }\left(\zeta \right)d{t}^{\nu }}$ to be strictly $LU$-convex at $(a^0,{\varphi }^0)\in \mathcal{O}$. Then, $(a^0,{\varphi }^0)\in \mathcal{O}$ is an optimal solution of the $LU$ type to $\left(Prob\right)$.

4. Main Results

The principal outcomes of this paper provide some links and relations for the mentioned variational models, namely $\left(Prob\right)$ and $(Split-Ineq)$.

The next result establishes the hypotheses under which a solution in $(Split-Ineq)$ also becomes an optimal solution of the $LU$ type of $\left(Prob\right)$.

Theorem 5.

Consider that $(a^0,{\varphi }^0)\in \mathcal{O}$ fulfills $(Split-Ineq)$ and that ${\displaystyle {\int }_{\Psi }{w}_{\nu }\left(\zeta \right)d{t}^{\nu }}$ is $LU$-convex at $(a^0,{\varphi }^0)\in \mathcal{O}$. Then, $(a^0,{\varphi }^0)\in \mathcal{O}$ is also a strong optimal solution of the $LU$ type to $\left(Prob\right)$.

Proof. 

By hypothesis, the pair $(a^0,{\varphi }^0)\in \mathcal{O}$ solves the split variational control inequality $(Split-Ineq)$. In contrast, suppose that $(a^0,{\varphi }^0)\in \mathcal{O}$ is not a strong optimal solution of the $LU$ type to $\left(Prob\right)$. Thus, there exists $(a,\varphi )\in \mathcal{O}$, fulfilling

$${\displaystyle {\int }_{\Psi }{w}_{\nu }\left(\zeta \right)d{t}^{\nu }{⪯}_{LU}{\int }_{\Psi }{w}_{\nu }\left({\zeta }^0\right)d{t}^{\nu },}$$

equivalent with

$${\displaystyle {\int }_{\Psi }{w}_{\nu }^L\left(\zeta \right)d{t}^{\nu }\le {\int }_{\Psi }{w}_{\nu }^L\left({\zeta }^0\right)d{t}^{\nu }\mathrm{and}{\int }_{\Psi }{w}_{\nu }^U\left(\zeta \right)d{t}^{\nu }\le {\int }_{\Psi }{w}_{\nu }^U\left({\zeta }^0\right)d{t}^{\nu }.}$$

(1)

By considering that the functional ${\displaystyle {\int }_{\Psi }{w}_{\nu }\left(\zeta \right)d{t}^{\nu }}$ is $LU$-convex at $(a^0,{\varphi }^0)\in \mathcal{O}$, we have

$${\displaystyle {\int }_{\Psi }{w}_{\nu }^L\left(\zeta \right)d{t}^{\nu }-{\int }_{\Psi }{w}_{\nu }^L\left({\zeta }^0\right)d{t}^{\nu }}$$

$${\displaystyle \ge {\int }_{\Psi }\left\{w_{\nu ,a}^L\left({\zeta }^0\right)\left(a-a^0\right)+w_{\nu ,a_{\gamma }}^L\left({\zeta }^0\right)D_{\gamma }\left(a-a^0\right)+w_{\nu ,\varphi }^L\left({\zeta }^0\right)\left(\varphi -{\varphi }^0\right)\right\}d{t}^{\nu },}$$

$${\displaystyle {\int }_{\Psi }{w}_{\nu }^U\left(\zeta \right)d{t}^{\nu }-{\int }_{\Psi }{w}_{\nu }^U\left({\zeta }^0\right)d{t}^{\nu }}$$

$${\displaystyle \ge {\int }_{\Psi }\left\{w_{\nu ,a}^U\left({\zeta }^0\right)\left(a-a^0\right)+w_{\nu ,a_{\gamma }}^U\left({\zeta }^0\right)D_{\gamma }\left(a-a^0\right)+w_{\nu ,\varphi }^U\left({\zeta }^0\right)\left(\varphi -{\varphi }^0\right)\right\}d{t}^{\nu },}$$

for all $(a,\varphi )\in \mathcal{O}$. In agreement with the inequalities given in $\left(1\right)$, the above inequalities yield

$${\displaystyle {\int }_{\Psi }\left\{w_{\nu ,a}^L\left({\zeta }^0\right)\left(a-a^0\right)+w_{\nu ,a_{\gamma }}^L\left({\zeta }^0\right)D_{\gamma }\left(a-a^0\right)+w_{\nu ,\varphi }^L\left({\zeta }^0\right)\left(\varphi -{\varphi }^0\right)\right\}d{t}^{\nu }\le 0,}$$

$${\displaystyle {\int }_{\Psi }\left\{w_{\nu ,a}^U\left({\zeta }^0\right)\left(a-a^0\right)+w_{\nu ,a_{\gamma }}^U\left({\zeta }^0\right)D_{\gamma }\left(a-a^0\right)+w_{\nu ,\varphi }^U\left({\zeta }^0\right)\left(\varphi -{\varphi }^0\right)\right\}d{t}^{\nu }\le 0,}$$

which contradicts that $(a^0,{\varphi }^0)\in \mathcal{O}$ is a solution to $(Split-Ineq)$. □

The reciprocal of the previous theorem is satisfied under the conditions formulated by the next theorem.

Theorem 6.

Consider $(a^0,{\varphi }^0)\in \mathcal{O}$ to be a strong optimal solution of the $LU$ type to $\left(Prob\right)$ and ${\displaystyle {\int }_{\Psi }-w_{\nu }\left(\zeta \right)d{t}^{\nu }}$ to be $LU$-convex at $(a^0,{\varphi }^0)\in \mathcal{O}$. Then, $(a^0,{\varphi }^0)\in \mathcal{O}$ solves the inequality $(Split-Ineq)$.

Proof. 

By hypothesis, we have that $(a^0,{\varphi }^0)\in \mathcal{O}$ is a strong optimal solution of the $LU$ type to $\left(Prob\right)$. In contrast, let us assume that $(a^0,{\varphi }^0)\in \mathcal{O}$ is not a solution of $(Split-Ineq)$. Thus, for $(a,\varphi )\in \mathcal{O}$, the inequalities

$${\displaystyle {\int }_{\Psi }\left\{w_{\nu ,a}^L\left({\zeta }^0\right)\left(a-a^0\right)+w_{\nu ,a_{\gamma }}^L\left({\zeta }^0\right)D_{\gamma }\left(a-a^0\right)+w_{\nu ,\varphi }^L\left({\zeta }^0\right)\left(\varphi -{\varphi }^0\right)\right\}d{t}^{\nu }\le 0,}$$

(2)

$${\displaystyle {\int }_{\Psi }\left\{w_{\nu ,a}^U\left({\zeta }^0\right)\left(a-a^0\right)+w_{\nu ,a_{\gamma }}^U\left({\zeta }^0\right)D_{\gamma }\left(a-a^0\right)+w_{\nu ,\varphi }^U\left({\zeta }^0\right)\left(\varphi -{\varphi }^0\right)\right\}d{t}^{\nu }\le 0}$$

(3)

hold. By considering the functional ${\displaystyle {\int }_{\Psi }-w_{\nu }\left(\zeta \right)d{t}^{\nu }}$ to be $LU$-convex at $(a^0,{\varphi }^0)\in \mathcal{O}$, this results in

$${\displaystyle {\int }_{\Psi }{w}_{\nu }^L\left(\zeta \right)d{t}^{\nu }-{\int }_{\Psi }{w}_{\nu }^L\left({\zeta }^0\right)d{t}^{\nu }}$$

$${\displaystyle \le {\int }_{\Psi }\left\{w_{\nu ,a}^L\left({\zeta }^0\right)\left(a-a^0\right)+w_{\nu ,a_{\gamma }}^L\left({\zeta }^0\right)D_{\gamma }\left(a-a^0\right)+w_{\nu ,\varphi }^L\left({\zeta }^0\right)\left(\varphi -{\varphi }^0\right)\right\}d{t}^{\nu }}$$

and

$${\displaystyle {\int }_{\Psi }{w}_{\nu }^U\left(\zeta \right)d{t}^{\nu }-{\int }_{\Psi }{w}_{\nu }^U\left({\zeta }^0\right)d{t}^{\nu }}$$

$${\displaystyle \le {\int }_{\Psi }\left\{w_{\nu ,a}^U\left({\zeta }^0\right)\left(a-a^0\right)+w_{\nu ,a_{\gamma }}^U\left({\zeta }^0\right)D_{\gamma }\left(a-a^0\right)+w_{\nu ,\varphi }^U\left({\zeta }^0\right)\left(\varphi -{\varphi }^0\right)\right\}d{t}^{\nu },}$$

for all pairs $(a,\varphi )\in \mathcal{O}$. In agreement with inequalities $\left(2\right)$ and $\left(3\right)$, the above inequalities yield

$${\int }_{\Psi }{w}_{\nu }^L\left(\zeta \right)d{t}^{\nu }\le {\int }_{\Psi }{w}_{\nu }^L\left({\zeta }^0\right)d{t}^{\nu }\mathrm{and}{\int }_{\Psi }{w}_{\nu }^U\left(\zeta \right)d{t}^{\nu }\le {\int }_{\Psi }{w}_{\nu }^U\left({\zeta }^0\right)d{t}^{\nu },$$

for $(a,\varphi )\in \mathcal{O}$. Equivalently, the inequality

$${\int }_{\Psi }{w}_{\nu }\left(\zeta \right)d{t}^{\nu }{⪯}_{LU}{\int }_{\Psi }{w}_{\nu }\left({\zeta }^0\right)d{t}^{\nu },$$

holds, for $(a,\varphi )\in \mathcal{O}$, which is a contradiction with the fact that $(a^0,{\varphi }^0)\in \mathcal{O}$ is a strong optimal solution of the $LU$ type of $\left(Prob\right)$. □

5. Numerical Applications

Let us consider the following optimization problem driven by interval-valued functionals:

$$\begin{array}{c}{\displaystyle \left(P_1\right)\underset{(a,\varphi )}{min}{\int }_{\Psi }{w}_{1}d{t}^1+w_{2}d{t}^2=\left[{\int }_{\Psi }{c}_1{\varphi }^2(d{t}^1+d{t}^2),{\int }_{\Psi }{c}_2{\varphi }^2(d{t}^1+d{t}^2)\right]}\\ \mathrm{subject}\mathrm{to}\\ D_{1}a=D_{2}a=l-\varphi ,\\ {\theta }^2-a^2\le 0,\\ a(0,0)=p,a(\tau ,\tau )=q,\end{array}$$

with $c_1,c_2,l,\theta ,p,q$ being positive real parameters associated with problem $\left(P_1\right)$, and $t\in \mathcal{M}={[0,\tau ]}^2,\Psi \subset \mathcal{M}$.

For the above-considered problem, we denote

$${\displaystyle P^L(a,\varphi )={\int }_{\Psi }{c}_1{\varphi }^2(d{t}^1+d{t}^2)\mathrm{and}{P}^U(a,\varphi )={\int }_{\Psi }{c}_2{\varphi }^2(d{t}^1+d{t}^2)}$$

and the condition $w_{\nu }^L\left(\zeta \right)\le w_{\nu }^U\left(\zeta \right)$ leads to $c_1\le c_2$. The convex subset of feasible solutions associated with $\left(P_1\right)$ is defined as

$${\displaystyle \mathcal{O}=\{(a,\varphi )\in \mathfrak{A}\times \mathfrak{R}\mid D_{1}a=D_{2}a=l-\varphi ,{\theta }^2-a^2\le 0,a(0,0)=p,a(\tau ,\tau )=q\}.}$$

From the conditions imposed on the problem $\left(P_1\right)$, we find $a=(l-\varphi )(t^1+t^2)+p$ and ${\displaystyle \varphi (\tau ,\tau )=l-\frac{q-p}{2\tau }}$. Denoting ${\displaystyle (a^0,{\varphi }^0)=(\frac{q-p}{2\tau }(t^1+t^2)+p,l-\frac{q-p}{2\tau })}$, the functionals $P^L(a,\varphi )$ and $P^U(a,\varphi )$ are convex at $(a^0,{\varphi }^0)$. Thus, the condition of $LU$-convexity from Theorem 5 is fulfilled. Also, the $(Split-Ineq)$ at $(a^0,{\varphi }^0)$ for our problem becomes

$${\displaystyle {\int }_{\Psi }2c_1{\varphi }^0\left(\varphi -{\varphi }^0\right)(d{t}^1+d{t}^2)>0\mathit{and}{\int }_{\Psi }2c_2{\varphi }^0\left(\varphi -{\varphi }^0\right)(d{t}^1+d{t}^2)>0.}$$

For a control function $\varphi (t^1,t^2)=\alpha t^1+\beta t^2$, by using the path independence of the involved functional, the condition returns to

$$(\alpha +\beta )\tau =l-{\displaystyle \frac{q-p}{2\tau }}<{\displaystyle \frac{\tau }{4}}(3\alpha +\beta ),$$

meaning

$${\displaystyle \frac{3}{2\tau }(l-\frac{q-p}{2\tau })<\alpha ,\beta =\frac{1}{\tau }(l-\frac{q-p}{2\tau })-\alpha .}$$

With $(Split-Ineq)$ also being accomplished, according to Theorem 5, the solution $(a^0,{\varphi }^0)$ becomes an optimal solution of the $LU$ type.

For the second problem, let us consider

$$\begin{array}{c}{\displaystyle \left(P_2\right)\underset{(a,\varphi )}{min}{\int }_{\Psi }{w}_{1}d{t}^1+w_{2}d{t}^2=\left[{\int }_{\Psi }{(\varphi -c_1)}^{2}d{t}^1+{(\varphi -c_2)}^{2}d{t}^2,{\int }_{\Psi }{\varphi }^2(d{t}^1+d{t}^2)\right]}\\ \mathrm{subject}\mathrm{to}\\ D_{1}a=D_{2}a=l-\varphi ,\\ {\theta }^2-a^2\le 0,\\ a(0,0)=p,a(\tau ,\tau )=q.\end{array}$$

We consider

$${\displaystyle P^L(a,\varphi )={\int }_{\Psi }{(\varphi -c_1)}^{2}d{t}^1+{(\varphi -c_2)}^{2}d{t}^2,P^U(a,\varphi )={\int }_{\Psi }{\varphi }^2(d{t}^1+d{t}^2)}$$

and, also, the feasible solution set is the same as for $\left(P_1\right)$. The condition $w_{\nu }^L\left(\zeta \right)\le w_{\nu }^U\left(\zeta \right)$ leads to $\varphi \ge c_1/2$, $\varphi \ge c_2/2$. The interval-valued functional $[P^L(a,\varphi ),P^U(a,\varphi )]$ is $LU$-convex at $(a^0,{\varphi }^0)$. The $(Split-Ineq)$ at $(a^0,{\varphi }^0)$ for problem $\left(P_2\right)$ becomes

$${\displaystyle {\int }_{\Psi }2\left(\varphi -{\varphi }^0\right)\left(({\varphi }^0-c_1)d{t}^1+({\varphi }^0-c_2)d{t}^2\right)>0\mathrm{and}{\int }_{\Psi }2{\varphi }^0\left(\varphi -{\varphi }^0\right)(d{t}^1+d{t}^2)>0.}$$

The following compatibility condition between parameters is obtained:

$$l-{\displaystyle \frac{q-p}{2\tau }}\ge {\displaystyle \frac{1}{2}}max(c_1,c_2).$$

By using a control function $\varphi (t^1,t^2)=\alpha t^1+\beta t^2$ again, one obtains the condition

$$2{\left({\varphi }^0\right)}^2-{\varphi }^0(c_1+c_2+(3\alpha +\beta )\tau /2+\alpha \tau c_1/2+(\alpha \tau +\beta \tau /2)c_2<0,$$

which, once fulfilled, enables $(a^0,{\varphi }^0)$ to become an optimal solution of the $LU$ type for the problem $\left(P_2\right)$.

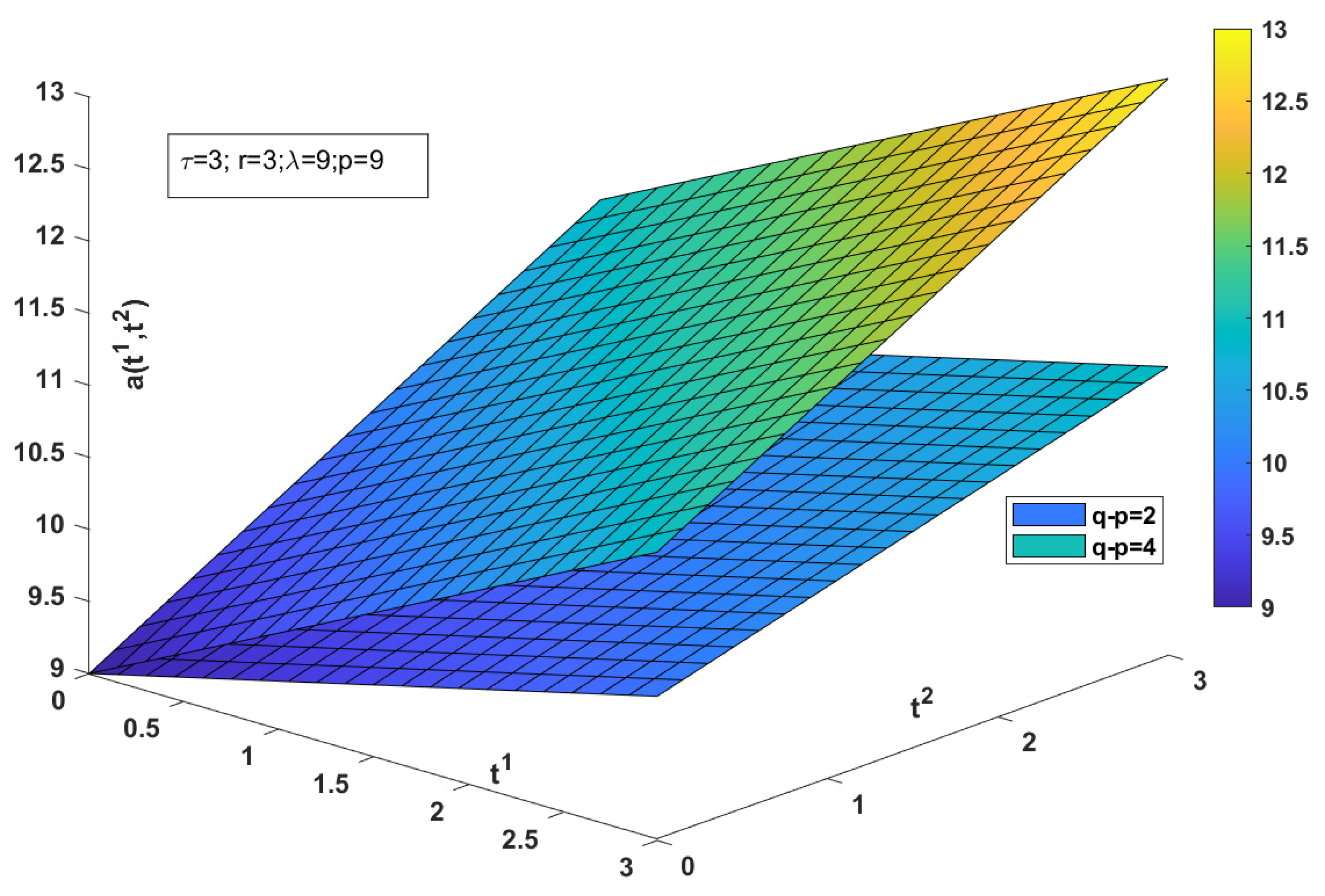
For the numerical case $\tau =3,l=3,\theta =9,p=9$ with $q-p=2$ and $q-p=4$, a graphical representation of the optimal solution is shown in Figure 1. In this picture, we can see the variation of an optimal solution with the difference of fixed conditions. Specifically, we can notice the distance between the two surfaces, i.e., when the difference between the fixed conditions is smaller, ($q-p=2$) then the surface is positioned lower than when the difference of fixed conditions is greater ($q-p=4$). This means that for large variations in boundary conditions, we will obtain optimal surfaces that are located higher.

Figure 1. Variation of an optimal solution with the difference of fixed conditions.

6. Conclusions

In this study, we formulated and proved some new results of the existence of solutions associated with a family of interval-valued minimization models. More precisely, we stated some characterization results on the set of solutions for the considered interval-valued minimization model by considering the solution set associated with some controlled split variational inequalities. These theoretical reciprocal results were also illustrated by suitable numerical experiments.

As further developments of the analysis provided in this study (that is, cases where $LU$-convexity fails to hold), we can mention the extension of the concept of $LU$-convexity to a more general one like $LU$-invexity and its various forms. In this way, this work will have greater applicability in various areas of science.