Semigroups and Evolution Equations in Modular Function Spaces

Abstract

This paper develops the theory of strongly continuous semigroups and abstract evolution equations in modular function spaces. We study the autonomous problem $\dot{u}\left(t\right)=Bu\left(t\right)$ with initial condition $u\left(0\right)=u_0\in L_{\rho }$, where B is the infinitesimal generator of a strongly continuous semigroup ${\left(S\left(t\right)\right)}_{t\ge 0}$ on $L_{\rho }$. Within this framework, we establish modular analogues of classical results from Banach-space semigroup theory, including criteria for $\rho$-boundedness and $\rho$-continuity, a Laplace resolvent representation of the generator, and explicit resolvent bounds in terms of the modular growth function ${\omega }_{\rho }$. Under a ${\Delta }_2$-type condition on the modular, we justify Steklov regularization of semigroup orbits, obtain domain inclusion and the resolvent identity, and derive spectral consequences for classes of operators naturally acting on $L_{\rho }$. The results show that the structural features of the classical semigroup framework persist in the modular topology, providing a unified approach to linear evolution in modular function spaces.

1. Introduction

The present paper is devoted to the study of abstract evolution equations in modular function spaces of the type $L_{\rho }$. Our aim is to extend the theory of strongly continuous semigroups and their infinitesimal generators to the modular framework and, in particular, to establish modular analogues of the fundamental results of semigroup theory developed for Banach spaces by Engel and Nagel [1] and Pazy [2].

We consider the autonomous abstract Cauchy problem

$$\dot{u}\left(t\right)=Bu\left(t\right),u\left(0\right)=u_0\in L_{\rho },$$

(1)

where $B:D\left(B\right)\subset L_{\rho }\to L_{\rho }$ denotes the (possibly unbounded) infinitesimal generator of a strongly continuous semigroup ${\left(S\left(t\right)\right)}_{t\ge 0}$ acting on $L_{\rho }$. Equation (1) is the modular counterpart of the classical linear evolution problem in Banach spaces; however, convergence, continuity, and differentiability are formulated here in the modular sense.

Working in modular spaces broadens the classical semigroup theory to a flexible analytical setting that can accommodate nonstandard growth and heterogeneous structures. The modular approach, developed systematically by Khamsi and Kozłowski [3], is based on a convex regular modular $\rho :{\mathcal{M}}_{\infty }\to [0,\infty ]$ and the topology of modular convergence. Within this framework, Bachar [4] established modular versions of key tools for linear evolution, including the construction of strongly continuous semigroups, the treatment of resolvents via Laplace-type representations, and operator bounds expressed through the growth function associated with $\rho$. These developments connect the classical semigroup theory of Engel–Nagel [1] and Pazy [2] with the nonlinear modular analysis of Khamsi–Kozłowski [3].

In this paper, we investigate generation, continuity, and spectral properties of strongly continuous semigroups on $L_{\rho }$. We identify conditions that ensure the existence of generators, derive modular resolvent representations together with explicit bounds, and justify the regularization of semigroup orbits in the modular topology. The results show that many structural features of the classical theory persist in $L_{\rho }$ once the norm topology is replaced by modular convergence. Under a standard ${\Delta }_2$-type assumption, the modular $\rho$ is equivalent to the associated Luxembourg norm, so the functional analysis result of the classical theory is preserved. Nevertheless, in this work, we formulate our a priori exponential bounds for the semigroup, the Laplace-type resolvent representations, and the generator domain characterizations primarily in modular form rather than in terms of the Luxembourg norm, since $\rho$ is the natural energy functional arising from the evolution problem and yields slightly sharper and more transparent quantitative estimates, which are particularly convenient from the numerical viewpoint. This effect is illustrated in Example 1, where a simple multiplication semigroup is used to demonstrate the potential difficulties that may occur in a purely Luxembourg norm-based numerical analysis. In this setting, the Luxembourg norm requires solving a nontrivial implicit equation, whereas the modular behavior is given explicitly and yields sharper and more transparent estimates.

The paper is organized as follows. Section 2 recalls the main concepts for $L_{\rho }$, including convex regular modulars, $\rho$-continuity, the ${\Delta }_2$-type condition, and the associated growth function. Section 3 develops the abstract evolution equation and semigroup framework in $L_{\rho }$: we formulate the notion of solution in the modular sense, construct strongly continuous semigroups from $\rho$-bounded generators via their exponential series, derive modular exponential bounds, and Laplace-type resolvent representations with explicit constants, and establish domain inclusion and generator identities using Steklov regularization.

2. Modular Spaces and Notation

We recall the fundamental notions of modular function spaces that form the analytical foundation of our work. The presentation follows the general framework of [3], the formulation in [4]. These concepts provide the functional setting for studying $\rho$-continuity, modular convergence, and the generation of semigroups in $L_{\rho }$.

Let $(0,T)$ be a finite interval endowed with the Lebesgue $\sigma$-algebra $\Sigma$, and denote by ${\mathcal{M}}_{\infty }$ the space of all extended real-valued measurable functions on $(0,T)$. A mapping $\rho :{\mathcal{M}}_{\infty }\to [0,\infty ]$, as introduced in Definition 3.1 of [3], is called a regular convex function pseudomodular if it is nontrivial, even, convex, monotone, orthogonally subadditive, and satisfies both the Fatou property and order continuity on the underlying lattice. If, in addition, $\rho \left(f\right)=0$ implies that $f=0$$\rho$ almost everywhere ($\rho$-a.e.), then $\rho$ is called a regular convex function modular. We denote by M the set of measurable functions that are finite $\rho$-a.e., identifying functions that coincide outside a $\rho$-null set.

Definition 1

(Convex regular modular [3,4]). A mapping $\rho :{\mathcal{M}}_{\infty }\to [0,\infty ]$ is called a convex regular modular if, for all $\varphi ,\psi \in {\mathcal{M}}_{\infty }$ and $a\in [0,1]$,

(i) 

$\rho \left(\varphi \right)=0$ if and only if $\varphi =0$ ρ-a.e.;

(ii) 

$\rho \left(a\varphi \right)=\rho \left(\varphi \right)$ whenever $\left|a\right|=1$;

(iii) 

$\rho (a\varphi +(1-a\left)\psi \right)\le a\rho \left(\varphi \right)+(1-a)\rho \left(\psi \right)$.

Given a convex regular modular $\rho$, the associated modular function space is defined by

$$L_{\rho }:=\left\{f\in M:\rho \left(\lambda f\right)<\infty \mathrm{for}\mathrm{some}\lambda >0\right\}.$$

The space $L_{\rho }$ is equipped with the Luxembourg norm

$${\parallel f\parallel }_{\rho }:=inf\left\{t>0:\rho \left(\frac{1}{t}f\right)\le 1\right\},f\in L_{\rho },$$

(2)

and the topology of $\rho$-continuity is induced by the modular itself.

Throughout, we assume the ${\Delta }_2$-type condition

$${\omega }_{\rho }\left(2\right):=inf\left\{K>0:\rho \left(2f\right)\le K\rho \left(f\right)\mathrm{for}\mathrm{all}f\in L_{\rho }\right\}<\infty ,$$

(3)

which ensures the topological equivalence between $\rho$ and ${\parallel ·\parallel }_{\rho }$. In particular, the convexity estimate

$$\rho (f+g)\le {\displaystyle \frac{{\omega }_{\rho }\left(2\right)}{2}}\left(\rho \left(f\right)+\rho \left(g\right)\right),f,g\in L_{\rho },$$

(4)

holds. The corresponding growth function is given by

$${\omega }_{\rho }\left(t\right):=sup\left\{{\displaystyle \frac{\rho \left(tf\right)}{\rho \left(f\right)}}:0<\rho \left(f\right)<\infty \right\},t\ge 0,$$

(5)

and remains finite for all $t>0$ under assumption (3). Moreover, the Fatou property yields the lower semicontinuity

$$\rho \left(f\right)\le \underset{n\to \infty }{lim\; inf}\rho \left(f_n\right)\mathrm{whenever}{f}_n\to f\rho \text{-}\mathrm{a}.\mathrm{e}..$$

(6)

We next recall the notions of $\rho$-bounded operators and strongly continuous semigroups.

Definition 2

($\rho$-bounded operator [4]). A linear operator $B:L_{\rho }\to L_{\rho }$ is called $\rho$-bounded if there exists a constant $M_B>0$ such that

$$\rho \left(Bf\right)\le M_B\rho \left(f\right),f\in L_{\rho }.$$

The smallest such constant $M_B$ is referred to as the$\rho$-bound of B.

Definition 3

(Strongly continuous semigroup [3,4]). A family ${\left(S\left(t\right)\right)}_{t\ge 0}$ of operators on $L_{\rho }$ is called a strongly continuous semigroup if the following conditions hold:

(i) 

$S\left(0\right)=I_{L_{\rho }}$;

(ii) 

$S(t+s)=S\left(t\right)S\left(s\right)$ for all $t,s\ge 0$;

(iii) 

for each $f\in L_{\rho }$, the function $t\mapsto \rho \left(S\right(t)f-f)$ is continuous on $[0,\infty )$.

If only conditions (i)–(ii) are satisfied, ${\left\{S\left(t\right)\right\}}_{t\ge 0}$ is said to possess the algebraic semigroup property. The infinitesimal generator B of $S(·)$ is defined by

$$Bf=\underset{t\downarrow 0}{lim}{\displaystyle \frac{S\left(t\right)f-f}{t}}\mathrm{in}{L}_{\rho },D\left(B\right):=\left\{f\in L_{\rho }:\underset{t\downarrow 0}{lim}\frac{S\left(t\right)f-f}{t}\mathrm{exists}\right\}.$$

Lemma 1

([3,4]). If $B\in \mathcal{L}\left(L_{\rho }\right)$ is ρ-bounded with constant $M_B>0$, then there exists ${\tilde{M}}_B:=max\{M_B,1\}>1$ such that

$${\parallel Bf\parallel }_{\rho }\le {\tilde{M}}_B{\parallel f\parallel }_{\rho },f\in L_{\rho }.$$

The space $L_{\rho }$, endowed with the topology of $\rho$-continuity, serves as the functional setting for all subsequent developments. This framework will be used to construct strongly continuous semigroups, to analyze their spectral properties, and to derive resolvent estimates in the modular space $L_{\rho }$.

3. The Abstract Evolution Equation and Semigroup Framework

Let ${\left(S\left(t\right)\right)}_{t\ge 0}$ be a strongly continuous semigroup on $L_{\rho }$ with infinitesimal generator $B,D\left(B\right)$ in the modular sense, as discussed in [3,4]. Throughout this section, we study the autonomous abstract Cauchy problem in the sense of $L_{\rho }$, $\rho$-a.e.,

$$\dot{u}\left(t\right)=Bu\left(t\right),t\ge 0,$$

(7a)

$$u\left(0\right)=u_0.$$

(7b)

Equation (7) provides the abstract framework for the analysis of linear evolution processes generated by the semigroup ${\left(S\left(t\right)\right)}_{t\ge 0}$ on $L_{\rho }$. In this setting, the dynamics of the system are governed by the generator B, and the semigroup $S\left(t\right)$ yields the modular representation

$$u\left(t\right)=S\left(t\right)u_0,\mathrm{in}{L}_{\rho },\rho \text{-}\mathrm{a}.\mathrm{e}.,t\ge 0,$$

whenever $u_0\in D\left(B\right)$. Our aim is to establish conditions ensuring $\rho$-continuity, exponential boundedness, and modular resolvent representations for strongly continuous semigroups acting in the space $L_{\rho }$. The results presented in Theorems 1 and 2 constitute modular analogues of the classical results of Engel and Nagel [1].

Definition 4.

A ρ-continuous function $u:[0,\infty )\to L_{\rho }$ is called a solution of the abstract evolution Equation (7) with initial value $u_0\in L_{\rho }$ if the following conditions are satisfied:

(i) 

u is right-differentiable at $t=0$ in the modular sense, i.e., there exists $v\in L_{\rho }$ such that

$$\underset{h\to 0^{+}}{lim}\rho \left({\displaystyle \frac{u\left(h\right)-u\left(0\right)}{h}}-v\right)=0,\mathit{and}\mathit{we}\mathit{set}{\dot{u}}_{+}\left(0\right):=v;$$

(ii) 

for every $t>0$ there exists $\dot{u}\left(t\right)\in L_{\rho }$ such that

$$\underset{h\to 0}{lim}\rho \left({\displaystyle \frac{u(t+h)-u\left(t\right)}{h}}-\dot{u}\left(t\right)\right)=0,$$

and the mapping $t\mapsto \dot{u}\left(t\right)$ is ρ-continuous on $(0,\infty )$;

(iii) 

$u\left(t\right)\in D\left(B\right)$ for all $t\ge 0$;

(iv) 

the evolution equation holds in the modular sense,

$$\dot{u}\left(t\right)=Bu\left(t\right)\mathit{in}{L}_{\rho },\rho \text{-}a.e.,t>0,u\left(0\right)=u_0.$$

In order to illustrate the role of $\rho$-bounded operators in the theory of semigroups, we next show that such operators naturally give rise to strongly continuous semigroups via their exponential series representation. This construction provides the appropriate analogue of the classical bounded generator theorem from Banach-space semigroup theory as developed in [1,2], and it ensures that the essential features of the classical theory, such as strong continuity, the semigroup property, and the existence of an infinitesimal generator, carry over to the modular setting. The modular counterpart of this result was studied in detail in [4], where it is shown that the boundedness condition on the operator suffices to guarantee the existence of a well-defined strongly continuous semigroup together with the corresponding convergence properties of its exponential series.

Lemma 2.

Let ρ be a convex, regular modular satisfying the ${\Delta }_2$-type condition, and let $B\in \mathcal{L}\left(L_{\rho }\right)$ be ρ-bounded with constant $M_B>0$ in the sense of Definition 2. For $t\ge 0$ define

$$S\left(t\right)\varphi :=\sum _{n=0}^{\infty }{\displaystyle \frac{t^n}{n!}}{B}^n\varphi ,\varphi \in L_{\rho },$$

where the series converges in the modular topology. Then ${\left\{S\left(t\right)\right\}}_{t\ge 0}$ is a strongly continuous semigroup on $L_{\rho }$, $S\left(0\right)=I_{L_{\rho }}$, $S(t+s)=S\left(t\right)S\left(s\right)$ for all $t,s\ge 0$, and

$$\rho \left(S\left(t\right)\varphi \right)\le C\left(t\right)e^{M_{B}t}\rho \left(\varphi \right),C\left(t\right):={\displaystyle \frac{{\omega }_{\rho }\left(e^t\right)}{e^t}},t\ge 0,\varphi \in L_{\rho }.$$

(8)

Proof. 

The proof follows the modular semigroup construction developed in [4]. Since $\rho$ satisfies the ${\Delta }_2$-type condition, the growth function

$${\omega }_{\rho }\left(\lambda \right):=sup\left\{{\displaystyle \frac{\rho \left(\lambda u\right)}{\rho \left(u\right)}}:0<\rho \left(u\right)<\infty \right\},\lambda \ge 0,$$

is finite for all $\lambda >0$, increasing, convex, and submultiplicative [4]. We use the following convexity-scaling inequality: if $c_k\ge 0$ and $A={\sum }_k{c}_k\in (0,\infty )$, then

$$\rho \left(\sum _k{c}_k{y}_k\right)\le {\displaystyle \frac{{\omega }_{\rho }\left(A\right)}{A}}\sum _k{c}_k\rho \left(y_k\right),$$

(9)

which follows from convexity of $\rho$ and the property $\rho \left(Az\right)\le {\omega }_{\rho }\left(A\right)\rho \left(z\right)$.

For $t\ge 0$, set $c_n=t^n/n!$ and $A=e^t$. Applying (9) to $y_n=B^n\varphi$ gives

$$\rho \left(S\left(t\right)\varphi \right)=\rho \left(\sum _{n=0}^{\infty }{\displaystyle \frac{t^n}{n!}}{B}^n\varphi \right)\le {\displaystyle \frac{{\omega }_{\rho }\left(e^t\right)}{e^t}}\sum _{n=0}^{\infty }{\displaystyle \frac{t^n}{n!}}\rho \left(B^n\varphi \right).$$

Since B is $\rho$-bounded, $\rho \left(B^n\varphi \right)\le M_B^n\rho \left(\varphi \right)$, and hence

$$\rho \left(S\left(t\right)\varphi \right)\le {\displaystyle \frac{{\omega }_{\rho }\left(e^t\right)}{e^t}}\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(M_{B}t\right)}^n}{n!}}\rho \left(\varphi \right)=C\left(t\right)e^{M_{B}t}\rho \left(\varphi \right).$$

The series defining $S\left(t\right)\varphi$ therefore converges in the modular topology, and inequality (8) follows.

To verify the semigroup property, define the partial sums

$$S_N\left(t\right)\varphi :=\sum _{n=0}^N{\displaystyle \frac{t^n}{n!}}{B}^n\varphi .$$

For $s,t\ge 0$, the algebraic Cauchy product gives

$$S_N\left(t\right)S_M\left(s\right)\varphi =\sum _{k=0}^{N+M}{a}_k^{N,M}(t,s)B^k\varphi ,a_k^{N,M}(t,s):=\sum _{\begin{array}{c}n+m=k\\ 0\le n\le N,0\le m\le M\end{array}}{\displaystyle \frac{t^n{s}^m}{n!m!}}.$$

For each fixed k, $a_k^{N,M}(t,s)\to b_k(t,s):={\displaystyle \frac{{(t+s)}^k}{k!}}$ as $N,M\to \infty$, and ${\sum }_k{b}_k(t,s)=e^{t+s}$. Applying (9) to ${\sum }_k{b}_k(t,s)B^k\varphi$ and using $\rho \left(B^k\varphi \right)\le M_B^k\rho \left(\varphi \right)$ gives

$$\rho \left(\sum _{k=0}^{\infty }{b}_k(t,s)B^k\varphi \right)\le {\displaystyle \frac{{\omega }_{\rho }\left(e^{t+s}\right)}{e^{t+s}}}\sum _{k=0}^{\infty }{\displaystyle \frac{{(t+s)}^k{M}_B^k}{k!}}\rho \left(\varphi \right)=C(t+s)e^{M_B(t+s)}\rho \left(\varphi \right).$$

By dominated convergence in the modular sense, it follows that

$$\underset{N,M\to \infty }{lim}\rho \left(S_N\left(t\right)S_M\left(s\right)\varphi -\sum _{k=0}^{\infty }{b}_k(t,s)B^k\varphi \right)=0,$$

and hence $S\left(t\right)S\left(s\right)\varphi =S(t+s)\varphi$ for all $t,s\ge 0$. Since $S\left(0\right)=I_{L_{\rho }}$, the family ${\left\{S\left(t\right)\right\}}_{t\ge 0}$ satisfies the algebraic semigroup property.

To show strong continuity at $t=0$, define ${\Lambda }_{\varphi }\left(t\right):=\rho (S\left(t\right)\varphi -\varphi )$. From the definition of $S\left(t\right)$,

$$S\left(t\right)\varphi -\varphi =\sum _{n=1}^{\infty }{\displaystyle \frac{t^n}{n!}}{B}^n\varphi =t\left(B\varphi +\sum _{n=2}^{\infty }{\displaystyle \frac{t^{n-1}}{n!}}{B}^n\varphi \right).$$

Applying (9) and using $\rho \left(B^n\varphi \right)\le M_B^n\rho \left(\varphi \right)$ yields

$${\Lambda }_{\varphi }\left(t\right)\le {\displaystyle \frac{{\omega }_{\rho }(e^t-1)}{e^t-1}}\sum _{n=1}^{\infty }{\displaystyle \frac{t^n{M}_B^n}{n!}}\rho \left(\varphi \right)={\displaystyle \frac{{\omega }_{\rho }(e^t-1)}{e^t-1}}\left(e^{M_{B}t}-1\right)\rho \left(\varphi \right)\underset{t\downarrow 0}{\to }0.$$

Hence $t\mapsto \rho \left(S\right(t)\varphi -\varphi )$ is continuous at $t=0$, and by the semigroup property, on all $[0,\infty )$.

Finally, for $t>0$ we compute

$${\displaystyle \frac{S\left(t\right)\varphi -\varphi }{t}}-B\varphi =\sum _{n=2}^{\infty }{\displaystyle \frac{t^{n-1}}{n!}}{B}^n\varphi .$$

Using the $\rho$-boundedness of B gives

$$\rho \left({\displaystyle \frac{S\left(t\right)\varphi -\varphi }{t}}-B\varphi \right)\le \sum _{n=2}^{\infty }{\displaystyle \frac{t^{n-1}}{n!}}{M}_B^n\rho \left(\varphi \right)=\left({\displaystyle \frac{e^{t{M}_B}-1}{t}}-M_B\right)\rho \left(\varphi \right)\underset{t\downarrow 0}{\to }0.$$

Thus, ${lim}_{t\downarrow 0}(S\left(t\right)\varphi -\varphi )/t=B\varphi$ in $L_{\rho }$ for all $\varphi \in D\left(B\right)$, and B is the infinitesimal generator of the strongly continuous semigroup ${\left\{S\left(t\right)\right\}}_{t\ge 0}$. □

We now consider the integral (Laplace) representation of the resolvent under the growth hypothesis of Lemma 2. The corresponding $\rho$-boundedness estimate for the resolvent depends on the modular growth function ${\omega }_{\rho }$ and on the $\rho$-boundedness constant $M_B$ of the generator B. Let $\overline{\omega }\in {\mathbb{R}}_{+}$ denote a threshold to be specified below. The precise bound is stated in the following Theorem; its magnitude is quantified in terms of ${\omega }_{\rho }$ and $M_B$, and an explicit estimate is provided in Remark 2.

Theorem 1

(Laplace resolvent). Under the hypotheses and notation of Lemma 2, let $\lambda >\overline{\omega }$ and set

$$K_{\lambda }:={\int }_0^{\infty }C\left(t\right)e^{-(\lambda -M_B)t}dt.$$

If $K_{\lambda }<\infty$, then for every $\varphi \in L_{\rho }$ the Laplace integral

$$R(\lambda ,B)\varphi :={\int }_0^{\infty }{e}^{-\lambda t}S\left(t\right)\varphi dt$$

exists in $L_{\rho }$ and defines a linear ρ–bounded operator $R(\lambda ,B)\in \mathcal{L}\left(L_{\rho }\right)$ with

$$\rho \left(R(\lambda ,B)\varphi \right)\le c_{\rho }\left(\lambda \right)K_{\lambda }\rho \left(\varphi \right),$$

where

$$c_{\rho }\left(\lambda \right)=\left\{\begin{array}{cc}1,\hfill & \lambda \ge 1,\hfill \\ {\displaystyle max\left\{1,{\omega }_{\rho }\left(e\right){\lambda }^{1-ln{\omega }_{\rho }\left(e\right)}\right\},}\hfill & 0<\lambda <1.\hfill \end{array}\right.$$

Proof. 

Fix $\lambda >\overline{\omega }$ and $\varphi \in L_{\rho }$. For $T>0$ set

$$R_T\varphi :={\int }_0^T{e}^{-\lambda t}S\left(t\right)\varphi dt,$$

where the integral is taken in the Bochner sense [3]. Let $0=t_0<t_1<\cdots <t_n=T$ be a partition of $[0,T]$ and define

$$x_n:=\sum _{i=0}^{n-1}{\alpha }_{i}S\left(t_i\right)\varphi ,{\alpha }_i:=e^{-\lambda t_i}(t_{i+1}-t_i)\ge 0,\beta :=\sum _{i=0}^{n-1}{\alpha }_i.$$

By the Lebesgue dominated convergence theorem for Bochner integrals, we have

$$\parallel x_n-R_T{\varphi \parallel }_{\rho }⟶0\mathrm{as}\left|\tau \right|:=\underset{0\le i\le n}{sup}|t_{i+1}-t_i|⟶0,$$

that is, $x_n\to R_T\varphi$ in the Luxembourg norm ${\parallel ·\parallel }_{\rho }$; see [3] for details. Moreover, since the modular $\rho$ satisfies the ${\Delta }_2$-type condition, norm convergence implies modular convergence, and hence

$$\rho (x_n-R_T\varphi )⟶0,$$

Normalize $w_i:={\alpha }_i/\beta$ so that ${\sum }_{i=0}^{n-1}{w}_i=1$, and write

$$x_n=\beta \sum _{i=0}^{n-1}{w}_{i}S\left(t_i\right)\varphi .$$

Using the growth function estimation $\rho \left(\beta u\right)\le {\omega }_{\rho }\left(\beta \right)\rho \left(u\right)$ and the convexity of $\rho$, we obtain

$$\begin{array}{cc}\hfill \rho \left(x_n\right)& =\rho \left(\beta \sum _{i=0}^{n-1}{w}_{i}S\left(t_i\right)\varphi \right)\le {\omega }_{\rho }\left(\beta \right)\rho \left(\sum _{i=0}^{n-1}{w}_{i}S\left(t_i\right)\varphi \right)\hfill \\ & \le {\omega }_{\rho }\left(\beta \right)\sum _{i=0}^{n-1}{w}_i\rho \left(S\left(t_i\right)\varphi \right)={\displaystyle \frac{{\omega }_{\rho }\left(\beta \right)}{\beta }}\sum _{i=0}^{n-1}{\alpha }_i\rho \left(S\left(t_i\right)\varphi \right).\hfill \end{array}$$

By Lemma 2, $\rho \left(S\left(t_i\right)\varphi \right)\le C\left(t_i\right)e^{M_B{t}_i}\rho \left(\varphi \right)$ for all $t_i\ge 0$. Consequently,

$$\rho \left(x_n\right)\le {\displaystyle \frac{{\omega }_{\rho }\left(\beta \right)}{\beta }}\rho \left(\varphi \right)\sum _{i=0}^{n-1}C\left(t_i\right)e^{-(\lambda -M_B)t_i}(t_{i+1}-t_i).$$

Moreover, since ${\alpha }_i=e^{-\lambda t_i}(t_{i+1}-t_i)$, we have

$$\beta =\sum _{i=0}^{n-1}{e}^{-\lambda t_i}(t_{i+1}-t_i)\le {\int }_0^T{e}^{-\lambda t}dt={\displaystyle \frac{1-e^{-\lambda T}}{\lambda }}\le {\displaystyle \frac{1}{\lambda }}.$$

• If $\lambda \ge 1$, then $\beta \le 1$, and by the homogeneity of $\rho$ we have ${\omega }_{\rho }\left(\beta \right)\le \beta$. Hence

  $$\rho \left(x_n\right)\le \rho \left(\varphi \right)\sum _{i=0}^{n-1}C\left(t_i\right)e^{-(\lambda -M_B)t_i}(t_{i+1}-t_i).$$
• If $0<\lambda <1$, then $\beta \le \frac{1}{\lambda }$ and $\frac{1}{\lambda }>1$. The ${\Delta }_2$-type condition implies that the growth function ${\omega }_{\rho }$ is submultiplicative,

  $${\omega }_{\rho }\left(st\right)\le {\omega }_{\rho }\left(s\right){\omega }_{\rho }\left(t\right),s,t\ge 1,$$

  and monotone in t. For $\beta >1$, write $\beta =e^{m+\theta }$ with $m:=\lfloor ln\beta \rfloor \in \mathbb{N}$ and $\theta \in [0,1)$, where $\lfloor t\rfloor$ denotes the floor of t, i.e., the greatest integer less than or equal to t. Then

  $${\omega }_{\rho }\left(\beta \right)={\omega }_{\rho }\left(e^{m+\theta }\right)\le {\omega }_{\rho }{\left(e\right)}^m{\omega }_{\rho }\left(e^{\theta }\right)\le {\omega }_{\rho }{\left(e\right)}^{m+1}\le {\omega }_{\rho }\left(e\right){\beta }^{ln{\omega }_{\rho }\left(e\right)}.$$
  Combining the above inequalities, we obtain

  $${\displaystyle \frac{{\omega }_{\rho }\left(\beta \right)}{\beta }}\le {\omega }_{\rho }\left(e\right){\beta }^{ln{\omega }_{\rho }\left(e\right)-1}\le {\omega }_{\rho }\left(e\right){\left(\frac{1}{\lambda }\right)}^{ln{\omega }_{\rho }\left(e\right)-1}={\omega }_{\rho }\left(e\right){\lambda }^{1-ln{\omega }_{\rho }\left(e\right)}.$$

Passing to the limit along the partition and using the Fatou property of $\rho$ for Bochner integrals under the ${\Delta }_2$-type condition (see [3]), we obtain

$$\rho \left(R_T\varphi \right)\le c_{\rho }\left(\lambda \right)\rho \left(\varphi \right){\int }_0^{T}C\left(t\right)e^{-(\lambda -M_B)t}dt.$$

To pass from T to ∞, observe that for $0<T_1<T_2$ the same estimate yields

$$\rho \left(R_{T_2}\varphi -R_{T_1}\varphi \right)\le c_{\rho }\left(\lambda \right)\rho \left(\varphi \right){\int }_{T_1}^{T_2}C\left(t\right)e^{-(\lambda -M_B)t}dt\underset{T_1,T_2\to \infty }{\to }0.$$

Hence, the sequence ${\left\{R_T\varphi \right\}}_{T>0}$ is Cauchy in the modular topology of $L_{\rho }$. Since $\rho$ satisfies the ${\Delta }_2$-type condition, it follows that

$$\rho \left(R_{T_2}\varphi -R_{T_1}\varphi \right)\to 0⟹{\parallel R_{T_2}\varphi -R_{T_1}\varphi \parallel }_{\rho }\to 0,$$

and thus ${\left\{R_T\varphi \right\}}_{T>0}$ is also Cauchy in the Luxembourg norm. Therefore,

$$\parallel R_T{\varphi -R(\lambda ,B)\varphi \parallel }_{\rho }⟶0\mathrm{as}T\to \infty ,$$

that is, $R_T\varphi \to R(\lambda ,B)\varphi$ in the Luxembourg norm. By the ${\Delta }_2$-type condition, this implies modular convergence as well, namely

$$\rho \left(R_T\varphi -R(\lambda ,B)\varphi \right)⟶0,T\to \infty .$$

By the lower semicontinuity of $\rho$ and the preceding bound, we obtain

$$\begin{array}{cc}\hfill \rho \left(R(\lambda ,B)\varphi \right)& \le c_{\rho }\left(\lambda \right)\underset{T\to \infty }{lim\; inf}\rho \left(R_T\varphi \right)\hfill \\ \hfill & \le c_{\rho }\left(\lambda \right)\left({\int }_0^{\infty }C\left(t\right)e^{-(\lambda -M_B)t}dt\right)\rho \left(\varphi \right)=c_{\rho }\left(\lambda \right)K_{\lambda }\rho \left(\varphi \right).\hfill \end{array}$$

Consequently, $R(\lambda ,B)\in \mathcal{L}\left(L_{\rho }\right)$ is $\rho$-bounded with bound $K_{\lambda }$. Linearity follows directly from the linearity of the Bochner integral. □

It is often necessary to control the behavior of the resolvent as $\lambda$ approaches the origin. In particular, for applications in spectral analysis, it is important to know that the prefactor $c_{\rho }\left(\lambda \right)$ remains bounded on compact subintervals of $(0,1)$. This guarantees that the resolvent family does not lose its $\rho$-boundedness when passing to small values of $\lambda$, so that only the constants in the estimates are affected, while the essential operator properties such as linearity, existence, and domain inclusion remain unchanged. The following remark makes this uniformity explicit.

Remark 1.

Let $0<{\lambda }_0<1$. For all $\lambda \in [{\lambda }_0,1)$ the constant $c_{\rho }\left(\lambda \right)$ is uniformly bounded by

$$c_{\rho }\left(\lambda \right)\le max\left\{1,{\omega }_{\rho }\left(e\right){\lambda }_0^{1-ln{\omega }_{\rho }\left(e\right)}\right\}.$$

For $\lambda \ge 1$ we simply have $c_{\rho }\left(\lambda \right)=1$, so the bound is trivial. Hence the resolvent remains a ρ-bounded linear operator for every $\lambda >\overline{\omega }$, where the threshold $\overline{\omega }$ is chosen so that $K_{\lambda }<\infty$. Only the multiplicative constant $c_{\rho }\left(\lambda \right)$ in the bound depends on the growth function ${\omega }_{\rho }$ and on the range of λ.

To use the resolvent bounds effectively later, it is convenient to give explicit estimates for $K_{\lambda }$ under the ${\Delta }_2$-type condition and to indicate which growth constant yields the sharper bound.

Remark 2.

Assume ρ satisfies the ${\Delta }_2$-type condition and, in Proposition 2, take $C\left(t\right)={\omega }_{\rho }\left(e^t\right)/e^t$. Then, for $\lambda >\overline{\omega }$,

$$K_{\lambda }={\int }_0^{\infty }C\left(t\right)e^{-(\lambda -M_B)t}dt={\int }_0^{\infty }{\omega }_{\rho }\left(e^t\right)e^{-(\lambda -M_B+1)t}dt.$$

• Next, we establish explicit bounds together with the smallest λ factor. Since the ${\Delta }_2$-type condition implies the finiteness and submultiplicativity of ${\omega }_{\rho }$, see Lemma 3.1 in [3] and also [5,6], for $t\ge 0$,

  $${\omega }_{\rho }\left(e^t\right)\le {\omega }_{\rho }{\left(e\right)}^{\lceil t\rceil }\le {\omega }_{\rho }\left(e\right)e^{(ln{\omega }_{\rho }\left(e\right))t}.$$
  where $\lceil ·\rceil$ stands for the ceiling function, i.e., $\lceil t\rceil :=min\{n\in \mathbb{Z}:n\ge t\}$. Consequently,

  $$K_{\lambda }\le {\omega }_{\rho }\left(e\right){\int }_0^{\infty }{e}^{-(\lambda -M_B+1-ln{\omega }_{\rho }\left(e\right))t}dt={\displaystyle \frac{{\omega }_{\rho }\left(e\right)}{\lambda -M_B+1-ln{\omega }_{\rho }\left(e\right)}},$$
  valid whenever $\lambda >M_B-1+ln{\omega }_{\rho }\left(e\right)$. Since $e<2^2$ and ${\omega }_{\rho }$ is submultiplicative, ${\omega }_{\rho }\left(e\right)\le {\omega }_{\rho }\left(2^2\right)\le {\omega }_{\rho }{\left(2\right)}^2$, hence the alternative bound

  $$K_{\lambda }\le {\displaystyle \frac{{\omega }_{\rho }{\left(2\right)}^2}{\lambda -M_B+1-2ln{\omega }_{\rho }\left(2\right)}},\lambda >M_B-1+2ln{\omega }_{\rho }\left(2\right).$$
  When applying Lemma 1, the resolvent estimate takes the form

  $$\rho \left(R(\lambda ,B)\varphi \right)\le c_{\rho }\left(\lambda \right)K_{\lambda }\rho \left(\varphi \right),$$
  with

  $$c_{\rho }\left(\lambda \right)=\left\{\begin{array}{cc}1,\hfill & \lambda \ge 1,\hfill \\ {\omega }_{\rho }\left(e\right){\lambda }^{1-ln{\omega }_{\rho }\left(e\right)},\hfill & 0<\lambda <1,\hfill \end{array}\right.$$
  and, equivalently, $c_{\rho }\left(\lambda \right)\le {\omega }_{\rho }\left(2\right){\lambda }^{1-{log}_2{\omega }_{\rho }\left(2\right)}$ if one prefers ${\omega }_{\rho }\left(2\right)$.
• Which bound is sharper? Since ${\omega }_{\rho }\left(e\right)\le {\omega }_{\rho }{\left(2\right)}^2$, we have $ln{\omega }_{\rho }\left(e\right)\le 2ln{\omega }_{\rho }\left(2\right)$, hence for any fixed λ,

  $$\lambda -M_B+1-ln{\omega }_{\rho }\left(e\right)\ge \lambda -M_B+1-2ln{\omega }_{\rho }\left(2\right).$$
  Therefore, on the common admissible range $\lambda >M_B-1+2ln{\omega }_{\rho }\left(2\right)$,

  $${\displaystyle \frac{{\omega }_{\rho }\left(e\right)}{\lambda -M_B+1-ln{\omega }_{\rho }\left(e\right)}}\le {\displaystyle \frac{{\omega }_{\rho }{\left(2\right)}^2}{\lambda -M_B+1-2ln{\omega }_{\rho }\left(2\right)}}.$$
  Thus, the bound with ${\omega }_{\rho }\left(e\right)$ is uniformly sharper than the one with ${\omega }_{\rho }{\left(2\right)}^2$.

In particular, one may choose

$$\overline{\omega }:=M_B-1+ln{\omega }_{\rho }\left(e\right),$$

so that $K_{\lambda }<\infty$ for all $\lambda >\overline{\omega }$. With this choice, the resolvent estimate holds with the sharper bound, namely

$$K_{\lambda }\le {\displaystyle \frac{{\omega }_{\rho }\left(e\right)}{\lambda -M_B+1-ln{\omega }_{\rho }\left(e\right)}}.$$

Before the next result we regularize the semigroup orbit by the short-time Steklov average

$$u_{\epsilon }\left(t\right):={\displaystyle \frac{1}{\epsilon }}{\int }_0^{\epsilon }S(t+s)\varphi ds,t>0,\epsilon >0.$$

(10)

This standard regularization places $u_{\epsilon }\left(t\right)$ in the generator’s domain $D\left(B\right)$, legitimizes differentiation with respect to t in the modular space $L_{\rho }$, and will be used to justify generator identities in $L_{\rho }$.

Theorem 2.

Under the hypotheses and notation of Lemma 2, let $\varphi \in L_{\rho }$ and define $u_{\epsilon }$ by (10) for $\epsilon >0$ and $t>0$. Then $u_{\epsilon }$ is ρ-continuous on $[0,\infty )$, and $u_{\epsilon }\left(t\right)\in D\left(B\right)$ for every $t>0$, with

$$B{u}_{\epsilon }\left(t\right)={\displaystyle \frac{S(t+\epsilon )\varphi -S\left(t\right)\varphi }{\epsilon }}\mathrm{in}{L}_{\rho },t>0.$$

Moreover, the mapping $t\mapsto u_{\epsilon }\left(t\right)$ is ρ-continuous on every bounded interval, and

$${\displaystyle \frac{d}{dt}}{u}_{\epsilon }\left(t\right)=B{u}_{\epsilon }\left(t\right)\mathrm{in}{L}_{\rho },\rho \text{-}a.e.,t>0.$$

(11)

Finally, for each fixed $t\ge 0$ one has

$$\rho \left(u_{\epsilon }\left(t\right)-S\left(t\right)\varphi \right)\underset{\epsilon \downarrow 0}{\to }0,\mathit{equivalently},u\left(t\right)=S\left(t\right)\varphi \rho \text{-}\mathit{almost}\mathit{everywhere},$$

where

$$\rho \left(u_{\epsilon }\left(t\right)-u\left(t\right)\right)\underset{\epsilon \downarrow 0}{\to }0.$$

Proof. 

Fix $t>0$ and $\epsilon >0$. By the semigroup’s algebraic properties,

$$u_{\epsilon }\left(t\right)={\displaystyle \frac{1}{\epsilon }}{\int }_0^{\epsilon }S\left(t\right)S\left(s\right)\varphi ds=S\left(t\right)\left({\displaystyle \frac{1}{\epsilon }}{\int }_0^{\epsilon }S\left(s\right)\varphi ds\right)=:S\left(t\right)v_{\epsilon },$$

where

$$v_{\epsilon }:={\displaystyle \frac{1}{\epsilon }}{\int }_0^{\epsilon }S\left(s\right)\varphi ds\in L_{\rho }.$$

(12)

We first show that the integral in (12) is well defined in $L_{\rho }$. For each $s\ge 0$, $S\left(s\right)\in \mathcal{L}\left(L_{\rho }\right)$ by Lemma 2, hence $S\left(s\right)\varphi \in L_{\rho }$. The growth estimate together with Lemma 1 yields, for $s\in [0,\epsilon ]$,

$$\rho \left(S\left(s\right)\varphi \right)\le C\left(s\right)e^{M_{B}s}\rho \left(\varphi \right)\Rightarrow {\parallel S\left(s\right)\varphi \parallel }_{\rho }\le max\{C\left(s\right)e^{M_{B}s},1\}{\parallel \varphi \parallel }_{\rho }.$$

Thus, the map $s\mapsto S\left(s\right)\varphi$ is measurable and bounded on $[0,\epsilon ]$. Since $\rho$ satisfies the ${\Delta }_2$-type condition, $L_{\rho }$ is complete with respect to the Luxembourg norm ${\parallel ·\parallel }_{\rho }$. Hence $s\mapsto S\left(s\right)\varphi$ is Bochner integrable in the Banach space $(L_{\rho },\parallel ·{\parallel }_{\rho })$, and the integrals in (12) and (10) are well defined.

We show that $v_{\epsilon }\in D\left(B\right)$ and

$$B{v}_{\epsilon }={\displaystyle \frac{S\left(\epsilon \right)\varphi -\varphi }{\epsilon }}.$$

(13)

Using the algebraic properties (i)–(ii) of the semigroup given in Definition 3, we have

$$S(t+s)=S\left(t\right)S\left(s\right),S\left(0\right)=I_{L_{\rho }}.$$

Hence,

$${\displaystyle \frac{S\left(h\right)v_{\epsilon }-v_{\epsilon }}{h}}={\displaystyle \frac{1}{\epsilon }}{\int }_0^{\epsilon }{\displaystyle \frac{S\left(h\right)S\left(s\right)\varphi -S\left(s\right)\varphi }{h}}ds={\displaystyle \frac{1}{\epsilon }}{\int }_0^{\epsilon }{\displaystyle \frac{S(s+h)\varphi -S\left(s\right)\varphi }{h}}ds.$$

To justify the next step, note that by the substitution $\sigma =s+h$,

$${\int }_0^{\epsilon }\left(S(s+h)\varphi -S\left(s\right)\varphi \right)ds={\int }_h^{\epsilon +h}S\left(\sigma \right)\varphi d\sigma -{\int }_0^{\epsilon }S\left(\sigma \right)\varphi d\sigma .$$

Using the identity

$${\int }_h^{\epsilon +h}=\left({\int }_0^{\epsilon +h}-{\int }_0^h\right),$$

we obtain

$${\int }_0^{\epsilon }\left(S(s+h)\varphi -S\left(s\right)\varphi \right)ds={\int }_{\epsilon }^{\epsilon +h}S\left(\sigma \right)\varphi d\sigma -{\int }_0^{h}S\left(\sigma \right)\varphi d\sigma .$$

Reparametrizing both integrals over $[0,h]$ by $\sigma =\epsilon +\tau$ and $\sigma =\tau$ yields

$${\int }_0^{\epsilon }\left(S(s+h)\varphi -S\left(s\right)\varphi \right)ds={\int }_0^h\left(S(\epsilon +\tau )-S\left(\tau \right)\right)\varphi d\tau .$$

Hence,

$${\displaystyle \frac{S\left(h\right)v_{\epsilon }-v_{\epsilon }}{h}}={\displaystyle \frac{1}{\epsilon h}}{\int }_0^h\left(S(\epsilon +\tau )-S\left(\tau \right)\right)\varphi d\tau ={\displaystyle \frac{1}{\epsilon }}{A}_h\left((S\left(\epsilon \right)-I_{L_{\rho }})\varphi \right),$$

where

$$A_h:={\displaystyle \frac{1}{h}}{\int }_0^{h}S\left(\tau \right)d\tau .$$

Since the semigroup S is strongly continuous on $L_{\rho }$, we have

$$\rho \left(S\left(\tau \right)\varphi -\varphi \right)\underset{\tau \downarrow 0}{\to }0.$$

By the $\rho$-boundedness of the semigroup and Proposition 2, there exists $M_B>0$ such that

$$\rho \left(S\left(\tau \right)\varphi \right)\le C\left(\tau \right)e^{M_B\tau }\rho \left(\varphi \right),0\le \tau \le h_0,$$

where $C\left(\tau \right)={\omega }_{\rho }\left(e^{\tau }\right)/e^{\tau }$. Hence, using (4),

$$\rho \left(S\left(\tau \right)\varphi -\varphi \right)\le {\displaystyle \frac{{\omega }_{\rho }\left(2\right)}{2}}\left(\rho \left(S\right(\tau \left)\varphi \right)+\rho \left(\varphi \right)\right)\le \frac{1}{2}{\omega }_{\rho }\left(2\right)\left(C\left(\tau \right)e^{M_B\tau }+1\right)\rho \left(\varphi \right),0\le \tau \le h_0.$$

Fix $0<h\le h_0$ and let $0=t_0<t_1<\cdots <t_n=h$ be a partition with mesh $\left|\tau \right|:={max}_{0\le i\le n-1}(t_{i+1}-t_i).$ Set the weights $w_i:=(t_{i+1}-t_i)/h$, so that $w_i\ge 0$ and ${\sum }_{i=0}^{n-1}{w}_i=1$. Define

$$Z_n:=\sum _{i=0}^{n-1}{w}_i\left(S\left(t_i\right)\varphi -\varphi \right).$$

Since $\rho$ is convex, we have

$$\rho \left(Z_n\right)\le \sum _{i=0}^{n-1}{w}_i\rho \left(S\left(t_i\right)\varphi -\varphi \right).$$

Moreover, using the pointwise bound above,

$$\rho \left(Z_n\right)\le {\displaystyle \frac{{\omega }_{\rho }\left(2\right)}{2}}{\displaystyle \frac{1}{h}}\sum _{i=0}^{n-1}{\int }_{t_i}^{t_{i+1}}\left(C\left(t_i\right)e^{M_B{t}_i}+1\right)\rho \left(\varphi \right)d\tau$$

$$\le {\displaystyle \frac{{\omega }_{\rho }\left(2\right)}{2}}\left(\underset{0\le t\le h}{sup}\left(C\left(t\right)e^{M_{B}t}+1\right)\right)\rho \left(\varphi \right),$$

so $\left\{\rho \left(Z_n\right)\right\}$ is uniformly bounded for refinements of the partition.

Since $S(·)\varphi$ is strongly continuous on $L_{\rho }$, the step functions ${\sum }_{i=0}^{n-1}{1}_{[t_i,t_{i+1})}\left(\tau \right)S\left(t_i\right)\varphi$ converge to $S(·)\varphi$ in $L_{\rho }$ as $\left|\tau \right|\to 0$ on $[0,h]$. Hence,

$$Z_n⟶{\displaystyle \frac{1}{h}}{\int }_0^h\left(S\left(\tau \right)\varphi -\varphi \right)d\tau \mathrm{in}{L}_{\rho }.$$

By the Fatou lower semicontinuity (6),

$$\rho \left({\displaystyle \frac{1}{h}}{\int }_0^h\left(S\left(\tau \right)\varphi -\varphi \right)d\tau \right)\le \underset{\left|\tau \right|\to 0}{lim\; inf}\rho \left(Z_n\right)\le \underset{\left|\tau \right|\to 0}{lim\; inf}\sum _{i=0}^{n-1}{w}_i\rho \left(S\left(t_i\right)\varphi -\varphi \right).$$

Since $t\mapsto \rho \left(S\left(t\right)\varphi -\varphi \right)$ is continuous and bounded on $[0,h]$, the right-hand side equals

$${\displaystyle \frac{1}{h}}{\int }_0^h\rho \left(S\left(\tau \right)\varphi -\varphi \right)d\tau .$$

Therefore, we obtain the modular averaging inequality

$$\rho \left(A_h\varphi -\varphi \right)=\rho \left({\displaystyle \frac{1}{h}}{\int }_0^h\left(S\left(\tau \right)\varphi -\varphi \right)d\tau \right)\le {\displaystyle \frac{1}{h}}{\int }_0^h\rho \left(S\left(\tau \right)\varphi -\varphi \right)d\tau .$$

Finally, since $\rho \left(S\left(\tau \right)\varphi -\varphi \right)\to 0$ as $\tau \downarrow 0$ and is bounded on $[0,h]$ by $\frac{1}{2}{\omega }_{\rho }\left(2\right)\left(C\left(\tau \right)e^{M_B\tau }+1\right)\rho \left(\varphi \right)$, we conclude that

$$\rho (A_h\varphi -\varphi )\underset{h\downarrow 0}{\to }0.$$

Therefore $\rho (A_h\varphi -\varphi )\to 0$ as $h\downarrow 0$, i.e., $A_h\varphi \to \varphi$ in $L_{\rho }$; in particular, $A_h\to I_{L_{\rho }}$ pointwise on $L_{\rho }$. Let $\psi :=(S\left(\epsilon \right)-I_{L_{\rho }})\varphi$. Using

$${\displaystyle \frac{S\left(h\right)v_{\epsilon }-v_{\epsilon }}{h}}={\displaystyle \frac{1}{\epsilon }}{A}_h\psi ,{\displaystyle \frac{S\left(\epsilon \right)\varphi -\varphi }{\epsilon }}={\displaystyle \frac{1}{\epsilon }}\psi ,$$

we obtain

$${\displaystyle \frac{S\left(h\right)v_{\epsilon }-v_{\epsilon }}{h}}-{\displaystyle \frac{S\left(\epsilon \right)\varphi -\varphi }{\epsilon }}={\displaystyle \frac{1}{\epsilon }}(A_h-I_{L_{\rho }})\psi .$$

By the growth function bound of the modular,

$$\rho \left({\displaystyle \frac{1}{\epsilon }}(A_h-I_{L_{\rho }})\psi \right)\le {\omega }_{\rho }\left(\frac{1}{\epsilon }\right)\rho \left((A_h-I_{L_{\rho }})\psi \right)\underset{h\downarrow 0}{\to }0,$$

since $\rho \left((A_h-I_{L_{\rho }})\psi \right)\to 0$ as $h\downarrow 0$. Hence,

$${\displaystyle \frac{S\left(h\right)v_{\epsilon }-v_{\epsilon }}{h}}\underset{h\downarrow 0}{\overset{L_{\rho }}{\to }}{\displaystyle \frac{S\left(\epsilon \right)\varphi -\varphi }{\epsilon }}.$$

This shows that $v_{\epsilon }\in D\left(B\right)$ and that identity (13) holds. We now prove that $u_{\epsilon }$ is $\rho$-continuous on $[0,\infty )$. Since $u_{\epsilon }\left(t\right)=S\left(t\right)v_{\epsilon }$ and $S\left(t\right)$ is strongly continuous, we have, for any $t_1,t_2\ge 0$,

$$u_{\epsilon }\left(t_2\right)-u_{\epsilon }\left(t_1\right)=\left(S(t_2-t_1)-I_{L_{\rho }}\right)S\left(t_1\right)v_{\epsilon },$$

which implies

$$\rho \left(u_{\epsilon }\left(t_2\right)-u_{\epsilon }\left(t_1\right)\right)=\rho \left(S(t_2-t_1)S\left(t_1\right)v_{\epsilon }-S\left(t_1\right)v_{\epsilon }\right)\underset{t_2\to t_1}{\to }0.$$

Thus, $u_{\epsilon }$ is $\rho$-continuous on $[0,\infty )$. We now verify (11). From (10),

$$u_{\epsilon }\left(t\right)={\displaystyle \frac{1}{\epsilon }}{\int }_t^{t+\epsilon }S\left(r\right)\varphi dr,B{u}_{\epsilon }\left(t\right)={\displaystyle \frac{S(t+\epsilon )\varphi -S\left(t\right)\varphi }{\epsilon }}.$$

For $h>0$, we compute

$${\displaystyle \frac{u_{\epsilon }(t+h)-u_{\epsilon }\left(t\right)}{h}}={\displaystyle \frac{1}{h}}·{\displaystyle \frac{1}{\epsilon }}{\int }_t^{t+\epsilon }\left(S(r+h)\varphi -S\left(r\right)\varphi \right)dr={\displaystyle \frac{1}{h}}{\int }_t^{t+h}B{u}_{\epsilon }\left(s\right)ds.$$

Let $f\left(s\right):=B{u}_{\epsilon }\left(s\right)$. By the growth estimate for $S\left(t\right)$ and inequality (4),

$$\rho \left(f\left(t\right)\right)={\displaystyle \frac{1}{\epsilon }}\rho \left(S(t+\epsilon )\varphi -S\left(t\right)\varphi \right)\le {\displaystyle \frac{{\omega }_{\rho }\left(2\right)}{2\epsilon }}\left(C(t+\epsilon )e^{M_B(t+\epsilon )}+C\left(t\right)e^{M_{B}t}\right)\rho \left(\varphi \right),$$

where $C\left(t\right)={\omega }_{\rho }\left(e^t\right)/e^t$. Thus, $t\mapsto \rho \left(f\right(t\left)\right)$ is integrable on every finite interval $[0,T]$.

Fix $t>0$ and define $g_t\left(s\right):=\rho \left(f\left(s\right)-f\left(t\right)\right)$. Using (4), one has

$$g_t\left(s\right)\le {\displaystyle \frac{{\omega }_{\rho }\left(2\right)}{2}}\left(\rho \left(f\right(s\left)\right)+\rho \left(f\right(t\left)\right)\right),$$

so $g_t\in L^1(0,T)$. By the scalar Lebesgue differentiation theorem,

$${\displaystyle \frac{1}{h}}{\int }_t^{t+h}{g}_t\left(s\right)ds\underset{h\downarrow 0}{\to }0\mathrm{for}\mathrm{a}.\mathrm{e}.t>0.$$

Applying the convexity of $\rho$, we obtain

$$\rho \left({\displaystyle \frac{1}{h}}{\int }_t^{t+h}\left(f\left(s\right)-f\left(t\right)\right)ds\right)\le {\displaystyle \frac{1}{h}}{\int }_t^{t+h}\rho \left(f\left(s\right)-f\left(t\right)\right)ds={\displaystyle \frac{1}{h}}{\int }_t^{t+h}{g}_t\left(s\right)ds\underset{h\downarrow 0}{\to }0.$$

Hence, in the modular sense,

$$\rho \left({\displaystyle \frac{1}{h}}{\int }_t^{t+h}f\left(s\right)ds-f\left(t\right)\right)\underset{h\downarrow 0}{\to }0,$$

that is,

$$\rho \left({\displaystyle \frac{u_{\epsilon }(t+h)-u_{\epsilon }\left(t\right)}{h}}-B{u}_{\epsilon }\left(t\right)\right)\underset{h\downarrow 0}{\to }0\mathrm{for}\mathrm{a}.\mathrm{e}.t>0.$$

Therefore, ${\displaystyle \frac{d}{dt}}{u}_{\epsilon }\left(t\right)=B{u}_{\epsilon }\left(t\right)$ for a.e. $t>0$ in $L_{\rho }$.

Finally, using convexity of $\rho$ and $\rho$-continuity of $s\mapsto S(t+s)\varphi$ at $s=0$, we obtain

$$\rho \left(u_{\epsilon }\left(t\right)-S\left(t\right)\varphi \right)=\rho \left({\displaystyle \frac{1}{\epsilon }}{\int }_0^{\epsilon }\left(S(t+s)\varphi -S\left(t\right)\varphi \right)ds\right)\le {\displaystyle \frac{1}{\epsilon }}{\int }_0^{\epsilon }\rho \left(S(t+s)\varphi -S\left(t\right)\varphi \right)ds\underset{\epsilon \downarrow 0}{\to }0.$$

This completes the proof. □

Before stating the corollary, we recall the admissible range for $\lambda$. Under the ${\Delta }_2$-type condition and with $C\left(t\right)={\omega }_{\rho }\left(e^t\right)/e^t$, Remark 2 shows that

$$K_{\lambda }={\int }_0^{\infty }{\omega }_{\rho }\left(e^t\right)e^{-(\lambda -M_B+1)t}dt$$

is finite already for $\lambda >M_B-1+ln{\omega }_{\rho }\left(e\right)$ (or, equivalently, for $\lambda >M_B-1+2ln{\omega }_{\rho }\left(2\right)$, using ${\omega }_{\rho }\left(e\right)\le {\omega }_{\rho }{\left(2\right)}^2$). Hence, the resolvent estimate from Lemma 1 remains valid on this enlarged half-line, with the small-$\lambda$ prefactor $c_{\rho }\left(\lambda \right)$ given in Remark 2. In the proof below, however, we employ the Laplace representation

$$R(\lambda ,B)\varphi ={\int }_0^{\infty }{e}^{-\lambda t}S\left(t\right)\varphi dt,$$

which requires $\lambda >\overline{\omega }$. Once the domain inclusion and resolvent identity have been established in this range, the explicit bounds for $K_{\lambda }$ allow us to extend the estimates to the full region $\lambda >M_B-1+ln{\omega }_{\rho }\left(e\right)$, which will be the framework for the subsequent spectral analysis in $L_{\rho }$.

Corollary 1.

Under the hypotheses of Proposition 2, for every $\lambda >\overline{\omega }$, the Laplace resolvent

$$R(\lambda ,B)\varphi :={\int }_0^{\infty }{e}^{-\lambda t}S\left(t\right)\varphi dt$$

is well defined in $L_{\rho }$, belongs to $\mathcal{L}\left(L_{\rho }\right)$, and satisfies

$$\rho \left(R(\lambda ,B)\varphi \right)\le c_{\rho }\left(\lambda \right)K_{\lambda }\rho \left(\varphi \right),\varphi \in L_{\rho },$$

(14)

where

$$C\left(t\right):={\displaystyle \frac{{\omega }_{\rho }\left(e^t\right)}{e^t}},K_{\lambda }:={\int }_0^{\infty }C\left(t\right)e^{-(\lambda -M_B)t}dt,$$

and

$$c_{\rho }\left(\lambda \right)=\left\{\begin{array}{cc}1,\hfill & \lambda \ge 1,\hfill \\ {\omega }_{\rho }\left(e\right){\lambda }^{1-ln{\omega }_{\rho }\left(e\right)},\hfill & 0<\lambda <1.\hfill \end{array}\right.$$

Moreover, $R(\lambda ,B)L_{\rho }\subset D\left(B\right)$ and $(\lambda I-B)R(\lambda ,B)=I$ on $L_{\rho }$.

Proof. 

The existence of $R(\lambda ,B)$ as a Bochner integral in $L_{\rho }$ and the estimate (14) follow directly from Lemma 1 with the same $C(·)$ and $K_{\lambda }$. The prefactor $c_{\rho }\left(\lambda \right)$ coincides with that obtained there and equals 1 for $\lambda \ge 1$.

We now derive an integral identity for $BS\left(t\right)\varphi$ that will be useful later. Fix $\varphi \in L_{\rho }$ and recall the Steklov regularization (10),

$$u_{\epsilon }\left(t\right):={\displaystyle \frac{1}{\epsilon }}{\int }_0^{\epsilon }S(t+s)\varphi ds,\epsilon >0,t>0.$$

By Theorem 2, $u_{\epsilon }\left(t\right)\in D\left(B\right)$ for every $t>0$, $u_{\epsilon }$ is $\rho$-continuous on $[0,\infty )$, and

$$u_{\epsilon }^{\prime }\left(t\right)=B{u}_{\epsilon }\left(t\right)\mathrm{in}{L}_{\rho },\rho \text{-}\mathrm{a}.\mathrm{e}.,t>0,$$

while

$$\rho \left(u_{\epsilon }\left(t\right)-S\left(t\right)\varphi \right)\underset{\epsilon \downarrow 0}{\to }0\mathrm{for}\mathrm{each}\mathrm{fixed}t\ge 0.$$

On any finite interval $[0,T]$, the mapping $t\mapsto \rho \left(u_{\epsilon }^{\prime }\left(t\right)\right)$ belongs to $L^1(0,T)$ (equivalently, $t\mapsto \parallel u_{\epsilon }^{\prime }{\left(t\right)\parallel }_{\rho }\in L^1(0,T)$), using the ${\Delta }_2$-type condition on $\rho$ to compare the modular and the Luxembourg norm and to guarantee Bochner integrability of $u_{\epsilon }^{\prime }$ in $L_{\rho }$. Hence, the modular fundamental theorem of calculus (Bochner integration by parts) applies to $t\mapsto e^{-\lambda t}{u}_{\epsilon }\left(t\right)$ on $[0,T]$ and yields

$${\int }_0^T{e}^{-\lambda t}{u}_{\epsilon }^{\prime }\left(t\right)dt=\lambda {\int }_0^T{e}^{-\lambda t}{u}_{\epsilon }\left(t\right)dt-{\left[e^{-\lambda t}{u}_{\epsilon }\left(t\right)\right]}_0^T\mathrm{in}{L}_{\rho }.$$

Using $u_{\epsilon }^{\prime }\left(t\right)=B{u}_{\epsilon }\left(t\right)$ a.e., we obtain

$${\int }_0^T{e}^{-\lambda t}B{u}_{\epsilon }\left(t\right)dt=\lambda {\int }_0^T{e}^{-\lambda t}{u}_{\epsilon }\left(t\right)dt-{\left[e^{-\lambda t}{u}_{\epsilon }\left(t\right)\right]}_0^T.$$

Letting $\epsilon \downarrow 0$ and using the modular dominated convergence theorem (which applies because $S\left(t\right)$ is $\rho$-bounded and satisfies the growth estimate (8)), we pass to the limit in each term and obtain

$${\int }_0^T{e}^{-\lambda t}BS\left(t\right)\varphi dt=\lambda {\int }_0^T{e}^{-\lambda t}S\left(t\right)\varphi dt-{\left[e^{-\lambda t}S\left(t\right)\varphi \right]}_0^T.$$

As $T\to \infty$, the boundary term at T satisfies

$$\rho \left(e^{-\lambda T}S\left(T\right)\varphi \right)\le e^{-(\lambda -M_B)T}C\left(T\right)\rho \left(\varphi \right)\underset{T\to \infty }{\to }0,$$

since $\lambda >M_B$, and the boundary term at 0 equals $-\varphi$. Hence

$${\int }_0^{\infty }{e}^{-\lambda t}BS\left(t\right)\varphi dt=\lambda {\int }_0^{\infty }{e}^{-\lambda t}S\left(t\right)\varphi dt-\varphi \mathrm{in}{L}_{\rho }.$$

(15)

We now prove that $R(\lambda ,B)\varphi \in D\left(B\right)$ and that the resolvent identity holds. Set

$$u:=R(\lambda ,B)\varphi ={\int }_0^{\infty }{e}^{-\lambda t}S\left(t\right)\varphi dt\in L_{\rho }.$$

For $h>0$, using the semigroup property and a change in variables, we obtain

$$\begin{array}{cc}\hfill S\left(h\right)u& ={\int }_0^{\infty }{e}^{-\lambda t}S\left(h\right)S\left(t\right)\varphi dt={\int }_0^{\infty }{e}^{-\lambda t}S(t+h)\varphi dt\hfill \\ & ={\int }_h^{\infty }{e}^{-\lambda (s-h)}S\left(s\right)\varphi ds=e^{\lambda h}{\int }_h^{\infty }{e}^{-\lambda s}S\left(s\right)\varphi ds.\hfill \end{array}$$

Hence

$$\begin{array}{cc}\hfill S\left(h\right)u-u& =\left(e^{\lambda h}{\int }_h^{\infty }{e}^{-\lambda s}S\left(s\right)\varphi ds\right)-{\int }_0^{\infty }{e}^{-\lambda t}S\left(t\right)\varphi dt\hfill \\ & =(e^{\lambda h}-1){\int }_h^{\infty }{e}^{-\lambda s}S\left(s\right)\varphi ds-{\int }_0^h{e}^{-\lambda t}S\left(t\right)\varphi dt.\hfill \end{array}$$

Dividing by h gives

$${\displaystyle \frac{S\left(h\right)u-u}{h}}={\displaystyle \frac{e^{\lambda h}-1}{h}}{\int }_h^{\infty }{e}^{-\lambda s}S\left(s\right)\varphi ds-{\displaystyle \frac{1}{h}}{\int }_0^h{e}^{-\lambda t}S\left(t\right)\varphi dt.$$

(16)

We show that the right-hand side converges in $L_{\rho }$ (in the modular sense) to $\lambda u-\varphi$ as $h\downarrow 0$.

First, note that

$${\displaystyle \frac{e^{\lambda h}-1}{h}}⟶\lambda \mathrm{as}h\downarrow 0.$$

Moreover, by the definition of u and the growth estimate (8), the family

$$v_h:={\int }_h^{\infty }{e}^{-\lambda s}S\left(s\right)\varphi ds$$

converges in $L_{\rho }$ to u as $h\downarrow 0$, and $\rho$-bounded for small $h>0$ by dominated convergence in the modular sense. Hence

$${\displaystyle \frac{e^{\lambda h}-1}{h}}{v}_h⟶\lambda u\mathrm{in}{L}_{\rho }\mathrm{as}h\downarrow 0.$$

For the second term in (16), set

$$A_h\varphi :={\displaystyle \frac{1}{h}}{\int }_0^{h}S\left(t\right)\varphi dt.$$

In the proof of Theorem 2, we established the modular averaging inequality

$$\rho (A_h\varphi -\varphi )\underset{h\downarrow 0}{\to }0.$$

Since $e^{-\lambda t}\to 1$ as $t\downarrow 0$ and $\rho \left(S\right(t\left)\varphi \right)$ is integrably bounded on $[0,1]$, the same argument with the weights $e^{-\lambda t}$ yields

$$\rho \left({\displaystyle \frac{1}{h}}{\int }_0^h{e}^{-\lambda t}S\left(t\right)\varphi dt-\varphi \right)\underset{h\downarrow 0}{\to }0.$$

Thus

$${\displaystyle \frac{1}{h}}{\int }_0^h{e}^{-\lambda t}S\left(t\right)\varphi dt⟶\varphi \mathrm{in}{L}_{\rho }\mathrm{as}h\downarrow 0.$$

Combining these two limits in (16), we obtain

$$\rho \left({\displaystyle \frac{S\left(h\right)u-u}{h}}-(\lambda u-\varphi )\right)\underset{h\downarrow 0}{\to }0.$$

By the definition of the infinitesimal generator in the modular sense, this shows that $u\in D\left(B\right)$ and

$$Bu=\lambda u-\varphi ,\mathrm{i}.\mathrm{e}.(\lambda I-B)u=\varphi .$$

Since $u=R(\lambda ,B)\varphi$, we have proved that $R(\lambda ,B)\varphi \in D\left(B\right)$ and that $(\lambda I-B)R(\lambda ,B)=I$ on $L_{\rho }$, which completes the proof. □

We now illustrate the abstract framework with a simple but very flexible class of examples, namely multiplication semigroups associated with integral modulars. Starting from a general convex modular $\rho$ of integral type, we obtain a natural $\rho$-bounded semigroup ${\left(S\left(t\right)\right)}_{t\ge 0}$ and can then specialize to the Orlicz–Luxembourg setting. This will also allow us to compare, in a concrete situation, the simplicity of modular estimates with the implicit character of the Luxembourg norm. Let $(\Omega ,\Sigma ,\mu )$ be a $\sigma$-finite measure space and let $\rho$ be a convex function modular on $L^0(\Omega )$ of the form

$$\rho \left(f\right):={\int }_{\Omega }M\left(x,\left|f\right(x\left)\right|\right)d\mu \left(x\right),$$

where for a.e. $x\in \Omega$ the function $t\mapsto M(x,t)$ is increasing on $[0,\infty )$. Consider a bounded measurable function $q:\Omega \to [0,\infty )$ and, for $t\ge 0$, define

$$\left(S\left(t\right)f\right)\left(x\right):=e^{-tq\left(x\right)}f\left(x\right),f\in L_{\rho }.$$

Then, using only the monotonicity of $t\mapsto M(x,t)$ and the fact that $0\le e^{-tq\left(x\right)}\le 1$, we obtain for each $t\ge 0$

$$\rho \left(S\left(t\right)f\right)={\int }_{\Omega }M\left(x,e^{-tq\left(x\right)}\left|f\left(x\right)\right|\right)d\mu \left(x\right)\le {\int }_{\Omega }M\left(x,\left|f\right(x\left)\right|\right)d\mu \left(x\right)=\rho \left(f\right).$$

Hence ${\left(S\left(t\right)\right)}_{t\ge 0}$ is $\rho$-bounded with bound 1. If, in addition, the modular $\rho$ satisfies the ${\Delta }_2$-type condition (3), then the associated growth function ${\omega }_{\rho }$ is finite for all $t>0$, the standing assumptions of this paper are fulfilled, and we can regard ${\left(S\left(t\right)\right)}_{t\ge 0}$ as a strongly continuous semigroup in the sense of Definition 3. In this case, all the results developed in this section (exponential bounds, resolvent representation, domain characterization) apply directly to this family. The proof uses only the explicit modular $\rho$ and no norm structure.

A particularly important example of this abstract construction is provided by the classical Orlicz setting. Let $\Phi :[0,\infty )\to [0,\infty )$ be convex and increasing, satisfy $\Phi \left(0\right)=0$, and fulfill a ${\Delta }_2$-type condition, and set

$$M(x,t):=\Phi \left(t\right),\rho \left(f\right):={\int }_{\Omega }\Phi \left(\right|f\left(x\right)\left|\right)d\mu \left(x\right).$$

Then $L_{\rho }=L^{\Phi }(\Omega )$ is the corresponding Orlicz space with Luxembourg norm

$${\parallel f\parallel }_{\Phi }:=inf\left\{\lambda >0:\rho (f/\lambda )\le 1\right\},$$

and modular convergence is equivalent to convergence in ${\parallel ·\parallel }_{\Phi }$. In particular, the inequality $\rho \left(S\right(t\left)f\right)\le \rho \left(f\right)$ implies that ${\left(S\left(t\right)\right)}_{t\ge 0}$ is also bounded with respect to the Luxembourg norm, but this information is encoded only indirectly through the implicit infimum in the definition of ${\parallel ·\parallel }_{\Phi }$. Indeed, if we fix $t\ge 0$ and $f\in L^{\Phi }(\Omega )$, then

$${\parallel f\parallel }_{\Phi }=inf\left\{\lambda >0:{\int }_{\Omega }\Phi \left(\left|f\right(x\left)\right|/\lambda \right)d\mu \left(x\right)\le 1\right\}.$$

If ${\lambda >\parallel f\parallel }_{\Phi }$, then by definition

$${\int }_{\Omega }\Phi \left(\left|f\right(x\left)\right|/\lambda \right)d\mu \left(x\right)\le 1.$$

Since $\left|S\left(t\right)f\left(x\right)\right|=e^{-tq\left(x\right)}\left|f\left(x\right)\right|\le \left|f\left(x\right)\right|$ and $\Phi$ is increasing, we obtain

$${\int }_{\Omega }\Phi \left(\left|S\right(t\left)f\right(x\left)\right|/\lambda \right)d\mu \left(x\right)\le {\int }_{\Omega }\Phi \left(\left|f\right(x\left)\right|/\lambda \right)d\mu \left(x\right)\le 1,$$

$${\parallel f\parallel }_{\Phi }=inf\left\{\lambda >0:{\int }_{\Omega }\Phi \left(\left|f\right(x\left)\right|/\lambda \right)d\mu \left(x\right)\le 1\right\}.$$

Hence, for every ${\lambda >\parallel f\parallel }_{\Phi }$ we have

$${\int }_{\Omega }\Phi \left(\left|f\right(x\left)\right|/\lambda \right)d\mu \left(x\right)\le 1.$$

Since $\left|S\left(t\right)f\left(x\right)\right|=e^{-tq\left(x\right)}\left|f\left(x\right)\right|\le \left|f\left(x\right)\right|$ and $\Phi$ is increasing,

$${\int }_{\Omega }\Phi \left(\left|S\right(t\left)f\right(x\left)\right|/\lambda \right)d\mu \left(x\right)\le {\int }_{\Omega }\Phi \left(\left|f\right(x\left)\right|/\lambda \right)d\mu \left(x\right)\le 1,$$

so every ${\lambda >\parallel f\parallel }_{\Phi }$ is also admissible for $S\left(t\right)f$. Therefore

$${\parallel S\left(t\right)f\parallel }_{\Phi }=inf\left\{\lambda >0:{\int }_{\Omega }\Phi \left(\left|S\right(t\left)f\right(x\left)\right|/\lambda \right)d\mu \left(x\right)\le 1\right\}\le {inf\{\lambda >\parallel f\parallel }_{\Phi }{\}=\parallel f\parallel }_{\Phi }.$$

In other words,

$${\parallel S\left(t\right)f\parallel }_{\Phi }\le {\parallel f\parallel }_{\Phi },t\ge 0.$$

This computation shows that, even in this very simple multiplication setting, establishing boundedness in the Luxembourg norm already requires working with the implicit infimum in the norm definition and exploiting the special structure of $S\left(t\right)$, whereas the corresponding modular estimate follows in a single step from the explicit integral form of $\rho$ together with the monotonicity of $\Phi$. In the next example, we illustrate this difficulty by a numerical simulation of the Luxembourg norm for a multiplication semigroup, highlighting the role of modular estimates.

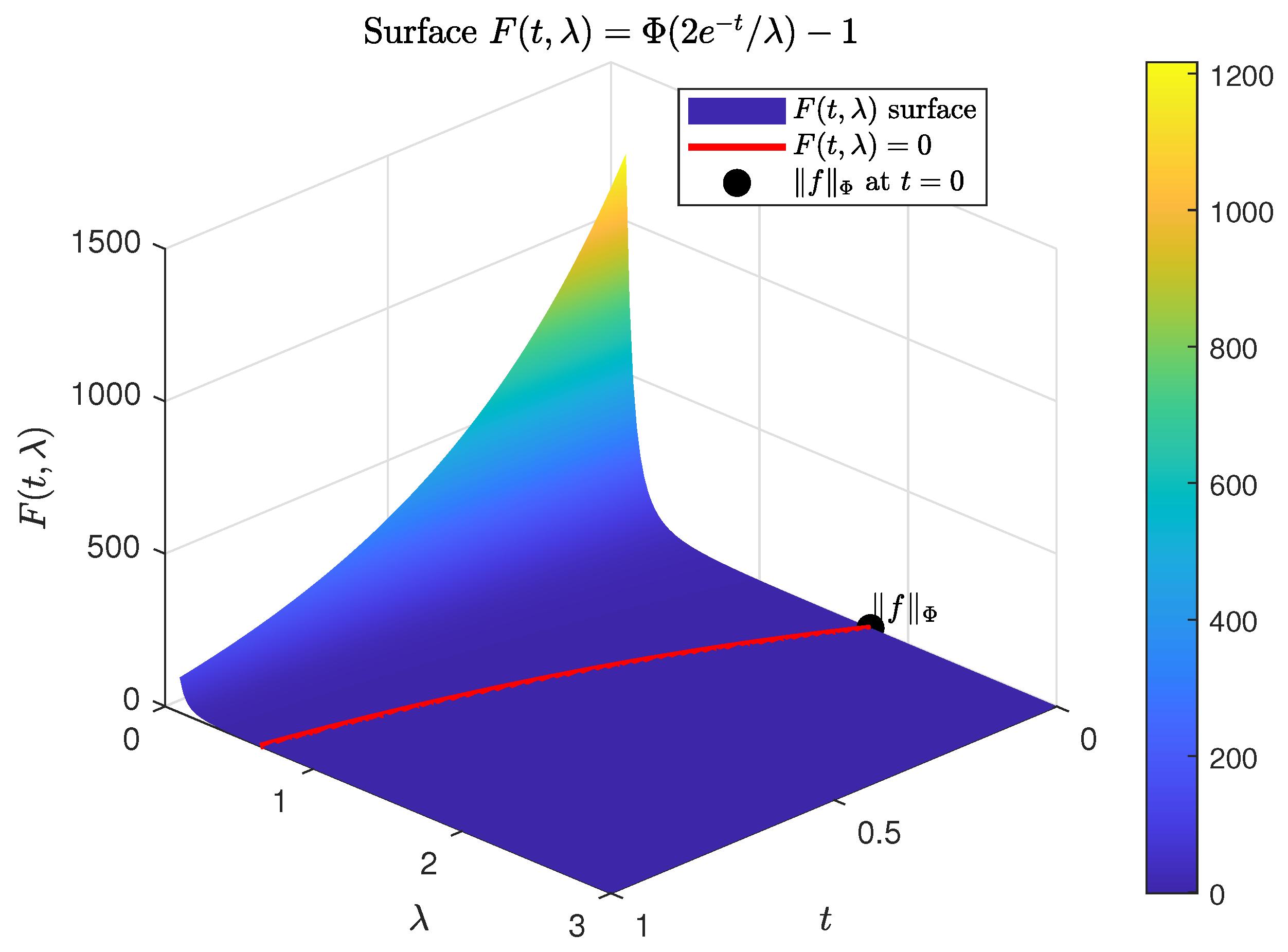
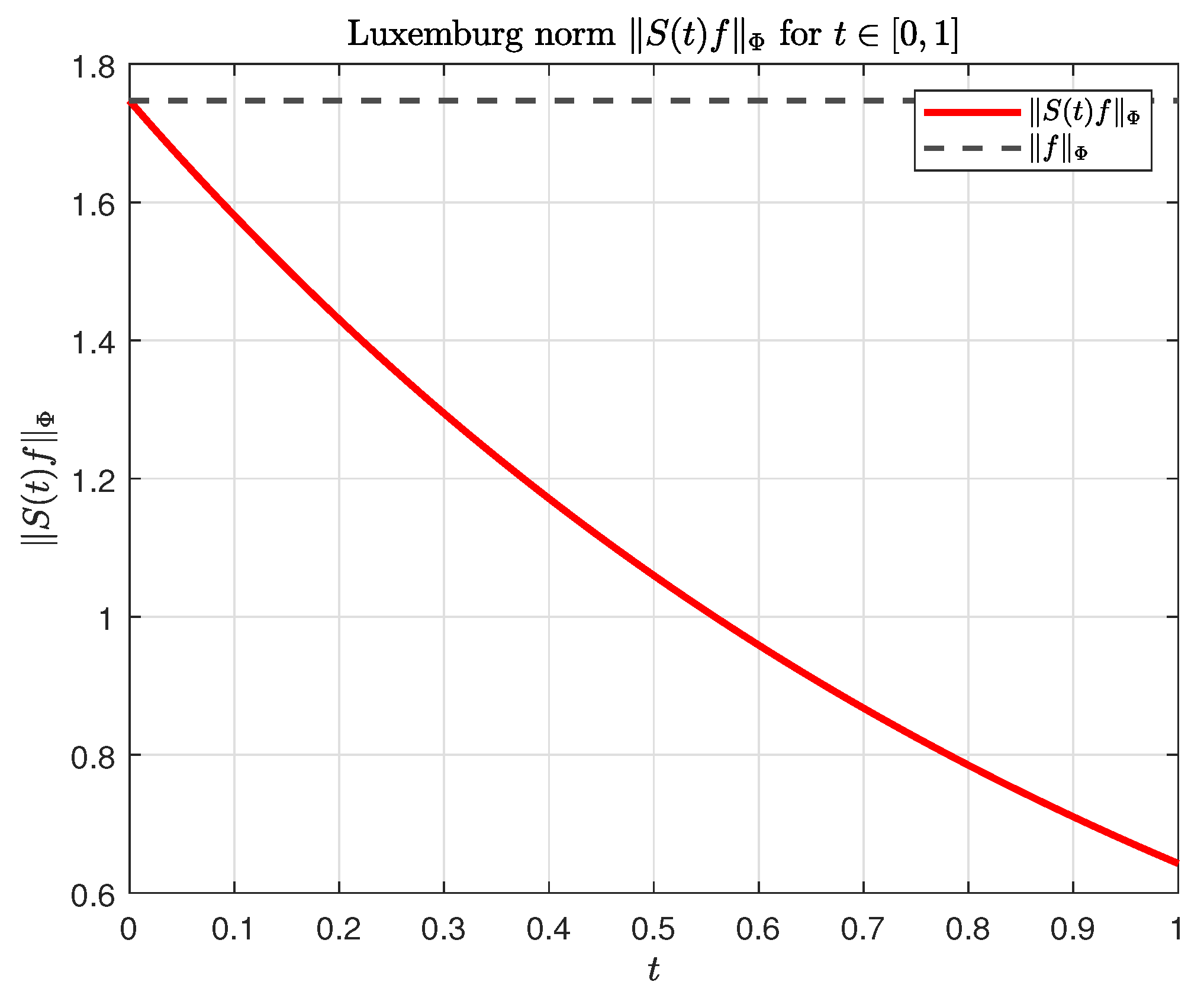
Example 1.

To illustrate this difference numerically, let $\Omega =(0,1)$ with Lebesgue measure and consider

$$\Phi \left(t\right):=t^{2}log(1+t),t\ge 0.$$

Then $\Phi \left(0\right)=0$, Φ is increasing and convex on $[0,\infty )$, and one easily checks that

$$\Phi \left(2t\right)=4t^{2}log(1+2t)\le 8t^{2}log(1+t)=8\Phi \left(t\right),t\ge 0,$$

so Φ satisfies a ${\Delta }_2$-type condition. The associated modular is

$$\rho \left(f\right):={\int }_0^1\Phi \left(\right|f\left(x\right)\left|\right)dx,$$

and the Luxembourg norm is

$${\parallel f\parallel }_{\Phi }:=inf\left\{\lambda >0:{\int }_0^1\Phi \left(\left|f\right(x\left)\right|/\lambda \right)dx\le 1\right\}.$$

Take the constant function $f\left(x\right)\equiv 2$ on $(0,1)$ and the multiplication semigroup with $q\left(x\right)\equiv 1$, so that

$$\left(S\left(t\right)g\right)\left(x\right)=e^{-t}g\left(x\right),t\ge 0.$$

For this choice,

$$\rho \left(f\right)={\int }_0^1\Phi \left(2\right)dx=\Phi \left(2\right)=4log\left(3\right),$$

and for every $t>0$,

$$\rho \left(S\left(t\right)f\right)={\int }_0^1\Phi \left(2e^{-t}\right)dx=\Phi \left(2e^{-t}\right)<\Phi \left(2\right)=\rho \left(f\right),$$

Thus, the ρ-boundedness of ${\left(S\left(t\right)\right)}_{t\ge 0}$ is obtained immediately from the modular estimate.

In contrast, the Luxembourg norm of f is determined by the implicit equation

$${\int }_0^1\Phi \left(2/\lambda \right)dx=1⟺\Phi (2/\lambda )=1,$$

that is,

$${\left({\displaystyle \frac{2}{\lambda }}\right)}^{2}log\left(1+{\displaystyle \frac{2}{\lambda }}\right)=1.$$

This nonlinear equation has no closed-form solution and must be solved numerically to obtain ${\parallel f\parallel }_{\Phi }$. Likewise, for each fixed $t>0$ the norm ${\parallel S\left(t\right)f\parallel }_{\Phi }$ is given implicitly by

$${\left({\displaystyle \frac{2e^{-t}}{\lambda }}\right)}^{2}log\left(1+{\displaystyle \frac{2e^{-t}}{\lambda }}\right)=1.$$

Thus, even for this very simple constant function and a bounded multiplication semigroup, the Luxembourg norm leads to transcendental equations, whereas the corresponding modular estimates are immediate. This concrete example explains why, in practice, semigroup bounds are more naturally derived at the modular level, even in ${\Delta }_2$-type condition settings where the Luxembourg norm is available. To visualize this implicit dependence. Figure 1 shows the surface

$$F(t,\lambda )=\Phi \left(2e^{-t}/\lambda \right)-1,$$

together with the zero level set $F(t,\lambda )=0$ corresponding to $\lambda \left(t\right)={\parallel S\left(t\right)f\parallel }_{\Phi }$. Figure 2 displays the graph of $t\mapsto {\parallel S\left(t\right)f\parallel }_{\Phi }$ on $[0,1]$ and the horizontal line $t\mapsto {\parallel f\parallel }_{\Phi }$. Both plots underline that obtaining the Luxembourg norm requires solving a nontrivial implicit equation, while the modular behavior $t\mapsto \rho \left(S\right(t\left)f\right)$ is given explicitly.

Figure 1. Surface $F(t,\lambda )=\Phi (2e^{-t}/\lambda )-1$ and the zero level curve $F(t,\lambda )=0$ giving $\lambda \left(t\right)={\parallel S\left(t\right)f\parallel }_{\Phi }$.

Figure 2. Luxembourg norm $t\mapsto {\parallel S\left(t\right)f\parallel }_{\Phi }$ for $t\in [0,1]$ and ${\parallel f\parallel }_{\Phi }$.