The Conservative Field of Coupled Newton–Coulomb Sources: Component Coupling Constants, Mass ⇌ Charge Cross-Forces, and Radiation from Reissner–Nordström Black Hole Mergers

Abstract

We investigate a combined conservative field, in which classical gravitational and electrostatic sources also exhibit mutual interactions. Hitherto neglected, the coupling between mass and charge may be necessary for constructing a unified conservative force field generated by a single underlying source. We determine the coupling constant of the cross-field components as the geometric mean (G-M) of Newton’s G and Coulomb’s K constants, in both SI units and dimensionless form. Consequently, for two identical objects, the cross-force ($F_{\times }$) is the G-M of the familiar Newton ($F_{\mathrm{g}}$) and Coulomb ($F_{\mathrm{e}}$) forces, so that $F_{\times }=\sqrt{F_{\mathrm{g}}{F}_{\mathrm{e}}}$, where $F_{\mathrm{g}}\ll F_{\times }\ll F_{\mathrm{e}}$. Remarkably, such cross-forces should be measurable in torsion balance experiments involving a suspended neutral mass interacting with a partially ionized gas. Furthermore, we apply our new formulation to estimate the dimensionless amplitude $\parallel {\mathcal{h}}_{\alpha \beta }^{\mathrm{TT}}\parallel$ of gravitational waves that are emitted by inspiraling Reissner–Nordström (RN) black hole binaries, expressed in terms of ratios of the four fundamental lengths of the problem: the distance to the binary D, the binary separation R, the Schwarzschild radius $R_S\propto 2M$ of mass M, and the RN charge (Q) length scale $L_Q\propto 2Q$. In this classical setting with speeds much lower than the speed of light c in vacuum, the surprising appearance of the maximum relativistic tension force $F_{\max }=c^4/\left(4G\right)$ is duly noted.

1. Introduction

In a classical grand-unified framework, conservative long-range fields must arise from a single underlying principle governing the two fundamental properties known as inertial mass and static charge, along with their interactions with other fields. In such a setting, the field components themselves are expected to interact, much like those of the electromagnetic (EM) field. Yet the possibility of a coupling between mass and charge has largely been overlooked, since Coulomb’s law and Newton’s law of gravitation treat their sources independently.

Charges never exist in isolation; they are always bound to material objects. This strongly suggests that the conservative field inherently carries both sources together, making it difficult to conceive of them as acting entirely independently. In fact, one might even argue that a subtle form of blending is already encoded in these sources, since attraction of a test particle is a property shared by both mass and negative charge (their field lines are identical). Further corroborating evidence comes from the formal analogies between general relativity and classical electrodynamics that effectively describe the geometrical properties of spacetime by various sets of Maxwell equations for the ‘gravitational electric’ and ‘gravitational magnetic’ fields [1,2,3,4].

1.1. Principles of Source Coupling and Field Components

Here, we investigate the “GravElectroMagnetic” (GEM) forces that arise in a combined conservative long-range field, in which mass and charge are intrinsically coupled. The specific form of this coupling is carefully developed through a series of assumptions and procedures:

• By convention, all attractive (repulsive) force components are taken to be positive (negative).
• Coulomb’s law and Newton’s law of gravitation are the fundamental principles governing interactions between charges and masses, respectively. Symbolically, we write $F_{Q\to q},F_{M\to m}$ for the actions and $F_{q\to Q},F_{m\to M}$ for the reactions, respectively.
• As usual, the coupling constants in the force laws are Coulomb’s constant K for charges and Newton’s gravitational constant G for masses. In dimensionless form, they appear in the definitions of the fine-structure constant (FSC) ${\mathrm{\alpha }}_{\mathrm{e}}$ and the gravitational coupling constant (GCC) ${\mathrm{\alpha }}_{\mathrm{g}}$, respectively—but these definitions are written in terms of Planck’s constant h [5,6], not Dirac’s ℏ [7,8], and they are adopted as the new standard forms for the reasons explained in depth in Refs. [9,10].
• The coupling constant of the cross-forces $F_{Q\to m},F_{M\to q}$ and the corresponding reactions $F_{m\to Q},F_{q\to M}$ is determined to be the geometric mean (G-M) $\sqrt{GK}$ on dimensional grounds. A new, dimensionless, cross-coupling constant (CCC) ${\mathrm{\alpha }}_{\times }$ then emerges, the G-M $\sqrt{{\mathrm{\alpha }}_{\mathrm{e}}{\mathrm{\alpha }}_{\mathrm{g}}}$, which is also defined in terms of Planck’s constant h, not Dirac’s ℏ. The coupling constants and the magnitudes of the various force components are summarized in

  Table 1. Coupling constants and magnitudes of the force components of the combined conservative field.

  Pairwise	Force	Force	Coupling	Definition
  Interaction	Constant	Magnitude	Constant	(Using Planck’s h)
  $M\to m$	$G$	$(\mathit{GM})m/R^2$	GCC	${\mathrm{\alpha }}_{\mathrm{g}}={\mathit{Gm}}_{\mathrm{e}}^2/(hc)$
  $Q\to q$	$K$	$(\mathit{KQ})q/R^2$	FSC	${\mathrm{\alpha }}_{\mathrm{e}}={\mathit{Ke}}^2/(hc)$
  $M\to q$	$\sqrt{\mathit{GK}}$	$(\sqrt{\mathit{GK}}M)q/R^2$	CCC	${\mathrm{\alpha }}_{\times }=\sqrt{{\mathrm{\alpha }}_{\mathrm{g}}{\mathrm{\alpha }}_{\mathrm{e}}}$
  $Q\to m$	$\sqrt{\mathit{GK}}$	$(\sqrt{\mathit{GK}}Q)m/R^2$	CCC	${\mathrm{\alpha }}_{\times }=\sqrt{{\mathrm{\alpha }}_{\mathrm{g}}{\mathrm{\alpha }}_{\mathrm{e}}}$

  Notes. $G$: Newton’s constant; $K$: Coulomb’s constant; $m_{\mathrm{e}}$: Electron mass; $e$: Elementary charge; $h$: Planck’s constant; $c$: Speed of light in vacuum [11]; $R$: Distance or separation of masses; ${\mathrm{\alpha }}_{\mathrm{e}}$: Fine-structure constant (FSC) [12]; ${\mathrm{\alpha }}_{\mathrm{g}}$: Gravitational coupling constant (GCC); ${\mathrm{\alpha }}_{\times }$: Cross-coupling constant (CCC) [10]. All dimensionless coupling constants are defined in terms of Planck’s $h$, not Dirac’s ℏ. The parentheses in the magnitudes of the forces (column 3) highlight the source terms of the combined field.

  .
• Newton’s third law of action–reaction is assumed to remain valid in the presence of cross-forces. However, this assumption does not uniquely determine the signs of the cross-force components $Q\to m,M\to q$, or the corresponding reactions. There are two possibilities for mass–charge interactions: mass behaves either as a negative charge or as a positive charge. Consequently, a choice must be made on how the sources of the combined field should behave during mutual interactions, all the while obeying Newton’s third law of motion.
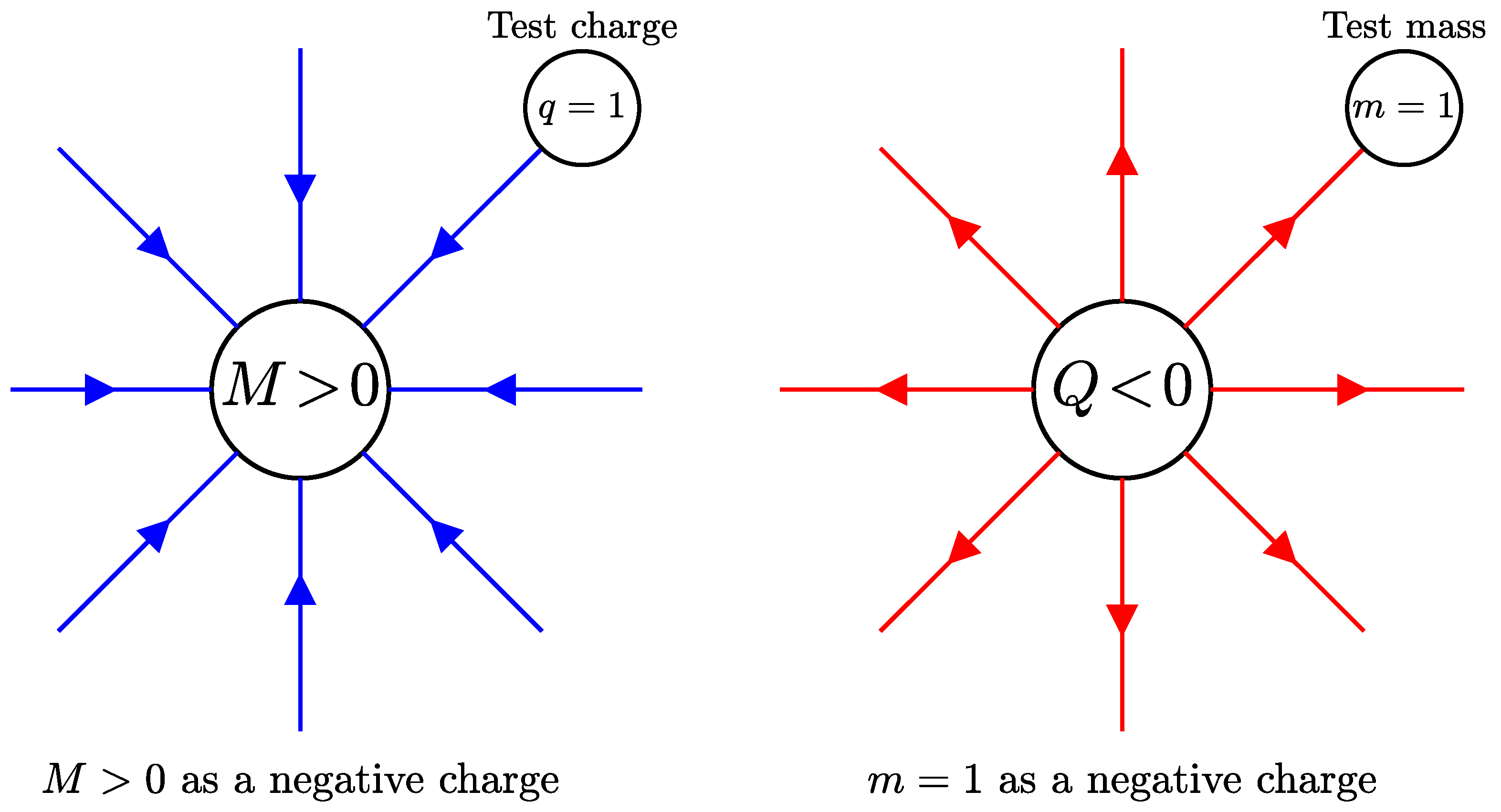
• We assume that mass behaves as a negative charge in its interactions with charges, so that a test charge ($q=1$) will be attracted by a mass M, and a test mass ($m=1$) will be repelled by a negative charge Q (Figure 1). This choice is based on the similarity of the conventional force fields that are generated by a mass and a negative charge, where the radial field lines converge toward both of these sources (Figure 2). This assumption will have to be experimentally tested (see item 8 below).
• Thus, $F_{+Q\to m},F_{M\to +q}$ are attractive force components, and $F_{-Q\to m},F_{M\to -q}$ are repulsive force components. The signs of the various force components are summarized in

  Table 2. Attractive (+) and repulsive (−) conservative force components. The matrix is symmetric, so the reaction forces obey the same sign rules. There is no need for an equivalence principle of masses in this scheme: all masses are inertial, and they are rendered sources of gravity only when multiplied by Newton’s $G$ [10]. Similarly, charges scaled by Coulomb’s $K$ act as sources of electric fields.

  		Subjected to Force
  		+m	−q	+q
  Sources	$\mathbf{+}\mathit{M}$	+	−	+
  	$\mathbf{-}\mathit{Q}$	−	−	+
  	$\mathbf{+}\mathit{Q}$	+	+	−

  .
• On the basis advocated above, we reject the notion that mass may behave as a positive charge in its interactions with charges of any type. However, Newton’s third law of motion would be valid under this alternative hypothesis. The question of which hypothesis is right (or whether both of them are flawed) can be resolved by torsion balance experiments utilizing an electrically neutral mass interacting with a partially ionized gas.

1.2. Outline

The remainder of the paper is organized as follows:

• In Section 2, we determine the coupling constant of the cross-forces acting between masses and charges and the conservative net forces of the interactions $(M,\pm Q)\to (m,\pm q)$, where capital letters denote the field sources, and lower-case letters denote the objects subjected to forcing.
• In Section 3, we estimate the magnitudes of the cross-forces between a neutral mass and an ionized xenon gas, with the prospect of measuring the effect in torsion balance experiments.
• In Section 4, we apply the new formulation to estimate the characteristic amplitude of radiation emitted by two inspiraling Reissner–Nordström (RN) black holes.
• In Section 5, we summarize our results and present our conclusions.

2. Newton–Coulomb Couplings, Cross-Forces, and Resultant GEM Forces

2.1. Dimensional Analysis of Cross-Forces and Effective Gravity

In general, we use capital letters to denote the sources M and Q of the conservative field and lower-case letters to indicate the masses (m) and the charges (q) that are subjected to cross-forces of the types $\{M\to q,Q\to m\}$. It can be shown that a cross-force law of the form $F\propto Mq/R^2$ or $F\propto Qm/R^2$ requires a proportionality constant with dimensions of ${(\left[G\right]·\left[K\right])}^{1/2}$. The dimensional analysis proceeds as follows:

$$\begin{array}{ccccc}\left[G\right]·{\displaystyle \frac{{\left[M\right]}^2}{{\left[R\right]}^2}}\sim \left[F\right]\sim \left[K\right]·{\displaystyle \frac{{\left[Q\right]}^2}{{\left[R\right]}^2}}& \Rightarrow & \hfill \left[F\right]·\left[F\right]& \sim & \left(\left[G\right]·{\displaystyle \frac{{\left[M\right]}^2}{{\left[R\right]}^2}}\right)·\left(\left[K\right]·{\displaystyle \frac{{\left[Q\right]}^2}{{\left[R\right]}^2}}\right)\hfill \\ & \Rightarrow & \hfill {\left[F\right]}^2& \sim & \left(\left[G\right]·\left[K\right]\right)·\left({\displaystyle \frac{{\left[M\right]}^2{\left[Q\right]}^2}{{\left[R\right]}^4}}\right)\hfill \\ & \Rightarrow & \hfill \left[F\right]& \sim & {\left(\left[G\right]·\left[K\right]\right)}^{1/2}·\left({\displaystyle \frac{\left[M\right]\left[Q\right]}{{\left[R\right]}^2}}\right).\hfill \end{array}$$

(1)

Thus, the CCC that appears in both types of cross-forces is the G-M $\sqrt{GK}$ of Newton’s constant G and Coulomb’s constant K, irrespective of whether the source term involves mass M acting on charge q or charge Q acting on mass m. The G-M $\sqrt{GK}$ has been determined to 10 significant digits in SI units (Table C2 in Ref. [10]):

$$\sqrt{GK}=0.7744872895{\mathrm{m}}^3{\mathrm{s}}^{-2}{\mathrm{C}}^{-1}.$$

(2)

The SI units in Equation (2) reveal the significance of this constant: Since $\left({\mathrm{m}}^3{\mathrm{s}}^{-2}\right)$ is the SI unit of the gravitational parameter $GM$ (the source of gravity) [13,14], $\left[G\right]=\left({\mathrm{m}}^3{\mathrm{s}}^{-2}\right){\mathrm{kg}}^{-1}$ expresses the strength of this source per kilogram, and the G-M $\left[\sqrt{GK}\right]=\left({\mathrm{m}}^3{\mathrm{s}}^{-2}\right){\mathrm{C}}^{-1}$ expresses the strength of the same source per coulomb. The notion of an intrinsic coupling within the combined field is alluded to by these dimensional relations.

Furthermore, the other G-M of G and K, viz., $\left[\sqrt{G/K}\right]={\mathrm{C}\mathrm{kg}}^{-1}$, leaves the source term out and directly describes coulombs per kilogram. This G-M guides us to define the effective gravitational constant $G_{★}$ [10] as

$$G_{★}\equiv {\displaystyle \frac{G}{K}}=\left(4\pi {\epsilon }_0\right)G,$$

(3)

where $K=1/\left(4\pi {\epsilon }_0\right)$, and ${\epsilon }_0$ is the electric permittivity of the vacuum. The units of $G_{★}$ are ${\left(\mathrm{C}{\mathrm{kg}}^{-1}\right)}^2$. Then, we also see that

$$\left[G_{★}\right]{\left[M\right]}^2={\left[Q\right]}^2,$$

(4)

which is a familiar relation between the units of mass and charge. In particular, $G_{★}{M}_{\mathrm{P}}^2=Q_{\mathrm{P}}^2$ in Planck (P) units and $G_{★}{M}_{\mathrm{S}}^2=e^2$ in Stoney (S) units [10].

2.2. The Significance of the Effective Gravitational Constant $G_{★}$

The G-M of Newton’s G and Coulomb’s K (Equation (2)) is the coupling constant of the cross-forces, so the postulated interaction between masses and charges does not introduce another universal constant. Nevertheless, it is rather odd that the combined GEM field is characterized by two seemingly independent constants, G and K. One would expect a single GEM constant, just as it was found for the electroweak field [9,10], in which the weak coupling constant ${\mathrm{\alpha }}_{\mathrm{w}}$ is related to the FSC ${\mathrm{\alpha }}_{\mathrm{e}}$ (defined in Table 1) by

$${\mathrm{\alpha }}_{\mathrm{w}}=\sqrt{{\mathrm{\alpha }}_{\mathrm{e}}}.$$

(5)

This G-K relation puzzle is resolved in a unified GEM-weak field, where all three constants are related and the effective gravitational constant $G_{★}$ (Equation (3)) assumes a prominent role. The constants of the three fundamental forces are related by

$${\mathrm{\alpha }}_{\mathrm{w}}={\displaystyle \frac{e}{Q_{\mathrm{P}}}}={\displaystyle \frac{e}{\sqrt{G_{★}}{M}_{\mathrm{P}}}},$$

(6)

where $M_{\mathrm{P}}$ is the Planck mass (defined in terms of Planck’s h) and $Q_{\mathrm{P}}$ is the Planck charge [10]. This relation is equivalent to

$${\mathrm{\alpha }}_{\mathrm{w}}\sqrt{G_{★}}={\displaystyle \frac{1}{{\aleph }_{\mathrm{A}}}}\left({\displaystyle \frac{e}{m_{\mathrm{e}}}}\right),$$

(7)

where ${\aleph }_{\mathrm{A}}$ is the “reduced Avogadro number” (reduced by a factor of ≈ 10, as derived in Ref. [10]).

In Equation (7), the combination of constants $G,K$, and ${\mathrm{\alpha }}_{\mathrm{w}}$ (or the FSC ${\mathrm{\alpha }}_{\mathrm{e}}$; Equation (5)) collected on the left-hand side is expressed in terms of the properties of the electron (${\aleph }_{\mathrm{A}}$ is the number of electrons in ≈ 0.1 moles). This equation effectively relates $\sqrt{G_{★}}$ to the ratio $(e/m_{\mathrm{e}})$, a result that was expected on dimensional grounds, since both terms have SI units of C kg⁻¹. Thus, much like the electroweak constants ${\mathrm{\alpha }}_{\mathrm{e}}$ and ${\mathrm{\alpha }}_{\mathrm{w}}$, the GEM constants G and K are not independent.

2.2.1. Numerical Equations for $G_{★}$ and G

On the other hand, recent work has shown that Newton’s G can be obtained in a fundamentally different way—using strictly SI units—as follows:

First, we obtain $G_{★}$ from the numerical equality (Equation (30) in Ref. [10])

$$\mathcal{N}\left(\sqrt{G_{★}}\right)={\displaystyle \frac{\mathcal{N}\left(k_{\mathrm{B}}\right)}{\mathcal{N}\left(e\right)}}\times {10}^{-6},$$

(8)

where the numerical function $\mathcal{N}\left(x\right)$ retains only the numerical value of x, and $k_{\mathrm{B}}$ is Boltzmann’s constant. This numerical relation indicates that entropy and charge information is encoded into $G_{★}$.

Next, we obtain Coulomb’s K from the electric permittivity of the vacuum ${\epsilon }_0$, viz.,

$$K\equiv {\displaystyle \frac{1}{4\pi {\epsilon }_0}}.$$

(9)

Finally, we combine Equations (8) and (9), and we solve for G. We determine that the numerical value of G in the SI system of units is

$$\mathcal{N}\left(G\right)={\displaystyle \frac{{10}^{-12}}{\mathcal{N}\left(4\pi {\epsilon }_0\right)}}{\left[{\displaystyle \frac{\mathcal{N}\left(k_{\mathrm{B}}\right)}{\mathcal{N}\left(e\right)}}\right]}^2=6.674015081\times {10}^{-11},$$

(10)

a value that is precise to 10 significant digits [10] owing to the exceptional measurement precision of $k_{\mathrm{B}}$, e, and ${\epsilon }_0$ [11].

2.2.2. Remarks

It is worth noting that, although precise, the numerical equality (10) that produces the SI value of G is also the first instance in physics in which the term $\left(4\pi {\epsilon }_0\right)e^2$ appears as a product in the denominator of the fraction on the right-hand side.

Furthermore, since the vacuum permittivity ${\epsilon }_0$ in the denominator is a lower limit in nature, it seems that the deduced SI value of G is a maximum in nature.

It is rather ironic that the extremely weak gravitational constant G, as we know it and have measured it, turns out to be a natural upper limit dictated by the vacuum, just as the speed of light in vacuum c. The difference of course is that c is a kinematical upper limit, whereas G is a maximized dynamical constant of the gravitational field.

2.3. The Components of the Conservative Force Field

Accounting explicitly for the signs of the force components given in Table 1 and Table 2, we write the net forces $F_{\mathrm{net}}$ in the various cases as follows:

• $\begin{array}{ccccccccccccc}\mathrm{Source}(M,+Q)\hfill & \to \hfill & (m,+q)& :& F_{\mathrm{net}}& =& {\left|F\right|}_{M\to m}& +& {\left|F\right|}_{M\to +q}& +& {\left|F\right|}_{+Q\to m}& -& {\left|F\right|}_{+Q\to +q}.\end{array}$
• $\begin{array}{ccccccccccccc}\mathrm{Source}(M,-Q)\hfill & \to \hfill & (m,-q)& :& F_{\mathrm{net}}& =& {\left|F\right|}_{M\to m}& -& {\left|F\right|}_{M\to -q}& -& {\left|F\right|}_{-Q\to m}& -& {\left|F\right|}_{-Q\to -q}.\end{array}$
• $\begin{array}{ccccccccccccc}\mathrm{Source}(M,+Q)\hfill & \to \hfill & (m,-q)& :& F_{\mathrm{net}}& =& {\left|F\right|}_{M\to m}& -& {\left|F\right|}_{M\to -q}& +& {\left|F\right|}_{+Q\to m}& +& {\left|F\right|}_{+Q\to -q}.\end{array}$
• $\begin{array}{ccccccccccccc}\mathrm{Source}(M,-Q)\hfill & \to \hfill & (m,+q)& :& F_{\mathrm{net}}& =& {\left|F\right|}_{M\to m}& +& {\left|F\right|}_{M\to +q}& -& {\left|F\right|}_{-Q\to m}& +& {\left|F\right|}_{-Q\to +q}.\end{array}$

All four cases can be condensed into one equation, if the charges Q and q are allowed to carry their own signs implicitly. Then, we write the net force in the general form

$$\begin{array}{ccc}{F}_{\mathrm{net}}& =& \left({\displaystyle \frac{1}{R^2}}\right)·\left[\left(GM+\sqrt{GK}Q\right)m-\left(KQ-\sqrt{GK}M\right)q\right]\hfill \\ & =& \left({\displaystyle \frac{K}{R^2}}\right)·\left[\left(G_{★}M+\sqrt{G_{★}}Q\right)m-\left(Q-\sqrt{G_{★}}M\right)q\right].\hfill \end{array}$$

(11)

or, equivalently, in the matrix form

$$\begin{array}{ccc}{F}_{\mathrm{net}}& =& \left({\displaystyle \frac{1}{R^2}}\right)·\left[\begin{array}{cc}M& Q\end{array}\right]\left[\begin{array}{cc}G& \sqrt{GK}\phantom{i}\\ \sqrt{GK}& -K\end{array}\right]\left[\begin{array}{c}m\\ q\end{array}\right]\hfill \\ & =& \left({\displaystyle \frac{K}{R^2}}\right)·\left[\begin{array}{cc}M& Q\end{array}\right]\left[\begin{array}{cc}{G}_{★}& \sqrt{G_{★}}\phantom{x}\\ \sqrt{G_{★}}& -1\end{array}\right]\left[\begin{array}{c}m\\ q\end{array}\right].\hfill \end{array}$$

(12)

The $2\times 2$ interaction matrix

$${\mathcal{I}}_{★}=\left[\begin{array}{cc}{G}_{★}& \sqrt{G_{★}}\phantom{i}\\ \sqrt{G_{★}}& -1\end{array}\right],$$

(13)

is symmetric, i.e., identical to its transpose ${\left({\mathcal{I}}_{★}\right)}^{\mathrm{T}}$. Its eigenvalues (${\mathrm{\lambda }}_{\mathrm{e}},{\mathrm{\lambda }}_{\mathrm{g}}$) are real, and its eigenvectors (${\overrightarrow{\upsilon }}_{\mathrm{e}},{\overrightarrow{\upsilon }}_{\mathrm{g}}$) are orthogonal. These eigenvectors define independent normal modes of interaction. Since $G\ll K$, then $G_{★}\ll 1$, and the eigenvalues are ${\mathrm{\lambda }}_{\mathrm{e}}\approx -(1+G_{★})$ and ${\mathrm{\lambda }}_{\mathrm{g}}\approx 2G_{★}$ to the first order in $G_{★}$. The corresponding eigenvectors in this approximation are ${\overrightarrow{\upsilon }}_{\mathrm{e}}\approx {\left[\begin{array}{cc}\sqrt{G_{★}}& -1\end{array}\right]}^{\mathrm{T}}$ and ${\overrightarrow{\upsilon }}_{\mathrm{g}}\approx {\left[\begin{array}{cc}+1& \sqrt{G_{★}}\end{array}\right]}^{\mathrm{T}}$.

In the physical regime where $G_{★}\ll 1$, the two normal modes are identified as predominantly electrical and gravitational, respectively. The off-diagonal components∼$\sqrt{G_{★}}$ indicate that each mode is weakly coupled to the other interaction. The eigenvalues of the system then show that the electrical mode $\propto exp\left({\mathrm{\lambda }}_{\mathrm{e}}t\right)$ decays rapidly in time t at a rate of ${\mathrm{\lambda }}_{\mathrm{e}}\approx -1$, whereas the gravitational mode $\propto exp\left({\mathrm{\lambda }}_{\mathrm{g}}t\right)$ is nearly quasistatic and evolves very slowly at a rate of ${\mathrm{\lambda }}_{\mathrm{g}}\approx 2G_{★}\ll 1$. As a result, once the fast electrical mode has decayed, the long-term evolution of the system is governed primarily by the very slow gravitational interactions.

2.4. Dimensionless Coupling Constants and Forces Between Electrons

Applied to two interacting electrons of mass $m_{\mathrm{e}}$ and charge $-e<0$, Equation (11) becomes

$$F_{\mathrm{net}}={\displaystyle \frac{1}{R^2}}\left(G{m}_{\mathrm{e}}^2-2\sqrt{GK}e{m}_{\mathrm{e}}-K{e}^2\right)\left(\mathrm{repulsive}\right),$$

(14)

where the dominant Coulomb force ($\propto -e^2$) and the two cross-forces ($\propto -e{m}_{\mathrm{e}}$) are all repulsive. The cross-force components cancel out only in a $e^{+}\rightleftharpoons e^{-}$ interaction, for which $Qm+Mq=0$ in Equation (11) and the net force $F_{\mathrm{net}}\simeq +K{e}^2/R^2$ is predominantly due to Coulomb attraction.

A dimensionless coupling constant of the combined field is defined for each component of the net force (14) in reference to the product ($hc$), where h is Planck’s constant and c is the speed of light in vacuum. Thus, we define the GCC, the CCC, and the FSC as

$${\mathrm{\alpha }}_{\mathrm{g}}\equiv {\displaystyle \frac{G{m}_{\mathrm{e}}^2}{hc}}=2.787972231\times {10}^{-46},$$

(15)

$${\mathrm{\alpha }}_{\times }\equiv {\displaystyle \frac{\sqrt{GK}e{m}_{\mathrm{e}}}{hc}}=5.690323437\times {10}^{-25},$$

(16)

and

$${\mathrm{\alpha }}_{\mathrm{e}}\equiv {\displaystyle \frac{K{e}^2}{hc}}=1.161409732\times {10}^{-3}\simeq {\displaystyle \frac{1}{861}},$$

(17)

respectively. The numerical values of these constants were determined from CODATA and PDG measurements [11,12] and the new data obtained in Refs. [9,10].

It is easy to show that the coupling constants are related, as they should be in the combined field: the CCC is precisely the G-M of the FSC and the GCC, viz.,

$${\mathrm{\alpha }}_{\times }=\sqrt{{\mathrm{\alpha }}_{\mathrm{g}}{\mathrm{\alpha }}_{\mathrm{e}}}.$$

(18)

Thus, we see that the coupling constants $\{{\mathrm{\alpha }}_{\mathrm{g}},{\mathrm{\alpha }}_{\times },{\mathrm{\alpha }}_{\mathrm{e}}\}$ form a growing geometric progression, in which ${\mathrm{\alpha }}_{\mathrm{g}}\ll {\mathrm{\alpha }}_{\times }\ll {\mathrm{\alpha }}_{\mathrm{e}}$, and the common ratio $\sqrt{{\mathrm{\alpha }}_{\mathrm{e}}/{\mathrm{\alpha }}_{\mathrm{g}}}\simeq 2.04\times {10}^{21}$ represents the square root of the ratio $(E_{\mathrm{e}}/E_{\mathrm{g}})$ of the electrostatic to the gravitational potential energy of two electrons separated by any distance R.

As a result, the net force (14) between the two electrons can be written as

$$\begin{array}{ccc}{F}_{\mathrm{net}}& =& {\displaystyle \frac{hc}{R^2}}\left(-{\mathrm{\alpha }}_{\mathrm{e}}-2\sqrt{{\mathrm{\alpha }}_{\mathrm{g}}{\mathrm{\alpha }}_{\mathrm{e}}}+{\mathrm{\alpha }}_{\mathrm{g}}\right)\hfill \\ & =& {\displaystyle \frac{hc}{R^2}}\left(-{\mathrm{\alpha }}_{\mathrm{e}}\right)\left(1+2\sqrt{{\mathrm{\beta }}_{\mathrm{g}}}-{\mathrm{\beta }}_{\mathrm{g}}\right)\hfill \\ & \simeq & F_{\mathrm{Coulomb}}\left(1+2\sqrt{{\mathrm{\beta }}_{\mathrm{g}}}\right)\left(\mathrm{repulsive}\right).\hfill \end{array}$$

(19)

where the normalized GCC ${\mathrm{\beta }}_{\mathrm{g}}\equiv {\mathrm{\alpha }}_{\mathrm{g}}/{\mathrm{\alpha }}_{\mathrm{e}}\simeq 2.40\times {10}^{-43}$ [10], and the term $-{\mathrm{\beta }}_{\mathrm{g}}$ was neglected in the last step.

Thus, the perturbation to the Coulomb force between electrons effectively arises from the cross-forces. Their relative amplitude ($2\sqrt{{\mathrm{\beta }}_{\mathrm{g}}}\sim {10}^{-21}$) is many orders of magnitude larger than that of the purely gravitational component, which was neglected. This disparity raises the prospect of detecting the cross-forces (should they exist) in gravitational experiments that involve an ionized gas and a neutral mass. Some typical estimates are obtained in Section 3 below.

3. Action–Reaction Cross-Forces of Type  $\mathit{Q}\rightleftharpoons \mathit{m}$  in Torsion Balance Experiments

Consider a partially ionized noble gas of mass M and total ionic charge Q interacting with a neutral mass m, located at distance R. For the interaction $(M,Q)\to (m,q)$ with $Q>0$ and $q=0$, Equation (11) reduces to

$$F_{\mathrm{net}}=F_{\mathrm{Newton}}\left(1+{\displaystyle \frac{Q}{\sqrt{G_{★}}M}}\right)\left(\mathrm{attractive}\right),$$

(20)

where $F_{\mathrm{Newton}}=GMm/R^2$, and $G_{★}$ is given by Equation (3). The cross-term is positive and enhances the Newtonian force.

For a torsion balance setup, we choose a test mass of $m=12$ g and a xenon (${}_{54}\mathrm{X}\mathrm{e}$) attractor with mass $M=12$ g and a relatively small ionization fraction $\mathrm{\chi }$ (to be determined). The ${}_{54}\mathrm{X}\mathrm{e}$ attractor is pressurized to 10 atm at room temperature (300 K) to reduce its volume to easily manageable Lab levels. Under these conditions, the ideal gas law predicts a volume of $V=225$ cm³ (0.225 L) for 0.0914 moles (12 g) of ${}_{54}\mathrm{X}\mathrm{e}$ gas (standard atomic weight 131.293 g mol⁻¹ [15]).

The two masses are separated by a distance of $r=12$ cm, so that the Newtonian force of attraction, $F_{\mathrm{Newton}}=6.67\times {10}^{-13}$ N, is barely measurable in the Lab. On the other hand, we would like the cross-force to be easily measurable in the Lab, so we choose its magnitude to be $F_{\times }=1\times {10}^{-8}$ N, which implies that $Q/\left(\sqrt{G_{★}}M\right)=1.50\times {10}^4$. Then, the required xenon charge is

$$Q=+15.5\mathrm{nC},$$

(21)

corresponding to a low ionization fraction of

$$\mathrm{\chi }={\displaystyle \frac{Q/e}{N_{\mathrm{Xe}}}}=1.76\times {10}^{-12},$$

(22)

where $N_{\mathrm{Xe}}=5.50\times {10}^{22}$ is the total number of atoms in 12 grams of ${}_{54}\mathrm{X}\mathrm{e}$ gas.

Finally, for a rod with a typical lever arm of $\mathsf{\ell }=2.5$ cm, the generated torque is

$$\mathrm{\tau }=F_{\times }\mathsf{\ell }=2.50\times {10}^{-10}\mathrm{N}\mathrm{m},$$

(23)

and for a torsion constant of $k=1\times {10}^{-9}$ N m rad⁻¹ (typical of Lab-utilized tungsten or quartz fibers), the maximum angular deflection of the suspended rod is

$${\theta }_{\max }={\displaystyle \frac{\mathrm{\tau }}{k}}=0.250\mathrm{rad}={14.3}^{\circ }.$$

(24)

The above values fall within the operational range of modern torsion balance metrology (e.g., Refs. [16,17,18,19,20,21,22,23,24] and references therein); therefore, if cross-forces do exist, their effects should be detectable with current experimental techniques using Faraday cages to achieve electrostatic shielding of the equipment [25,26,27,28,29,30].

4. Radiation from Inspiraling Reissner–Nordström Black Holes

4.1. Preliminaries

An RN black hole is characterized by two independent length scales corresponding to its physical properties, the field sources M and Q [31,32]: the Schwarzschild radius

$$R_S={\displaystyle \frac{2GM}{c^2}},$$

(25)

and the charge radius

$$R_Q={\displaystyle \frac{\sqrt{GK}\left|Q\right|}{c^2}},$$

where c is the speed of light in vacuum. Acceptable $R_Q$ values that prevent the appearance of naked singularities [33] fall in the range of

$$0\le R_Q\le {\displaystyle \frac{R_S}{2}}.$$

For our purposes, we choose a different strategy: we define an alternative charge length scale $L_Q$ that carries a factor of 2 in analogy with $R_S$, as well as the sign of the charge Q if one or both black holes of a binary carry a negative charge, viz.,

$$L_Q\equiv {\displaystyle \frac{2\sqrt{GK}Q}{c^2}},$$

(26)

for which the acceptable range to avoid naked singularities now is

$$|L_Q|\le R_S.$$

(27)

Then, by substituting Equations (25) and (26) into Equation (11), we write the conservative resultant force between equal-mass ($M=m$) RN black holes in three cases of interest (equal charges $q=Q$, opposite charges $q=-Q$, and one zero charge $q=0$):

$$\begin{array}{c}\hfill \begin{array}{cccc}\hfill \mathrm{Case}1,& Qq=+Q^2\hfill & \hfill :& F_{\mathrm{net}}=F_{\max }\left(R_S^2-L_Q^2+2R_S{L}_Q\right)R^{-2};\hfill \\ \hfill \mathrm{Case}2,& Qq=-Q^2\hfill & \hfill :& F_{\mathrm{net}}=F_{\max }\left(R_S^2+L_Q^2\right)R^{-2};\hfill \\ \hfill \mathrm{Case}3,& q=0\hfill & \hfill :& F_{\mathrm{net}}=F_{\max }\left(R_S^2+R_S{L}_Q\right)R^{-2};\hfill \end{array}\end{array}$$

(28)

where R is the separation of the black holes, and $F_{\max }=c^4/\left(4G\right)$ is the maximum tension force established in general relativity [34,35,36,37] (notably, one-fourth of the Planck unit of force $F_{\mathrm{P}}=c^4/G$ [10,38]). Furthermore, $L_Q<0$ when even one of the black holes carries a negative charge.

4.1.1. Maximum Force $F_{\max }$

The significance of the maximum tension force is that $F_{\max }$ has indeed appeared in our classical analysis of GEM forces. Up until now, it was commonly believed that a maximum force could not be obtained in Newtonian gravity [35], although it was found in some modified theories of gravity that are applicable to black hole binaries (e.g., Moffat, Brans–Dicke, and pure Lovelock theories [37]).

The “absence” of $F_{\max }$ from Newtonian mechanics was previously attributed in part to the absence of Planck’s constant h from the definition of the Planck force $F_{\mathrm{P}}$ [35]. We see that this conjecture is not confirmed: when we consider all force components of the combined GEM field, force $F_{\max }$ appears naturally as the leading factor of the net force. We expect that $R_S^2+L_Q^2<R^2$ (even for $R=2R_S$, when the horizons of the black holes touch), which then implies that the classical net forces $F_{\mathrm{net}}$ in binaries containing Schwarzschild and/or RN black holes do obey the condition that

$$F_{\mathrm{net}}<F_{\max }={\displaystyle \frac{c^4}{4G}}.$$

(29)

4.1.2. Net Forces $F_{\mathrm{net}}$ in Cases 1–3

The net forces (28) can be further simplified by introducing the dimensionless ratio $\mathsf{\varphi }$ between the source terms of the combined GEM field, defined as

$$\mathsf{\varphi }\equiv {\displaystyle \frac{L_Q}{R_S}}={\displaystyle \frac{Q}{\sqrt{G_{★}}M}},$$

(30)

where $\mathsf{\varphi }<0$ when at least one of the black holes in a binary carries a negative charge. Under these conditions, Equation (28) can be rewritten as

$$\begin{array}{c}\hfill \begin{array}{cccc}\hfill \mathrm{Case}1,& Qq=+Q^2\hfill & \hfill :& F_{\mathrm{net}}=F_{\max }\left(1-{\mathsf{\varphi }}^2+2\mathsf{\varphi }\right){\left(R_S/R\right)}^2;\hfill \\ \hfill \mathrm{Case}2,& Qq=-Q^2\hfill & \hfill :& F_{\mathrm{net}}=F_{\max }\left(1+{\mathsf{\varphi }}^2\right){\left(R_S/R\right)}^2;\hfill \\ \hfill \mathrm{Case}3,& q=0\hfill & \hfill :& F_{\mathrm{net}}=F_{\max }\left(1+\mathsf{\varphi }\right){\left(R_S/R\right)}^2.\hfill \end{array}\end{array}$$

(31)

Now, interpreting Cases 2 and 3 is straightforward, but Case 1 presents additional subtleties:

• In Case 3, the ratio $\mathsf{\varphi }\in [-1,+1]$, and the surviving component of the cross-force (term $+\mathsf{\varphi }$) is repulsive only if $Q<0$.
• In Case 2, the ratio $\mathsf{\varphi }\in [-1,+1]$ as well; the Coulomb force is attractive (term $+{\mathsf{\varphi }}^2$), and the cross-forces vanish.
• In Case 1, when $\mathsf{\varphi }<1-\sqrt{2}$, the net force is repulsive and the black holes move apart. Models involving two negatively charged black holes with $\mathsf{\varphi }<1-\sqrt{2}$ are not of interest, since the emitted GEM waves die out rapidly (their amplitudes decrease with separation as $1/R$ [39,40,41]). Such models are therefore excluded from the subsequent analysis of Case 1 by adopting the restricted range

  $$1-\sqrt{2}\le \mathsf{\varphi }\le 1\left(\mathrm{Case}1\right).$$

  (32)

  which corresponds to non-repulsive net forces $F_{\mathrm{net}}\ge 0$.

4.2. Radiation Amplitudes

In linearized gravity, the typical amplitude A of the perturbation of the flat spacetime metric ${\mathrm{\eta }}_{\alpha \beta }$ (i.e., the “metric perturbation” $\parallel {\mathcal{h}}_{\alpha \beta }^{\mathrm{TT}}\parallel$ with $A\equiv \parallel {\mathcal{h}}_{\alpha \beta }^{\mathrm{TT}}\parallel \ll 1$) is estimated to be (pages 996–1000 in Ref. [39] and Equations (4.38)–(4.40) in Ref. [40]) of the order of

$$A={\displaystyle \frac{G}{c^4}}\left({\displaystyle \frac{2}{D}}\right)\left|{\displaystyle \frac{d^2}{d{t}^2}}\left(I_{\mathrm{RN}}\right)\right|={\displaystyle \frac{1}{F_{\mathrm{P}}}}\left({\displaystyle \frac{2}{D}}\right)\left|{\displaystyle \frac{d^2}{d{t}^2}}\left(I_{\mathrm{RN}}\right)\right|,$$

(33)

where t represents time, $I_{\mathrm{RN}}=\mu R^2={\displaystyle \frac{1}{2}}M{R}^2$ is the moment of inertia of the RN binary ($\mu$ is the reduced mass), and D is the distance of the binary system from the observer.

We assume that the masses M of the black holes do not vary in time, in which case Equation (33) takes the equivalent forms

$$\begin{array}{cc}\hfill A& ={\displaystyle \frac{1}{F_{\mathrm{P}}}}\left({\displaystyle \frac{M}{D}}\right)\left|{\displaystyle \frac{d^2}{d{t}^2}}\left(R^2\right)\right|\hfill \\ \hfill & ={\displaystyle \frac{2}{F_{\mathrm{P}}}}\left({\displaystyle \frac{R}{D}}\right)\left|M{\displaystyle \frac{d^{2}R}{d{t}^2}}+{\displaystyle \frac{M}{R}}{\left({\displaystyle \frac{dR}{dt}}\right)}^2\right|\hfill \\ \hfill & ={\displaystyle \frac{2}{F_{\mathrm{P}}}}\left({\displaystyle \frac{R}{D}}\right)\left|-F_{\mathrm{net}}+{\displaystyle \frac{M{V}^2}{R}}\right|;\hfill \end{array}$$

(34)

in these equations, the separation $R\left(t\right)$ is a decreasing function of time, the radial velocity is $V\left(t\right)=dR/dt<0$, and the net force $F_{\mathrm{net}}>0$ is attractive (item 1 in Section 1.1).

Next, we adopt the equality $M{V}^2/R=F_{\mathrm{net}}/3$, and we cast Equation (34) in a compact form, viz.,

$$A={\displaystyle \frac{4}{3}}\left({\displaystyle \frac{R}{D}}\right){\displaystyle \frac{F_{\mathrm{net}}}{F_{\mathrm{P}}}}={\displaystyle \frac{1}{3}}\left({\displaystyle \frac{R}{D}}\right){\displaystyle \frac{F_{\mathrm{net}}}{F_{\max }}}.$$

(35)

The relation $M{V}^2/R=F_{\mathrm{net}}/3$ follows from the autonomous differential equation

$$R{R}^{″}=-3{\left(R^{\prime }\right)}^2,$$

(36)

where primes denote derivatives with respect to time t and the acceleration $R^{″}<0$ during the inspiral. The general solution describing orbital decay is $R\left(t\right)\propto {(1-t/{\mathrm{\tau }}_{\mathrm{c}})}^{1/4}$, where ${\mathrm{\tau }}_{\mathrm{c}}$ is the so-called “coalescence time”, defined by the condition that $R\left({\mathrm{\tau }}_{\mathrm{c}}\right)=0$ [41,42,43,44]. This solution effectively describes energy losses in the system: the power that is radiated away by GEM waves is precisely equal to the rate of decrease of the binary’s orbital energy [45,46,47].

4.2.1. Schwarzschild Black Holes

For conventional gravitational waves in the absence of Coulomb and cross-forces ($\mathsf{\varphi }=0$), all three cases presented in Equation (31) reduce to the Schwarzschild attractive force

$$F_S=F_{\max }{\left({\displaystyle \frac{R_S}{R}}\right)}^2.$$

(37)

Then, Equation (35) produces an estimate of the expected amplitude of gravitational waves $A_S$ from a pair of Schwarzschild black holes (SBHs), viz.,

$$A_S={\displaystyle \frac{R_S^2}{3RD}}.$$

(38)

When the horizons of two SBHs touch, $R=2R_S$ and $A_S=R_S/\left(6D\right)$. As an example, for $M=5M_{\odot }$, $D=8$ kpc, and horizons touching, the wave amplitude is quite large, viz., $A_S\simeq 1\times {10}^{-17}$. But for a binary separation of $R=1$ pc at the same distance D, Equation (38) gives $A_S\simeq 1\times {10}^{-29}$, a signal that is weaker by 12 orders of magnitude.

4.2.2. Reissner–Nordström Black Holes

In general, the three cases presented in Equation (31), combined with Equation (35), yield the following GEM wave amplitudes for the corresponding $\mathsf{\varphi }$-ranges that characterize RN black hole inspirals:

$$\begin{array}{c}\hfill \begin{array}{cccccc}\hfill \mathrm{Case}1,& Qq=+Q^2\hfill & \hfill :& A=A_S\left(1-{\mathsf{\varphi }}^2+2\mathsf{\varphi }\right)\hfill & \hfill ,& \mathrm{for}(1-\sqrt{2})\le \mathsf{\varphi }\le 1;\hfill \\ \hfill \mathrm{Case}2,& Qq=-Q^2\hfill & \hfill :& A=A_S\left(1+{\mathsf{\varphi }}^2\right)\hfill & \hfill ,& \mathrm{for}-1\le \mathsf{\varphi }\le 1;\hfill \\ \hfill \mathrm{Case}3,& q=0\hfill & \hfill :& A=A_S\left(1+\mathsf{\varphi }\right)\hfill & \hfill ,& \mathrm{for}-1\le \mathsf{\varphi }\le 1;\hfill \end{array}\end{array}$$

(39)

where $A_S$ is given by Equation (38).

In these cases, RN pairs of “extremal black holes” (EBHs) with $\left|\mathsf{\varphi }\right|=1$ are of special interest [48,49]. Their GEM wave amplitudes are

$$A_{\mathrm{EBHs}}=\left\{\begin{array}{ccc}0& ,& \mathrm{for}Q<0\mathrm{and}q=0;\hfill \\ 2A_S& ,& \mathrm{in}\mathrm{all}\mathrm{the}\mathrm{other}\mathrm{cases}.\hfill \end{array}\right.$$

(40)

The corresponding extremal net forces, derived from Equations (31) and (37), are as follows:

$$F_{\mathrm{EBHs}}=\left\{\begin{array}{ccc}0& ,& \mathrm{for}Q<0\mathrm{and}q=0;\hfill \\ 2F_S& ,& \mathrm{in}\mathrm{all}\mathrm{the}\mathrm{other}\mathrm{cases}.\hfill \end{array}\right.$$

(41)

Extremal black hole binaries with $Q<0$ and $q=0$ constitute one of two new classes of stationary equilibria arising solely from the inclusion of cross-forces. The second class emerges in Case 1 for $Q=q=(1-\sqrt{2})\sqrt{G_{★}}M$ (i.e., $\mathsf{\varphi }=1-\sqrt{2}<0$). These equilibria are discussed further in Section 4.3 below.

4.3. GEM Radiation, Extremal Black Holes, and Two Classes of Stationary Equilibria

In the nominal case of gravitational radiation from black hole mergers, a pair of SBHs are subject to an attractive force $F_S>0$ (Equation (37)), and the emitted gravitational waves have a typical amplitude $A_S$, given by Equation (38).

Considering now Equations (39)–(41), the following types of black hole binaries (RN–RN and RN–SBH pairs) are of current theoretical interest:

(a)

RN black hole mergers with negligible charges ($\left|\mathsf{\varphi }\right|\ll 1$) are also effectively described by the nominal SBH mergers. However, the first-order approximations of $\mathcal{O}\left(\mathsf{\varphi }\right)$ are different in Cases 1–3: the slopes of the linear terms in Equation (39) are 2, 0, and 1, respectively.

(b)

Case 1: Black holes with the same mass M and the same negative charge $Q=(1-\sqrt{2})\sqrt{G_{★}}M$ are in stationary equilibrium ($F_{\mathrm{net}}=0$ and $A=0$). These models are discussed in more detail below.

(c)

Case 3: An RN black hole with a charge-to-mass ratio of $Q/M=-\sqrt{G_{★}}=-86.173333$ pC/kg (i.e., $\mathsf{\varphi }=-1$) is also in stationary equilibrium, with an SBH of mass $m=M$ ($F_{\mathrm{net}}=0$), and no gravitational or GEM waves are emitted by the pair ($A=0$). This equilibrium is established by the balance between the attractive Newtonian forces $M\rightleftharpoons m$ and the repulsive cross-forces $Q\rightleftharpoons m$, since $Q<0$.

(d)

All other pairs of EBHs of equal mass M and at least one positive charge Q (Equations (40) and (41)) are bound by an attractive net force of magnitude $F_{\mathrm{EBHs}}=2F_S$ and emit GEM waves of amplitude $A_{\mathrm{EBHs}}=2A_S$, which grows at twice the rate of conventional gravitational waves during the inspiral.

4.3.1. Majumdar–Papapetrou RN–RN Binaries

The famous relativistic Majumdar–Papapetrou stationary equilibrium solution [50,51] is not realized in the above cases because of the inclusion of cross-forces. This equilibrium was originally established in extremal RN black holes of equal mass M and equal charge $Q=\pm \sqrt{G_{★}}M$ (hence, $\left|\mathsf{\varphi }\right|=1$), in which the Newtonian gravitational attraction cancels exactly the Coulomb repulsion [52,53,54,55]. However, there exists an analogue of the Majumdar–Papapetrou model, in which $m=M$ and $Qq=+Q^2\ne 0$ (a Case 1 model in Equation (39); item (b) above): For equal masses and charges, the net force is

$$F_{\mathrm{net}}=F_S\left(1-{\mathsf{\varphi }}^2+2\mathsf{\varphi }\right),$$

(42)

and a stationary equilibrium does arise for

$$\mathsf{\varphi }\equiv {\mathsf{\varphi }}_{\mathrm{eq}}=1-\sqrt{2}\simeq -0.4142,$$

(43)

corresponding to a ratio of $Q/M\simeq -35.694163$ pC/kg. Naturally, no GEM waves are emitted from this RN–RN configuration ($A=0$ from Equation (39) with $\mathsf{\varphi }={\mathsf{\varphi }}_{\mathrm{eq}}$ in Case 1).

4.3.2. Extremal RN–RN Binaries

Equation (40) shows that extremal RN–RN GEM waves are twice as strong and carry four times the energy flux of SBH–SBH gravitational waves (item (d) above). However, extremal RN black holes have not been observed, and only recently has it been shown that such objects can form through gravitational collapse [49,56]. These developments motivate a renewed examination of such models. For instance, a $5M_{\odot }$ RN black hole would require a charge excess or deficit of roughly ${10}^{16}$ moles of electrons ($\left|Q\right|$∼${10}^{21}$ C), corresponding to an ionization fraction of only∼${10}^{-18}$, since five solar masses contain about ${10}^{34}$ moles of hydrogen atoms. For further details on the theoretically expected charge range in RN black holes and the limiting value of $\mathsf{\varphi }\equiv L_Q/R_S=\pm 1$ for extremal Majumdar–Papapetrou solutions, see Refs. [57,58,59], the online summaries [48,60,61], and the recent works [49,56,62,63,64].

5. Summary and Conclusions

In this work, we have investigated the conservative GEM fields generated by charged masses ($M,Q$) interacting with other charged masses ($m,q$). The appearance of force components due to cross-interactions between masses and charges ($M\rightleftharpoons q$ and $Q\rightleftharpoons m$) is the key new element introduced in the calculations. The steps taken in the analysis and the empirical results obtained from applications are summarized as follows:

• The adopted principles of source coupling and the new and old GEM/EM forces were described in Section 1.1 and in Table 1. These principles are experimentally testable (Section 3).
• Newton’s third law of motion holds for all resultant forces, but the mass in cross-terms was assumed to behave in analogy to a negative charge (Table 2), because both masses and negative charges invariably attract test particles with positive intrinsic properties. This assumption can also be tested experimentally (Section 3).
• The dimensional coupling constant of the cross-forces was determined in Section 2.1 as the G-M of Newton’s G and Coulomb’s K (Equation (2)), and the resulting net forces due to both masses and charges were determined in Section 2.3 (Equations (11) and (12)).
• The dimensionless coupling constants corresponding to Newton’s law of gravity, Coulomb’s law, and the new cross-force components were defined in Section 2.4 (Equations (15)–(17) and Table 1) using the dimensional constants of the classical force laws, properties of the electron ($e,m_{\mathrm{e}}$), Planck’s constant h (not Dirac’s ℏ [9,10]), and the speed of light c.
• The cross-force ($F_{\times }$) between identical objects is the G-M of the familiar Newton ($F_{\mathrm{g}}$) and Coulomb ($F_{\mathrm{e}}$) forces, so that $F_{\mathrm{g}}\ll F_{\times }\ll F_{\mathrm{e}}$. If present, these cross-forces should be measurable in torsion balance experiments involving suspended masses interacting with partially ionized gases. As an application of the new formulation, we obtained related estimates for setting up such experiments in Section 3.
• In another application, we determined in Section 4 the typical amplitude $A=\parallel {\mathcal{h}}_{\alpha \beta }^{\mathrm{TT}}\parallel$ of GEM waves from extremal RN–RN black holes of the same mass and charge magnitude. It was found that $A=2A_S$, where $A_S$ is the amplitude of gravitational waves from a pair of inspiraling Schwarzschild black holes (see Equations (37) and (38) for SBH–SBH binaries).
• In the classical treatment of GEM forces in black hole binaries (Section 4), it is striking that the maximum relativistic tension force $F_{\max }=c^4/\left(4G\right)$ emerges naturally (Equation (28)), even though this limit was discovered in relativistic calculations and was not anticipated to appear in a classical framework [34,35].
• Because of the inclusion of cross-forces, the relativistic Majumdar–Papapetrou [50,51] stationary solution for extremal RN black holes ($\mathsf{\varphi }=\pm 1$ in Equation (30) and $Q/M\simeq \pm 86.17$ pC/kg) shifts to a unique lower (non-extremal) negative charge value, viz., $\mathsf{\varphi }=1-\sqrt{2}\simeq -0.4142$ and $Q/M\simeq -35.69$ pC/kg (Section 4.3). This threshold serves as a separatrix: in our models, identical RN black holes with a $\mathsf{\varphi }$-ratio in the negative range of

  $$-1\le \mathsf{\varphi }<1-\sqrt{2},$$

  do repel one another, whereas there are no repelling RN–RN or RN–SBH pairs in the absence of cross-forces.
• The cross-forces in RN–SBH binaries with $M=m$ are also responsible for the emergence of another class of stationary nonradiating equilibria (item (c) in Section 4.3). In this class, the RN black hole is always extremal and negatively charged ($\mathsf{\varphi }=-1$), with a charge-to-mass ratio of $Q/M\simeq -86.17$ pC/kg.