Abstract
This work explores the dynamics of quantum Fisher information (QFI) in open quantum systems coupled to squeezed reservoirs, providing a mathematical framework for analyzing parameter estimation precision under decoherence. We analyze QFI in two-qubit systems undergoing pure dephasing, considering the effects of squeezing parameter, phase difference, and coupling strength within an Ohmic spectral density model. The decoherence factor shows how reservoir engineering influences coherence loss. Numerical results demonstrate that optimal squeezing and local bath configurations enhance QFI preservation, while collective couplings accelerate decay. We also examine the interplay with von Neumann entropy, highlighting their inverse correlation, where increased mixedness reduces metrological sensitivity.
Keywords:
quantum fisher information; squeezed reservoirs; quantum dynamics; parameter estimation; von Neumann entropy MSC:
81P40; 81Q93; 81P45; 81S22
1. Introduction
In quantum theory, the precision of parameter estimation (P-E) is crucial across numerous scientific and technological domains, where novel approaches to assessing parameter sensitivity often lead to significant breakthroughs and technological advancements. A primary goal in quantum estimation is to enhance and maintain resolution accuracy by determining the values of an unknown parameter that characterizes a quantum system. P-E has been extensively studied to address practical challenges such as loss and decoherence [1,2,3,4,5,6,7]. Fisher information (FI), introduced by Fisher [8], is a key concept in parameter estimation (P-E) theory. Within this framework, QFI, which quantifies a quantum state’s sensitivity to the parameter variations, is a fundamental concept. Quantum estimation theory provides methods to identify optimal measurements for systems, especially when the parameter of interest is not directly accessible. The quantum version of the Cramér–Rao inequality establishes a lower bound governed by QFI [9], making QFI a central challenge to address. QFI represents the maximum information extractable from a specific measurement process for a given parameter. The QFI is an essential and fundamental quantifier extensively investigated across diverse physical contexts and frameworks. Recent studies have examined factorization dynamics linking QFI to quantum coherence, with both theoretical frameworks and experimental validations [10]. These findings reveal how coherence influences QFI scaling, with implications for quantum-sensing applications. Advances in non-Hermitian quantum models demonstrate that QFI can achieve super-Heisenberg scaling for magnetic field estimation in finite systems [11]. These findings highlight a dynamic interplay between Hermitian and non-Hermitian terms, enabling enhanced precision in dynamical quantum evolutions. A recent study on multiparameter qubit estimation introduced scrambling operations to address parameter uncertainty and incompatibility, enhancing the quantum Cramér–Rao bound [12]. This method offers practical solutions for joint estimation, surpassing sequential approaches when parameter uncertainty is reduced. While this work examines single-parameter estimation, where QFI is a scalar quantifying sensitivity to , in multiparametric scenarios the QFI forms a matrix , with symmetric logarithmic derivatives satisfying for parameters . Differences arise due to parameter incompatibility, where off-diagonal elements of the QFI matrix reflect trade-offs in simultaneous estimation, potentially requiring the quantum Cramér–Rao bound (with weight matrix W and d parameters) rather than the simple scalar bound. For the two-qubit dephasing model here, extending to multiparametric estimation could reveal enhanced precision in local baths, as collective couplings might amplify incompatibility via correlated noise in , leading to a non-commuting generator set and necessitating scrambling operations [12] to approach the bound—contrasting the monotonic, decoherence-limited scalar QFI decay observed in our single-parameter case. Additionally, investigation applied QFI to cosmic qubits in non-Markovian environments for Hubble parameter estimation, distinguishing thermalization dynamics [13]. These results underscore QFI’s utility in probing cosmological phenomena amidst environmental noise.
The purity of a quantum state, quantified as the trace of the density operator squared, provides a fundamental measure of its deviation from a pure configuration, with maximal purity indicating a coherent superposition free from statistical mixing and minimal purity signifying a fully mixed state in a given Hilbert space dimension. Mixedness, inversely related to purity, encapsulates the inherent uncertainty arising from ensemble averaging or environmental decoherence, and is alternatively gauged by the von Neumann entropy, which attains zero for pure states and its extremum for equiprobable mixtures, thereby serving as a cornerstone for assessing quantum information content. Recent investigations have elucidated the sensitivity of these metrics to variations in Planck’s constant, demonstrating that for Gaussian states, a reduction in this fundamental parameter diminishes purity and escalates entropy [14]. Complementary approaches have derived tight bounds on von Neumann entropy solely from purity measurements, facilitating the operational quantification of entanglement and coherence in multipartite systems without necessitating complete spectral decomposition [15]. In the realm of topological quantum matter, extensions of entanglement entropy to mixed states via convex-roof constructions preserve diagnostic capabilities for topological order, even under local noise, where mixedness modulates the persistence of long-range correlations [16]. Moreover, novel entanglement measures based on reduction-induced variations in partial von Neumann entropy offer intuitive and computationally efficient tools for bipartite mixed states, bridging theoretical insights with practical applications in quantum resource theory [17].
In quantum open-systems theory, the environmental reservoir is conventionally initialized in a thermal equilibrium state or a vacuum state. Nevertheless, progress in quantum reservoir engineering enables the preparation of nonthermal states. For example, squeezed reservoirs can be realized through Josephson parametric amplification in superconducting quantum circuits or via coherent manipulation of a trapped impurity within a double-well potential [18,19]. The application of nonthermal reservoirs has produced substantial insights in theoretical quantum investigations. A contemporary study [20] analyzed the Wigner quasiprobability distribution for photon-added squeezed-vacuum states [21,22,23], which holds relevance for quantum metrological protocols. Within non-Markovian open-system dynamics, squeezed reservoirs exert a pivotal regulatory influence [24,25,26]. Moreover, inquiries into squeezed thermal reservoirs have broadened to encompass quantum thermodynamic processes [27,28,29,30,31,32]. Additionally, squeezed thermal and vacuum reservoirs profoundly affect diverse quantum phenomena, including abrupt entanglement decay [25,33], violation of Leggett–Garg type inequalities [34], prolongation of quantum superposition lifetimes in Schrödinger-cat states [35], and related effects [36,37,38].
This work furthers our exploration of physical systems and physical processes that might result in high estimation precision. Specifically, we address this problem and discuss possible implications that might lead to useful techniques for maintaining and improving the precision of P-E. In this case, we examine the feasibility of maintaining and adjusting the QFI initially defined in a two-qubit system interacting with squeezed reservoirs. We demonstrate that by tuning the squeezing parameter, phase difference, and coupling strength, the QFI can be preserved and even improved during the dynamics. We demonstrate that long-term protection of quantum FI may be accomplished without being impacted by the decoherence effect by carefully choosing the model parameters.
The manuscript is organized as follows. In Section 2, the physical dephasing model with the exact solution is introduced. Section 3 is devoted to the dynamics of QFI and von Neumann entropy in a two-qubit system, locally subjected to spatially separated squeezed reservoirs or a common reservoir. A summary of our findings is presented in Section 4.
2. Modeling Pure Dephasing with a Squeezed Reservoir
This section explores a pure dephasing framework involving a two-qubit system, where each qubit either interacts independently with its own squeezed thermal reservoir or both qubits couple to a shared squeezed thermal bath. The following subsections elaborate on these two distinct configurations.
2.1. Individual Qubits Coupled to Separate Baths
We first examine the scenario where two qubits are linked to separate, identical squeezed thermal reservoirs through nondemolition interactions. To analyze this setup, we start with a single two-level system described by the Hamiltonian
which interacts with a bosonic environment given by
The interaction between the qubit and the reservoir is governed by the nondemolition Hamiltonian
where defines the Pauli z-operator, with and representing the excited and ground states of the qubit, respectively, and denoting the qubit’s transition frequency. The terms indicate the frequency of the mth reservoir mode, and are the creation and annihilation operators for that mode, and represents the coupling strength between the qubit and each mode. The total Hamiltonian of the combined system-reservoir is . Since acts only on the reservoir degrees of freedom, . Combined with , this implies , ensuring that the expectation value of the system energy, , is conserved over time for any initial state. This conservation prevents transitions between the qubit’s energy eigenstates (|e⟩ and |g⟩), resulting in constant populations and . In contrast, in general, as the interaction can induce fluctuations in the reservoir modes without net energy transfer to the system. This nondemolition form of (coupled via ) distinguishes the model from typical dissipative baths, where interactions involving or would enable energy exchange, driving the system toward a thermal Gibbs state with modified populations. Here, the reservoir induces only pure dephasing, affecting coherences (off-diagonal terms) while preserving the diagonal populations, which is ideal for studying decoherence without relaxation.
To derive the dynamics of a single qubit, we assume an initial separable state , with the reservoir initialized in a squeezed thermal state
where , T is the temperature, and N is a normalization factor. The squeezing operator is , with , where and denote the squeezing strength and phase, respectively. Since the combined qubit–reservoir system is isolated but , this implies that the energy of the system is always conserved, and the populations on each level of the qubit remain unchanged over time; evolution is described in the interaction picture with respect to . In this picture, the time–evolution operator is unitary and takes the form
with the interaction-picture unitary operator , and . By tracing out the reservoir degrees of freedom, the reduced density matrix of the qubit in the basis is written as
where is the decoherence factor defined by [27,39,40]
We employ an Ohmic spectral density, , commonly used in spin-boson systems [27], where is a dimensionless dissipation parameter, is the phase difference between the squeezing and coupling phases, and is the cutoff frequency. At zero temperature (), , and the reservoir is effectively a squeezed vacuum. Solving the integral in Equation (7) yields
with time-dependent terms , , and , where . In the high-temperature limit, , and the decoherence factor retains the form of Equation (8), but with modified coefficients
Our focus is the dephasing behavior of a two-qubit system, where each qubit interacts separately with its own squeezed thermal bath via energy-conserving coupling. Using the method outlined in [41,42,43,44], we compute the reduced density matrix for the two-qubit system, . Using Kraus operators diagonal in the basis, the single-qubit map is
and for two qubits,
The matrix elements are
with coefficients from single-qubit maps.
In the two-qubit basis (indices 1 to 4), the diagonal elements remain unchanged due to population conservation
The off-diagonal elements incorporate the decoherence factors from each bath
with Hermitian conjugates ensuring . For non-identical baths, distinct and would apply, but here identical reservoirs yield the symmetric form. Finally, the temporal evolution of the density matrix for the two-qubit system, expressed within the two-qubit basis, is formally articulated as follows
This matrix describes the evolution of a two-qubit system under local baths (denoted ). In pure dephasing, diagonal elements remain unchanged, while off-diagonal elements decay over time as evolves.
2.2. Two Qubits Coupled to a Shared Bath
Next, we consider a scenario where two identical qubits interact with a single squeezed thermal reservoir through energy-preserving interactions. The total Hamiltonian is
with j indexing the qubits and m the bath modes. Here, both qubits share identical coupling strengths to the reservoir. Following the technique in [45], the reduced density matrix for the two-qubit system, , is derived in the same basis
where denotes the common bath, and is as given in Equation (7). This expression captures the dynamics of two qubits under a shared squeezed thermal bath. Notably, in this setup, the diagonal elements and off-diagonal terms and stay constant, while others decay as progresses.
3. Quantum Fisher Information and Purity
In this section, we examine the QFI to evaluate the sensitivity of a two-qubit system’s time-evolved states to a parameter , encoded via a local unitary operation, under two distinct environmental interactions: (i) each qubit coupled to its own squeezed thermal bath, as governed by Equation (6), and (ii) both qubits coupled to a shared squeezed thermal bath, as described by Equation (9). The QFI serves as a pivotal metric in quantum metrology, quantifying the precision with which can be estimated, thus shedding light on the impact of bath configurations on the precision of P-E. We start with the initial pure state , where x and y are real coefficients satisfying the normalization condition , yielding the initial density matrix
in the basis . The parameter is introduced through the unitary operator , with the generator , where acts on qubit A and is the identity on qubit B. The QFI, denoted , is calculated using the formula
where and are the eigenvalues and eigenvectors of the time-evolved state . In order to study the purity of the two-qubit states in the dephasing model, the von Neumann entropy is employed as a fundamental quantifier, defined as
where it measures mixedness by vanishing for pure states and achieving mixed two-qubit configurations for nonzero entropy value. For the time-evolved density matrices and , this entropy is derived from their spectral decompositions, revealing how the temporal degradation of state purity induced by interactions with squeezed thermal reservoirs. Within this quantum open-system framework, the entropy evolution elucidates how reservoir-squeezing parameters regulate coherence dissipation, manifested through the decoherence function that governs off-diagonal decay, consequently influencing the overall mixedness.
Figure 1 illustrates the temporal evolution of the QFI in a two-qubit system subjected to pure dephasing due to interactions with squeezed-vacuum reservoirs, initialized in the pure entangled state . The figure comprises two panels: (a) depicts the dynamics under local reservoir couplings and (b) shows the case of collective reservoir coupling. In both panels, the QFI is plotted against the dimensionless time , with curves corresponding to different phase differences . Solid is for , dot-dashed is for , dashed is for , and dotted is for , with fixed parameters and . In Figure 1, phase differences , , , and illustrate the transition from minimal () to maximal () protective effects, with intermediates highlighting tunable control; fixed and . The QFI reaches its maximum value at , reflecting the optimal sensitivity of the pure entangled state to phase variations. In both panels, the QFI exhibits monotonic decay from its initial value toward zero as time progresses, driven by dephasing from the squeezed reservoirs, resulting from the exponential suppression of off-diagonal elements in the density matrix, governed by the decoherence factor. The hyperbolic terms involving q and the trigonometric dependence on modulate the effective noise strength, allowing squeezing to either amplify or mitigate decoherence compared to an unsqueezed thermal bath. The dependence on reveals a tunable control mechanism. When , the QFI decays most rapidly, leading to accelerated loss of coherence, whereas at , it decays most slowly, with intermediate values like and showing decay rates between these extremes. Comparing Figure 1a,b, the collective coupling in (b) generally results in faster QFI decay across all , particularly at longer times, where the collective case approaches asymptotic zero more rapidly. In the local bath scenario, off-diagonal elements like decay with , whereas in the shared bath, the exponent for is , causing faster erasure of the initial QFI. This amplification occurs because the shared bath correlates noise, enhancing the effective dephasing rate for the qubit state during dynamics. Physically, these results highlight the role of reservoir engineering in open quantum systems, which can be harnessed to extend the coherence time of entangled states, thereby enhancing the quantum advantage in metrological tasks and implying a lower Cramér–Rao bound for estimating . Notably, for the specific initial state considered, independent local baths preserve QFI better than a shared bath, underscoring the importance of aligning the environmental configuration with the quantum state’s symmetry.
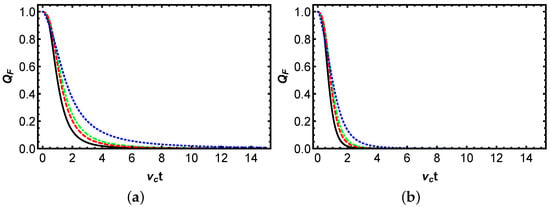
Figure 1.
Time-dependent behavior of the QFI for a two-qubit system interacting with a squeezed reservoir at zero temperature, characterized by varying phase difference . Panels (a,b) illustrate the QFI dynamics for local and collective reservoir couplings, respectively. The solid curve corresponds to , the dot-dashed curve to , and the dashed curve to , and the dotted curve to . The initial quantum state is defined by parameters , with a qubit–reservoir coupling strength of and a reservoir-squeezing parameter of .
Figure 2 presents the temporal dynamics of the QFI for a two-qubit system undergoing pure dephasing with parameters . The figure is divided into two panels: (a) illustrates dynamics under local reservoir couplings, where each qubit interacts with an independent squeezed bath, and (b) depicts collective coupling, where both qubits share a common bath. In both panels, QFI is plotted against the dimensionless time . The curves correspond to varying squeezing parameters q. Solid is for , dot-dashed is for , dashed is for , and dotted is for , with fixed coupling strength and phase difference . Figure 2 varies , , , and at fixed and to span low-to-high squeezing strengths, modulating effective noise suppression. Both panels show QFI decaying monotonically to zero due to dephasing, driven by the decoherence factor . The squeezing parameter q modulates decoherence: at , QFI decays slowly, as minimal squeezing offers limited noise suppression, delaying coherence loss. When , QFI decay is faster, with stronger squeezing; intermediate and yield graded decay rates, reflecting the increasing suppression of via the term. Panel (b) exhibits faster QFI decay than (a) due to the collective bath’s enhanced dephasing effect. These findings highlight reservoir engineering’s role in quantum metrology, where higher squeezing mitigates decoherence, tightening the Cramér–Rao bound for -estimation and that local baths outperform collective ones for this state, emphasizing the need to tailor environmental interactions to the qubits’state.
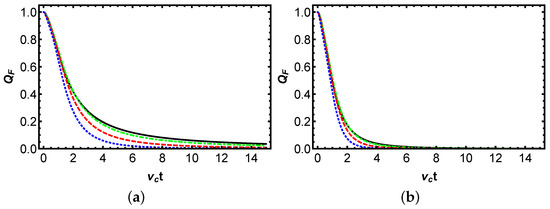
Figure 2.
Time-dependent dynamics of the QFI for a two-qubit system interacting with a squeezed reservoir at zero temperature, characterized by varying squeezing parameter q. Panels (a,b) depict the evolution of QFI under local and collective reservoir couplings, respectively. The solid curve corresponds to , the dot-dashed curve to , the dashed curve to , and the dotted curve to . The initial quantum state is defined by parameters , with a qubit–reservoir coupling strength of and a phase difference of .
In Figure 3, the time evolution of the QFI for a two-qubit system QFI is plotted against dimensionless time under pure dephasing for various values of the coupling strengths . The solid for , dot-dashed for , dashed for , and dotted for , with fixed squeezing parameter and phase difference . In Figure 3, , , , and at fixed and capture weak-to-strong coupling regimes, where low mimics near-isolated evolution and higher amplifies bath-induced dephasing. Both panels of the figure demonstrate a monotonic decrease of the QFI to zero, driven by dephasing induced by the decoherence factor . The coupling strength regulates the intensity of dephasing. A weak results in the slowest QFI decay by limiting bath-induced phase noise, thereby preserving QFI; a strong (dotted) accelerates decay by amplifying noise through an increased ; intermediate values and yield progressive decay rates, aligning with the linear dependence of in . Panel (b) exhibits a faster QFI reduction compared to (a), as collective coupling enhances dephasing, where off-diagonal elements such as decay as versus in the local configuration. These findings highlight the influence of reservoir engineering on quantum metrology, where a weaker system–bath coupling reduces decoherence, improving the Cramér–Rao bound for -estimation and sustaining measurement precision against environmental noise.
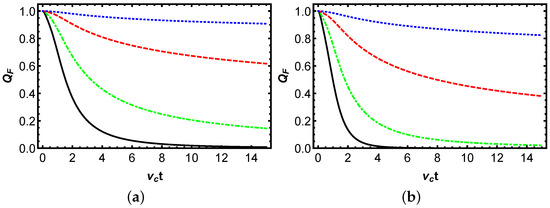
Figure 3.
Temporal dynamics of the QFI for a two-qubit system interacting with a squeezed reservoir at zero temperature, characterized by varying qubit–reservoir coupling strength . Panels (a,b) illustrate the evolution of QFI under local and collective reservoir couplings, respectively. The solid curve corresponds to , the dot-dashed curve to , the dashed curve to , and the dotted curve to . The initial quantum state is defined by parameters , with a reservoir-squeezing parameter and a phase difference .
Figure 4 depicts the time-dependent von Neumann entropy S in a two-qubit system under pure dephasing in squeezed-vacuum reservoirs at zero temperature, initialized in the Bell state. The Figure 4a,b show the entropy evolution for local and collective couplings, respectively, plotted against dimensionless time with curves for varying phase difference . The function S starts at 0 for the pure initial state and rises monotonically toward 1, indicating increasing mixedness due to dephasing that affects off-diagonal coherences governed by . Interestingly, the phase modulates the rate, with yielding the fastest entropy growth via enhanced noise alignment, while minimizes it by quadrature suppression, and intermediate values show transitional rates. Furthermore, the panel (b) exhibits quicker entropy accumulation than (a), as collective noise correlates fluctuations to amplify dephasing during the dynamics. Physically, this highlights how phase tuning in engineered reservoirs controls purity degradation. Compared to QFI, which quantifies phase sensitivity and decays inversely with S, high entropy correlates with low QFI, as mixedness diminishes metrological utility. Figure 5 presents the temporal von Neumann entropy dynamics for the same initial state versus with varying squeezing q at and . We can observe that the function S increases from 0 to approach 1, with lower q accelerating growth due to insufficient noise reduction, whereas higher q slows it, and mid-range q produces intermediate increases reflecting hyperbolic modulation in . In contrast to QFI, which decreases more rapidly at low squeezing parameter q, the rise in von Neumann entropy S exhibits an inverse correlation with QFI’s decline, underscoring that S quantifies the degree of purity, whereas QFI reflects the loss of extractable information. Figure 6 illustrates von Neumann entropy versus for varying coupling with . It is observed that the von Neumann entropy S rises monotonically from a pure state to maximum mixing, with higher coupling strength accelerating this increase through enhanced scaling, lower slowing it by reducing bath interactions, and intermediate values producing a range of intermediate rates. Physically, this highlights the dominant role of coupling strength in determining dephasing intensity, where a minimal approximates isolated quantum evolution, preserving coherence. In relation to QFI, the rise in entropy inversely correlates with QFI’s decline, as increased coupling reduces sensitivity while boosting mixedness, though low in local setups optimizes both entropy and QFI, facilitating metrological precision. The selections of the parameters not only demonstrate the monotonic, decoherence-limited QFI decay but also underscore optimal configurations for preserving metrological sensitivity in local versus collective baths.
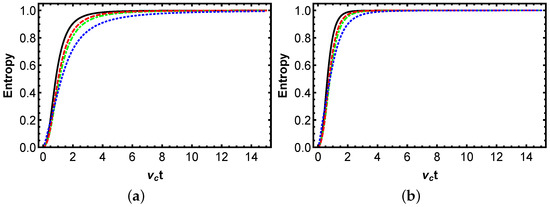
Figure 4.
Time-dependent behavior of the von Neumann entropy for a two-qubit system interacting with a squeezed reservoir at zero temperature, characterized by varying phase difference . Panels (a,b) illustrate the QFI dynamics for local and collective reservoir couplings, respectively. The solid curve corresponds to , the dot-dashed curve to , the dashed curve to , and the dotted curve to . The initial quantum state is defined by parameters , with a qubit–reservoir coupling strength of and a reservoir-squeezing parameter of .
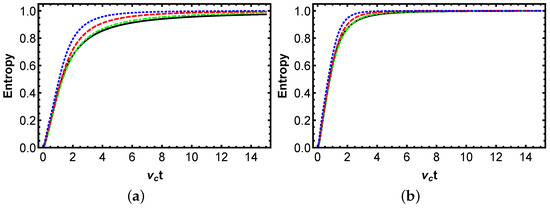
Figure 5.
Time-dependent dynamics of the von Neumannn entropy for a two-qubit system interacting with a squeezed reservoir at zero temperature, characterized by varying squeezing parameter q. Panels (a,b) depict the evolution of QFI under local and collective reservoir couplings, respectively. The solid curve corresponds to , the dot-dashed curve to , the dashed curve to , and the dotted curve to . The initial quantum state is defined by parameters , with a qubit–reservoir coupling strength of and a phase difference of .
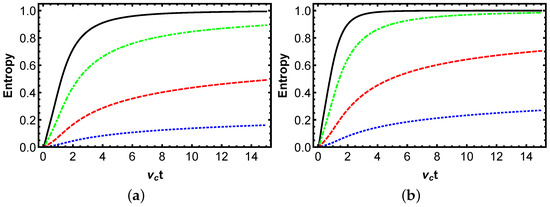
Figure 6.
Temporal dynamics of the von Neumannn entropy for a two-qubit system interacting with a squeezed reservoir at zero temperature, characterized by varying qubit–reservoir coupling strength . Panels (a,b) illustrate the evolution of QFI under local and collective reservoir couplings, respectively. The solid curve corresponds to , the dot-dashed curve to , the dashed curve to , and the dotted curve to . The initial quantum state is defined by parameters , with a reservoir-squeezing parameter and a phase difference .
The observed preservation of QFI under optimal reservoir parameters—such as higher squeezing q, , and weaker coupling in local bath configurations—directly enhances the precision of estimating , as dictated by the quantum Cramér–Rao inequality, which bounds the variance , where M is the number of measurements. In the local bath case, the slower decay of off-diagonal terms (e.g., for ) maintains higher QFI values over longer , potentially reducing the estimation error by up to a factor of 2 compared to collective couplings, where decay is amplified (e.g., ). This suggests practical advantages for quantum-sensing protocols, where squeezed reservoirs could extend the operational timescale for phase estimation in noisy environments, outperforming unsqueezed thermal baths by suppressing the effective noise strength. Conversely, suboptimal parameters (e.g., or strong ) accelerate QFI loss, widening the Cramér–Rao bound and limiting metrological sensitivity, as evidenced by the inverse correlation with von Neumann entropy S, where increased mixedness erodes the quantum advantage.
Figure 7 () and Figure 8 () reveal the tight mutual relations among QFI, von Neumann entropy S, and -norm coherence . In the local bath configuration, moderate and suitable q yield extended regions of high QFI and high accompanied by low S, with this preservation effect significantly enhanced under the optimal phase difference in Figure 8, demonstrating effective mitigation of coherence loss and sustained metrological usefulness with minimal mixedness. In contrast, collective couplings exhibit broader and more rapid degradation across the parameter space, resulting in low QFI, low , and high S even for moderate parameters. The inverse correlations are evident throughout both figures—decoherence drives the exponential loss of off-diagonal elements ( decay), which in turn increases mixedness (S rise) and erodes parameter sensitivity (QFI drop)—consistent with the proportionality of and .
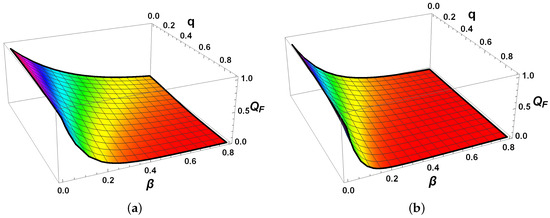
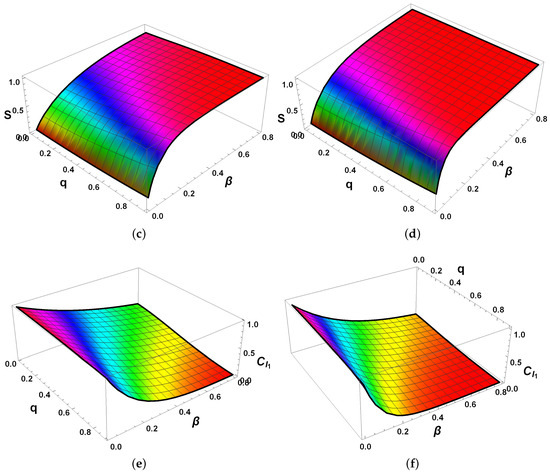
Figure 7.
QFI , von Neumann entropy S, and -norm coherence for the two-qubit system as functions of parameters and q at fixed time , with phase difference . The initial state is the maximally coherent X-state with . Panels (a,b) show QFI under local and collective reservoir couplings, respectively. Panels (c,d) display the von Neumann entropy S for local and collective couplings, respectively. Panels (e,f) present the -norm coherence under local and collective couplings, respectively.
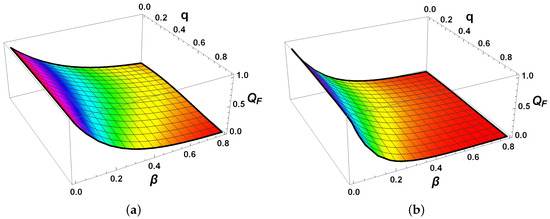
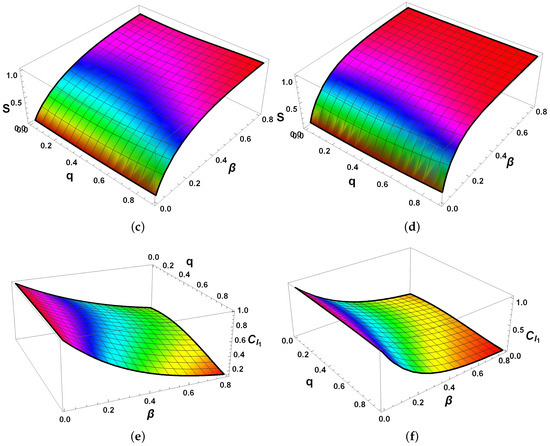
Figure 8.
QFI , von Neumann entropy S, and -norm coherence for the two-qubit system as functions of parameters and q at fixed time , with phase difference . The initial state is the maximally coherent X-state with . Panels (a,b) show QFI under local and collective reservoir couplings, respectively. Panels (c,d) display the von Neumann entropy S for local and collective couplings, respectively. Panels (e,f) present the -norm coherence under local and collective couplings, respectively.
4. Conclusions
In conclusion, this work has elucidated the dynamics of quantum Fisher information (QFI) in open quantum systems coupled to squeezed reservoirs, offering a mathematical framework for analyzing the precision of parameter estimation under decoherence. Our analysis of QFI in two-qubit systems undergoing pure dephasing has demonstrated the significant influence of the squeezing parameter, phase difference, and coupling strength within an Ohmic spectral density model. The decoherence factor reveals how reservoir engineering can effectively modulate QFI loss. Numerical results indicate that optimal squeezing and local bath configurations substantially enhance QFI preservation, whereas collective couplings accelerate decay. Additionally, the interplay with von Neumann entropy highlights an inverse correlation, wherein increased mixedness diminishes metrological sensitivity. These findings underscore the potential of squeezed reservoirs to mitigate decoherence, paving the way for improved quantum sensing and metrology applications. In comparison with recent work on prethermal Floquet time crystals as quantum sensors of AC fields [46], where QFI achieves superlinear scaling ( with ) in the prethermal regime due to many-body correlations and robustness against disorder, our results demonstrate that squeezed reservoirs in two-qubit dephasing models can preserve and enhance QFI through tunable parameters like squeezing strength and phase difference, offering a complementary approach for maintaining metrological precision in open quantum systems. Future work could extend this framework to multipartite systems or incorporate amplitude damping to further explore practical implementations in quantum technologies.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2503).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef]
- Dowling, J.P. Quantum optical metrology—The lowdown on high-N00N states. Contemp. Phys. 2008, 49, 125–143. [Google Scholar] [CrossRef]
- Jones, J.A.; Karlen, S.D.; Fitzsimons, J.; Ardavan, A.; Benjamin, S.C.; Briggs, G.A.D.; Morton, J.J.L. Magnetic field sensing beyond the standard quantum limit using 10-Spin NOON States. Science 2009, 324, 1166–1168. [Google Scholar] [CrossRef]
- Simmons, S.; Jones, J.A.; Karlen, S.D.; Ardavan, A.; Morton, J.J.L. Magnetic field sensors using 13-spin cat states. Phys. Rev. A 2010, 82, 022330. [Google Scholar] [CrossRef]
- Higgins, B.L.; Berry, D.W.; Bartlett, S.D.; Wiseman, H.M.; Pryde, G.J. Entanglement-free Heisenberg-limited phase estimation. Nature 2007, 450, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Demkowicz-Dobrzanski, R.; Dorner, U.; Smith, B.J.; Lundeen, J.S.; Wasilewski, W.; Banaszek, K.; Walmsley, I.A. Quantum phase estimation with lossy interferometers. Phys. Rev. A 2009, 80, 013825. [Google Scholar] [CrossRef]
- Berrada, K. Optimizing Parameter Estimation Precision in Open Quantum Systems. Axioms 2025, 14, 368. [Google Scholar] [CrossRef]
- Fisher, R.A. Theory of statistical estimation. In Mathematical Proceedings of the Cambridge Philosophical Society; Fisher, R.A., Bennett, J.H., Eds.; University of Adelaide Press: Adelaide, Australia, 1925; Volume 22, pp. 700–725. [Google Scholar]
- Cramer, H. Mathematical Methods of Statistics; Princeton University Press: Princeton, NJ, USA, 1946. [Google Scholar]
- Zhao, X.; Yu, X.; Li, L.; Zhou, W.; Zhang, C. Factorization dynamics and quantum Fisher information in bipartite entanglement. Sci. Adv. 2025, 11, eadv8132. [Google Scholar] [CrossRef]
- Agarwal, K.D.; Konar, T.K.; Chandra Lakkaraju, L.G.; De, A.S. Critical quantum metrology using non-Hermitian spin model with RT-symmetry. arXiv 2025, arXiv:2503.24331. [Google Scholar] [CrossRef]
- He, J.; Paris, M.G.A. Scrambling for precision: Optimizing multiparameter qubit estimation with sloppiness and incompatibility. arXiv 2025, arXiv:2503.08235. [Google Scholar] [CrossRef]
- Feng, J. Quantum Fisher information of a cosmic qubit in non-Markovian de Sitter spacetime. J. High Energy Phys. 2025, 2025, 29. [Google Scholar]
- Gosson, M.A.d. On the sensitivity of the purity and entropy of mixed quantum states on variations of Planck’s constant. Quantum Stud. Math. Found. 2025, 12, 16. [Google Scholar] [CrossRef]
- Zhang, T.; Smith, G.; Smolin, J.A.; Liu, L.; Peng, X.-J.; Zhao, Q.; Girolami, D.; Ma, X.; Yuan, X.; Lu, H. Quantification of entanglement and coherence with purity detection. Npj Quantum Inf. 2024, 10, 60. [Google Scholar] [CrossRef]
- Wang, T.-T.; Song, M.; Meng, Z.Y.; Grover, T. An analog of Topological Entanglement Entropy for Mixed States. PRX Quantum 2025, 6, 010358. [Google Scholar] [CrossRef]
- Zhu, J.-M. Reduction-induced variations in partial von Neumann entropy. arXiv 2024, arXiv:2412.17027v3. [Google Scholar]
- Murch, K.W.; Weber, S.J.; Beck, K.M.; Ginossar, E.; Siddiqi, I. Reduction of the radiative decay of atomic coherence in squeezed vacuum. Nature 2013, 499, 62–65. [Google Scholar] [CrossRef]
- Bar-Gill, N.; Rao, D.D.B.; Kurizki, G. Creating Nonclassical States of Bose-Einstein Condensates by Dephasing Collisions. Phys. Rev. Lett. 2011, 107, 010404. [Google Scholar] [CrossRef] [PubMed]
- Akhtar, N.; Wu, J.; Peng, J.-X.; Liu, W.-M.; Xianlong, G. Sub-Planck structures and sensitivity of the superposed photon-added or photon-subtracted squeezed-vacuum states. Phys. Rev. A 2023, 107, 052614. [Google Scholar] [CrossRef]
- Akhtar, N.; Sanders, B.C.; Xianlong, G. Sub-Planck phase-space structure and sensitivity for SU(1,1) compass states. Phys. Rev. A 2022, 106, 043704. [Google Scholar] [CrossRef]
- Dey, S.; Nair, S.S. Generalized photon-subtracted squeezed vacuum states. J. Phys. A Math. Theor. 2020, 53, 385305. [Google Scholar] [CrossRef]
- Biswas, A.; Agarwal, G.S. Nonclassicality and decoherence of photon-subtracted squeezed states. Phys. Rev. A 2007, 75, 032104. [Google Scholar] [CrossRef]
- Ablimit, A.; Ren, F.-H.; He, R.-H.; Xie, Y.-Y.; Wang, Z.-M. Effects of non-Markovian squeezed bath on the dynamics of open systems. Physica A 2023, 630, 129251. [Google Scholar] [CrossRef]
- Ali, M.M.; Chen, P.-W.; Goan, H.-S. Decoherence-free subspace and disentanglement dynamics for two qubits in a common non-Markovian squeezed reservoir. Phys. Rev. A 2010, 82, 022103. [Google Scholar] [CrossRef]
- He, Z.; Zeng, H.-S.; Chen, Y.; Yao, C. Non-Markovian dynamics of a dephasing model in a squeezed thermal bath. Laser Phys. Lett. 2019, 16, 065204. [Google Scholar] [CrossRef]
- You, Y.-N.; Li, S.-W. Entropy dynamics of a dephasing model in a squeezed thermal bath. Phys. Rev. A 2018, 97, 012114. [Google Scholar] [CrossRef]
- Agarwalla, B.K.; Jiang, J.-H.; Segal, D. Quantum efficiency bound for continuous heat engines coupled to noncanonical reservoirs. Phys. Rev. B 2017, 96, 104304. [Google Scholar] [CrossRef]
- Klaers, J.; Faelt, S.; Imamoglu, A.; Togan, E. Squeezed Thermal Reservoirs as a Resource for a Nanomechanical Engine beyond the Carnot Limit. Phys. Rev. X 2017, 7, 031044. [Google Scholar] [CrossRef]
- Roßnagel, J.; Abah, O.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Nanoscale heat engine beyond the Carnot limit. Phys. Rev. Lett. 2014, 112, 030602. [Google Scholar] [CrossRef] [PubMed]
- de Assis, R.J.; Sales, J.S.; da Cunha, J.A.R.; de Almeida, N.G. Universal two-level quantum Otto machine under a squeezed reservoir. Phys. Rev. E 2020, 102, 052131. [Google Scholar] [CrossRef]
- de Assis, R.J.; Sales, J.S.; Mendes, U.C.; de Almeida, N.G. Two-level quantum Otto heat engine operating with unit efficiency far from the quasi-static regime under a squeezed reservoir. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 095501. [Google Scholar] [CrossRef]
- Hernandez, M.; Orszag, M. Decoherence and disentanglement for two qubits in a common squeezed reservoir. Phys. Rev. A 2008, 78, 042114. [Google Scholar] [CrossRef]
- Naikoo, J.; Banerjee, S.; Jayannavar, A.M. Violation of Leggett-Garg-type inequalities in a driven two-level atom interacting with a squeezed thermal reservoir. Phys. Rev. A 2019, 100, 062132. [Google Scholar] [CrossRef]
- Teh, R.Y.; Drummond, P.D.; Reid, M.D. Overcoming decoherence of Schrödinger cat states formed in a cavity using squeezed-state inputs. Phys. Rev. Res. 2020, 2, 043387. [Google Scholar] [CrossRef]
- Banerjee, S.; Ghosh, R. Dynamics of decoherence without dissipation in a squeezed thermal bath. J. Phys. A Math. Theor. 2007, 40, 13735–13746. [Google Scholar] [CrossRef]
- Drummond, P.D.; Ficek, Z. Quantum Squeezing; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Wang, Y.; Li, C.; Sampuli, E.M.; Song, J.; Jiang, Y.; Xia, Y. Quantum state transfer in noisy environments. Phys. Rev. A 2019, 99, 023833. [Google Scholar] [CrossRef]
- Berrada, K.; Raffah, B.; Eleuch, H. Long-time protection of correlations and coherence in squeezed thermal bath. Chaos Solitons Fractals 2021, 143, 110501. [Google Scholar] [CrossRef]
- Basit, A.; Ali, H.; Li, P.-B.; Xianlong, G. Effects of reservoir squeezing on trace-distance correlations and emergence of the pointer basis. Phys. Rev. A 2023, 107, 042432. [Google Scholar] [CrossRef]
- Bellomo, B.; Franco, R.L.; Compagno, G. Non-Markovian effects on the dynamics of entanglement. Phys. Rev. Lett. 2007, 99, 160502. [Google Scholar] [CrossRef]
- Bellomo, B.; Franco, R.L.; Maniscalco, S.; Compagno, G. Two-qubit entanglement dynamics for two different non-Markovian environments. Phys. Scr. 2010, 2010, 014014. [Google Scholar] [CrossRef]
- Berrada, K.; Bougouffa, S. Controlling open quantum systems: Quantum correlations as resources during the transition from Markovian to non-Markovian dynamics. Phys. Lett. A 2025, 552, 130624. [Google Scholar] [CrossRef]
- Berrada, K.; Bougouffa, S. Quantum Steering and Fidelity in a Two-Photon System Subjected to Symmetric and Asymmetric Phasing Interactions. Symmetry 2025, 17, 647. [Google Scholar] [CrossRef]
- Palma, G.M.; Suominen, K.-A.; Ekert, A.K. Quantum computers and dissipation. Proc. R. Soc. A 1996, 452, 567–584. [Google Scholar]
- Shukla, R.K.; Chotorlishvili, L.; Mishra, S.K.; Iemini, F. Prethermal Floquet time crystals in chiral multiferroic chains and applications as quantum sensors of AC fields. Phys. Rev. B 2025, 111, 024315. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).