Convergence-Equivalent DF and AR Iterations with Refined Data Dependence: Non-Asymptotic Error Bounds and Robustness in Fixed-Point Computations

Abstract

Recent developments in fixed-point theory have focused on iterative techniques for approximating solutions, yet there remain important questions about whether different methods are equivalent and how well they resist perturbations. In this study, two recently proposed algorithms, referred to as the DF and AR iteration methods, are shown to be connected by proving that they converge similarly when applied to contraction mappings in Banach spaces, provided that their control sequences meet specific, explicit conditions. This work extends previous research on data dependence by removing restrictive assumptions related to both the perturbed operator and the algorithmic parameters, thereby increasing the range of situations where the results are applicable. Utilizing a non-asymptotic analysis, the authors derive improved error bounds for fixed-point deviations under operator perturbations, achieving a tightening of these estimates by a factor of 3–15 compared to earlier results. A key contribution of this study is the demonstration that small approximation errors lead only to proportionally small deviations from equilibrium, which is formalized in bounds of the form $\parallel s^{*}-{\tilde{s}}^{*}\parallel \le O(\epsilon /(1-\lambda ))$. These theoretical findings are validated through applications involving integral equations and examples from function spaces. Overall, this work unifies the convergence analysis of different iterative methods, enhances guarantees regarding stability, and provides practical tools for robust computational methods in areas such as optimization, differential equations, and machine learning. By relaxing structural constraints and offering a detailed sensitivity analysis, this study significantly advances the design and understanding of iterative algorithms in applied mathematics.

1. Introduction and Preliminaries

Throughout the course of this study, $\mathbb{N}$ will denote the set of natural numbers. Let $\mathcal{C}$ be a non-empty closed and convex subset of the Banach space $\mathcal{B}$ equipped with a norm $∥·∥$. We define $\mathbb{S}:\mathcal{C}\to \mathcal{C}$ as a mapping, and $\mathrm{Fix}\left(\mathbb{S}\right)=\left\{x\in \mathcal{C}:\mathbb{S}x=x\right\}$ as the set encompassing all fixed points of $\mathbb{S}$ within $\mathcal{C}$.

Since Banach’s pioneering contribution in 1922 [1], the Banach contraction principle, based on the class of contraction mappings, has attracted significant attention in mathematical research. A mapping $\mathbb{S}:\mathcal{C}\to \mathcal{C}$ on a normed space $(\mathcal{C},\parallel ·\parallel )$ is called a contraction if there exists a constant $\lambda \in [0,1)$ such that

$$(\forall x,y\in \mathcal{C})\parallel \mathbb{S}x-\mathbb{S}y\parallel \le \lambda \parallel x-y\parallel .$$

(1)

Owing to its fundamental properties and strong potential for addressing complex problems across various disciplines, this class of mappings has been extensively studied under different structural frameworks. Consequently, it has emerged as a powerful tool in fixed-point theory. However, recognizing both the strengths and inherent limitations of contraction mappings, researchers have introduced more generalized classes that relax certain constraints while extending their applicability under broader conditions (see [2,3,4,5,6,7,8]). These generalized mappings have been investigated in terms of stability, existence, and uniqueness of fixed points, data dependence, and other qualitative aspects within diverse mathematical settings, including metric, topological, and normed spaces (see [9,10,11,12,13,14,15,16]). Moreover, numerous iterative algorithms have been developed to approximate the fixed points of such mappings, specifically addressing the challenges posed by modern computational problems (see [17,18,19,20,21,22,23,24,25]). While classical fixed-point iterations, such as those of Picard and Krasnoselskij, continue to serve as fundamental methods for solving nonlinear equations, emerging applications in high-dimensional optimization, machine learning, and perturbed dynamical systems expose the limitations of these traditional approaches. These domains require algorithms that offer enhanced stability, accelerated convergence, and robustness to approximation errors. To meet these demands, recent contributions by Filali et al. [26] and Alam and Rohen [27] have introduced two distinct approaches, hereinafter referred to as the “DF iteration algorithm” (Algorithm 1) and “AR iteration algorithm” (Algorithm 2), respectively, which will be examined in detail in the subsequent sections.

Algorithm 1: DF iteration algorithm

Input: A mapping $\mathbb{S}$,

initial point $x_0\in \mathcal{C}$,

$\left\{{\rho }_n\right\}$, $\left\{{\sigma }_n\right\}$, $\left\{{\tau }_n\right\}\subset [0,1]$,

and budget N.

1: for $n=0,1,2,\dots ,N$ do

2: $w_n=\mathbb{S}\left(\left(1-{\tau }_n\right)x_n+{\tau }_n\mathbb{S}{x}_n\right)$

$y_n={\mathbb{S}}^2{w}_n$

$z_n=\mathbb{S}\left(\left(1-{\sigma }_n\right)\mathbb{S}{y}_n+{\sigma }_n\mathbb{S}{w}_n\right)$

$x_{n+1}=\mathbb{S}\left(\left(1-{\rho }_n\right)\mathbb{S}{y}_n+{\rho }_n\mathbb{S}{z}_n\right)$

3: end for

Output: Approximate solution $x_N$

Algorithm 2: AR iteration algorithm

Input: A mapping $\mathbb{S}$,

initial point $x_0\in \mathcal{C}$,

$\left\{{\rho }_n^{*}\right\}$, $\left\{{\sigma }_n^{*}\right\}$ , $\left\{{\tau }_n^{*}\right\}\subset [0,1],$,

and budget N.

1: for $n=0,1,2,\dots ,N$ do

2: $w_n^{*}=\mathbb{S}\left(\left(1-{\tau }_n^{*}\right)x_n^{*}+{\tau }_n^{*}\mathbb{S}{x}_n^{*}\right)$

$y_n^{*}=\mathbb{S}\left(\left(1-{\sigma }_n^{*}\right)w_n^{*}+{\sigma }_n^{*}\mathbb{S}{w}_n^{*}\right)$

$z_n^{*}=\mathbb{S}\left(\left(1-{\rho }_n^{*"}\right)y_n^{*}+{\rho }_n^{*}\mathbb{S}{y}_n^{*}\right)$

$x_{n+1}^{*}={\mathbb{S}}^2{z}_n^{*}$

3: end for

Output: Approximate solution $x_N^{*}$

Both studies presented a range of theoretical results, including convergence and stability analyses, as well as insights into the sensitivity of fixed points with respect to perturbations in contraction mappings. More specifically, the authors derived the following results concerning the data dependence of fixed points:

Theorem 1.

Let $\mathbb{S}$, $\tilde{\mathbb{S}}:\mathcal{C}\to \mathcal{C}$ be two contractions with contractivity constant $\lambda \in [0,1)$ and fixed points $s_{*}$ and ${\tilde{s}}_{*}$, respectively. Suppose that there exists a maximum admissible error $\epsilon >0$ such that $∥\mathbb{S}x-\tilde{\mathbb{S}}x∥\le \epsilon$ for all $x\in \mathcal{C}$ (in this case, $\mathbb{S}$ and $\tilde{\mathbb{S}}$ are called approximate operators of each other).

(i) ([26], Theorem 5) Let $\left\{x_n\right\}$ and $\left\{{\tilde{x}}_n\right\}$ be the iterative sequences generated by the DF iteration algorithm associated with $\mathbb{S}$ and $\tilde{\mathbb{S}}$, respectively. If the sequences $\left\{{\rho }_n\right\}$, $\left\{{\sigma }_n\right\}$, $\left\{{\tau }_n\right\}$ in the DF iteration algorithm satisfy the conditions $1/2\le {\rho }_n\le {\tau }_n$ for all $n\in \mathbb{N}$ and ${\displaystyle \sum _{n=1}^{\infty }}{\rho }_n(1-\lambda )=\infty$, then it holds that

$$∥s_{*}-{\tilde{s}}_{*}∥\le {\displaystyle \frac{15\epsilon }{1-\lambda }}.$$

(2)

(ii) ([27], Theorem 8) Let $\left\{x_n^{*}\right\}$ and $\left\{{\tilde{x}}_n^{*}\right\}$ be the iterative sequences generated by the AR iteration algorithm associated with $\mathbb{S}$ and $\tilde{\mathbb{S}}$, respectively. If the sequences $\left\{{\rho }_n^{*}\right\}$, $\left\{{\sigma }_n^{*}\right\}$, $\left\{{\tau }_n^{*}\right\}$ in the DF iteration algorithm satisfy either of

$$\sum _{n=1}^{\infty }{\rho }_n^{*}(1-\lambda )=\infty ,\sum _{n=1}^{\infty }{\sigma }_n^{*}(1-\lambda )=\infty ,and\sum _{n=1}^{\infty }{\tau }_n^{*}\left(1-\lambda \right)=\infty ,$$

then it holds that

$$∥s_{*}-{\tilde{s}}_{*}∥\le {\displaystyle \frac{15\epsilon }{1-\lambda }}.$$

(3)

We should immediately point out that, in both results, the restrictions imposed on the control sequences $\left\{{\rho }_n\right\}$, $\left\{{\sigma }_n\right\}$, $\left\{{\tau }_n\right\}$, $\left\{{\rho }_n^{*}\right\}$, $\left\{{\sigma }_n^{*}\right\}$, $\left\{{\tau }_n^{*}\right\}\subset [0,1]$ and the imposed contraction condition on the mapping $\tilde{\mathbb{S}}$, significantly restrict the applicability of these theories. Indeed, when $\mathbb{S}$ and $\tilde{\mathbb{S}}$ are approximate operators of each other and $\mathbb{S}$ is a $\lambda -$contraction, the mapping $\tilde{\mathbb{S}}$ satisfies the following condition for all x, $y\in \mathcal{C}$:

$$\begin{array}{cc}\hfill ∥\tilde{\mathbb{S}}x-\tilde{\mathbb{S}}y∥& \le ∥\tilde{\mathbb{S}}x-\mathbb{S}x∥+∥\mathbb{S}x-\mathbb{S}y∥+∥\mathbb{S}y-\tilde{\mathbb{S}}y∥\hfill \\ \hfill & \le \lambda ∥x-y∥+\mu ,\hfill \end{array}$$

(4)

where $\mu =2\epsilon$. This demonstrates that $\tilde{\mathbb{S}}$ inherits a weakened contraction-like property, deviating from strict contractivity by an additive constant $\mu$ dependent on the approximation error $\epsilon$. As is evident, any contraction mapping satisfies condition (4). However, as the following example illustrates, a mapping $\tilde{\mathbb{S}}$ that satisfies (4) does not necessarily satisfy the contraction condition given in (1).

Example 1.

Consider the space $\mathcal{C}=[0,1]\subset \mathbb{R}$ equipped with the usual absolute value norm. Define the mappings $\mathbb{S},\tilde{\mathbb{S}}:\mathcal{C}\to \mathcal{C}$ as follows:

$$\mathbb{S}x={\displaystyle \frac{x}{4}}\mathit{and}\tilde{\mathbb{S}}x=\left\{\begin{array}{cc}{\displaystyle \frac{1-x}{4}},\hfill & 0\le x\le {\displaystyle \frac{1}{2}},\hfill \\ {\displaystyle \frac{2-x}{4}},\hfill & {\displaystyle \frac{1}{2}}<x\le 1.\hfill \end{array}\right.$$

Then, we have

$$\left|\tilde{\mathbb{S}}x-\mathbb{S}x\right|\le {\displaystyle \frac{1}{4}}\mathit{for}\mathit{all}x\in \mathcal{C}.$$

So, we can choose $\epsilon =1/4$. Since $\tilde{\mathbb{S}}$ is discontinuous, it does not qualify as a contraction. However, it possesses a unique fixed point at $1/5$. On the other hand, the mapping $\tilde{\mathbb{S}}$ satisfies condition (4) with $\lambda =1/4$ and $\mu =1/2$. To verify this, we examine the following cases:

Cases 1 and 2: If $x,y\in [0,1/2]$ or $x,y\in (1/2,1]$, then for any $\mu >0$, we have

$$\left|\tilde{\mathbb{S}}x-\tilde{\mathbb{S}}y\right|\le {\displaystyle \frac{1}{4}}\left|x-y\right|\le {\displaystyle \frac{1}{4}}\left|x-y\right|+\mu .$$

Cases 3 and 4: If $x\in [0,1/2]$ and $y\in (1/2,1]$(or vice versa), then

$$\left|\tilde{\mathbb{S}}x-\tilde{\mathbb{S}}y\right|=\left|-{\displaystyle \frac{1}{4}}-\left({\displaystyle \frac{x}{4}}-{\displaystyle \frac{y}{4}}\right)\right|\le {\displaystyle \frac{1}{4}}\left|x-y\right|+{\displaystyle \frac{1}{4}}.$$

Thus, considering all cases together, we conclude that the mapping $\tilde{\mathbb{S}}$ satisfies condition (4) with $\lambda =1/4$ and $\mu =1/2$. (Note that while the theory requires $\mu =2\epsilon =1/2$, this example shows that $\mu =1/4$ is sufficient for the inequality to hold, indicating a tighter bound for this specific mapping.)

The example provided below illustrates that the condition delineated in (4) lacks sufficiency in ensuring the existence of fixed points for a mapping $\tilde{\mathbb{S}}$.

Example 2.

Let us consider the set $\mathcal{C}=[0,1]\subset \mathbb{R}$, equipped with the norm induced by the usual absolute value metric. Define the mappings $\mathbb{S},\tilde{\mathbb{S}}:\mathcal{C}\to \mathcal{C}$, as follows:

$$\mathbb{S}={\displaystyle \frac{8}{49}}x\mathit{and}\tilde{\mathbb{S}}x=\left\{\begin{array}{cc}{\displaystyle \frac{x+2}{x+3}},\hfill & 0\le x<{\displaystyle \frac{1}{2}},\hfill \\ {\displaystyle \frac{x+1}{x+3}},\hfill & {\displaystyle \frac{1}{2}}\le x\le 1.\hfill \end{array}\right.$$

Then, we have

$$\left|\tilde{\mathbb{S}}x-\mathbb{S}x\right|\le {\displaystyle \frac{2}{3}}\mathit{for}\mathit{all}x\in \mathcal{C}.$$

So, we can choose $\epsilon =2/3$. We now demonstrate that the mapping $\tilde{\mathbb{S}}$ satisfies the inequality in (4) under four cases.

Cases 1 and 2: If $x,y\in \left[0,1/2\right)$ or $x,y\in \left[1/2,1\right]$, then for any $\mu >0$, we obtain

$$\left|\tilde{\mathbb{S}}x-\tilde{\mathbb{S}}y\right|=\left|{\displaystyle \frac{x-y}{\left(x+3\right)\left(y+3\right)}}\right|\le {\displaystyle \frac{1}{9}}\left|x-y\right|\le {\displaystyle \frac{1}{9}}\left|x-y\right|+\mu ,$$

and

$$\left|\tilde{\mathbb{S}}x-\tilde{\mathbb{S}}y\right|=\left|{\displaystyle \frac{2x-2y}{\left(x+3\right)\left(y+3\right)}}\right|\le {\displaystyle \frac{8}{49}}\left|x-y\right|\le {\displaystyle \frac{8}{49}}\left|x-y\right|+\mu ,$$

respectively. Hence, in both cases, the mapping $\tilde{\mathbb{S}}$ satisfies the inequality in (4) for any $\lambda \in \left[8/49,1\right)$ and any $\mu >0$.

Cases 3 and 4: If $x\in \left[0,1/2\right)$ and $y\in \left[1/2,1\right]$ (or vice versa), then $\tilde{\mathbb{S}}x=(x+2)/(x+3)$ and $\tilde{\mathbb{S}}y=(y+1)/(y+3)$. It is important to note that for every $x\in \left[0,1/2\right)$

$${\displaystyle \frac{\mathrm{d}\tilde{\mathbb{S}}}{\mathrm{d}x}}={\displaystyle \frac{1}{{\left(x+3\right)}^2}}>0,$$

and for every $y\in \left[1/2,1\right]$

$${\displaystyle \frac{\mathrm{d}\tilde{\mathbb{S}}}{\mathrm{d}y}}={\displaystyle \frac{2}{{\left(y+3\right)}^2}}>0,$$

indicating that $\tilde{\mathbb{S}}x$ and $\tilde{\mathbb{S}}y$ are increasing functions. Consequently,

$$\left|\tilde{\mathbb{S}}x-\tilde{\mathbb{S}}y\right|=\left|{\displaystyle \frac{x+2}{x+3}}-{\displaystyle \frac{y+1}{y+3}}\right|$$

reaches its maximum value when $y=1/2$ and $x=1/2$. This implies that

$$\underset{x\in [0,1/2),y\in [1/2,1]}{sup}\left|\tilde{\mathbb{S}}x-\tilde{\mathbb{S}}y\right|={\displaystyle \frac{2}{7}},$$

meaning that for every $x\in \left[0,1/2\right)$ and $y\in \left[1/2,1\right]$, $\left|\tilde{\mathbb{S}}x-\tilde{\mathbb{S}}y\right|\le 2/7$. On the other hand, employing similar arguments, we obtain

$$\underset{x\in \left[0,1/2\right),y\in \left[1/2,1\right]}{inf}\left|x-y\right|=0,$$

indicating that for every $x\in \left[0,1/2\right)$ and $y\in \left[1/2,1\right]$, $0\le \left|x-y\right|$. Thus, if $x\in \left[0,1/2\right)$ and $y\in \left[1/2,1\right]$, then for any $\lambda \in \left[0,1\right)$ and any $\mu \ge 2/7$, the following inequality holds:

$$\left|\tilde{\mathbb{S}}x-\tilde{\mathbb{S}}y\right|\le \lambda \left|x-y\right|+\mu .$$

As a result, for every $x,y\in [0,1]$, the mapping $\tilde{\mathbb{S}}$ satisfies the inequality in (4) for any $\lambda \in \left[8/49,1\right)$ and for any $\mu \ge 2/7$. (Note that while the theory guarantees the inequality for $\mu =2\epsilon =4/3$, this example demonstrates that a smaller $\mu =2/7$ is sufficient, indicating a tighter bound for this specific mapping). However, upon solving the equation $\tilde{\mathbb{S}}x=x$, we find that for $x\in \left[0,1/2\right)$, $x=-1\pm \sqrt{3}\notin \left[0,1/2\right)$, and for $x\in \left[1/2,1\right]$, $x=-1\pm \sqrt{2}\notin \left[1/2,1\right]$. Consequently, the mapping $\tilde{\mathbb{S}}$ does not possess any fixed points for $x\in [0,1]$.

By Banach’s fixed-point theorem, the contraction mapping $\mathbb{S}:\mathcal{C}\to \mathcal{C}$ guarantees the existence of a unique fixed point $s_{*}\in \mathcal{C}$. However, the approximate operator $\tilde{\mathbb{S}}:\mathcal{C}\to \mathcal{C}$, while satisfying inequality (4) deviates from strict contractivity because of the additive perturbation term $\mu =2\epsilon >0$. Although $\tilde{\mathbb{S}}$, lacks the classical contraction property, its structural proximity to $\mathbb{S}$ permits an analysis of fixed-point stability. Specifically, if $\mu$ is sufficiently small—as a consequence of the bounded approximation error $\epsilon$—the fixed points of $\tilde{\mathbb{S}}$, should they exist (say ${\tilde{s}}_{*}$), lie within a neighborhood of $s_{*}$. By utilizing inequality (4) and employing a non-asymptotic approach, we derive a concrete upper bound for $∥s_{*}-{\tilde{s}}_{*}∥$ without relying on asymptotic assumptions, as required in Theorem 1. Specifically, we establish the following bound:

$$\begin{array}{cc}\hfill ∥s_{*}-{\tilde{s}}_{*}∥& \le ∥\mathbb{S}{s}_{*}-\tilde{\mathbb{S}}{s}_{*}∥+∥\tilde{\mathbb{S}}{s}_{*}-\tilde{\mathbb{S}}{\tilde{s}}_{*}∥\hfill \\ \hfill & \le \epsilon +\lambda ∥s_{*}-{\tilde{s}}_{*}∥+2\epsilon ,\hfill \end{array}$$

which leads to

$$∥s_{*}-{\tilde{s}}_{*}∥\le {\displaystyle \frac{3\epsilon }{1-\lambda }}.$$

(5)

This result formalizes the intuition that small perturbations in the operator propagate controllably to its equilibria. While $\tilde{\mathbb{S}}$ does not inherently inherit the contraction property, the weakened inequality still enables meaningful conclusions about fixed-point proximity, illustrating the robustness of contraction-based frameworks under bounded approximations. Such insights are pivotal in applied settings, where numerical or modeling errors require tolerance analyses in dynamical systems and iterative algorithms.

The preceding discussions indicate that the applicability of the data-dependence results in parts (i) and (ii) of Theorem 1 can be further extended by relaxing the contraction assumption imposed on the mapping $\tilde{\mathbb{S}}$ and instead treating $\tilde{\mathbb{S}}$ merely as an approximate operator of the mapping $\mathbb{S}$.

In this study, we establish a convergence-equivalence result between the DF and AR iteration algorithms in approximating the fixed point of a contraction mapping. Moreover, we derive enhanced versions of the data-dependence results in parts (i) and (ii) of Theorem 1 by not only removing the contraction condition imposed on the mapping $\tilde{\mathbb{S}}$ but also eliminating the constraints on the control sequences $\left\{{\rho }_n\right\}$, $\left\{{\sigma }_n\right\}$, $\left\{{\tau }_n\right\}$, $\left\{{\rho }_n^{*}\right\}$, $\left\{{\sigma }_n^{*}\right\}$, $\left\{{\tau }_n^{*}\right\}\subset \left[0,1\right]$.

The following lemma plays a key role in establishing our results:

Lemma 1

([28]). Let ${\left\{{\Phi }_n^i\right\}}_{n=0}^{\infty }$, $i=1,2,3,$ be three sequences such that ${\Phi }_n^i\ge 0$ for each $n\in \mathbb{N}$, $i=1,2,3,$ ${\Phi }_n^3\in (0,1)$ for all $n\ge n_0$, ${\displaystyle \sum _{n=1}^{\infty }}{\Phi }_n^3=\infty$, ${\Phi }_n^2=o\left({\Phi }_n^3\right)$, and

$$(\forall n\in \mathbb{N}){\Phi }_{n+1}^1\le \left(1-{\Phi }_n^3\right){\Phi }_n^1+{\Phi }_n^2.$$

It then holds that $\underset{n\to \infty }{lim}{\Phi }_n^1=0$.

2. Main Results

In this section, we establish our main theoretical findings concerning the convergence behavior of the iterative processes under consideration. In particular, we compare the trajectories generated by the DF iteration and the AR iteration when applied to a contraction mapping. The significance of the following theorem lies in the fact that it provides conditions under which both iterative schemes not only converge to the unique fixed point $s_{*}$ of $\mathbb{S}$, but also approach each other asymptotically. This comparison allows us to assess the relative stability and efficiency of the algorithms, and highlights the robustness of their convergence under mild assumptions on the control sequences. We will now state the results precisely:

Theorem 2.

Let $\mathbb{S}:\mathcal{C}\to \mathcal{C}$ be a λ-contraction mapping with a fixed point $s_{*}$. Consider the sequences $\left\{x_n\right\}$ and $\left\{x_n^{*}\right\}$, which are generated by the DF and AR iteration algorithms, respectively. The following statements are equivalent:

(i) Define the sequence $\left\{M_n\right\}$ for all $n\in \mathbb{N}$ as

$$M_n=max\left\{1-{\tau }_n(1-\lambda ),\left[1-{\rho }_n^{*}(1-\lambda )\right]\left[1-{\sigma }_n^{*}(1-\lambda )\right]\left[1-{\tau }_n^{*}\left(1-\lambda \right)\right]\right\}.$$

If the sequence ${\left\{{\displaystyle \frac{2{\lambda }^5{M}_n}{{\tau }_n(1-\lambda )}}\right\}}_{n=0}^{\infty }$ is bounded and ${\displaystyle \sum _{n=0}^{\infty }}{\tau }_n=\infty$, then the sequence ${\left\{x_n-x_n^{*}\right\}}_{n=0}^{\infty }$ converges strongly to 0, and ${\left\{x_n\right\}}_{n=0}^{\infty }$ converges strongly to $s_{*}$.  

(ii) Define the sequence $\left\{M_n^{\prime }\right\}$ for all $n\in \mathbb{N}$ as

$$\begin{array}{cc}\hfill M_n^{\prime }=max\left\{\right[1-& min\left\{{\rho }_n^{*},{\sigma }_n^{*},{\tau }_n^{*}\right\}(1-\lambda )],\hfill \\ \hfill & \left[1-{\rho }_n\left(1-\left((1-{\sigma }_n){\lambda }^2+{\sigma }_n\right)\right)\right]\left[1-{\tau }_n(1-\lambda )\right]\}.\hfill \end{array}$$

If the sequence ${\left\{{\displaystyle \frac{2{\lambda }^5{M}_n^{\prime }}{min\left\{{\rho }_n^{*},{\sigma }_n^{*},{\tau }_n^{*}\right\}(1-\lambda )}}\right\}}_{n=0}^{\infty }$ is bounded and ${\displaystyle \sum _{n=0}^{\infty }}min\left\{{\rho }_n^{*},{\sigma }_n^{*},{\tau }_n^{*}\right\}=\infty$, then the sequence ${\left\{x_n^{*}-x_n\right\}}_{n=0}^{\infty }$ converges strongly to zero and ${\left\{x_n^{*}\right\}}_{n=0}^{\infty }$ converges strongly to $s_{*}$.

Proof. 

(i) Using the inequality in (1) and employing the DF and AR iteration algorithms, we achieve the following for every $n\in \mathbb{N}$:

$$\begin{array}{cc}\hfill ∥x_{n+1}-x_{n+1}^{*}∥& =∥\mathbb{S}\left(\left(1-{\rho }_n\right)\mathbb{S}{y}_n+{\rho }_n\mathbb{S}{z}_n\right)-{\mathbb{S}}^2{z}_n^{*}∥\hfill \\ \hfill & \le \lambda ∥\left(1-{\rho }_n\right)\mathbb{S}{y}_n+{\rho }_n\mathbb{S}{z}_n-\mathbb{S}{z}_n^{*}∥\hfill \\ \hfill & \le \lambda ∥\left(1-{\rho }_n\right)\mathbb{S}{y}_n+{\rho }_n\mathbb{S}{z}_n-s_{*}∥+\lambda ∥s_{*}-\mathbb{S}{z}_n^{*}∥\hfill \\ \hfill & \le \lambda \left(1-{\rho }_n\right)∥\mathbb{S}{y}_n-\mathbb{S}{s}_{*}∥+\lambda {\rho }_n∥\mathbb{S}{z}_n-\mathbb{S}{s}_{*}∥+\lambda ∥\mathbb{S}{s}_{*}-\mathbb{S}{z}_n^{*}∥\hfill \\ \hfill & \le {\lambda }^2\left(1-{\rho }_n\right)∥y_n-s_{*}∥+{\lambda }^2{\rho }_n∥z_n-s_{*}∥+{\lambda }^2∥s_{*}-z_n^{*}∥\hfill \\ \hfill & \le {\lambda }^2\left(1-{\rho }_n\right)∥{\mathbb{S}}^2{w}_n-s_{*}∥+{\lambda }^2{\rho }_n∥\mathbb{S}\left(\left(1-{\sigma }_n\right)\mathbb{S}{y}_n+{\sigma }_n\mathbb{S}{w}_n\right)-s_{*}∥\hfill \\ \hfill & +{\lambda }^2∥\mathbb{S}\left(\left(1-{\rho }_n^{*}\right)y_n^{*}+{\rho }_n^{*}\mathbb{S}{y}_n^{*}\right)-s_{*}∥\hfill \\ \hfill & \le {\lambda }^4\left[1-{\rho }_n+{\rho }_n\left\{\left(1-{\sigma }_n\right){\lambda }^2+{\sigma }_n\right\}\right]∥w_n-s_{*}∥\hfill \\ \hfill & +{\lambda }^3\left[1-{\rho }_n^{*}(1-\lambda )\right]∥y_n^{*}-s_{*}∥\hfill \\ \hfill & \le {\lambda }^5\left[1-{\rho }_n+{\rho }_n\left\{\left(1-{\sigma }_n\right){\lambda }^2+{\sigma }_n\right\}\right]\left[1-{\tau }_n(1-\lambda )\right]∥x_n-s_{*}∥\hfill \\ \hfill & +{\lambda }^5\left[1-{\rho }_n^{*}(1-\lambda )\right]\left[1-{\sigma }_n^{*}(1-\lambda )\right]\left[1-{\tau }_n^{*}(1-\lambda )\right]∥x_n^{*}-s_{*}∥\hfill \\ \hfill & \le \left[1-{\tau }_n(1-\lambda )\right]∥x_n-x_n^{*}∥+2{\lambda }^5{M}_n∥x_n^{*}-s_{*}∥.\hfill \end{array}$$

(6)

where

$$M_n=max\left\{1-{\tau }_n(1-\lambda ),\left[1-{\rho }_n^{*}(1-\lambda )\right]\left[1-{\sigma }_n^{*}(1-\lambda )\right]\left[1-{\tau }_n^{*}\left(1-\lambda \right)\right]\right\}.$$

Now, we set the following for every $n\in \mathbb{N}$:

$$\begin{array}{cc}\hfill {\Phi }_n^1& :=∥x_n-x_n^{*}∥\ge 0,\hfill \\ \hfill {\Phi }_n^3& :={\tau }_n(1-\lambda )\in (0,1),\hfill \\ \hfill {\Phi }_n^2& :=2{\lambda }^5{M}_n∥x_n^{*}-s_{*}∥.\hfill \end{array}$$

Since ${\left\{{\displaystyle \frac{2{\lambda }^5{M}_n}{{\tau }_n(1-\lambda )}}\right\}}_{n=0}^{\infty }$ is bounded, there exists a number $\mu >0$ such that for every $n\in \mathbb{N}$, the following holds:

$$\left|{\displaystyle \frac{2{\lambda }^5{M}_n}{{\tau }_n(1-\lambda )}}\right|<\mu .$$

Moreover, since ${lim}_{n\to \infty }∥x_n^{*}-s_{*}∥=0$ according to ([27], Theorem 3), for any given $\epsilon >0$, there exists an $n_0\in \mathbb{N}$ such that for all $n\ge n_0$, $∥x_n^{*}-s_{*}∥<\epsilon /\mu$. Thus, for every $n\ge n_0$, we have

$$\left|{\displaystyle \frac{2{\lambda }^5{M}_n}{{\tau }_n(1-\lambda )}}\right|∥x_n^{*}-s_{*}∥<\epsilon$$

which implies $\underset{n\to \infty }{lim}{\Phi }_n^2/{\Phi }_n^3=0$, i.e., ${\Phi }_n^2=o\left({\Phi }_n^3\right)$. Consequently, the inequality in (6) satisfies all the requirements of Lemma 1 and, therefore, we obtain $\underset{n\to \infty }{lim}∥x_n-x_n^{*}∥=0$. On the other hand, since $∥x_n-s_{*}∥\le ∥x_n-x_n^{*}∥+∥x_n^{*}-s_{*}∥$, we can conclude that $\underset{n\to \infty }{lim}∥x_n-s_{*}∥=0$.

(ii) Utilizing the inequality in (1) with AR and DF iteration algorithms, we obtain the following for all $n\in \mathbb{N}$:

$$\begin{array}{cc}\hfill ∥x_{n+1}^{*}-x_{n+1}∥\le & ∥{\mathbb{S}}^2{z}_n^{*}-s_{*}∥+∥s_{*}-\mathbb{S}\left(\left(1-{\rho }_n\right)\mathbb{S}{y}_n+{\rho }_n\mathbb{S}{z}_n\right)∥\hfill \\ \hfill \le & {\lambda }^2∥z_n^{*}-s_{*}∥+{\lambda }^2\left\{\left(1-{\rho }_n\right)∥s_{*}-y_n∥+{\rho }_n∥s_{*}-z_n∥\right\}\hfill \\ \hfill \le & {\lambda }^3\left[1-{\rho }_n^{*}\left(1-\lambda \right)\right]∥y_n^{*}-s_{*}∥\hfill \\ \hfill & +{\lambda }^4\left\{\left(1-{\rho }_n\right)∥s_{*}-w_n∥+{\rho }_n\left[\left(1-{\sigma }_n\right)∥s_{*}-y_n∥+{\sigma }_n∥s_{*}-w_n∥\right]\right\}\hfill \\ \hfill \le & {\lambda }^5\left[1-{\rho }_n^{*}(1-\lambda )\right]\left[1-{\sigma }_n^{*}(1-\lambda )\right]\left[1-{\tau }_n^{*}(1-\lambda )\right]∥x_n^{*}-s_{*}∥\hfill \\ \hfill & +{\lambda }^5\left[1-{\rho }_n\left(1-\left(\left(1-{\sigma }_n\right){\lambda }^2+{\sigma }_n\right)\right)\right]\left[1-{\tau }_n(1-\lambda )\right]∥s_{*}-x_n∥\hfill \\ \hfill \le & {\lambda }^5\left[1-{\rho }_n^{*}(1-\lambda )\right]\left[1-{\sigma }_n^{*}(1-\lambda )\right]\left[1-{\tau }_n^{*}(1-\lambda )\right]∥x_n^{*}-x_n∥\hfill \\ \hfill & +{\lambda }^5\left[1-{\rho }_n^{*}(1-\lambda )\right]\left[1-{\sigma }_n^{*}(1-\lambda )\right]\left[1-{\tau }_n^{*}(1-\lambda )\right]∥x_n-s_{*}∥\hfill \\ \hfill & +{\lambda }^5\left[1-{\rho }_n\left(1-\left(\left(1-{\sigma }_n\right){\lambda }^2+{\sigma }_n\right)\right)\right]\left[1-{\tau }_n\left(1-\lambda \right)\right]∥s_{*}-x_n∥\hfill \\ \hfill \le & \left[1-min\left\{{\rho }_n^{*},{\sigma }_n^{*},{\tau }_n^{*}\right\}(1-\lambda )\right]∥x_n^{*}-x_n∥\hfill \\ \hfill & +{\lambda }^5\left[1-min\left\{{\rho }_n^{*},{\sigma }_n^{*},{\tau }_n^{*}\right\}(1-\lambda )\right]∥x_n-s_{*}∥\hfill \\ \hfill & +{\lambda }^5\left[1-{\rho }_n\left(1-\left(\left(1-{\sigma }_n\right){\lambda }^2+{\sigma }_n\right)\right)\right]\left[1-{\tau }_n(1-\lambda )\right]∥x_n-s_{*}∥\hfill \\ \hfill \le & \left[1-min\left\{{\rho }_n^{*},{\sigma }_n^{*},{\tau }_n^{*}\right\}(1-\lambda )\right]∥x_n^{*}-x_n∥+2{\lambda }^5{M}_n^{\prime }∥x_n-s_{*}∥,\hfill \end{array}$$

(7)

where

$$M_n^{\prime }=\left\{\left[1-min\left\{{\rho }_n^{*},{\sigma }_n^{*},{\tau }_n^{*}\right\}(1-\lambda )\right],\left[1-{\rho }_n\left(1-\left(\left(1-{\sigma }_n\right){\lambda }^2+{\sigma }_n\right)\right)\right]\left[1-{\tau }_n(1-\lambda )\right]\right\}.$$

Define the following for all $n\in \mathbb{N}$:

$$\begin{array}{cc}\hfill {\Phi }_n^1& :=∥x_n^{*}-x_n∥\ge 0,\hfill \\ \hfill {\Phi }_n^3& :=min\left\{{\rho }_n^{*},{\sigma }_n^{*},{\tau }_n^{*}\right\}(1-\lambda )\in (0,1),\hfill \\ \hfill {\Phi }_n^2& :=2{\lambda }^5{M}_n^{\prime }∥x_n-s_{*}∥.\hfill \end{array}$$

Given that ${\left\{{\displaystyle \frac{2{\lambda }^5{M}_n^{\prime }}{min\left\{{\rho }_n^{*},{\sigma }_n^{*},{\tau }_n^{*}\right\}\left(1-\lambda \right)}}\right\}}_{n=0}^{\infty }$ is bounded, there exists $\mu >0$ such that for all $n\in \mathbb{N}$:

$$\left|{\displaystyle \frac{2{\lambda }^5{M}_n^{\prime }}{min\left\{{\rho }_n^{*},{\sigma }_n^{*},{\tau }_n^{*}\right\}(1-\lambda )}}\right|<\mu .$$

Furthermore, as $\underset{n\to \infty }{lim}∥x_n-s_{*}∥=0$ according to ([26], Theorem 2), for any $\epsilon >0$, there exists an $n_0\in \mathbb{N}$ such that for all $n\ge n_0$, $∥x_n-s_{*}∥<\epsilon /\mu$. Hence, for each $n\ge n_0$

$$\left|{\displaystyle \frac{2{\lambda }^5{M}_n^{\prime }}{min\left\{{\rho }_n^{*},{\sigma }_n^{*},{\tau }_n^{*}\right\}(1-\lambda )}}\right|∥x_n-s_{*}∥<\epsilon .$$

This implies $\underset{n\to \infty }{lim}{\Phi }_n^2/{\Phi }_n^3=0$ or ${\Phi }_n^2=o\left({\Phi }_n^3\right)$. Thus, the inequality in (7) satisfies the conditions of Lemma 1, leading to $\underset{n\to \infty }{lim}∥x_n^{*}-x_n∥=0$. Moreover, since

$$∥x_n^{*}-s_{*}∥\le ∥x_n^{*}-x_n∥+∥x_n-s_{*}∥,$$

we conclude that $\underset{n\to \infty }{lim}∥x_n^{*}-s_{*}∥=0$.    □

To demonstrate the applicability of Theorem 2, we will now provide an example based on a nonlinear differential equation. This example serves two purposes. First, it shows how an abstract contraction mapping arising from an integral operator can be constructed in a concrete functional setting. Second, it illustrates that the theoretical convergence results established in Theorem 2 can be verified numerically by examining the behavior of the DF and AR iteration schemes. In particular, we consider an initial value problem whose solution can be reformulated as a fixed-point problem, and then show that the corresponding operator is indeed a contraction mapping. This allows us to apply Theorem 2 directly and validate the convergence through numerical simulations.

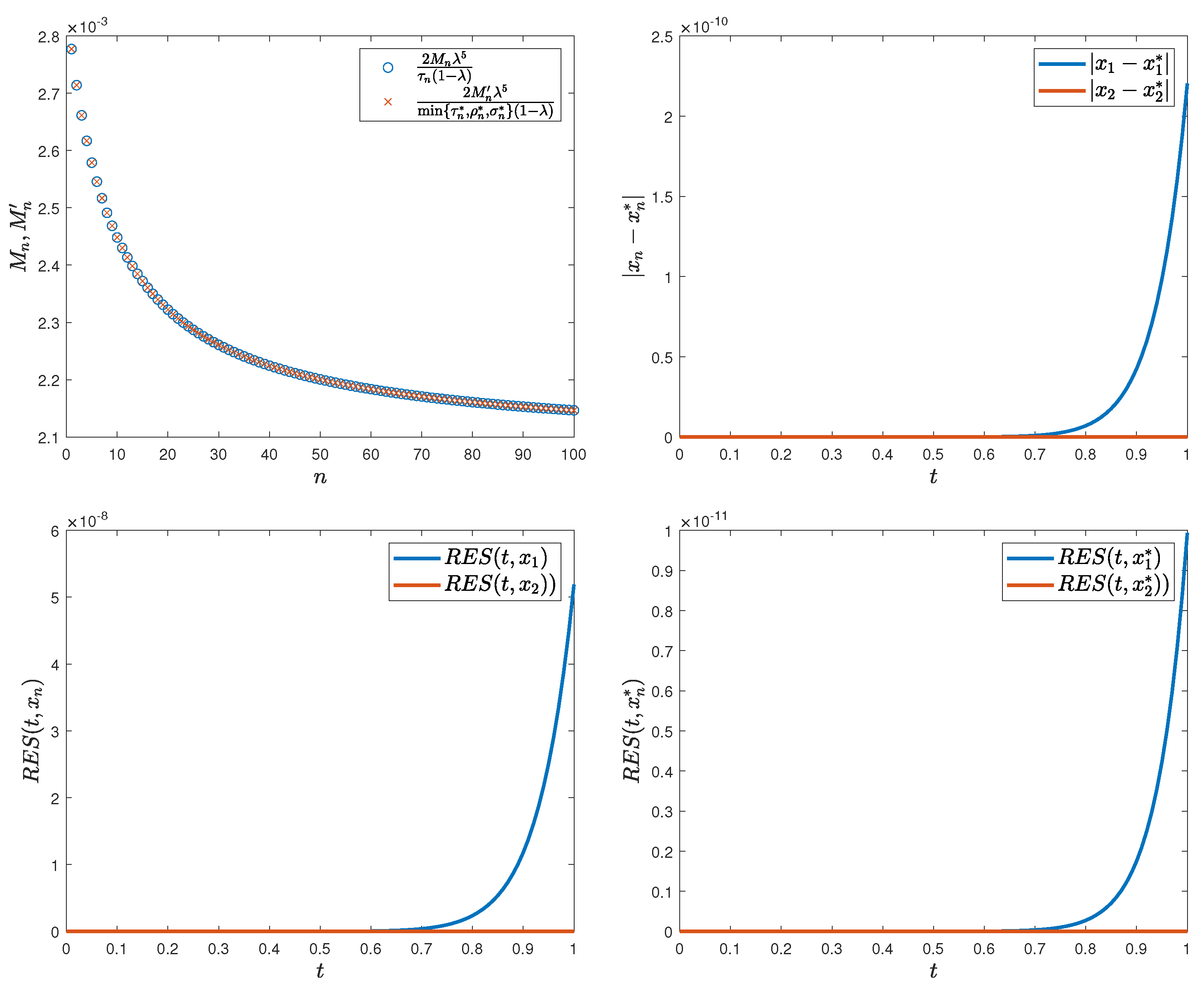
Example 3.

Let $C^2[0,1]$ denote the set of functions defined on $[0,1]$ that possess continuous second-order derivatives, equipped with the supremum norm ${∥·∥}_{\infty }$. It is well known that $\mathcal{B}=\left(C^2[0,1],{∥·∥}_{\infty }\right)$ forms a Banach space. Now, consider the following initial value problem:

$${\displaystyle \frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}}u\left(t\right)={\displaystyle \frac{u^2\left(t\right)}{2}}-{\displaystyle \frac{u\left(t\right)}{2}}+{\displaystyle \frac{1}{2}},u\left(0\right)=1,{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}u\left(0\right)=1.$$

(8)

A potential solution to this problem can be expressed in the following integral form:

$$u\left(t\right)=1+{\int }_0^t\left[1+{\int }_0^s\left({\displaystyle \frac{u^2\left(x\right)}{2}}-{\displaystyle \frac{u\left(x\right)}{2}}+{\displaystyle \frac{1}{2}}\right)\mathrm{d}x\right]\mathrm{d}s.$$

Now, let $\mathcal{C}=\left\{u\left(t\right)\in B:0\le u\left(t\right)\le 1\right\}\subset \mathcal{B}$. Then, the operator $\mathbb{S}:\mathcal{C}\to \mathcal{C}$, defined as

$$\mathbb{S}\left(u\right)\left(t\right)=1+{\int }_0^t\left[1+{\int }_0^s\left({\displaystyle \frac{u^2\left(x\right)}{2}}-{\displaystyle \frac{u\left(x\right)}{2}}+{\displaystyle \frac{1}{2}}\right)\mathrm{d}x\right]\mathrm{d}s,$$

is a contraction mapping. Indeed, it satisfies the contraction property

$$\begin{array}{cc}\hfill \left|\mathbb{S}\left(u\right)-\mathbb{S}\left(v\right)\right|=& \left|{\int }_0^t\left\{{\int }_0^s\left[\left({\displaystyle \frac{u^2\left(x\right)}{2}}-{\displaystyle \frac{u\left(x\right)}{2}}+{\displaystyle \frac{1}{2}}\right)-\left({\displaystyle \frac{v^2\left(x\right)}{2}}-{\displaystyle \frac{v\left(x\right)}{2}}+{\displaystyle \frac{1}{2}}\right)\right]\mathrm{d}x\right\}\mathrm{d}s\right|\hfill \\ \hfill \le & \left|{\int }_0^t\left\{{\int }_0^s{∥\left({\displaystyle \frac{u^2\left(x\right)}{2}}-{\displaystyle \frac{u\left(x\right)}{2}}+{\displaystyle \frac{1}{2}}\right)-\left({\displaystyle \frac{v^2\left(x\right)}{2}}-{\displaystyle \frac{v\left(x\right)}{2}}+{\displaystyle \frac{1}{2}}\right)∥}_{\infty }\mathrm{d}x\right\}\mathrm{d}s\right|\hfill \\ \hfill \le & {∥{\int }_0^t\left\{{\int }_0^s\mathrm{d}x\right\}\mathrm{d}s∥}_{\infty }{∥\left({\displaystyle \frac{u^2\left(t\right)}{2}}-{\displaystyle \frac{u\left(t\right)}{2}}+{\displaystyle \frac{1}{2}}\right)-\left({\displaystyle \frac{v^2\left(t\right)}{2}}-{\displaystyle \frac{v\left(t\right)}{2}}+{\displaystyle \frac{1}{2}}\right)∥}_{\infty }\hfill \\ \hfill \le & {\displaystyle \frac{3}{10}}{∥u\left(t\right)-v\left(t\right)∥}_{\infty }.\hfill \end{array}$$

Now, for each $n\ge 1$, we consider the following sequences:

$$\begin{array}{cc}\hfill {\tau }_n& =1-{\displaystyle \frac{1}{n+10}},{\rho }_n=1-{\displaystyle \frac{1}{{(n+10)}^2}},{\sigma }_n=1-{\displaystyle \frac{1}{{(n+10)}^2}},\hfill \\ \hfill {\tau }_n^{*}& =1-{\displaystyle \frac{1}{n+10}},{\rho }_n^{*}=1-{\displaystyle \frac{1}{n+10}},{\sigma }_n^{*}=1-{\displaystyle \frac{1}{n+10}}.\hfill \end{array}$$

As illustrated in Figure 1 (top left), the sequences

$${\left\{{\displaystyle \frac{2M_n{\lambda }^5}{{\tau }_n(1-\lambda )}}\right\}}_{n\ge 1}and{\left\{{\displaystyle \frac{2M_n^{\prime }{\lambda }^5}{min\left\{{\tau }_n^{*},{\rho }_n^{*},{\sigma }_n^{*}\right\}(1-\lambda )}}\right\}}_{n\ge 1}$$

are both bounded, thereby satisfying the hypotheses of Theorem 2. Let

$$\mathrm{RES}(t,x_n)=\left|{\displaystyle \frac{{\mathrm{d}}^2}{\mathrm{d}t}}{x}_n\left(t\right)-\left({\displaystyle \frac{x_n^2\left(t\right)}{2}}-{\displaystyle \frac{x_n\left(t\right)}{2}}+{\displaystyle \frac{1}{2}}\right)\right|$$

be the residual error for $n>0$. Figure 1 (top right) shows that, starting with the initial norm ${∥x_0-x_0^{*}∥}_{\infty }=0$, where $x_0\left(t\right)=x_0^{*}\left(t\right)=t+1$, the sequence ${\left\{{∥x_n-x_n^{*}∥}_{\infty }\right\}}_{n\ge 1}$ converges to 0, while the diagrams below, together with

Table 1. Numerical values of the residual errors $\mathrm{RES}(t,x_n)$ and $\mathrm{RES}(t,x_n^{*})$ for $n=1$ and 2.

t	$\mathbf{RES}(\mathit{t},{\mathit{x}}_1)$	$\mathbf{RES}(\mathit{t},{\mathit{x}}_2)$	$\mathbf{RES}(\mathit{t},{\mathit{x}}_1^{*})$	$\mathbf{RES}(\mathit{t},{\mathit{x}}_2^{*})$
0.	0.	0.	0.	0.
0.1	$6.39(-20)$	$2.10(-40)$	$2.08(-22)$	$2.10(-33)$
0.2	$1.14(-16)$	$1.53(-32)$	$1.89(-20)$	$1.53(-31)$
0.3	$1.10(-14)$	$1.17(-27)$	$4.97(-19)$	$1.17(-30)$
0.4	$3.19(-13)$	$4.56(-26)$	$1.28(-17)$	$4.56(-26)$
0.5	$4.72(-12)$	$1.28(-24)$	$2.15(-16)$	$1.28(-24)$
0.6	$4.56(-11)$	$2.98(-19)$	$2.49(-15)$	$2.99(-23)$
0.7	$3.27(-10)$	$6.09(-19)$	$2.22(-14)$	$6.10(-21)$
0.8	$1.89(-9)$	$1.13(-18)$	$1.63(-13)$	$1.13(-20)$
0.9	$9.25(-9)$	$1.96(-17)$	$1.03(-12)$	$1.97(-18)$
1.	$3.98(-8)$	$3.21(-17)$	$5.78(-12)$	$3.22(-17)$

, illustrate that the sequences ${\left\{x_n\right\}}_{n\ge 1}$ and ${\left\{x_n^{*}\right\}}_{n\ge 1}$ converge to the fixed point of the mapping $\mathbb{S}$. Numbers in parentheses indicate decimal exponents.

Algorithms 3 and 4 provide theoretical error bounds when the exact operator $\mathbb{S}$ is replaced by a perturbed operator $\tilde{\mathbb{S}}$, which can be interpreted as an approximation arising in practical applications. To illustrate the usefulness of this result, we consider a modified nonlinear differential equation. Such an example demonstrates how the admissible error $\epsilon$ can be explicitly quantified in a functional setting, and how the theoretical estimates (9)–(10) compare with the actual numerical deviations observed in practice.

Theorem 3.

Let $\mathbb{S}:\mathcal{C}\to \mathcal{C}$ be a λ-contraction mapping with a fixed point $s_{*}$, and let $\tilde{\mathbb{S}}:\mathcal{C}\to \mathcal{C}$ be a mapping. Consider the sequences $\left\{{\tilde{x}}_n\right\}$ and $\left\{{\tilde{x}}_n^{*}\right\}$ generated by the DF and AR iteration algorithms associated with $\tilde{\mathbb{S}}$, which are defined as follows:

Algorithm 3: DF iteration algorithm for $\tilde{\mathbb{S}}$

Input: A mapping $\tilde{\mathbb{S}}$,

initial point $x_0\in \mathcal{C}$,

$\left\{{\rho }_n\right\}$, $\left\{{\sigma }_n\right\}$, $\left\{{\tau }_n\right\}\subset [0,1]$,

and budget N.

1: for $n=0,1,2\dots ,N$ do

2: ${\tilde{w}}_n=\tilde{\mathbb{S}}\left(\left(1-{\tau }_n\right){\tilde{x}}_n+{\tau }_n\tilde{\mathbb{S}}{\tilde{x}}_n\right)$

${\tilde{y}}_n={\tilde{\mathbb{S}}}^2{\tilde{w}}_n$

${\tilde{z}}_n=\tilde{\mathbb{S}}\left(\left(1-{\sigma }_n\right)\tilde{\mathbb{S}}{\tilde{y}}_n+{\sigma }_n\tilde{\mathbb{S}}{\tilde{w}}_n\right)$

${\tilde{x}}_{n+1}=\tilde{\mathbb{S}}\left(\left(1-{\rho }_n\right)\tilde{\mathbb{S}}{\tilde{y}}_n+{\rho }_n\tilde{\mathbb{S}}{\tilde{z}}_n\right)$

3: end for

Output: Approximate solution ${\tilde{x}}_N$

Algorithm 4: AR iteration algorithm for $\tilde{\mathbb{S}}$

Input: A mapping $\tilde{\mathbb{S}}$,

initial point $x_0\in \mathcal{C}$,

$\left\{{\rho }_n^{*}\right\}$, $\left\{{\sigma }_n^{*}\right\}$, $\left\{{\tau }_n^{*}\right\}\subset [0,1]$,

and budget N.

1: for $n=0,1,2\dots ,N$ do

2: ${\tilde{w}}_n^{*}=\tilde{\mathbb{S}}\left(\left(1-{\tau }_n^{*}\right){\tilde{x}}_n^{*}+{\tau }_n^{*}\tilde{\mathbb{S}}{\tilde{x}}_n^{*}\right)$

${\tilde{y}}_n^{*}=\tilde{\mathbb{S}}\left(\left(1-{\sigma }_n^{*}\right){\tilde{w}}_n^{*}+{\sigma }_n^{*}\tilde{\mathbb{S}}{\tilde{w}}_n^{*}\right)$

${\tilde{z}}_n^{*}=\tilde{\mathbb{S}}\left(\left(1-{\rho }_n^{*}\right){\tilde{y}}_n^{*}+{\rho }_n^{*}\tilde{\mathbb{S}}{\tilde{y}}_n^{*}\right)$

${\tilde{x}}_{n+1}^{*}={\tilde{\mathbb{S}}}^2{\tilde{z}}_n^{*}$

3: end for

Output: Approximate solution ${\tilde{x}}_N^{*}$

Suppose the following conditions hold:

(C1) There exists a maximum admissible error $\epsilon >0$ such that

$$(\forall x\in \mathcal{C})∥\mathbb{S}x-\tilde{\mathbb{S}}x∥\le \epsilon ,$$

(C2) There exists ${\tilde{s}}_{*}\in \mathcal{C}$ such that $\tilde{\mathbb{S}}{\tilde{s}}_{*}={\tilde{s}}_{*}$ and both iterative sequences $\left\{{\tilde{x}}_n\right\}$ and $\left\{{\tilde{x}}_n^{*}\right\}$ converge to ${\tilde{s}}_{*}$.

Then, the following bounds hold for the iterative sequences $\left\{{\tilde{x}}_n\right\}$ and $\left\{{\tilde{x}}_n^{*}\right\}$, respectively:

$$∥s_{*}-{\tilde{s}}_{*}∥\le {\displaystyle \frac{{\left({\lambda }^2+1\right)}^2\left(\lambda +1\right)}{1-{\lambda }^5}}\epsilon$$

(9)

and

$$∥s_{*}-{\tilde{s}}_{*}∥\le {\displaystyle \frac{\left({\lambda }^4+{\lambda }^3+{\lambda }^2+1\right)\left(\lambda +1\right)}{1-{\lambda }^5}}\epsilon .$$

(10)

Proof. 

We begin by deriving the bound presented in (9) for the term $∥s_{*}-{\tilde{s}}_{*}∥$, utilizing the DF iteration algorithms associated with the mappings $\mathbb{S}$ and $\tilde{\mathbb{S}}$. Using the contraction property of $\mathbb{S}$, condition (C1), and the DF iteration algorithm for both $\mathbb{S}$ and $\tilde{\mathbb{S}}$, we obtain the following estimates:

$$\begin{array}{cc}\hfill ∥w_n-{\tilde{w}}_n∥& \le ∥\mathbb{S}\left(\left(1-{\tau }_n\right)x_n+{\tau }_n\mathbb{S}{x}_n\right)-\mathbb{S}\left(\left(1-{\tau }_n\right){\tilde{x}}_n+{\tau }_n\tilde{\mathbb{S}}{\tilde{x}}_n\right)∥\hfill \\ \hfill & +∥\mathbb{S}\left(\left(1-{\tau }_n\right){\tilde{x}}_n+{\tau }_n\tilde{\mathbb{S}}{\tilde{x}}_n\right)-\tilde{\mathbb{S}}\left(\left(1-{\tau }_n\right){\tilde{x}}_n+{\tau }_n\tilde{\mathbb{S}}{\tilde{x}}_n\right)∥\hfill \\ \hfill & \le \lambda ∥\left(\left(1-{\tau }_n\right)x_n+{\tau }_n\mathbb{S}{x}_n\right)-\left(\left(1-{\tau }_n\right){\tilde{x}}_n+{\tau }_n\tilde{\mathbb{S}}{\tilde{x}}_n\right)∥+\epsilon \hfill \\ \hfill & \le \lambda \left[1-{\tau }_n(1-\lambda )\right]∥x_n-{\tilde{x}}_n∥+\lambda {\tau }_n\epsilon +\epsilon ,\hfill \\ \hfill ∥y_n-{\tilde{y}}_n∥& \le ∥\mathbb{S}\left(\mathbb{S}{w}_n\right)-\mathbb{S}\left(\tilde{\mathbb{S}}{\tilde{w}}_n\right)∥+∥\mathbb{S}\left(\tilde{\mathbb{S}}{\tilde{w}}_n\right)-\tilde{\mathbb{S}}\left(\tilde{\mathbb{S}}{\tilde{w}}_n\right)∥\hfill \\ \hfill & \le \lambda \left\{∥\mathbb{S}{w}_n-\mathbb{S}{\tilde{w}}_n∥+∥\mathbb{S}{\tilde{w}}_n-\tilde{\mathbb{S}}{\tilde{w}}_n∥\right\}+\epsilon \hfill \\ \hfill & \le {\lambda }^2∥w_n-{\tilde{w}}_n∥+(\lambda +1)\epsilon ,\hfill \\ \hfill ∥z_n-{\tilde{z}}_n∥& \le ∥\mathbb{S}\left(\left(1-{\sigma }_n\right)\mathbb{S}{y}_n+{\sigma }_n\mathbb{S}{w}_n\right)-\mathbb{S}\left(\left(1-{\sigma }_n\right)\tilde{\mathbb{S}}{\tilde{y}}_n+{\sigma }_n\tilde{\mathbb{S}}{\tilde{w}}_n\right)∥\hfill \\ \hfill & +∥\mathbb{S}\left(\left(1-{\sigma }_n\right)\tilde{\mathbb{S}}{\tilde{y}}_n+{\sigma }_n\tilde{\mathbb{S}}{\tilde{w}}_n\right)-\tilde{\mathbb{S}}\left(\left(1-{\sigma }_n\right)\tilde{\mathbb{S}}{\tilde{y}}_n+{\sigma }_n\tilde{\mathbb{S}}{\tilde{w}}_n\right)∥\hfill \\ \hfill & \le \lambda ∥\left(1-{\sigma }_n\right)\left(\mathbb{S}{y}_n-\tilde{\mathbb{S}}{\tilde{y}}_n\right)+{\sigma }_n\left(\mathbb{S}{w}_n-\tilde{\mathbb{S}}{\tilde{w}}_n\right)∥+\epsilon \hfill \\ \hfill & \le {\lambda }^2\left\{\left(1-{\sigma }_n\right)∥y_n-{\tilde{y}}_n∥+{\sigma }_n∥w_n-{\tilde{w}}_n∥\right\}+(\lambda +1)\epsilon ,\hfill \\ \hfill ∥x_{n+1}-{\tilde{x}}_{n+1}∥& \le ∥\mathbb{S}\left(\left(1-{\rho }_n\right)\mathbb{S}{y}_n+{\rho }_n\mathbb{S}{z}_n\right)-\mathbb{S}\left(\left(1-{\rho }_n\right)\tilde{\mathbb{S}}{\tilde{y}}_n+{\rho }_n\tilde{\mathbb{S}}{\tilde{z}}_n\right)∥\hfill \\ \hfill & +∥\mathbb{S}\left(\left(1-{\rho }_n\right)\tilde{\mathbb{S}}{\tilde{y}}_n+{\rho }_n\tilde{\mathbb{S}}{\tilde{z}}_n\right)-\tilde{\mathbb{S}}\left(\left(1-{\rho }_n\right)\tilde{\mathbb{S}}{\tilde{y}}_n+{\rho }_n\tilde{\mathbb{S}}{\tilde{z}}_n\right)∥\hfill \\ \hfill & \le \lambda \left\{\left(1-{\rho }_n\right)\left\{∥\mathbb{S}{y}_n-\mathbb{S}{\tilde{y}}_n∥+\epsilon \right\}+{\rho }_n\left\{∥\mathbb{S}{z}_n-\mathbb{S}{\tilde{z}}_n∥+\epsilon \right\}\right\}+\epsilon \hfill \\ \hfill & \le {\lambda }^2\left\{\left(1-{\rho }_n\right)∥y_n-{\tilde{y}}_n∥+{\rho }_n∥z_n-{\tilde{z}}_n∥\right\}+(\lambda +1)\epsilon ,\hfill \end{array}$$

By combining these inequalities, we obtain

$$\begin{array}{cc}\hfill ∥x_{n+1}-{\tilde{x}}_{n+1}∥& \le {\lambda }^5\left[\left(1-{\rho }_n\right)+{\rho }_n{\lambda }^2\left(1-{\sigma }_n\right)+{\rho }_n{\sigma }_n\right]\left[1-{\tau }_n\left(1-\lambda \right)\right]∥x_n-{\tilde{x}}_n∥\hfill \\ \hfill & +{\lambda }^4\left[\left(1-{\rho }_n\right)+{\rho }_n{\lambda }^2\left(1-{\sigma }_n\right)+{\rho }_n{\sigma }_n\right]\left(\lambda {\tau }_n\epsilon +\epsilon \right)\hfill \\ \hfill & +{\lambda }^2\left[\left(1-{\rho }_n\right)+{\rho }_n{\lambda }^2\left(1-{\sigma }_n\right)\right](\lambda +1)\epsilon +{\lambda }^2{\rho }_n(\lambda +1)\epsilon +(\lambda +1)\epsilon .\hfill \end{array}$$

(11)

Since for every $n\in \mathbb{N}$, ${\rho }_n$, ${\sigma }_n$, and ${\tau }_n\in [0,1]$ and $\lambda \in [0,1)$, we conclude that

$$∥x_{n+1}-{\tilde{x}}_{n+1}∥\le {\lambda }^5∥x_n-{\tilde{x}}_n∥+\left({\lambda }^4+2{\lambda }^2+1\right)(\lambda +1)\epsilon .$$

From ([26], Theorem 2), we have $\underset{n\to \infty }{lim}{x}_n=s_{*}$ and under assumption (C2), we also have $\underset{n\to \infty }{lim}{\tilde{x}}_n={\tilde{s}}_{*}$. Taking the limit on both sides of the final inequality yields

$$∥s_{*}-{\tilde{s}}_{*}∥\le {\displaystyle \frac{{\left({\lambda }^2+1\right)}^2\left(\lambda +1\right)}{1-{\lambda }^5}}\epsilon .$$

Next, we derive the bound specified in (10) for the quantity $∥s_{*}-{\tilde{s}}_{*}∥$ by utilizing the AR iteration algorithms associated with the mappings $\mathbb{S}$ and $\tilde{\mathbb{S}}$. By leveraging the contraction property of $\mathbb{S}$, assumption (C1), and the AR iteration algorithm for both $\mathbb{S}$ and $\tilde{\mathbb{S}}$, the following estimates can be derived in a manner similar to the previous ones:

$$\begin{array}{cc}\hfill ∥w_n^{*}-{\tilde{w}}_n^{*}∥\le & \lambda \left[1-{\tau }_n^{*}(1-\lambda )\right]∥x_n^{*}-{\tilde{x}}_n^{*}∥+\lambda {\tau }_n^{*}\epsilon +\epsilon ,\hfill \\ \hfill ∥y_n^{*}-{\tilde{y}}_n^{*}∥\le & \lambda \left[1-{\sigma }_n^{*}(1-\lambda )\right]∥w_n^{*}-{\tilde{w}}_n^{*}∥+\lambda {\sigma }_n^{*}\epsilon +\epsilon ,\hfill \\ \hfill ∥z_n-{\tilde{z}}_n∥\le & \lambda \left[1-{\rho }_n^{*}(1-\lambda )\right]∥y_n^{*}-{\tilde{y}}_n^{*}∥+\lambda {\rho }_n^{*}\epsilon +\epsilon ,\hfill \\ \hfill ∥x_{n+1}-{\tilde{x}}_{n+1}∥\le & {\lambda }^2∥z_n^{*}-{\tilde{z}}_n^{*}∥+(\lambda +1)\epsilon .\hfill \end{array}$$

By successively substituting these bounds, we obtain the following:

$$\begin{array}{cc}\hfill ∥x_{n+1}-{\tilde{x}}_{n+1}∥& \le {\lambda }^5\left[1-{\rho }_n^{*}(1-\lambda )\right]\left[1-{\sigma }_n^{*}(1-\lambda )\right]\left[1-{\tau }_n^{*}(1-\lambda )\right]∥x_n^{*}-{\tilde{x}}_n^{*}∥\hfill \\ \hfill & +{\lambda }^4\left[1-{\rho }_n^{*}(1-\lambda )\right]\left[1-{\sigma }_n^{*}(1-\lambda )\right]\left(\lambda {\tau }_n^{*}\epsilon +\epsilon \right)\hfill \\ \hfill & +{\lambda }^3\left[1-{\rho }_n^{*}(1-\lambda )\right]\left(\lambda {\sigma }_n^{*}\epsilon +\epsilon \right)+{\lambda }^2\left(\lambda {\rho }_n^{*}\epsilon +\epsilon \right)+(\lambda +1)\epsilon .\hfill \end{array}$$

(12)

Since for every $n\in \mathbb{N}$, ${\rho }_n^{*}$, ${\sigma }_n^{*}$, and ${\tau }_n^{*}\in [0,1]$ and $\lambda \in \left[0,1\right)$, it follows that

$$∥x_{n+1}-{\tilde{x}}_{n+1}∥\le {\lambda }^5∥x_n^{*}-{\tilde{x}}_n^{*}∥+\left({\lambda }^4+{\lambda }^3+{\lambda }^2+1\right)(\lambda +1)\epsilon .$$

From ([27], Theorem 3), we know that $\underset{n\to \infty }{lim}{x}_n=s_{*}$, and under assumption (C2), we also have $\underset{n\to \infty }{lim}{\tilde{x}}_n={\tilde{s}}_{*}$. Taking limits on both sides of the last inequality, we finally obtain

$$∥s_{*}-{\tilde{s}}_{*}∥\le {\displaystyle \frac{\left({\lambda }^4+{\lambda }^3+{\lambda }^2+1\right)\left(\lambda +1\right)}{1-{\lambda }^5}}\epsilon ,$$

which completes the proof. □

To clarify the applicability of Theorem 3, we present a concrete example constructed from a nonlinear differential equation. This will allow us to explicitly see how the perturbation of the operator affects the fixed point and how the theoretical error bounds are reflected in practice.

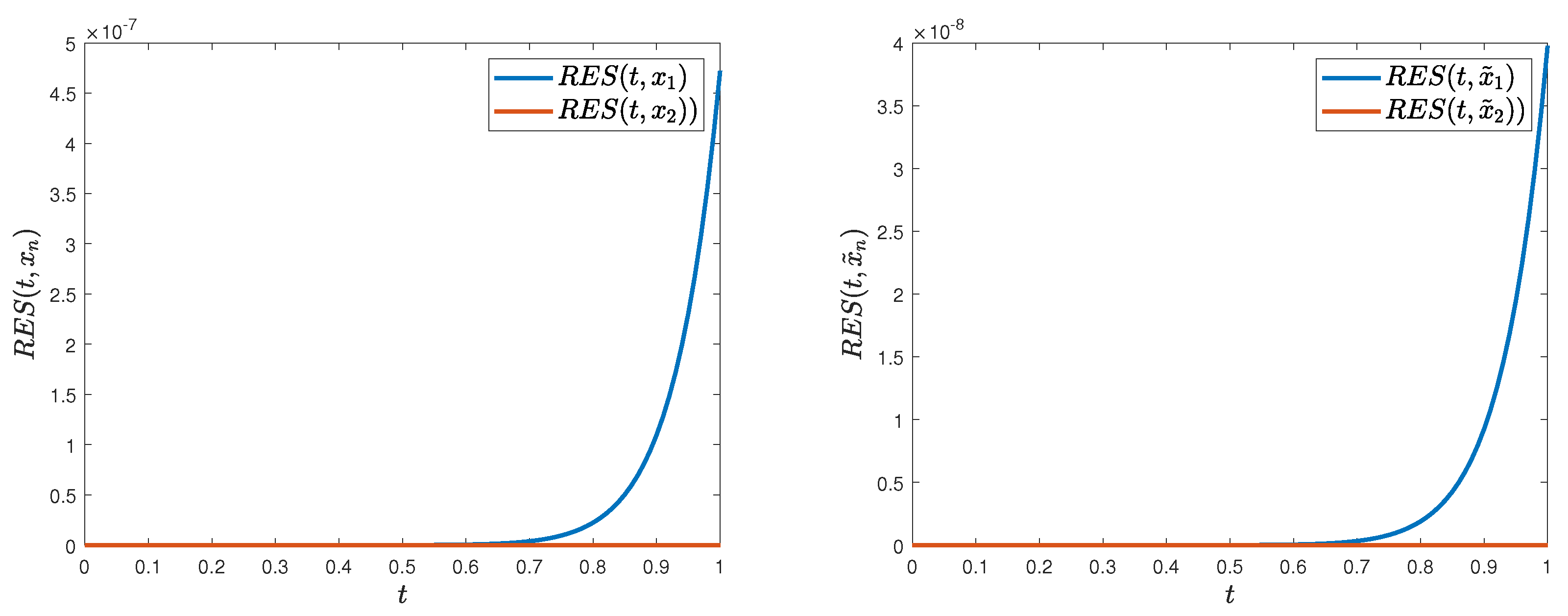
Example 4.

Let $\mathcal{B}$, $\mathcal{C}$, $\mathbb{S}$, $\left\{{\rho }_n\right\}$, $\left\{{\sigma }_n\right\}$, $\left\{{\tau }_n\right\}$, $\left\{{\rho }_n^{*}\right\}$, $\left\{{\sigma }_n^{*}\right\}$, and $\left\{{\tau }_n^{*}\right\}$ be defined as in Example 3. We now consider the following second-order initial value problem

$${\displaystyle \frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}}u\left(t\right)={\displaystyle \frac{u^2\left(t\right)}{2}}-{\displaystyle \frac{u\left(t\right)}{2}}+{\displaystyle \frac{u^2\left(t\right)-u^3\left(t\right)}{{10}^2}}+{\displaystyle \frac{1}{2}},u\left(0\right)=1,{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}u\left(0\right)=1.$$

A possible solution to this problem can be formulated as an integral equation:

$$u\left(t\right)=1+{\int }_0^t\left(1+{\int }_0^s\left({\displaystyle \frac{u^2\left(x\right)}{2}}-{\displaystyle \frac{u\left(x\right)}{2}}+{\displaystyle \frac{u^2\left(x\right)-u^3\left(x\right)}{{10}^2}}+{\displaystyle \frac{1}{2}}\right)\mathrm{d}x\right)\mathrm{d}s.$$

Define an operator $\tilde{\mathbb{S}}:\mathcal{C}\to \mathcal{C}$ as follows:

$$\tilde{\mathbb{S}}\left(u\right)\left(t\right)=1+{\int }_0^t\left(1+{\int }_0^s\left({\displaystyle \frac{u^2\left(x\right)}{2}}-{\displaystyle \frac{u\left(x\right)}{2}}+{\displaystyle \frac{u^2\left(x\right)-u^3\left(x\right)}{{10}^2}}+{\displaystyle \frac{1}{2}}\right)\mathrm{d}x\right)\mathrm{d}s.$$

Thus, we can establish the following bound:

$$\begin{array}{cc}\hfill \left|\mathbb{S}\left(u\right)-\tilde{\mathbb{S}}\left(u\right)\right|=& |1+{\int }_0^t\left(1+{\int }_0^s\left({\displaystyle \frac{u^2\left(x\right)}{2}}-{\displaystyle \frac{u\left(x\right)}{2}}+{\displaystyle \frac{1}{2}}\right)\mathrm{d}x\right)\mathrm{d}s\hfill \\ \hfill & -\left(1+{\int }_0^t\left(1+{\int }_0^s\left({\displaystyle \frac{u^2\left(x\right)}{2}}-{\displaystyle \frac{u\left(x\right)}{2}}+{\displaystyle \frac{u^2\left(x\right)-u^3\left(x\right)}{{10}^2}}+{\displaystyle \frac{1}{2}}\right)\mathrm{d}x\right)\mathrm{d}s\right)|\hfill \\ \hfill \le & \left|{\int }_0^t\left({\int }_0^s\left({\displaystyle \frac{u^2\left(x\right)-u^3\left(x\right)}{{10}^2}}+{\displaystyle \frac{1}{2}}\right)\mathrm{d}x\right)\mathrm{d}s\right|\hfill \\ \hfill \le & {\displaystyle \frac{1}{2}}{∥{\displaystyle \frac{u^2\left(t\right)-u^3\left(t\right)}{{10}^2}}∥}_{\infty }<7.42\times {10}^{-4}=\epsilon .\hfill \end{array}$$

The obtained value $7.42\times {10}^{-4}$ represents the admissible tolerance ε, showing that the error in the approximation does not exceed this bound. As in Example 3, we introduce the residual error for the sequence $\left\{{\tilde{x}}_n\right\}$ by

$$\mathrm{RES}(t,{\tilde{x}}_n)=\left|{\displaystyle \frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}}{\tilde{x}}_n\left(t\right)-\left({\displaystyle \frac{{\tilde{x}}_n^2\left(t\right)}{2}}-{\displaystyle \frac{{\tilde{x}}_n\left(t\right)}{2}}+{\displaystyle \frac{{\tilde{x}}_n^2\left(t\right)-{\tilde{x}}_n^3\left(t\right)}{{10}^2}}+{\displaystyle \frac{1}{2}}\right)\right|.$$

From

Table 2. Numerical values of the residual errors $\mathrm{RES}(t,{\tilde{x}}_n)$ and $\mathrm{RES}(t,{\tilde{x}}_n^{*})$ for $n=1$ and 2.

t	$\mathbf{RES}(\mathit{t},{\tilde{\mathit{x}}}_1)$	$\mathbf{RES}(\mathit{t},{\tilde{\mathit{x}}}_2)$	$\mathbf{RES}(\mathit{t},{\tilde{\mathit{x}}}_1^{*})$	$\mathbf{RES}(\mathit{t},{\tilde{\mathit{x}}}_2^{*})$
0.	0.	0.	0.	0.
0.1	$7.19(-20)$	$8.42(-40)$	$1.90(-24)$	$2.79(-37)$
0.2	$1.30(-16)$	$1.12(-33)$	$4.09(-21)$	$3.62(-33)$
0.3	$1.27(-14)$	$2.00(-27)$	$4.38(-19)$	$6.26(-29)$
0.4	$3.73(-13)$	$1.55(-26)$	$1.45(-17)$	$4.74(-25)$
0.5	$5.60(-12)$	$7.65(-22)$	$2.56(-16)$	$2.28(-24)$
0.6	$5.49(-11)$	$2.82(-22)$	$3.06(-15)$	$8.25(-23)$
0.7	$4.01(-10)$	$8.53(-20)$	$2.79(-14)$	$2.44(-21)$
0.8	$2.36(-9)$	$2.22(-20)$	$2.10(-13)$	$6.25(-20)$
0.9	$1.18(-8)$	$5.15(-19)$	$1.36(-12)$	$1.43(-18)$
1.	$5.19(-8)$	$1.08(-18)$	$7.90(-12)$	$2.99(-18)$

and Figure 2, starting with the initial function ${\tilde{x}}_0\left(t\right)={\tilde{x}}_0^{*}\left(t\right)=t+1$, it is evident that the sequences ${\left\{{\tilde{x}}_n\right\}}_{n\ge 1}$ and ${\left\{{\tilde{x}}_n^{*}\right\}}_{n\ge 1}$ exhibit convergence toward a fixed point of $\tilde{\mathbb{S}}$. As a result, all the conditions of Theorem 3 are satisfied, thereby confirming the validity of the estimates in (9) and (10), as demonstrated below:

$${∥s_{*}-{\tilde{s}}_{*}∥}_{\infty }\le 8.55\times {10}^{-4}\le 1.15\times {10}^{-3}={\displaystyle \frac{{\left({\lambda }^2+1\right)}^2\left(\lambda +1\right)}{1-{\lambda }^5}}\epsilon ,$$

$${∥s_{*}-{\tilde{s}}_{*}∥}_{\infty }\le 9.678\times {10}^{-4}\le 1.38\times {10}^{-3}={\displaystyle \frac{\left({\lambda }^4+{\lambda }^3+{\lambda }^2+1\right)\left(\lambda +1\right)}{1-{\lambda }^5}}\epsilon .$$

The numerical estimates demonstrate that the deviations $|s^{*}-{\tilde{s}}^{*}{|}_{\infty }$ are bounded by $8.55\times {10}^{-4}$ and $9.678\times {10}^{-4}$, which remain well within the respective theoretical tolerances ${\displaystyle \frac{{\left({\lambda }^2+1\right)}^2\left(\lambda +1\right)}{1-{\lambda }^5}}\epsilon$ and ${\displaystyle \frac{\left({\lambda }^4+{\lambda }^3+{\lambda }^2+1\right)\left(\lambda +1\right)}{1-{\lambda }^5}}\epsilon$, thereby confirming both the accuracy of the numerical scheme and the sharpness of the established analytical bounds.

The numerical outcomes presented in Table 2 and Figure 2 highlight two important observations. First, the residual errors decrease rapidly with each iteration, confirming the strong convergence of both DF and AR schemes towards the fixed point of $\tilde{\mathbb{S}}$. Second, the measured deviations between $s_{*}$ and ${\tilde{s}}_{*}$ remain well within the analytical error bounds derived in Theorem 3. This shows that estimates (9) and (10) are not only mathematically valid, but also numerically sharp. Consequently, Example 4 provides concrete evidence of the stability and reliability of the proposed iterative methods when small perturbations are introduced into the underlying operator.

Remark 1.

(1) The estimates provided in Theorem 3 within (9) and (10) for the quantity $∥s_{*}-{\tilde{s}}_{*}∥$ offer substantially more precise approximations than the corresponding ones presented in parts (i) and (ii) of Theorem 1. Additionally, a comparative analysis of the estimates given in (9) and (10) reveals that the bound in (9) exhibits superior accuracy compared to that in (10).

Furthermore, by utilizing the identity

$${\displaystyle \frac{1}{1-{\lambda }^{k+1}}}\sum _{i=0}^k{\lambda }^i={\displaystyle \frac{1}{1-\lambda }},\mathit{for}\mathit{all}k\in \mathbb{N},$$

we derive the following asymptotic results:

(D1) Taking the limit as $n\to \infty$ under the assumption that ${\rho }_n$, ${\sigma }_n$, ${\tau }_n\to 0$, the inequality given in (11) leads to

$$∥s_{*}-{\tilde{s}}_{*}∥\le {\displaystyle \frac{{\lambda }^4+{\lambda }^3+{\lambda }^2+\lambda +1}{1-{\lambda }^5}}\epsilon ={\displaystyle \frac{\epsilon }{1-\lambda }}.$$

(13)

(D2) As $n\to \infty$, assuming ${\rho }_n$, ${\sigma }_n$, ${\tau }_n\to 1$, the inequality from (11) results in

$$∥s_{*}-{\tilde{s}}_{*}∥\le {\displaystyle \frac{{\lambda }^5+{\lambda }^4+{\lambda }^3+{\lambda }^2+\lambda +1}{1-{\lambda }^6}}\epsilon ={\displaystyle \frac{\epsilon }{1-\lambda }}.$$

(14)

(D3) Taking the limit as $n\to \infty$ with ${\rho }_n^{*}$, ${\sigma }_n^{*}$, ${\tau }_n^{*}\to 0$, the inequality from (12) yields

$$∥s_{*}-{\tilde{s}}_{*}∥\le {\displaystyle \frac{{\lambda }^4+{\lambda }^3+{\lambda }^2+\lambda +1}{1-{\lambda }^5}}\epsilon ={\displaystyle \frac{\epsilon }{1-\lambda }}.$$

(15)

(D4) Finally, as $n\to \infty$ under the condition ${\rho }_n^{*}$, ${\sigma }_n^{*}$, ${\tau }_n^{*}\to 1$, applying the limit to the inequality in (12) gives

$$∥s_{*}-{\tilde{s}}_{*}∥\le {\displaystyle \frac{{\lambda }^7+{\lambda }^6+{\lambda }^5+{\lambda }^4+{\lambda }^3+{\lambda }^2+\lambda +1}{1-{\lambda }^8}}\epsilon ={\displaystyle \frac{\epsilon }{1-\lambda }}.$$

(16)

Based on these results, it follows that in cases (D1) and (D2), the estimates obtained in (13) and (14) are more precise than the bound in (9). Similarly, for cases (D3) and (D4), the estimates in (15) and (16) yield more refined approximations than that in (10).

(2) Let the mappings $\mathbb{S}$ and $\tilde{\mathbb{S}}$ be as defined in Theorem 3. Then, we observe that

$$\begin{array}{cc}\hfill ∥s_{*}-{\tilde{s}}_{*}∥& =∥\mathbb{S}{s}_{*}-\tilde{\mathbb{S}}{\tilde{s}}_{*}∥\hfill \\ \hfill & \le ∥\mathbb{S}{s}_{*}-\mathbb{S}{\tilde{s}}_{*}∥+∥\mathbb{S}{\tilde{s}}_{*}-\tilde{\mathbb{S}}{\tilde{s}}_{*}∥\hfill \\ \hfill & \le \lambda ∥s_{*}-{\tilde{s}}_{*}∥+\underset{x\in \mathcal{C}}{sup}∥\mathbb{S}x-\tilde{\mathbb{S}}x∥,\hfill \end{array}$$

where, due to condition (C1), we have

$$\underset{x\in \mathcal{C}}{sup}∥\mathbb{S}x-\tilde{\mathbb{S}}x∥\le \epsilon ,$$

which leads to

$$∥s_{*}-{\tilde{s}}_{*}∥\le {\displaystyle \frac{\epsilon }{1-\lambda }}.$$

(17)

Thus, using a more straightforward approach, we obtain a tighter bound for $∥s_{*}-{\tilde{s}}_{*}∥$ compared to those provided in (9) and (10).

(3)

Table 3. Comparison of the coefficients of $\epsilon /(1-\lambda )$ across these bounds for a typical $\lambda \in [0,1)$.

Bound in	Coefficient	Improvement Factor (vs. Original 15)
(2) or (3)	15	–
(5)	3	$5\times$
(9)	${\displaystyle \frac{{\left({\lambda }^2+1\right)}^2\left(\lambda +1\right)}{{\lambda }^4+{\lambda }^3+{\lambda }^2+\lambda +1}}$	≈3–6×
(10)	${\displaystyle \frac{\left({\lambda }^4+{\lambda }^3+{\lambda }^2+1\right)\left(\lambda +1\right)}{{\lambda }^4+{\lambda }^3+{\lambda }^2+\lambda +1}}$	≈3–5×
(13)–(16)	1	$15\times$
(17)	1	$15\times$

presents a comparison of the results obtained from the analyses conducted to establish an upper bound for $∥s_{*}-{\tilde{s}}_{*}∥$:

Example 5.

Let $\mathcal{B}$, $\mathcal{C}$, $\mathbb{S}$, and $\tilde{\mathbb{S}}$ be defined as in Example 4.

(D1) Consider the parametrized sequences $\left\{{\tau }_n\right\}$, $\left\{{\rho }_n\right\}$, $\left\{{\sigma }_n\right\}$, prescribed by

$${\tau }_n={\displaystyle \frac{1}{n+10}},{\rho }_n={\displaystyle \frac{1}{{(n+10)}^2}},{\sigma }_n={\displaystyle \frac{1}{{(n+10)}^2}}$$

for all $n\ge 1$. These sequences exhibit asymptotic behavior ${\tau }_n,{\rho }_n,{\sigma }_n\to 0$ as n $\to \infty$. As empirically validated by Figure 3, the iterative sequence ${\left\{x_n\right\}}_{n\ge 1}$, starting with the initial $x_0\left(t\right)=t+1$, converges to the fixed point of $\mathbb{S}$, while ${\left\{{\tilde{x}}_n\right\}}_{n\ge 1}$, starting with the initial ${\tilde{x}}_0\left(t\right)=t+1$, converges to the fixed point of $\tilde{\mathbb{S}}$. A quantitative assessment yields

$${∥s_{*}-{\tilde{s}}_{*}∥}_{\infty }\le 9.55\times {10}^{-4}\le 1.05\times {10}^{-3}={\displaystyle \frac{\epsilon }{1-\lambda }}.$$

(D2) Building on Example 4, define the sequences

$${\tau }_n=1-{\displaystyle \frac{1}{n+10}},{\rho }_n=1-{\displaystyle \frac{1}{{(n+10)}^2}},{\sigma }_n=1-{\displaystyle \frac{1}{{(n+10)}^2}}$$

for all $n\ge 1$. Here, ${\tau }_n,{\rho }_n,{\sigma }_n\to 1$ as $n\to \infty$. Graphical results in Figure 3 (left and right) confirm that ${\left\{x_n\right\}}_{n\ge 1}$ and ${\left\{{\tilde{x}}_n\right\}}_{n\ge 1}$, starting with the initial $x_0\left(t\right)={\tilde{x}}_0\left(t\right)=t+1$, converge to $s_{*}$ and ${\tilde{s}}_{*}$, respectively. The error propagation adheres to the bound:

$${∥s_{*}-{\tilde{s}}_{*}∥}_{\infty }\le 8.55\times {10}^{-4}\le 1.05\times {10}^{-3}={\displaystyle \frac{\epsilon }{1-\lambda }}.$$

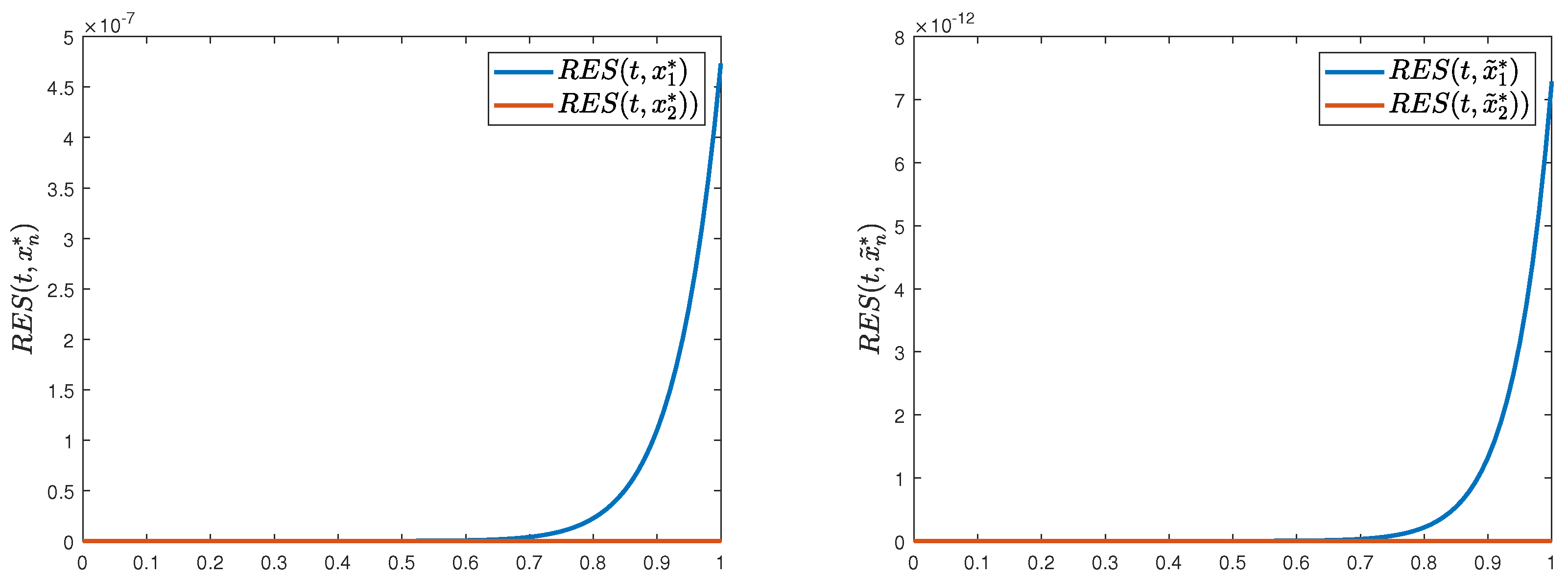
(D3) Let the sequences $\left\{{\tau }_n^{*}\right\}$, $\left\{{\rho }_n^{*}\right\}$, and $\left\{{\sigma }_n^{*}\right\}$ be specified via

$${\tau }_n^{*}={\displaystyle \frac{1}{(n+10)}},{\rho }_n^{*}={\displaystyle \frac{1}{n+10}},{\sigma }_n^{*}={\displaystyle \frac{1}{n+10}}$$

for all $n\ge 1$. These sequences satisfy ${\tau }_n^{*}$, ${\rho }_n^{*}$, ${\sigma }_n^{*}\to 0$ as n $\to \infty$. As depicted in Figure 4 (left and right), ${\left\{x_n^{*}\right\}}_{n\ge 1}$ and ${\left\{{\tilde{x}}_n^{*}\right\}}_{n\ge 1}$, starting with the initial $x_0^{*}\left(t\right)={\tilde{x}}_0^{*}\left(t\right)=t+1$, converge to $s_{*}$ and ${\tilde{s}}_{*}$, respectively. The deviation between fixed points is bounded by

$${∥s_{*}-{\tilde{s}}_{*}∥}_{\infty }\le 8.73\times {10}^{-4}\le 1.05\times {10}^{-3}={\displaystyle \frac{\epsilon }{1-\lambda }}.$$

(D4) Adopting the framework of Example 4, define

$${\tau }_n^{*}=1-{\displaystyle \frac{1}{n+10}},{\rho }_n^{*}=1-{\displaystyle \frac{1}{n+10}},{\sigma }_n^{*}=1-{\displaystyle \frac{1}{n+10}}$$

for all $n\ge 1$. Then, ${\tau }_n^{*}$, ${\rho }_n^{*}$, ${\sigma }_n^{*}\to 1$ as n $\to \infty$. Starting with the initial $x_0^{*}\left(t\right)={\tilde{x}}_0^{*}\left(t\right)=t+1$, Figure 1 (bottom-right) and Figure 2 (right) illustrate the convergence of ${\left\{x_n^{*}\right\}}_{n\ge 1}$ and ${\left\{{\tilde{x}}_n^{*}\right\}}_{n\ge 1}$ to $s_{*}$ and ${\tilde{s}}_{*}$, respectively. The empirical error remains well within the theoretical upper limit

$${∥s_{*}-{\tilde{s}}_{*}∥}_{\infty }\le 9.678\times {10}^{-4}\le 1.05\times {10}^{-3}={\displaystyle \frac{\epsilon }{1-\lambda }}.$$

3. Discussion

The equivalence of convergence between the DF and AR algorithms (Theorem 2) underscores a deeper structural symmetry in their iterative mechanisms, which had not been previously recognized. This finding simplifies comparative analyses in applications where algorithm selection is non-trivial. Our data-dependence results (Theorem 3) significantly improve upon the works of Filali et al. [26] and Alam et al. [27], by removing the requirement for $\tilde{\mathbb{S}}$ to be a strict contraction, instead permitting it to satisfy a weakened inequality $∥\tilde{\mathbb{S}}x-\tilde{\mathbb{S}}y∥\le \lambda ∥x-y∥+\mu$. This generalization is critical for real-world scenarios where numerical approximations or noisy data inherently violate strict contractivity. A notable limitation lies in the assumption of a uniform bound $\epsilon$ on $∥\mathbb{S}x-\tilde{\mathbb{S}}x∥$, which may not hold in unbounded domains. Additionally, while our focus on Banach spaces covers a broad class of problems, extending these results to metric spaces with non-linear structures—such as hyperbolic or CAT(0) spaces—remains an open challenge.

4. Conclusions

The primary contribution of this study is the derivation of enhanced data-dependence estimates without imposing stringent contraction conditions on the perturbed operator. By employing a non-asymptotic approach, we establish explicit error bounds on the perturbations of fixed points, given by $∥s_{*}-{\tilde{s}}_{*}∥\le \mathcal{O}\left(\epsilon /(1-\lambda )\right)$, and demonstrate that small perturbations in the operator systematically propagate to their corresponding equilibria in a controlled and quantifiable manner. These refined estimates offer stronger theoretical guarantees compared to existing results, thereby improving the robustness of the framework in practical applications where numerical approximations and modeling inaccuracies are unavoidable. Furthermore, we characterize the conditions under which the DF and AR iteration algorithms exhibit equivalent convergence behavior, providing a unified theoretical perspective on their properties. Our analysis reveals that, under specific conditions, both algorithms demonstrate comparable stability and sensitivity characteristics. Additionally, we refine the data-dependence analysis in the context of contraction mappings by relaxing restrictive assumptions on control sequences and underlying mappings, thereby broadening the scope and applicability of asymptotic data-dependence results. These findings are substantiated through rigorous theoretical analysis and illustrative examples. The insights derived from this study contribute to a deeper understanding of fixed-point approximation methods and their sensitivity to perturbations. Future research directions include extending these results to more general classes of contractive mappings and investigating their implications in optimization, differential equations, and machine learning algorithms.