A Novel Robust Transformation Approach to Finite Population Median Estimation Using Monte Carlo Simulation and Empirical Data

Abstract

This study develops an improved family of estimators for estimating the finite population median within a two-phase sampling method. The proposed estimators, which use transformation techniques to reduce survey costs when full auxiliary information is unavailable, yield more accurate results than traditional methods. These transformations employ robust statistical measures such as Hodges–Lehmann location, Gini mean difference, and Bowley’s skewness, which strengthen resistance against outliers and heavy-tailed distributions. Through the use of these modern tools within the two-phase sampling framework, the proposed estimators achieve greater flexibility and robustness compared to conventional quantile-based approaches. A first-order approximation is employed to derive the bias and mean squared error expressions. The performance of the proposed estimators is examined through simulation experiments across multiple distributional scenarios and validated using real datasets against standard approaches. Findings based on percent relative efficiency confirm that the proposed estimators improve the accuracy and efficiency of median estimation in two-phase sampling, demonstrating superiority over conventional methods across various practical scenarios.

1. Introduction

In survey methodology, the median is widely recognized as a reliable measure of central tendency, especially under skewed distributions or when outliers are present. The stratified two-phase sampling design enhances the efficiency of such estimation by first obtaining auxiliary information within each stratum and then selecting a sub-sample in the second phase for detailed measurement. This arrangement is useful when full auxiliary data are initially absent, since it reduces costs while preserving accuracy. As a result, the combined use of stratification and two-phase sampling provides a practical framework for precise and dependable median estimation in complex populations. More details about auxiliary information can be found at [1,2,3,4].

In many areas of applied statistics, the median has proven to be a more reliable summary measure than the mean, particularly when populations are skewed or contain a high frequency of extreme values. Its robustness has made it valuable in fields such as economic surveys, medical outcome analysis, and environmental monitoring, where averages may be misleading. A key aspect of improving median estimation has been the use of auxiliary variables, which allow researchers to reduce cost while increasing precision. Early studies provided the theoretical groundwork [5,6,7], followed by the introduction of improved estimators such as ratio and regression forms [8,9]. As the discipline advanced, methods incorporating two-phase or double-sampling designs, as well as approaches utilizing multiple auxiliary variables, further enhanced efficiency [10,11,12,13]. More recent contributions emphasize the role of robust, transformation-based estimators under both simple and stratified designs [14,15,16,17,18], reflecting the ongoing importance of median estimation in survey methodology [19,20,21,22,23,24,25].

In many real-world applications, survey data are rarely symmetric and often include extreme observations. Agricultural yields fluctuate due to weather patterns, industrial outputs may be distorted by production defects, and educational test scores frequently deviate from normality. In such contexts, the median provides a more stable and reliable indicator of central tendency than the mean. However, traditional estimators such as ratio, regression, product, and exponential types were mostly developed under the assumption of normality and symmetry. As a result, they are highly sensitive to skewness and outliers, leading to inefficiency in complex populations. Motivated by the limitations of traditional approaches and supported by recent contributions by employing the methodologies outlined in [26,27,28], we develop a new class of estimators under a stratified two-phase sampling design. Stratification ensures that population heterogeneity is properly represented, while the two-phase design allows auxiliary information from the first phase to be utilized before more detailed data are collected in the second phase. By applying transformation techniques, the proposed estimators achieve improved robustness and precision, reducing sensitivity to irregularities in the data. The combined use of stratification, two-phase sampling, and transformations ensures higher efficiency and greater consistency, making the proposed estimators well suited for practical survey applications.

Rationale for the Proposed Class of Estimators

In addition to the conventional sample median, a number of robust summary measures have been proposed to capture distributional features such as location, scale, skewness, and tail behavior. These measures serve as useful transformation components that can improve the efficiency and reliability of median-based estimation, particularly in the presence of outliers or departures from normality. The motivation for introducing this new family of estimators with robust transformations can be summarized as follows:

• Handling outliers and heavy tails: Conventional median-type estimators often lose efficiency when the auxiliary variable is affected by extreme values. Robust transformations such as Hodges–Lehmann location and Gini mean difference, and resistant averages such as trimmed and winsorized means provide stable adjustments that reduce the influence of outliers.
• Quartile-based measures: Median ratio, Bowley’s skewness, interquartile range, geometric quartile mean, quartile deviation, and percentile ranges describe spread and asymmetry.
• Robust dispersion: The median absolute deviation and skewness-adjusted indices help reduce the influence of extreme values.
• Variability and shape: The coefficient of variation and Moors’ kurtosis provide insight into variability and tail behavior, especially in skewed or heavy-tailed data.
• Improved efficiency: By combining resistant measures of location, scale, and shape, the proposed class can achieve lower bias and mean squared error compared to traditional quantile-based methods.
• Novelty in median estimation: While robust measures such as trimmed means or Gini mean difference have been studied in the context of mean estimation, their use in designing median estimators under two-phase sampling has not been explored. This gives the proposed class originality and adds value to the literature.
• Practical Relevance: Many real-life datasets in economics, health, and social sciences exhibit skewness or contain irregular observations. The proposed transformations make the estimators more reliable for such applications.
• Overall contribution: Together, these measures and transformations enhance the efficiency, stability, and reliability of median-based estimation in the presence of outliers or non-normality.

2. Survey Design and Preliminaries

A comprehensive discussion of the methods used for the proposed median class of estimators and those previously introduced by various authors is presented in this section. Consider a population of N members, written as $T=\{T_1,T_2,\dots ,T_N\}.$ The research investigates a study variable Y along with an auxiliary variable X. From this population, a simple random sample without replacement (SRSWOR) of size n is selected, producing observed values $y_i$ and $x_i$ for $i=1,\dots ,n$. While Y and X are strongly related, the median ${\Phi }_x$ for X in the population remains unknown. The stages of the two-phase sampling method are specified as follows.

(i)

The process begins with selecting a sample of $m_1$ elements. At this stage, information is collected only on the auxiliary factor x, which is then used to approximate the median value ${\Phi }_x$ of the population.

(ii)

A second-phase sub-sample of size $m_2$ ($m_2<m_1$) is taken from the first-phase selection. At this stage, data are collected on both the main study characteristic y and the auxiliary factor x.

Population medians of the study and auxiliary variables are represented by ${\Phi }_y$ and ${\Phi }_x$. From the first-phase data, the median is written as ${\varphi }_x^{\prime }$, while the second-phase produces the estimators ${\widehat{\varphi }}_y$ and ${\widehat{\varphi }}_x$. The probability density functions for these population medians are denoted by $f_y({\Phi }_y)$ and $f_x({\Phi }_x)$. The relationship between ${\Phi }_y$ and ${\Phi }_x$ is quantified by the correlation coefficient ${\rho }_{yx}$, given by:

$$\rho ({\Phi }_y,{\Phi }_x)=4P_{11}(y,x)-1,$$

where $P_{11}$ represents

$$P(y\le {\Phi }_y\cap x\le {\Phi }_x).$$

The following expressions for relative error and corresponding expected values serve as the basis for first-order approximations of biases and mean squared errors:

$${\varphi }_0=\left({\displaystyle \frac{{\widehat{\varphi }}_y-{\Phi }_y}{{\Phi }_y}}\right),{\varphi }_1=\left({\displaystyle \frac{{\widehat{\varphi }}_x-{\Phi }_x}{{\Phi }_x}}\right),{\varphi }_2=\left({\displaystyle \frac{{\acute{\varphi }}_x-{\Phi }_x}{{\Phi }_x}}\right),$$

such that $E\left({\varphi }_i\right)=0$ for $i=0,1,2$.

Moreover,

$$E\left({\varphi }_0^2\right)={\lambda }_1{\Phi }_{C_y}^2,$$

$$E\left({\varphi }_1^2\right)={\lambda }_1{\Phi }_{C_x}^2,$$

$$E\left({\varphi }_2^2\right)={\lambda }_2{\Phi }_{C_x}^2,$$

$$E\left({\varphi }_0{\varphi }_1\right)={\lambda }_1{\Phi }_{C_{yx}}={\rho }_{yx}{\Phi }_{C_y}{\Phi }_{C_x},$$

$$E\left({\varphi }_0{\varphi }_2\right)={\lambda }_2{\Phi }_{C_{yx}}={\rho }_{yx}{\Phi }_{C_y}{\Phi }_{C_x},$$

$$E\left({\varphi }_1{\varphi }_2\right)={\lambda }_2{\Phi }_{C_x}^2,$$

where

$${\Phi }_{C_y}={\displaystyle \frac{1}{{\Phi }_y{f}_y({\Phi }_y)}},$$

$${\Phi }_{C_x}={\displaystyle \frac{1}{{\Phi }_x{f}_x({\Phi }_x)}},$$

are the mathematical representations of the population coefficients of variation for the medians of Y and X, and

$${\lambda }_1={\displaystyle \frac{1}{4}}\left({\displaystyle \frac{N-m_2}{m_2\times N}}\right),$$

$${\lambda }_2={\displaystyle \frac{1}{4}}\left({\displaystyle \frac{N-m_1}{m_1\times N}}\right),$$

$${\lambda }_3={\displaystyle \frac{1}{4}}\left({\displaystyle \frac{m_1-m_2}{m_1\times m_2}}\right).$$

3. Existing Approaches for Median Estimation

The median estimators outlined below are reviewed and will later serve as benchmarks for comparison prior to presenting the proposed class of estimators. These estimators, developed by various researchers, along with their bias, variance, and mean squared error expressions are presented as follows:

The usual sample median estimator and its variance formula proposed by [5] are presented below.

$${\widehat{\varphi }}_{GR}={\widehat{\varphi }}_y$$

and

$$Var({\widehat{\varphi }}_y)={\lambda }_1{\Phi }_y^2{\Phi }_{C_y}^2.$$

(1)

In the context of two-phase sampling, [10] introduced a ratio-based estimator designed to enhance estimation efficiency, defined as:

$${\widehat{\varphi }}_{SA}=\left({\displaystyle \frac{\widehat{{\varphi }_y}}{\widehat{{\varphi }_x}}}\right){\acute{\varphi }}_x.$$

The first-order approximations for the bias and mean squared error (MSE) of ${\widehat{M}}_{SA}$ are expressed as:

$$Bias\left({\widehat{\varphi }}_{SA}\right)\cong {\lambda }_3{\Phi }_y\left({\Phi }_{C_x}^2-{\Phi }_{C_{yx}}\right)$$

(2)

and

$$MSE\left({\widehat{\varphi }}_{SA}\right)\cong {\Phi }_y^2\left[{\lambda }_1{\Phi }_{C_y}^2+{\lambda }_3\left({\Phi }_{C_x}^2-2{\Phi }_{C_{yx}}\right)\right].$$

(3)

According to the formulation in [12], the difference-type estimator ${\widehat{\varphi }}_S$ is defined as:

$${\widehat{\varphi }}_S={\widehat{\varphi }}_y+d_1\left({\acute{\varphi }}_x-{\widehat{\varphi }}_x\right).$$

Using the first-order approximation, the minimum mean squared error expression for ${\widehat{\varphi }}_S$ at the optimum value of $d_1$ is given by:

$$MSE{\left({\widehat{\varphi }}_S\right)}_{min}\cong {\Phi }_y^2{\Phi }_{C_y}^2\left({\lambda }_1-{\lambda }_3{\rho }_{yx}^2\right),$$

(4)

where

$$d_{1\left(opt\right)}={\displaystyle \frac{{\rho }_{yx}{\Phi }_y{\Phi }_{C_y}}{{\Phi }_x{\Phi }_{C_x}}}.$$

Under two-phase sampling, the median forms of the exponential ratio and product estimators introduced by [29] are presented below:

$${\widehat{\varphi }}_{Re}={\widehat{\varphi }}_y\exp \left({\displaystyle \frac{{\acute{\varphi }}_x-{\widehat{\varphi }}_x}{{\acute{\varphi }}_x+{\widehat{\varphi }}_x}}\right)$$

and

$${\widehat{\varphi }}_{Pe}={\widehat{\varphi }}_y\exp \left({\displaystyle \frac{{\widehat{\varphi }}_x-{\acute{\varphi }}_x}{{\acute{\varphi }}_x+{\widehat{\varphi }}_x}}\right).$$

At the first-order level of approximation, the expressions for the biases and mean squared errors of $({\widehat{\varphi }}_{Re},{\widehat{\varphi }}_{Pe})$ are given below:

$$Bias\left({\widehat{\varphi }}_{Re}\right)\cong {\displaystyle \frac{{\lambda }_3}{8}}{\Phi }_y\left(3{\Phi }_{C_x}^2-4{\Phi }_{C_{yx}}\right),$$

(5)

$$Bias\left({\widehat{\varphi }}_{Pe}\right)\cong {\displaystyle \frac{{\lambda }_3}{8}}{\Phi }_y\left(3{\Phi }_{C_x}^2+4{\Phi }_{C_{yx}}\right),$$

(6)

$$MSE\left({\widehat{\varphi }}_{Re}\right)\cong {\displaystyle \frac{{\Phi }_y^2}{4}}\left[4{\lambda }_1{\Phi }_{C_y}^2+{\lambda }_3{\Phi }_{C_x}^2\left(1-4V\right)\right]$$

(7)

and

$$MSE\left({\widehat{\varphi }}_{Pe}\right)\cong {\displaystyle \frac{{\Phi }_y^2}{4}}\left[4{\lambda }_1{\Phi }_{C_y}^2+{\lambda }_3{\Phi }_{C_x}^2\left(1+4V\right)\right],$$

(8)

where

$$V={\displaystyle \frac{{\rho }_{yx}{\Phi }_{C_y}}{{\Phi }_{C_x}}}.$$

The difference-based estimators for median estimation proposed by [9,13] are defined as follows:

$${\widehat{\varphi }}_R=d_2{\widehat{\varphi }}_y+d_3\left({\acute{\varphi }}_x-{\widehat{\varphi }}_x\right),$$

$${\widehat{\varphi }}_{G_1}=\left[d_4{\widehat{\varphi }}_y+d_5\left({\acute{\varphi }}_x-{\widehat{\varphi }}_x\right)\right]\left({\displaystyle \frac{{\acute{\varphi }}_x}{{\widehat{\varphi }}_x}}\right),$$

$${\widehat{\varphi }}_{G_2}=\left[d_6{\widehat{\varphi }}_y+d_7\left({\acute{\varphi }}_x-{\widehat{\varphi }}_x\right)\right]\left({\displaystyle \frac{{\acute{\varphi }}_x-{\widehat{\varphi }}_x}{{\acute{\varphi }}_x+{\widehat{\varphi }}_x}}\right).$$

The optimal values of $d_i$$(i=2,3,\dots ,7)$ yield the following first-order approximation formulas for the minimum biases and mean squared errors of the estimators $({\widehat{\varphi }}_R,{\widehat{\varphi }}_{G_1},{\widehat{\varphi }}_{G_2})$:

$$Bias{\left({\widehat{\varphi }}_R\right)}_{min}\cong -{\Phi }_y\left[{\displaystyle \frac{{\lambda }_1{\Phi }_y^2{\Phi }_{C_x}^2-{\lambda }_3{\Phi }_{C_{yx}}^2}{{\Phi }_x^2\left(1+{\lambda }_1{\Phi }_{C_y}^2\right)-{\lambda }_3{\Phi }_{C_{yx}}^2}}\right],$$

(9)

$$Bias{\left({\widehat{\varphi }}_{G_1}\right)}_{min}\cong {\Phi }_y\left(d_{4(opt)}-1\right)+{\lambda }_3\left[d_{4(opt)}{\Phi }_y\left({\Phi }_{C_x}^2-{\Phi }_{C_{yx}}\right)+d_{5(opt)}{\Phi }_x{\Phi }_{C_x}^2\right],$$

(10)

$$Bias{\left({\widehat{\varphi }}_{G_2}\right)}_{min}\cong {\Phi }_y\left[-1+{\displaystyle \frac{{\lambda }_3}{4}}{\Phi }_{C_x}^2\left\{-1+d_{6(opt)}\left({\displaystyle \frac{{\Phi }_x+8{\rho }_{yx}{\Phi }_y}{{\Phi }_x}}\right)\right\}\right],$$

(11)

$$MSE{\left({\widehat{M}}_R\right)}_{min}\cong {\Phi }_y^2\left[{\displaystyle \frac{{\lambda }_1{\Phi }_{C_y}^2{\Phi }_{C_x}^2-{\lambda }_3{\Phi }_{C_{yx}}^2}{{\Phi }_{C_x}^2\left(1+{\lambda }_1{\Phi }_{C_y}^2\right)-{\lambda }_3{\Phi }_{C_{yx}}^2}}\right],$$

(12)

$$\begin{array}{cc}\hfill MSE{\left({\widehat{\varphi }}_{G_1}\right)}_{min}\cong & Bias{\left({\widehat{\varphi }}_{G_1}\right)}_{min}^2+{\lambda }_1{\Phi }_y^2{d}_{4(\mathrm{opt})}^2{\Phi }_{C_y}^2+{\lambda }_3\left[{\Phi }_{C_x}^2{\left(d_{4(\mathrm{opt})}{\Phi }_y+d_{5(\mathrm{opt})}{\Phi }_x\right)}^2\right.\hfill \\ \hfill & \left.-2d_{4(\mathrm{opt})}{\Phi }_y{\Phi }_{C_{yx}}\left(d_{4(\mathrm{opt})}{\Phi }_y+d_{5(\mathrm{opt})}{\Phi }_x\right)\right]\hfill \end{array}$$

(13)

and

$$MSE{\left({\widehat{\varphi }}_{G_2}\right)}_{min}\cong Bias{\left({\widehat{\varphi }}_{G_2}\right)}_{min}+{\displaystyle \frac{{\lambda }_3}{4}}{d}_{6(opt)}^2{\Phi }_y^2{\Phi }_{C_x}^2,$$

(14)

where

$$d_{2(opt)}={\displaystyle \frac{{\Phi }_{C_x}^2}{{\Phi }_{C_x}^2\left(1+{\lambda }_1{\Phi }_{C_y}^2\right)-{\lambda }_3{\Phi }_{C_{yx}}^2}},$$

$$d_{3(opt)}={\displaystyle \frac{{\Phi }_y{\Phi }_{C_{yx}}}{{\Phi }_x\left[{\Phi }_{C_x}^2\left(1+{\lambda }_1{\Phi }_{C_y}^2\right)-{\lambda }_3{\Phi }_{C_{yx}}^2\right]}},$$

$$d_{4(opt)}=\left[{\displaystyle \frac{{\Phi }_{C_x}^2}{{\Phi }_{C_x}^2\left(1+{\lambda }_1{\Phi }_{C_y}^2\left\{1+{\lambda }_3{\Phi }_{C_x}^2\right\}\right)+{\lambda }_3{\Phi }_{C_{yx}}^2\left(1+{\Phi }_{C_x}^2\right)}}\right],$$

$$d_{5(opt)}={\Phi }_y\left[{\displaystyle \frac{{\Phi }_{C_x}^2\left({\lambda }_1{\Phi }_{C_y}^2-1\right)+{\Phi }_{C_{yx}}\left(1-{\lambda }_3{\Phi }_{C_{yx}}\right)}{{\Phi }_{C_x}^2\left(1+{\lambda }_1{\Phi }_{C_y}^2\left\{1+{\lambda }_3{\Phi }_{C_x}^2\right\}\right)+{\lambda }_3{\Phi }_{C_{yx}}^2\left(1+{\Phi }_{C_x}^2\right)}}\right],$$

$$d_{6(opt)}={\displaystyle \frac{1}{8}}\left[{\displaystyle \frac{8-{\lambda }_2{\Phi }_{C_x}^2}{1+{\lambda }_1{\Phi }_{C_x}^2\left(1-{\rho }_{yx}^2\right)}}\right],$$

and

$$d_{7\left(opt\right)}={\displaystyle \frac{{\Phi }_y}{{\Phi }_x}}\left[{\displaystyle \frac{1}{2}}+d_{6\left(opt\right)}\left({\displaystyle \frac{{\rho }_{yx}{\Phi }_y}{{\Phi }_x}}\right)-1\right].$$

4. Proposed Class of Robust Median Estimators

Inspired by the modified forms of estimators proposed by employing the methodologies outlined in [26,27,28], we introduce a generalized double exponential class of median estimators for two-phase sampling. This approach utilizes various transformations of the auxiliary variable to estimate the finite population median. The new family of estimators is presented below:

$${\widehat{\varphi }}_V={\widehat{\varphi }}_y\exp \left[{\displaystyle \frac{{\tau }_1\left({\widehat{\varphi }}_x-{\acute{\varphi }}_x\right)}{{\tau }_1\left({\acute{\varphi }}_x+{\widehat{\varphi }}_x\right)+2{\tau }_2}}\right]\exp \left[{\displaystyle \frac{{\tau }_3\left({\acute{\varphi }}_x-{\widehat{\varphi }}_x\right)}{{\tau }_3\left({\acute{\varphi }}_x+{\widehat{\varphi }}_x\right)+2{\tau }_4}}\right],$$

(15)

where the symbols ${\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4$ denote known population quantities related to the auxiliary variable X. In practice, they are computed from the first-phase sample where X is observed, but for theoretical derivations they may be computed from the full population. Starting from Equation (15), we introduce new estimators by selecting different combinations of these population quantities; the specific settings appear in

Table 1. New suggested transformations for proposed estimators under two-phase sampling.

Estimator	${\mathit{\tau }}_1$	${\mathit{\tau }}_2$	${\mathit{\tau }}_3$	${\mathit{\tau }}_4$
${\widehat{\varphi }}_{V_1}$	Hodges–Lehmann(X)	GMD(X)	1	Winsor_range10%(X)
${\widehat{\varphi }}_{V_2}$	Trim–Mean10%(X)	Winsorized Mean10%(X)	1	MAD(X)
${\widehat{\varphi }}_{V_3}$	$Q_3-Q_1$	Skew_adj(X)	1	CV(X)
${\widehat{\varphi }}_{V_4}$	Median_ratio$(Q_3/Q_1)$	1	1	Bowley_skewness(X)
${\widehat{\varphi }}_{V_5}$	$\log (1+HL(X))$	$\log (1+GMD(X))$	1	$\log (1+IQR)$
${\widehat{\varphi }}_{V_6}$	$\sqrt{Q_1·Q_3}$	$Q_3-Q_1$	1	$X_{90\%}-X_{10\%}$
${\widehat{\varphi }}_{V_7}$	Hodges–Lehmann$(X)$	MAD(X)	1	Skew_adj(X)
${\widehat{\varphi }}_{V_8}$	$1/(1+CV(X))$	$1/(1+Kurtosis(X))$	1	$Q_3/Q_2$

.

The specific choices of ${\tau }_1$–${\tau }_4$ in Table 1 are motivated by their robustness and ability to capture essential features of the auxiliary variable X. For instance, measures such as the Hodges–Lehmann estimator, trimmed mean, and Winsorized mean provide central tendency estimates that are less sensitive to outliers, while quantities like the interquartile range, median absolute deviation (MAD), and skewness adjustments reflect the spread and asymmetry of the distribution. By combining these transformations in the proposed exponential ratio–product framework, the estimators utilize both location and variability information from X, enhancing efficiency and robustness in the two-phase sampling design.

• Hodges–Lehmann:

  $$HL(X)=\mathrm{median}\left({\displaystyle \frac{X_i+X_j}{2}}:1\le i\le j\le m_1\right),$$
• Gini Mean Difference:

  $$GMD(X)={\displaystyle \frac{1}{m_1(m_1-1)}}\sum _{1\le i<j\le m_1}|X_i-X_j|,$$
• Trimmed Mean (10%): Let $k_1=⌊0.10m_1⌋.$ Then

  $$T{M}_{10\%}(X)={\displaystyle \frac{1}{m_1-2k}}\sum _{i=k+1}^{m_1-k}{X}_{(i)},k=\lfloor 0.1m_1\rfloor ,$$
• Winsorized Mean (10%): Let $k_1=⌊0.10m_1⌋.$ Then

  $$W{M}_{10\%}(X)={\displaystyle \frac{1}{m_1}}\left(k_1{X}_{(k_1+1)}+\sum _{i=k_1+1}^{m_1-k_1}{X}_{(i)}+k_1{X}_{(m_1-k_1)}\right),$$
• Median ratio:

  $$MR(X)={\displaystyle \frac{Q_3}{Q_1}},$$
• Bowley Skewness:

  $$BSkew(X)={\displaystyle \frac{Q_3+Q_1-2Q_2}{Q_3-Q_1}},$$
• Inter quartile range:

  $$QR(X)=Q_3-Q_1,$$
• Geometric Quartile Mean:

  $$\sqrt{Q_1·Q_3},$$
• Quartile Deviation:

  $$QD(X)={\displaystyle \frac{Q_3-Q_1}{2}},$$
• 10–90% Range:

  $$R_{10-90}(X)=X_{(0.90m_1)}-X_{(0.10m_1)},$$
• Median Absolute Deviation (MAD):

  $$MAD(X)=\mathrm{median}(|X_i-Q_2|),i=1,\dots ,m_1,$$
• Skewness Adjusted:

  $$Skew\_adj(X)={\displaystyle \frac{Q_3-2Q_2+Q_1}{Q_3-Q_1}},$$
• Coefficient of Variation:

  $$CV(X)={\displaystyle \frac{S_X}{Q_2}},$$
• Moors’ kurtosis: Let $Q_p$ be the sample quantile of order $p.$ It is simple, bounded, and robust, making it a suitable choice when the target is the median. Using octiles $Q_{k/8}$:

  $$M_K={\displaystyle \frac{(Q_{7/8}-Q_{5/8})+(Q_{3/8}-Q_{1/8})}{Q_{6/8}-Q_{2/8}}}.$$

Theorem 1 provides the theoretical foundation for the proposed median-based estimators under two-phase sampling. It establishes key properties, such as bias and mean squared error expressions, which are essential for understanding their efficiency and reliability. Including this theorem helps to explain why the proposed estimators perform better under different population distributions and correlation scenarios.

Theorem 1.

A two-phase sampling scheme is considered in which ${\widehat{\varphi }}_V$ is defined as an exponential ratio–product type estimator for the finite population median ${\Phi }_y$. The corresponding bias and mean squared error formulations are given below:

$$\begin{array}{c}Bias\left({\widehat{\varphi }}_V\right)\cong {\Phi }_y\left[{\displaystyle \frac{1}{2}}\left(r_1-r_2\right){\lambda }_3{\Phi }_{C_{yx}}-{\displaystyle \frac{1}{8}}\left(r_1^2-r_2^2-2r_1{r}_2\right){\lambda }_3{\Phi }_{C_x}^2\right]\hfill \end{array}$$

and

$$\begin{array}{c}MSE\left({\widehat{\varphi }}_V\right)\cong {\Phi }_y^2\left[{\lambda }_1{\Phi }_{C_y}^2+{\displaystyle \frac{1}{4}}{\lambda }_3{\Phi }_{C_x}^2\left(r_1^2+r_2^2-2r_1{r}_2\right)+{\lambda }_3{\Phi }_{C_{yx}}\left(r_1-r_2\right)\right].\hfill \end{array}$$

Proof. 

The detailed derivation is given in Appendix A. □

5. Theoretical Comparison with Existing Estimators

In this section, we demonstrate that the proposed estimator, denoted by ${\widehat{\varphi }}_V$, consistently outperforms each of the existing estimators presented in Section 2. The superiority of ${\widehat{\varphi }}_V$ is established through a set of explicit inequalities, which highlight its improved efficiency and reduced error in comparison. These inequalities not only provide a rigorous theoretical justification but also confirm the practical advantages of adopting ${\widehat{\varphi }}_V$ over its counterparts.

(i)

By comparing the mean squared error of the newly proposed family of estimators (A4) with the variance of the sample median (1), we arrive at the following condition:

$$MSE({\widehat{\varphi }}_y)>MSE\left({\widehat{\varphi }}_V\right)\mathrm{if}$$

$${\displaystyle \frac{1}{4}}{\Phi }_{C_x}^2\left(r_1^2+r_2^2-2r_1{r}_2\right)+{\Phi }_{C_{yx}}(r_1-r_2)>0.$$

(ii)

By comparing Equation (A4) for the proposed family of estimators with the MSE in Equation (3), we obtain the condition stated below:

$$MSE({\widehat{\varphi }}_{SA})>MSE\left({\widehat{\varphi }}_V\right)\mathrm{if}$$

$${\Phi }_{C_x}^2\left(r_1^2+r_2^2-2r_1{r}_2\right)+4{\Phi }_{C_{yx}}\left(2+r_1-r_2\right)<4{\Phi }_{C_x}^2.$$

(iii)

Examining the mean squared error of the proposed estimators in Equation (A4) against the MSE in Equation (4) leads to the following condition:

$$MSE{({\widehat{\varphi }}_S)}_{min}>MSE\left({\widehat{\varphi }}_V\right)\mathrm{if}$$

$${\Phi }_{C_x}^2\left(r_1^2+r_2^2-2r_1{r}_2\right)+4{\varphi }_{C_{yx}}(r_1-r_2)>4{\Phi }_{C_y}^2{\rho }_{yx}^2.$$

(iv)

Evaluating the MSE of the proposed family of estimators (A4) in relation to the expression in Equation (7) provides the following condition, which is important for establishing their comparative efficiency:

$$MSE({\widehat{\varphi }}_{Re})>MSE\left({\widehat{\varphi }}_V\right)\mathrm{if}$$

$${\Phi }_{C_x}^2\left(1-4V\right)>{\Phi }_{C_x}^2\left(r_1^2+r_2^2-2r_1{r}_2\right)+4{\Phi }_{C_{yx}}(r_1-r_2).$$

(v)

A comparison of Equation (A4) for the proposed family of estimators with the MSE in Equation (8) yields the condition below:

$$MSE({\widehat{\varphi }}_{Pe})>MSE\left({\widehat{\varphi }}_V\right)\mathrm{if}$$

$${\varphi }_{C_x}^2\left(1+4V\right)>{\Phi }_{C_x}^2\left(r_1^2+r_2^2-2r_1{r}_2\right)+4{\Phi }_{C_{yx}}(r_1-r_2).$$

(vi)

By comparing the MSE expression of the proposed family of estimators in Equation (A4) with the MSE of the sample median in Equation (12), the following condition is derived.

$$MSE{({\widehat{\varphi }}_R)}_{min}>MSE\left({\widehat{\varphi }}_V\right)\mathrm{if}$$

$${\displaystyle \frac{1}{4}}{\Phi }_{C_x}^2\left(r_1^2+r_2^2-2r_1{r}_2\right)+{\Phi }_{C_{yx}}(r_1-r_2)>{\displaystyle \frac{{\Phi }_{C_{yx}}^2}{{\Phi }_{C_x}^2\left(1+{\lambda }_1{\Phi }_{C_y}^2\right)-{\lambda }_3{\Phi }_{C_{yx}}^2}}.$$

(vii)

By comparing the MSE of the newly developed family of estimators (A4) with the MSE in equation ${\widehat{\varphi }}_{G_1}$, the following condition is obtained, capturing their relative performance:

$$MSE{({\widehat{\varphi }}_{G_1})}_{min}>MSE\left({\widehat{\varphi }}_V\right)\mathrm{if}$$

$${\displaystyle \frac{B_{G_1}}{{\lambda }_3}}+{\mathrm{\Psi }}_{G_1}>\frac{1}{4}{\Phi }_{C_x}^2\left(r_1^2+r_2^2-2r_1{r}_2\right)+{\Phi }_{C_{yx}}(r_1-r_2),$$

where

$${\mathrm{\Psi }}_{G_1}={\Phi }_{C_x}^2{\left(d_{4(opt)}{\Phi }_y+d_{5(opt)}{\Phi }_x\right)}^2-2d_{4(opt)}{\Phi }_y{\Phi }_{C_{yx}}\left(d_{4(opt)}{\Phi }_y+d_{5(opt)}{\Phi }_x\right)$$

and

$$B_{G_1}={\displaystyle \frac{Bias{\left({\widehat{\varphi }}_{G_1}\right)}_{min}^2}{{\Phi }_y^2}}+{\lambda }_1(d_{4(opt)}^2-1){\Phi }_{C_y}^2.$$

(viii)

Evaluating the MSE of the proposed family of estimators (A4) relative to the MSE in Equation (14) leads to a specific condition, which highlights their comparative performance:

$$MSE{({\widehat{\Phi }}_{G_2})}_{min}>MSE\left({\widehat{\varphi }}_V\right)\mathrm{if}$$

$${\displaystyle \frac{B_{G_2}}{{\lambda }_3}}+{\displaystyle \frac{1}{4}}{d}_{6(opt)}^2{\Phi }_{C_x}^2-{\displaystyle \frac{{\lambda }_1}{{\lambda }_3}}{\Phi }_{C_y}^2>{\displaystyle \frac{1}{4}}{\Phi }_{C_x}^2\left(r_1^2+r_2^2-2r_1{r}_2\right)+{\Phi }_{C_{yx}}(r_1-r_2),$$

where

$$B_{G_2}={\displaystyle \frac{Bias{\left({\widehat{\varphi }}_{G_2}\right)}_{min}}{{\Phi }_y^2}}.$$

6. Results and Discussion

In this section, the efficiency of the proposed family of estimators is evaluated in relation to existing methods. For this purpose, five distinct simulated populations are constructed based on appropriate positively skewed probability distributions. Furthermore, three practical datasets are employed to validate and support the empirical performance of the proposed estimators.

6.1. Monte Carlo Simulation Study

The most appropriate distribution for median estimation is determined by the nature of the dataset and the distribution’s properties. Because the median resists the influence of skewness, extreme observations, and non-normal patterns, it becomes particularly advantageous in such contexts. In this study, the variable X is generated from one of the five distributions described below.

• Population 1: The random variable X follows a Cauchy distribution characterized by parameters $t_1=18$ and $t_2=11.$ Since the Cauchy distribution does not have a defined mean or variance, the theoretical population correlation with Y is undefined. For our simulation, we used a correlation of ${\rho }_{yx}=-0.53,$ which refers to the sample correlation calculated from the generated data set and reflects the observed inverse association between X and $Y.$
• Population 2: X follows a uniform distribution bounded between 16 and 22, and is statistically independent of Y in terms of correlation (${\rho }_{yx}=0$).
• Population 3: The variable X is modeled using an exponential distribution with a strong skew, where the rate parameter is $\alpha =0.5$. Its correlation with Y is positive and equals ${\rho }_{yx}=0.85$.
• Population 4: The random variable X is distributed as a gamma law with shape $a_1=14$ and scale $a_2=8$. Its dependence on Y is positive, with ${\rho }_{yx}=0.67$.
• Population 5: The variable X is assumed to follow a log-normal distribution with mild skewness, defined by parameters ${\mu }_1=7$ and ${\mu }_2=2$. Its correlation with Y is $0.59$.

6.2. Simulation Steps Under Two-Phase Sampling

The percent relative efficiencies (PREs) of both the proposed and existing estimators were examined for each distribution and correlation scenario defined above. All computations were performed in R software (latest v. 4.4.0) to assess their robustness and efficiency. The simulation procedure consists of the following steps:

• Population setup: Generate the study population by selecting one of the five distributions for the auxiliary variable X (Cauchy, Uniform, Exponential, Gamma, or Log-normal) with their specified parameters, where $N=1400.$ For each unit, the corresponding study variable Y is obtained from

  $$Y={\rho }_{yx}\times X+e,e\sim N(0,1).$$
• First-phase sampling: From the generated population of size N, draw a simple random sample of size $m_1$. At this stage, only the values of the auxiliary variable X are recorded.
• Second-Phase Sampling: From the first-phase sample, select a subsample of size $m_2$$(m_2<m_1)$. For the units in this subsample, observe both the auxiliary variable X and the study variable Y.
• Estimator formation: Using the information from phase-I and the paired $(X,Y)$ observations from phase II, construct the proposed estimators based on the sample median.
• Repetition: Repeat the above process a large number of times (for instance, 25,000 iterations) to assess the sampling behavior of the estimators.
• Performance assessment: For each estimator, mean squared error (MSE), relative efficiency, and, when applicable, the coverage probability of confidence intervals.
• Comparison across populations: Finally, compare the results across the five populations to evaluate how the estimators perform under heavy-tailed, skewed, and moderately correlated settings.

The following formulas are used to calculate the MSEs and PREs:

$$MSE{({\widehat{\varphi }}_t)}_{min}={\displaystyle \frac{{\sum }_{s=1}^{25000}{\left({\widehat{\varphi }}_{ts}-{\Phi }_y\right)}^2}{25000}}$$

and

$$PRE={\displaystyle \frac{MSE\left({\widehat{\varphi }}_y\right)}{MSE{({\widehat{\varphi }}_t)}_{min}}}\times 100,$$

where t ($t=y,SA,S,Re,Pe,R,G_1,G_2,V_1,V_2,\dots ,V_8$).

6.3. Application to Survey Data

This part of the paper provides an empirical evaluation based on three real population datasets, with their details outlined below. The MSEs for the existing estimators and the proposed estimators of the population median ${\widehat{\Phi }}_y$ of y are shown in

Table 2. A statistical summary of the various datasets.

Symbols	Set 1 (Statistic)	Set 2 (Statistic)	Set 3 (Statistic)
N	36	36	36
${\Phi }_x$	168.5	1016.5	171.5
${\Phi }_y$	10,484.5	115,223.5	10,494
$f_x({\Phi }_x)$	0.00015	0.00022	0.00019
$f_x({\Phi }_y)$	0.00016	0.00024	0.00021
$HL$	199.50	1027	201.25
$GMD$	192.22	441.95	396.49
$T{M}_{10\%}$	235.50	1019.13	236.00
$W{M}_{10\%}$	270.67	1031.61	270.67
$Q_1$	89.5	729	87.5
$Q_3$	347	1242.25	352.5
$MR$	3.88	1.703	4.03
$BSkew$	0.386	−0.1225	0.366
$QR$	257.5	512.25	175.62
$QD$	128.75	256.125	265
$R_{10-90}$	751	844	762.5
$MAD$	92.50	289	99
$Skew\_adj$	0.386	−0.1225	0.366
$CV$	2.60	0.396	2.64
$M_K$	2.10	1.125	2.18
${\rho }_{yx}$	0.912	0.796	0.519
${\lambda }_1$	0.0107	0.0242	0.0288
${\lambda }_2$	0.0035	0.0123	0.0140
${\lambda }_3$	0.00072	0.0119	0.0148

,

Table 3. A comparison of PRE across five populations.

Estimator	Pop1	Pop2	Pop3	Pop4	Pop5
${\widehat{\varphi }}_{GR}$	100.00	100.00	100.00	100.00	100.00
${\widehat{\varphi }}_{SA}$	196.15	169.71	95.99	190.70	151.17
${\widehat{\varphi }}_S$	164.68	159.12	99.42	232.71	139.17
${\widehat{\varphi }}_{Re}$	160.64	169.87	114.34	159.98	193.08
${\widehat{\varphi }}_{Pe}$	60.91	90.10	72.55	60.59	47.22
${\widehat{\varphi }}_R$	199.77	244.77	127.85	242.25	200.80
${\widehat{\varphi }}_{G_1}$	224.02	199.57	154.70	252.88	230.97
${\widehat{\varphi }}_{G_2}$	200.79	238.59	143.50	250.09	255.57
${\widehat{\varphi }}_{V_1}$	274.81	300.02	191.82	281.45	261.83
${\widehat{\varphi }}_{V_2}$	284.20	310.00	200.71	292.62	274.32
${\widehat{\varphi }}_{V_3}$	284.42	300.00	188.92	299.87	299.23
${\widehat{\varphi }}_{V_4}$	300.65	319.99	199.79	200.30	259.98
${\widehat{\varphi }}_{V_5}$	296.34	280.01	179.73	278.66	269.67
${\widehat{\varphi }}_{V_6}$	272.02	315.02	254.16	281.47	251.80
${\widehat{\varphi }}_{V_7}$	301.87	325.00	239.22	260.07	270.99
${\widehat{\varphi }}_{V_8}$	294.46	276.00	205.80	255.72	310.09

and

Table 4. PRE values among real data sets.

Estimator	Set 1	Set 2	Set 3
${\widehat{\varphi }}_y$	100.00	100.00	100.00
${\widehat{\varphi }}_{SA}$	134.54	123.16	143.53
${\widehat{\varphi }}_S$	140.82	145.87	155.98
${\widehat{\varphi }}_{Re}$	130.74	142.56	175.06
${\widehat{\varphi }}_{Pe}$	95.62	65.92	86.49
${\widehat{\varphi }}_R$	206.36	245.20	216.71
${\widehat{\varphi }}_{G_1}$	239.47	252.38	274.63
${\widehat{\varphi }}_{G_2}$	227.10	285.95	251.85
${\widehat{\varphi }}_{V_1}$	251.88	310.43	290.91
${\widehat{\varphi }}_{V_2}$	258.79	315.91	301.07
${\widehat{\varphi }}_{V_3}$	292.68	298.08	299.37
${\widehat{\varphi }}_{V_4}$	299.47	302.83	308.74
${\widehat{\varphi }}_{V_5}$	286.98	299.55	284.46
${\widehat{\varphi }}_{V_6}$	261.80	290.24	310.50
${\widehat{\varphi }}_{V_7}$	257.94	331.82	334.29
${\widehat{\varphi }}_{V_8}$	297.72	352.29	321.82

.

Population 1.

We use data from the 2013 edition of Punjab Development Statistics [30] (p. 226), which records the number of registered factories in 2010 and their corresponding employment across different districts and divisions. This dataset serves as a practical benchmark for comparing the proposed estimators with existing approaches. The Pakistan Bureau of Statistics website provides a download link: https://www.pbs.gov.pk/content/microdata (accessed on 27 August 2025).

• Y: Denotes the average number of employees per district in 2010, reflecting workforce distribution across regions.
• X: Represents the total value of factory registrations in the same year, indicating the scale of industrial activity in each district.

Population 2.

We use data from the 2014 edition of Punjab Development Statistics [31] (p. 135) to study a real finite population of gender-specific enrollment in government primary and middle schools, capturing both boys’ and girls’ enrollment across different districts. This dataset provides a comprehensive view of the distribution of students, allowing for an empirical evaluation of the proposed estimators under realistic population conditions. The Pakistan Bureau of Statistics website provides access to the microdata at: https://www.pbs.gov.pk/content/microdata (accessed on 27 August 2025).

• Y: Aggregate number of students registered in all schools during the 2012–2013 academic session.
• X: Total number of government-managed middle school institutions recorded for the 2012–2013 academic session.

Population 3.

We consider a real finite population using data from the 2013 edition of Punjab Development Statistics [30] (p. 226). The dataset provides detailed information on the number of registered factories and employment levels across various districts and divisions, including both employment distribution and factory registration counts for the year 2012. We use this dataset to apply and evaluate the performance of our proposed estimators, allowing us to examine their effectiveness under realistic population conditions. It is accessible for download on the Pakistan Bureau of Statistics website using the following URL: https://www.pbs.gov.pk/content/microdata (accessed on 27 August 2025).

• Y: Aggregate employment across all industrial sectors in each district.
• X: Fraction of registered factories in the corresponding district for the year 2012.

The datasets are summarized in Table 2, and the percent relative efficiencies of the proposed and existing estimators, derived from both simulated and real data, are displayed in Table 3 and Table 4. These comparisons emphasize the practical effectiveness of the proposed methods, confirming their improved precision over conventional estimators.

6.4. Analysis of Simulation and Empirical Results

Results show that the proposed transformation-based estimators outperform existing methods by attaining higher PRE values in both simulated and real-life datasets. Their ability to remain accurate under symmetric, skewed, and heavy-tailed distributions further demonstrates their robustness. The estimators consistently outperform traditional methods, particularly when data contain outliers or deviate from normality, making them highly adaptable to practical situations. They also remain stable across different sample sizes, ensuring reliable results even for small or finite populations. Table 3 and Table 4 summarize these findings and emphasize the consistent superiority of the proposed methods.

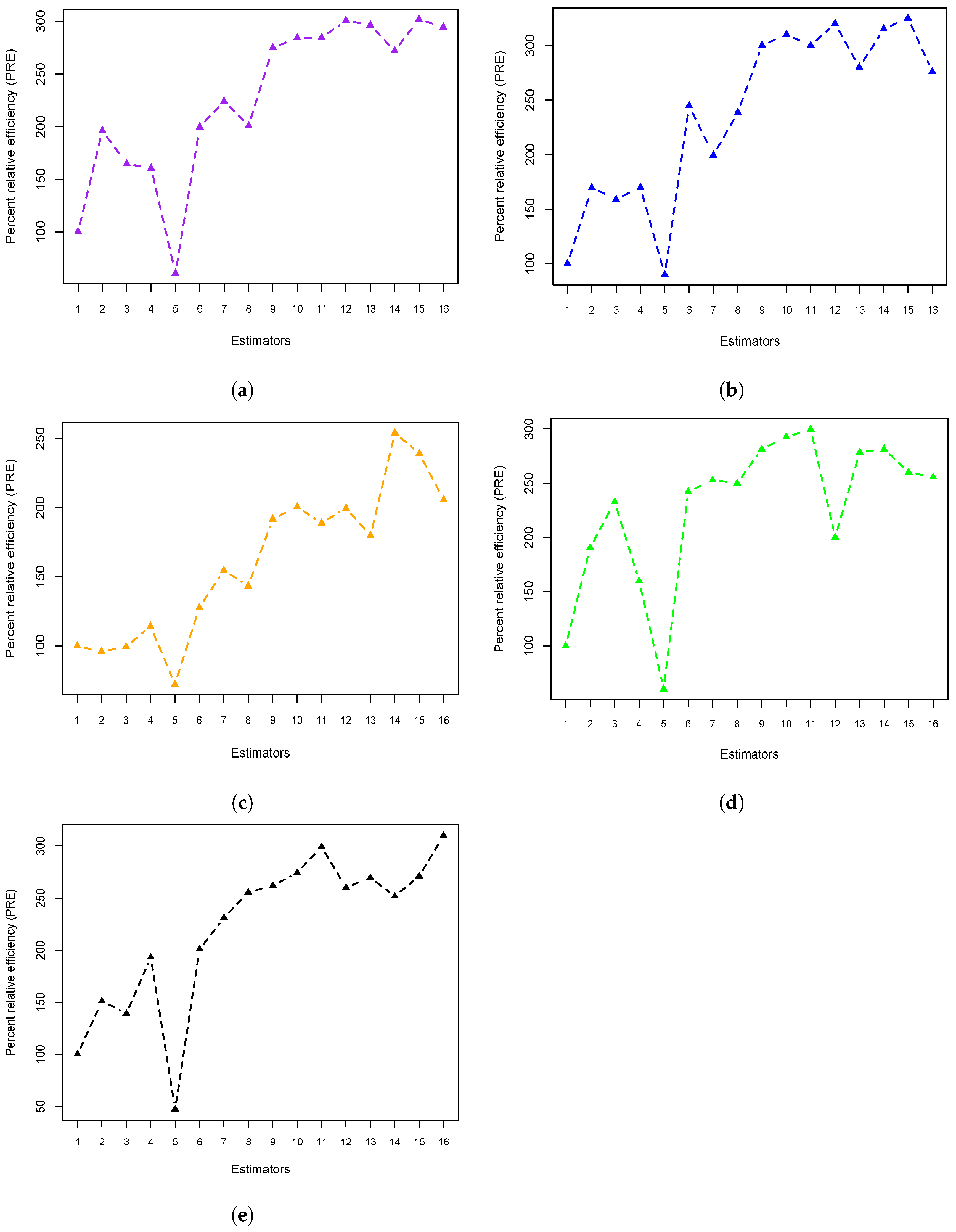
• Performance on simulated data: Table 3 provides strong evidence that the proposed estimators consistently deliver higher percent relative efficiency (PRE) than conventional approaches. This advantage is observed across a broad range of distributions including all five different cases. The graphical representation in Figure 1 further illustrates this pattern, where the proposed estimators are repeatedly identified as the most efficient, appearing across all scenarios. Such findings confirm their robustness under diverse distributional conditions.
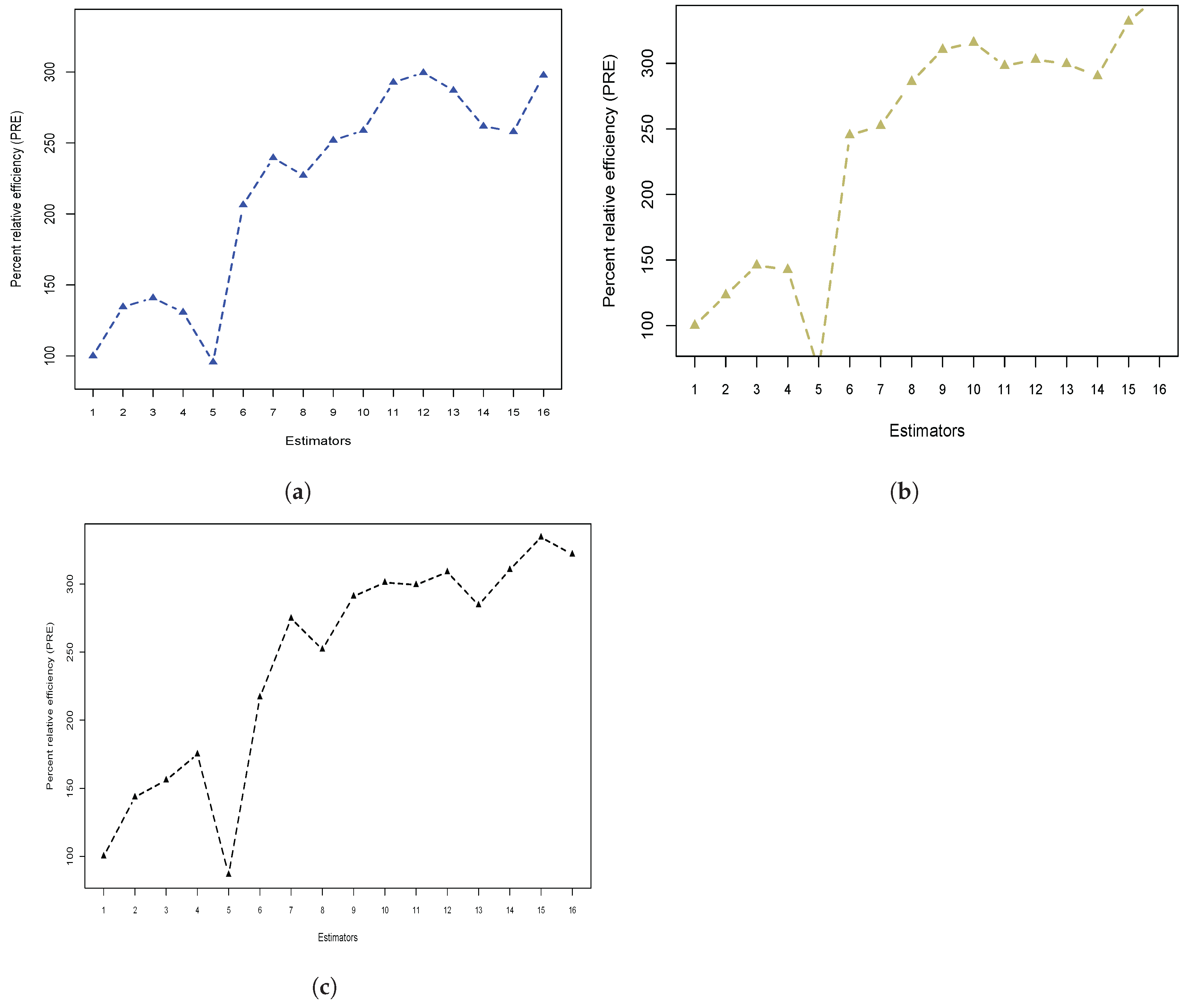
• Application to real data sets: The benefits of the proposed estimators are not confined to artificial populations; they extend convincingly to real-world data. Table 4 summarizes their performance across socio-economic and environmental populations, where they consistently achieve higher PRE values than their traditional counterparts. This trend is echoed in Figure 2, which clearly highlights the superiority of the proposed methods over exponential and difference-type estimators in all three populations considered. These results underscore the practical reliability of the proposed class of estimators when applied to empirical datasets.
• Impact of correlation and sample size: Another important aspect of efficiency is its stability across varying survey conditions. Figure 1 and Figure 2 indicate that the proposed estimators maintain their effectiveness regardless of the correlation level between the study and auxiliary variables. Complementary evidence from Table 3 and Table 4 shows that efficiency does not deteriorate even when the second-phase sample size $m_2$ is much smaller than the first-phase size $m_1.$ This property is particularly valuable for practitioners conducting surveys with limited resources, as it ensures that reliable results can still be obtained under constrained sampling conditions.

7. Conclusions and Research Directions

This study presents a transformed class of median estimators developed for two-phase sampling when auxiliary information is expensive to obtain. Applying transformation strategies, the proposed estimators demonstrate clear improvements in efficiency and precision compared with conventional approaches.

Explicit expressions for bias and mean squared error were obtained, together with conditions under which these estimators consistently dominate classical counterparts. Theoretical properties were further confirmed through Monte Carlo experiments across different distributions and real survey applications, where the proposed methods consistently recorded higher PRE values.

Based on the PRE values reported in Table 3 and Table 4, the ${\widehat{\varphi }}_{V_i}$ estimators consistently demonstrate superior performance across both artificial and real data sets. Specifically, for the artificial populations, the top three ${\widehat{\varphi }}_{V_i}$ estimators are ${\widehat{\varphi }}_{V_7}$, ${\widehat{\varphi }}_{V_3}$, and ${\widehat{\varphi }}_{V_6}$, as they exhibit the highest average PRE values across the five populations. For the real data sets, the leading estimators are ${\widehat{\varphi }}_{V_8}$, ${\widehat{\varphi }}_{V_7}$, and ${\widehat{\varphi }}_{V_4}$, which consistently achieve the largest PRE values across all three data sets. These results indicate that these ${\widehat{\varphi }}_{V_i}$ estimators provide the most efficient and reliable performance for the populations considered.

This study lays a strong foundation for robust median estimation under two-phase sampling, but several directions remain for future work. A natural extension is adapting these transformation-based estimators to stratified and multistage sampling, where auxiliary information is partly available at different levels. The proposed median-based estimators align with advances in robust and non-parametric statistics. By utilizing auxiliary information in a manner resistant to skewness and outliers, these estimators complement existing robust methods and offer practical value when standard parametric assumptions do not hold. Using multiple auxiliary variables together may also improve stability, especially in surveys where no single auxiliary measure explains population variability well.

Another direction lies in developing variance estimation procedures and confidence interval construction for the proposed estimators, whose applicability in practical survey settings can be expanded. Additionally, exploring their performance under nonresponse, measurement error, or incomplete auxiliary data can strengthen their robustness for real-life applications.