Extremal Trees for Logarithmic VDB Topological Indices

Abstract

Vertex-degree-based (VDB) topological indices have been applied in the study of molecular structures and chemical properties. At present, the exponential VDB index has been studied extensively. Naturally, we began to consider the logarithmic VDB index $ln{\mathcal{T}}_f$. In this paper, we first discuss the necessity of a logarithmic VDB index, and then present sufficient conditions so that $P_n$ and $S_n$ are the only trees with the smallest and greatest values of $ln{\mathcal{T}}_f\left(T\right)$. As applications, the minimal and maximal trees of some logarithmic VDB indices are determined. Through our work, we found that the logarithmic VDB index $ln{\mathcal{T}}_f$ has excellent discriminability, but the relevant results are not completely opposite to the exponential VDB index. The study of logarithmic VDB indices is an interesting but difficult task that requires further resolution.

1. Introduction

Topological indices (or chemical indices) have a significant role in studying the structures and properties of molecular compounds. Related studies have shown that topological indices are closely related to physico-chemical properties or biological activity [1,2]. Vertex-degree-based (VDB) topological indices, as an important type of topological index, have long been considered and applied in QSPR/QSAR research [3,4]. Due to their significance in application, much mathematical and chemical literature for the extremal values and extremal graphs have been published, and they are often considered and verified to have some excellent chemical properties. For relevant research, see [5,6,7].

Throughout the whole paper, the considered graphs are simple, connected and undirected. For a graph G with order n, the sets of vertices and edges are denoted by $V\left(G\right)$ and $E\left(G\right)$, respectively. We use $d_G\left(u\right)$, or $d\left(u\right)$ for short, to represent the degree of vertex v. For a vertex $v\in G$, if $d_G\left(v\right)=1$, we say that v is pendent. If the edge $\left\{uv\right\}\in E\left(G\right)$, then the two vertices u and v are adjacent. The vertex set adjacent to v is known as its neighbor, which is denoted by $N_G\left(v\right)$ or by $N\left(v\right)$ for short. If $\left\{uv\right\}\notin E\left(G\right)$, the graph $G+\left\{uv\right\}$ represents the resulting graph by adding the edge $\left\{uv\right\}$ from G. Meanwhile, we use $G-\left\{uv\right\}$, which represents the resulting graph by deleting the edge $\left\{uv\right\}$ in G for the edge $\left\{uv\right\}\in E\left(G\right)$. Let $P_n$, $S_n$, and ${\mathbb{T}}_n$ denote the path, star, and set of trees with order n, respectively. We use $S_{r,n-r}$ to represent a double star with the degrees of the two centers being r and $n-r$, where $2\le r\le \lfloor {\displaystyle \frac{n}{2}}\rfloor$. For more notations and symbols, the readers can refer to

Table 1. A list of acronyms and symbols.

Symbol	Explanation
$d\left(x\right)$	Degree of vertex x
$N\left(x\right)$	Neighbors of vertex x
$P_n$	Path with order n
$S_n$	Star with order n
$S_{r,n-r}$	Double star with two centers
${\mathbb{T}}_n$	Set of trees with order n
${\mathcal{T}}_f$	VDB (vertex-degree-based) index
$e^{{\mathcal{T}}_f}$	The exponential of a VDB index
$ln{\mathcal{T}}_f$	The logarithm of a VDB index
$f(x,y)$	A real symmetric function
$\beta (x,y)$	$=e^{f(x,y)}$
$\gamma (x,y)$	$=lnf(x,y)$
${\displaystyle \frac{\partial f}{\partial x}}$	Partial derivative
${\displaystyle \frac{{\partial }^{2}f}{\partial x^2}}$	Second partial derivative

at the end of this section.

A general vertex-degree-based (VDB for short) index of G is defined as

$${\mathcal{T}}_f={\mathcal{T}}_f\left(G\right)=\sum _{\left\{uv\right\}\in E\left(G\right)}f(d\left(u\right),d\left(v\right)),$$

where $f(x,y)$ is a real symmetric function for $x,y\ge 1$. To learn more about the relevant results, the readers can refer to [8,9,10]. In particular, in [8], Gutman collected a few significant and well-investigated VDB topological indices.

In 2019, In [11], Rada first defined the exponential of ${\mathcal{T}}_f$ as

$$e^{{\mathcal{T}}_f}=e^{{\mathcal{T}}_f}\left(G\right)=\sum _{\left\{uv\right\}\in E\left(G\right)}{e}^{f\left(d\right(u),d(v\left)\right)} = \sum _{\left\{uv\right\}\in E\left(G\right)}\beta (d\left(u\right),d\left(v\right)),$$

where $f(x,y)=f(y,x)$ is a binary function for $x,y\ge 1$.

The study of VDB topological indices has attracted increasing attention, especially in order to determine the extremal values of ${\mathcal{T}}_f$ or $e^{{\mathcal{T}}_f}$ for some special types of graphs. The authors of [12] provide a good method to obtain whether the star $S_n$ or path $P_n$ are the extremal trees for VDB indices. Additionally, if $f(x,y)$ is concave upwards and increasing on $x>0$, the maximum trees of $T_f$ were determined in [13]. In [14], Gao provided some conditions for binary function $f(x,y)$. If $f(x,y)$ matches some conditions, then the necessary and sufficient conditions for a chemical tree being the largest ${\mathcal{T}}_f$ are attained. Very recently, the authors of [15] gave sufficient conditions for $P_n$ being the only smallest $e^{{\mathcal{T}}_f}$ tree, and the sufficient conditions for $S_n$ being the only largest $e^{{\mathcal{T}}_f}$ tree. For research on ${\mathcal{T}}_f$ or $e^{{\mathcal{T}}_f}$, the readers can refer to [16,17,18,19].

2. Necessity of the Logarithmic VDB Topological Indices

However, the functions involved in VDB indices studied in previous literature did not include logarithmic functions, and the more complete results are mainly the VDB indices in the form of the exponential function in [11]. As an inverse function of the exponential function, theoretically, the logarithmic form of the VDB indices should also be improved. Thus, we introduce a new VDB topological index, the logarithmic VDB index $ln{\mathcal{T}}_f\left(G\right)$ of a graph G:

$$ln{\mathcal{T}}_f=ln{\mathcal{T}}_f\left(G\right)=\sum _{\left\{uv\right\}\in E\left(G\right)}lnf\left(d\right(u),d(v\left)\right)=\sum _{uv\in E\left(G\right)}\gamma (d\left(u\right),d\left(v\right)),$$

where $f(x,y)=f(y,x)$ is a binary function for $x,y\ge 1$.

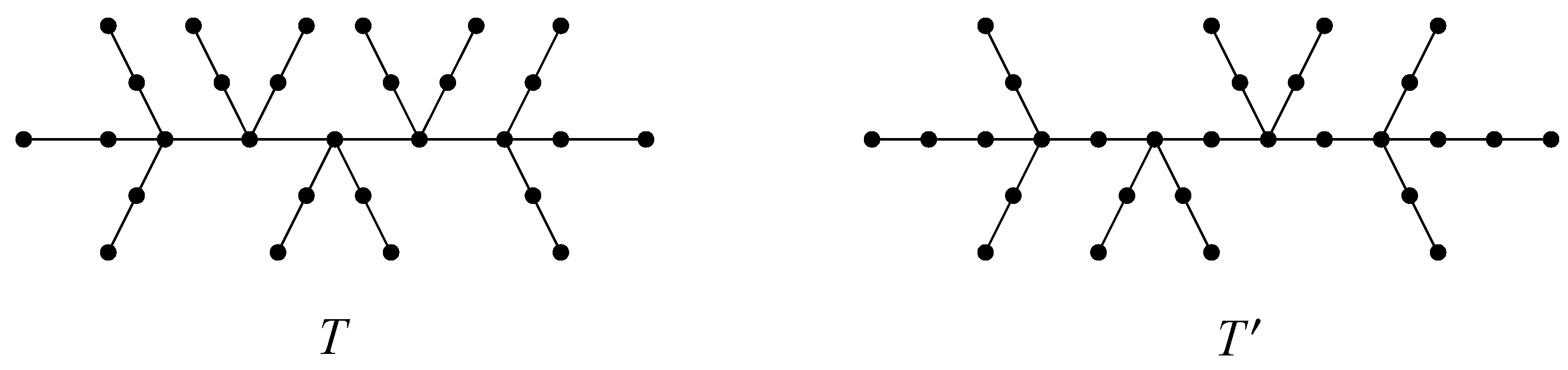
Besides its theoretical significance, the logarithmic of $ln{\mathcal{T}}_f$ has an excellent discriminative property. For example, T and $T^{\prime }$ are depicted in Figure 1. Clearly, $T\ncong T^{\prime }$ but $\chi \left(T\right)=\chi \left(T^{\prime }\right)={\displaystyle \frac{36+2\sqrt{2}}{2\sqrt{2}}}$, where the Randič index $\chi \left(T\right)={\sum }_{\left\{uv\right\}\in E\left(T\right)}{\displaystyle \frac{1}{\sqrt{\left(d\right(u\left)d\right(v\left)\right)}}}$.

Meanwhile, we can calculate the values of the exponential Randič index $e^{\chi }$ and the logarithmic Randič index $ln\chi$; the detailed process is as follows:

$$e^{\chi }=12e^{{\displaystyle \frac{1}{\sqrt{2}}}}+12e^{{\displaystyle \frac{1}{\sqrt{8}}}}+4e^{{\displaystyle \frac{1}{4}}}\approx 46.56,$$

$$e^{\chi }=10e^{{\displaystyle \frac{1}{\sqrt{2}}}}+16e^{{\displaystyle \frac{1}{\sqrt{8}}}}+2e^{{\displaystyle \frac{1}{2}}}\approx 46.36,$$

$$ln\chi \left(T\right)=12ln{\displaystyle \frac{1}{\sqrt{2}}}+12ln{\displaystyle \frac{1}{\sqrt{8}}}+4ln{\displaystyle \frac{1}{4}}\approx -22.18,$$

$$ln\chi \left(T^{\prime }\right)=10ln{\displaystyle \frac{1}{\sqrt{2}}}+16ln{\displaystyle \frac{1}{\sqrt{8}}}+2ln{\displaystyle \frac{1}{2}}\approx -21.49.$$

From

Table 2. The values of three types of Randič indices for trees T and $T^{\prime }$.

Indices	T	${\mathit{T}}^{\prime }$
The general VDB index of $\chi$	${\displaystyle \frac{36+2\sqrt{2}}{2\sqrt{2}}}$	${\displaystyle \frac{36+2\sqrt{2}}{2\sqrt{2}}}$
The exponential VDB index of $e^{\chi }$	46.56	46.36
The logarithmic VDB index of $ln\chi$	−22.18	−21.49

, we can conclude that $\chi \left(T\right)=\chi \left(T^{\prime }\right)$, $e^{\chi \left(T\right)}\ne e^{\chi \left(T^{\prime }\right)}$, and $ln\chi \left(T\right)\ne ln\chi \left(T^{\prime }\right)$. That is to say, for trees T and $T^{\prime }$, the general Randič index has no discriminability, while both the exponential Randič index and logarithmic Randič index have a discrimination property. As is well-known, the Randič index has been widely applied in various aspects of chemical research. Therefore, as a class of VDB topological indices, studying the logarithmic VDB index has theoretical significance and practical value.

In this paper, we mainly focus on the extremal trees for the logarithmic index $ln{\mathcal{T}}_f$. In Section 4, we present sufficient conditions for $P_n$ being the only tree with minimal values of $ln{\mathcal{T}}_f\left(T\right)$. In Section 5, we obtain the sufficient conditions for $S_n$ being the only tree with maximal and minimal values of $ln{\mathcal{T}}_f\left(T\right)$. In addition, as applications, the minimal and maximal trees of some logarithmic VDB indices are determined in Section 6.

3. Preliminaries

In the remainder of this paper, suppose that $\gamma (x,y)=lnf(x,y)$, and $f(x,y)=f(y,x)$ is the symmetric function for $x,y\ge 1$. Now, we will first provide some useful lemmas for the later sections.

Lemma 1.

Let $\gamma (x,y)=lnf(x,y)$, and $f(x,y)>0$. Then,

(1) If ${\displaystyle \frac{\partial f}{\partial x}}>0$, then $\gamma (x,y)$ is strictly increasing on $x\ge 1$;

(2) If ${\displaystyle \frac{\partial f}{\partial x}}<0$, then $\gamma (x,y)$ is strictly decreasing on $x\ge 1$.

Proof. 

As ${\displaystyle \frac{\partial \gamma }{\partial x}}={(lnf(x,y))}_x^{\prime }={\displaystyle \frac{\frac{\partial f}{\partial x}}{f(x,y)}}$, thus $\gamma (x,y)$ is strictly increasing under the conditions of $f>0$ and ${\displaystyle \frac{\partial f}{\partial x}}>0$. Likewise, result (2) holds. □

Lemma 2.

Let $\gamma (x,y)=lnf(x,y)$, where $f(x,y)>0$ is a symmetric function for $x,y\ge 1$. For any $r\ge 1$, if $f(x_1,y_1)·f(x_2,y_2)\cdots f(x_r,y_r)\ge f(x_1^{\prime },y_1^{\prime })·f(x_2^{\prime },y_2^{\prime })\cdots f(x_r^{\prime },y_r^{\prime })$. then,

$$\gamma (x_1,y_1)+\gamma (x_2,y_2)+\cdots +\gamma (x_r,y_r)\ge \gamma (x_1^{\prime },y_1^{\prime })+\gamma (x_2^{\prime },y_2^{\prime })+\cdots +\gamma (x_r^{\prime },y_r^{\prime }).$$

Proof. 

Since $\gamma (x,y)=lnf(x,y)$, according to the condition of lemma, we obtain the following:

$$\begin{array}{ccc}\hfill & \gamma (x_1,y_1)+\gamma (x_2,y_2)+\cdots +\gamma (x_r,y_r)-\left(\gamma (x_1^{\prime },y_1^{\prime })+\gamma (x_2^{\prime },y_2^{\prime })+\cdots +\gamma (x_r^{\prime },y_r^{\prime })\right)\hfill & \\ \hfill & =ln{\displaystyle \frac{f(x_1,y_1)·f(x_2,y_2)\cdots f(x_r,y_r)}{f(x_1^{\prime },y_1^{\prime })·f(x_2^{\prime },y_2^{\prime })\cdots f(x_r^{\prime },y_r^{\prime })}}\ge ln1=0.\hfill \end{array}$$

Hence, the lemma is proven. □

Lemma 3.

If $f(x,y)={\left(xy\right)}^{\alpha }(\alpha >0)$, then $f(x,y)=g\left(x\right)h\left(y\right)$, and $g{(r+1)}^{r+1}·g{(s+1)}^{s+1}<g\left(1\right)·g{(r+s+1)}^{r+s+1}$, where $r\ge 1$ and $s\ge 1$.

Proof. 

Clearly, $f(x,y)={\left(xy\right)}^{\alpha }=g\left(x\right)h\left(y\right)$, where $g\left(x\right)=x^{\alpha }$, and $h\left(y\right)=y^{\alpha }$. In the following, we will verify that $g{(r+1)}^{r+1}·g{(s+1)}^{s+1}<g\left(1\right)·g{(r+s+1)}^{r+s+1}$.

In general, assuming that $r\le s$, note that

$$\begin{array}{ccc}\hfill & g{(r+s+1)}^{r+s+1}={(r+s+1)}^{\alpha (r+s+1)}\hfill & \\ \hfill & ={(s+1)}^{\alpha (s+1)}·{\left({\displaystyle \frac{r+s+1}{s+1}}\right)}^{\alpha (s+1)}·{(r+s+1)}^{\alpha r}\hfill & \\ \hfill & =g{(s+1)}^{s+1}·{\left({\displaystyle \frac{r+s+1}{s+1}}\right)}^{\alpha (s+1)}·{(r+s+1)}^{\alpha r},\hfill \end{array}$$

thus, the lemma is true if the equality $g{(r+1)}^{r+1}={(r+1)}^{\alpha (r+1)}<{\left({\displaystyle \frac{r+s+1}{s+1}}\right)}^{\alpha (s+1)}·{(r+s+1)}^{\alpha r}$ holds, i.e.,

$$\begin{array}{cc}& {\left({\displaystyle \frac{r+s+1}{s+1}}\right)}^{s+1}·{\left({\displaystyle \frac{r+s+1}{s+1}}\right)}^{r+1}>1+r.\end{array}$$

If $r=1,2$, then:

$$\begin{array}{cc}& {\left({\displaystyle \frac{r+s+1}{s+1}}\right)}^{s+1}·{\left({\displaystyle \frac{r+s+1}{r+1}}\right)}^s=\left\{\begin{array}{cc}{\left({\displaystyle \frac{3}{2}}\right)}^2\left({\displaystyle \frac{3}{2}}\right)>1+1=2,\hfill & \hfill \mathrm{if}\mathrm{s}=\mathrm{r}=1,\\ {\left({\displaystyle \frac{5}{3}}\right)}^2\left({\displaystyle \frac{5}{3}}\right)>1+2=3,\hfill & \hfill \mathrm{if}\mathrm{s}=\mathrm{r}=2.\end{array}\right.\end{array}$$

and

$$\begin{array}{ccc}& {\left({\displaystyle \frac{r+s+1}{s+1}}\right)}^{s+1}·{\left({\displaystyle \frac{r+s+1}{r+1}}\right)}^r>{\left({\displaystyle \frac{r+s+1}{r+1}}\right)}^r\hfill & \\ & =\left\{\begin{array}{cc}{\left({\displaystyle \frac{1+2+1}{2}}\right)}^1=2\ge 1+1=2,\hfill & \hfill \mathrm{if}\mathrm{s}>\mathrm{r}=1,\\ {\left({\displaystyle \frac{2+3+1}{2}}\right)}^2=4\ge 1+2=3,\hfill & \hfill \mathrm{if}\mathrm{s}>\mathrm{r}=2.\end{array}\right.\hfill \end{array}$$

If $s\ge 3$, and because $s\ge r$, then:

$$\begin{array}{ccc}\hfill & {\left({\displaystyle \frac{r+s+1}{s+1}}\right)}^{s+1}·{\left({\displaystyle \frac{r+s+1}{r+1}}\right)}^r>{\left({\displaystyle \frac{r+s+1}{r+1}}\right)}^r\ge {\left({\displaystyle \frac{2r+1}{r+1}}\right)}^r={(1+{\displaystyle \frac{r}{r+1}})}^r\hfill & \\ \hfill & \ge C_r^0+C_r^1{\displaystyle \frac{r}{r+1}}+C_r^2{\left({\displaystyle \frac{r}{r+1}}\right)}^2+C_r^3{\left({\displaystyle \frac{r}{r+1}}\right)}^3\hfill & \\ \hfill & =1+{\displaystyle \frac{r^2}{r+1}}+{\displaystyle \frac{r(r-1)r^2}{2{(r+1)}^2}}+{\displaystyle \frac{r(r-1)(r-2)r^3}{6{(r+1)}^3}}\hfill & \\ \hfill & \ge 1+{\displaystyle \frac{r^2}{r+1}}+{\displaystyle \frac{r^3}{{(r+1)}^2}}+{\displaystyle \frac{r^3(r-2)}{{(r+1)}^3}}\hfill & \\ \hfill & \ge 1+r.\hfill \end{array}$$

Hence, the lemma has been proven. □

Lemma 4.

Let there be a binary function $f(x,y)={\displaystyle \frac{xy}{x+y}}$, where $x,y\ge 1$. Then,

(1) ${\displaystyle \frac{\partial f}{\partial x}}<0$, ${\displaystyle \frac{{\partial }^{2}f}{\partial x^2}}·f-{\left({\displaystyle \frac{\partial f}{\partial x}}\right)}^2<0$; and

(2) $f{(1,r)}^{r-1}·f{(1,n-r)}^{n-r-1}·f(r,n-r)>f{(1,n-1)}^{n-1}$, where $2\le r\le \lfloor {\displaystyle \frac{n}{2}}\rfloor$.

Proof. 

(1) Since ${\displaystyle \frac{\partial f}{\partial x}}={\displaystyle \frac{y-xy}{{(x+y)}^2}}$, and $x,y\ge 1$, thus ${\displaystyle \frac{\partial f}{\partial x}}<0$. Note that

$$\begin{array}{cc}& {\displaystyle \frac{{\partial }^{2}f}{\partial x^2}}={({\displaystyle \frac{y-xy}{{(x+y)}^2}})}^{\prime }={\displaystyle \frac{xy-y^2-2y}{{(x+y)}^3}},\end{array}$$

and therefore,

$$\begin{array}{cc}& {\displaystyle \frac{{\partial }^{2}f}{\partial x^2}}·f-{\left({\displaystyle \frac{\partial f}{\partial x}}\right)}^2={\displaystyle \frac{(xy-y^2-2y)xy}{{(x+y)}^4}}-{\displaystyle \frac{{(y-xy)}^2}{{(x+y)}^4}}={\displaystyle \frac{-x{y}^3-y^2}{{(x+y)}^4}}<0.\end{array}$$

(2) Substituting $f(x,y)={\displaystyle \frac{xy}{x+y}}$ into $f{(1,r)}^{r-1}·f{(1,n-r)}^{n-r-1}·f(r,n-r)>f{(1,n-1)}^{n-1}$ yields that

$$\begin{array}{cc}& {\left({\displaystyle \frac{r}{r+1}}\right)}^{r-1}·{\left({\displaystyle \frac{n-r}{n+1-r}}\right)}^{n-1-r}·{\displaystyle \frac{r(n-r)}{n}}>{\left({\displaystyle \frac{n-1}{n}}\right)}^{n-1},\end{array}$$

i.e.,

$$\begin{array}{cc}& {\displaystyle \frac{r^r·(n+1-r)}{{(r+1)}^{r-1}·n}}·{\left({\displaystyle \frac{n-r}{n+1-r}}\right)}^{n-r}>{\left({\displaystyle \frac{n-1}{n}}\right)}^{n-1}.\end{array}$$

Hence, to complete the lemma’s proof, it is only necessary to prove the following:

$$\begin{array}{cc}& {\displaystyle \frac{r^r·(n+1-r)}{{(r+1)}^{r-1}·n}}>1,and{\left({\displaystyle \frac{n-r}{n+1-r}}\right)}^{n-r}>{\left({\displaystyle \frac{n-1}{n}}\right)}^{n-1}.\end{array}$$

Let us first consider ${\displaystyle \frac{r^r·(n+1-r)}{{(r+1)}^{r-1}·n}}>1$. Note that

$$\begin{array}{ccc}\hfill & {\left({\displaystyle \frac{r}{r+1}}\right)}^{r-1}={(1-{\displaystyle \frac{1}{r+1}})}^{r-1}\hfill & \\ \hfill & =C_{r-1}^0-C_{r-1}^1{\displaystyle \frac{1}{r+1}}+C_{r-1}^2{\left({\displaystyle \frac{1}{r+1}}\right)}^2-\cdots +C_{r-1}^{r-1}{(-{\displaystyle \frac{1}{r+1}})}^{r-1}\hfill & \\ \hfill & >1-{\displaystyle \frac{r-1}{r+1}}={\displaystyle \frac{2}{r+1}}.\hfill \end{array}$$

Thus, we obtain the following:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{r^r·(n+1-r)}{{(r+1)}^{r-1}·n}}={\left({\displaystyle \frac{r}{r+1}}\right)}^{r-1}·{\displaystyle \frac{r(n+1-r)}{n}}>{\displaystyle \frac{2}{r+1}}·{\displaystyle \frac{r(n+1-r)}{n}}.\hfill \end{array}$$

In the following, we only need to prove that ${\displaystyle \frac{2}{r+1}}·{\displaystyle \frac{r(n+1-r)}{n}}\ge 1$. Let $f\left(r\right)=2r(n+1-r)-(r+1)n$, where $2\le r\le \lfloor {\displaystyle \frac{n}{2}}\rfloor$. Since $f^{\prime }\left(r\right)=n-4r+2,$ then $f_{min}=\{f\left(2\right),f\left({\displaystyle \frac{n}{2}}\right)\}=f\left({\displaystyle \frac{n}{2}}\right)=0.$ This implies that $f\left(r\right)\ge 0$, and therefore,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{r^r·(n+1-r)}{{(r+1)}^{r-1}·n}}>{\displaystyle \frac{2}{r+1}}·{\displaystyle \frac{r(n+1-r)}{n}}\ge 1.\hfill \end{array}$$

Now, let us turn to prove ${\left({\displaystyle \frac{n-r}{n+1-r}}\right)}^{n-r}>{\left({\displaystyle \frac{n-1}{n}}\right)}^{n-1}$. Let $y={\left({\displaystyle \frac{n-r}{n+1-r}}\right)}^{n-r}$, where $2\le r\le \lfloor {\displaystyle \frac{n}{2}}\rfloor$. Since

$$\begin{array}{cc}\hfill & y^{\prime }={\left({\displaystyle \frac{n-r}{n+1-r}}\right)}^{n-r}(-ln{\displaystyle \frac{n-r}{n+1-r}}-{\displaystyle \frac{1}{n+1-r}}),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & g^{\prime }\left(r\right)={(-ln{\displaystyle \frac{n-r}{n+1-r}}-{\displaystyle \frac{1}{n+1-r}})}^{\prime }={\displaystyle \frac{1}{{(n+1-r)}^2(n-r)}}>0,\hfill \end{array}$$

thus, we have

$$\begin{array}{cc}\hfill & g\left(r\right)\ge g\left(1\right)=ln{\displaystyle \frac{n}{n-1}}-{\displaystyle \frac{1}{n}}\ge ln{\displaystyle \frac{4}{3}}-{\displaystyle \frac{1}{4}}>0.\hfill \end{array}$$

That is to say, y is increasing, and hence,

$$\begin{array}{cc}\hfill & {\left({\displaystyle \frac{n-r}{n+1-r}}\right)}^{n-r}>y\left(1\right)={\left({\displaystyle \frac{n-1}{n}}\right)}^{n-1}.\hfill \end{array}$$

Therefore, combining the above two inequations, the lemma proof is completed. □

4. Sufficient Conditions for $P_n$ Is the Minimum Tree

In this section, sufficient conditions for $P_n$ being the minimal tree among all $ln{\mathcal{T}}_f\left(T\right)$ are given. We present the following transformation first.

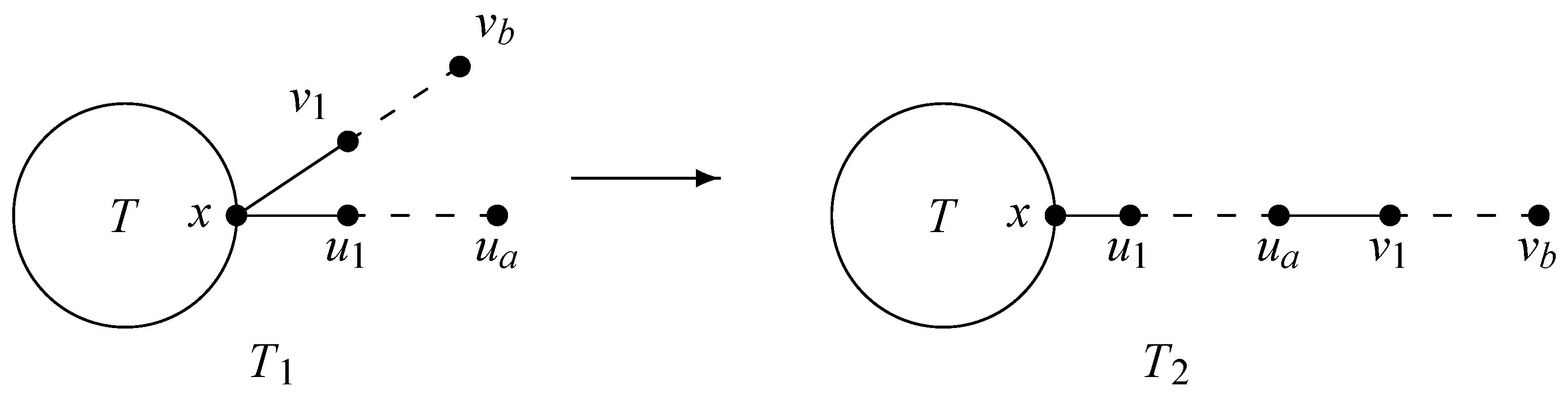
Transformation 1. Assume that $T\in {\mathbb{T}}_n$, and let x be the vertex in T. $T_1$ is the tree obtained from T by adding two pendent paths $P_1$ and $P_2$ attached at x, where $P_1=x{u}_1{u}_2\cdots u_a$, $P_2=x{v}_1{v}_2\cdots v_b$, $a\ge b\ge 1$, and $d_{T_1}\left(x\right)\ge 3$. $T_2$ is the resulting graph obtained from $T_1$ by removing edge $\left\{x{v}_1\right\}$ and connecting a new edge $\left\{u_a{v}_1\right\}$, i.e., $T_2=T_1-\left\{x{v}_1\right\}+\left\{u_a{v}_1\right\}$. $T_1$ and $T_2$ are depicted in Figure 2. Clearly, $T_1,T_2\in {\mathbb{T}}_n$.

Lemma 5.

Let $T_1$ and $T_2$ be the graphs in Transformation 1 (see Figure 2), where $a=b=1$. If $f(x,y)$ matches conditions $f(x,y)>0$, ${\displaystyle \frac{\partial f}{\partial x}}>0$, and $f^2(1,x+2)\ge f(2,x+1)·f(2,1)$, then $ln{\mathcal{T}}_f\left(T_1\right)>ln{\mathcal{T}}_f\left(T_2\right)$.

Proof. 

Denote $d_{T_1}\left(x\right)=k+2$, where $k\ge 1$, and $N_T\left(x\right)=N_{T_1}\left(x\right)\setminus \{u_1,u_2\}=\{w_1,\cdots ,w_k\}$. Since $a=b=1$, then $d_{T_1}\left(u_1\right)=d_{T_1}\left(v_1\right)=1$. Thus, we have the following:

$$\begin{array}{ccc}\hfill & ln{\mathcal{T}}_f\left(T_1\right)-ln{\mathcal{T}}_f\left(T_2\right)\hfill & \\ \hfill & =2\gamma (k+2,1)+{\Sigma }_{i=1}^k\gamma (k+2,d_T\left(w_i\right))-\left(\gamma (k+1,2)+\gamma (2,1)+{\Sigma }_{i=1}^k\gamma (k+1,d_T\left(w_i\right))\right)\hfill & \\ \hfill & ={\Sigma }_{i=1}^k\left(\gamma (k+2,d_T\left(w_i\right))-\gamma (k+1,d_T\left(w_i\right))\right)+2\gamma (k+2,1)-\gamma (k+1,2)-\gamma (2,1).\hfill \end{array}$$

Since $f(x,y)>0$ and ${\displaystyle \frac{\partial f}{\partial x}}>0$, by Lemma 1, we obtain ${\Sigma }_{i=1}^k\left(\gamma (k+2,d_T\left(w_i\right))-\gamma (k+1,d_T\left(w_i\right))\right)>0$. Using Lemma 2, we have

$$ln{\mathcal{T}}_f\left(T_1\right)-ln{\mathcal{T}}_f\left(T_2\right)>2\gamma (k+2,1)-\gamma (k+1,2)-\gamma (2,1)\ge 0.$$

Thus, the lemma is completed. □

Lemma 6.

Let $T_1$ and $T_2$ be the graphs in Transformation 1 (see Figure 2), where $a>b=1$. If $f(x,y)$ matches conditions $f(x,y)>0$, ${\displaystyle \frac{\partial f}{\partial x}}>0$, and $f(1,x+2)·f(2,x+2)\ge f(2,x+1)·f(2,2)$, then $ln{\mathcal{T}}_f\left(T_1\right)>ln{\mathcal{T}}_f\left(T_2\right)$.

Proof. 

Denote $d_{T_1}\left(x\right)=k+2$, where $k\ge 1$, and $N_T\left(x\right)=N_{T_1}\left(x\right)\setminus \{u_1,u_2\}=\{w_1,\cdots ,w_k\}$. Since $a>b=1$, then $d_{T_1}\left(u_1\right)=2$, and $d_{T_1}\left(v_1\right)=1$. Therefore, we have the following:

$$\begin{array}{ccc}\hfill & ln{\mathcal{T}}_f\left(T_1\right)-ln{\mathcal{T}}_f\left(T_2\right)\hfill & \\ \hfill & =\gamma (k+2,1)+\gamma (k+2,2)+\gamma (2,1)+{\Sigma }_{i=1}^k\gamma (k+2,d_T\left(w_i\right))\hfill & \\ \hfill & -\left(\gamma (k+1,2)+\gamma (2,2)+\gamma (2,1)+{\Sigma }_{i=1}^k\gamma (k+1,d_T\left(w_i\right))\right)\hfill & \\ \hfill & ={\Sigma }_{i=1}^k\left(\gamma (k+2,d_T\left(w_i\right))-\gamma (k+1,d_T\left(w_i\right))\right)\hfill & \\ \hfill & +\gamma (k+2,1)+\gamma (k+2,2)-\gamma (k+1,2)-\gamma (2,2).\hfill \end{array}$$

According to $f(x,y)>0$ and ${\displaystyle \frac{\partial f}{\partial x}}>0$, by Lemma 1, we have ${\Sigma }_{i=1}^k\left(\gamma (k+2,d_T\left(w_i\right))-\gamma (k+1,d_T\left(w_i\right))\right)>0$. This, together with Lemma 2, implies that

$$ln{\mathcal{T}}_f\left(T_1\right)-ln{\mathcal{T}}_f\left(T_2\right)>\gamma (k+2,1)+\gamma (k+2,2)-\gamma (k+1,2)-\gamma (2,2)\ge 0.$$

Hence, we finished the proof. □

Lemma 7.

Let $T_1$ and $T_2$ be the graphs in Transformation 1 (see Figure 2), where $a\ge b>1$. If $f(x,y)$ matches conditions $f(x,y)>0$, ${\displaystyle \frac{\partial f}{\partial x}}>0$, and $f^2(2,x+2)·f(2,1)\ge f(2,x+1)·f^2(2,2)$, then $ln{\mathcal{T}}_f\left(T_1\right)>ln{\mathcal{T}}_f\left(T_2\right)$.

Proof. 

Denote $d_{T_1}\left(x\right)=k+2$, where $k\ge 1$, and $N_T\left(x\right)=N_{T_1}\left(x\right)\setminus \{u_1,u_2\}=\{w_1,\cdots ,w_k\}$. Since $a\ge b>1$, then $d_{T_1}\left(u_1\right)=d_{T_1}\left(v_1\right)=2$. Hence, we have the following:

$$\begin{array}{ccc}\hfill & ln{\mathcal{T}}_f\left(T_1\right)-ln{\mathcal{T}}_f\left(T_2\right)\hfill & \\ \hfill & =2\gamma (k+2,2)+2\gamma (2,1)+\gamma (2,1)+{\Sigma }_{i=1}^k\gamma (k+2,d_T\left(w_i\right))\hfill & \\ \hfill & -\left(\gamma (k+1,2)+2\gamma (2,2)+\gamma (2,1)+{\Sigma }_{i=1}^k\gamma (k+1,d_T\left(w_i\right))\right)\hfill & \\ \hfill & ={\Sigma }_{i=1}^k\left(\gamma (k+2,d_T\left(w_i\right))-\gamma (k+1,d_T\left(w_i\right))\right)\hfill & \\ \hfill & +2\gamma (k+2,2)+\gamma (2,1)-\gamma (k+1,2)-2\gamma (2,2).\hfill \end{array}$$

By ${\displaystyle \frac{\partial f}{\partial x}}>0$, and Lemma 1, we have ${\Sigma }_{i=1}^p\left(\gamma (k+2,d_T\left(w_i\right))-\gamma (k+1,d_T\left(w_i\right))\right)>0$. Now, applying Lemma 2, we have the following:

$$ln{\mathcal{T}}_f\left(T_1\right)-ln{\mathcal{T}}_f\left(T_2\right)>2\gamma (k+2,2)+\gamma (2,1)-\gamma (k+1,2)-2\gamma (2,2)\ge 0.$$

Thus, the proof is done. □

With the help of lemmas, we now present the core theorem.

Theorem 1.

Let $T\in {\mathbb{T}}_n$, assuming that $f(x,y)$ satisfies the following conditions:

$\left(1\right)f(x,y)>0$, ${\displaystyle \frac{\partial f}{\partial x}}>0$;

$\left(2\right)f^2(1,x+2)\ge f(2,x+1)·f(2,1)$;

$\left(3\right)f(1,x+2)·f(2,x+2)\ge f(2,x+1)·f(2,2)$; and

$\left(4\right)f^2(2,x+2)·f(2,1)\ge f(2,x+1)·f^2(2,2)$;

• then $ln{\mathcal{T}}_f\left(T\right)\ge ln{\mathcal{T}}_f\left(P_n\right)$, if and only if $T\cong P_n$ the equality holds.

Proof. 

Conditions (1)–(4) are satisfied for the results of Lemmas 5–7. If $T\ncong P_n$, then, using Transformation 1 repeatedly, $T^{\prime }$ is attained from T. Moreover, according to Lemmas 5–7, we have $ln{\mathcal{T}}_f\left(T\right)>ln{\mathcal{T}}_f\left(T^{\prime }\right)$. Therefore, $ln{\mathcal{T}}_f\left(T\right)\ge ln{\mathcal{T}}_f\left(P_n\right)$, where T is isomorphic to $P_n$, the equality holds. Thus, the proof is completed. □

5. Sufficient Conditions for ${\mathbf{S}}_{\mathbf{n}}$ Being Extremal Trees

In Section 4, we present sufficient conditions for $S_n$ being the extremal trees among all $ln{\mathcal{T}}_f\left(T\right)$. We introduce Transformation 2 first.

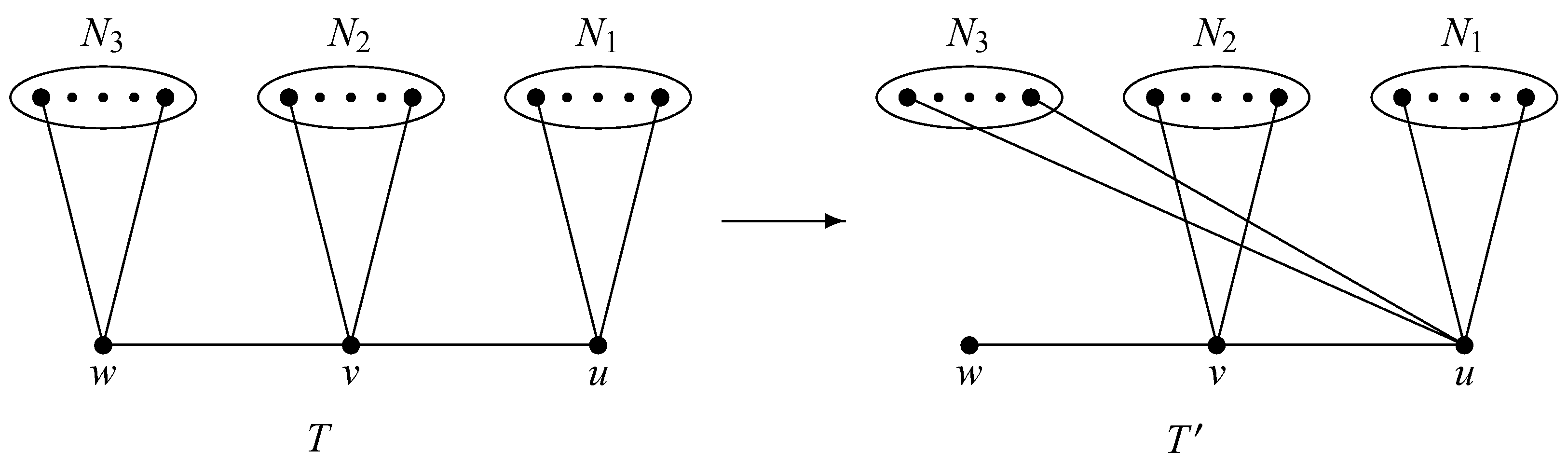
Transformation 2. Let $T\in {\mathbb{T}}_n$, $\{wv,uv\}\in E\left(T\right)$, where $d_T\left(w\right)\le d_T\left(u\right)\le 2$. Let $N_3=N\left(w\right)\setminus \left\{v\right\}$, $N_2=N\left(v\right)\setminus \{u,w\}$, and $N_1=N\left(u\right)\setminus \left\{v\right\}$. In T, replacing the edge $\left\{w{w}_i\right\}$ with $\left\{u{w}_i\right\}$ at each vertex $w_i\in N_3$, we then obtain a new tree $T^{\prime }$; see Figure 3. Clearly, $T^{\prime }\in {\mathbb{T}}_n$.

With the help of Transformation 2, we first give sufficient conditions for the star $S_n$ is the maximal tree among all $ln{\mathcal{T}}_f\left(T\right)$.

Lemma 8.

Let T and $T^{\prime }$ be the graphs in Transformation 2 (see Figure 3). If $f(x,y)=g\left(x\right)h\left(y\right)$ is a real symmetric function with $x,y\ge 1$, and meets the condition $g{(r+1)}^{r+1}·g{(s+1)}^{s+1}<g\left(1\right)·g{(r+s+1)}^{r+s+1}$, then $ln{\mathcal{T}}_f\left(T\right)<ln{\mathcal{T}}_f\left(T^{\prime }\right)$.

Proof. 

For convenience, suppose that $N_3=\{w_1,w_2,\cdots ,w_r\}$ and $N_1=\{u_1,u_2,\cdots ,u_s\}$, where $r\le s$. Thus, we have $d_T\left(w\right)=r+1$, $d_T\left(u\right)=s+1$, and:

$$\begin{array}{ccc}\hfill & ln{\mathcal{T}}_f\left(T\right)-ln{\mathcal{T}}_f\left(T^{\prime }\right)\hfill & \\ \hfill & ={\Sigma }_{i=1}^r\left(\gamma (r+1,d_T\left(w_i\right))-\gamma (r+s+1,d_T\left(w_i\right))\right)+{\Sigma }_{i=1}^s(\gamma (s+1,d_T\left(u_i\right))\hfill & \\ \hfill & -\gamma (r+s+1,d_T\left(u_i\right)))+\gamma (r+1,d_T\left(v\right))+\gamma (s+1,d_T\left(v\right))\hfill & \\ \hfill & -\gamma (1,d_T\left(v\right))-\gamma (r+s+1,d_T\left(v\right))\hfill & \\ \hfill & =ln\prod _{i=1}^r{\displaystyle \frac{f(r+1,d_T\left(w_i\right))}{f(r+1+s,d_T\left(w_i\right))}}\prod _{i=1}^s{\displaystyle \frac{f(s+1,d_T\left(u_i\right))}{f(r+s+1,d_T\left(u_i\right))}}{\displaystyle \frac{f(r+1,d_T\left(v\right))·f(s+1,d_T\left(v\right))}{f(1,d_T\left(v\right))·f(r+s+1,d_T\left(v\right))}}.\hfill \end{array}$$

Since the same expressions $d_T\left(w_i\right)$, $d_T\left(u_i\right)$, and $d_T\left(v\right)$ are included in the above equation, therefore, under the condition $f(x,y)=g\left(x\right)h\left(y\right)$, the above equation simplified as follows:

$$\begin{array}{ccc}\hfill & ln{\mathcal{T}}_f\left(T\right)-ln{\mathcal{T}}_f\left(T^{\prime }\right)\hfill & \\ \hfill & =ln\prod _{i=1}^r{\displaystyle \frac{g(r+1)}{g(r+s+1)}}·\prod _{i=1}^s{\displaystyle \frac{g(s+1)}{g(r+s+1)}}·{\displaystyle \frac{g(r+1)·g(s+1)}{g\left(1\right)·g(r+s+1)}}\hfill & \\ \hfill & =ln{\displaystyle \frac{g{(r+1)}^{r+1}·g{(s+1)}^{s+1}}{g\left(1\right)·g{(r+s+1)}^{r+s+1}}}.\hfill \end{array}$$

Furthermore, by Lemma 2, we can easily obtain $ln{\mathcal{T}}_f\left(T\right)-ln{\mathcal{T}}_f\left(T^{\prime }\right)<0$. Hence, the lemma has been proven. □

Theorem 2.

Let $T\in {\mathbb{T}}_n$. If $f(x,y)=g\left(x\right)h\left(y\right)$ for any $x,y\ge 1$, and $g\left(x\right)$ meets the condition $g{(r+1)}^{r+1}·g{(s+1)}^{s+1}<g\left(1\right)·g{(r+s+1)}^{r+s+1}$, and then the star $S_n$ is the maximal tree among all $ln{\mathcal{T}}_f\left(T\right)$.

Proof. 

Let T be a tree with n vertices, $\left|p\right(T\left)\right|$ represents the sum of pendent vertices. If $\left|p\right(T\left)\right|=n-2$ or $n-1$, then T can only be the double star $S_{r,n-r}$ or star $S_n$, where $2\le r\le \lfloor {\displaystyle \frac{n}{2}}\rfloor$. Thus, assume that $\left|p\right(T\left)\right|\le n-3$ for the rest of the proof.

Assume that $T_0$ is a new tree obtained by removing all pendent vertices from T. Then, we have $|V\left(T_0\right)|=n-|p\left(T\right)|\ge n-(n-3)=3$. Moreover, the degree of $v\in V\left(T_0\right)$ is greater than or equal 2. Let us consider two edges; suppose that $\left\{uv\right\}$ and $\left\{vw\right\}$, such that $\{uv,vw\}\subseteq E\left(T\right)$. Without loss of generality, let $d_T\left(u\right)\ge d_T\left(v\right)$. Note that $d_T\left(u\right)\ge 2$, and $d_T\left(w\right)\ge 2$. By Transformation 2, a new tree $T^{\prime }$ is generated from T, while satisfying $|p\left(T^{\prime }\right)|-|p\left(T\right)|=1$. According to Lemma 8, $ln{\mathcal{T}}_f\left(T\right)<ln{\mathcal{T}}_f\left(T^{\prime }\right)$.

If $\left|p\right(T^{\prime }\left)\right|$ is not equal to $n-2$, then using Transformation 2 again for $T^{\prime }$, we can finally obtain the double star $S_{r,n-r}$. Therefore, applying Lemma 8, we have $ln{\mathcal{T}}_f\left(T\right)<ln{\mathcal{T}}_f\left(T^{\prime }\right)$.

Hence, to complete the proof, it is just needed to prove that $ln{\mathcal{T}}_f\left(S_{r,n-r}\right)<ln{\mathcal{T}}_f\left(S_n\right)$. Note that

$$\begin{array}{ccc}\hfill & ln{\mathcal{T}}_f\left(S_{r,n-r}\right)\hfill & \\ \hfill & =(r-1)lnf(1,r)+(n-1-r)lnf(1,n-r)+lnf(r,n-r)\hfill & \\ \hfill & =lnf{(1,r)}^{r-1}·f{(1,n-r)}^{n-1-r}·f(r,n-r).\hfill & \\ \hfill & ln{\mathcal{T}}_f\left(S_n\right)=(n-1)lnf(1,n-1)=lnf{(1,n-1)}^{n-1}.\hfill \end{array}$$

Thus,

$$\begin{array}{ccc}\hfill & ln{\mathcal{T}}_f\left(S_{r,n-r}\right)-ln{\mathcal{T}}_f\left(S_n\right)\hfill & \\ \hfill & =lnf{(1,r)}^{r-1}·f{(1,n-r)}^{n-r-1}·f(r,n-r)-lnf{(1,n-1)}^{n-1}\hfill & \\ \hfill & =ln{\displaystyle \frac{f{(1,r)}^{r-1}·f{(1,n-r)}^{n-r-1}·f(r,n-r)}{f{(1,n-1)}^{n-1}}}.\hfill \end{array}$$

By substituting the condition into above equation, we can obtain the following:

$$\begin{array}{ccc}\hfill & ln{\mathcal{T}}_f\left(S_{r,n-r}\right)-ln{\mathcal{T}}_f\left(S_n\right)\hfill & \\ \hfill & =ln{\displaystyle \frac{g{\left(1\right)}^{n-2}·g{\left(r\right)}^{r-1}·g{(n-r)}^{n-r-1}·g\left(r\right)·g(n-r)}{g{\left(1\right)}^{n-1}·g{(n-1)}^{n-1}}}\hfill & \\ \hfill & =ln{\displaystyle \frac{g{\left(r\right)}^r·g{(n-r)}^{n-r}}{g\left(1\right)·g{(n-1)}^{n-1}}}\hfill & \\ \hfill & <ln1=0.\hfill \end{array}$$

Hence, the theorem holds. □

In the remainder of this section, by utilizing the monotonicity and concavity of functions, we will give sufficient conditions for the star $S_n$ being the minimal tree of $ln{\mathcal{T}}_f$.

Lemma 9.

Assuming that T and $T^{\prime }$ are trees in Transformation 2 (see Figure 3), if $f(x,y)$ meets the conditions $f(x,y)>0$, ${\displaystyle \frac{\partial f}{\partial x}}<0$, and ${\displaystyle \frac{{\partial }^{2}f}{\partial x^2}}·f-{\left({\displaystyle \frac{\partial f}{\partial x}}\right)}^2<0$, then $ln{\mathcal{T}}_f\left(T\right)>ln{\mathcal{T}}_f\left(T^{\prime }\right)$.

Proof. 

Denote $N_3=\{w_1,w_2,\cdots ,w_r\}$ and $N_1=\{u_1,u_2,\cdots ,u_s\}$, where $r\le s$. Similar to Lemma 8, we have $d_T\left(w\right)=r+1$,$d_T\left(u\right)=s+1$, and

$$\begin{array}{ccc}\hfill & ln{\mathcal{T}}_f\left(T\right)-ln{\mathcal{T}}_f\left(T^{\prime }\right)\hfill & \\ \hfill & ={\Sigma }_{i=1}^r\left(\gamma (r+1,d_T\left(w_i\right))-\gamma (r+s+1,d_T\left(w_i\right))\right)\hfill & \\ \hfill & +{\Sigma }_{j=1}^s\left(\gamma (s+1,d_T\left(u_j\right))-\gamma (r+s+1,d_T\left(u_j\right))\right)\hfill & \\ \hfill & +\gamma (r+1,d_T\left(v\right))+\gamma (s+1,d_T\left(v\right))-\gamma (1,d_T\left(v\right))-\gamma (r+s+1,d_T\left(v\right)).\hfill \end{array}$$

By Lemma 1, $\gamma (x,y)$ is decreasing on x. Then, for $i=1,2,\cdots ,r$,

$$\begin{array}{cc}\hfill & \left(\gamma (r+1,d_T\left(w_i\right))-\gamma (r+s+1,d_T\left(w_i\right))\right)>0,\hfill \end{array}$$

and for $j=1,2,\cdots ,s$,

$$\begin{array}{cc}\hfill & \left(\gamma (s+1,d_T\left(u_j\right))-\gamma (r+s+1,d_T\left(u_j\right))\right)>0.\hfill \end{array}$$

Since

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{\partial }^2\gamma (x,y)}{\partial x^2}}={\displaystyle \frac{\partial \left(\frac{f^{\prime }(x,y)}{f(x,y)}\right)}{\partial x}}={\displaystyle \frac{\frac{{\partial }^{2}f}{\partial x^2}·f-{\left(\frac{\partial f}{\partial x}\right)}^2}{f^2}}<0,\hfill \end{array}$$

thus, $\gamma (x,y)$ is concave down on x. Hence,

$$\begin{array}{cc}\hfill & \gamma (r+1,d_T\left(v\right))+\gamma (s+1,d_T\left(v\right))\ge \gamma (1,d_T\left(v\right))+\gamma (r+s+1,d_T\left(v\right)).\hfill \end{array}$$

Combining the above two equations, the lemma holds true. □

Theorem 3.

Let $T\in {\mathbb{T}}_n$. If $f(x,y)$ meet the following conditions:

(1) $f(x,y)>0$, ${\displaystyle \frac{\partial f}{\partial x}}<0$, ${\displaystyle \frac{{\partial }^{2}f}{\partial x^2}}·f-{\left({\displaystyle \frac{\partial f}{\partial x}}\right)}^2<0$, and

(2) $f{(1,r)}^{r-1}·f{(1,n-r)}^{n-r-1}·f(r,n-r)>f{(1,n-1)}^{n-1}$,

• then, the star $S_n$ is the minimal tree of $ln{\mathcal{T}}_f\left(T\right)$.

Proof. 

First, we will prove the minimal tree of $ln{\mathcal{T}}_f\left(T\right)$ is $S_{d,n-d}$ or $S_n$. Let $\left|p\right(T\left)\right|$ represent the sum of pendent vertices in T. If $\left|p\right(T\left)\right|=n-2$ or $n-1$, then T can only be the double star $S_{r,n-r}$ or star $S_n$, where $2\le r\le \lfloor {\displaystyle \frac{n}{2}}\rfloor$. Thus, we assume that $\left|p\right(T\left)\right|\le n-3$ for the rest of the proof.

Assuming that $T_0$ is a new tree obtained by removing all pendent vertices from T, we have $|V\left(T_0\right)|=n-|p\left(T\right)|\ge 3$, and $d_T\left(v\right)\ge 2$ for any $v\in V\left(T_0\right)$. Now, consider two edges, and suppose that $\left\{uv\right\}$ and $\left\{vw\right\}$, such that $\{uv,vw\}\subseteq E\left(T\right)$. Without loss of generality, let $d_T\left(u\right)\ge d_T\left(v\right)$. By Transformation 2, a new tree $T^{\prime }$ is generated from T, such that $|p\left(T^{\prime }\right)|-|p\left(T\right)|=1$. According to Lemma 9, we have $ln{\mathcal{T}}_f\left(T\right)<ln{\mathcal{T}}_f\left(T^{\prime }\right)$.

If $\left|p\right(T^{\prime }\left)\right|$ is not equal to $n-2$, then using Transformation 2 again for $T^{\prime }$, we can finally obtain the double star $S_{r,n-r}$. Therefore, according to Lemma 9, $ln{\mathcal{T}}_f\left(T\right)<ln{\mathcal{T}}_f\left(T^{\prime }\right)$.

Second, we will prove that $ln{\mathcal{T}}_f\left(S_n\right)<ln{\mathcal{T}}_f\left(S_{r,n-r}\right)$. Note that

$$\begin{array}{ll}& ln{\mathcal{T}}_f\left(S_{r,n-r}\right)\\ & =(r-1)lnf(1,r)+(n-r-1)lnf(1,n-r)+lnf(r,n-r)\\ & =lnf{(1,r)}^{r-1}·f{(1,n-r)}^{n-r-1}·f(r,n-r).\\ & ln{\mathcal{T}}_f\left(S_n\right)=(n-1)lnf(1,n-1)=lnf{(1,n-1)}^{n-1}.\end{array}$$

By the condition $f{(1,r)}^{r-1}·f{(1,n-r)}^{n-r-1}·f(r,n-r)>f{(1,n-1)}^{n-1}$, we obtain the following:

$$\begin{array}{l}ln{\mathcal{T}}_f\left(S_{r,n-r}\right)-ln{\mathcal{T}}_f\left(S_n\right)\\ =lnf{(1,r)}^{r-1}·f{(1,n-r)}^{n-r-1}·f(r,n-r)-lnf{(1,n-1)}^{n-1}\\ =ln{\displaystyle \frac{f{(1,r)}^{r-1}·f{(1,n-r)}^{n-r-1}·f(r,n-r)}{f{(1,n-1)}^{n-1}}}\\ >ln1=0.\end{array}$$

Therefore, the theorem holds true. □

6. Applications

Note that if $f(x,y)=\sqrt{\left(xy\right)}$, ${\left(xy\right)}^{\alpha }(\alpha \ge 1)$, $x^2+y^2$, $\sqrt{x^2+y^2}$, $\sqrt{{(x-1)}^2+{(y-1)}^2}$, ${(x+y)}^{\alpha }(\alpha \ge 1)$, $x+y+xy$, ${(x+y+xy)}^2$, $(x+y)xy$, ${(x+y+xy)}^2$, and $\sqrt{(x+y)xy}$, then the conditions of Theorem 1 are matched. Thus, as an application of Theorem 1, we declare that the minimal tree is $P_n$ for the logarithmic VDB indices labeled in

Table 3. Extremal trees of $ln{\mathcal{T}}_f$.

Indices	$\mathit{f}(\mathit{x},\mathit{y})$	Min	Max
Inverse sum index	${\displaystyle \frac{xy}{x+y}}$	$S_n$
Reciprocal Randič index	$\sqrt{\left(xy\right)}$	$P_n$	$S_n$
General second Zagreb index	${\left(xy\right)}^{\alpha }(\alpha \ge 1)$	$P_n$	$S_n$
Forgotten index	$x^2+y^2$	$P_n$
Sombor index	$\sqrt{x^2+y^2}$	$P_n$
Reduced Sombor index	$\sqrt{{(x-1)}^2+{(y-1)}^2}$	$P_n$
General first Zagreb index	${(x+y)}^{\alpha }(\alpha \ge 1)$	$P_n$
First Gourava index	$x+y+xy$	$P_n$
First hyper-Gourava index	${(x+y+xy)}^2$	$P_n$
Second Gourava index	$(x+y)xy$	$P_n$
Second hyper-Gourava index	${\left((x+y)xy\right)}^2$	$P_n$
Product-connectivity Gourava index	$\sqrt{(x+y)xy}$	$P_n$

.

Likewise, if $f(x,y)=\sqrt{\left(xy\right)}$, or ${\left(xy\right)}^{\alpha }(\alpha \ge 1)$, by Lemma 3, the conditions of Theorem 2 are established. Thus, according to Theorem 2, the maximal tree is $S_n$ for the logarithmic reciprocal Randič index and general second Zagreb index. Similarly, if $f(x,y)={\displaystyle \frac{xy}{x+y}}$, by Lemma 4, the conditions of Theorem 3 are established. Therefore, by applying Theorem 3, the minimal tree is $S_n$ for the logarithmic Inverse sum index. The main results are depicted in Table 3.

7. Conclusions

Our main contribution consists in introducing the logarithmic VDB index $ln{\mathcal{T}}_f$ and investigating the minimal and maximal trees for $ln{\mathcal{T}}_f\left(T\right)$. In Section 2, the logarithmic VDB index is shown to have excellent discriminability, and its research is of theoretical significance and practical value.

As the inverse function of the exponential VDB index, we speculated that the corresponding extremum results may be opposite. However, based on our work in Section 4 and Section 5, this is not the case. This implies that the logarithmic VDB index $ln{\mathcal{T}}_f$ is interesting.

However, due to the fact that logarithmic functions do not have good monotonicity and convexity, the study of $ln{\mathcal{T}}_f$ has become very complex, to the extent that in Table 3, we only determined maximal values of $ln{\mathcal{T}}_f\left(T\right)$ for $f(x,y)=\sqrt{\left(xy\right)}$, and ${\left(xy\right)}^{\alpha }(\alpha \ge 1)$. Therefore, the study of the logarithmic VDB index is an interesting but difficult task that requires further resolution.