Greedoids and Violator Spaces

Abstract

This research explores the interplay between violator spaces and greedoids—two distinct theoretical frameworks developed independently. Violator spaces were introduced as a generalization of linear programming, while greedoids were designed to characterize combinatorial structures where greedy algorithms yield optimal solutions. These frameworks have, until now, existed in isolation. This paper bridges the gap by showing that greedoids can be defined using a modified violator operator. The established connections not only deepen our understanding of these theories but also provide a new characterization of antimatroids.

1. Preliminaries

The primary objective of the paper is to establish connections between two combinatorial concepts: violator spaces and greedoids. Violator spaces emerged as a generalization of Linear Programming (LP) problems. LP-type problems were introduced and studied by Matoušek, Sharir, and Welzl [1,2] as a combinatorial framework encompassing linear programming and other computational geometric problems. Subsequently, Matoušek [3] introduced violator spaces as a simpler framework that generalizes LP-type problems. Violator spaces provide an abstract structure that facilitates the formulation and design of efficient algorithms for solving optimization problems across diverse areas, such as computational geometry [4], computational algebra [5], and machine learning [6].

Greedoids were introduced in an effort to characterize combinatorial structures where the greedy algorithm yields optimal solutions [7,8]. Numerous examples of greedoids appear in various areas of mathematics [9,10]. This work explores the relationships between violator spaces and greedoids, showing that greedoids can be defined using a variant of the violator operator. These interrelations provide a new characterization of antimatroids.

2. Violator Spaces

Definition 1 

([3]). A violator space is a pair $(E,\nu )$, where E is a finite set and ν is a violator operator, i.e., a mapping $2^E\to 2^E$, such that for all subsets $X,Y\subseteq E$ the following properties are satisfied:

V1: $X\cap \nu \left(X\right)=\varnothing$ (consistency);

V2: $(X\subseteq Y$ and $Y\cap \nu \left(X\right)=\varnothing )\Rightarrow \nu (X)=\nu (Y)$ (locality).

Let $(E,\nu )$ be a violator space. Let $\phi \left(X\right)=E-\nu \left(X\right)$. So, if $\nu$ is defined by (3) then

$$\phi \left(X\right)=\{a\in E:w(X\cup a)=w(X\left)\right\}.$$

(1)

Theorem 1 

([11]). Let E be a finite set and $\nu ,\phi :2^E\to 2^E$ two mappings, such that $\phi \left(X\right)=E-\nu \left(X\right)$ for all $X\subseteq E$. Then, $(E,\nu )$ is a violator space if and only if φ satisfies

C1: $X\subseteq \phi \left(X\right)$ (extensivity);

C2: $(X\subseteq Y\subseteq \phi (X\left)\right)\Rightarrow \phi \left(X\right)=\phi \left(Y\right)$ (self-convexity).

Thus, we have two equivalent approaches to defining violator spaces:

• the classic one—$(E,\nu )$, where the ground set E is equipped with the mapping $\nu$ satisfying consistency and locality;
• the dual one—$(E,\phi )$, where the ground set E is equipped with the mapping $\phi$ satisfying extensivity and self-convexity.

In what follows, a pair $(E,\phi )$, where E is a finite set and $\phi$ is a mapping satisfying extensivity and self-convexity, will be considered a violator space as well.

Since a violator operator $\phi$ is extensive it may be interpreted as a type of a “closure” operator. The concept of closure appears in many disciplines, including topology, algebra, logic, geometry, convexity analysis, graph theory, etc. It is also known by other names, such as span, hull, and envelope. For instance, the convex hull operator on the Euclidean space is a classic example of a closure operator.

Definition 2. 

Let E be a finite set; $\tau :2^E\to 2^E$ is a closure operator on E if for all subsets $X,Y\subseteq E$ the following properties are satisfied:

CL1: $X\subseteq \tau \left(X\right)$ (extensivity);

CL2: $X\subseteq Y\Rightarrow \tau \left(X\right)\subseteq \tau \left(Y\right)$ (isotonicity);

CL3: $\tau \left(\tau \right(X\left)\right)=\tau \left(X\right)$ (idempotence).

It is proved that every closure operator is a violator operator, since isotonicity and idempotence imply self-convexity, and extensivity with self-convexity implies idempotence [11]. However, not each violator operator is a closure operator, since it does not have to satisfy isotonicity.

Let us consider some additional properties of violator operators.

Lemma 1. 

Let $(E,\phi )$ be a violator space. Then, $X\subseteq \phi \left(Y\right)\iff \phi \left(Y\right)=\phi (Y\cup X)$ for all $X,Y\subseteq E$.

Proof. 

“If”: Let $\phi \left(Y\right)=\phi (Y\cup X)$. Since extensivity implies $X\subseteq Y\cup X\subseteq \phi (Y\cup X)$, we conclude with $X\subseteq \phi \left(Y\right)$.

“Only if”: If $X\subseteq \phi \left(Y\right)$ then $Y\subseteq Y\cup X\subseteq \phi \left(Y\right)$. Hence, by self-convexity, $\phi \left(Y\right)=\phi (Y\cup X)$. □

Proposition 1. 

Let E be a finite set. For each extensive operator $\phi :2^E\to 2^E$ self-convexity is equivalent to the following property:

C22: $(X\subseteq \phi (Y)\wedge Y\subseteq \phi (X\left)\right)\Rightarrow \phi \left(X\right)=\phi \left(Y\right)$ for all $X,Y\subseteq E$.

Proof. 

1. C2 ⇒ C22: From Lemma 1 $(X\subseteq \phi (Y)\wedge Y\subseteq \phi (X\left)\right)\Rightarrow \phi \left(Y\right)=\phi (X\cup Y)=\phi \left(X\right)$. Hence, $\phi \left(X\right)=\phi \left(Y\right)$.

2. C22 ⇒C2: $(X\subseteq Y\subseteq \phi (X\left)\right)\Rightarrow X\subseteq \phi \left(Y\right)\wedge Y\subseteq \phi \left(X\right)$ (from extensivity). Then, C22 implies $\phi \left(X\right)=\phi \left(Y\right)$. □

Lemma 2 

([11]). Let $(E,\phi )$ be a violator space. Then,

$\phi \left(X\right)=\phi \left(Y\right)\Rightarrow \phi (X\cup Y)=\phi \left(X\right)=\phi \left(Y\right)$

2.1. Uniquely Generated Violator Spaces

Let $(E,\alpha )$ be an arbitrary space with the operator $\alpha :2^E\to 2^E$. $B\subseteq E$ is a generator of $X\subseteq E$ if $\alpha \left(B\right)=\alpha \left(X\right)$. A basis of X is an inclusion-minimal set $B\subseteq E$ (not necessarily included in X) with $\alpha \left(B\right)=\alpha \left(X\right)$. A space $(E,\alpha )$ is uniquely generated if every set $X\subseteq E$ has a unique basis.

Proposition 2 

([11]). A violator space $(E,\phi )$ is uniquely generated if and only if for every $X,Y\subseteq E$

$$\phi \left(X\right)=\phi \left(Y\right)\Rightarrow \phi (X\cap Y)=\phi \left(X\right)=\phi \left(Y\right).$$

(2)

It is known that a closure operator $\tau$ is uniquely generated if and only if it satisfies the anti-exchange property [10,12,13]:

$$p,q\notin \tau \left(X\right)\wedge p\in \tau (X\cup q)\Rightarrow q\notin \tau (X\cup p).$$

We extend this characterization to violator spaces in the following:

Theorem 2 

([11]). Let $(E,\phi )$ be a violator space. Then, $(E,\phi )$ is uniquely generated if and only if the operator φ satisfies the anti-exchange property.

An element x of a subset $X\subseteq E$ is an extreme point of X if $x\notin \alpha (X-x)$. The set of extreme points of X is denoted by $ex\left(X\right)$.

Proposition 3 

([11]). For violator spaces: $x\in ex\left(X\right)$ if and only if $\phi \left(X\right)\ne \phi (X-x)$.

Theorem 3 

([11]). Let $(E,\phi )$ be a violator space. Then, $(E,\phi )$ is uniquely generated if and only if for every set $X\subseteq E$, $\phi \left(X\right)=\phi \left(ex\right(X\left)\right)$.

Corollary 1 

([11]). Let $(E,\phi )$ be a uniquely generated violator space. Then, for every $X\subseteq E$ the set $ex\left(X\right)$ is the unique basis of X.

2.2. LP-Type Problems

A different way to define violator spaces, consistent with their historical development, is through their introduction as a framework that generalizes LP-type problems.

An LP-type problem is defined by a finite set E of constraints and a value $w\left(X\right)$ associated with every subset $X\subseteq E$. These values can be real numbers or elements of any other linearly ordered set. The mapping $X\to w\left(X\right)$ must satisfy the axioms outlined in the following definition.

Definition 3 

([3]). An LP-type problem is a quadruple $(E,w,W,\le )$, where E is a finite set, W is a set linearly ordered by ≤, and w is a mapping $2^E\to W$, such that for all subsets $X,Y\subseteq E$ the following properties are satisfied:

V11: $X\subseteq Y\Rightarrow w\left(X\right)\le w\left(Y\right)$ (monotonicity);

V22: for all $X\subseteq Y$, if $w\left(X\right)=w\left(Y\right)$ and there exists $a\in E$ such that $w\left(Y\right)<w(Y\cup a)$ then $w\left(X\right)<w(X\cup a)$ (locality).

A classic example of an LP-type problem is the computation of the smallest circle that contains all of a given finite set of points in the Euclidean plane. In this case, E represents a set of points in the plane, and $w\left(X\right)$ is the radius of the smallest circle that encloses all points of X. Monotonicity of w is straightforward. To demonstrate locality, observe that for $X\subseteq Y$ if $w\left(X\right)=w\left(Y\right)$ then X and Y share the same smallest enclosing circle. If $w\left(Y\right)<w(Y\cup a)$ then a lies outside this circle, which, in turn, means $w\left(X\right)<w(X\cup a)$.

For an LP-type problem $(E,w,W,\le )$ and for $X\subseteq E$, a basis of X is an inclusion-minimal subset B of X with $w\left(B\right)=w\left(X\right)$. Solving an LP-type problem $(E,w,W,\le )$ means identifying a basis of E.

Let us again illustrate this, using the smallest circle problem. A basis of X is a minimal subset of points that share the same enclosing circle as X. Specifically, all points in this basis lie on the boundary of the circle.

The set of all constraints violating $X\subseteq E$, denoted as $\nu \left(X\right)$, is defined as

$$\nu \left(X\right)=\{a\in E:w(X\cup a)>w(X\left)\right\}.$$

(3)

This set includes all elements a in the ground set E that are not in X and, when added to X, cause the objective function w to increase. For the smallest circle problem, the violated constraints of X are precisely the points that lie outside the smallest enclosing circle of X.

One can see that the condition $w\left(X\right)=w\left(Y\right)$ generally does not suffice for $\nu \left(X\right)=\nu \left(Y\right)$. For example [3], if $w\left(X\right)=\left|X\right|$ for all $X\subseteq E$ then any X of the same size will have the same $w\left(X\right)$; however, $\nu \left(X\right)=E-X$, and so no distinct sets X share the value of $\nu \left(X\right)$. Thus, we can see that w by itself does not capture the combinatorial structure of the problem. To describe the “structure” of an LP-type problem Matoušek et al. [3] introduced the concept of a violator space and proved that every LP-type problem can naturally be converted into a violator space with violator mapping $\nu$ but that the reverse is not necessarily true.

Proposition 4 

([3]). Consider an LP-type problem $(E,w,W,\le )$, and let ν be its violator mapping defined by (3). Then, $(E,\nu )$ is a violator space and $(E,\nu )$ is basis-equivalent to $(E,w,W,\le )$.

Take a small example, to illustrate how LP-type systems really create a violator space and bases.

Example 1. 

Build the simplest LP-type system whose atoms a, b, c, d have weights 1, 2, 2, 3, respectively. The full definition of the function w, the corresponding function ν, and the bases are shown in

Table 1. An example involving four elements.

X	$\mathit{w}\left(\mathit{X}\right)$	$\mathit{\nu }\left(\mathit{X}\right)$	Bases
$\left\{a\right\}$	1	$\{b,c,d\}$	$\left\{a\right\}$
$\left\{b\right\}$	2	$\left\{d\right\}$	$\left\{b\right\}$
$\left\{c\right\}$	2	$\left\{d\right\}$	$\left\{c\right\}$
$\left\{d\right\}$	3	∅	$\left\{d\right\}$
$\{a,b\}$	2	$\left\{d\right\}$	$\left\{b\right\}$
$\{a,c\}$	2	$\left\{d\right\}$	$\left\{c\right\}$
$\{a,d\}$	3	∅	$\left\{d\right\}$
$\{b,c\}$	2	$\left\{d\right\}$	$\left\{b\right\},\left\{c\right\}$
$\{b,d\}$	3	∅	$\left\{d\right\}$
$\{c,d\}$	3	∅	$\left\{d\right\}$
$\{a,b,c\}$	2	$\left\{d\right\}$	$\left\{b\right\},\left\{c\right\}$
$\{a,b,d\}$	3	∅	$\left\{d\right\}$
$\{a,c,d\}$	3	∅	$\left\{d\right\}$
$\{b,c,d\}$	3	∅	$\left\{d\right\}$
$\{a,b,c,d\}$	3	∅	$\left\{d\right\}$

.

It is easy to see that the operator w is monotone and satisfies locality. It is not a uniquely generated space, since the subsets $\{b,c\}$ and $\{a,b,c\}$ each have two bases.

In the previous example, the violator operator $\nu$ is also a closure operator, as it is monotone. Consider another example, which encapsulates all the previous definitions and illustrates the basic concepts of LP-type problems.

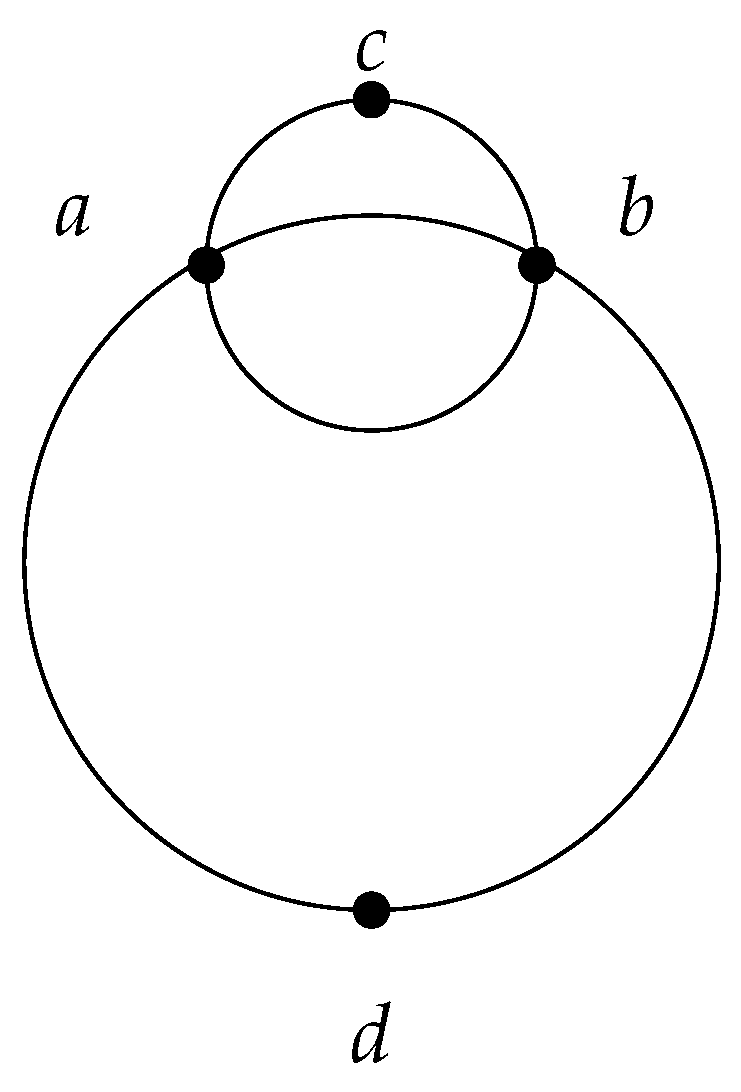
Example 2. 

Let $E=\{a,b,c,d\}$ be four points in the Euclidean plane, such that point c lies on the boundary of the circle passing through points a and b.

Let us sort the radii of the enclosing circles by size. For each point from E, the radius of its circle is 0. The radius of the circle that encloses the pair of points $(a,c)$ or $(b,c)$ is half the distance between the two points. The radius of the circle that encloses both points a and b is equal to the radius of the circle that encloses all three points a, b, and c, making it the third-largest radius. The next-largest radius is for the pairs $(a,d)$ and $(b,d)$, and so on.

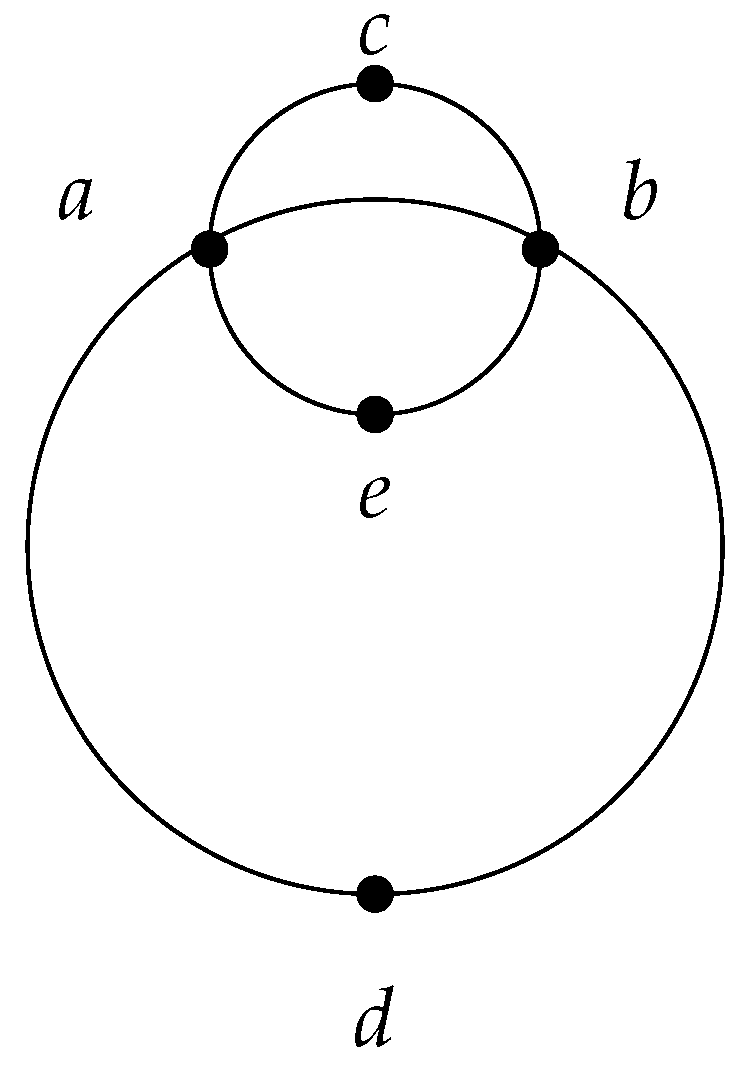
The full definitions of the function w and the corresponding functions ν and φ are shown in

Table 2. An example of four points in a coordinate system.

X	$\mathit{w}\left(\mathit{X}\right)$	$\mathit{\nu }\left(\mathit{X}\right)$	$\mathit{\phi }\left(\mathit{X}\right)$
$\left\{a\right\}$	0	$\{b,c,d\}$	$\left\{a\right\}$
$\left\{b\right\}$	0	$\{a,c,d\}$	$\left\{b\right\}$
$\left\{c\right\}$	0	$\{a,b,d\}$	$\left\{c\right\}$
$\left\{d\right\}$	0	$\{a,b,c\}$	$\left\{d\right\}$
$\{a,b\}$	2	$\left\{d\right\}$	$\{a,b,c\}$
$\{a,c\}$	1	$\{b,d\}$	$\{a,c\}$
$\{a,d\}$	3	$\{b,c\}$	$\{a,d\}$
$\{b,c\}$	1	$\{a,d\}$	$\{b,c\}$
$\{b,d\}$	3	$\{a,c\}$	$\{b,d\}$
$\{c,d\}$	5	∅	$\{a,b,c,d\}$
$\{a,b,c\}$	2	$\left\{d\right\}$	$\{a,b,c\}$
$\{a,b,d\}$	4	$\left\{c\right\}$	$\{a,b,d\}$
$\{a,c,d\}$	5	∅	$\{a,b,c,d\}$
$\{b,c,d\}$	5	∅	$\{a,b,c,d\}$
$\{a,b,c,d\}$	5	∅	$\{a,b,c,d\}$

.

It is easy to see that the operator w is monotone and satisfies locality. However, the operator $\phi \left(X\right)$ does not satisfy monotonicity. Indeed, while $X=\{a,b\}\subseteq Y=\{a,b,d\}$, $\phi \left(X\right)=\{a,b,c\}⊈\phi \left(Y\right)=\{a,b,d\}$ (see Table 1 and Figure 1). From this example, we can also gain a better understanding of the notion of basis. Thus, the basis of the subset $\{a,b,c\}$ is the pair $\{a,b\}$, and the basis of E is a pair $\{c,d\}$. Note that a unique basis is not always guaranteed. If we add another point e on the circle passing through points $\{a,b\}$, exactly opposite point c, we obtain two bases for $\{a,b,c,e\}$: the pair $\{a,b\}$ and the pair $\{c,e\}$ (see Figure 2).

3. Greedoids

The concept of a greedoid was introduced by Bernhard Korte and László Lovász around 1980 as a way to generalize the notion of structures that can be optimized using greedy algorithms [7].

Definition 4. 

A set system $(E,\mathcal{F})$ is a greedoid if the following properties are satisfied:

(i) $\varnothing \in \mathcal{F}$;

(ii) $X,Y\in \mathcal{F},\left|X\right|<\left|Y\right|\Rightarrow \exists y\in Y-X$, such that $X\cup y\in \mathcal{F}$ (augmentation property).

Elements of $\mathcal{F}$ are called feasible sets.

The rank function of a greedoid is defined as follows:

$$r\left(X\right)=max\left\{\right|A|:A\subseteq X,A\in \mathcal{F}\}.$$

Theorem 4 

([10]). A function $r:2^E\to Z^{+}$ is the rank function of a greedoid if and only if for all $X,Y\subseteq E$ and all $x,y\in E$ the following conditions hold:

(1.1) $r(\varnothing )=0$

(1.2) $r\left(X\right)\le \left|X\right|$ (subcardinality)

(1.3) $X\subseteq Y$ implies $r\left(X\right)\le r\left(Y\right)$ (monotonicity)

(1.4) $r\left(X\right)=r(X\cup x)=r(X\cup y)$ implies $r\left(X\right)=r(X\cup x\cup y)$ (local submodularity).

Moreover, the greedoid is uniquely determined by its rank function:

$$\mathcal{F}=\{X:r(X)=|X\left|\right\}.$$

(4)

So, the pair $(E,r)$ may be considered as a greedoid with $\mathcal{F}$ defined by (4).

3.1. LP-Type Problems and Greedoids

The rank function r of a greedoid satisfies all the properties of the mapping w of an LP-type problem. It is monotone (Theorem 4) and satisfies the locality.

Proposition 5. 

Let $(E,\mathcal{F})$ be a greedoid with rank function r. Then, $r\left(X\right)=r\left(Y\right)$ and $r\left(Y\right)<r(Y\cup a)$ implies $r\left(X\right)<r(X\cup a)$ for all $X\subseteq Y$ and $a\in E$.

Proof. 

If $X\subseteq Y$ and $r\left(X\right)=r\left(Y\right)$ there is a maximal feasible set $A\subseteq X$, with $\left|A\right|=r\left(X\right)=r\left(Y\right)$. In addition, there is a feasible set $C\subseteq (Y\cup a)$, with $\left|C\right|>\left|A\right|$. Since A is a maximal feasible set in Y, $C⊈Y$, $a\notin Y$ and $a\in C$. Then (from the augmentation property), there exists $x\in C$ for which $A\cup x\in \mathcal{F}$. Since A is a maximal feasible set in Y, $x\notin Y$, and so $x=a$, i.e., $A\cup a$ is a feasible set, and then $r\left(X\right)<r(X\cup a)$. □

Thus, each greedoid $(E,r)$ may be considered as an LP-type problem $(E,r,Z^{+},\le )$.

Note that the family $\mathcal{F}$ is the family of all the bases of an LP-type problem, since for each proper subset A of a feasible set,

$$X\in \mathcal{F},r\left(A\right)\le \left|A\right|<\left|X\right|=r\left(X\right).$$

However, if the bases of an LP-type problem $(E,w,Z^{+},\le )$ form a greedoid, a function w does not have to be a greedoid’s rank function. For example, every monotone function w with different values on each element of $2^E$ turns all subsets of E to bases. While the bases constitute a greedoid, a function w does not have to satisfy subcardinality.

Let us build a specific LP-type problem $(E,w,Z^{+},\le )$, where E is a finite set and w is a mapping $2^E\to Z^{+}$, such that for all subsets $X,Y\subseteq E$ the following properties are satisfied:

(1) $w(\varnothing )=0$;

(2) $w\left(X\right)\le \left|X\right|$ (subcardinality);

(3) $X\subseteq Y$ implies $w\left(X\right)\le w\left(Y\right)$ (monotonicity);

(4) For all $X\subseteq Y$ if $w\left(X\right)=w\left(Y\right)$ and there exists $a\in E$ such that $w\left(Y\right)<w(Y\cup a)$ then $w\left(X\right)<w(X\cup a)$ (locality).

The property (4) may be reformulated as follows:

(5) For all $X\subseteq Y$ and $a\in E$ with $w\left(X\right)=w\left(Y\right)$ and $w\left(X\right)=w(X\cup a)$ we have $w\left(Y\right)=w(Y\cup a)$.

Proposition 6. 

Let w be a monotone mapping on $2^E$. Then, locality (5) is equivalent to local submodularity (1.4).

Proof. 

1. Let w satisfy locality and $w\left(X\right)=w(X\cup x)=w(X\cup y)$. Denote $Y=X\cup x$. Then, $X\subseteq Y$, $w\left(X\right)=w\left(Y\right)$ and $w\left(X\right)=w(X\cup y)$; then, (from (5)) we have $w\left(X\right)=w\left(Y\right)=w(Y\cup y)=w(X\cup x\cup y)$.

2. Let w satisfy local submodularity, $X\subseteq Y\subseteq E$, $a\in E$, $w\left(X\right)=w\left(Y\right)$, and $w\left(X\right)=w(X\cup a)$. By repeatedly applying local submodularity we prove that $w\left(Y\right)=w(Y\cup a)$. It is easy to see that the proposition is correct for $a\in Y$. Let $Y-X=\{y_1,y_2,\dots ,y_n\}$. From monotonicity it follows that $w\left(X\right)=w(X\cup y_1)=w\left(Y\right)$. Hence, $w\left(X\right)=w(X\cup a)=w(X\cup y_1)$. Local submodularity implies $w\left(X\right)=w(X\cup y_1\cup a)$. Denote $Y_k=X\cup \{y_1,y_2,\dots ,y_k\}$.

Prove by induction on n that $w\left(X\right)=w(Y_k\cup a)$ for each $1\le k\le n$. From monotonicity it follows that $w\left(X\right)=w\left(Y_k\right)$ for each $1\le k\le n$. Then, $w\left(X\right)=w(Y_k\cup a)=w(Y_k\cup y_{k+1})$ implies $w\left(X\right)=w(Y_{k+1}\cup a)$. Thus, $w\left(X\right)=w\left(Y\right)=w(Y_n\cup a)=w(Y\cup a)$. □

In fact, the property of local submodularity may be extended as follows.

Corollary 2. 

If $X,Y\subseteq E$ such that $w\left(X\right)=w\left(Y\right)=w(X\cap Y)$ then $w(X\cap Y)=w(X\cup Y)$.

Theorem 4 implies that an LP-type problem with mapping $w(\varnothing )=0$ and $w\left(X\right)\le \left|X\right|$ determines a greedoid $(E,w)$ by $\mathcal{F}=\{X:w\left(X\right)=\left|X\right|\}$.

3.2. Violator and Rank Closure Operators on Greedoids

Define (rank) closure operator of greedoids ([10]): $\sigma \left(X\right)=\{x:r(X\cup x)=r(X\left)\right\}$. The operator is extensive ($CL1$) and idempotent ($CL3$), but it does not have to be an isotone operator. So, $\sigma$ is not always a closure operator. At the same time, the definition of $\sigma$ coincides with the definition of a violator operator (1). The following theorem supports the interpretation of greedoids as a subclass of violator spaces, since Properties (i) and (ii) define a violator operator.

Theorem 5 

([14]). A mapping $\sigma :2^E\to 2^E$ is the closure operator of some greedoid $(E,\mathcal{F})$ if and only if

(i) $X\subseteq \sigma \left(X\right)$

(ii) $(X\subseteq Y\subseteq \sigma (X\left)\right)\Rightarrow \sigma \left(X\right)=\sigma \left(Y\right)$

(iii) if $z\notin \sigma (X\cup x-z)$ for all $z\in X\cup x$ and $x\in \sigma (X\cup y)$ then $y\in \sigma (X\cup x)$.

Moreover, if σ satisfies (i), (ii), and (iii) then

$\mathcal{F}=\{X\subseteq E:\forall x\in X:x\notin \sigma (X-x\left)\right\}$.

Based on the definition of extreme points, we have

$$\mathcal{F}=\{X\subseteq E:X=ex(X\left)\right\}.$$

Then, the following condition $z\notin \sigma (X\cup x-z)$ for all $z\in X\cup x$ is equivalent to $X\cup x\in \mathcal{F}$, and so the property (iii) may be rewritten as follows:

$$(X\cup x\in \mathcal{F})\wedge (x\in \sigma (X\cup y\left)\right)\Rightarrow y\in \sigma (X\cup x).$$

(5)

Define $\mathcal{B}=\{X\subseteq E:\forall Y\subset X:\sigma (X)\ne \sigma (Y\left)\right\}$—the family of bases with respect to operator $\sigma$.

Proposition 7. 

$\mathcal{B}=\mathcal{F}$ for each violator operator σ.

Proof. 

If $X\in \mathcal{B}$, i.e., for all $Y\subset X:\sigma \left(X\right)\ne \sigma \left(Y\right)$ then for all $x\in X$ holds $\sigma \left(X\right)\ne \sigma (X-x)$, and so (from Proposition 3) $x\notin \sigma (X-x)$. Then, $\mathcal{B}\subseteq \mathcal{F}$. If $X\notin \mathcal{B}$ then there exists $Y\subset X$, such that $\sigma \left(X\right)=\sigma \left(Y\right)$. Hence, for each $x\in X-Y$ self-convexity implies $\sigma \left(X\right)=\sigma (X-x)$, i.e., $x\in \sigma (X-x)$. This concludes the proof, with $\mathcal{F}\subseteq \mathcal{B}$. □

It is worth mentioning that Property (iii) is not necessary for $\mathcal{F}$ to be a greedoid.

Example 3. 

Let $E=\{1,2,3\}$. Define $\phi \left(X\right)=X$ for each $X\subseteq E$ except $\phi \left(\right\{1\left\}\right)=\phi \left(\right\{1,3\left\}\right)=\{1,3\}$. It is easy to check that the space $(E,\phi )$ is a uniquely generated violator space (it satisfies both extensivity and convexity) where the family of bases $\mathcal{F}=P\left(\right\{1,2,3\left\}\right)-\{1,3\}$ forms a greedoid. At the same time, operator φ does not satisfy (5), which is equivalent to (iii). Indeed, if $X=\varnothing ,x=3,y=1$ then $X\cup x=\left\{3\right\}\in \mathcal{F}$, $x\in \phi (X\cup y)=\phi \left(\right\{1\left\}\right)=\{1,3\}$, but $y\notin \phi (X\cup x)=\phi \left(\right\{3\left\}\right)$.

If we consider the rank function of the greedoid, we can see that $r\left(\right\{1\left\}\right)=r\left(\right\{3\left\}\right)=r\left(\right\{1,3\left\}\right)$, and so $\sigma \left(\right\{1\left\}\right)=\sigma \left(\right\{3\left\}\right)=\{1,3\}$. Then, for this function σ the property (iii) holds and we have a not-uniquely-generated violator space.

Thus, the same family of bases may be obtained by different mappings.

3.3. Antimatroids—Uniquely Generated Greedoids

An antimatroid is a combinatorial structure related to the concept of a greedoid, and it describes a process where elements are added to a set in a sequential manner, subject to certain constraints. Antimatroids have many applications. Thus, game theory provides a framework in which antimatroids are interpreted as permission structures for coalitions [15]. In mathematical psychology, antimatroids are used to describe the feasible states of knowledge of a human learner [16,17].

Antimatroids have various definitions. We will use the following.

Definition 5. 

An antimatroid is a greedoid closed under union.

To provide an equivalent definition, we need to introduce the concept of accessibility.

Definition 6. 

An accessible set system $(E,\mathcal{F})$ is a set system in which every non-empty feasible set $X\in \mathcal{F}$ contains an element x, such that $X-x$ is feasible.

By definition, the family of feasible sets of a greedoid is an accessible set system.

Lemma 3 

([10]). For an accessible set system $(E,\mathcal{F})$ the following statements are equivalent:

(A1) $(E,\mathcal{F})$ is an antimatroid

(A2) $\mathcal{F}$ is closed under union

(A3) $A,A\cup x,A\cup y\in \mathcal{F}$ implies $A\cup \{x,y\}\in \mathcal{F}$.

Proposition 8. 

An antimatroid is a uniquely generated greedoid.

Proof. 

Let $\mathcal{F}$ be an antimatroid. Since each antimatroid is a greedoid, it remains to prove that the greedoid is uniquely generated. Suppose there are two bases, $B_1$ and $B_2$, such that $\sigma \left(B_1\right)=\sigma \left(B_2\right)$. Since $\mathcal{F}$ is a family of bases then $B_1,B_2\in \mathcal{F}$. Hence, $B_1\cup B_2\in \mathcal{F}$, because $\mathcal{F}$ is an antimatroid. But $\sigma (B_1\cup B_2)=\sigma \left(B_1\right)$ (see Lemma 2). Contradiction. □

Since, for each greedoid $\sigma$ is a violator operator, Theorem 2 implies the following.

Corollary 3. 

The operator σ of each antimatroid satisfies the anti-exchange property.

Theorem 6. 

The family $\mathcal{F}$ is an antimatroid if and only if $\mathcal{F}$ is a uniquely generated greedoid.

Proof. 

It remains to be proven that each uniquely generated greedoid is an antimatroid. Suppose $A,A\cup x,A\cup y\in \mathcal{F}$ but $A\cup \{x,y\}\notin \mathcal{F}$. Then, $x,y\notin \sigma \left(A\right)$, $x\in \sigma (A\cup y)$ and $y\in \sigma (A\cup x)$. Contradiction to anti-exchange property. □

4. Conclusions

We have shown that greedoids can be defined using a variant of the violator operator. The connections between violator spaces and greedoids have enabled us to provide a new characterization of antimatroids.

To gain further structural insights into antimatroids, one can explore co-spanning relations. Given an operator $\sigma$, two sets X and Y are co-spanning if $\sigma \left(X\right)=\sigma \left(Y\right)$. The equivalence relation known as co-spanning has been studied for greedoids [10], and it has been shown that this relation uniquely determines greedoids.

Similar equivalence relations have also been explored for violator spaces [11,18,19]. It is known that violator operators are closed under union (Lemma 2) and satisfy the following property [11]:

$$(X\subseteq Y\subseteq Z)\wedge \left(\phi \right(X)=\phi (Z\left)\right)\Rightarrow \phi \left(X\right)=\phi \left(Y\right)=\phi \left(Z\right)$$

which we refer to as convexity, in accordance with Monjardet [20], since this property addresses all sets lying between two given sets.

Based on this property, it was proved [19] that the equivalence classes of a co-spanning relation are closed under union and convex if and only if they arise from a co-spanning relation of a violator space. Moreover, a co-spanning partition to intervals ${\left[A\right]}_{\phi }=[ex\left(A\right),\phi \left(A\right)]$ corresponds to a uniquely generated violator space. We extended this approach to antimatroids and convex geometries, with the initial results available in [21]. Further investigation of these structures could lead to new characterizations of antimatroids and other combinatorial structures.

It seems very appealing to generalize our findings to the infinite case. As we see it, topological spaces may provide the main motivation for such a generalization [22].