1. Introduction
For notations and graph-theoretical terminologies not defined here, we follow [
1]. All graphs in this paper are undirected, simple and finite. Let
be a graph, where
is the vertex set and
is the edge set. Let
be the order of
G and
be the size of
G. For a vertex
, the neighborhood of
u in
G is
is adjacent to
, and the degree of
u in
G is
. The minimum degree
of
G is min
. For an edge
,
is the edge-degree of
e in
G. The minimum edge-degree of
G, denoted by
, is
. Obviously,
, with the equality holding if and only if there is an edge
such that
. For a vertex set
, the
of
U in
G, denoted by
, is the graph with the vertex set
U, and the two vertices
u and
v in
U are adjacent if and only if they are adjacent in
G.
For two nonempty subsets , denotes the set of edges with one end in X and the other in Y. When , the set is called an edge-cut of G associated with X. The edge-connectivity of a graph G is defined as the cardinality of a minimum edge-cut of G. It is well known that . Thus, a graph G is said to be maximally edge-connected if , and a graph G is said to be super edge-connected if each minimum edge-cut isolates a vertex of G. By the two definitions above, we know that a super edge-connected graph must be maximally edge-connected. But the converse is not true. For instance, the cycle of an order of at least four is maximally edge-connected but not super edge-connected.
As an interconnection network can be modeled by a graph, the edge-connectivity can be used to measure the network reliability. But there is a deficiency, which allows all edges incident with a vertex to fail simultaneously. This situation is highly improbable in practical network applications. For compensating this deficiency, all kinds of concepts extending the edge-connectivity were proposed. Esfahanian and Hakimi [
2] introduced the notion of restricted edge-connectivity. If an edge set
satisfying
G–
S is disconnected and each component of
G–
S has at least two vertices, then
S is called a restricted edge-cut. The restricted edge-connectivity of
G, denoted by
, is the cardinality of a minimum restricted edge-cut of
G if
G has at least one. It was proved in [
2] that if
G is not a star and its order is at least four, then
. In this case, a graph
G is said to be maximally restricted edge-connected if
; a graph
G is said to be super restricted edge-connected if each minimum restricted edge-cut isolates an edge of
G. By these two definitions, we know that a super restricted edge-connected graph must be maximally restricted edge-connected. But the converse is not true. For instance, the cycle of an order of at least six is maximally restricted edge-connected but not super restricted edge-connected.
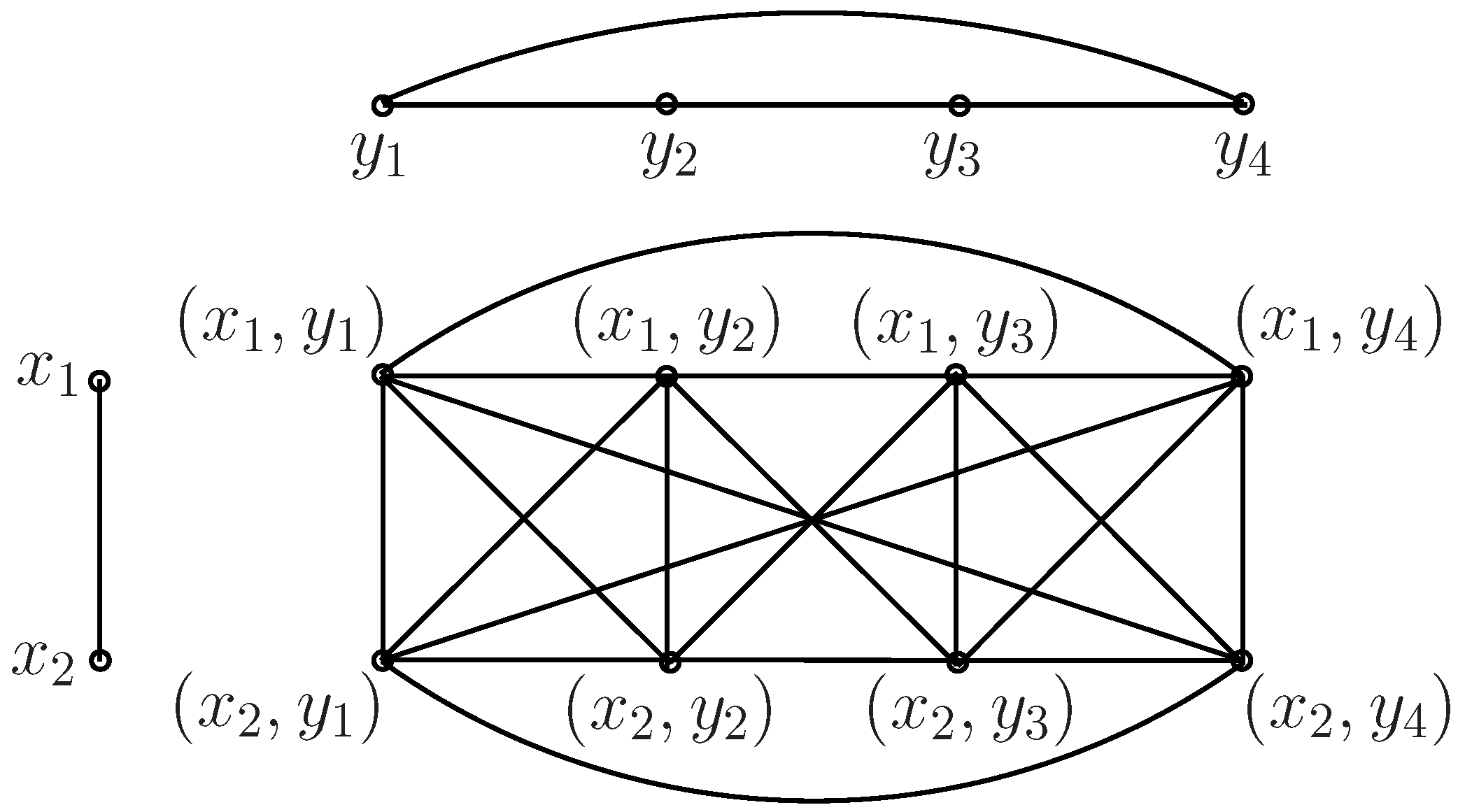
The concept of the graph product is utilized to construct larger graphs from smaller ones. There are various kinds of graph products, including Cartesian products, direct products and strong products, etc. Given two graphs
G and
H, the vertex sets of the Cartesian product
, the direct product
and the strong product
are all
. For two distinct vertices
and
, they are adjacent in
if and only if
and
is an edge in
H, or
and
is an edge in
G; they are adjacent in
if and only if
is an edge in
G and
is an edge in
H; and they are adjacent in
if and only if
and
is an edge in
H, or
and
is an edge in
G, or
is an edge in
G and
is an edge in
H. Clearly, the edge set of
is the union of the edge sets of
and
. See
Figure 1 for an illustration of the strong product graph
.
In [
3], Klavžar and Špacapan obtained the edge-connectivity of the Cartesian product of two nontrivial connected graphs. Shieh [
4] characterized the super edge-connected Cartesian product graphs of two maximally edge-connected regular graphs. For the results on the restricted edge-connectivity of Cartesian product graphs, see [
5,
6,
7] for references.
Brešar and Špacapan [
8] gave some lower and upper bounds on the edge-connectivity of the direct product of two nontrivial connected graphs. The edge-connectivity of the direct product of a nontrivial connected graph and a complete graph was obtained by Cao, Brglez, Špacapan and Vumar [
9]. In [
10], Špacapan studied the the edge-connectivity of the direct product of two nontrivial connected graphs. He not only obtained the expression of the edge-connectivity but also characterized the structure of each minimum edge-cut in these direct product graphs. In [
11], Ma, Wang and Zhang determined the restricted edge-connectivity of the direct product of a nontrivial connected graph and a complete graph. In [
12], Bai, Tian and Yin further studied the super restricted edge-connectedness of the direct product of a nontrivial connected graph and a complete graph.
The edge-connectivity of the strong products of two nontrivial connected graphs was determined by Brešar and Špacapan in [
13]. Ou and Zhao [
14] studied the restricted edge-connectivity of the strong product of two triangle-free connected graphs. In [
15], Wang, Mao, Ye and Zhao presented an expression of the restricted edge-connectivity of the strong product graphs with two maximally restricted edge-connected graphs.
Motivated by the results above, in this paper, we study the restricted edge-connectivity of the strong product of a nontrivial connected graph with a path, or a cycle or a complete graph. As corollaries, we give some sufficient conditions for these strong product graphs to be maximally restricted edge-connected and super restricted edge-connected. In the next section, we introduce some definitions and lemmas. The main results are presented in
Section 3. We provide some conclusion remarks in the last section.
2. Preliminary
The path, the cycle and the complete graph of order n are denoted by , and , respectively.
Let G and H be two graphs. Define a natural projection p on as follows: for any . For any given vertex x in G, the subgraph induced by in is denoted by . Analogously, for any given vertex y in H, the subgraph induced by in is denoted by . Obviously, and .
In the following lemma, the edge-connectivity of the strong product of two connected nontrivial graphs is presented.
Lemma 1 ([
13])
. Let G and H be two connected nontrivial graphs. Then, Let H be a connected graph. Define , where , is the strong product of the complete graph with only one vertex a and H and is the strong product of the complete graph with only one vertex b and H. By this definition, it can be verified that is connected if and only if H is connected.
Lemma 2 ([
16])
. Let H be a connected graph and S be an edge cut of , where . If the vertices of are in different components of and the vertices of are also in different components of , then . Since for any , we have . Thus, the following lemma holds.
Lemma 3 ([
7])
. Let G be a connected graph. If X is a nonempty subset of , then for any , we have , with all equalities holding if and only if X is a minimum-degree vertex. Lemma 4 ([
2])
. If G is not a star and its order is at least four, then exists and . Lemma 5 ([
14])
. Let G and H be two connected nontrivial graphs. Then, 3. Main Results
Lemma 6. Let G and H be two connected nontrivial graphs of orders m and n, respectively. Then, min.
Proof. Let be a minimum edge-cut of G. Then, is a restricted edge-cut of . By , we have . Analogously, let be a minimum edge-cut of H. Then, is a restricted edge-cut of . By , we have . Thus, min. □
Lemma 7. Let G and H be two connected nontrivial graphs of orders m and n, respectively. Assume S is a minimum restricted edge-cut of and and are two components of –S. If each vertex satisfies and , or each vertex satisfies and , then or .
Proof. Denote and .
Assume each vertex
satisfies
and
. For
, denote
,
. By Lemma 2, we have
for any edge
. Thus,
Analogously, if each vertex satisfies and , then we have . □
Theorem 1. Let G be a connected nontrivial graph of order m. Then, = min, where .
Proof. Denote . Let and , where for . Since and , we have min min by Lemma 6. By Lemmas 4 and 5, . Therefore, .
Now, it is sufficient to prove . Let S be a minimum restricted edge-cut of . Then –S has exactly two components, say and , where and . We consider two cases in the following.
Case 1. Each vertex satisfies and , or each vertex satisfies and .
Assume each vertex satisfies and . Then, by Lemma 7, . Analogously, if each vertex satisfies and , then .
Case 2. There exists a vertex and a vertex such that and or and .
Without loss of generality, assume
and
. By the assumption, we know
and
are contained in
. Let
. Without loss of generality, assume
. For
, denote
,
. For any
, we have
by the definition of the strong product. Hence,
Subcase 2.1. .
When
, we know that
, that is,
. Since
is a connected graph, we have
is connected. If
, then
. If
, by
is connected, then there exists a vertex
such that
. Without loss of generality, assume
and
. Let
. By Lemma 3,
. Thus, by (
1), we have
Subcase 2.2. .
By Lemma 3 and
, we have
For any
, we have
, and for any
, we have
. It follows that
If
, then by (
2), we have
. Therefore, we only need to consider
. There are three subcases in the following.
Subcase 2.2.1. .
If
, then
and
. Furthermore, by (
3), we have
. Thus, by (
1), we obtain that
.
If
, then by (
2) and (
3), we have
Subcase 2.2.2. .
If
, then
. By Lemma 2, we obtain that
. By (
1), we have
.
If
, then by (
3), we have
when
. Suppose
. Since
and
, we have
. Thus, by Lemma 2, we have
Hence, by (
1), we have
.
If
, then by (
2) and (
3), we have
.
Subcase 2.2.3. .
If
, then
. By Lemma 2, we obtain that
. Thus, by (
1), we have
.
Now, we consider
. Let
. If
is connected, then, by a similar argument as Subcase 2.1, we can also obtain
. If
is not connected, then
must contain isolated vertices. Therefore,
. By (
3), it follows that
. Hence, by (
1), we obtain
This proof is thus complete. □
Theorem 2. Let G be a connected nontrivial graph of order m. Then , where .
Proof. Denote . Let and , where for (). Since and , we have min min by Lemma 6. By Lemmas 4 and 5, . Therefore, .
Now, it is sufficient to prove . Let S be a minimum restricted edge-cut of . Then –S has exactly two components, say and , where and . We consider two cases in the following.
Case 1. Each vertex satisfies and , or each vertex satisfies and .
Assume each vertex satisfies and . Then, by Lemma 7, . Analogously, if each vertex satisfies and , then .
Case 2. There exists a vertex and a vertex such that and or and .
Without loss of generality, assume
and
. By the assumption, we know
and
are contained in
. Let
, where the addition is a modular
n operation. Without loss of generality, assume
. For
, denote
,
. For any vertex
, we have
. Then,
. Analogously,
. Hence,
Subcase 2.1. .
When
, we know that
, that is,
. Since
is a connected graph, we have
is connected. If
, then
. If
, then by Lemma 3 and (
4), we have
Subcase 2.2. .
By Lemma 3 and (
4), we have
If
, then we have
. Therefore, we only need to consider
, that is,
and
, or
and
or
and
. Without loss of generality, assume
. By (
3) and (
5), we have
This proof is thus complete. □
Theorem 3. Let G be a connected nontrivial graph of order m. Then, , where .
Proof. Denote . Let and . Since and , we have min min by Lemma 6. By Lemmas 4 and 5, we have . Therefore, .
Now, it is sufficient to prove . Let S be a minimum restricted edge-cut of . Then –S has exactly two components, say and , where and . We consider two cases in the following.
Case 1. Each vertex satisfies and , or each vertex satisfies and .
Assume each vertex satisfies and . Then, by Lemma 7, . Analogously, if each vertex satisfies and , then .
Case 2. There exists a vertex and a vertex such that and or and .
Without loss of generality, assume
and
. By the assumption, we know
and
are contained in
. Since any two distinct vertices are adjacent in
, by renaming the vertices of
, we can let
. Furthermore, assume
. For
, let
,
. Denote
. By the definition of the strong product, for any
, we have
. Hence,
Subcase 2.1. .
When
, we know that
, that is,
. Since
is a connected graph, we have
is connected. If
, then
. If
, then by (
7), we have
Subcase 2.2. .
Subcase 2.2.1. For each , .
By Lemma 2, we have
Since
, we know that
. By (
7), we have
Let and . Since and , we have and . Thus, we obtain .
Subcase 2.2.2. There are at least two integers in , say 1 and 2, such that .
By
, we have
for any
. Analogously,
, for any
. Denote
. Then,
. By Lemma 2, we have
Recall that
and
, then
and
. If
, then
and
. Therefore,
. Otherwise, assume
. Then, by (
7), we have
Since for , we obtain .
Subcase 2.2.3. There is only one integer in , say 1, such that .
If there is a such that , then . By a similar argument as Subcase 2.2.1, we can also obtain . Thus, we assume for .
If
, then
. By Lemma 2, we have
Since
, by (
6), we have
Set . Recall that and . Then, we obtain .
Now, we consider
. Since
for any
, we obtain
for
. Thus,
By using inequality (
7), we obtain
This proof is thus complete. □
4. Concluding Remarks
In this paper, we obtain the restricted edge-connectivity of the strong product of a connected nontrivial graph with a path graph, a cycle graph and a complete graph. The main results are the following three theorems.
Theorem 4. Let G be a connected nontrivial graph of order m. Then = min, where .
Theorem 5. Let G be a connected nontrivial graph of order m. Then , where .
Theorem 6. Let G be a connected nontrivial graph of order m. Then , where .
Since , and , Theorems 4–6 imply the following three corollaries, respectively.
Corollary 1. Let G be a connected nontrivial graph of order m. If min, then is maximally restricted edge-connected, where .
Corollary 2. Let G be a connected nontrivial graph of order m. If min, then is maximally restricted edge-connected, where .
Corollary 3. Let G be a connected nontrivial graph of order m. If min, then is maximally restricted edge-connected, where .
By checking through the proof of Theorem 1, we find that min or min when both and . The proof of Theorem 2 implies that min or when both and . From the proof of Theorem 3, we obtain that min or when both and . Thus, we have the following three corollaries.
Corollary 4. Let G be a connected nontrivial graph of order m. If min, then is super restricted edge-connected, where .
Corollary 5. Let G be a connected nontrivial graph of order m. If min, then is super restricted edge-connected, where .
Corollary 6. Let G be a connected nontrivial graph of order m. If min, then is super restricted edge-connected, where .