Finding Set Extreme 3-Uniform Hypergraphs Cardinality through Second-Order Signatures

Abstract

This paper continues the study of second-order signature properties—the characterization of the extreme 3-uniform hypergraph. Previously, bases were used to count extreme 3-uniform hypergraphs. However, the algorithm using this mechanism is extremely labor-intensive. The structure of the signature allows us to use it as a more efficient basis for the same problem. Here, we establish the nature of the mutual correspondence between the kind of second-order signature and extreme hypergraphs, and we present a new algorithm to find the power of the set of extreme 3-uniform hypergraphs through the set of their characteristic-signatures. New results obtained with the proposed tool are also presented.

1. Introduction

The theory of hypergraphs separated from graph theory in the second half of the last century. It was pioneered by Berge [1]. He introduced the concept of hypergraphs and formulated the first problems related to them [2]. A number of researchers immediately directed their eyes to the new subject and, by analogy with graphs, generalized some of the available results to the theory of hypergraphs. The constructed theory, as is now well seen, has a wide field of practical applications. Let us note only some of them: computer network modeling and design [3,4], including wireless nets [5]; the modeling of transport networks and calculation of loads on them [6]; social interaction analysis [7] and filtering music tracks [8,9]; database design [10] and neural network design [11,12,13]; cryptography [14,15,16,17]; and data visualization [18]. At the same time, hypergraphs themselves are rather amorphous structures, which led to the necessity to distinguish between various classes of hypergraphs with essentially different parameters and constraints: hypertrees [19], hypernetworks [6], and uniform hypergraphs [20,21,22,23,24,25] (also known as complexes [26]).

Hypergraph models are widely used in solving a number of problems: extreme problems [27,28], covers [29,30], coloring [21,22], pathfinding [31,32,33], the internal structure of a hypergraph—its topology [20,34], hypergraph storage [35,36,37,38,39], and structures of random hypergraphs [40,41].

It should be noted that in the classes of problems on coverings, on interior topology, and on storage, there arises a question related to the estimation of the set of hypergraphs of a particular kind. A number of fundamental works are devoted to the problems of estimating the power of graphs [42,43,44,45,46,47,48], but for hypergraphs such work has not been carried out in general; presumably, it is connected with the extremely indeterminate structure of hypergraphs, which led to a number of estimates in particular cases. In this way, the problems of enumerating hypergraphs and the problems of determining the power of a set only for certain classes of hypergraphs were solved [49,50,51,52,53].

Usually, to work with hypergraphs, an incidence matrix or a list of hyperedges is used. In the case of a large number of vertices, the matrix becomes very sparse, and the list of edges makes it possible to construct the hypergraph structure itself, but for many algorithms is not possible to directly apply it. For k-uniform hypergraphs [54], a number of algorithms use a representation in the form of an adjacency matrix. However, the amount of RAM used for it is proportional to $n^k$ bytes, where n is the number of vertices of the hypergraph. In addition to those indicated, there is another representation: a vector of degrees of vertices of a uniform hypergraph [23,36,37,55]; however, it has its own drawback: the ambiguity of the correspondence between the vector and the hypergraph realized from it, that is, for one vector there can be several implementations. It is worth noting that there is a separate class of uniform hypergraphs—extremal ones. These are hypergraphs that have a one-to-one correspondence with their vectors. In other words, their vector of vertex degrees corresponds to only one uniform hypergraph of the corresponding dimension [38].

For this class of hypergraphs, a new construction was developed: “base” [54]. In an extremal hypergraph, vertices are numbered in descending order of vertex degree, and vertices in hyperedges are ordered in ascending order of vertex numbers. Then, a partial order relationship can be established between hyperedges, which is defined according to the following principle: one hyperedge is smaller than another if each vertex number of the first edge is less than or equal to the number of the corresponding vertex from the second edge. The “base” contains only “maximal” edges that are included in the hypergraph and do not have a single large edge from this hypergraph. Thus, the “base” takes up less space in memory than a list of hyperedges, but it is not convenient for all algorithms from a practical point of view.

In [39], we describe another approach to the representation of an extremal 2-uniform hypergraph: the signature. It is given as a non-negative integer having exactly 1 digit less than the vertices in the hypergraph in binary representation. Also, here we prove a theorem about the power of the set of extremal 2-uniform hypergraphs that can be constructed on n vertices. In addition, algorithms for transforming signatures into the adjacency matrix and vice versa are described here. This allows us to proceed to the choice of the most appropriate extremal 2-uniform hypergraph for storage depending on the problem.

In [56,57], a new representation is given for an extremal 3-uniform hypergraph, and operations under signatures are described.

In works [14,15,16,17], the possibility of using extreme uniform hypergraphs as a key element for a new method of data encryption is presented. This method is topological; the higher the order of uniformity of the hypergraph, the larger the key space at the same number of vertices involved. To analyze the topological approach to encryption, it is necessary to be able to more precisely estimate the power of the key space, and in fact we are talking about the power of the set of extreme k-uniform hypergraphs. Unfortunately, at the moment, all of the estimates for this set are oversampled except for the case $k=2$, i.e., extreme graphs. In the case $k=3$, the results are known for $n<17$, which is not enough to find theoretical power estimates for the set of extreme 3-uniform hypergraphs. The counting method itself is directly related to the representation of an extreme hypergraph—a base. The structure of the base makes it quite easy to enumerate all its possible variants but makes it almost a simple enumeration. Thanks to the second-order signature representation, which appeared in the works of [56,57], as well as operations on these representations of extreme 3 uniform hypergraphs, we are able to propose a new, more efficient algorithm for calculating the cardinality of a set.

Although work on high-order signatures is still in progress, we can still develop algorithms for finding the power of the set of second-order signatures, which will also help us in solving the problem of enumerating extreme 3 uniform hypergraphs.

In this work, the algorithm used in [49] will be analyzed, and its analogue, working on the basis of second-order signatures, will be presented.

2. Definitions

The algorithms and results considered in the following relate to the counting of extreme 3-uniform hypergraphs. To work with them, it is worth to briefly describe their peculiarities and mutual and characteristic features.

Definition 1.

A hypergraph is a set of vertices and a set of hyper edges, each of which is incident to a certain set of vertices [2].

Since hypergraphs are unbounded, it is important for many studies to consider k-uniform hypergraphs.

Definition 2.

A k-uniform hypergraph (hereafter, UH) is a hypergraph in which each hyperedge is incident to exactly k vertices.

Uniform hypergraphs, having another name, can be found in topology (complexes of order $k-1$ [26,36]) and in graph theory (simple graphs without loops).

Hypergraphs in computer memory are traditionally represented in several ways: a list of hyper edges, an adjacency matrix, and an incident matrix. Each has both advantages and disadvantages. They are mainly compared in the categories of memory footprint and applicability to different algorithms.

In [37], we present another form of hypergraph storage: a vector of degrees of its vertices. Since we do not consider directed hypergraphs at this stage, the degree of a vertex is taken to be the sum of the weights of all hyperbranes incident to the vertex. However, this characteristic allows us to efficiently store information about a hypergraph but does not allow us to unambiguously reconstruct it from such a vector since for most hypergraphs there is at least one non-isomorphic hypergraph having the same vector of vertex degrees.

This led to the study of a separate class: extreme uniform hypergraphs ($EUH$). This class is characterized by the fact that each $EUH$ corresponds mutually unambiguously to its vector of vertex degrees and has no non-isomorphic hypergraphs with the same vector. Also, in $EUH$ the coordinates are ordered by decreasing degrees.

For $EUH$, there are several characteristics that allow one to describe it uniquely. In [54], the “base” was considered.

There are two approaches to determine the “base”: through the adjacency matrix of a uniform hypergraph and through the list of edges. Let us use the second way.

Let the k-extreme uniform hypergraph be given in which all vertices are numbered from 1 to n in decreasing order of vertex degree. Then, each hypergraph can be denoted by a set of k indices of the form $\{p_1,p_2,\dots ,p_k\}$, with $p_1<p_2<\dots p_k$. The definition of the base is directly related to the partial order constructed on the set of such index sets.

We will assume that a hyperedge p is smaller than a hyperedge q if for each pair of indices of the associated sets $\{p_1,p_2,\dots ,p_k\}$ and $\{q_1,q_2,\dots ,q_k\}$, the condition $p_i⩽q_i$ is satisfied.

The relation $p>q$ is defined similarly.

Definition 3.

Let $H(V_n,S)$—$EU{H}_n^k$, where $V_n$ is the set of vertices and S is the set of hyperedges. A hyperedge $p\in S$ and its associated tuple of indices $\{p_1,p_2,\dots ,p_k\}$ are called maximal in H if

(1) 

$\forall q\in S$ either $q<p$ or the partial order relation between p and q is not established;

(2) 

$\forall \{t_1,t_2,\dots ,t_k\}<\{p_1,p_2,\dots ,p_k\}$$\exists t\in S$.

Definition 4.

The set of all maximal index sets on H is the “base” of H—$EUH$.

Also, one way to specify $EUH$ is to use a random base since there is one and only one $EUH$ for each base.

Definition 5.

Let B be a base containing some number of the elements of dimension k. Let us construct all index tuples for which any element of the base is maximal. For the obtained set of index tuples, we can obtain the associated set of hyperedges $S_B$; then, the hypergraph $H(V_n,S_B)$ is $EU{H}_n^k$.

In [39], the <<signature>> for $EU{H}_n^2$ is presented. In [56], an extension of the notion of signature is presented: a second-order signature, or vector of signatures, for $EU{H}_n^3$.

A brief description of the basis is given in the introduction. Here, we will present an explanation of the nature of the signature and the signature vector.

In the adjacency matrix $EU{H}_n^2$, all cells have values 0 and 1. Except for the main diagonal, all ones and all zeros are separated by a broken line running along the boundaries of the cells: 1 is closer to the smaller indices of the matrix, and 0 is closer to the larger ones. Coding the segments of this broken line with 0’s and 1’s depending on the direction of movement sets the signature.

Example 1.

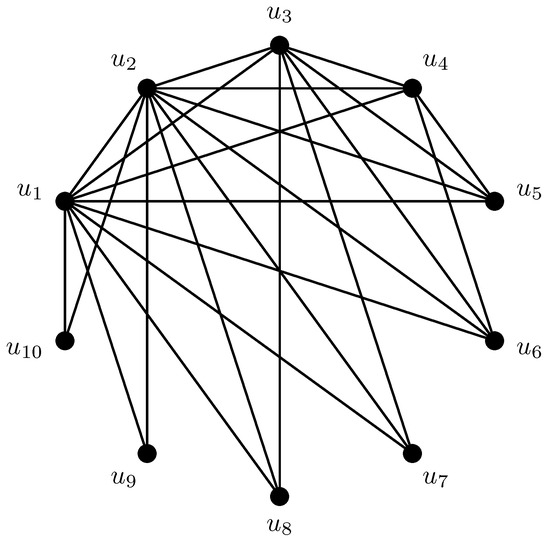
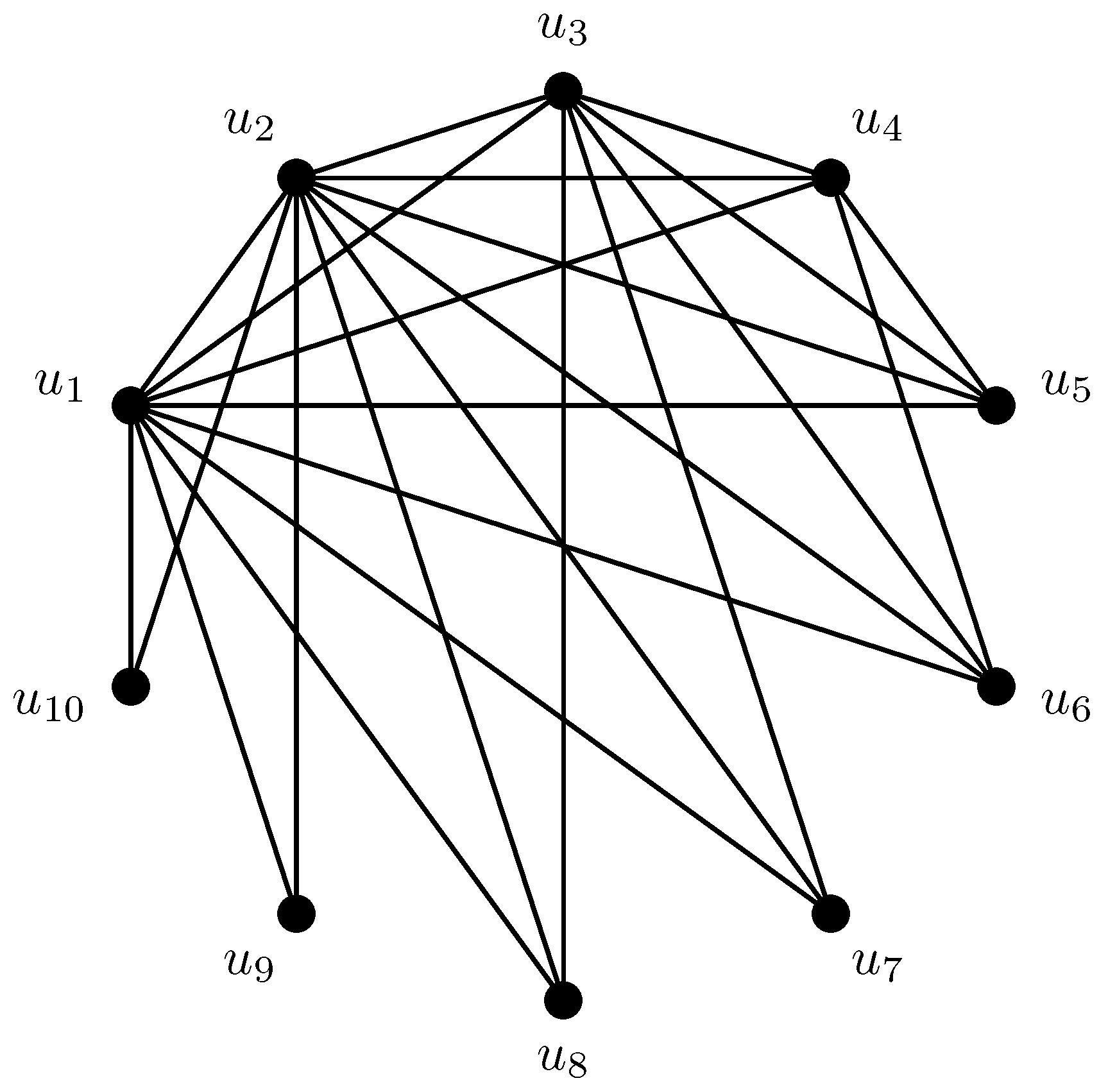
Let $EU{H}_{10}^2$$H=H(V_{10},S)$, where S is an associated set of tuples $\left\{\right\{1,2\}$, $\{1,3\}$, $\{1,4\}$, $\{1,5\}$, $\{1,6\}$, $\{1,7\}$, $\{1,8\}$, $\{1,9\}$, $\{1,10\}$, $\{2,3\}$, $\{2,4\}$, $\{2,5\}$, $\{2,6\}$, $\{2,7\}$, $\{2,8\}$, $\{2,9\}$, $\{2,10\}$, $\{3,4\}$, $\{3,5\}$, $\{3,6\}$, $\{3,7\}$, $\{3,8\}$, $\{4,5\}$, $\{4,6\}\}$:

1. 

A hypergraph is shown in Figure 1;

2. 

Its adjacency matrix is shown in Figure 2;

3. 

Its base $B\left(H\right)=\left\{\right\{2,10\}$, $\{3,8\}$, $\{4,6\}\}$;

4. 

Its signature $\sigma \left(H\right)={110010010}_2={402}_{10}$.

For $EU{H}_n^3$, a cubic adjacency matrix is required. But its behavior is similar to that of the square adjacency matrix $EU{H}_n^2$: 1 and 0 are also grouped into 2 non-overlapping clusters (1 closer to cell $x_{111}$, 0 closer to cell $x_{nnn}$). If we divide the cubic matrix into slices, relative to one of the dimensions, we obtain n-slices, for each of which we can construct a signature. The only difference between such signatures is that in a slice we consider only cells with two other indices larger than the slice index. The set of obtained signatures forms a vector of signatures. It should be noted that the last pair of coordinates of such a vector will always be zero, so it is unnecessary to add them to the vector.

Example 2.

Consider the adjacency matrix (see Figure 3) of the hypergraph $H(V_6,S)$, where $S=\left\{\right\{1,2,3\}$ , {1, 2, 4}, {1, 2, 5}, {1, 2, 6}, {1, 3, 4}, {1, 3, 5}, {1, 3, 6}, {1, 4, 5}, {2, 3, 4}, {2, 3, 5}, {2, 4, 5}, $\{3,4,5\}\}$. Here, the dark colour indicates empty cells that cannot correspond to any hyperedge of any $UH$ in the adjacency matrix. The cells that are not used to form the second-order signature are highlighted in medium grey.

The second-order signature for H—${\sigma }^2=({1101}_2,{011}_2,{01}_2,0_2)=(13,3,1,0)$ is shown in Figure 4.

Base $B\left(H\right)=\left\{\right\{1,3,6\},\{3,4,5\left\}\right\}$.

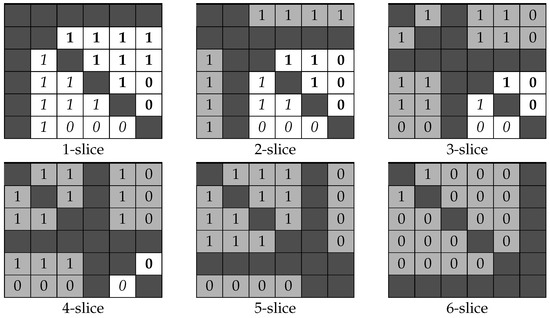
Figure 3. The adjacency matrix for $EU{H}_6^3$ from Example 2.

Figure 3. The adjacency matrix for $EU{H}_6^3$ from Example 2.

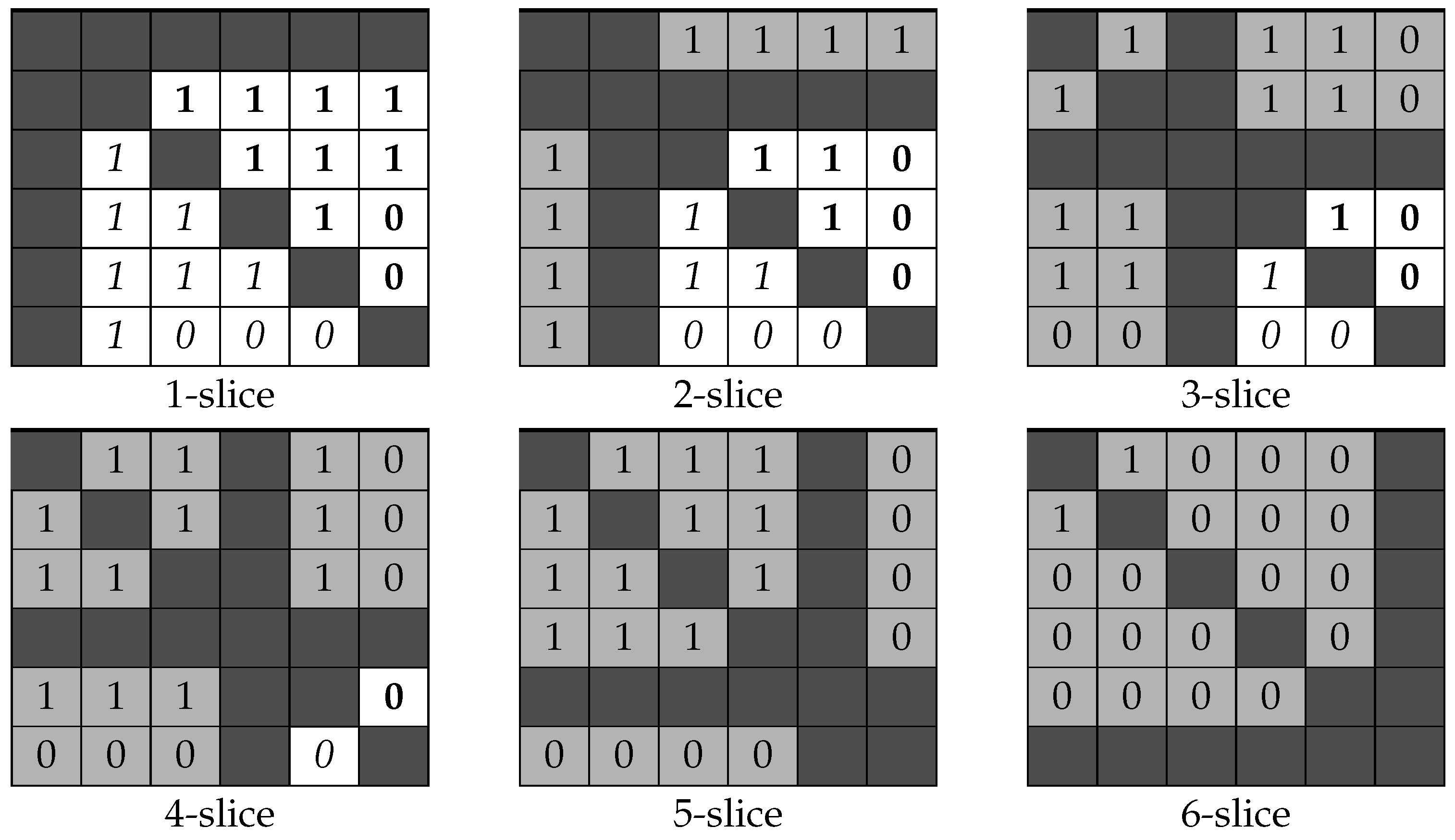
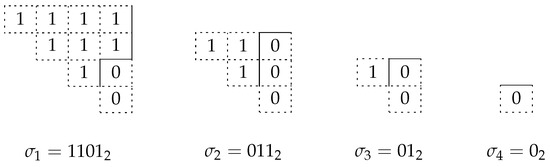
Figure 4. ${\sigma }^2({\sigma }_1,{\sigma }_2,{\sigma }_3,{\sigma }_4)$ for $EU{H}_6^3$ from Example 2.

Figure 4. ${\sigma }^2({\sigma }_1,{\sigma }_2,{\sigma }_3,{\sigma }_4)$ for $EU{H}_6^3$ from Example 2.

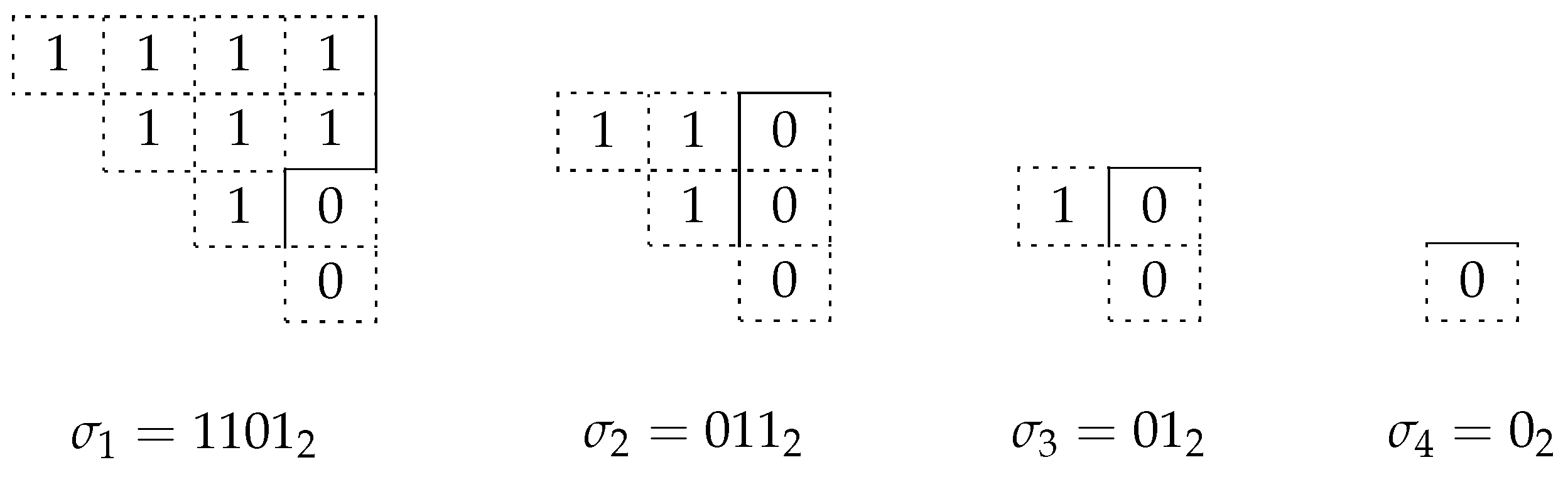
In [56], we also introduced the notion of a truncated signature and defined the relation of including one signature into another through the notion of truncation.

The truncation operation allows us to specify constraints for the next numbered signature. And the inclusion relation describes all of the signatures that can have an index greater than that of the included signature in the vector of signatures.

3. Results

3.1. An Approach to Calculating the Cardinality of a Set of Extremal 3-Uniform Hypergraphs through “Base” Counting

Here, we will consider an algorithm for finding the cardinality of the set $EU{H}_n^3$. Unlike the set $EU{H}_n^2$, for which the cardinality ($2^{n-1}$) is precisely known, theoretical estimates have not yet been obtained for the set $EU{H}_n^3$. Only experimental data are known, obtained through listing another characteristic $EU{H}_n^3$ — “base”.

Base, like signature, is a one-to-one characteristic for $EU{H}_n^k$. Moreover, it can be specified for any k, in contrast to the signature, which is currently defined only for $k=2$ and $k=3$.

The algorithm presented in [49] can be briefly described as an enumeration algorithm with the construction of lengthening chains of single-element bases that create a composite base. To form the base, a set of all combinations of index sets is pre-created: $Ckn$ is the set of all combinations of k integers, from 1 to n, ordered in ascending order ($Ckn$ is ordered in lexicographical order, for example, if $n=5$ and $k=3$; then, $Ckn=\left\{\right\{1,2,3\}$, {1, 2, 4}, {1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 4}, {2, 3, 5}, {2, 4, 5}, $\{3,4,5\}\}$).

The algorithm is recursive and looks like this:

Algorithm 1 initiation: CalcBases(k, n, −1, 1).

Algorithm 1 CalcBases: Calculating the power of a set of bases.
Require: $k>1$	▹k is dimension of $EUH$;
Require: $n⩾k$	▹n is number of vertices $EUH$;
Require: $B\left[\right]$	▹B —a set of elements from $Ckn$, ordered in ascending order in lexicographical order, in which for each pair of elements the partial order relation is not defined;
Require: $p>0$	▹p—sequence number of the last checked element from $Ckn$;
Require: $lc⩾0$	▹$lc$—accumulated chain length;
Require: $BN\left[\right]$	▹$BN\left[\right]$—a null array to store the number of bases consisting of the corresponding number of elements.
for $i\leftarrow p$; $i<\mathrm{len}\left(Ckn\right)$; i++ do     if IsBase(B, $Ckn\left[i\right]$ then         $BN[i-lc]$++         CalcBases(k, n, $i+1$, $lc+1$, GroupBase(B, $Ckn\left[i\right]$))     end if end for

The IsBase function checks each element of the first argument for a partial order relationship with the second argument. If the relationship exists for at least one pair of elements, then the function is returned as false; otherwise, it is returned as true.

The GroupBase function returns a new base—the union of the first argument, the old base; and the second argument—the new base element.

It is also important to note that the maximum number of elements in the base has so far only been estimated for the cases $k=2$ and $k=3$. In [49], the following estimates for the maximum base length are obtained $ML{B}_n^k$:

$$ML{B}_n^2=⌊\frac{1}{2}n⌋,$$

$$ML{B}_n^3=⌊\frac{1}{8}n(n-2)⌋.$$

For extreme uniform hypergraphs of a higher order, there are no exact estimates. In this case, we can hypothesize that $ML{B}_n^k$ is of the form $O\left(n^k\right)$ or is more complicated.

Direct analysis of the complexity of the obtained algorithm is difficult due to its recursive nature, as is the barely predictable process of the branching of chains of constructed bases. Therefore, in order to evaluate the growth of computational complexity, let us look at the experimental data obtained using the developed algorithm.

Table 1. The number of bases and the time taken to find them at different n.

n	${\mathit{B}}_{\mathit{n}}^3$	Time, c.	${\mathit{t}}_{\mathit{n}}/{\mathit{t}}_{\mathit{n}-1}$
3	2	<0.001
4	5	<0.001
5	16	<0.001
6	66	0.002	2
7	352	0.004	2
8	2431	0.011	2.75
9	21,760	0.021	1.9
10	252,586	0.045	2.14
11	3,803,648	0.062	1.4
12	74,327,145	0.181	2.9
13	1,885,102,080	3.6	19.9
14	62,062,015,500	118.5	32.9
15	2,652,584,509,440	5300	44.7
16	147,198,472,495,020	304,636	57.5

has the following form: the first column contains n—the number of hypergraph vertices; the second column contains the number of different bases found on n; the third column specifies the time spent on the algorithm execution; and the last column shows the ratio between the spent seconds at n and $n-1$.

It can be seen that when the number of vertices is small ($n<12$), the computation time is small and may contain a number of overheads associated with the representation of the algorithm in the program, as well as random fluctuations of the influence of the operating system. With a larger number of vertices, it is easy to see that the running time of the algorithm grows faster than the exponential function, which allows us to estimate the complexity of the algorithm as greater than the exponential one.

3.2. Counting Included First-Order Signatures

Having obtained an estimate of the complexity of the base counting algorithm, we will try to create an algorithm for finding extremal 3-uniform hypergraphs by finding second-order signatures.

To do this, we will use the already described property of signatures—the relation of inclusion of first-order signatures. The main property of including signatures is that each of the included signatures allows you to partially set $EU{H}_n^3$ at its own level. In this case, to describe the entire $EU{H}_n^3$ it is necessary to specify $n-2$ first-order signatures, which together form a second-order signature.

Recall the logic of how the signature inclusion relation works.

Let the signature $\sigma$ be given on p digits. Let us build a truncated signature $\widehat{\sigma }$ containing one less digit (we discard the first digit of $\sigma$) and set the highest digit of $\widehat{\sigma }$ equal to 1 to 0. The signatures included in $\sigma$ must satisfy the following condition: for each $0⩽k⩽p-1$, the sum of the highest k binary digits does not exceed the sum of the highest k binary digits of $\widehat{\sigma }$.

Each signature at one level restricts the possible signatures at the next level. For example, as shown in the [56] for $\sigma =25$, the signatures $0,1,2,2,3,4,5,8,9$ will be included. And the signature $\sigma =2^p-1$ includes all signatures from 0 to $2^{p-1}-1$.

Note that $\forall \sigma =2^k:\widehat{\sigma }=0$.

If for a given signature of the form $2^{n-1}$ we construct all possible signatures included in it, and for each included signature we repeat the search for the included ones, and so on until all new signatures are equal to 0, then we obtain all of the possible vectors of signatures describing all $EU{H}_n^3$. The algorithm for counting all second-order signatures is presented below.

To fully describe this algorithm, we need to define the function for checking the included signatures. To do this, we first define the function of finding the highest digit of a number because to determine whether a signature is enabled, we need to remove the highest digit from the main signature. And when comparing signatures, it is necessary to start from the highest single bit.

Now, you can also set the function to check if the signature is enabled.

Algorithm 2 initiation: CalcSignatures2($2^{n-1}-1$).

Let us estimate the complexity of the resulting Algorithm 2.

First, let us consider the MaxBit Algorithm 3 since it has only one cycle that is executed at most n, where n is the number of digits in the considered signature. Accordingly, its complexity in the worst case is $O\left(n\right)$.

For the IsSinS Algorithm 4, the complexity is similarly computed and is also $O\left(n\right)$.

Algorithm 2 CalcSignatures2: Counting the power of the set of second-order signatures given by the first coordinate.

Require:  $s⩾0$                  ▹s—signature (first coordinate of the second-order signature). $res\leftarrow 1$ $mb\leftarrow$ MaxBit(s) $ns\leftarrow s-mb$ for $j\leftarrow 1$; $j<ns+1$; j++ do     if IsSinS($ns$, j) then         $res\leftarrow res+\mathrm{CalcSignatures}2\left(j\right)$     end if end for   return res

Algorithm 3 MaxBit: finding the highest digit of a number.

Require:  $a⩾0$ $p\leftarrow 0$ while (a >> 1) > 0 do     $a\leftarrow a$ >> 1     $p\leftarrow p+1$ end while   return 1 << p

For the basic Algorithm 2, the complexity is determined by its main loop. The loop tries half of all signatures from the one being checked, checks for each of them, and then calls the main algorithm from the smaller signature.

That is, to call the function to find the number of possible second-order signatures built on n vertices, we obtain the following number of operations $T_{2^{n-1}-1}$:

$$T_{2^{n-1}-1}=\sum _{m=0}^{2^{n-2}-1}{T}_m{log}_{2}m<\sum _{m=0}^{2^{n-2}-1}{T}_m{log}_2{2}^{n-1}=(n-1)\sum _{m=0}^{2^{n-2}-1}{T}_m.$$

It should be noted that $T_0=T_1=O\left(1\right)$. Suppose that $T_i⩾T_{i_1}$. Then,

$$\begin{array}{c}{T}_{2^{n-1}-1}<(n-1)T_{2^{n-2}-1}\frac{2^{n-2}-1-0}{2}{2}^{n-2}<(n-1)T_{2^{n-2}-1}{2}^{n-3}{2}^{n-2}=\hfill \\ \hfill =(n-1)!\prod _{t=0}^{n-2}{2}^{n-2-t}{2}^{n-3-t}=(n-1)!2^{{\sum }_{t=0}^{n-3}(n-2-t)+(n-3-t)}=(n-1)!2^{(n-3)(n-2)}.\end{array}$$

(1)

Remark 1.

The resulting complexity score (1) of Algorithm 2 is an overestimate since not every signature is smaller in value than the other one included in it.

Algorithm 4 IsSinS: checking relation of inclusion between signatures.

Require:  $a⩾0$                  ▹a—first signature Require:  $b⩾0$                  ▹b—testing sinature if  $a<b$ then      return 0 end if if $a=b$ then      return 1 end if $c\leftarrow 0$ $ap\leftarrow \mathrm{MaxBit}(a)$ while ($c⩾0$) && $ap$ do     if a & $ap$ then         $c\leftarrow c+1$     end if     if b & $ap$ then         $c\leftarrow c-1$     end if     $ap\leftarrow ap$ >> 1 end while if $c⩾0$ then      return 1 else      return 0 end if

When running the algorithm, it should be understood that the output is the sum of all possible chains of subordinate signatures that are possible given the initial signature that defines the lower slice of the adjacency matrix with significant cells. The result of the algorithm counting the included signatures for different initial values is presented in

Table 2. Number of enabled signatures for signature ${\sigma }_0$ in the range from 0 to 31.

${\mathit{\sigma }}_0$	Count $\mathit{\sigma }\subset {\mathit{\sigma }}_0$	${\mathit{\sigma }}_0$	Count $\mathit{\sigma }\subset {\mathit{\sigma }}_0$
0	1	16	1
1	1	17	2
2	1	18	3
3	2	19	5
4	1	20	4
5	2	21	8
6	3	22	11
7	5	23	16
8	1	24	5
9	2	25	11
10	3	26	17
11	5	27	27
12	4	28	21
13	8	29	39
14	11	30	50
15	16	31	66

.

In Table 2, you can see a relationship between the values:

Theorem 1.

Let S be a vector of the number of signatures included for ${\sigma }_0=\overline{1,2^{n-1}-1}$; then, it can be divided into four equal length quartiles from $q_0=(s_0,\dots ,s_{2^{n-3}-1})$ to $q_3=(s_{2^{n-2}+2^{n-3}},\dots ,s_{2^{n-1}-1})$, with the values in $q_1$ corresponding to the values in $q_2$.

Proof. 

Consider the i-th signatures from quartiles $q_1$ and $q_2$. They differ by the first two bits (see

Table 3. Bitwise representation of signatures from $q_1$ and $q_2$ when $n=6$.

${\mathit{\sigma }}_{1\mathit{i}}$	BIN(${\mathit{\sigma }}_{1\mathit{i}}$)	${\mathit{\sigma }}_{2\mathit{i}}$	BIN(${\mathit{\sigma }}_{2\mathit{i}}$)
8	01000	16	10000
9	01001	17	10001
10	01010	18	10010
11	01011	19	10011
12	01100	20	10100
13	01101	21	10101
14	01110	22	10110
15	01111	23	10111

); if the two higher bits of the signature from $q_1$ are 0 and 1, then the signatures from the second quartile have the first bits 1 and 0, respectively. Let ${\sigma }_{1i}$ be a signature from quartile $q_1$, standing in it at number i, and let ${\sigma }_{2i}$ be a signature from quartile $q_2$ at the same number; then, ${\widehat{\sigma }}_{1i}={\widehat{\sigma }}_{2i}$, i.e., the truncation of these signatures will be the same. This naturally leads to the equality $\left|{\sigma }_{{\sigma }_{1i}}^2\left(n\right)\right|=\left|{\sigma }_{{\sigma }_{2i}}^2\left(n\right)\right|$.    □

Example 3.

If we look at the Table 2, we can see an example of the quartile division of the number of included signatures. Consider the vectors of values for all signatures less than the maximum for the current n.

• $n=3$—the maximal signature is equal to $2^{3-1}-1=3$:

$$q_0=\left(1\right),q_1=\left(1\right),q_2=\left(1\right),q_3=\left(2\right).$$

• $n=4$—the maximal signature is equal to $2^{4-1}-1=7$:

$$q_0=(1,1),q_1=(1,2),q_2=(1,2),q_3=(3,5).$$

• $n=5$—the maximal signature is equal to $2^{5-1}-1=15$:

$$q_0=(1,1,1,2),q_1=(1,2,3,5),q_2=(1,2,3,5),q_3=(4,8,11,16).$$

• $n=6$—the maximal signature is equal to $2^{6-1}-1=31$:

$$q_0=(1,1,1,2,1,2,3,5),q_1=(1,2,3,5,4,8,11,16)$$

$$q_2=(1,2,3,5,4,8,11,16),q_3=(5,11,17,27,21,39,50,66).$$

As we can see, in each case $q_1=q_2$.

In general, the algorithm for finding included signatures is also essentially an algorithm that builds chains of signatures included in one another. This effect can be used to further improve the algorithm for counting second-order signatures since no significant increase in speed was achieved compared to the basic algorithm.

Let us consider the principles of using this property in practice.

• It is necessary to implement a structure for storing previously obtained values, for signatures that are smaller than the one under study by two binary orders.
• For a new signature, only a quarter of the time it is necessary to look for the inclusion of other signatures.

Next theorem is derived from Theorem 1.

Theorem 2.

Let us here call ${\sigma }_{{\sigma }_0}^2\left(n\right)$ the set of all second-order signatures of $n-2$ coordinates whose first coordinate is equal to ${\sigma }_0$—the signature defining the lower significant layer of the adjacency matrix. Then, the power of the set ${\sigma }_{{\sigma }_0}^2\left(n\right)$ has the following form:

$$\left|{\sigma }_{{\sigma }_0}^2\left(n\right)\right|=\left\{\begin{array}{c}\left|{\sigma }_{{\sigma }_0}^2(n-1)\right|,\mathrm{if}{\sigma }_0<2^{n-2},\hfill \\ \left|{\sigma }_{{\sigma }_0-2^{n-3}}^2(n-1)\right|,\mathrm{if}{2}^{n-2}⩽{\sigma }_0<2^{n-2}+2^{n-3},\hfill \\ {\displaystyle \sum _{{\sigma }_i\subset {\sigma }_0}\left|{\sigma }_{{\sigma }_i}^2(n-1)\right|,\mathrm{if}{\sigma }_0>2^{n-2}+2^{n-3}.}\hfill \end{array}\right.$$

Proof. 

The first equation is valid because each signature is smaller than the previous one by at least one bit. At the same time, if the highest bit is 0, it means that at least one vertex in the extreme hypergraph is isolated and does not affect the construction of the hypergraph itself. That is, on n vertices in this configuration we can build exactly as many extreme hypergraphs as on $n-1$, provided that we have removed the isolated vertex.

The second equation follows from Theorem 1.

The latter expression is given by the algorithm for finding the power as a recursive appeal to the power of the set of second-order signatures having one less coordinate and defined by the first coordinate included in the signature ${\sigma }_0$.    □

Example 4.

Let us consider the functioning of the theorem on the example of the second half of Table 2. According to Theorem 2, we already know the first values for the number of signatures included in the signatures from 0 to 15. The third quarter is duplicated from the second quarter according to Theorem 1. It remains for us to find the last quarter of the table. To do this, we need to obtain all the signatures included in the signatures from 24 to 31. Let us show them in

Table 4. Included signatures and their cardinality for ${\sigma }_0=\overline{48,63}$.

${\mathit{\sigma }}_0$	${\mathit{\sigma }}_{\mathit{i}}\subset {\mathit{\sigma }}_0$	$\sum {\mathit{\sigma }}_{{\mathit{\sigma }}_{\mathit{i}}}^2$
24	$(0,1,2,4,8)$	$1+1+1+1+1=5$
25	$(0,1,2,3,4,5,8,9)$	$1+1+1+2+1+2+1+2=11$
26	$(0,1,2,3,4,5,6,8,9,10)$	$1+1+1+2+1+2+3+1+2+3=17$
27	$(0,1,2,3,4,5,6,7,8,9,10,11)$	$1+1+1+2+1+2+3+5+1+2+3+5=27$
28	$(0,1,2,3,4,5,6,8,9,10,12)$	$1+1+1+2+1+2+3+1+2+3+4=21$
29	$(0,1,2,3,4,5,6,7,8,9,10,11,12,13)$	$1+1+1+2+1+2+3+5+1+2+3+5+4+8=39$
30	$(0,1,2,3,4,5,6,7,8,9,10,11,12,13,14)$	$1+1+1+2+1+2+3+5+1+2+3+5+4+8+11=50$
31	$(0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)$	$1+1+1+2+1+2+3+5+1+2+3+5+4+8+11+16=66$

. We can see that the found values repeat the last quarter of Table 2.

Based on the obtained theorem, we can refine Algorithm 5 (CalcSignatures2M) for finding the power of the set of second-order signatures with a given first coordinate as follows: let us add the storage of values for previously found sets to the function of searching for new signatures, and let us add a division into quartiles when choosing an action for a signature.

Algorithm 5 initiation: CalcSignatures2M($2^n-1$, $2^n$).

This algorithm must be run for each of the unknown signatures, starting from the previous n, that is, to find the second half of $\left|{\sigma }_{{\sigma }_0}^2(n+1)\right|$, it is necessary to know $\left|{\sigma }_{{\sigma }_0}^2\left(n\right)\right|$. This allows one, firstly, to approach the finding of values sequentially and to save intermediate results, and secondly, it significantly accelerates the calculation itself since to find the power of the set of all possible second-order signatures on $n-2$ coordinates it is enough to find $2^{n-2}$ values.

The application of this algorithm is shown in

Table 5. The cardinality of second-order signatures set generated by the signature ${\sigma }_n=2^{n-1}-1$, where n—the number of vertices from $EU{H}_n^3$, and the time taken to find them at different n.

n	${\mathit{\sigma }}_{\mathit{n}}$	$\left|{\mathit{\sigma }}_{2^{\mathit{n}-1}-1}^2\left(\mathit{n}\right)\right|$	Time, c.	Parallel Time, c.
3	3	2	<0.001	<0.001
4	7	5	<0.001	<0.001
5	15	16	<0.001	<0.001
6	31	66	<0.001	<0.001
7	63	352	<0.001	<0.001
8	127	2431	<0.001	<0.001
9	255	21,760	0.001	<0.001
10	511	252,586	0.002	0.001
11	1023	3,803,648	0.003	0.002
12	2,047	74,327,145	0.008	0.003
13	4095	1,885,102,080	0.028	0.006
14	8191	62,062,015,500	0.101	0.015
15	16,383	2,652,584,509,440	0.428	0.047
16	32,767	147,198,472,495,020	1.729	0.171
17	65,535	10,606,175,914,819,584	6.742	0.725
18	131,071	992,340,657,705,109,416	27.981	2.994

.

Algorithm 5 CalcSignatures2M: Modified power calculation of the set of second-order signatures generated by a specified signature.

Require:  s                                                                      ▹s—signature. Require:  $level$                                            ▹$level$—maximum signature value + 1 relative to the current signature. Require:  R                        ▹R—global data array with dimension $2^{l}evel$, where the found set powers are stored, indexed according to the value of the generating signature ($R\left[0\right]=R\left[1\right]=1$). if $R\left[s\right]>0$ then   return  $R\left[s\right]$ end if $res\leftarrow 1$ $mb=\mathrm{MaxBit}(s)$ $ns\leftarrow s-mb$ $l1\leftarrow level$ >> 1 $l2\leftarrow level$ >> 2 if $s<l1+l2$ then   return $R[s-l2]$ end if for $j\leftarrow 1$; $j<ns+1$; j++ do     if IsSinS($ns$, j) > 0 then         $res=res+\mathrm{CalcSignatures}2\mathrm{M}(j,level)$     end if end for   return res

The complexity estimation of Algorithm 5 is similar to the previous one, but it is worth noting that the recursive call for each included signature occurs no more than once. The reason is that the number of subordinate signatures is calculated only once for each signature under investigation. In addition, for each vertex level, only signatures from quartile $q3$ need to be considered, which also lowers the number of operations. In fact, for each of the signatures we have to find all the signatures included once while checking them for inclusion; hence, the number of operations $T_{2^{n-1}-1}$ can be estimated as

$$T_{2^{n-1}-1}=(n-1)2^{n-2}.$$

Remark 2.

Thus, we can estimate the complexity of Algorithm 5 as $O\left(n{2}^{n-2}\right)$.

To find values at $n>18$, we need to switch to 128-bit numbers, which by some estimation will suffice up to $n=27$.

Remark 3.

The considered algorithm can be easily parallelized into threads provided that OpenMP technology is used, which allows one to productively distribute iterations of the for loop between threads that will use different processor cores. For example, Table 5 shows the time when processing data on a 20-core Core i7-12700H processor. When analyzing the performance of parallelizing iterations, you should keep in mind the architecture of the processor and the inequality of its cores.

4. Discussion

We have obtained an elegant and more efficient algorithm for finding the power of the set $EU{H}_n^3$. This problem makes not only theoretical but also practical sense if we remember that this parameter is taken into account when used as a key in the topological encryption algorithm [14].

It should be understood that the second-order signature is described only for 3-uniform hypergraphs, which does not currently allow us to construct an appropriate algorithm for $EU{H}_n^k$ when $k>3$.

Therefore, the main directions for the development of further research are assumed to be the definition of high-order signatures, and eventually the general form of the signature ${\sigma }^k$. It is also planned to continue studying the properties of the first- and second-order signatures, which will possibly improve the existing algorithms for determining the power of the set $EU{H}_n^3$, as well as open the way and the rule of their enumeration.

However, it should be noted that the basic CalcBases algorithm, although inferior to the new one in performance, allows us to separately find the number of bases that have the same number of elements. This can further help in understanding the overall logic of bases, and the structure of $EU{H}_n^3$ itself. In addition, this algorithm allows us to search for bases for $EU{H}_n^4$ and a higher order, while the counting time is significantly increased. For example, we obtained the following values for the power of the set $EU{H}_n^4$ (

Table 6. The number of $EU{H}_n^4$ and the time taken to find them at different n.

n	${\mathit{B}}_{\mathit{n}}^3$	Time, c.
4	2	<0.001
5	6	<0.001
6	32	<0.001
7	352	<0.001
8	9304	0.002
9	683,464	0.04
10	161,960,220	6
11	143,145,033,004	3827

). Hence, we should not completely abandon the algorithms on bases and should continue to investigate them from the point of view of further optimization.