Extremal Sombor Index of Graphs with Cut Edges and Clique Number

Abstract

The Sombor index is defined as $SO\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}}\sqrt{d^2\left(u\right)+d^2\left(v\right)}$, where $d\left(u\right)$ and $d\left(v\right)$ represent the number of edges in the graph G connected to the vertices u and v, respectively. In this paper, we characterize the largest and second largest Sombor indexes with a given number of cut edges. Moreover, we determine the upper and lower sharp bounds of the Sombor index with a given number of clique numbers, and we characterize the extremal graphs.

1. Introduction

In graph theory, studying extremal graphs and indices for a class of graphs with given parameters is an interesting problem. Recently, Gutman introduced a novel topological index, named the Sombor index in [1] and defined as $SO\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}}\sqrt{d^2\left(u\right)+d^2\left(v\right)}$, where $d\left(u\right)$ and $d\left(v\right)$ represent the number of edges connected to vertices u and v in G, respectively, and further established some mathematical properties for the index. Chen et al. in [2] considered the extremal values of the Sombor index of trees with some given parameters such as matching number, pendent vertices, diameter, segment number, and branching number. In the meantime, the corresponding extremal trees are characterized. Li et al. showed the extremal graphs with respect to the Sombor index among all the n-order trees with a given diameter [3]. In [4], Redžpović studied the chemical applicability of the Sombor index. In addition, Cruz et al. in [5] determined the extremal chemical graphs and hexagonal systems for the Sombor index. In [6], Zhou et al. studied the Sombor index of trees and unicyclic graphs with a given maximum degree. In [7], they found the maximum Sombor index of unicyclic graphs with a fixed girth. In [8], they showed applications of the Sombor index. For more studies in this direction, one may refer to [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24].

Let $G=\left(V\right(G),E(G\left)\right)$ be a finite, simple, and connected graph with $V\left(G\right)={\displaystyle \bigcup _{i=1}^n}{V}_i$ and $E\left(G\right)={\displaystyle \bigcup _{i=1}^m}{E}_i$. For any vertex $v\in V\left(G\right)$, we denote $N_G\left(v\right)=\left\{u\right|uv\in E\left(G\right)\}$ and $N_G\left[v\right]=\left\{u\right|uv\in E\left(G\right)\}\cup \left\{v\right\}$. The degree $d\left(v\right)$ of the vertex v is the number of edges connected to the vertex v. The vertex v is called pendent vertex if $d\left(v\right)=1$. The stem is the vertex adjacent to at least one pendent vertex, and the pendent edge is the edge incident with the pendent vertex and the stem. If $u,v\in G$, then the distance $d(u,v)$ is the length of the shortest path connecting the two vertices u and v. We use $P_n,C_n$, and $K_{1,n-1}$ to represent the path, cycle, and star graph with n vertices, respectively.

A clique is a subset $V^{\prime }\in V\left(G\right)$ that makes $G\left[V^{\prime }\right]$ to a complete graph. The order of the largest complete subgraph in graph G is called the clique number $\psi \left(G\right)$ of G. The chromatic number $\chi \left(G\right)$ of the graph G is the minimum number of colors needed to stain each vertex on a graph so that the two adjacent vertices are different colors. See reference [25] for some notations and terms that we have not mentioned here.

Let ${\mathcal{C}}_{n,k}$ be a class of graphs having n vertices and k cut edges. Denote $E^{\prime }=\{e_1,e_2,\cdots ,e_k\}$. It can be divided into two classes, namely, pendent edges with size $k^{\prime }$, and non-pendent edges with size $k-k^{\prime }$. We know the resulting graph $G-E^{\prime }$ are either 2-edge-connected graphs or isolated vertices. The maximum number of cut edges in a connected graph with n vertices and at least one cycle is limited to $n-3$; therefore, we assume that the graph G with cut edges and k ($k\ge 1$) is less than or equal to $n-3$.

In this paper, we determine the Sombor index of the graph with a given number of cut edges and determine the types of the graphs with the largest and second largest Sombor indexes. At the same time, we use clique number to determine the upper and lower sharp bounds for the Sombor index in ${\mathcal{C}}_{n,k}$. We will introduce some graph transformations.

2. The Extremal Graph of the Sombor Index with Cut Edges

If any graphs $G_1$ and $G_2$ with $V\left(G_1\right)\cap V\left(G_2\right)=\left\{v\right\}$, then label the graph as $G_{1}v{G}_2$. If the graphs $G_1,G_2,\cdots ,G_t$$(t\ge 2)$ share a common vertex v, then the graph is labeled as $G_{1}v{G}_{2}v\cdots v{G}_t$. In the same way, if there is a cut edge $uv$ between any graphs $G_1$ and $G_2$ with $u\in V\left(G_1\right)$ and $v\in V\left(G_2\right)$, in the same way, we label this graph as $G_{1}uv{G}_2$. According to the definition and direct computation, we can obtain the following results.

Lemma 1. 

Let $G=(V,E)$ be a graph and $u,v\in V\left(G\right)$. If $uv$ is not an edge in $E\left(G\right)$, we have $SO\left(G\right)<SO(G+uv)$. If $uv$ is an edge in $E\left(G\right)$, then we have $SO\left(G\right)>SO(G-uv)$.

Proof. 

Since the increase (or decrease) in a new edge in the graph increases (or decreases) by some vertex degree, the lemma obviously holds. □

Here, we explain the graph transformation I on graph $G\in {\mathcal{C}}_{n,k}$. Denote that $G=G_{1}uv{G}_2$ is a graph that does not contain cut edge $uv$, where $G_1$ and $G_2$ are both 2-edge-connected graphs (Figure 1a). Let $G^{*}=G-\left\{uv\right\}+\left\{u\left(v\right)w\right\}$ (Figure 1b). Then, the resulting graph $G^{*}$ is obtained from G via the graph transformation I. Since the graph $G^{*}$ posses k cut edges, the number of pendent vertices increases by 1.

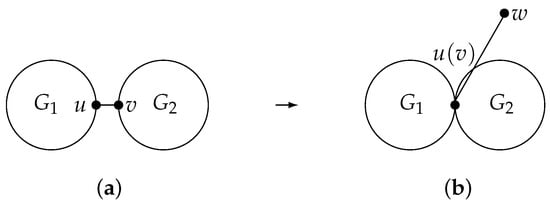
Figure 1. The graph transformation I: $G\to G^{*}$. (a) G. (b) $G^{*}$.

Lemma 2. 

Suppose that $G^{*}$ is the graph derived by $G\in {\mathcal{C}}_{n,k}$ using the graph transformation I, as described in Figure 1. Then, $SO\left(G^{*}\right)>SO\left(G\right)$.

Proof. 

Set $N_G\left(u\right)-\left\{v\right\}=\{u_1,u_2,\cdots ,u_r\}$ and $N_G\left(v\right)-\left\{u\right\}=\{v_1,v_2,\cdots ,v_s\}$ with $r,s\ge 2$. Then, $d_G\left(u\right)=r+1$, $d_G\left(v\right)=s+1$, and $d_{G^{*}}\left(u\left(v\right)\right)=r+s+1$. It is clear that the vertices $u_1,u_2,\cdots ,u_r$ are in $V\left(G_1\right)$; and $v_1,v_2,\cdots ,v_s$ are in $V\left(G_2\right)$ by assumption. Further,

$$\begin{array}{cc}\hfill SO\left(G^{*}\right)-SO\left(G\right)& =\sqrt{\sum _{x\in N_{G^{*}}\left(u\right)}{d}_{G^{*}}^2\left(x\right)+d_{G^{*}}^2\left(u\right)}-\sqrt{\sum _{x\in N_G\left(u\right)\backslash v}{d}_G^2\left(x\right)+d_G^2\left(u\right)}\hfill \\ \hfill & -\sqrt{\sum _{x\in N_G\left(v\right)\backslash u}{d}_G^2\left(x\right)+d_G^2\left(v\right)}=\sqrt{1+{(r+s+1)}^2}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +\sqrt{\sum _{x\in N_G\left(u\right)\backslash v}{d}_G^2\left(x\right)+{(r+s+1)}^2}+\sqrt{\sum _{x\in N_G\left(v\right)\backslash u}{d}_G^2\left(x\right)+{(r+s+1)}^2}\hfill \\ \hfill & -\sqrt{\sum _{x\in N_G\left(u\right)\backslash v}{d}_G^2\left(x\right)+{(r+1)}^2}-\sqrt{\sum _{x\in N_G\left(v\right)\backslash u}{d}_G^2\left(x\right)+{(s+1)}^2}\hfill \\ \hfill & -\sqrt{{(r+1)}^2+{(s+1)}^2}=\sqrt{1+{(r+s+1)}^2}\hfill \\ \hfill & +\sqrt{\sum _{i=1}^r{d}_G^2\left(u_i\right)+{(r+s+1)}^2}+\sqrt{\sum _{j=1}^s{d}_G^2\left(v_j\right)+{(r+s+1)}^2}\hfill \\ \hfill & -\sqrt{\sum _{i=1}^r{d}_G^2\left(u_i\right)+{(r+1)}^2}-\sqrt{\sum _{j=1}^s{d}_G^2\left(v_j\right)+{(s+1)}^2}-\sqrt{{(r+1)}^2+{(s+1)}^2}\hfill \\ \hfill & =\left(\sqrt{1+{(r+s+1)}^2}-\sqrt{{(r+1)}^2+{(s+1)}^2}\right)\hfill \\ \hfill & +\left(\sqrt{\sum _{i=1}^r{d}_G^2\left(u_i\right)+{(r+s+1)}^2}-\sqrt{\sum _{i=1}^r{d}_G^2\left(u_i\right)+{(r+1)}^2}\right)\hfill \\ \hfill & +\left(\sqrt{\sum _{j=1}^s{d}_G^2\left(v_j\right)+{(r+s+1)}^2}-\sqrt{\sum _{j=1}^s{d}_G^2\left(v_j\right)+{(s+1)}^2}\right).\hfill \end{array}$$

Note that

$$\begin{array}{cc}\hfill & \sqrt{1+{(r+s+1)}^2}-\sqrt{{(r+1)}^2+{(s+1)}^2}>0.\hfill \\ \hfill & \sqrt{\sum _{i=1}^r{d}_G^2\left(u_i\right)+{(r+s+1)}^2}-\sqrt{\sum _{i=1}^r{d}_G^2\left(u_i\right)+{(r+1)}^2}>0.\hfill \\ \hfill & \sqrt{\sum _{j=1}^s{d}_G^2\left(v_j\right)+{(r+s+1)}^2}-\sqrt{\sum _{j=1}^s{d}_G^2\left(v_j\right)+{(s+1)}^2}>0.\hfill \end{array}$$

where $d_G\left(u_i\right),d_G\left(v_j\right)\ge 1$ and $SO\left(G^{*}\right)-SO\left(G\right)>0$. We have finished. □

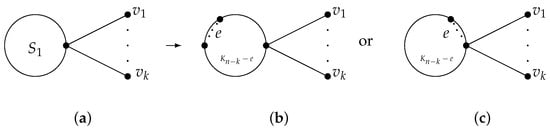
Here, we explain the graph transformation II on a graph $G\in {\mathcal{C}}_{n,k}$. Set $uv$ as not a pendent cut edge in $G=G_{1}uv{K}_{1,r}$, Figure 2a. Let $G^{**}=G_{1}u{K}_{1,r+1}$ (Figure 2b). In this way, the graph $G^{**}$ is attained at G by applying graph transformation II.

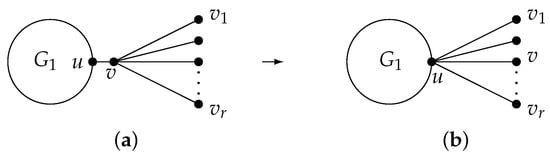
Figure 2. The graph transformation II: $G\to G^{**}$. (a) G. (b) $G^{**}$.

Based on the graph transformation II, we obtain:

Lemma 3. 

Let $G_1$ be a 2-edge-connected graph and $uv$ be a non-pendent cut edge of $G=G_{1}uv{K}_{1,r}$; $G^{**}$ will be the resulting graph from G by applying the graph transformation II (Figure 2). Then, we have $SO\left(G^{**}\right)>SO\left(G\right)$.

Either a cut edge or a non-pendent edge can be transformed into a pendent edge via graph transformations I and II, as shown in Figure 3.

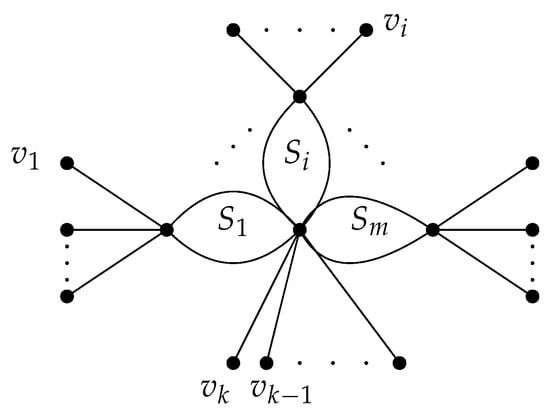
Figure 3. The graph $G_{k^{″}}^{*}$.

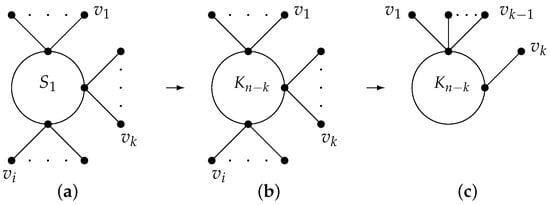
Here, we explain the graph transformation III on graph $G\in {\mathcal{C}}_{n,k}$. Assume that $u,v\in V\left(G\right)$ and the vertices $u_1,u_2,\cdots ,u_s$ are pendent vertices adjacent to vertex u; the vertices $v_1,v_2,\cdots ,v_t$ are pendent vertices adjacent to vertex v, as shown in Figure 4a. Let $G^{\prime }=G-\{u{u}_1,u{u}_2,\cdots ,u{u}_s\}+\{v{u}_1,v{u}_2,\cdots ,v{u}_s\}$, as shown in Figure 4b. Then, $G^{\prime }$ is the resulting graph from G through graph transformation III.

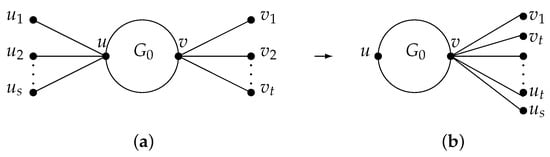
Figure 4. The graph transformation III: $G\to G^{\prime }$. (a) G. (b) $G^{\prime }$.

Lemma 4. 

Let $G^{\prime }$ be a graph obtained from G by applying the graph transformation III (Figure 3). Then, $SO\left(G^{\prime }\right)>SO\left(G\right)$.

By repeating this transformation in the graph, all pendent edges are connected to the same vertex.

We will discuss the graph of ${\mathcal{C}}_{n,k}$ with the largest Sombor index in the following. Let $K_n$ be a complete graph with n vertices, and $Q_n^k$ be a graph obtained by connecting k independent vertices to one of the vertices of $K_{n-k}$.

Theorem 1. 

In all connected graphs in ${\mathcal{C}}_{n,k}$, the Sombor index takes the maximum value on $Q_n^k$, i.e., the graph obtained by connecting k independent vertices to one of the vertex of the graph $K_{n-k}$.

Proof. 

According to above lemmas, we provide the Sombor index for graphs in ${\mathcal{C}}_{n,k}$ that achieve the upper bound.

Claim 1. If a graph $G\in {\mathcal{C}}_{n,k}$, then $SO\left(G\right)\le SO\left(G^{*}\right)$.

Let $G\in {\mathcal{C}}_{n,k}$ and $G\ncong G^{*}$, then based on the above lemmas, we know $SO\left(G\right)<SO\left(G^{*}\right)$. Obviously, the equality holds when $G\cong G^{*}$.

Claim 2. For two graphs $G^{*}$ and H in Figure 4, $SO\left(G^{*}\right)\le SO\left(H\right)$, the equality holds when $G^{*}\cong H$.

Assume $G\in {\mathcal{C}}_{n,k}$ is a graph with cut edges $\{e_1,e_2,\cdots e_k\}$. Then, via Lemma 1, we have $SO(G+e)>SO\left(G\right)$, where $e\notin E\left(G\right)$. Recall that by adding some edges to 2-edge-connected graphs $S_i$ for $i\in \{1,2,\cdots ,m\}$, it is converted to the complete subgraphs $K_{n_i+1} for(i\in \{1,2,\cdots ,m\}$; therefore, the graph $G^{*}$ is converted to the graph H, which has k cut edges, so that $H\subset G\in {\mathcal{C}}_{n,k}$. According to Lemma 1, if $G^{*}\subset H$, then we have $SO\left(G^{*}\right)<SO\left(H\right)$ and the equality holds when $G^{*}\cong H$.

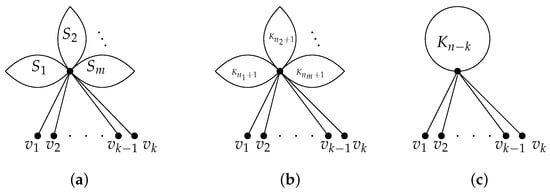
Claim 3. For two graphs H and $Q_n^k$ in Figure 5, we have $SO\left(H\right)\le SO\left(Q_n^k\right)$, and the equality holds when $H\cong Q_n^k$, i.e., $m=1$.

Figure 5. Simple graphs $G^{*}$, H and $Q_n^k$ with k cut edges. (a) $G^{*}$. (b) H. (c) $Q_n^k$.

The graph H becomes the graph $Q_n^k$ if we connect every pair of vertices in the complete subgraphs $K_{n_i+1}(i\in \{1,2,\cdots ,m\})$ of H and it has k cut edges. Obviously, $Q_n^k\in {\mathcal{C}}_{n,k}$ and $H\subset Q_n^k$. Therefore, using Lemma 1, we obtain $SO\left(H\right)<SO\left(Q_n^k\right)$, and the equality holds when $H\cong Q_n^k$, i.e., $m=1$.

With the above three claims, the theorem holds. □

In the following, we characterize the graph with the second largest Sombor index in ${\mathcal{C}}_{n,k}$.

Theorem 2. 

In all graphs $G\in {\mathcal{C}}_{n,k}$ and $G\ncong Q_n^k$, it holds that $SO\left(G\right)\le SO\left(G_2\right)$; the equality holds when $G\cong G_2$.

Proof of Theorem 2. 

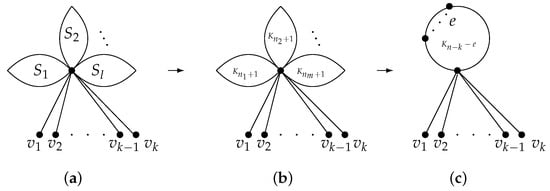
For all graphs $G\in {\mathcal{C}}_{n,k}$, if G achieves the maximum $SO\left(G\right)$, then it must be one of the graphs shown in Figure 6, namely $G_1,G_2$, or $G_3$.

Figure 6. Simple graphs $G_1$, $G_2$, and $G_3$ with cut edges. (a) $G_1$. (b) $G_2$. (c) $G_3$.

Recall that either a cut edge or a non-pendent cut edge can eventually be transformed into a pendent edge by repeating the graph transformation I or II. We denote the resulting graph as $G_{k^{″}}^{*}$ in Figure 3, where $S_i$ for $1\le i\le m$ represents the 2-edge-connected graphs. Then, we have $SO\left(G_{k^{″}}^{*}\right)\ge SO\left(G\right)$. In Figure 3, $k^{″}$ represents the number of non-pendent vertices attached to cut edges. In the following, we will discuss two cases according to parameters m and $k^{″}$.

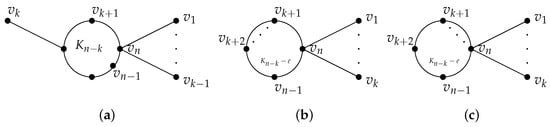
Case 1. If $m=1$.

If $k^{″}=1$, additional edges are added to the vertices of the subgraph $S_1$ which is 2-edge-connected; via transformation, $S_1$ turns into $G_2$ or $G_3$ (see Figure 7). By adding an additional edge to either $G_2$ or $G_3$, then it becomes the graph $Q_n^k$. Therefore, based on the Lemma 1, it holds that

$$SO\left(G\right)\le SO\left(G_{k^{″}}^{*}\right)\le SO\left(G_2\right)\le SO\left(Q_n^k\right)\mathrm{or}SO\left(G\right)\le SO\left(G_{k^{″}}^{*}\right)\le SO\left(G_3\right)\le SO\left(Q_n^k\right).$$

Figure 7. The graphs with $m=1$, $k^{″}=1$. (a) $G_{k^{″}}^{*}$. (b) $G_2$. (c) $G_3$.

If $k^{″}\ge 2$, edges are initially added to the vertices of the $S_1$ which is a 2-edge-connected subgraph, and it is converted to $K_{n-k}$, denoting the graph as $H_1$ (See Figure 8). By applying Lemma 1, we obtain $SO\left(H\right)\ge SO\left(G_{k^{″}}^{*}\right)$. Next, repeating the graph transformation III on graph H, at last we obtain $G_1$. If we move only one edge from $G_1$, it becomes $Q_n^k$. By repeating this transformation in the graph, each pendent edge is attached to the same vertex. Via Lemma 4, we have $SO\left(G\right)\le SO\left(H_1\right)\le SO\left(G_1\right)\le SO\left(Q_n^k\right).$

Figure 8. The graph transformation with $m=1$, $k^{″}\ge 2$. (a) $G_{k^{″}}^{*}$. (b) $H_1$. (c) $G_1$.

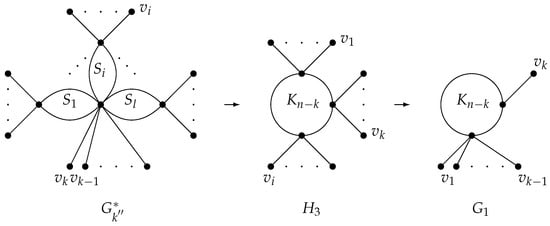
Case 2. If $m\ge 2$, we consider the same way in Case 1.

If $k^{″}=1$, the complete graphs $K_{i+1}(i=1,2,\cdots ,m)$ are constructed by adding edges to the 2-edge-connected subgraphs $S_i(i=1,2,\cdots ,m)$ in $G_{k^{″}}^{*}$, forming the graph $H_2$ (Figure 9). Then, we have $SO\left(H_2\right)\ge SO(G_{k^{″}}^{*})$ via Lemma 1. Add some edges between $K_{n_i+1}(i=1,2,\cdots ,m)$, composing the graph $G_2$ (Figure 9). If adding another edge to $G_2$, it becomes $Q_n^k$. Via Lemma 1, it holds that $SO(G_{k^{″}}^{*})\le SO\left(H_2\right)\le SO\left(G_2\right)\le SO\left(Q_n^k\right).$

Figure 9. The graph transformation with $m\ge 2$, $k^{″}=1$. (a) $G_{k^{″}}^{*}$. (b) $H_2$. (c) $G_2$.

If $k^{″}\ge 2$, add some edges to $S_i(i=1,2,\cdots ,m)$ of $G_{k^{″}}^{*}$ to obtain the complete graph $K_{n_i+1}(i=1,2,\cdots ,m)$; by adding edges among $K_{n_i+1}(i=1,2,\cdots ,m)$, we can obtain the graph $H_3$. Finally, we can obtain the graph $G_1$ by applying the graph transformation III on $H_3$, and we can obtain the graph $Q_n^k$ by adding an edge to $G_1$ (Figure 10). Then, according to the above lemmas, it holds that $SO(G_{k^{″}}^{*})\le SO\left(H_3\right)\le SO\left(G_1\right)\le SO\left(Q_n^k\right)$.

Figure 10. The graph transformation with $m\ge 2$, $k^{″}\ge 2$.

From the above cases, we know that the second largest value of the Sombor index is taken by one of the graphs $G_1,G_2$, and $G_3$. In our next work, we only need to compare the Sombor index of $G_1,G_2$, and $G_3$. Therefore,

$$\begin{array}{cc}\hfill SO\left(G_1\right)& =(k-1)\sqrt{{(n-2)}^2+1}+\sqrt{{(n-2)}^2+{(n-k)}^2}+\sqrt{{(n-k)}^2+1}\hfill \\ \hfill & +\sqrt{{(n-2)}^2+{(n-k-1)}^2}(n-k-2)+\sqrt{{(n-k)}^2+{(n-k-1)}^2}\hfill \\ \hfill & +\sqrt{2{(n-k-1)}^2}(n-k-3).\hfill \\ \hfill SO\left(G_2\right)& =k\sqrt{{(n-1)}^2+1}+\sqrt{{(n-1)}^2+{(n-k-2)}^2}+\sqrt{{(n-1)}^2+{(n-k-1)}^2}(n-k)\hfill \\ \hfill & +\sqrt{2{(n-k-1)}^2}(n-k-4)+\sqrt{{(n-k-2)}^2+{(n-k-1)}^2}(2n-2k-5).\hfill \\ \hfill SO\left(G_3\right)& =k\sqrt{{(n-2)}^2+1}+(n-k-2)(\sqrt{{(n-k-2)}^2+{(n-k-1)}^{{}^2}}\hfill \\ \hfill & +\sqrt{{(n-2)}^2+{(n-k-1)}^{{}^2}})+\sqrt{2{(n-k-1)}^2}(n-k-3).\hfill \end{array}$$

Therefore, we compare the graph $G_2$ with the graph $G_1$, where $n\ge k+3$ and $k\ge 1$, then, through direct calculation, we have $SO\left(G_2\right)-SO\left(G_1\right)>0$.

Next, we compare the graph $G_2$ with the graph $G_1$ using easy calculation, where $n\ge k+3$ and $k\ge 1$, then $SO\left(G_2\right)-SO\left(G_3\right)>0$. Therefore, the Sombor index attained the maximum value on $G_2$. The theorem is proven. □

3. Extremal Sombor Index of Graphs with a Clique Number

Let ${\chi }_{n,k}$ and ${\psi }_{n,k}$ be a class of graphs with n vertices, and chromatic number k and clique number k, respectively.

Let $Q_n\left(k\right)$ be a complete k-partite graph with a partition set differing in size by no more than 1. Let $T_k\left({(n-k)}^1\right)$ be the graph in which a vertex of a a complete graph $K_k$ is connected to a path graph $P_{n-k+1}$ (see Figure 11). Next, we will prove that the graph $Q_n\left(k\right)$ and the tadpole graph $T_k\left({(n-k)}^1\right)$ has a maximal and minimal Sombor index in ${\psi }_{n,k}$, respectively.

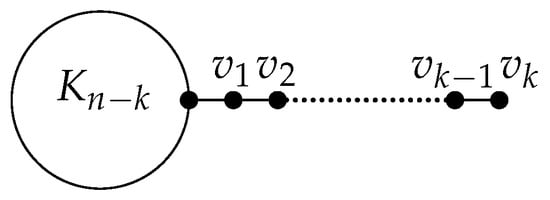
Figure 11. The tadpole graph $T_k\left({(n-k)}^1\right)$.

In order to obtain our main result, we first provide some necessary lemmas. From the definition of the Sombor index of the graph, these lemmas are obvious and fundamental.

Assume that ${\displaystyle \sum _{i=1}^k}{n}_i=n$. Set $Q_{n_1,n_2,\cdots ,n_k}$ as the complete k-partite graph with n vertices, and the number of the partition set as $n_1,n_2,\cdots ,n_k$, respectively.

Lemma 5. 

$SO\left(Q_{n_1,n_2,\cdots ,n_k}\right)={\displaystyle \sum _{s=1}^k}{\displaystyle \sum _{t=s+1}^k}{n}_s{n}_t\sqrt{{(n-n_s)}^2+{(n-n_t)}^2}.$

Proof. 

In a partition set of size $n_j$ of $Q_{n_1,n_2,\cdots ,n_k}$ for $j\in \{1,2,\cdots ,k\}$, the degree of each vertex is $n-n_j$ between two partition sets of sizes $n_i,n_j$, where $1\le i<j\le k$, respectively. In $Q_{n_1,n_2,\cdots ,n_k}$, there are $n_i{n}_j$ edges connected to two sets. In addition, the degrees of the two vertices incident with each of these edges are $n-n_i$ and $n-n_j$, respectively. Then, we have $SO\left(Q_{n_1,n_2,\cdots ,n_k}\right)={\displaystyle \sum _{s=1}^k}{\displaystyle \sum _{t=s+1}^k}{n}_s{n}_t\sqrt{{(n-n_s)}^2+{(n-n_t)}^2}$, and we complete the proof of the lemma. □

In the next, we consider the maximal Sombor index of graphs from ${\chi }_{n,k}$. The set ${\chi }_{n,k}$ contains connected graph $K_1$ when $k=1$, and the only graph in ${\chi }_{n,k}$ is the complete graph $K_n$ when $k=n$.

Lemma 6. 

Let $G\in {\chi }_{n,k}$ be the graph with a maximal Sombor index. Then, $G\cong Q_{n_1,n_2,\cdots ,n_k}$.

Proof. 

The lemma holds immediately based on Lemma 1, and by the definition of the set ${\chi }_{n,k}$. □

Further, we will introduce some notations. If $u,v\in V\left(G\right)$ are not the same vertices in graph G for $p,q>0$, we denote by $G_{u,v}(p,q)$ the graph from G by attaching a path of length p and q at the vertex u and v of G, respectively. For $v\in V\left(G\right)$, let $G_v\left(l\right)$ be the graph attaining at v a path of length l. Let $1\le k\le n-2$, and through the graph transformations, we get the following Lemma:

Lemma 7. 

Let G be a connected graph with $G\ne K_1$; v is a vertex in G. $G_v(k,n-1-k)$ is the graph resulting from attaching at v two paths of lengths k and $n-1-k$, respectively. Then, $SO\left(G_v(k,n-1-k)\right)>SO\left(G_v(n-1)\right)$.

By repeating the above lemma, it is easy to obtain the following result.

Remark 1 

([6]). When the tree T with t vertices on the graph G is replaced by the path $P_{t+1}$, then $SO\left(G\right)$ of the graph decreases.

Remark 2 

([6]). Assume $s,t>0$, and two vertices $u,v\in V\left(G\right)$ so that $d\left(u\right)\ge d\left(v\right)>1$. Then, $SO\left(G_{u,v}(s,t)\right)>SO\left(G_v(s+t)\right)$.

Now, we first consider the maximal Sombor index for a graph from ${\chi }_{n,k}$. In the discussion in this part, we assume that the graph G has k chromatic numbers for $1<k<n$ and $n=kq+r$, $(0\le r<k)$, where $q=\lfloor \frac{n}{k}\rfloor$.

Lemma 8. 

Let $G\in {\chi }_{n,k}$, then

$$\begin{array}{cc}\hfill SO\left(G\right)& \le SO\left(Q_n\left(k\right)\right)\hfill \\ \hfill & =\left({\displaystyle \genfrac{}{}{0pt}{}{k-r}{2}}\right){⌊\frac{n}{k}⌋}^2\sqrt{2{(n-\lfloor \frac{n}{k}\rfloor )}^2}\hfill \\ \hfill & +r(k-r)⌊\frac{n}{k}⌋⌈\frac{n}{k}⌉\sqrt{{(n-\lfloor \frac{n}{k}\rfloor )}^2+{(n-\lceil \frac{n}{k}\rceil )}^2}\hfill \\ \hfill & +\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right){⌈\frac{n}{k}⌉}^2\sqrt{2(n-{\lceil \frac{n}{k}\rceil }^2)},\hfill \end{array}$$

where the first equality holds when $G\cong Q_n\left(k\right)$.

Proof. 

For any graph $G\in {\chi }_{n,k}$, there are k color classes, and each color class is an independent set. If the order of k classes is $n_1,n_2,\cdots ,n_k$, according to Lemma 6 and by ${\chi }_{n,k}$, it takes the maximal Sombor index, which is the complete k-partite graph $Q_{n_1,n_2,\cdots ,n_k}$. Suppose that a graph $G\in {\chi }_{n,k}$ takes the maximal Sombor index. We claim that G is $Q_n\left(k\right)$. On the contrary, suppose that $n_p$ and $n_q$ represent the size of vertices of two classes, $1\le p<q\le k$, such that $n_q-n_p\ge 2$. Let ${\displaystyle \sum _i^j}{n}_i=0$ if $j<i$ for convenience. Thus, using Lemma 5, we obtain:

$$\begin{array}{cc}\hfill SO\left(Q_{n_1,n_2,\cdots ,n_p,\cdots ,n_q,\cdots ,n_k}\right)& =\sum _{i=1}^{p-1}\sum _{j=i+1}^k{n}_i{n}_j\sqrt{{(n-n_i)}^2+{(n-n_j)}^2}\hfill \\ \hfill & +\sum _{i=p+1}^{q-1}\sum _{\begin{array}{c}j=i+1\\ j\ne q\end{array}}^k{n}_i{n}_j\sqrt{{(n-n_i)}^2+{(n-n_j)}^2}\hfill \\ \hfill & +\sum _{i=q+1}^k\sum _{j=i+1}^k{n}_i{n}_j\sqrt{{(n-n_i)}^2+{(n-n_j)}^2}\hfill \\ \hfill & +n_p(n-n_p)(\sum _{i=1}^{p-1}\sqrt{{(n-n_i)}^2+{(n-n_j)}^2}\hfill \\ \hfill & +\sum _{j=p+1}^k\sqrt{{\left(n_j\right)}^2+{(n-n_j)}^2})\hfill \\ \hfill & +n_q(n-n_q)(\sum _{i=1}^{p-1}\sqrt{n_i^2+{(n-n_j)}^2}\hfill \\ \hfill & +\sum _{j=p+1}^{q-1}\sqrt{n_j^2+{(n-n_j)}^2}+\sum _{j=q+1}^k\sqrt{n_j^2+{(n-n_j)}^2}).\hfill \end{array}$$

Let

$$\begin{array}{cc}\hfill A_1& =\sum _{i=1}^{p-1}\sum _{j=i+1}^k{n}_i{n}_j\sqrt{{(n-n_i)}^2+{(n-n_j)}^2},A_2=\sum _{i=p+1}^{q-1}\sum _{\begin{array}{c}j=i+1\\ j\ne q\end{array}}^k{n}_i{n}_j\sqrt{{(n-n_i)}^2+{(n-n_j)}^2},\hfill \\ \hfill A_3& =\sum _{i=q+1}^k\sum _{j=i+1}^k{n}_i{n}_j\sqrt{{(n-n_i)}^2+{(n-n_j)}^2},and\hfill \\ \hfill B& =\sum _{i=1}^{p-1}\sqrt{n_i^2+{(n-n_i)}^2}+\sum _{i=q+1}^{q-1}\sqrt{n_i^2+{(n-n_i)}^2}+\sum _{j=q+1}^k\sqrt{n_i^2+{(n-n_i)}^2}.\hfill \end{array}$$

Then, we have

$$\begin{array}{cc}\hfill SO\left(Q_{n_1,n_2,\cdots ,n_p,\cdots ,n_q,\cdots ,n_k}\right)& =A_1+A_2+A_3+\left(n(n_p+n_q)-(n_p^2+n_q^2)\right)\sum _{i=1}^{p-1}\sqrt{n_i^2+{(n-n_i)}^2}\hfill \\ \hfill & +\left(n{n}_p(1-p)+n_q(n-n_q)\right)\sum _{i=p+1}^{q-1}\sqrt{n_i^2+{(n-n_i)}^2}\hfill \\ \hfill & +\left(n_p(n-n_p)+n_q(n-n_q)\right)\sum _{j=q+1}^k\sqrt{n_i^2+{(n-n_i)}^2}\hfill \\ \hfill & +n_p{n}_q(n-n_p)(n-n_q)=A_1+A_2+A_3\hfill \\ \hfill & +\left(n(n_p+n_q)-(n_p^2+n_q^2)\right)B+n{n}_p{n}_q(1-p)(n-n_q),\hfill \end{array}$$

$$\begin{array}{cc}\hfill SO\left(Q_{n_1,n_2,\cdots ,n_{p+1},\cdots ,n_{q-1},\cdots ,n_k}\right)& =A_1+A_2+A_3\hfill \\ \hfill & +\left((n_p+1)(n-n_p-1)+(n_q-1)(n-n_q+1)\right)B\hfill \\ \hfill & +(n_p+1)(n_q-1)(n-n_p-1)(n-n_q+1).\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill SO\left(Q_{n_1,n_2,\cdots ,n_{p+1},\cdots ,n_{q-1},\cdots ,n_k}\right)& -SO\left(Q_{n_1,n_2,\cdots ,n_p,\cdots ,n_q,\cdots ,n_k}\right)=2(n_q-n_p-1)B\hfill \\ \hfill & +(n_p{n}_q+n_q-n_p-1)(n-n_p-1)(n-n_q+1)\hfill \\ \hfill & -n_p{n}_q(n-n_p)(n-n_q)\hfill \\ \hfill & \ge n_p{n}_q\left((n-n_p)-(n-n_q)-1\right)\hfill \\ \hfill & >n_q-n_p-1>0.\hfill \end{array}$$

This contradicts the maximality of the Sombor index of G. We know that $n=r+k\lfloor \frac{n}{k}\rfloor =r\lceil \frac{n}{k}\rceil +(k-r)\lfloor \frac{n}{k}\rfloor$. Combining with Lemma 5, the values of Sombor index $SO\left(Q_n\left(k\right)\right)$ can be obtained immediately. □

Lemma 9 

([26]). Assume that $G_1=(V,E_1)$ is the graph, $\psi \left(G\right)\le k$. Then, there is a k-partite graph $G_2=(V,E_2)$, and it holds that $d_{G_1}\left(v\right)\le d_{G_2}\left(v\right)$ for $v\in V$.

According to the above lemmas, we obtain:

Theorem 3. 

Let $G\in {\psi }_{n,k}$. Then,

$$\begin{array}{cc}\hfill SO\left(G\right)& \le \left({\displaystyle \genfrac{}{}{0pt}{}{k-r}{2}}\right){⌊\frac{n}{k}⌋}^2\sqrt{2{(n-\lfloor \frac{n}{k}\rfloor )}^2}\hfill \\ \hfill & +r(k-r)⌊\frac{n}{k}⌋⌈\frac{n}{k}⌉\sqrt{{(n-\lfloor \frac{n}{k}\rfloor )}^2+{(n-\lceil \frac{n}{k}\rceil )}^2}\hfill \\ \hfill & +\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right){⌈\frac{n}{k}⌉}^2\sqrt{2(n-{\lceil \frac{n}{k}\rceil }^2)},\hfill \end{array}$$

the equality holds when $G\cong Q_n\left(k\right)$.

Proof. 

It is trivial that when $k=n$, then we assume that $k<n$. Assume that G from ${\psi }_{n,k}$ has the maximum Sombor index. Let $G\in {\chi }_{n,k}$. If not, from the case $\psi \left(G\right)=k$ of Lemma 9, we obtain the k-partite graph $G_2$ with the same set of vertices as G makes $v\in V\left(G\right)=V\left(G_2\right)$, $d_G\left(v\right)\le d_{G_2}\left(v\right)$. Clearly, $G_2\in {\psi }_{n,k}$. According to the definition, we obtain $SO\left(G_2\right)\ge SO\left(G\right)$. According to Lemma 8, this theorem holds immediately due to the uniqueness of extremal graphs in ${\chi }_{n,k}$. □

Theorem 4. 

Let $G\in {\psi }_{n,k}$, then $SO\left(G\right)\ge \left(\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)-(k-1)\right)\sqrt{2{(k-1)}^2}+(k-1)\sqrt{k^2+{(k-1)}^2}$$+\sqrt{k^2+4}+2\sqrt{2}(n-k-2)+\sqrt{5}$, where equality holds when $G\cong T_k\left({(n-k)}^1\right)$.

Proof. 

Assume that the graph $G_1\in {\psi }_{n,k}$ has the smallest Sombor index. Using the definition of ${\psi }_{n,k}$, $G_1$ has a subgraph $Q_k$, which is a complete graph. Let $V\left(Q_k\right)=\{v_1,v_2,\cdots ,v_k\}$. Via Lemma 1, $G_1$ is a graph obtained via $Q_k$ by connecting some trees rooted in some vertices of $Q_k$. From $G_1$, let $V_0=\left\{v_i\right|i\in \{1,2,\cdots ,k\}$, $d_{G_1}\left(v_i\right)>k-1$ (i.e., there is a tree connected to $v_i$ for any vertex $v_i\in V_0$, and vertices in $V_0$ are labeled as $v_1,v_2,\cdots ,v_t$, with $k\ge t$.

From Lemma 9, all trees connected to some vertices of $Q_k$ must be paths in $G_1$, i.e., all vertices of $V_0$ of $G_1$ have degree k. Suppose that $|V_0|=1$. Contrary to assumption, we can find two vertices at least, such that $v_i,v_j\in V_0$. The graph $G_{v_i,v_j}(p_i,p_j)$ is denoted by $G_1$. However, from the graph transformation, $G_1\cong G_{v_i,v_j}(p_i,p_j)$ is converted into $G_{v_i}(p_i+p_j)$ or $G_{v_j}(p_i+p_j)$ with a smaller Sombor index. In this way, it contradicts the choice of $G_1$. Hence, $G_1\cong T_k\left({(n-k)}^1\right)$, and through simple calculation, we have $SO\left(T_k\left({(n-k)}^1\right)\right)=\left(\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)-(k-1)\right)\sqrt{2{(k-1)}^2}+(k-1)\sqrt{k^2+{(k-1)}^2}+\sqrt{k^2+4}+2\sqrt{2}(n-k-2)+\sqrt{5}.$

This theorem is proven. □

4. Conclusions

In this paper, firstly, we determine the Sombor index of the graph with a given number of cut edges and we determine the types of graphs with the largest and second largest Sombor indexes through the graph transformations I, II, and III. Secondly, we use the clique number to characterize the extremal graphs for the Sombor index, and we provide the upper and lower bounds for the index. As a result, we provide the following results in Table 1.

Table 1. Main results.

Class of Graph	Extremal Graph	Maximum or Minimum
${\mathcal{C}}_{n,k}$	$Q_n^k$	maximum
${\chi }_{n,k}$	$Q_n\left(k\right)$	maximum
${\psi }_{n,k}$	$T_k\left({(n-k)}^1\right)$	minimum

5. Notations

We provide some symbols in Table 2 in the following.

Table 2. Notations.

Symbol	Definition
${\mathcal{C}}_{n,k}$	The set of graphs having n vertices and k cut edges
$Q_n^k$	The graph obtained by connecting k independent vertices to one of the vertices of $K_{n-k}$
${\chi }_{n,k}$	The set of chromatic number k of connected graphs with n vertices
${\psi }_{n,k}$	The set of clique number k of connected graphs with n vertices
$Q_n\left(k\right)$	The complete k-partite graph and its partition sets differ in size by no more than 1
$T_k\left({(n-k)}^1\right)$	The graph in which a vertex on a complete graph $K_k$ is connected to a pendent vertex on a path graph $P_{n-k+1}$
$Q_{n_1,n_2,\cdots ,n_k}$	The complete k-partite graph with n vertices; the number of the partition set is $n_1,n_2,\cdots ,n_k$, respectively
$G_{u,v}(p,q)$	The graph attained from G by attaching at u a path of length p and at v a path of length q
$G_v\left(l\right)$	The graph attained at v a path of length l