Analytical Solution of Generalized Bratu-Type Fractional Differential Equations Using the Homotopy Perturbation Transform Method
Abstract
1. Introduction
Basic Definitions
2. Basic Homotopy Perturbation Transform Approach
3. Existence and Uniqueness of the Solution
4. Main Result
5. Convergence Analysis
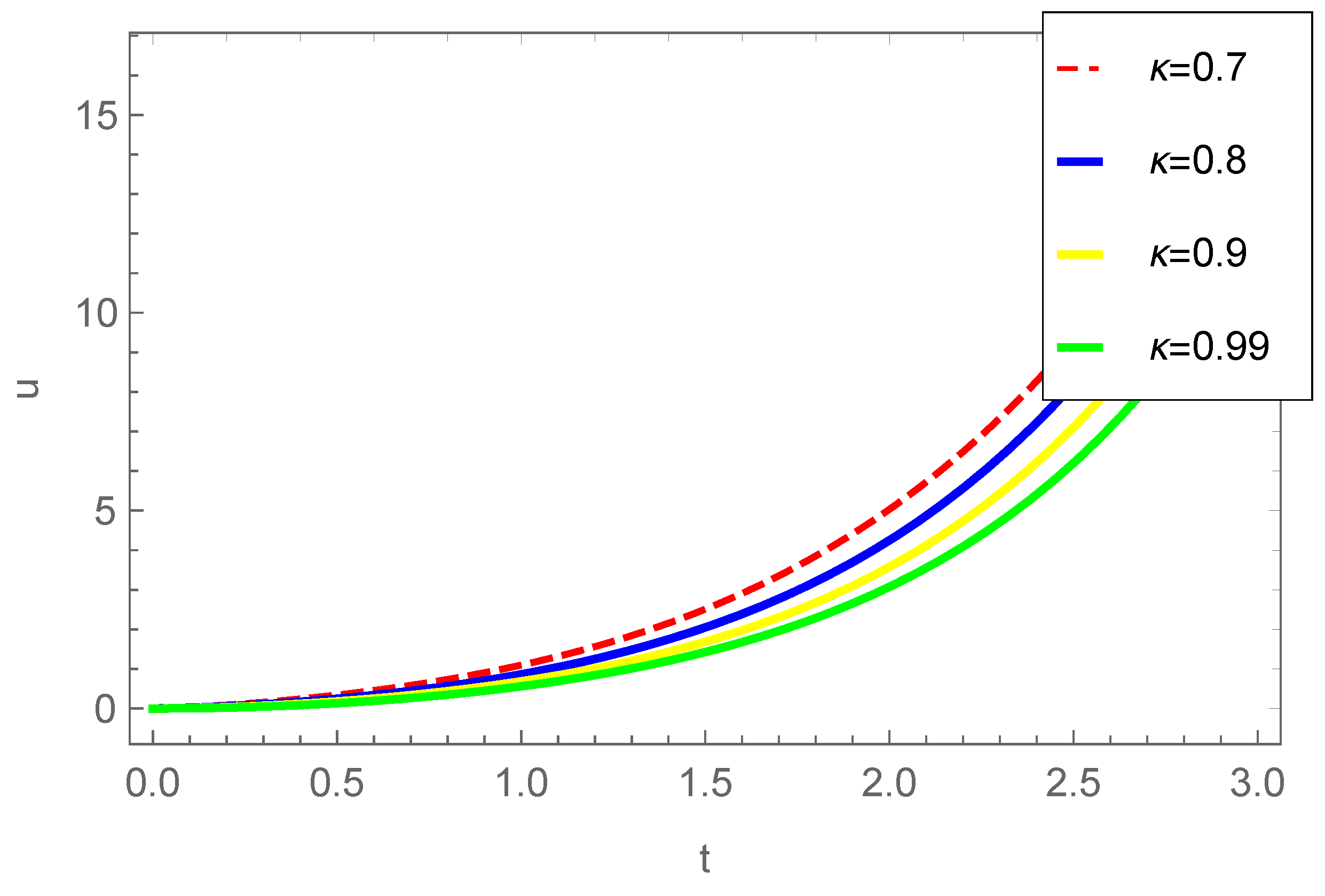
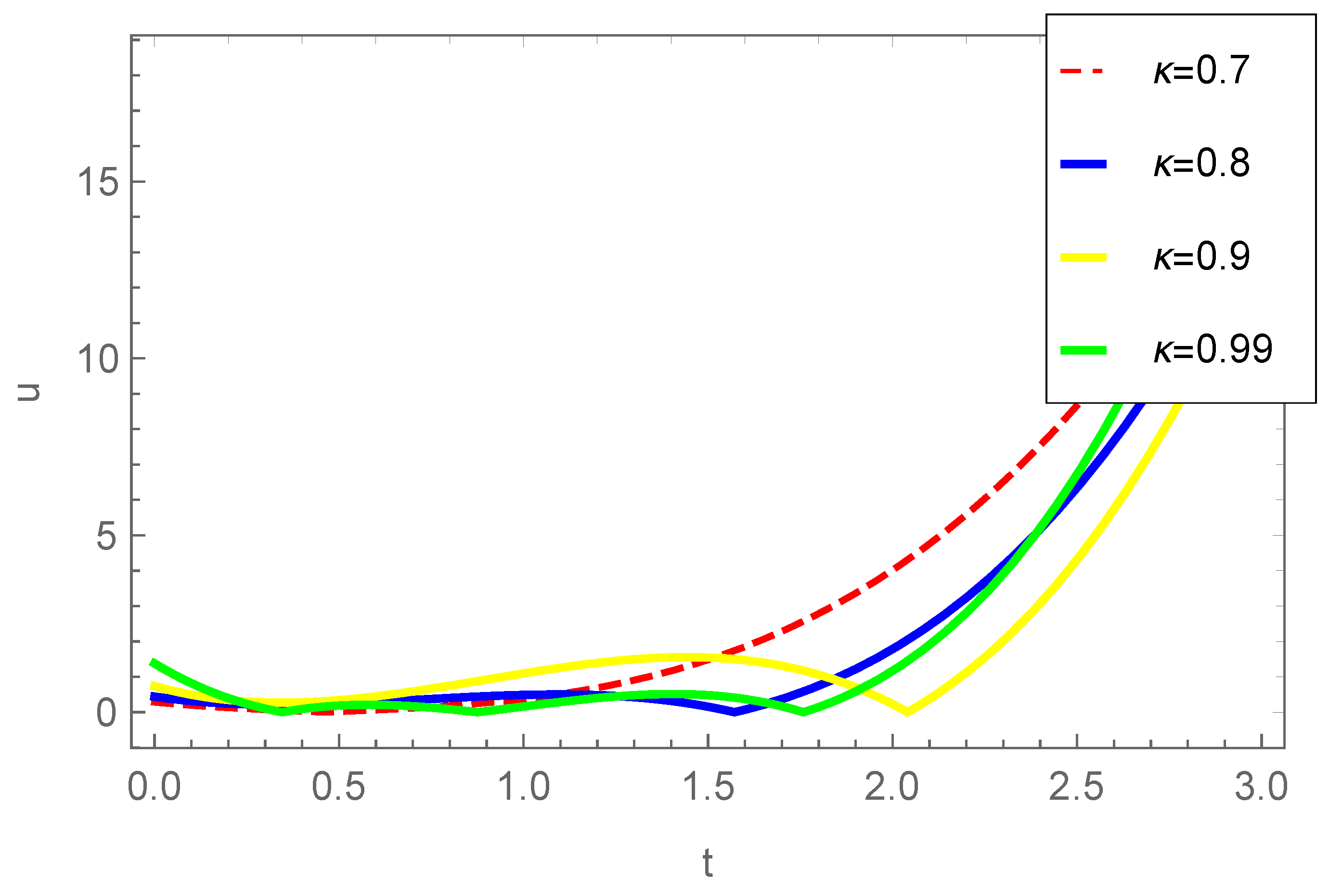
6. Special Cases
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; A Wiley-Interscience Publication: New York, NY, USA, 1993; ISBN 0-471-58884-9. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus-Theory and Applications of Differentiation and Integration to Arbitrary Order, 1st ed.; Mathematics in Science and Engineering: New York, NY, USA; London, UK, 1974; ISBN 978-012-525-550-9. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, 1st ed.; North-Holland Mathematics Studies: Amsterdam, The Netherlands, 2006; ISBN 978-0-444-51832-3. [Google Scholar]
- Podlubny, I. Fractional Differential Equations—An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, 1st ed.; Mathematics in Science and Engineering: New York, NY, USA; London, UK, 1999; ISBN 978-0-12-558840-9. [Google Scholar]
- Zhou, Y. Basic Theory of Fractional Differential Equations; World Scientific: Beijing, China, 2014; ISBN 978-981-4579-89-6. [Google Scholar]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science Publisher: New York, NY, USA, 2012; ISBN 978-1-938576-01-0. [Google Scholar]
- Yang, X.J.; Gao, F.; Srivastava, H.M. Exact travelling wave solutions for the local fractional two-dimensional Burger’s type equations. J. Comput. Appl. Math. 2017, 73, 203–210. [Google Scholar] [CrossRef]
- Atangana, A. On the new fractional derivative and application to non-linear Fisher’s reaction-diffusion equation. Appl. Math. Comput. 2016, 273, 948–956. [Google Scholar] [CrossRef]
- Saad, K.M.; Atangana, A.; Baleanu, D. New fractional derivatives with non-singular kernel applied to the Burgers equation. Chaos 2018, 28, 63–109. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. Solving a multi-order fractional differential equation using adomian decomposition. Appl. Math. Comput. 2007, 189, 541–548. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A reliable modification of Adomian decomposition method. Appl. Math. Comput. 1999, 102, 77–86. [Google Scholar] [CrossRef]
- Biazar, J.; Babolian, E.; Islam, R. Solution of the system of ordinary differential equations by Adomian decomposition method. Appl. Math. Comput. 2004, 147, 713–719. [Google Scholar] [CrossRef]
- Hashim, I.; Abdulaziz, O.; Momani, S. Homotopy Analysis Method for Fractional IVPs. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 674–684. [Google Scholar] [CrossRef]
- Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2014, 147, 499–513. [Google Scholar] [CrossRef]
- Liao, S. Notes on the homotopy analysis method: Some definitions and theorems. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 983–997. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S.; Erturk, V.S. Generalized differential transform method for solving a space- and time-fractional diffusion-wave equation. Phys. Lett. A 2007, 370, 379–387. [Google Scholar] [CrossRef]
- Abdulaziz, O.; Hashim, I.; Momani, S. Solving systems of fractional differential equations by homotopy-perturbation method. Phys. Lett. A 2008, 372, 451–459. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- Khan, Y. An effective modification of the laplace decomposition method for nonlinear equations. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 1373–1376. [Google Scholar] [CrossRef]
- Khan, Y. Homotopy perturbation transform method for nonlinear equations using He’s polynomials. Comput. Math. Appl. 2011, 61, 1963–1967. [Google Scholar] [CrossRef]
- Khan, M.; Gondal, M.A.; Hussain, I.; Vanani, S.K. A new comparative study between homotopy analysis transform method and homotopy perturbation transform method on a semi infinite domain. Math. Comput. Model. 2012, 55, 1143–1150. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Swroop, R. Numerical solution of time- and space-fractional coupled Burger’s equations via homotopy algorithm. Alex. Eng. J. 2016, 55, 1753–1763. [Google Scholar] [CrossRef]
- Mohamed, M.S.; Hamed, Y.S. Solving the convection–diffusion equation by means of the optimal q-homotopy analysis method (Oq-HAM). Results Phys. 2016, 6, 20–25. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for solving boundary value problems. Phys. Lett. A 2006, 350, 87–88. [Google Scholar] [CrossRef]
- He, J.H. The homotopy perturbation method for nonlinear oscillators with discontinuities. Appl. Math. Comput. 2004, 151, 287–292. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Gomez-Aguilar, J.F.; Atangana, A. New insight in fractional differentiation: Power, exponential decay and Mittag–Leffler laws and applications. Eur. Phys. J. Plus 2017, 132, 1–21. [Google Scholar] [CrossRef]
- Gomez-Aguilar, J.F.; Atangana, A. Decolonisation of fractional calculus rules: Breaking commutativity and associativity to capture more natural phenomena. Eur. Phys. J. Plus 2018, 133, 166. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Swroop, R.; Kumar, S. An efficient computational approach for time-fractional Rosenau–Hyman equation. Neural Comput. Appl. 2017, 30, 3063–3070. [Google Scholar] [CrossRef]
- Ascher, U.M.; Matheij, R.; Russell, R.D. Numerical Solution of Boundary Value Problems for Ordinary Differential Equations; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1995; ISBN 978-089-871-354-1. [Google Scholar]
- Chandrasekhar, S. An Introduction to the Study of Stellar Structure; Dover: Chicago, IL, USA, 1957; ISBN 978-0-486-60413-8. [Google Scholar]
- Ghazanfari, B.; Sepahvandzadeh, A. Homotopy perturbation method for solving fractional Bratu-type equation. J. Math. Model. 2015, 2, 143–155. [Google Scholar]
- Ghazanfari, B.; Sepahvandzadeh, A. Solving fractional Bratu-type equations by modified variational iteration method. Selcuk. J. Appl. Math. 2014, 39, 23–29. [Google Scholar]
- Ghazanfari, B.; Sepahvandzadeh, A. Adomian decomposition method for solving fractional Bratu-type equations. J. Math. Comput. Sci. 2014, 8, 236–244. [Google Scholar] [CrossRef]
- Ghomanjani, F.; Shateyi, S. Numerical solution for fractional Bratu’s initial value problem. Open Phys. 2017, 15, 1045–1048. [Google Scholar] [CrossRef]
- Demir, D.D.; Zeybek, A. The numerical solution of fractional Bratu-type differential equations. ITM Web Conf. 2017, 13, 1–11. [Google Scholar] [CrossRef]
- Yi, M.; Sun, K.; Huang, J.; Wang, L. Numerical solution of fractional integrodifferential equations of bratu type by using CAS wavelets. J. Appl. Math. 2013, 2013, 801395. [Google Scholar] [CrossRef]
- Kukushkin, M.V. Abstract Fractional Calculus for m-accretive Operators. Int. J. Appl. Math. 2021, 34, 1–41. [Google Scholar] [CrossRef]
- Kukushkin, M.V. On Solvability of the Sonin–Abel Equation in the Weighted Lebesgue Space. Fractal Fract. 2021, 5, 77. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications, 1st ed.; Gordon and Breach, Yverdon; CRC Press: Boca Raton, FL, USA, 1993; ISBN 2881248640. [Google Scholar]
- Luchko, Y.; Yamamoto, M. General time-fractional diffusion equation: Some uniqueness and existence results for the initial boundary value problems. Fract. Calc. Appl. Anal. 2016, 19, 676–695. [Google Scholar] [CrossRef]
- Oliveira, D.S.; Oliveira, E.C.D. On a Caputo-type fractional derivative. Adv. Pure Appl. Math. 2018, 10, 81–91. [Google Scholar] [CrossRef]
- Qureshi, S.; Rangaig, N.A.; Baleanu, D. New Numerical Aspects of Caputo-Fabrizio Fractional Derivative Operator. Mathematics 2019, 7, 374. [Google Scholar] [CrossRef]
- Yadav, S.; Pandey, R.K.; Shukla, A.K. Numerical approximations of Atangana–Baleanu Caputo derivative and its application. Chaos Solitons Fractals 2019, 118, 58–64. [Google Scholar] [CrossRef]
- Demiray, S.T.; Bulut, H.; Belgacem, F.B.M. Sumudu Transform Method for Analytical Solutions of Fractional Type Ordinary Differential Equations. Math. Probl. Eng. 2014, 2015, 131690. [Google Scholar] [CrossRef]
- Atangana, A.; Akgul, A. Can transfer function and Bode diagram be obtained from Sumudu transform. Alex. Eng. J. 2019, 59, 1971–1984. [Google Scholar] [CrossRef]
- Bodkhe, D.S.; Panchal, S.K. On Sumudu Transform Of Fractional Derivatives and Its Applications to Fractional Differential Equations. Asian J. Math. Comput. 2016, 11, 69–77. [Google Scholar]
- Dubey, V.P.; Kumar, R.; Kumar, D. Analytical study of fractional Bratu-type equation arising in electro-spun organic nanofibers elaboration. Phys. A 2019, 521, 762–772. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhamzi, G.; Gouri, A.; Alkahtani, B.S.T.; Dubey, R.S. Analytical Solution of Generalized Bratu-Type Fractional Differential Equations Using the Homotopy Perturbation Transform Method. Axioms 2024, 13, 133. https://doi.org/10.3390/axioms13020133
Alhamzi G, Gouri A, Alkahtani BST, Dubey RS. Analytical Solution of Generalized Bratu-Type Fractional Differential Equations Using the Homotopy Perturbation Transform Method. Axioms. 2024; 13(2):133. https://doi.org/10.3390/axioms13020133
Chicago/Turabian StyleAlhamzi, Ghaliah, Aafrin Gouri, Badr Saad T. Alkahtani, and Ravi Shanker Dubey. 2024. "Analytical Solution of Generalized Bratu-Type Fractional Differential Equations Using the Homotopy Perturbation Transform Method" Axioms 13, no. 2: 133. https://doi.org/10.3390/axioms13020133
APA StyleAlhamzi, G., Gouri, A., Alkahtani, B. S. T., & Dubey, R. S. (2024). Analytical Solution of Generalized Bratu-Type Fractional Differential Equations Using the Homotopy Perturbation Transform Method. Axioms, 13(2), 133. https://doi.org/10.3390/axioms13020133





