Response Analysis and Vibration Suppression of Fractional Viscoelastic Shape Memory Alloy Spring Oscillator Under Harmonic Excitation

Abstract

This study investigates the dynamic behavior and vibration mitigation of a fractional single-degree-of-freedom (SDOF) viscoelastic shape memory alloy spring oscillator system subjected to harmonic external forces. A fractional derivative approach is employed to characterize the viscoelastic properties of shape memory alloy materials, leading to the development of a novel fractional viscoelastic model. The model is then theoretically examined using the averaging method, with its effectiveness being confirmed through numerical simulations. Furthermore, the impact of various parameters on the system’s low- and high-amplitude vibrations is explored through a visual response analysis. These findings offer valuable insights for applying fractional sliding mode control (SMC) theory to address the system’s vibration control challenges. Despite the high-amplitude vibrations induced by the fractional order, SMC effectively suppresses these vibrations in the shape memory alloy spring system, thereby minimizing the risk of catastrophic events.

1. Introduction

Viscoelastic materials, distinct from purely viscous substances and elastomers, exhibit both strain sensitivity and spring-like elastic characteristics. These unique properties have led to their widespread application across various research domains [1,2,3]. Recently, there has been a growing interest in integrating viscoelasticity into engineering systems, such as mechanical and machinery systems, to gain a more comprehensive understanding of their dynamic responses [4,5].

Traditionally, viscoelastic properties have been modeled using integer-order frameworks like the classical Maxwell, Voigt, and Kelvin models [1]. However, these models fall short of accurately capturing the intricate mechanical behavior of viscoelastic materials. To address this limitation, researchers have turned to fractional derivatives, which incorporate time memory, offering a more nuanced representation of viscoelastic behavior. This shift has led to the development of fractional-order models, such as the fractional Maxwell, Poynting–Thomson, and Kelvin–Voigt models [6,7,8,9,10].

Bagley [11] made significant contributions to the foundational theory of fractional viscoelastic materials. AIJarbouh [12] utilized transformation methods and fractional derivatives to investigate the rheological characteristics of these materials. Wang [13] employed the fractional order Kelvin–Voigt model to analyze the mechanical behavior of viscoelastic saturated soil, confirming the validity of solutions for fractional viscoelastic systems under varying loads. Liu et al. [14] developed a vibration model for fractional viscoelastic piles based on viscoelastic mechanics, obtaining numerical solutions through numerical integration. Their study indicates that the fractional order significantly affects the mechanical characteristics of viscoelastic materials.

Research on fractional dynamic systems has led to the development of various analytical and numerical methods to analyze their dynamic responses [15,16,17,18,19,20,21,22,23,24]. These methods are essential for understanding how system parameters influence behavior. For instance, Rudinger [25] employed frequency domain techniques to study linear fractional systems under Gaussian white noise, while Shen et al. [26] utilized averaging methods for both linear and nonlinear systems with fractional derivatives. Liu [27] applied stochastic averaging to explore the dynamic response and vibration suppression in viscoelastic wing models with fractional constitutive relations.

In the field of shape memory alloys, significant advancements have also been made in fractional calculus. M. E. Reyes-Melo et al. [28] developed a fractional Zener model for NiTi shape memory alloys, investigating the application of fractional calculus in dynamic analysis. Manzoor et al. [29] examined vibration reduction systems in shape memory alloys using fractional homotopic perturbation methods. Despite these developments, there is still limited research focused on nonlinear dynamic systems with fractional damping under harmonic excitation. This highlights the necessity of studying the dynamic behavior of shape memory alloy spring oscillators in such contexts. Such investigations not only contribute to a better understanding of the performance of shape memory alloys in practical applications but also provide a theoretical foundation for the further development of related technologies.

This paper addresses this gap by focusing on the dynamic response and vibration suppression of a fractional viscoelastic shape memory alloys spring oscillator under harmonic excitation. Section 2 introduces the model, while Section 3 derives the amplitude–frequency response equation using the averaging method, validating theoretical results through numerical simulations. The transition from low- to high-amplitude vibrations is visualized under varying system parameters. To prevent structural damage from high-amplitude vibrations, Section 4 discusses the application of fractional sliding mode control for vibration suppression. Finally, Section 5 concludes the paper, summarizing the key findings and implications and the next future work.

2. The Fractional SDOF Shape Memory Alloy Model

This section establishes a fractional-order viscoelastic shape memory alloy spring oscillator model under harmonic excitation, based on existing knowledge of fractional-order derivatives and existing shape memory alloy models.

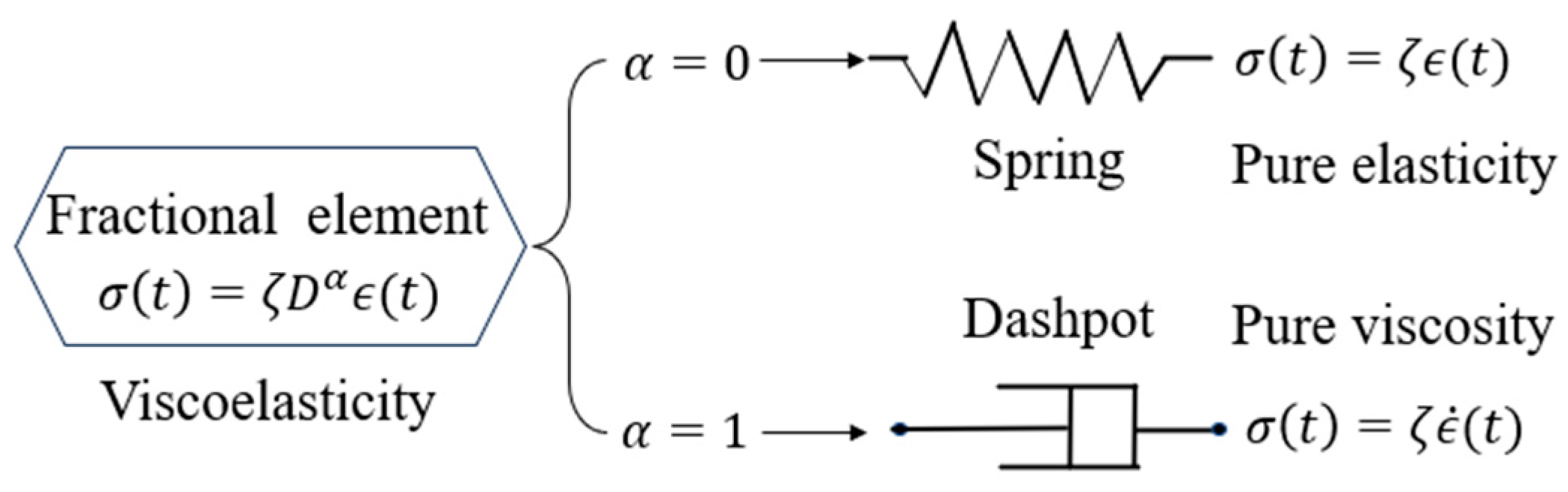
2.1. Preliminaries

We begin by outlining the fundamental definitions and properties of fractional calculus. Various definitions of fractional-order derivatives have been proposed, with the Riemann–Liouville and Caputo definitions being the most prevalent. Notably, the Caputo definition retains the same initial conditions as the classical integer-order derivatives, making it more applicable in fields such as physics and engineering [30,31]. Consequently, we will utilize the Caputo definition in this discussion.

Before presenting the various definitions, we assume that the function $f\left(t\right)$ is continuously differentiable; $\alpha$ is the fractional order.

Definition 1

([30]). The $\alpha$-order Grunwald–Letnikov fractional-order integral operator is given by

$${}_a{}^{GL}I_t^{\alpha }f\left(t\right)=\underset{h\to 0+}{\lim }{\displaystyle \frac{1}{h^{\alpha }}}{\sum }_{j=0}^{{\displaystyle \frac{t-a}{h}}}{\left(-1\right)}^j\left(\begin{array}{c}\alpha \\ j\end{array}\right)f(t-jh),$$

(1)

where  $\left(\begin{array}{c}\alpha \\ j\end{array}\right)={\displaystyle \frac{\alpha \left(\alpha -1\right)\left(\alpha -2\right)\cdots (\alpha -j+1)}{j!}}$, $\alpha >0$.

Definition 2

([30]). The $\alpha$-order Riemann–Liouville fractional-order integral operator is defined as follows

$${}^{RL}I_{a+}^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_a^t{\displaystyle \frac{f\left(\tau \right)}{{(t-\tau )}^{1-\alpha }}}d\tau , t>a, \alpha >0,$$

(2)

$${}^{RL}I_{b-}^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_t^b{\displaystyle \frac{f\left(\tau \right)}{{(\tau -t)}^{1-\alpha }}}d\tau , t<b, \alpha >0,$$

(3)

where  $\mathsf{\Gamma }(·)$ denotes Euler’s Gamma function.

Definition 3

([30]). The operator for the α-order Riemann–Liouville fractional derivative is defined as follows:

$${}_a{}^{RL}D_t^{\alpha }f\left(t\right)=({{\displaystyle \frac{d}{dt}})}^n{I}_{a+}^{n-\alpha }f\left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(n-\alpha \right)}}({{\displaystyle \frac{d}{dt}})}^n{\int }_a^t{\displaystyle \frac{f\left(\tau \right)}{{\left(t-\tau \right)}^{\alpha -n+1}}}d\tau ,$$

(4)

where $n=\left[\alpha \right]+1$, $n-1\le \alpha <n$, $t>a$.

When $0<\alpha <1$, the definition can be simplified to

$${}_a{}^{RL}D_t^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(1-\alpha \right)}}{\displaystyle \frac{d}{dt}}{\int }_a^t{\displaystyle \frac{f\left(\tau \right)}{{\left(t-\tau \right)}^{\alpha }}}d\tau , t>a.$$

(5)

Definition 4

([30]). The $\alpha$-order Caputo fractional-order derivative operator is written as

$${}_a{}^{C}D_t^{\alpha }f\left(t\right)=I_{a+}^{n-\alpha }{f}^{\left(n\right)}\left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}{\int }_a^t{\displaystyle \frac{f^{\left(n\right)}\left(\tau \right)}{{(t-\tau )}^{\alpha -n+1}}}d\tau ,$$

(6)

where $n=\left[\alpha \right]+1$, $n-1\le \alpha <n$, $t>a$.

When $0<\alpha \le 1$, $n=1$, the above definition is simplified as

$${}_a{}^{C}D_t^{\alpha }f\left(t\right)=I_{a+}^{1-\alpha }{f}^{\prime }\left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}{\int }_a^t{\displaystyle \frac{f^{\prime }\left(\tau \right)}{{(t-\tau )}^{\alpha }}}d\tau , 0<\alpha \le 1, t>a.$$

(7)

To simplify notation, the Caputo fractional-order derivative operator  ${}_a{}^{C}D_t^{\alpha }$ will be represented as  $D^{\alpha }$ hereafter.

Property 1

([30]). For a function $f\left(t\right)$ that is continuously differentiable, we can state that

$$D^{p_1}f\left(t\right)D^{p_2}f\left(t\right)=D^{p_2}f\left(t\right)D^{p_1}f\left(t\right)=D^{p_1+p_2}f\left(t\right).$$

(8)

where  $p_1$ and  $p_2$ are the fractional orders.

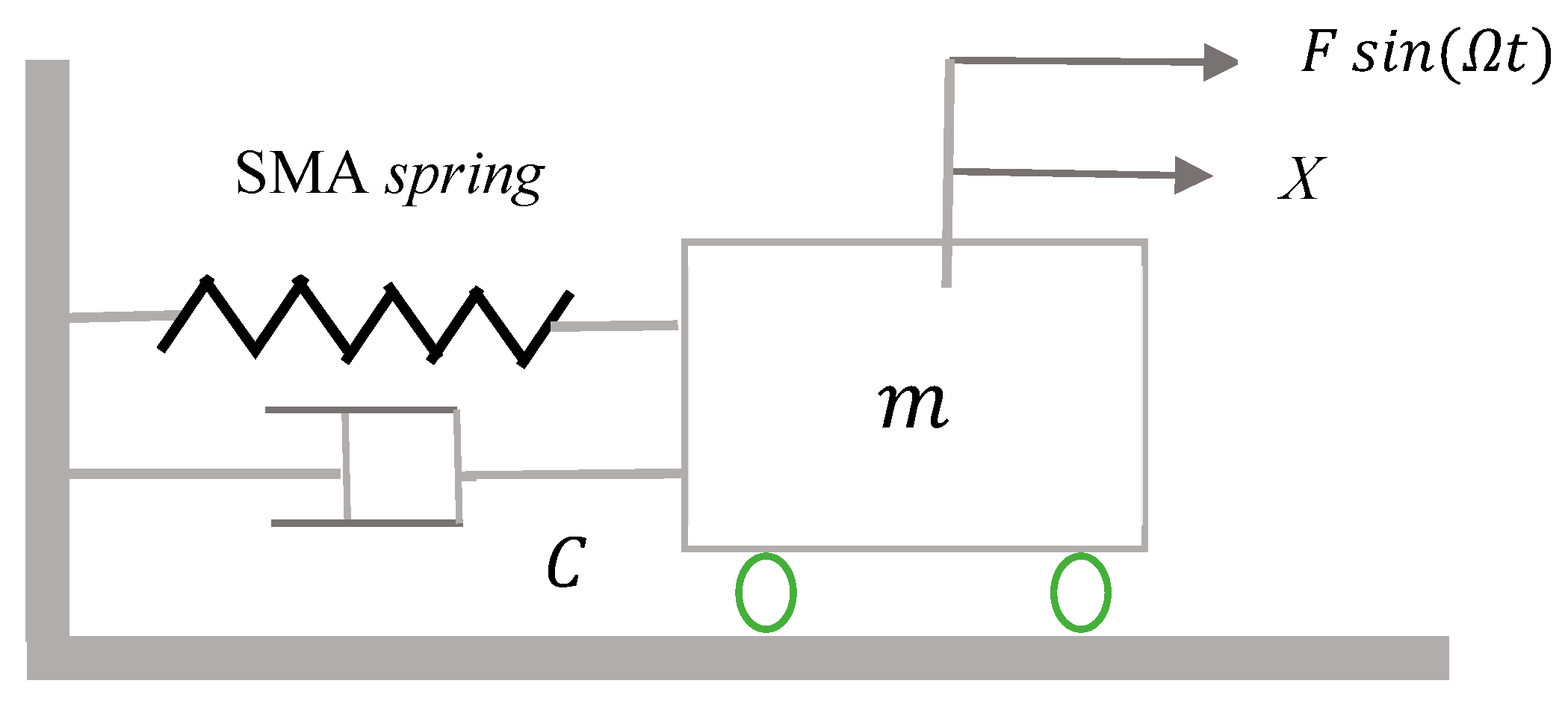
2.2. Model Description

This system is a single-degree-of-freedom oscillator utilizing a shape memory alloy, depicted in Figure 1. It features a mass $m$ that experiences a periodic force $Fsin\left(\Omega t\right)$, along with a linear damper $c$ and a shape memory alloy spring connected to a fixed support.

In this study, the polynomial constitutive model introduced by Falk [32] is utilized to characterize the spring restoring force of the shape memory alloy oscillator. The constitutive equation is given by

$$\sigma =a_1\left(T-T_M\right)ϵ-a_2{ϵ}^3+a_3{ϵ}^5,$$

(9)

in which $a_1$, $a_2$, and $a_3$ are positive material constants, $\sigma$ is stress, $T$ is temperature, $T_M$ is critical temperature for martensitic transformation, and $ϵ$ is strain. For the shape memory alloy, $T_A$ (the critical temperature for austenite transformation) and $T_M$ are both key temperature parameters. The connection between these parameters and the positive material constants $a_1$, $a_2$, and $a_3$ is as follows:

$$T_A=T_M+{\displaystyle \frac{a_2^2}{4a_1{a}_3}},$$

(10)

Consequently, the restoring force model for the shape memory alloy spring can be formulated as follows:

$$K\left(X,T\right)=\overline{a_1}\left(T-T_M\right)X-\overline{a_2}{X}^3+\overline{a_3}{X}^5,$$

(11)

where $\overline{a_1}=a_{1}A/L, \overline{a_2}=a_{2}A/L^3, \overline{a_3}=a_{3}A/L^5$, $A$ is the area of shape memory alloy spring wire, $L$ represents original length of shape memory alloy spring, and $x$ is the displacement.

According to Newton’s second law, considering mass, damping, and the restoring force of the spring, the motion-governing equation of the shape memory alloy oscillator is obtained:

$$m\ddot{X}+c\dot{X}+\overline{a_1}\left(T-T_M\right)X-\overline{a_2}{X}^3+\overline{a_3}{X}^5=F\mathit{sin}\left(\Omega t\right).$$

(12)

Now, we introduce the following dimensionless transformations:

$$x={\displaystyle \frac{X}{L}}, \theta ={\displaystyle \frac{T}{T_M}}, {\tau ={\omega }_{0}t,\omega }_0^2={\displaystyle \frac{a_{1}A{T}_M}{mL}}, \omega ={\displaystyle \frac{\Omega }{{\omega }_0}},$$

$$N=\theta -1, r={\displaystyle \frac{c}{m{\omega }_0}}, B=-{\displaystyle \frac{a_{2}A}{mL{\omega }_0^2}}, E={\displaystyle \frac{a_{3}A}{mL{\omega }_0^2}}, f={\displaystyle \frac{F}{mL{\omega }_0^2}}.$$

where $x$, $r$, $\tau$, $\omega$, $\theta$, and $f$ are the dimensionless displacement, damping coefficient, time, frequency of periodic external excitation, temperature, and amplitude, respectively.

Because shape memory alloys display varying properties based on temperature $\theta$, we focus exclusively on the range where the phase remains stable in the alloy, specifically when $\theta >1$, and take ${\Omega }^2=N$, $N>0$.

The dimensionless equation for the shape memory alloy oscillator can be rephrased as follows [33]:

$$\ddot{x}+r\dot{x}+Nx+B{x}^3+E{x}^5=f\mathit{sin}\left(\omega \tau \right).$$

(13)

In this study, the Caputo fractional-order derivative is utilized to characterize the viscoelastic behavior of shape memory alloy materials. The simple fractional element model shown in Figure 2 was first proposed by Scott-Blair [34]. The stress–strain constitutive relationship of the fractional Scott-Blair model can be expressed as:

$$\sigma \left(t\right)={\zeta D}^{\alpha }ϵ\left(t\right), 0\le \alpha \le 1,$$

(14)

where $\sigma \left(t\right)$ and $ϵ\left(t\right)$ are the stress and strain, respectively. The constants $\zeta$ and $\alpha$ are specific to the material, with $\zeta$ indicating the viscosity coefficient and $\alpha$ representing the order of the fractional derivative. To realize the theoretical analysis of the shape memory alloy system, we consider $D^{\alpha }$ as the definition of the Caputo fractional derivative (7). As the order $\alpha$ transitions from zero to one, the behavior of the fractional element shifts from exhibiting pure elasticity to demonstrating pure viscosity [7].

The Scott-Blair damping element model has been utilized to characterize viscoelastic materials and has been validated with experimental data [35]. By leveraging the characteristics of the fractional damping element, we substitute the traditional viscous damping component in the classical linear viscoelastic model with a fractional damping element, thereby creating a fractional constitutive relationship model for viscoelastic materials.

Considering Scott-Blair’s model (14) and supposing that the oscillator created from shape memory alloy exhibits weak nonlinearity, a SDOF viscoelastic shape memory alloy spring oscillator model with harmonic excitation is established by incorporating a small parameter $0<\epsilon \ll 1$ as

$$\ddot{x}+{\epsilon }^{2}r\dot{x}+{\Omega }_0^{2}x+{\epsilon }^{2}B{x}^3+{\epsilon }^{2}E{x}^5+{\epsilon }^2{kD}^{\alpha }x={\epsilon }^{2}f\mathit{sin}\left(\omega \tau \right).$$

(15)

3. Amplitude–Frequency Relation

The average method is utilized for the SDOF fractional viscoelastic shape memory alloy system, leading to the derivation of its amplitude–frequency response relationship. The effectiveness of this approach is confirmed through a numerical analysis of the system’s response. Following this, we investigate the impact of various system parameters on the response in detail. Notably, we found that the amplitude–frequency response exhibits a jump between high and low amplitudes, with high-amplitude vibrations being identified as undesirable and needing suppression in the subsequent section.

3.1. Theoretical Analysis via the Averaging Method

To apply the averaging method, we reformulate the viscoelastic shape memory alloy system (15) as follows:

$$\ddot{x}+{\omega }^{\ast 2}={\epsilon }^{2}g\left(x\right),$$

(16)

where

$${\omega }^{\ast 2}={\Omega }_0^2(1+{\epsilon }^2\delta ),$$

(17)

$$g\left(x\right)={\delta \Omega }_0^{2}x+fsin\left(\omega t\right)-(r\dot{x}+B{x}^3+E{x}^5+k{D}^{\alpha }x),$$

(18)

in which $\delta =({\omega }^{\ast 2}/{\Omega }_0^2-1)/{\epsilon }^2$ is the detuning parameter. We focus solely on the primary resonance, specifically when ${\omega }^{\ast }=\omega$.

Suppose that

$$x=a\left(t\right)\mathit{cos}\theta , \dot{x}=-\omega a\left(t\right)\mathit{sin}\theta , \theta =\omega t+\phi ,$$

(19)

in which $a$ and $\phi$ represent the amplitude and phase of $x$, respectively, and they are slowly varying functions of time. Substituting Equation (19) into Equation (16), then

$$\dot{a}=-{\displaystyle \frac{{\epsilon }^2}{\omega }}g\left(x\right)sin\theta =-{\displaystyle \frac{{\epsilon }^2}{\omega }}\left[P_1\right(x)+P_2(x\left)\right]sin\theta ,$$

(20)

$$\dot{\phi }=-{\displaystyle \frac{{\epsilon }^2}{a\omega }}g\left(x\right)cos\theta =-{\displaystyle \frac{{\epsilon }^2}{a\omega }}\left[P_1\right(x)+P_2(x\left)\right]cos\theta ,$$

(21)

where

$$P_1\left(x\right)=\sigma {\Omega }_0^{2}x+fsin\left(\omega t\right)-r\dot{x}+B{x}^3+E{x}^5,$$

(22)

$$P_2\left(x\right)=-k{D}^{\alpha }x,$$

(23)

By averaging over the time interval $[0,T]$, we obtain the following averaged equations:

$$\dot{a}=-{\displaystyle \frac{{\epsilon }^2}{T\omega }}{\int }_0^T[P_1\left(x\right)+P_2\left(x\right)]sin\theta d\theta ,$$

(24)

$$\dot{\phi }=-{\displaystyle \frac{{\epsilon }^2}{Ta\omega }}{\int }_0^T[P_1\left(x\right)+P_2\left(x\right)]cos\theta d\theta .$$

(25)

According to the averaging principle [27,36], if $P_1\left(x\right)$ and $P_2\left(x\right)$ are periodic functions, one option is to choose $T=2\pi$; alternatively, we can take $T$ to approach infinity.

To begin with, expanding the integrals in Equation (24) results in:

$${\dot{a}=A}_1+A_2, \dot{\phi }{=B}_1+B_2,$$

(26)

in which $A_1$ and $B_1$ represent the first part of Equations (24) and (25); $A_2$ and $B_2$ represent the second part of Equations (24) and (25).

For the first part, through calculation, we can obtain

$$A_1=-{\displaystyle \frac{{\epsilon }^2}{2\omega }}fcos\phi -{\displaystyle \frac{{\epsilon }^2}{2}}ra,$$

(27)

$$B_1=-{\displaystyle \frac{{\epsilon }^2}{2a\omega }}(\sigma {\Omega }_0^{2}a-fsin\phi -{\displaystyle \frac{3}{4}}B{a}^3-{\displaystyle \frac{5}{8}}E{a}^5).$$

(28)

To compute the second part, we introduce the following two key formulas [27,36]:

$$\underset{T\to \infty }{\mathit{lim}}{\int }_0^T{\displaystyle \frac{sin\left(\Omega t\right)}{t^{\alpha }}}dt={\Omega }^{\alpha -1}\Gamma \left( 1-\alpha \right)cos\left({\displaystyle \frac{\mathsf{\alpha }\mathsf{\pi }}{2}}\right),$$

(29)

$$\underset{T\to \infty }{\mathit{lim}}{\int }_0^T{\displaystyle \frac{cos\left(\Omega t\right)}{t^{\alpha }}}dt={\Omega }^{\alpha -1}\Gamma \left( 1-\alpha \right)sin\left({\displaystyle \frac{\alpha \pi }{2}}\right).$$

(30)

Then, according to the Caputo fractional-order derivation definition, we obtain

$$\begin{array}{cc}{A}_2& =-{\displaystyle \frac{{\epsilon }^2}{2\pi \omega }}{\int }_0^{2\pi }{P}_2\left(x\right)sin\theta d\theta =-\underset{T\to \infty }{\mathit{lim}}{\displaystyle \frac{{\epsilon }^2}{\omega }}{\displaystyle \frac{1}{T}}{\int }_0^T{P}_2\left(x\right)sin\theta d\theta \\ & =\underset{T\to \infty }{lim}{\displaystyle \frac{{\epsilon }^{2}k}{{\epsilon }^{2}T}}{\int }_0^T{D}^{\alpha }\left[acos\theta \right]sin\theta d\theta =-{\displaystyle \frac{{\epsilon }^{2}ak{\omega }^{\alpha -1}}{2}}sin\left({\displaystyle \frac{\alpha }{2}}\pi \right),\end{array}$$

(31)

$$\begin{array}{ll}{B}_2& =-\underset{T\to \infty }{\mathit{lim}}{\displaystyle \frac{{\epsilon }^2}{a\omega }}{\displaystyle \frac{1}{T}}{\int }_0^T{P}_2\left(x\right)cos\theta d\theta =-\underset{T\to \infty }{\mathit{lim}}{\displaystyle \frac{{\epsilon }^2}{a\omega }}{\displaystyle \frac{1}{T}}{\int }_0^T(-k)D^{\alpha }\left(acos\theta \right)d\theta \\ & ={\displaystyle \frac{{\epsilon }^{2}k{\omega }^{\alpha -1}}{2}}cos\left({\displaystyle \frac{\alpha \pi }{2}}\right).\end{array}$$

(32)

Hence, we have

$$\dot{a}=-{\displaystyle \frac{{\epsilon }^2}{2\omega }}fcos\phi -{\displaystyle \frac{{\epsilon }^2}{2}}ra-{\displaystyle \frac{{\epsilon }^{2}ak{\omega }^{\alpha -1}}{2}}sin\left({\displaystyle \frac{\alpha }{2}}\pi \right),$$

(33)

$$\dot{\phi }=-{\displaystyle \frac{{\epsilon }^2}{2\omega a}}[\sigma {\Omega }_0^{2}a-fsin\phi -{\displaystyle \frac{3}{4}} B{a}^3-{\displaystyle \frac{5}{8}} E{a}^5+ak{\omega }^{\alpha -1}\mathit{cos}\left({\displaystyle \frac{\alpha }{2}}\pi \right)],$$

(34)

Next, considering the significance to the actual engineering vibrations, we mainly study the steady-state response of the system. Let $\dot{a}=0$ and $\dot{\phi }=0$; eliminating the parameter $\phi$, we have the amplitude–frequency equations

$$f^2={[ra\omega +ak{\omega }^{\alpha }sin({\displaystyle \frac{\alpha }{2}}\pi \left)\right]}^2+{[a\sigma {\Omega }_0^2-{\displaystyle \frac{3}{4}} B{a}^3-{\displaystyle \frac{5}{8}} E{a}^5+ak{\omega }^{\alpha }\mathit{cos}\left({\displaystyle \frac{\mathsf{\alpha }}{2}}\mathsf{\pi }\right)]}^2.$$

(35)

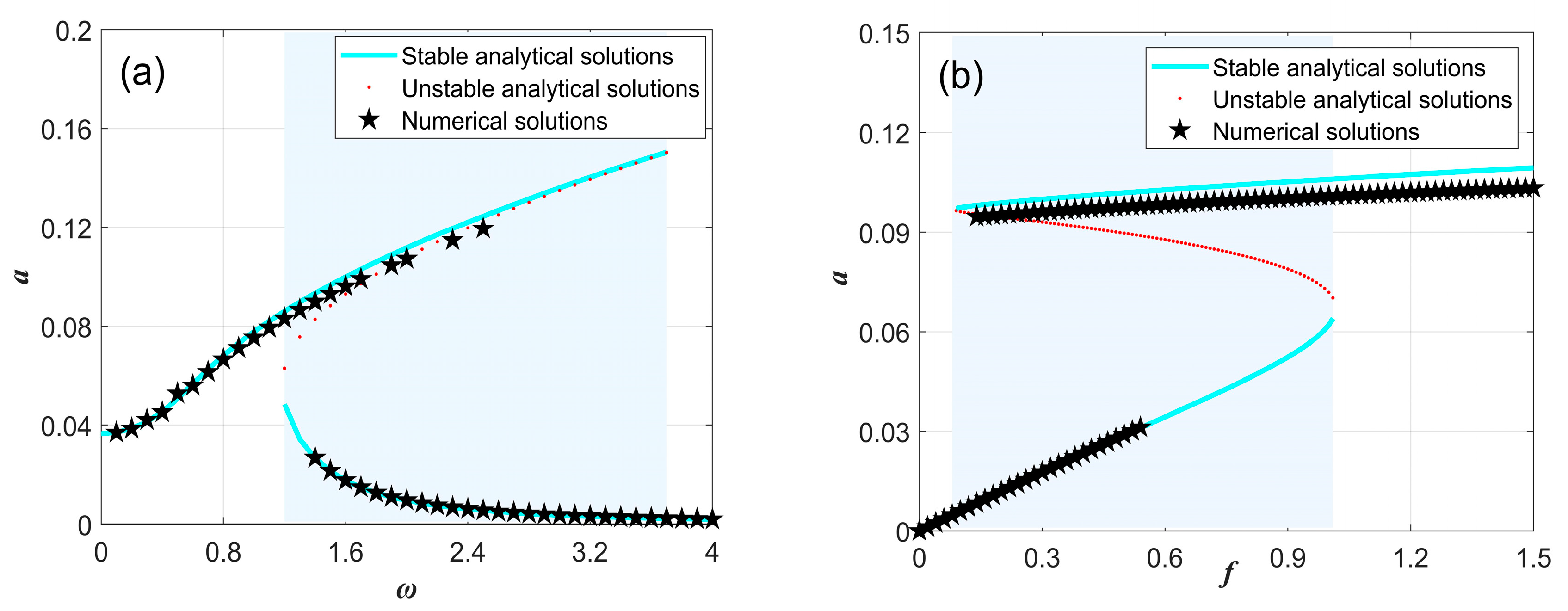
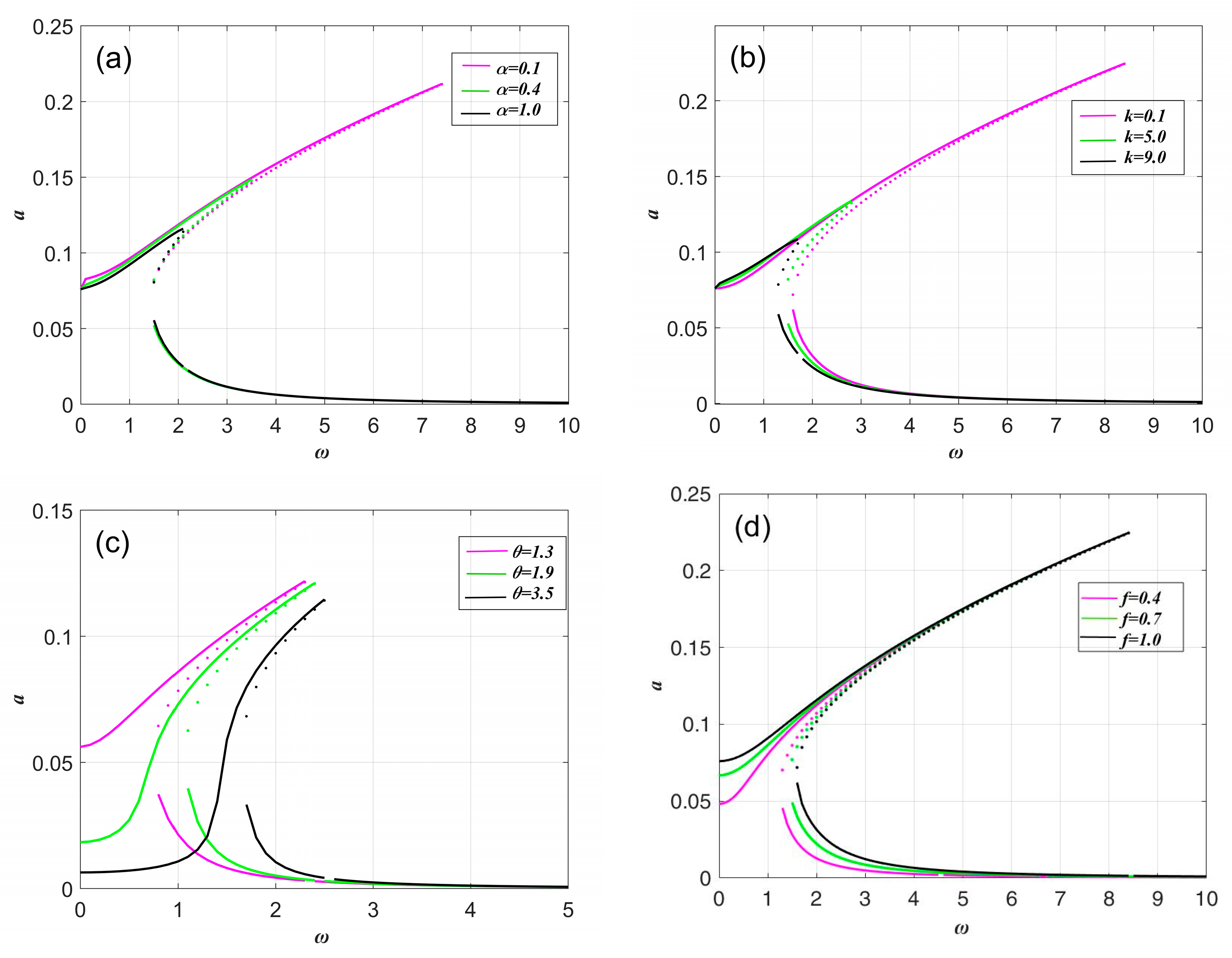
3.2. Numerical Verifications

To confirm the accuracy of the approximate analytical solution derived from the average method, we perform numerical simulations. Then, we define the following state variables

$${u=D}^{\alpha }x, {v=D}^{1-\alpha }u.$$

(36)

According to Property 1, the original SDOF viscoelastic shape memory alloy system can be reformulated into the following set of three-dimensional fractional differential equations:

$$\left\{\begin{array}{c}{D}^{\alpha }x=h\\ D^{1-\alpha }h=v\\ D^{1}v=a_{1}x{+a}_{2}h+a_{3}v+a_4{x}^3+a_5{x}^5+a_{6}sin\left(\omega t\right)\end{array}\right.,$$

(37)

where $\alpha$ is the fractional order, $a_1=-{\mathsf{\Omega }}_0^2$, $a_2=-{\epsilon }^{2}k$, $a_3=-{\epsilon }^{2}r$, $a_4=-{\epsilon }^{2}B$, $a_5=-{\epsilon }^{2}E$, and $a_6={\epsilon }^{2}f$.

In the following numerical simulation, the system parameters are given as $r=0.5, \theta =1.9, B=-1.3\times {10}^3, E=4.7\times {10}^5, \epsilon =\sqrt{0.1}$, and $f=0.16$. In addition, the initial value of the fractional derivative term is roughly taken as [35]

$$h\left(0\right)=x\left(0\right)cos\left({\displaystyle \frac{\alpha \pi }{2}}\right).$$

(38)

Figure 3 illustrates that the analytical results derived from Equation (35) closely align with the numerical results for the amplitude–frequency response described by Equation (15). Additionally, the multi-valued response phenomenon occurs within a specific range of frequency $\omega$ or amplitude $f$ of the external excitation, as indicated by the blue area in Figure 3. In fact, these multi-valued phenomena are attributed to the nonlinear term in the restoring force of the shape memory alloy spring, which includes two stable solutions and one unstable solution. In other words, as $\omega$ or $f$ reaches a certain critical point, stochastic transitions occur between the upper branch and the lower branch, leading to shifts from the upper branch to the lower branch and vice versa. In these ranges, two probable steady-state responses coexist, characterized by low-amplitude and high-amplitude vibrations, which can be considered a bistable behavior. Thus, the SDOF viscoelastic shape memory alloy oscillator demonstrates bistable behavior that is highly sensitive to the system’s initial conditions.

Next, by visualizing the response data under different system parameters, the impact of different parameters on the system amplitude–frequency response is discussed, and the transition phenomenon from low-amplitude to high-amplitude vibrations are revealed.

In Figure 4a, the amplitude–frequency response curves of the system with different fractional order $\alpha =0.1$, $\alpha =0.4$, and $\alpha =1.0$ are compared. It is found that with the increase in fractional order, the peak amplitude decreases, and the bistable region shifts to the left, resulting in a reduction of the related area; meanwhile, the curvature of the amplitude–frequency response curve also diminishes. When $\alpha =1.0$, that is, the integer order, the system generates a lower peak amplitude, indicating that fractional order yields a higher peak amplitude compared with traditional integer-order systems. The primary reason for this outcome is that the properties of viscoelastic materials are captured by fractional derivatives, which can simultaneously influence both the structural damping and stiffness of the system. Figure 4b gives the amplitude–frequency response images when the fractional coefficients $k=0.1$, $k=5.0$, and $k=9.0$. We observed that the phenomenon is similar to fractional order. These results indicate that the fractional derivative significantly impacts the nonlinear behavior of the viscoelastic shape memory alloy spring system, influencing its bistable characteristics. As the unique shape memory effect of shape memory alloy material is affected by temperature, Figure 4c shows the amplitude–frequency response of the system at different temperatures. With the increase in temperature, the bistable region shifts progressively to the right, leading to a reduction in its corresponding area, which means that the frequency range for the multivalued response region becomes narrower. In addition, we also study the influence of external harmonic excitation amplitude $f$ on the nonlinear amplitude–frequency response curve. As the amplitude of external excitation increases, the area of multi-value response area increases, as shown in Figure 4d.

To further demonstrate the jump phenomenon depicted in Figure 3, several time history and phase diagrams are presented in Figure 5. These diagrams illustrate that the steady-state responses of the fractional viscoelastic shape memory alloy spring oscillator are highly influenced by the initial conditions. When the initial conditions are $x\left(0\right)=0.01$ and $\dot{x}\left(0\right)=0.01$, as shown in Figure 5a,b, the limit cycle oscillation with high amplitude appears in the system state, corresponding to the upper half of the amplitude response in the bistable region. When the initial conditions are $x\left(0\right)=0.1$ and $\dot{x}\left(0\right)=0.1$, as shown in Figure 5c,d, the limit cycle oscillation with relatively low amplitude appears in the system state, corresponding to the lower half of the amplitude response in the bistable region. These two states are very undesirable in practice. Therefore, in order to ensure the normal operation of the shape memory alloy spring vibrator system, we will discuss the active vibration suppression of the fractional viscoelastic shape memory alloy system in the next section.

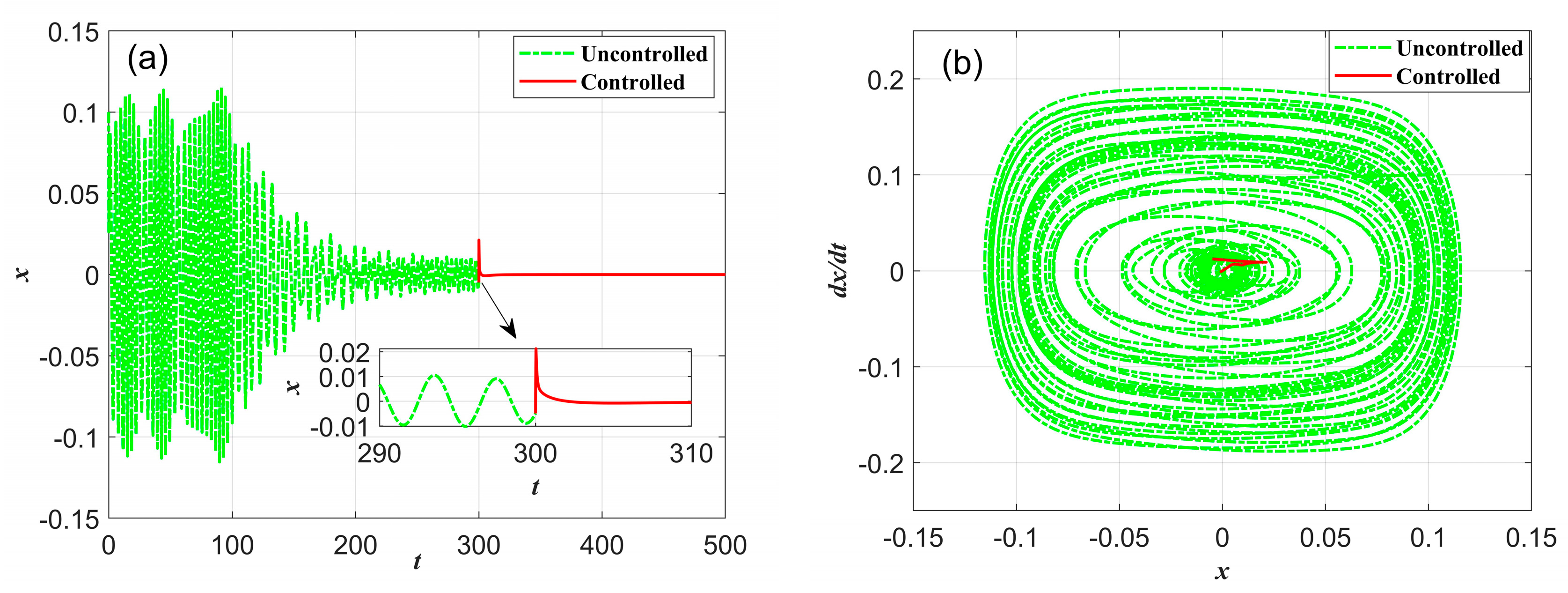
4. Active Vibration Suppression

This section first introduces relevant knowledge of fractional-order sliding mode control theory. Based on this foundation, a fractional-order sliding mode control law is designed. The asymptotic stability of the controlled fractional-order viscoelastic shape memory alloy spring oscillator system under the action of the sliding mode controller is then studied. Finally, numerical simulations are conducted to verify the effectiveness of the designed control law.

4.1. Design of Fractional Synovial Control Law

For the active vibration suppression of fractional viscoelastic shape memory alloy system, we consider applying a controller to realize it. Now, we rewrite the system (15) into the following vector form:

$$D^{\lambda }\mathit{x}=\mathit{M}\mathit{x}+\mathit{p}(\mathit{x},t)+\mathit{u}\left(t\right),$$

(39)

where $\lambda ={[p,1-p,1]}^T,\mathit{x}={[x,h,v]}^{\mathit{T}}\in {\mathbb{R}}^{3\times 1}$ are the system-state vectors. $\mathit{u}\left(t\right)$ is a control input vector, $\mathit{M}\in {\mathbb{R}}^{3\times 3}$ is a constant coefficient matrix, and $\mathit{p}\left(\mathit{x},t\right):{\mathbb{R}}^{3\times 1}\times {\mathbb{R}}_{+}\to {\mathbb{R}}^{3\times 1}$ is a nonlinear vector function, and the specific form is as follows:

$$M=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ a_1& a_2& a_3\end{array}\right], \mathit{p}\left(\mathit{x},t\right)=\left[\begin{array}{c}0\\ 0\\ a_4{x}^3+a_5{x}^5+a_6\sin \left(\omega t\right)\end{array}\right].$$

(40)

where $a_1=-{\Omega }_0^2$, $a_2=-{\epsilon }^{2}k$, $a_3=-{\epsilon }^2\gamma$, $a_4=-{\epsilon }^{2}B$, $a_5=-{\epsilon }^{2}E$, and $a_6={\epsilon }^{2}f$.

The purpose of vibration suppression is to develop a controller $\mathit{u}\left(t\right)$ that ensures

$$\underset{t\to \infty }{\mathit{lim}}‖\mathit{x}\left(t\right)‖=0.$$

(41)

To remove the nonlinear term $\mathit{p}(\mathit{x},t)$ in Equation (39), we choose the following control input vector:

$$\mathit{u}\left(t\right)=\mathit{H}\left(t\right)-\mathit{p}(\mathit{x},t),$$

(42)

in which $\mathit{H}\left(t\right)=\mathit{K}\mathit{w}\left(t\right)$, $\mathit{K}\in {\mathbb{R}}^{3\times 3}$ is a constant gain matrix to be given, and $\mathit{w}\left(t\right)\in {\mathbb{R}}^{3\times 3}$ is the control input signal and satisfies

$$\mathit{w}\left(t\right)=\left\{\begin{array}{c}{w}^{+}\left(t\right),\mathit{s}\left(t\right)\ge 0,\\ w^{-}\left(t\right),\mathit{s}\left(t\right)<0,\end{array}\right.$$

(43)

where $\mathit{s}\left(t\right)\in {\mathbb{R}}^{3\times 1}$ denotes a sliding surface vector function that needs to be designed to define the intended sliding mode behavior. Consequently, system (39) can be reformulated as

$$D^{\lambda }\mathit{x}=\mathit{M}\mathit{x}+\mathit{K}\mathit{w}\left(t\right).$$

(44)

When the system is controllable on the synovial surface, the sliding surface vector function that has been designed must fulfill

$$\mathit{s}\left(t\right)=0,\dot{\mathit{s}}\left(t\right)=0.$$

(45)

which assumes that the system state converges to the equilibrium point, representing the desired control objective. Therefore, an appropriate fractional-order integral surface vector function is defined as

$$\mathit{s}\left(t\right)=D^{\lambda -1}\mathit{x}-{\int }_0^t\left(\mathit{M}+\mathit{K}\right)\mathit{x}\left(s\right)ds,$$

(46)

Combining Equations (45) and (46), the equivalent control ${\mathit{w}}_{eq}\left(t\right)$ can be obtained as follows

$${\mathit{w}}_{eq}\left(t\right)=\mathit{x}.$$

(47)

However, the equivalent control law can only keep the state trajectory of the system on the sliding surface. In order to ensure that the state trajectory of the system far from the sliding surface converges to the expected sliding manifold, the controller chooses the following exponential reaching law:

$$\dot{\mathit{s}}\left(t\right)=-r\mathit{s}-\kappa sgn\left(\mathit{s}\right),$$

(48)

where $\mathrm{s}\mathrm{g}\mathrm{n}\left(\mathit{s}\right)={[\mathrm{s}\mathrm{g}\mathrm{n}\left(s_1\right),\mathrm{s}\mathrm{g}\mathrm{n}\left(s_2\right),\mathrm{s}\mathrm{g}\mathrm{n}\left(s_3\right)]}^T\in {\mathbb{R}}^{3\times 1}$; $s_1$, $s_2$, $s_3$ are elements in the synovial vector function $\mathit{s}$; $r$ and $\kappa$ are positive real numbers; and $\mathrm{s}\mathrm{g}\mathrm{n}\left(·\right)$ represents a sign function [37,38], namely

$$sgn\left(s_i\right)=\left\{\begin{array}{c}\begin{array}{ccc}1,& s_i>0,& \end{array}\\ \begin{array}{ccc}0,& s_i=0,& i=\mathrm{1,2},3\end{array}.\\ \begin{array}{ccc}-1,& s_i<0.& \end{array}\end{array}\right.$$

(49)

Therefore, according to Equations (46) and (48), the control law form of the system can be obtained:

$$\mathit{w}\left(t\right)={\mathit{K}}^{-1}[\mathit{K}\mathit{x}-r\mathit{s}-\kappa sgn(\mathit{s}\left)\right].$$

Furthermore, according to Equation (42), we construct the controller form of Equation (44) as follows

$$\mathit{u}\left(t\right)=\mathit{K}\mathit{x}-r\mathit{s}-\kappa sgn\left(\mathit{s}\right)-\mathit{p}(\mathit{x},t).$$

(50)

In summary, under the action of the controller (50), the fractional viscoelastic shape memory alloy system (39) can be written in the closed-loop form as follows:

$$D^{\lambda }\mathit{x}=\left(\mathit{M}+\mathit{K}\right)\mathit{x}-r\mathit{s}-\kappa sgn\left(\mathit{s}\right).$$

(51)

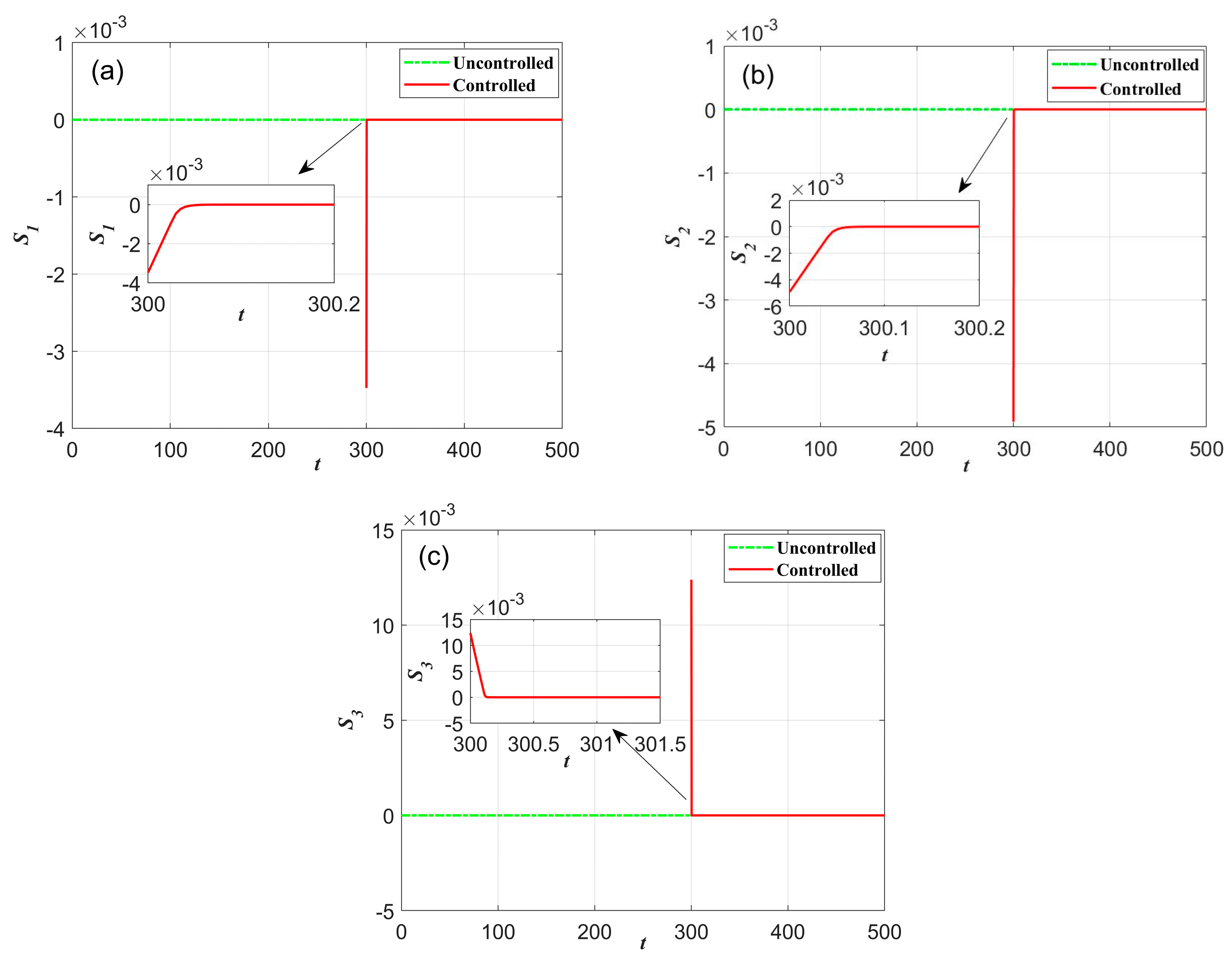
4.2. Asymptotic Stability Analysis

The next work is to analyze the asymptotic stability of the controlled fractional viscoelastic shape memory alloy system (39) when influenced by the sliding mode controller (50). Before proving the stability of the controlled fractional viscoelastic shape memory alloy system, the stability theorem of the fractional system is given, as follows:

Lemma 1

([30]). Consider the following autonomous linear fractional-order system

$$D^q\mathit{y}\left(t\right)=\mathit{C}\mathit{y}\left(t\right),\mathit{y}\left(0\right)={\mathit{y}}_0,$$

(52)

where $\mathit{y}={[y_1,y_2,\dots ,y_n]}^T\in {\mathbb{R}}^n$, $\mathit{C}={\left(c_{ij}\right)}_{n\times n}\in {\mathbb{R}}^{n\times n}$, and $\mathit{q}={[q_1,q_2,\dots ,q_n]}^T\in {\mathbb{R}}^n$, and $0<q_i\le 1$, $i=\mathrm{1,2},\dots ,n$. A fractional-order system is considered asymptotically stable if and only if

$$\left|arg\left(eig\left(\mathit{C}\right)\right)\right|>{\displaystyle \frac{\pi }{2}}\mathit{q},$$

(53)

where $arg(·)$  and $eig(·)$ represent the radial angle and the eigenvalue, respectively.

According to the stability theorem of fractional system in Lemma 1, we give the following theorem.

Theorem 1

([27]). If the controller (50) is selected, appropriate control parameters $r>0$ and $\kappa >0$ are selected, and a constant gain matrix  $\mathit{K}$ is selected, so that the following formula holds

$$\left|arg\left(eig\left(\mathit{M}+\mathit{K}\right)\right)\right|>{\displaystyle \frac{\pi }{2}}\mathit{\lambda },$$

(54)

where in that case, the controlled fractional viscoelastic shape memory alloy system (39) is regarded as asymptotically stable.

Proof. 

When sliding mode motion occurs, that is $\dot{s}\left(t\right)=0$, as indicated by Equation (46), we can derive the following:

$$\dot{\mathit{s}}\left(t\right)=D^{\lambda }\mathit{x}-\left(\mathit{M}+\mathit{K}\right)\mathit{x}=0.$$

(55)

Furthermore, the subsequent autonomous linear fractional-order system can be obtained:

$$D^{\lambda }\mathit{x}=\left(\mathit{M}+\mathit{K}\right)\mathit{x}.$$

(56)

If the constant gain matrix $\mathit{K}$ is chosen appropriately to satisfy condition (54), then the controlled fractional viscoelastic shape memory alloy system (39) is asymptotically stable according to Lemma 1. That is to say, when the sliding mode dynamics take place, the system trajectory will converge to zero.

This concludes the proof. □

One thing to note here is that in order to reduce the influence of controller chattering, in the actual sliding mode control, we choose the following saturation function instead of the sign function in the controller:

$$sat\left(s_i\right)=\left\{\begin{array}{c}\begin{array}{ccc}1,& s_i>\Delta , & \end{array}\\ \varrho s_i\begin{array}{ccc},& \left|s_i\right|\le \Delta ,& \varrho ={\displaystyle \frac{1}{\Delta }},i=\mathrm{1,2},3\end{array},\\ \begin{array}{ccc}-1,& s_i<-\Delta .& \end{array} \end{array}\right.$$

(57)

where $\Delta$ is a positive real number; it is taken as $\Delta =0.001$ in this paper.

4.3. Numerical Simulation

The effectiveness of the SMC strategy introduced in this paper is validated through numerical simulation. In the following numerical simulation, the initial conditions are set as $x_0=0.1$ and $\dot{x_0}=0.1$, other system parameters are the same as those in the previous section, and the time step is $∆t=0.005$. Therefore, the control parameters can be set to

$$\mathit{K}=\left[\begin{array}{ccc}1& 1& 0\\ -3& -1& 1\\ 10& 0& -8\end{array}\right], r=1.0, \kappa =0.1, \Delta =0.001.$$

(58)

It is straightforward to confirm that the matrix $\mathit{K}$ meets the requirement specified in condition (54). In fact, through calculation, all eigenvalues of the matrix $\mathit{M}+\mathit{K}$ are, respectively, ${\vartheta }_1=-14.3681, {\vartheta }_2=0.6840+5.1175\mathrm{i},{\vartheta }_3=0.6840-5.1175\mathrm{i}$. Then we have $\left|arg\left({\vartheta }_1\right)\right|=\pi >\pi {\lambda }_1/2$, $\left|arg\left({\vartheta }_2\right)\right|=1.4379>\pi {\lambda }_2/2$, and $\left|arg\left({\vartheta }_3\right)\right|=1.4379>\pi {\lambda }_3/2$; obviously, the condition (54) in Theorem 1 is satisfied.

We assume that the activation time of SMC is $t=300$ in these simulations. The simulation outcomes are presented in Figure 6, Figure 7 and Figure 8, and the partial enlargement of some results is given in the illustration. As can be seen from Figure 6, after adding the sliding mode controller, the system response quickly converges to zero, which proves the stability of the fractional viscoelastic shape memory alloy system. Additionally, the responses of the sliding mode function and the control input signal are presented in Figure 7 and Figure 8, where the chattering phenomenon of the controller can be observed. The numerical simulation results show that the SMC strategy proposed in this paper is very effective and feasible to suppress the large amplitude limit cycle oscillation in the fractional viscoelastic shape memory alloy system.

Furthermore, the performance of the SMC method will be analyzed from an energy perspective. According to the kinetic energy theorem, the energy consumption is equal to the change in kinetic energy [39]. Therefore, the needed energy cost (NEC) of control from the initial time to the subsequent time can be expressed as follows:

$$NEC\left(k\right)=\mathsf{{\rm E}}\left[\left|{\displaystyle \frac{1}{2}}u{v}_k^2-{\displaystyle \frac{1}{2}}u{v}_{k-1}^2\right|\right], k=t_{con}+1, t_{con}+2, \dots , T_{sim}.$$

(59)

Additionally, the cumulated energy cost (CEC) of the SMC can be expressed as

$$CEC\left(t\right)={\sum }_{k=t_{con}+1}^{t}NEC\left(k\right), k=t_{con}+1, t_{con}+2, \dots , T_{sim}.$$

(60)

where $v_k$ represents the speed at time $k$; $t_{con}$ and $T_{sim}$ represent the start time of control and the simulation duration, respectively. We set $t_{con}=300$ in the numerical simulation. The numerical results of energy consumption are illustrated in Figure 9 and Figure 10, and the illustrations are partially enlarged views. From the figures, it is evident that initially, a greater amount of energy is required to guide the state trajectory toward the predetermined sliding surface. However, as the process continues, the energy consumption of the system exhibits a downward trend. Once the sliding mode motion is achieved, only a small but non-zero energy input is necessary to maintain the system’s motion on the sliding mode surface. Furthermore, as illustrated in Figure 9 and Figure 10, a faster convergence speed of the controlled system response correlates with higher energy consumption. That is to say, if we aim for the drive system’s response to reach the desired control goal more quickly, it will require a greater input of energy.

5. Conclusions

This paper primarily investigated the response of a shape memory alloy spring oscillator system with fractional viscoelastic characteristics under harmonic excitation, achieving the suppression of catastrophic high-amplitude vibrations. Initially, the amplitude–frequency response of the system under primary resonance was derived using the averaging method. Numerical simulations of the response, conducted with the Monte Carlo method, confirmed the accuracy of the analytical results. This study then explored in detail how various system parameters influence the response. Notably, the fractional derivative significantly affected the nonlinear behavior of the viscoelastic shape memory alloy spring system, extending the region of multi-valued responses. To prevent the occurrence of undesirable high-amplitude vibrations, a sliding mode control (SMC) strategy was introduced into the fractional viscoelastic shape memory alloy system. An SMC quantity based on the fractional integral sliding mode function was constructed following an exponential reaching law, and the asymptotic stability of the spring oscillator was ensured based on the stability theorem for fractional systems. By visualizing the response under controlled conditions, the effectiveness of SMC in suppressing high-amplitude vibrations in fractional viscoelastic shape memory alloy systems was ultimately verified. Although the control framework for catastrophic high-amplitude vibrations was established based on a simple spring oscillator, our work may offer new insights for preventing structural damage in practical engineering applications.

In future research, the control framework proposed in this paper can be applied to more complex and realistic systems, such as multi-degree-of-freedom structures or systems with spatially distributed parameters. Additionally, the integration of the shape memory alloy spring oscillator system with other advanced materials, such as piezoelectric or magnetorheological materials, can be explored to enhance vibration suppression capabilities and develop hybrid systems with improved adaptability and efficiency.