Transient and Steady-State Analysis of an M/PH₂/1 Queue with Catastrophes

Abstract

In the paper, we consider the $P{H}_2$-distribution, which is a particular case of the $PH$-distribution. In other words, The first service phase is exponentially distributed, and the service rate is $\mu$. After the first service phase, the customer can to go away with probability p or continue the service with probability $(1-p)$ and service rate ${\mu }^{\prime }$. We study an analysis of an $M/P{H}_2/1$ queue model with catastrophes, which is regarded as a generalization of an $M/M/1$ queue model with catastrophes. Whenever a catastrophe happens, all customers will be cleaned up immediately, and the queuing system is empty. The customers arrive at the queuing system based on a Poisson process, and the total service duration has two phases. Transient probabilities and steady-state probabilities of this queuing system are considered using practical applications of the modified Bessel function of the first kind, the Laplace transform, and probability-generating function techniques. Moreover, some important performance measures are obtained in the system. Finally, numerical illustrations are used to discuss the system’s behavior, and conclusions and future directions of the model are given.

1. Introduction

Historical accidents can determine the mode and the value of necessity. Accidental events fill every aspect of our life. Any accidental event that is caused by a sudden change in the normal functioning of a system may be considered as a catastrophe. There are many queuing problems in life, but there are many accidental factors (such as COVID-19, computer systems, telecommunications systems, biological mathematics, ecology, marketing, etc.) that cause our queuing system to crash. If a system suffers from a catastrophe, it will take some time to recover. Catastrophe models have wide applications in different fields, including queue systems, telecommunication, mathematical biology, population dynamics, ecology, artificial intelligence, marketing, etc. Melikov [1] discussed single-server models of queuing-inventory systems (QIS) with catastrophes in warehouses and negative customers (n-customers) in service facilities. Studies on queuing models for birth–death processes with the catastrophic queue assume that a customer should always appear in the system throughout the whole process of providing services (see, for instance, Dharmraja [2], Singh Bura [3], Mishra [4], Kumar [5], Arizono [6], Granville [7], Vishnevsky [8], and Tang [9]). Many achievements in different fields have been nade by Jain and Kumar [10], Dabrowski [11], and reference therein.

The main purpose of this manuscript is to extend the basic version of an $M/M/1$ queue model with a catastrophe. To the best of our knowledge, the pioneering works analyzing queuing systems with catastrophes in the input flow were published by Krishna Kumar [12], where the authors= described transient probabilities, steady-state probabilities, and asymptotic behaviors of the server being idle and mean system size based on the diagram in Figure 1 (also see Jain and Kumar [10] and Krishna Kumar [13,14]). Dudin et al. [15] presented a thorough analysis of correlated input in queuing systems, and their work is unique in the sense that the entire manuscript is devoted to queues with correlated arrivals. For a special state-dependent queue model, they studied the reliability and availability, mean system size, and server failures of the version (see Di Crescenzo [16,17], Yashkov [18], Jain [19], Suranga Sampath [20], Kaliappan [21], and Paz [22], among others).

On the other hand, due to the excellent properties of the $PH$ distribution, it can almost approximate all distributions. A large number of researchers have performed significant work using the $PH$ distribution instead of an exponential distribution in recent years (see Sule Alfa [23] and Zhang [24]). Chakravarthy et al. [25] studied a queuing model of the type $MAP/PH/1$ in the context of the server going on vacations, the server breaking down due to external shocks, the server requiriing repairs, and the server being helped by a backup server during vacations and repairs (also see Klimenok et al. [26] and Choi et al. [27]). Baba [28] analyzed an $M/PH/1$ queue with phase-type working vacations and vacation interruptions, where the vacation time follows a phase-type distribution. Kim [29] gave expressions for the Laplace–Stieltjes transform of the waiting time. Liu [30] considered an $M/PH/1$ queue model subject to different service speeds. Many references similar to the $M/PH/1$ queue have already gained attention more recently (also see, e.g., Oliveira et al. [31], Sakuma, et al. [32], Jose, et al. [33], Liu, et al. [30], Dogan, et al. [34], Lakshmi et al. [35], and Sudhesh et al. [36]).

The $M/P{H}_2/1$ queue model study considers a public service system consisting of two service phases with different service capacities and qualities, such as medical or service transportation systems. Liu et al. studied the scenario where patients are divided into first-visit and referred patients, and the hospitals provide the patients with two service phases of “diagnosis” and “treatment” [37]. Chakravarthy et al. [25] studied a queuing model of the type $MAP/PH/1$ in the context of the server going on vacations, the server breaking down due to external shocks, the server requiring repairs, and the server being helped by a backup server during vacations and repairs (also see Klimenok et al. [26] and Choi et al. [27]). Based on these results, our objective in this manuscript is a descendant of an $M/M/1$ queue model according to catastrophes. As far as we know, there is no study of the transient probabilities in an $M/P{H}_2/1$ queue model according to catastrophes in the literature. The aim of our research is to present transient probabilities and steady-state probabilities when catastrophes occur. Moreover, we obtain performance indices such as mean and variance. Finally, numerical examples are discussed with respect to the effects of several parameters on the system performance indices. In the queue model, all customers based on a Poisson process with rate $\xi$ will be cleared when a catastrophe takes place. In addition, for the sake of convenience of understanding and use, the diagram in Figure 2 based on an $M/P{H}_2/1$ queue model according to catastrophes is introduced.

The results of this paper are organized as follows. In Section 2, a description of the $M/P{H}_2/1$ queue model with catastrophes under study is outlined. In Section 3, the transient probabilities of the system’s size are obtained using the modified Bessel function, the Laplace transform, and matrix transformation. In Section 4, we obtain the solution for the steady-state probabilities. In Section 5, we obtain some performance measures of the system. 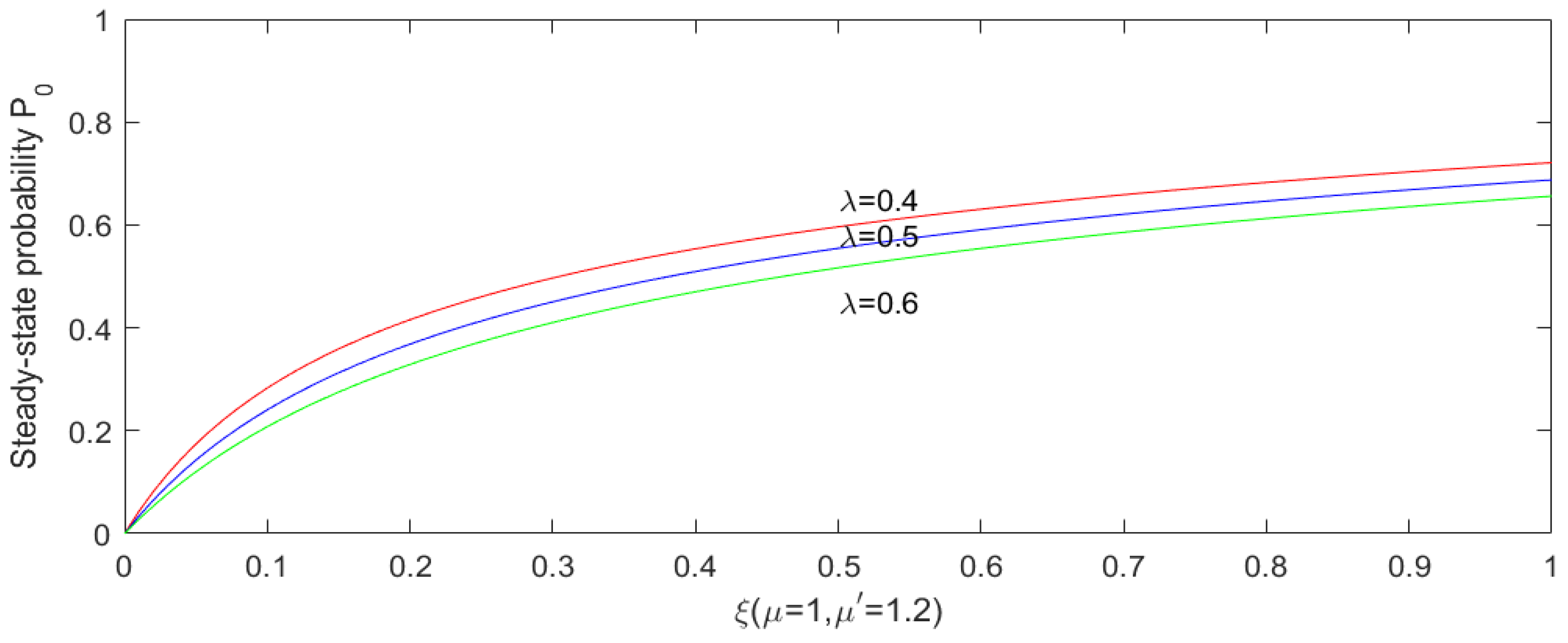In Section 6, numerical experiments are conducted to investigate the influence of catastrophes. Finally, we provide the conclusion and future research directions.

2. The Framework

A single server queuing system in which there are two service phases is considered on an FCFS basis; that is, the service time distribution in the queue model according to a Poisson arrival process has two different phases. The first service phase is exponentially distributed, and the service rate is $\mu$. When it is finished, the work will be checked immediately. There is a probability p that the work is found to be satisfactory, and the customer goes away. There is a $1-p$ probability that the customer requires extra measures, where the service time is exponentially distributed with service rate ${\mu }^{\prime }$. Once the second service operation is completed, the customer will automatically go away. Except for arrival processes and service processes, catastrophes may also take place at the service facilities as a Poisson process with parameter $\xi (\xi >0$). Whenever a catastrophe takes place in the system, the queuing system clears all the customers. In this paper, we assume that customers arrive according to a Poisson process with mean arrival rate $\lambda$ during times that the server is run. In this way, we have a queuing system of $M/P{H}_2/1$ queue with the possibility of catastrophes. The $M/P{H}_2/1$ queue model with catastrophes is shown in Figure 2 for the sake of simplicity.

For the convenience of understanding the queuing system, we will comprehensively elaborate on Figure 2 shown below. At most, one customer can be in the queuing system at any given time. Once the customer’s service begins, the customer will enter node 1. The time spent in the queuing system follows an exponential distribution with parameters of $\mu$. When the customer completes node 1, he leaves the queuing system with probability p and enters node 2 with probability q. The time spent at node 2 follows an exponential distribution of parameter ${\mu }^{\prime }$, and he leaves the queuing system from node 2. At any service time, catastrophes may occur at the service facility as a Poisson process with parameter $\xi$ in nodes 1 and 2.

We utilize the following notation. The queue model may be represented as a continuous time Markov chain in the following state-space:

$$\mathcal{S}=\left\{l\right(0\left)\right\}\cup \left\{l\right(1\left)\right\}\cup \left\{l\right(2\left)\right\}\cup \dots ,$$

where the zero state $l\left(0\right)$(={0}) indicates that the queue is an empty system; $l\left(n\right)=\left\{\right(n,1),$$(n,2),n\ge 1$}; the state $(n,j)$ indicates that there are n customers in the queue system, $n-1$ of whom are in the waiting room; and the customer in the service phase is at node j.

Changes of state take place when a new customer arrives, when a service is finished, or when the new arrival in the service moves from node 1 to node 2. At any service time, catastrophes may take place.

Whenever a catastrophe occurs, all the customers in the system will be immediately cleared. For the sake of understanding, the transitions between each node are given in

Table 1. The transitions.

No.	From	To	Rate	Range
1	0	(1, 1)	$\lambda$
2	(1, 1)	0	$\mu p+\xi$
3	$(n,1)$	$(n,2)$	$\mu q$	for $n\ge 1$
4	$(n,1)$	$(n-1,1)$	$\mu p$	for $n\ge 2$
5	(1, 2)	0	${\mu }^{\prime }+\xi$
6	$(n,2)$	$(n-1,1)$	${\mu }^{\prime }$	for $n\ge 2$
7	$(n,j)$	$(n+1,j)$	$\lambda$	for $n\ge 1,j=1,2$
8	$(n,j)$	0	$\xi$	for $n\ge 2,j=1,2$

below.

If $\xi$ is equal to zero, Table 1 clearly represents a specific $M/P{H}_2/1$ queue. In the following study, we assume that $\xi$ is greater than 0. We begin by letting $\{X\left(t\right);t\in R^{+}\}\in \{0,1,2,\cdots \}$ be the number of customers in the queuing system at moment t, and letting $\{Y\left(t\right);t\in R^{+}\}\in \{1,2\}$ be node 1 or 2 in the queuing system at moment t. If we order the states by level and, within a level, by the label of the service node, let $P_{n,j}\left(t\right)=P(X\left(t\right)=n,Y\left(t\right)=j),n=1,2,\cdots ,j=1,2,$ be the transient state probability that the time-dependent probability for the queuing system is in state j with customers n at moment t. Let $P_0\left(t\right)$ be the probability that there are zero customers in the system at moment t without the occurrence of catastrophes. Based on the above assumptions and the Chapman–Kolmogorov forward differential–difference equations, the transient state probabilities $P_{n,j}\left(t\right),n=1,2,\cdots ,j=1,2$ and the differential–difference equations for the queuing system under investigation can be written as follows:

$$\begin{array}{ccc}& & {\displaystyle \frac{d{P}_0\left(t\right)}{dt}}=-(\xi +\lambda )P_0\left(t\right)+\mu p{P}_{1,1}\left(t\right)+{\mu }^{\prime }{P}_{1,2}\left(t\right)+\xi ,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}& & {\displaystyle \frac{d{P}_{1,1}\left(t\right)}{dt}}=-(\mu +\lambda +\xi )P_{1,1}\left(t\right)+\lambda P_0\left(t\right)+\mu p{P}_{2,1}\left(t\right)+{\mu }^{\prime }{P}_{2,2}\left(t\right),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& & {\displaystyle \frac{d{P}_{1,2}\left(t\right)}{dt}}=-({\mu }^{\prime }+\lambda +\xi )P_{1,2}\left(t\right)+\mu q{P}_{1,1}\left(t\right),\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& & {\displaystyle \frac{d{P}_{n,1}\left(t\right)}{dt}}=-(\mu +\lambda +\xi )P_{n,1}\left(t\right)+\lambda P_{n-1,1}\left(t\right)+\mu p{P}_{n+1,1}\left(t\right)+{\mu }^{\prime }{P}_{n+1,2}\left(t\right),n\ge 2,\hfill \end{array}$$

(4)

$$\begin{array}{ccc}& & {\displaystyle \frac{d{P}_{n,2}\left(t\right)}{dt}}=-({\mu }^{\prime }+\lambda +\xi )P_{n,2}\left(t\right)+\lambda P_{n-1,2}\left(t\right)+\mu q{P}_{n,1}\left(t\right),n\ge 2.\hfill \end{array}$$

(5)

In general, we assume that initially, there are no customers in the queue system. In other words,

$$P_0\left(0\right)=1.$$

For the purpose of calculation, we have listed the notations and their meanings in a table (

Table 2. The notations and their meanings.

Notations	Range
${\mathbf{e}}_0$	${(1,0)}^T$
${\mathbf{e}}_1$	${(1,0,0)}^T$
${\mathbf{e}}_2$	${(0,1,0)}^T$
${\mathbf{e}}_3$	${(1,1,1)}^T$
${\mathbf{e}}_4$	${(1,1)}^T$
*	Denotes convolution
$\mathcal{L}\left(e^A\right)$	Laplace transform of matrix $e^A$
${\mathcal{L}}^{-1}\left(e^A\right)$	Laplace inverse transform of matrix $e^A$
I	2nd order identity matrix

).

3. Transient Probabilities

In this section, we study the behavior of the transient probabilities of an $M/P{H}_2/1$ queue model with catastrophes.

Let

$$P_n\left(t\right)={(P_{n,1}\left(t\right),P_{n,2}\left(t\right))}^T,n\ge 1.$$

By substituting Equations (2)–(5), we obtain the following:

$$\begin{array}{c}\hfill {\displaystyle \frac{d{P}_1\left(t\right)}{dt}}=A{P}_1\left(t\right)+\lambda P_0\left(t\right){\mathbf{e}}_0+C{P}_2\left(t\right),\end{array}$$

(6)

$$\begin{array}{c}\hfill {\displaystyle \frac{d{P}_n\left(t\right)}{dt}}=A{P}_n\left(t\right)+B{P}_{n-1}\left(t\right)+C{P}_{n+1}\left(t\right),n\ge 2.\end{array}$$

(7)

where

$$A=\left(\begin{array}{cc}-(\mu +\lambda +\xi )& 0\\ \mu q& -({\mu }^{\prime }+\lambda +\xi )\end{array}\right),B=\left(\begin{array}{cc}\lambda & 0\\ 0& \lambda \end{array}\right),C=\left(\begin{array}{cc}\mu p& {\mu }^{\prime }\\ 0& 0\end{array}\right).$$

We next discuss solving these equations using the generating functions method, and we assume that the number of customers arriving at the queue system is random. We define the following:

$$\begin{array}{ccc}\hfill Q\left(t\right)& =& {(Q_1\left(t\right),Q_2\left(t\right))}^T={(\sum _{k=0}^{\infty }{P}_{k+1,1}\left(t\right),\sum _{k=0}^{\infty }{P}_{k+1,2}\left(t\right))}^T,\hfill \\ \hfill H(z,t)& =& {(H_1(z,t),H_2(z,t))}^T={(\sum _{k=0}^{\infty }{P}_{k+1,1}\left(t\right)z^k,\sum _{k=0}^{\infty }{P}_{k+1,2}\left(t\right)z^k)}^T=\sum _{k=0}^{\infty }{P}_{k+1}\left(t\right)z^k.\hfill \end{array}$$

By substituting Equations (6) and (7), we obtain the following:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial H(z,t)}{\partial t}}=(A+zB+{\displaystyle \frac{1}{z}}C)H(z,t)+\lambda P_0\left(t\right){\mathbf{e}}_0-{\displaystyle \frac{1}{z}}C{P}_1\left(t\right).\end{array}$$

(8)

Integrating Equation (8) with respect to time ‘$t(t\ge 0)$’, we have the following:

$$\begin{array}{ccc}\hfill H(z,t)& =& {\int }_0^t\lambda P_0\left(y\right)e^{(A+zB+{\displaystyle \frac{1}{z}}C)(t-y)}{\mathbf{e}}_{0}dy-{\int }_0^t{\displaystyle \frac{1}{z}}{e}^{(A+zB+{\displaystyle \frac{1}{z}}C)(t-y)}C{P}_1\left(y\right)dy\hfill \\ & =& {\int }_0^t\lambda P_0\left(y\right)e^{\left[\lambda \right(z-1)-\mu -\xi ]I(t-y)}{e}^{M(t-y)}{\mathbf{e}}_{0}dy\hfill \\ & & -{\int }_0^t{\displaystyle \frac{1}{z}}{e}^{\left[\lambda \right(z-1)-\mu -\xi ]I(t-y)}{e}^{M(t-y)}C{P}_1\left(y\right)dy,\hfill \end{array}$$

(9)

where $M=\left(\begin{array}{cc}{\displaystyle \frac{\mu p}{z}}& {\displaystyle \frac{{\mu }^{\prime }}{z}}\\ \mu q& \mu -{\mu }^{\prime }\end{array}\right).$

Here,

$$\begin{array}{c}\hfill e^{\left[\lambda \right(z-1)-\mu -\xi ]It}=e^{\left[\lambda \right(z-1)-\mu -\xi ]t}I.\end{array}$$

(10)

By taking the Laplace transform on matrix $Mt$, we obtain the following:

$$\begin{array}{ccc}\hfill \mathcal{L}\left[e^{Mt}\right]& =& {\int }_0^{+\infty }{e}^{-stI}{e}^{Mt}dt={(sI-M)}^{-1}\hfill \\ & =& \left(\begin{array}{cc}{\displaystyle \frac{\mu -{\mu }^{\prime }-s_1}{s_2-s_1}}{\displaystyle \frac{1}{s-s_1}}+{\displaystyle \frac{\mu -{\mu }^{\prime }-s_2}{s_1-s_2}}{\displaystyle \frac{1}{s-s_2}}& {\displaystyle \frac{\frac{{\mu }^{\prime }}{z}}{s_1-s_2}}{\displaystyle \frac{1}{s-s_1}}-{\displaystyle \frac{\frac{{\mu }^{\prime }}{z}}{s_1-s_2}}{\displaystyle \frac{1}{s-s_2}}\\ {\displaystyle \frac{\mu q}{s_1-s_2}}{\displaystyle \frac{1}{s-s_1}}-{\displaystyle \frac{\mu q}{s_1-s_2}}{\displaystyle \frac{1}{s-s_2}}& {\displaystyle \frac{\frac{\mu p}{z}-s_1}{s_2-s_1}}{\displaystyle \frac{1}{s-s_1}}+{\displaystyle \frac{\frac{\mu p}{z}-s_2}{s_1-s_2}}{\displaystyle \frac{1}{s-s_2}}\end{array}\right),\hfill \end{array}$$

(11)

where $s_1={\displaystyle \frac{\frac{\mu p}{z}+\mu -{\mu }^{\prime }+\sqrt{{(\mu -{\mu }^{\prime }-\frac{\mu p}{z})}^2+\frac{4\mu {\mu }^{\prime }q}{z}}}{2}}={\displaystyle \frac{\frac{\mu p}{z}+\mu -{\mu }^{\prime }+\sqrt{\Delta }}{2}},$ $s_2={\displaystyle \frac{\frac{\mu p}{z}+\mu -{\mu }^{\prime }-\sqrt{{(\mu -{\mu }^{\prime }-\frac{\mu p}{z})}^2+\frac{4\mu {\mu }^{\prime }q}{z}}}{2}}={\displaystyle \frac{\frac{\mu p}{z}+\mu -{\mu }^{\prime }-\sqrt{\Delta }}{2}},\Delta ={(\mu -{\mu }^{\prime }-{\displaystyle \frac{\mu p}{z}})}^2+{\displaystyle \frac{4\mu {\mu }^{\prime }q}{z}}.$

By taking the Laplace inverse transform on matrix (11), we have the following:

$$\begin{array}{ccc}\hfill e^{Mt}& =& {\mathcal{L}}^{-1}\left[{(sI-M)}^{-1}\right]\hfill \\ \\ & =& \left(\begin{array}{cc}{\displaystyle \frac{\mu -{\mu }^{\prime }-s_1}{s_2-s_1}}{e}^{s_{1}t}+{\displaystyle \frac{\mu -{\mu }^{\prime }-s_2}{s_1-s_2}}{e}^{s_{2}t}& {\displaystyle \frac{\frac{{\mu }^{\prime }}{z}}{s_1-s_2}}{e}^{s_{1}t}-{\displaystyle \frac{\frac{{\mu }^{\prime }}{z}}{s_1-s_2}}{e}^{s_{2}t}\\ {\displaystyle \frac{\mu q}{s_1-s_2}}{e}^{s_{1}t}-{\displaystyle \frac{\mu q}{s_1-s_2}}{e}^{s_{2}t}& {\displaystyle \frac{\frac{\mu p}{z}-s_1}{s_2-s_1}}{e}^{s_{1}t}+{\displaystyle \frac{\frac{\mu p}{z}-s_2}{s_1-s_2}}{e}^{s_{2}t}\end{array}\right).\hfill \end{array}$$

(12)

For the convenience of calculation, using Equations (9)–(12), we can obtain the following:

$$\begin{array}{ccc}& & e^{\left[\lambda \right(z-1)-\mu -\xi ]It}{e}^{Mt}{\mathbf{e}}_0\hfill \\ & =& e^{(\lambda z+{\displaystyle \frac{\mu p}{2z}})t}{e}^{-{\displaystyle \frac{1}{2}}(\mu +{\mu }^{\prime }+2\lambda +2\xi )t}\left(\begin{array}{c}{\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\left(\frac{t}{2}\right)}^{2k}}{\left(2k\right)!}}{\Delta }^k-(\mu -{\mu }^{\prime }-{\displaystyle \frac{\mu p}{z}}){\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\left(\frac{t}{2}\right)}^{2k+1}}{(2k+1)!}}{\Delta }^k\\ 2\mu q{\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\left(\frac{t}{2}\right)}^{2k+1}}{(2k+1)!}}{\Delta }^k\end{array}\right)\hfill \\ & =& e^{(\lambda z+{\displaystyle \frac{\mu p}{2z}})t}{e}^{-{\displaystyle \frac{1}{2}}(\mu +{\mu }^{\prime }+2\lambda +2\xi )t}\sum _{k=0}^{\infty }\left(\begin{array}{c}{\displaystyle \frac{{\left(\frac{t}{2}\right)}^{2k}}{\left(2k\right)!}}-(\mu -{\mu }^{\prime }-{\displaystyle \frac{\mu p}{z}}){\displaystyle \frac{{\left(\frac{t}{2}\right)}^{2k+1}}{(2k+1)!}}\\ 2\mu q{\displaystyle \frac{{\left(\frac{t}{2}\right)}^{2k+1}}{(2k+1)!}}\end{array}\right){\Delta }^k.\hfill \end{array}$$

(13)

By using Equations (11) and (12) in Equation (9), we have the following:

$$\begin{array}{ccc}\hfill H(z,t)& =& {\int }_0^t[\lambda P_0\left(y\right)-{\displaystyle \frac{1}{z}}{F}^T{P}_1\left(y\right)]e^{(\lambda z+{\displaystyle \frac{\mu p}{2z}})(t-y)}{e}^{-{\displaystyle \frac{1}{2}}(\mu +{\mu }^{\prime }+2\lambda +2\xi )(t-y)}\hfill \\ & & ·\sum _{k=0}^{\infty }\left(\begin{array}{c}{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k}}{\left(2k\right)!}}-(\mu -{\mu }^{\prime }-{\displaystyle \frac{\mu p}{z}}){\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\\ 2\mu q{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\end{array}\right){\Delta }^{k}dy,\hfill \end{array}$$

(14)

where $F={(\mu p,{\mu }^{\prime })}^T.$

Using the Bessel Function identity (see Watson [38]) with $\alpha =\sqrt{2\lambda \mu p},\beta =\sqrt{2\lambda /\mu p}$ gives the following:

$$\begin{array}{ccc}& & e^{(\lambda z+{\displaystyle \frac{\mu p}{2z}})(t-y)}=\sum _{k=-\infty }^{\infty }{\left(\beta z\right)}^k{I}_k\left[\alpha (t-y)\right],\hfill \\ & & I_n\left(x\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{1}{k!\Gamma (k+n+1)}}{\left({\displaystyle \frac{x}{2}}\right)}^{n+2k},\left(\right|x|<\infty ,|\arg \left(x\right)|<\pi ),\hfill \end{array}$$

(15)

where $I_n(·)$ is the modified Bessel Function of first kind order n.

By using Equation (15) in Equation (14), we obtain the following:

$$\begin{array}{ccc}& & H(z,t)\hfill \\ & =& {\int }_0^t[\lambda P_0\left(y\right)-{\displaystyle \frac{1}{z}}{F}^T{P}_1\left(y\right)]\sum _{k=-\infty }^{\infty }{\left(\beta z\right)}^k{I}_k\left[\alpha (t-y)\right]e^{-{\displaystyle \frac{1}{2}}(\mu +{\mu }^{\prime }+2\lambda +2\xi )(t-y)}\hfill \\ & & ·\sum _{k=0}^{\infty }\left(\begin{array}{c}{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k}}{\left(2k\right)!}}-(\mu -{\mu }^{\prime }-{\displaystyle \frac{\mu p}{z}}){\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\\ 2\mu q{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\end{array}\right){\Delta }^{k}dy.\hfill \end{array}$$

(16)

Equating the coefficient of $z^n(n\ge 0)$ in Equation (16) gives the following:

$$\begin{array}{ccc}& & P_{n+1}\left(t\right)\hfill \\ & =& \sum _{i=0}^{\infty }{\int }_0^t\{\lambda P_0\left(y\right){\beta }^{n+i}{I}_{n+i}\left[\alpha (t-y)\right]e^{-{\displaystyle \frac{1}{2}}(\mu +{\mu }^{\prime }+2\lambda +2\xi )(t-y)}\hfill \\ & & ·\sum _{k=0}^{\infty }\sum _{\begin{array}{c}{i}_1+i_2+i_3=k\\ 2i_1+i_2=i\end{array}}\left(\begin{array}{c}{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k}}{\left(2k\right)!}}-(\mu -{\mu }^{\prime }){\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\\ 2\mu q{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\end{array}\right)\hfill \\ & & ·{\displaystyle \frac{k!}{i_1!i_2!i_3!}}{\left(\mu p\right)}^{2i_1}{(2\mu {\mu }^{\prime }+2\mu {\mu }^{\prime }q-2{\mu }^{2}p)}^{i_2}{(\mu -{\mu }^{\prime })}^{2i_3}\}dy\hfill \\ & & -\sum _{i=0}^{\infty }{\int }_0^t\{\lambda P_0\left(y\right){\beta }^{n+i+1}{I}_{n+i+1}\left[\alpha (t-y)\right]e^{-{\displaystyle \frac{1}{2}}(\mu +{\mu }^{\prime }+2\lambda +2\xi )(t-y)}\hfill \\ & & ·\sum _{k=0}^{\infty }\sum _{\begin{array}{c}{i}_1+i_2+i_3=k\\ 2i_1+i_2=i\end{array}}\left(\begin{array}{c}\mu p{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\\ 0\end{array}\right){\displaystyle \frac{k!}{i_1!i_2!i_3!}}{\left(\mu p\right)}^{2i_1}{(2\mu {\mu }^{\prime }+2\mu {\mu }^{\prime }q-2{\mu }^{2}p)}^{i_2}{(\mu -{\mu }^{\prime })}^{2i_3}\}dy\hfill \\ & & -\sum _{i=0}^{\infty }{\int }_0^t\{F^T{P}_1\left(y\right){\beta }^{n+i+1}{I}_{n+i+1}\left[\alpha (t-y)\right]e^{-{\displaystyle \frac{1}{2}}(\mu +{\mu }^{\prime }+2\lambda +2\xi )(t-y)}\hfill \\ & & ·\sum _{k=0}^{\infty }\sum _{\begin{array}{c}{i}_1+i_2+i_3=k\\ 2i_1+i_2=i\end{array}}\left(\begin{array}{c}{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k}}{\left(2k\right)!}}-(\mu -{\mu }^{\prime }){\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\\ 2\mu q{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\end{array}\right)\hfill \\ & & ·{\displaystyle \frac{k!}{i_1!i_2!i_3!}}{\left(\mu p\right)}^{2i_1}{(2\mu {\mu }^{\prime }+2\mu {\mu }^{\prime }q-2{\mu }^{2}p)}^{i_2}{(\mu -{\mu }^{\prime })}^{2i_3}\}dy\hfill \\ & & +\sum _{i=0}^{\infty }{\int }_0^t\{F^T{P}_1\left(y\right){\beta }^{n+i+2}{I}_{n+i+2}\left[\alpha (t-y)\right]e^{-{\displaystyle \frac{1}{2}}(\mu +{\mu }^{\prime }+2\lambda +2\xi )(t-y)}\hfill \\ & & ·\sum _{k=0}^{\infty }\sum _{\begin{array}{c}{i}_1+i_2+i_3=k\\ 2i_1+i_2=i\end{array}}\left(\begin{array}{c}\mu p{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\\ 0\end{array}\right){\displaystyle \frac{k!}{i_1!i_2!i_3!}}{\left(\mu p\right)}^{2i_1}{(2\mu {\mu }^{\prime }+2\mu {\mu }^{\prime }q-2{\mu }^{2}p)}^{i_2}{(\mu -{\mu }^{\prime })}^{2i_3}\}dy.\hfill \end{array}$$

(17)

Evaluation of ${\mathbf{P}}_{\mathbf{0}}\left(\mathbf{t}\right)$

Substituting $z=1$ in Equation (8) and taking the Laplace transform, we derive the following:

$$\begin{array}{c}\hfill \widehat{Q}\left(s\right)=\left(\begin{array}{c}-{\displaystyle \frac{s+{\mu }^{\prime }+\xi }{c_2\left(s\right)}}\\ -{\displaystyle \frac{\mu q}{c_2\left(s\right)}}\end{array}\right){\widehat{P}}_0\left(s\right)+\left(\begin{array}{c}{\displaystyle \frac{s+{\mu }^{\prime }+\xi }{s{c}_2\left(s\right)}}\\ {\displaystyle \frac{\mu q}{s{c}_2\left(s\right)}}\end{array}\right),\end{array}$$

(18)

where $c_2\left(s\right)=s+{\mu }^{\prime }+\lambda +\xi$, and $\widehat{Q}\left(s\right)={(Q_1\left(s\right),Q_2\left(s\right))}^T$ is the Laplace transform expression of $Q\left(t\right)={(Q_1\left(t\right),Q_2\left(t\right))}^T$.

We derive the following equation:

$$\begin{array}{c}\hfill {\mathbf{e}}_4^T\widehat{Q}\left(s\right)+{\widehat{P}}_0\left(s\right)={\displaystyle \frac{1}{s}},\end{array}$$

(19)

and its the Laplace inverse transform is of the form

$$\begin{array}{c}\hfill {\mathbf{e}}_4^{T}Q\left(t\right)+P_0\left(t\right)=1,\mathrm{for}\mathrm{any}t\ge 0,\end{array}$$

(20)

where ${\widehat{P}}_0\left(s\right)$ is the Laplace transform expression of $P_0\left(t\right)$. That is to say, in order to derive the expression of ${\widehat{P}}_0\left(s\right)$, we need to find another method.

From the second equation in matrix equation system (8), we determine the following:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial H_2(z,t)}{\partial t}}& =& \mu q{H}_1(z,t)+[-({\mu }^{\prime }+\lambda +\xi )+\lambda z]H_2(z,t).\hfill \end{array}$$

(21)

Integrating Equation (21) with respect to time ‘$t(t\ge 0)$’, we have the following:

$$\begin{array}{ccc}\hfill H_2(z,t)& =& {\int }_0^t\mu q{H}_1(z,y)e^{[-({\mu }^{\prime }+\lambda +\xi )+\lambda z](t-y)}dy\hfill \\ & =& {\int }_0^t\mu q{H}_1(z,y)e^{-({\mu }^{\prime }+\lambda +\xi )(t-y)}\sum _{n=0}^{\infty }{\displaystyle \frac{{\lambda }^n{z}^n{(t-y)}^n}{n!}}dy.\hfill \end{array}$$

(22)

Equating the coefficient of $z^k(k\ge 0)$ in Equation (22) gives the following:

$$\begin{array}{ccc}\hfill P_{k+1,2}\left(t\right)& =& \sum _{i=0}^k{\int }_0^t\mu q{P}_{i+1,1}\left(y\right)e^{-({\mu }^{\prime }+\lambda +\xi )(t-y)}{\displaystyle \frac{{\lambda }^{k-i}{(t-y)}^{k-i}}{(k-i)!}}dy.\hfill \end{array}$$

(23)

By taking the Laplace transform of Equation (23), we obtain the following:

$$\begin{array}{ccc}\hfill {\widehat{P}}_{k+1,2}\left(s\right)& =& \sum _{i=0}^k{\displaystyle \frac{\mu q{\lambda }^{k-i}}{c_2^{k-i+1}\left(s\right)}}{\widehat{P}}_{i+1,1}\left(s\right),\hfill \end{array}$$

(24)

where ${\widehat{P}}_{k+1,2}\left(s\right)$ is the Laplace transform expression of $P_{k+1,2}\left(t\right)$.

By taking the Laplace transform of Equations (4) and (5), we have the following:

$$\begin{array}{ccc}& & \mu (p{c}_2\left(s\right)+{\mu }^{\prime }q){\widehat{P}}_{n+1,2}\left(s\right)-[\lambda \mu p+c_1\left(s\right)c_2\left(s\right)]{\widehat{P}}_{n,2}\left(s\right)\hfill \\ & & +\left[\lambda (c_1\left(s\right)+c_2\left(s\right))\right]{\widehat{P}}_{n-1,2}\left(s\right)-{\lambda }^2{\widehat{P}}_{n-2,2}\left(s\right)=0,n\ge 3,\hfill \end{array}$$

(25)

where $c_1\left(s\right)=s+\mu +\lambda +\xi .$

By adding $n=3$ to ∞ on both sides of Equation (25), we find the following:

$$\begin{array}{ccc}\hfill a_2\left(s\right)Q_2\left(s\right)& =& \mu (p{c}_2\left(s\right)+{\mu }^{\prime }q)[{\widehat{P}}_{1,2}\left(s\right)+{\widehat{P}}_{2,2}\left(s\right)+{\widehat{P}}_{3,2}\left(s\right)]\hfill \\ & & -[\lambda \mu p+c_1\left(s\right)c_2\left(s\right)][{\widehat{P}}_{1,2}\left(s\right)+{\widehat{P}}_{2,2}\left(s\right)]+\lambda [c_1\left(s\right)+c_2\left(s\right)]{\widehat{P}}_{1,2}\left(s\right),\hfill \end{array}$$

(26)

where $a_2\left(s\right)=-c_1\left(s\right)c_2\left(s\right)+\lambda [c_1\left(s\right)+c_2\left(s\right)]+\mu p{c}_2\left(s\right)+\mu {\mu }^{\prime }q-\lambda \mu p-{\lambda }^2$ is a quadratic polynomial of s.

Using Equations (2), (3), and (5) in Equation (26), we can obtain the following:

$$\begin{array}{ccc}& & a_2\left(s\right)Q_2\left(s\right)\hfill \\ & =& {\displaystyle \frac{(s+\lambda +\xi )\{b_4\left(s\right)+\lambda \mu q[c_1\left(s\right)+c_2\left(s\right)]c_2\left(s\right)c_3\left(s\right)\}+\mu b_2\left(s\right)c_3\left(s\right)-c_2\left(s\right)d_5\left(s\right)}{\mu c_2\left(s\right)c_3^2\left(s\right)}}{\widehat{P}}_0\left(s\right)\hfill \\ & & +{\displaystyle \frac{c_2\left(s\right)f_5\left(s\right)-(s+\xi )\{b_4\left(s\right)+{\mu }^{2}q{c}_3^2\left(s\right)c_2\left(s\right)+\lambda \mu q[c_1\left(s\right)+c_2\left(s\right)]c_2\left(s\right)c_3\left(s\right)\}}{\mu s{c}_2\left(s\right)c_3^2\left(s\right)}}.\hfill \end{array}$$

(27)

where $b_2\left(s\right)=q\mu (s+\xi )[{\mu }^{\prime }q+p{c}_2\left(s\right)]-\lambda q[c_1\left(s\right)c_2\left(s\right)+\lambda \mu p]$ is a quadratic polynomial of s, $b_4\left(s\right)=q[c_1^2\left(s\right)c_2^2\left(s\right)+\mu p{c}_1\left(s\right)c_2^2\left(s\right)+\mu q{\mu }^{\prime }{c}_1\left(s\right)c_2\left(s\right)+\lambda {\mu }^{2}p{c}_2\left(s\right)+\lambda {\mu }^2{p}^2{c}_2\left(s\right)-\lambda \mu {\mu }^{\prime }{c}_2\left(s\right)$$-\lambda \mu q{\mu }^{\prime }{c}_1\left(s\right)+{\lambda }^2{\mu }^2{p}^2+\lambda {\mu }^2{\mu }^{\prime }pq]$ is a 4th degree polynomial of s, and both $d_5\left(s\right)=[\lambda \mu p+c_1\left(s\right)c_2\left(s\right)]q[c_1\left(s\right)c_2\left(s\right)(s+\lambda +\xi )+\mu p{(s+\lambda +\xi )}^2+\mu {\mu }^{\prime }(s+\xi )]$ and $f_5\left(s\right)=[\lambda \mu p+c_1\left(s\right)c_2\left(s\right)]q(s+\xi )[c_1\left(s\right)c_2\left(s\right)+\mu p(s+2\lambda +\xi )+\mu {\mu }^{\prime }]$ are univariate fifth-degree polynomials of $s,$ $c_3\left(s\right)=p{c}_2\left(s\right)+{\mu }^{\prime }q$.

The simultaneous equations of Equations (18) and (27) can be obtained:

$$\begin{array}{ccc}\hfill {\widehat{P}}_0\left(s\right)& =& {\displaystyle \frac{{\mu }^{2}q{c}_2\left(s\right)c_3^2\left(s\right)a_2\left(s\right)-f_6\left(s\right)c_4\left(s\right)}{d_6\left(s\right)s{c}_4\left(s\right)+{\mu }^{2}q{c}_3^2\left(s\right)s{a}_2\left(s\right)c_2\left(s\right)}},\hfill \end{array}$$

(28)

where $c_4\left(s\right)=s+{\mu }^{\prime }+\mu q+\xi$, and both $d_6\left(s\right)=d_5\left(s\right)c_2\left(s\right)-(s+\lambda +\xi )\{b_4\left(s\right)+\lambda \mu q[c_1\left(s\right)+c_2\left(s\right)][p{c}_2\left(s\right)+{\mu }^{\prime }q]c_2\left(s\right)\}+\mu b_2\left(s\right)[p{c}_2\left(s\right)+{\mu }^{\prime }q]$, $f_6\left(s\right)=c_2\left(s\right)f_5\left(s\right)-(s+\xi )\{b_4\left(s\right)+{\mu }^{2}q$${[p{c}_2\left(s\right)+{\mu }^{\prime }q]}^2{c}_2\left(s\right)+\lambda \mu q[c_1\left(s\right)+c_2\left(s\right)][p{c}_2\left(s\right)+{\mu }^{\prime }q]c_2\left(s\right)\}$ are univariate sixth-degree polynomials of s.

Through careful observation, we found that the numerator of the fraction in expression (28) is a seventh-degree polynomial of s, and its denominator is a eighth-degree polynomial of s. Therefore, we determine that Equation (28) can be decomposed into the sum of several simplest fractions using number theory. Furthermore, using MATLAB R2016a, we can obtain $P_0\left(t\right)$ through the Laplace inverse transform of Equation (28).

Through the Laplace inverse transformation, we obtain the following expression for $P_0\left(t\right)$:

$$\begin{array}{ccc}& & P_0\left(t\right)={\displaystyle \frac{1}{2\pi i}}{\int }_{\sigma -i\infty }^{\sigma +i\infty }{\displaystyle \frac{{\mu }^{2}q{c}_2\left(s\right)c^2\left(s\right)a_2\left(s\right)-f_6\left(s\right)c_4\left(s\right)}{d_6\left(s\right)s{c}_4\left(s\right)+{\mu }^{2}q{c}_3^2\left(s\right)s{a}_2\left(s\right)c_2\left(s\right)}}{e}^{st}ds.\hfill \end{array}$$

(29)

Evaluation of ${\mathbf{P}}_{\mathbf{1},\mathbf{1}}\left(\mathbf{t}\right),{\mathbf{P}}_{\mathbf{1},\mathbf{2}}\left(\mathbf{t}\right)$

By taking the Laplace transform of Equation (1), we have the following:

$$\begin{array}{c}\hfill F^T{\widehat{P}}_1\left(s\right)=(s+\lambda +\xi ){\widehat{P}}_0\left(s\right)-{\displaystyle \frac{s+\xi }{s}}.\end{array}$$

(30)

The remaining transient probabilities $P_0\left(t\right),P_{11}\left(t\right)$ and $P_{12}\left(t\right)$ can be obtained by solving the system of Equations (1)–(3). To do this, we rewrite the system of Equations (1)–(3) in the following matrix form:

$$\begin{array}{c}\hfill {\displaystyle \frac{dP\left(t\right)}{dt}}=DP\left(t\right)+\xi {\mathbf{e}}_1+F^T{P}_2\left(t\right){\mathbf{e}}_2,\end{array}$$

(31)

where

$$P\left(t\right)={(P_0\left(t\right),P_{11}\left(t\right),P_{12}\left(t\right))}^T,D=\left(\begin{array}{ccc}-(\lambda +\xi )& \mu p& {\mu }^{\prime }\\ \lambda & -(\mu +\lambda +\xi )& 0\\ 0& \mu q& -({\mu }^{\prime }+\lambda +\xi )\end{array}\right).$$

By taking the Laplace transform, the solution of (31) is obtained as follows:

$$\begin{array}{c}\hfill \widehat{P}\left(s\right)={(sI-D)}^{-1}\{{\displaystyle \frac{1}{s}}\xi {\mathbf{e}}_1+F^T{\widehat{P}}_2\left(s\right){\mathbf{e}}_2+P\left(0\right)\},\end{array}$$

(32)

where $P\left(0\right)={(1,0,0)}^T.$

We observe that

$$\begin{array}{c}\hfill {\mathbf{e}}_3^T\widehat{P}\left(s\right)={\widehat{P}}_0\left(s\right)+e_4^T\widehat{P_1}\left(s\right).\end{array}$$

(33)

Taking Equation (33) in Equation (32) and transforming, we have the following:

$$\begin{array}{c}\hfill {\mathbf{e}}_4^T{\widehat{P}}_1\left(s\right)={\mathbf{e}}_3^T{(sI-D)}^{-1}[{\displaystyle \frac{\xi \mathbf{e}}{s}}+P\left(0\right)]-{\widehat{P}}_0\left(s\right)+{\mathbf{e}}_3^T{(sI-D)}^{-1}{\mathbf{e}}_2{F}^T{\widehat{P}}_2\left(s\right).\end{array}$$

(34)

Taking the Laplace transform of Equation (2) and substituting $k=1$ in Equation (24) gives the following:

$$\begin{array}{ccc}\hfill {\widehat{P}}_2\left(s\right)& =& \left(\begin{array}{cc}{\displaystyle \frac{c_1\left(s\right)c_2^2\left(s\right)-\mu {\mu }^{\prime }\lambda q}{\mu [p{c}_2\left(s\right)+{\mu }^{\prime }q]c_2\left(s\right)}}& 0\\ {\displaystyle \frac{[c_1\left(s\right)c_2\left(s\right)+\lambda \mu p]q}{[p{c}_2\left(s\right)+{\mu }^{\prime }q]c_2\left(s\right)}}& 0\end{array}\right){\widehat{P}}_1\left(s\right)+\left(\begin{array}{c}{\displaystyle \frac{-\lambda c_2\left(s\right)}{\mu [p{c}_2\left(s\right)+{\mu }^{\prime }q]}}\\ {\displaystyle \frac{-\lambda q}{p{c}_2\left(s\right)+{\mu }^{\prime }q}}\end{array}\right){\widehat{P}}_0\left(s\right)\hfill \\ & =& {\widehat{\mathsf{\Phi }}}_1\left(s\right){\widehat{P}}_1\left(s\right)+{\widehat{\mathsf{\Phi }}}_0\left(s\right){\widehat{P}}_0\left(s\right),\hfill \end{array}$$

(35)

where ${\widehat{\mathsf{\Phi }}}_1\left(s\right)=\left(\begin{array}{cc}{\displaystyle \frac{c_1\left(s\right)c_2^2\left(s\right)-\mu {\mu }^{\prime }\lambda q}{\mu [p{c}_2\left(s\right)+{\mu }^{\prime }q]c_2\left(s\right)}}& 0\\ {\displaystyle \frac{[c_1\left(s\right)c_2\left(s\right)+\lambda \mu p]q}{[p{c}_2\left(s\right)+{\mu }^{\prime }q]c_2\left(s\right)}}& 0\end{array}\right)$, ${\widehat{\mathsf{\Phi }}}_0\left(s\right)=\left(\begin{array}{c}{\displaystyle \frac{-\lambda c_2\left(s\right)}{\mu [p{c}_2\left(s\right)+{\mu }^{\prime }q]}}\\ {\displaystyle \frac{-\lambda q}{p{c}_2\left(s\right)+{\mu }^{\prime }q}}\end{array}\right).$

Let

$$\begin{array}{c}\hfill det\left(s\right)={(sI-D)}^{-1}={\left({\widehat{d}}_{ij}\left(s\right)\right)}_{3\times 3}.\end{array}$$

(36)

We use algebraic methods to obtain ${(sI-D)}^{-1}$ as ${\displaystyle \frac{1}{|sI-D(s\left)\right|}}$ multiplied by the following:

$$\begin{array}{c}\hfill \left(\begin{array}{ccc}{c}_1\left(s\right)c_2\left(s\right)& \mu p{c}_2\left(s\right)+\mu {\mu }^{\prime }q& {\mu }^{\prime }{c}_1\left(s\right)\\ \lambda c_2\left(s\right)& (s+\lambda +\xi )c_2\left(s\right))& \lambda {\mu }^{\prime }\\ \lambda \mu q& \mu q(s+\lambda +\xi )& (s+\lambda +\xi )c_1\left(s\right)-\lambda \mu p\end{array}\right),\end{array}$$

where $|sI-D\left(s\right)|={(s+\lambda +\xi )}^3+(\mu +{\mu }^{\prime }){(s+\lambda +\xi )}^2+\mu ({\mu }^{\prime }-\lambda +q)(s+\lambda +\xi )-\mu {\mu }^{\prime }\lambda .$

Substituting Equation (35) into (34), we obtain the following:

$$\begin{array}{ccc}& & e_3^T{(sI-D)}^{-1}{\displaystyle \frac{1}{s}}\xi e_1+e_3^T{(sI-D)}^{-1}P\left(0\right)={\displaystyle \frac{\xi +s}{s}}({\widehat{d}}_{11}\left(s\right)+{\widehat{d}}_{21}\left(s\right)+{\widehat{d}}_{31}\left(s\right)),\hfill \\ & & e_3^T{(sI-D)}^{-1}{e}_2{E}^T{\widehat{Q}}_2\left(s\right)=({\widehat{d}}_{12}\left(s\right)+{\widehat{d}}_{22}\left(s\right)+{\widehat{d}}_{32}\left(s\right))F^T{\widehat{P}}_2\left(s\right).\hfill \end{array}$$

(37)

Taking Equation (37) in Equation (34) and transforming it, we have the following:

$$\begin{array}{ccc}\hfill e_4^T{\widehat{P}}_1\left(s\right)& =& {\displaystyle \frac{\xi +s}{s}}({\widehat{d}}_{11}\left(s\right)+{\widehat{d}}_{21}\left(s\right)+{\widehat{d}}_{31}\left(s\right))-{\widehat{P}}_0\left(s\right)\hfill \\ & & +({\widehat{d}}_{12}\left(s\right)+{\widehat{d}}_{22}\left(s\right)+{\widehat{d}}_{32}\left(s\right))F^T[{\widehat{\mathsf{\Phi }}}_1\left(s\right){\widehat{P}}_1\left(s\right)+{\widehat{\mathsf{\Phi }}}_0\left(s\right){\widehat{P}}_0\left(s\right)].\hfill \end{array}$$

(38)

From Equations (30) and (38), we also have the following:

$$\begin{array}{ccc}\hfill {\widehat{P}}_{11}\left(s\right)& =& {\displaystyle \frac{-det\left(s\right)[s+\lambda +\xi +\lambda {\mu }^{\prime }]}{({\mu }^{\prime }-\mu p)det\left(s\right)-\mu c_1^2\left(s\right)c_2\left(s\right)}}{\widehat{P}}_0\left(s\right)\hfill \\ & & +{\displaystyle \frac{det\left(s\right)[{\mu }^{\prime }\frac{s+\xi }{s}({\widehat{d}}_{12}\left(s\right)+{\widehat{d}}_{22}\left(s\right)+{\widehat{d}}_{32}\left(s\right))+\frac{s+\xi }{s}]}{(\mu -{\mu }^{\prime }p)det\left(s\right)-{\mu }^{\prime }{c}_1^2\left(s\right)c_2\left(s\right)}},\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill {\widehat{P}}_{12}\left(s\right)& =& {\displaystyle \frac{[det\left(s\right)-c_1^2\left(s\right)c_2\left(s\right)](s+\lambda +\xi )+\mu p\lambda det\left(s\right)]}{({\mu }^{\prime }-\mu p)det\left(s\right)-\mu c_1^2\left(s\right)c_2\left(s\right)}}{\widehat{P}}_0\left(s\right)\hfill \\ & & +{\displaystyle \frac{[det\left(s\right)-c_1^2\left(s\right)c_2\left(s\right)](-\frac{s+\xi }{s})-\mu pdet\left(s\right)\frac{s+\xi }{s}({\widehat{d}}_{11}\left(s\right)+{\widehat{d}}_{21}\left(s\right)+{\widehat{d}}_{31}\left(s\right))}{(\mu -{\mu }^{\prime }p)det\left(s\right)-{\mu }^{\prime }{c}_1^2\left(s\right)c_2\left(s\right)}}.\hfill \end{array}$$

(40)

Inverting Equations (39) and (40) yields the explicit expression for $P_{1,1}\left(t\right)$ and $P_{1,2}\left(t\right)$ as follows:

$$\begin{array}{ccc}\hfill P_{1,1}\left(t\right)& =& {\displaystyle \frac{1}{\mu }}[{\displaystyle \frac{1}{p}}·1\left(t\right)+{\displaystyle \frac{(\lambda +\xi )({\mu }^{\prime }+\lambda +\xi )}{{\mu }^{\prime }+p\lambda +p\xi }}\delta \left(t\right)\hfill \\ & & -{\displaystyle \frac{q({\mu }^{\prime 2}+q\lambda {\mu }^{\prime }+p{\mu }^{\prime }\xi +q{\xi }^2+p{\lambda }^2+2p\lambda \xi )}{p^2({\mu }^{\prime }+p\lambda +p\xi )}}{e}^{-{\displaystyle \frac{{\mu }^{\prime }+p\lambda +p\xi }{p}}t}]\ast P_0\left(t\right)\hfill \\ & & +{\displaystyle \frac{1}{\mu }}\left[{\displaystyle \frac{1}{p}}·1\left(t\right)+{\displaystyle \frac{({\mu }^{\prime }+\lambda +\xi )\xi }{{\mu }^{\prime }+p\lambda +p\xi }}\delta \left(t\right)-{\displaystyle \frac{q{\mu }^{\prime }}{p^2}}{e}^{-{\displaystyle \frac{{\mu }^{\prime }+p\lambda +p\xi }{p}}t}\right],\hfill \\ \hfill P_{1,2}\left(t\right)& =& \left[{\displaystyle \frac{q(\lambda +\xi )}{{\mu }^{\prime }+p\lambda +p\xi }}\delta \left(t\right)+{\displaystyle \frac{{\mu }^{\prime }q}{p({\mu }^{\prime }+p\lambda +p\xi )}}{e}^{-{\displaystyle \frac{{\mu }^{\prime }+p\lambda +p\xi }{p}}t}\right]\ast P_0\left(t\right)\hfill \\ & & +{\displaystyle \frac{q\xi }{{\mu }^{\prime }+p\lambda +p\xi }}\delta \left(t\right)+{\displaystyle \frac{q({\mu }^{\prime }+p\lambda )}{p({\mu }^{\prime }+p\lambda +p\xi )}}{e}^{-{\displaystyle \frac{{\mu }^{\prime }+p\lambda +p\xi }{p}}t}.\hfill \end{array}$$

(41)

where $\delta \left(t\right)$ is a Dirichlet Function and * denotes convolution.

Evaluation of ${\mathbf{P}}_{\mathbf{n},\mathbf{1}}\left(\mathbf{t}\right),{\mathbf{P}}_{\mathbf{n},\mathbf{2}}\left(\mathbf{t}\right),n\ge 1$

Taking the Laplace transform of Equation (30) gives the following:

$$\begin{array}{c}\hfill F^T{P}_1\left(t\right)=\left(1·1\left(t\right)+(\lambda +\xi )\delta \left(t\right)\right)\ast P_0\left(t\right)-1·1\left(t\right)+\xi \delta \left(t\right).\end{array}$$

(42)

From Equations (17), (29), and (42), we have the following:

$$\begin{array}{ccc}& & P_{n+1}\left(t\right)\hfill \\ & =& \sum _{i=0}^{\infty }{\int }_0^t\{\lambda P_0\left(y\right){\beta }^{n+i}{I}_{n+i}\left[\alpha (t-y)\right]e^{-{\displaystyle \frac{1}{2}}(\mu +{\mu }^{\prime }+2\lambda +2\xi )(t-y)}\hfill \\ & & ·\sum _{k=0}^{\infty }\sum _{\begin{array}{c}{i}_1+i_2+i_3=k\\ 2i_1+i_2=i\end{array}}\left(\begin{array}{c}{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k}}{\left(2k\right)!}}-(\mu -{\mu }^{\prime }){\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\\ 2\mu q{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\end{array}\right)\hfill \\ & & ·{\displaystyle \frac{k!}{i_1!i_2!i_3!}}{\left(\mu p\right)}^{2i_1}{(2\mu {\mu }^{\prime }+2\mu {\mu }^{\prime }q-2{\mu }^{2}p)}^{i_2}{(\mu -{\mu }^{\prime })}^{2i_3}\}dy\hfill \\ & & -\sum _{i=0}^{\infty }{\int }_0^t\{\lambda P_0\left(y\right){\beta }^{n+i+1}{I}_{n+i+1}\left[\alpha (t-y)\right]e^{-{\displaystyle \frac{1}{2}}(\mu +{\mu }^{\prime }+2\lambda +2\xi )(t-y)}\hfill \\ & & ·\sum _{k=0}^{\infty }\sum _{\begin{array}{c}{i}_1+i_2+i_3=k\\ 2i_1+i_2=i\end{array}}\left(\begin{array}{c}\mu p{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\\ 0\end{array}\right){\displaystyle \frac{k!}{i_1!i_2!i_3!}}{\left(\mu p\right)}^{2i_1}{(2\mu {\mu }^{\prime }+2\mu {\mu }^{\prime }q-2{\mu }^{2}p)}^{i_2}{(\mu -{\mu }^{\prime })}^{2i_3}\}dy\hfill \\ & & -\sum _{i=0}^{\infty }{\int }_0^t\{F^T{P}_1\left(y\right){\beta }^{n+i+1}{I}_{n+i+1}\left[\alpha (t-y)\right]e^{-{\displaystyle \frac{1}{2}}(\mu +{\mu }^{\prime }+2\lambda +2\xi )(t-y)}\hfill \\ & & ·\sum _{k=0}^{\infty }\sum _{\begin{array}{c}{i}_1+i_2+i_3=k\\ 2i_1+i_2=i\end{array}}\left(\begin{array}{c}{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k}}{\left(2k\right)!}}-(\mu -{\mu }^{\prime }){\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\\ 2\mu q{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\end{array}\right)\hfill \\ & & ·{\displaystyle \frac{k!}{i_1!i_2!i_3!}}{\left(\mu p\right)}^{2i_1}{(2\mu {\mu }^{\prime }+2\mu {\mu }^{\prime }q-2{\mu }^{2}p)}^{i_2}{(\mu -{\mu }^{\prime })}^{2i_3}\}dy\hfill \\ & & +\sum _{i=0}^{\infty }{\int }_0^t\{F^T{P}_1\left(y\right){\beta }^{n+i+2}{I}_{n+i+2}\left[\alpha (t-y)\right]e^{-{\displaystyle \frac{1}{2}}(\mu +{\mu }^{\prime }+2\lambda +2\xi )(t-y)}\hfill \\ & & ·\sum _{k=0}^{\infty }\sum _{\begin{array}{c}{i}_1+i_2+i_3=k\\ 2i_1+i_2=i\end{array}}\left(\begin{array}{c}\mu p{\displaystyle \frac{{\left(\frac{t-y}{2}\right)}^{2k+1}}{(2k+1)!}}\\ 0\end{array}\right){\displaystyle \frac{k!}{i_1!i_2!i_3!}}{\left(\mu p\right)}^{2i_1}{(2\mu {\mu }^{\prime }+2\mu {\mu }^{\prime }q-2{\mu }^{2}p)}^{i_2}{(\mu -{\mu }^{\prime })}^{2i_3}\}dy,\hfill \end{array}$$

(43)

where $P_0\left(y\right)$ and $F^T{P}_1\left(y\right)$ are given in Equations (29) and (42), respectively.

Thus, Equations (29), (41), and (43) completely determine all the system size probabilities.

4. Steady-State Probabilities

In this section, we seek analytical expressions for the steady-state probabilities of an $M/P{H}_2/1$ queue model with catastrophes. Let

$$\begin{array}{ccc}& & P_0=\underset{t\to \infty }{lim}{P}_0\left(t\right),\hfill \\ & & P_{n,1}=\underset{t\to \infty }{lim}{P}_{n,1}\left(t\right),n=1,2,\dots ,\hfill \\ & & P_{n,2}=\underset{t\to \infty }{lim}{P}_{n,2}\left(t\right),n=1,2,\dots .\hfill \end{array}$$

From Equation (28), we have the following:

$$\begin{array}{ccc}\hfill {\widehat{P}}_0\left(s\right)& =& {\displaystyle \frac{{\mu }^{2}q{c}_2\left(s\right)c_3^2\left(s\right)a_2\left(s\right)-f_6\left(s\right)c_4\left(s\right)}{d_6\left(s\right)s{c}_4\left(s\right)+{\mu }^{2}q{c}_3^2\left(s\right)s{a}_2\left(s\right)c_2\left(s\right)}}.\hfill \end{array}$$

By using Tauberian theorem, we obtain the following:

$$\begin{array}{ccc}\hfill P_0& =& {\displaystyle \frac{{\mu }^{2}q({\mu }^{\prime }+\lambda +\xi ){(\mu +p\lambda +p\xi )}^2+f_6}{d_6+{\mu }^{2}q({\mu }^{\prime }+\mu p+p\xi )({\mu }^{\prime }+\lambda +\xi )}}.\hfill \end{array}$$

(44)

where $d_6=d_5({\mu }^{\prime }+\lambda +\xi )-(\lambda +\xi )[b_4+\lambda \mu q(\mu +{\mu }^{\prime }+2\lambda +2\xi )({\mu }^{\prime }+p\lambda +p\xi )({\mu }^{\prime }+\lambda +\xi )]+\mu b_2({\mu }^{\prime }+\lambda +\xi )$, $f_6=({\mu }^{\prime }+\lambda +\xi )f_5-\xi [b_4+{\mu }^{2}q{({\mu }^{\prime }+p\lambda +p\xi )}^2({\mu }^{\prime }+\lambda +\xi )+\lambda \mu q(\mu +{\mu }^{\prime }+2\lambda +2\xi )({\mu }^{\prime }+p\lambda +p\xi )({\mu }^{\prime }+\lambda +\xi )],$ $d_5=q[\lambda \mu p+(\mu +\lambda +\xi )({\mu }^{\prime }+\lambda +\xi )][(\mu +\lambda +\xi )({\mu }^{\prime }+\lambda +\xi )(\lambda +\xi )+\mu p{(\lambda +\xi )}^2+\mu {\mu }^{\prime }\xi ]$, $f_5=q(s+\xi )[\lambda \mu p+(\mu +\lambda +\xi )({\mu }^{\prime }+\lambda +\xi )][(\mu +\lambda +\xi )({\mu }^{\prime }+\lambda +\xi )+\mu p(2\lambda +\xi )+\mu {\mu }^{\prime }],$ $b_4=q[{(\mu +\lambda +\xi )}^2{({\mu }^{\prime }+\lambda +\xi )}^2+\mu p(\mu +\lambda +\xi ){({\mu }^{\prime }+\lambda +\xi )}^2+\mu q{\mu }^{\prime }(\mu +\lambda +\xi )({\mu }^{\prime }+\lambda +\xi )+\lambda {\mu }^{2}p({\mu }^{\prime }+\lambda +\xi )+\lambda {\mu }^2{p}^2({\mu }^{\prime }+\lambda +\xi )-\lambda \mu {\mu }^{\prime }({\mu }^{\prime }+\lambda +\xi )-\lambda \mu q{\mu }^{\prime }(\mu +\lambda +\xi )+{\lambda }^2{\mu }^2{p}^2+\lambda {\mu }^2{\mu }^{\prime }pq],$ $b_2=q\mu \xi ({\mu }^{\prime }+p\lambda +p\xi )\lambda q[(\mu +\lambda +\xi )({\mu }^{\prime }+\lambda +\xi )+\lambda \mu p]$.

From Equations (28), (39), and (40), again using Tauberian theorem, we have the following:

$$\begin{array}{ccc}\hfill P_{1,1}& =& {\displaystyle \frac{({\mu }^{\prime }+\lambda +\xi )(\lambda +\xi )}{\mu ({\mu }^{\prime }+p\lambda +p\xi )}}{P}_0-{\displaystyle \frac{({\mu }^{\prime }+\lambda +\xi )\xi }{\mu ({\mu }^{\prime }+p\lambda +p\xi )}},\hfill \end{array}$$

(45)

$$\begin{array}{ccc}\hfill P_{1,2}& =& {\displaystyle \frac{q(\lambda +\xi )}{{\mu }^{\prime }+p\lambda +p\xi }}{P}_0-{\displaystyle \frac{q\xi }{{\mu }^{\prime }+p\lambda +p\xi }}.\hfill \end{array}$$

(46)

From Equations (4), (24), and (28), and again using Tauberian theorem, we have the following:

$$\begin{array}{ccc}\hfill P_{2,1}& =& {\displaystyle \frac{-\lambda ({\mu }^{\prime }+\lambda +\xi )}{\mu ({\mu }^{\prime }+p\lambda +p\xi )}}{P}_0+{\displaystyle \frac{(\mu +\lambda +\xi ){(\lambda +{\mu }^{\prime }+\xi )}^2-\mu {\mu }^{\prime }\lambda q}{\mu ({\mu }^{\prime }+p\lambda +p\xi )({\mu }^{\prime }+\lambda +\xi )}}{P}_{1,1},\hfill \end{array}$$

(47)

$$\begin{array}{ccc}\hfill P_{2,2}& =& {\displaystyle \frac{-\lambda q}{{\mu }^{\prime }+p\lambda +p\xi }}{P}_0+{\displaystyle \frac{[(\mu +\lambda +\xi )({\mu }^{\prime }+\lambda +\xi )+\lambda \mu p]q}{({\mu }^{\prime }+p\lambda +p\xi )({\mu }^{\prime }+\lambda +\xi )}}{P}_{1,1},\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill P_{3,1}& =& -{\displaystyle \frac{\lambda {({\mu }^{\prime }+\lambda +\xi )}^3+\mu {\mu }^{\prime }q{\lambda }^2}{\mu ({\mu }^{\prime }+p\lambda +p\xi ){({\mu }^{\prime }+\lambda +\xi )}^2}}{P}_{1,1}+{\displaystyle \frac{(\mu +\lambda +\xi ){({\mu }^{\prime }+\lambda +\xi )}^2-\mu {\mu }^{\prime }q\lambda }{\mu ({\mu }^{\prime }+\lambda +\xi )({\mu }^{\prime }+p\lambda +p\xi )}}{P}_{2,1},\hfill \end{array}$$

(49)

$$\begin{array}{ccc}\hfill P_{3,2}& =& {\displaystyle \frac{q\lambda [\lambda \mu p-{({\mu }^{\prime }+\lambda +\xi )}^2]}{({\mu }^{\prime }+p\lambda +p\xi ){({\mu }^{\prime }+\lambda +\xi )}^2}}{P}_{1,1}-{\displaystyle \frac{q[(\mu +\lambda +\xi )({\mu }^{\prime }+\lambda +\xi )+\lambda \mu p]}{({\mu }^{\prime }+\lambda +\xi )({\mu }^{\prime }+p\lambda +p\xi )}}{P}_{2,1}.\hfill \end{array}$$

(50)

Using a similar method for Equations (4), (24), and (45)–(50), using Tauberian theorem, we will calculate $P_{4,1},P_{4,2},P_{5,1},P_{5,2}$, ⋯.

Once the steady-state distribution is in hand, other performance measures of the system are subsequently obtained.

5. Performance Measures

Based on the transient probabilities, in this section, we demonstrate how to calculate relevant system performance measures.

5.1. Mean

Let $N\left(t\right)$ be the number of customers in the system at time t. The average number of customers in the system at time t is given as follows:

$$\begin{array}{c}\hfill E\left(N\left(t\right)\right)={\mathbf{e}}_4^T{P}_1\left(t\right)+\sum _{n=1}^{\infty }(n+1){\mathbf{e}}_4^T{P}_{n+1}\left(t\right)\end{array}$$

(51)

and

$$\begin{array}{c}\hfill {\displaystyle \frac{dE\left(N\right(t\left)\right)}{dt}}={\mathbf{e}}_4^T\sum _{n=1}^{\infty }n{\displaystyle \frac{d{P}_n\left(t\right)}{dt}}.\end{array}$$

(52)

From Equations (6) and (7), after considerable mathematical manipulations, the above equation will lead to the following differential equation:

$$\begin{array}{c}\hfill {\displaystyle \frac{dE\left(N\right(t\left)\right)}{dt}}=-\xi E\left(N\left(t\right)\right)+\lambda P_0\left(t\right)-{\mathbf{e}}_4^T{C}^2{P}_2\left(t\right)+\sum _{n=1}^{\infty }{\mathbf{e}}_4^{T}B{P}_n\left(t\right)-\sum _{n=1}^{\infty }{\mathbf{e}}_4^{T}C{P}_{n+2}\left(t\right).\end{array}$$

(53)

Therefore:

$$\begin{array}{ccc}\hfill E\left(N\right(t\left)\right)& =& \lambda {\int }_0^t{P}_0\left(y\right)e^{-\xi (t-y)}dy-{\mathbf{e}}_4^T{C}^2{\int }_0^t{P}_2\left(y\right)e^{-\xi (t-y)}dy\hfill \\ & & +\sum _{n=1}^{\infty }{\mathbf{e}}_4^{T}B{\int }_0^t{P}_n\left(y\right)e^{-\xi (t-y)}dy-\sum _{n=1}^{\infty }{\mathbf{e}}_4^{T}C{\int }_0^t{P}_{n+2}\left(y\right)e^{-\xi (t-y)}dy,\hfill \end{array}$$

(54)

where $P_0\left(t\right),P_1\left(t\right),$ and $P_n\left(t\right),n=2,3,\dots$ are given in Equations (29), (41), and (43), respectively.

5.2. Variance

The variance number of customers in the system at time t is given as follows:

$$\begin{array}{ccc}& & \mathrm{Var}\left(N\left(t\right)\right)=E\left(N^2\left(t\right)\right)-{\left[E\left(N\left(t\right)\right)\right]}^2,\hfill \\ & & \mathrm{Var}\left(N\left(t\right)\right)=r\left(t\right)-{\left[E\left(N\left(t\right)\right)\right]}^2,\hfill \end{array}$$

(55)

where

$$\begin{array}{c}\hfill r\left(t\right)=E\left(N^2\left(t\right)\right)={\mathbf{e}}_4^T{P}_1\left(t\right)+\sum _{n=1}^{\infty }{(n+1)}^2{\mathbf{e}}_4^T{P}_{n+1}\left(t\right).\end{array}$$

(56)

Then,

$$\begin{array}{c}\hfill {\displaystyle \frac{dr\left(t\right)}{dt}}={\mathbf{e}}_4^T{\displaystyle \frac{d{P}_1\left(t\right)}{dt}}+\sum _{n=1}^{\infty }{(n+1)}^2{\mathbf{e}}_4^T{\displaystyle \frac{d{P}_{n+1}\left(t\right)}{dt}}.\end{array}$$

(57)

From Equations (6), (7), and (56), after considerable mathematical manipulations, the above equation will lead to the following differential equation:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dr\left(t\right)}{dt}}& =& -\xi r\left(t\right)+(2\lambda -\mu p-{\mu }^{\prime })E\left(N\left(t\right)\right)+\lambda P_0\left(t\right)\hfill \\ & & +\sum _{n=1}^{\infty }{\mathbf{e}}_4^{T}B{P}_n\left(t\right)-\sum _{n=1}^{\infty }{\mathbf{e}}_4^{T}C{P}_n\left(t\right).\hfill \end{array}$$

(58)

Therefore,

$$\begin{array}{ccc}\hfill r\left(t\right)& =& (2\lambda -\mu p-{\mu }^{\prime }){\int }_0^{t}E\left(N\left(y\right)\right)e^{-\xi (t-y)}dy+\lambda {\int }_0^t{P}_0\left(y\right)e^{-\xi (t-y)}dy\hfill \\ & & +\sum _{n=1}^{\infty }{\int }_0^t{\mathbf{e}}_4^{T}B{P}_n\left(y\right)e^{-\xi (t-y)}dy-\sum _{n=1}^{\infty }{\int }_0^t{\mathbf{e}}_4^{T}C{P}_n\left(y\right)e^{-\xi (t-y)}dy.\hfill \end{array}$$

(59)

Using Equation (55), we obtain the following:

$$\begin{array}{ccc}\hfill \mathrm{Var}\left(N\right(t\left)\right)& =& (2\lambda -\mu p-{\mu }^{\prime }){\int }_0^{t}E\left(N\left(y\right)\right)e^{-\xi (t-y)}dy+\lambda {\int }_0^t{P}_0\left(y\right)e^{-\xi (t-y)}dy\hfill \\ & & +\sum _{n=1}^{\infty }{\int }_0^t{\mathbf{e}}_4^{T}B{P}_n\left(y\right)e^{-\xi (t-y)}dy-\sum _{n=1}^{\infty }{\int }_0^t{\mathbf{e}}_4^{T}C{P}_n\left(y\right)e^{-\xi (t-y)}dy-{\left[E\left(N\left(t\right)\right)\right]}^2,\hfill \end{array}$$

(60)

where $P_0\left(t\right),P_1\left(t\right)$, $P_n\left(t\right),n=2,3,\dots$ and $E\left(N\right(t\left)\right)$ are given in Equations (29), (41), (43) and (54), respectively.

6. Special Case and Numerical Examples

6.1. Special Case

• Case 1: For $p=1,{\mu }^{\prime }=0$, and $q=1-p=0,$ we observe that our model is reduced to the one studied by Oliveira Souza [31]. Equation (1) in Oliveira Souza [31] coincides with Equations (1)–(5), respectively.

6.2. Numerical Examples

In the subsection, we present a few numerical examples to investigate the steady-state probabilities. In all of the examples we take the service rate $\mu =1,{\mu }^{\prime }=1.2$, and $p=0.9,q=0.1$.

In Figure 3, the steady-state probability $P_0$ is plotted against the rate $\xi$ with the assumption that initially, the system is empty. All the probability curves increase with increasing rate $\xi$.

Figure 4 displays the steady-state probabilities $Q_1(={(P_{11},P_{12})}^T)$ in the system from three different values of the rate $\lambda$ and catastrophe rate. The steady-state probabilities $Q_1$ increase with increasing rate $\xi$ when rate $\xi$ is relatively small, then they gradually decrease and stabilize.

Figure 5 displays the steady-state probabilities $Q_n(=2,3,4)$ in the system for different values of the catastrophe rate. The steady-state probabilities $Q_n$ increase with increasing rate $\xi$. However, the probability $Q_n$ decreases with increasing n values.

In Figure 6, the transient probability $P_0\left(t\right)$ is plotted against time t with the assumption that initially, the system is empty. We observe that all the probability curves decrease with increasing time t. Moreover, with the passage of time, the transient probability $P_0\left(t\right)$ decreases from 1 and later tends towards a constant value.

7. Conclusions and Future Research

In this study, we have investigated a queue model according to catastrophes in which the service time has two phases. Customers enter the service system based on the Poisson process, and the service time for each customer in the system corresponds to the $PH$ distribution. To formulate the system and solve the transient probabilities, we combined the modified Bessel function and the Laplace transform. The steady-state probabilities of the system are presented. Some performance measures of the system, such as mean and variance, are studied. Finally, special cases and numerical examples are given.

In the future, due to the complexity of the real world, this study may be extended from one service to more than one unit service. We will consider comparing the waiting time in the following states between two queuing systems. Case 1: If $\mu$ and ${\mu }^{\prime }$ in two queuing systems have different values, but the sum of $\mu$ and ${\mu }^{\prime }$ is equal. Case 2: If $\mu$, ${\mu }^{\prime }$, and $\xi$ in two queueing systems have different values, but $\mu +{\mu }^{\prime }-\xi$ is a constant. Fractional queues, retrial queues, and vacation policy can also be interpreted in the system. We will demonstrate some applications of an $M/P{H}_2/1$ queue according to catastrophes. We will also consider whether it is feasible to use the duality between the $M/P{H}_2/1$ queue according to catastrophes and the fractional $M/P{H}_2/1$ queue according to catastrophes to solve problems of transient probabilities.