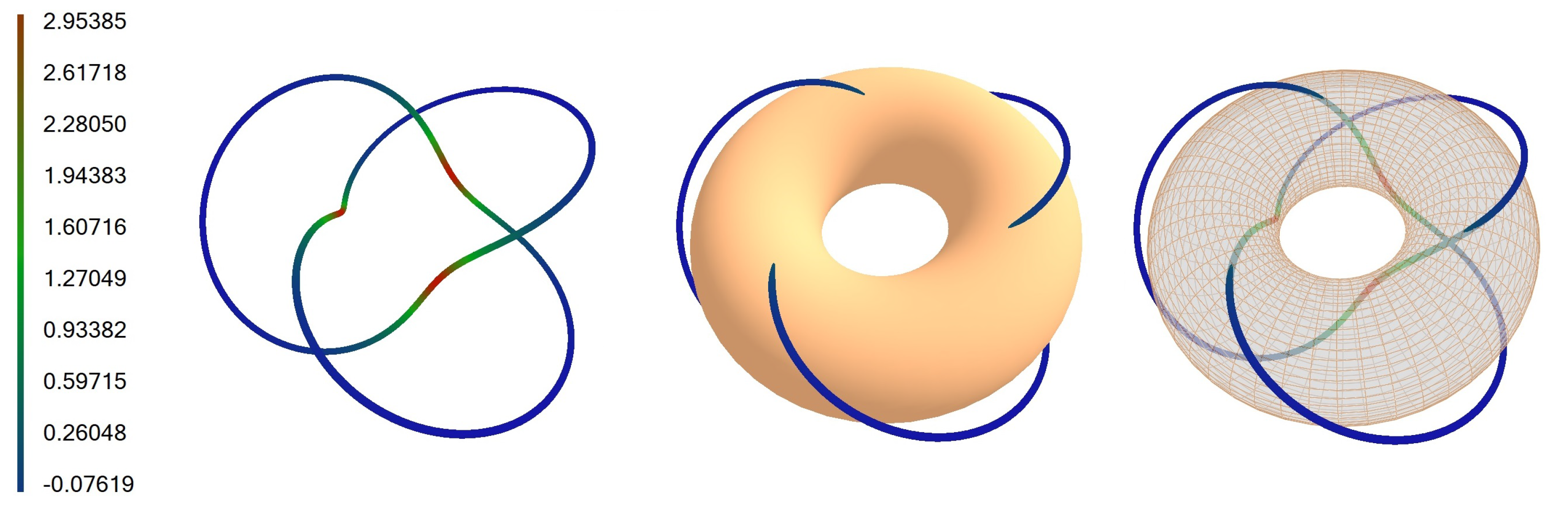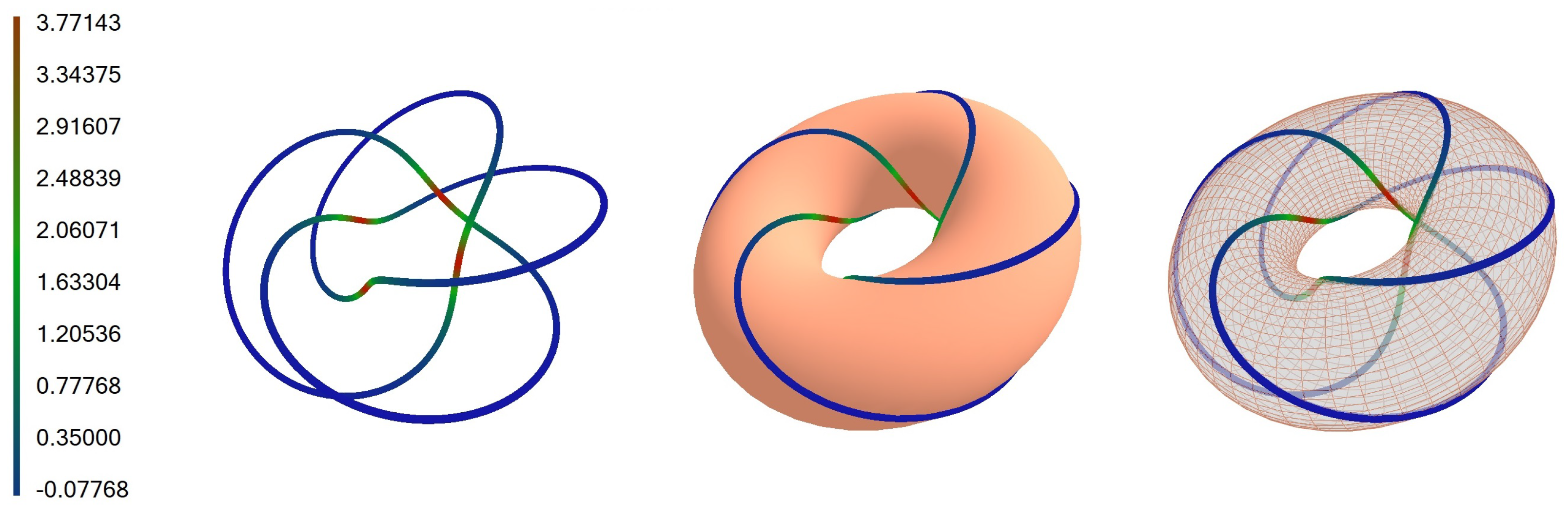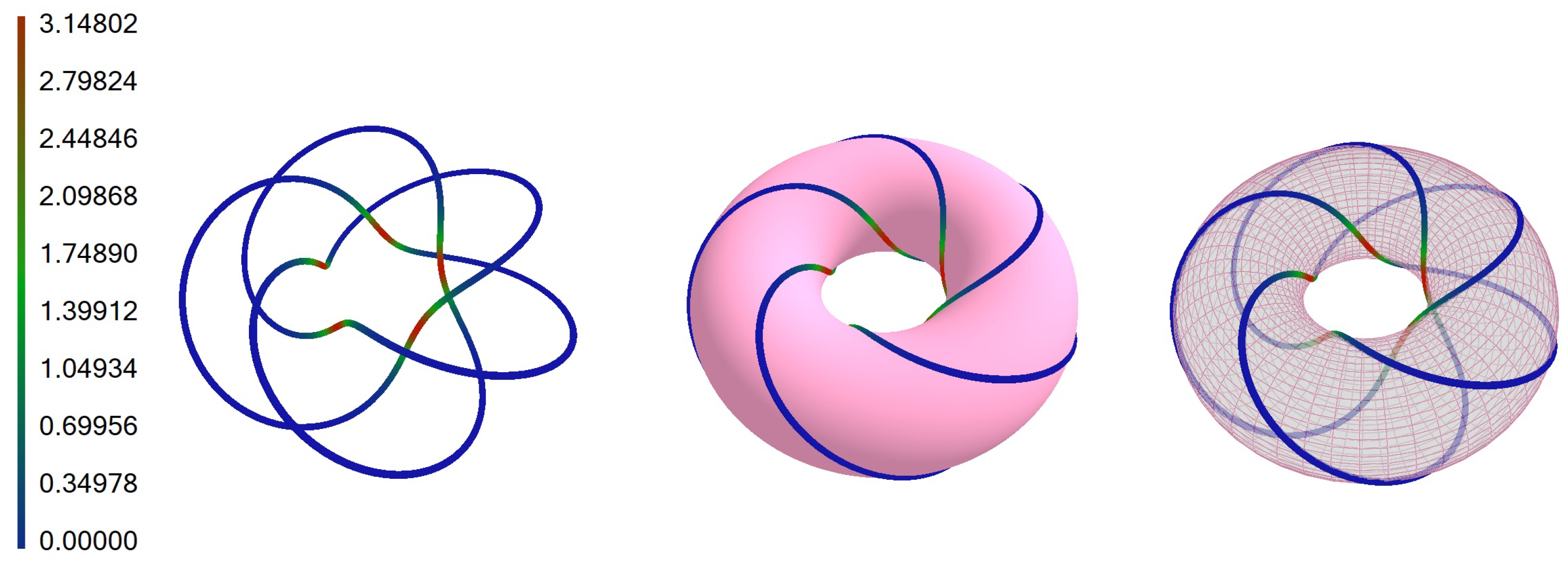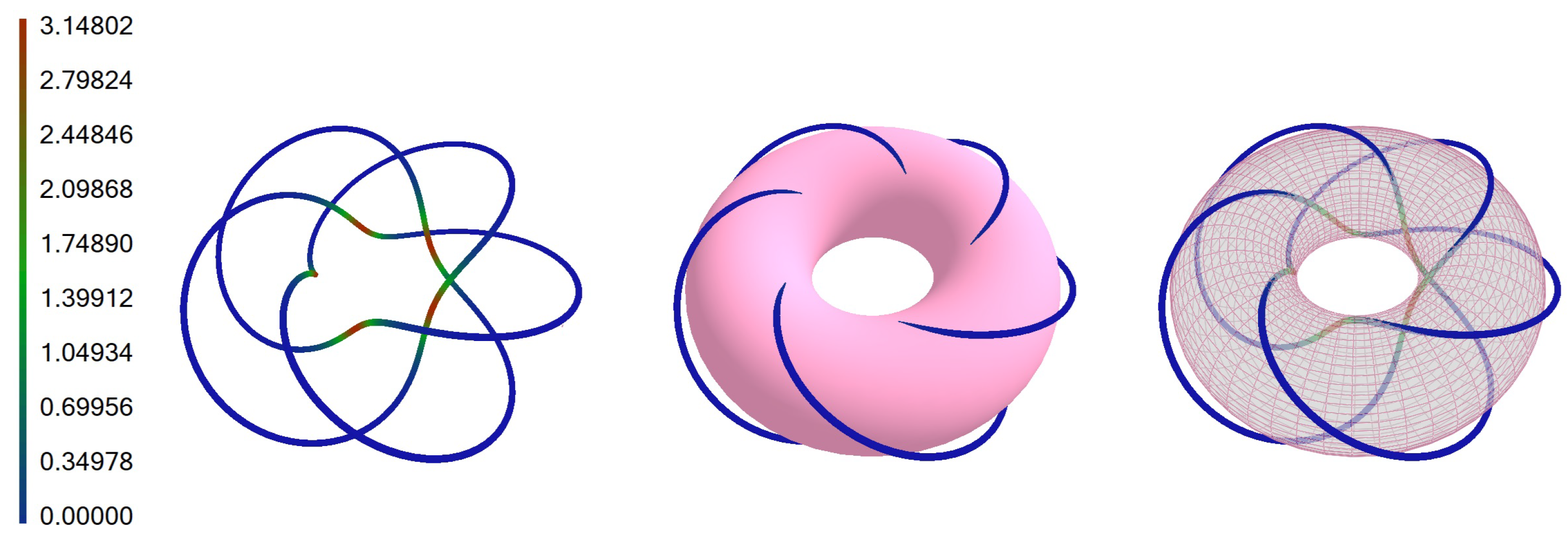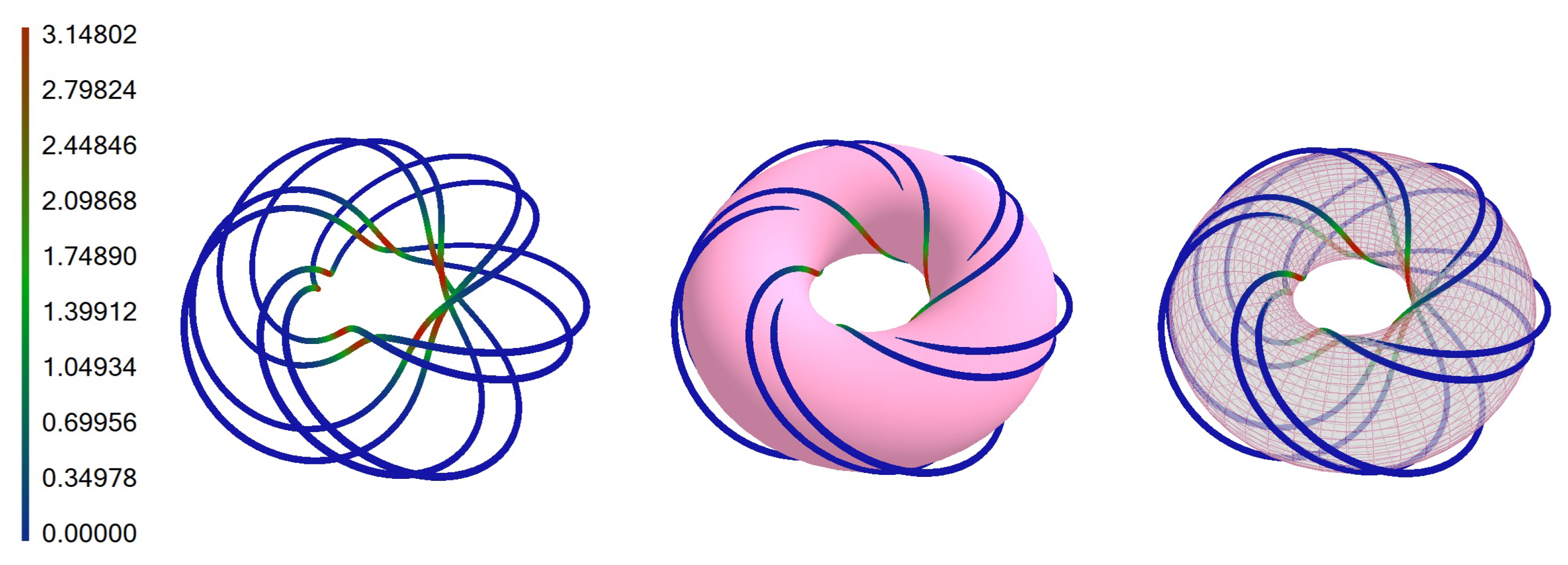On the Torsional Energy of Deformed Curves and Knots

Abstract

This paper deals with the study of torsional energy (total squared torsion) at infinitesimal bending of curves and knots in three dimensional Euclidean space. During bending, the curve is subject to change, and its properties are changed. The effect that deformation has on the curve is measured by variations. Here, we observe the infinitesimal bending of the second order and variations of the first and the second order that occur in this occasion. The subjects of study are curves and knots, in particular torus knots. We analyze various examples both analytically and graphically, using our own calculation and visualization software tool.

1. Introduction

Functionals that include curvature and torsion are often encountered when modeling the behavior of geometric objects. To better understand these objects and their shape, we consider corresponding functionals called energies. The integrals of the squared curvature and squared torsion are especially important, and they relate to the Willmore (bending) [1] and torsional energy of elastic filaments.

The torsional energy (total squared torsion) is one of the global properties of a curve C and is defined by the integral $E_{\tau }={\displaystyle \frac{1}{2}}{\int }_C{\tau }^2(s)ds,$ where s and $\tau$ are the arc length and the torsion of C, respectively. During various deformations, for instance, infinitesimal bending, the curves undergo changes, which also affects the change in torsional energy. Variational problems under different boundary conditions and the finding of critical curves have been intensively investigated under various points of view.

Knots are closed curves in space, without self-intersections. In particular, torus knots lie on the surface of a torus, wrapped uniformly around it. They are very important in many areas such as physics [2], biology (DNA) [3], mechanics [4] etc. The knowledge of functionals based on the squared curvature and torsion is essential in studying the shapes of knots. Thus, elastic filaments in the shapes of torus knots were studied in relation to bending and torsional energy in [5]. In terms of knot complexity given by the winding number, bending and torsional energy were discussed in [6]. In [7], in using a numerical approach based on the gradient descent method, the critical trajectories for bending and torsional energies and their projection onto the image plane under certain constraints were determined. The impact of the infinitesimal bending of the first order on the torsional energy on torus knots was considered in [8].

There are numerous studies related to curvature and torsion effects on curves and knots. Based on the research of W. Fenchel, K. Borsukm and W. Milnor, the first results about the total curvature of knots in three-dimensional space showed that it must exceed $4\pi$, while for an arbitrary closed curve, it is at least $2\pi$ [9]. Following the classical result related to total torsion, which states that the total torsion of a closed spherical curve is equal to zero, paper [10] gave a generalization of this result to Riemannian three-dimensional manifolds with constant curvature. Other generalizations were given in paper [11] about the total torsion of closed lines of curvature, and in [12] about the total torsion of knots under second-order infinitesimal bending. The application of curvature- and torsion-based functions is huge, for instance, the case of knotted polymers was discussed in [13]. In [14], the curvature and torsion of the tight trefoil knot were studied with the use of the so-called SONO algorithm. In [15], the authors proved that the average crossing number of a smooth knot K was less than the quadruple product of the rope length of K and its total curvature.

In this research, we deal with infinitesimal bending problems related to the torsional energy of curves and knots and consider second-order bending and variations. This paper is organized in the following way: In Section 2, a brief overview of second-order infinitesimal bending is given. In Section 3, the first and the second variation of the torsional energy is obtained, with some conclusions for plane curves and knots. In Section 4, torus knots under second-order infinitesimal bending are studied, with the condition that the family of bent curves is approximately on the initial torus, i.e., with a given precision. In Section 5, some examples of torus knots under infinitesimal bending are considered, together with graphical illustrations and numerical calculations.

2. Second-Order Infinitesimal Bending of Curve in ${\mathbb{R}}^{\mathbf{3}}$

Starting with the works of famous mathematicians such as A. D. Aleksandrov [16], N. V. Efimov [17], S. E. Kon-Fossen [18], I. Vekua [19], and many others, until the recent works of modern mathematicians (see O. Belova et al. [20], V. de Lessa and A. Meziani [21], U. Gözütok at al. [22], L. Rýparová [23], and M. Sherkuziyev [24]), the theory of infinitesimal bending has been intensively developed up to the present day. A lot of articles are devoted to the infinitesimal bending problems of curves and surfaces, and more recently, knots have become the subject of study [25]. Some other generalizations have lead to the study of bending on manifolds and to more general deformations [26]. Bellow, we will give a brief overview of the infinitesimal bending theory primarily based on [17,19,27,28].

Let us consider a biregular curve

$$C:\mathbf{r}=\mathbf{r}(u),u\in \mathcal{J}\subseteq \mathbb{R}$$

of a class $C^{\alpha },\alpha \ge 3$, included in a family of curves

$$C_{ϵ}:\tilde{\mathbf{r}}(u,ϵ)={\mathbf{r}}_{ϵ}(u)=\mathbf{r}(u)+ϵ\stackrel{(1)}{\mathbf{z}}(u)+{ϵ}^2\stackrel{(2)}{\mathbf{z}}(u),$$

(1)

where $ϵ\ge 0,ϵ\to 0$, $\mathcal{J}$ is an interval in $\mathbb{R}$, and we obtain C for $ϵ=0$ ($C=C_0$). The fields $\stackrel{(j)}{\mathbf{z}}(u)\in C^{\alpha },\alpha \ge 3,j=1,2$, are continuous vector functions defined at the points of C.

According to Efimov [17], a family of curves $C_{ϵ}$ is an infinitesimal bending of the second order of the curve C if

$$d{s}_{ϵ}^2-d{s}^2=o({ϵ}^2),$$

(2)

i.e., if the difference of the squares of the line elements of the deformed and the initial curve is an infinitesimal value of the order higher than the second with respect to $ϵ$. The field $\stackrel{(j)}{\mathbf{z}}=\stackrel{(j)}{\mathbf{z}}(u)$, where $j=1,2$, is the infinitesimal bending field of the order j of the curve C.

The previous condition is equivalent to the following system of equations [17,28]:

$$d\mathbf{r}·d\stackrel{(1)}{\mathbf{z}}=0,2d\mathbf{r}·d\stackrel{(2)}{\mathbf{z}}+d\stackrel{(1)}{\mathbf{z}}·d\stackrel{(1)}{\mathbf{z}}=0,$$

(3)

where · stands for the scalar product in ${\mathbb{R}}^3$.

If the curve C is parameterized by an arc length

$$C:\mathbf{r}=\mathbf{r}(s)=\mathbf{r}[u(s)],s\in \mathcal{I}=[0,L]\subseteq \mathbb{R},$$

(4)

then corresponding infinitesimal bending is in the form

$$C_{ϵ}:\tilde{\mathbf{r}}(s,ϵ)={\mathbf{r}}_{ϵ}(s)=\mathbf{r}(s)+ϵ\stackrel{(1)}{\mathbf{z}}(s)+{ϵ}^2\stackrel{(2)}{\mathbf{z}}(s).$$

Since the vector fields $\stackrel{(1)}{\mathbf{z}}$ and $\stackrel{(2)}{\mathbf{z}}$ are defined in the points of curve (4), they can be presented in the form

$$\stackrel{(j)}{\mathbf{z}}=\stackrel{(j)}{z}\mathbf{t}+\stackrel{(j)}{z_1}{\mathbf{n}}_1+\stackrel{(j)}{z_2}{\mathbf{n}}_2,j=1,2,$$

where $\mathbf{t}, {\mathbf{n}}_{\mathbf{1}},$ and ${\mathbf{n}}_2$ are the unit tangent, unit principal normal, and binormal vector fields of C, respectively, and $\stackrel{(j)}{z},\stackrel{(j)}{z_1},$ and $\stackrel{(j)}{z_2}$ are the functions of s.

In this case, the necessary and sufficient conditions for the second-order infinitesimal bending are given by the following equations:

$$\begin{array}{ll}{\stackrel{(1)}{z}}^{\prime }-k\stackrel{(1)}{z_1}=& 0,\\ {\stackrel{(2)}{z}}^{\prime }-k\stackrel{(2)}{z_1}=& -{\displaystyle \frac{1}{2}}\{{[k\stackrel{(1)}{z}+{\stackrel{(1)}{z_1}}^{\prime }-\tau \stackrel{(1)}{z_2}]}^2+{[\tau \stackrel{(1)}{z_1}+{\stackrel{(1)}{z_2}}^{\prime }]}^2\},\end{array}$$

(5)

where k is the curvature, $\tau$ is the torsion of C, and prime denotes derivative with respect to arc length s (see [27]).

Infinitesimal bending affects the change in geometric quantities, which is described by variations. If $\mathcal{A}=\mathcal{A}(u)$ is a magnitude that characterizes a geometric property on the curve C, then the corresponding magnitude on the curve $C_{ϵ}$ being an infinitesimal bending of the curve C will be denoted by ${\mathcal{A}}_{ϵ}={\mathcal{A}}_{ϵ}(u)$. According to Vekua [19], let the increase $\Delta \mathcal{A}$ in the magnitude $\mathcal{A}$ be presented in the form

$$\begin{array}{c}\hfill \Delta \mathcal{A}={\mathcal{A}}_{ϵ}-\mathcal{A}=ϵ\delta \mathcal{A}+{ϵ}^2{\delta }^2\mathcal{A}+\dots +{ϵ}^n{\delta }^n\mathcal{A}+\dots \end{array}$$

Then, the coefficients $\delta \mathcal{A},{\delta }^2\mathcal{A},\dots ,{\delta }^n\mathcal{A},\dots$ are the first, the second, …, the n-th variation in the geometric magnitude $\mathcal{A}$, respectively, under the infinitesimal bending $C_{ϵ}$ of the curve C.

It is simply shown that under the second-order infinitesimal bending of the curve, the first and second variations of the line element $ds$ vanish, i.e., $\delta (ds)={\delta }^2(ds)=0$. In paper [27], the first and second variations of some important geometric quantities of the curves were determined.

3. Change in Torsional Energy under Infinitesimal Bending

Let

$$C:\mathbf{r}=\mathbf{r}(s),s\in \mathcal{I},$$

be a biregular curve parameterized by the arc length s. Half of the integral of the square of torsion along $\mathcal{I}$, ie.

$$E_{\tau }={\displaystyle \frac{1}{2}}{\int }_{\mathcal{I}}{\tau }^2(s)ds,$$

is called the torsional energy of the given curve C.

The following theorem is about the change in torsional energy during the infinitesimal bending of the second order.

Theorem 1.

During the infinitesimal bending of the second order of the curve C, the first variation of the torsional energy is

$$\begin{array}{ll}\delta E_{\tau }& ={\int }_{\mathcal{I}}\left\{\left[{\displaystyle \frac{3}{2}}k{\tau }^2+{\displaystyle \frac{{{\tau }^{\prime }}^2}{k}}+2\tau {\left({\displaystyle \frac{{\tau }^{\prime }}{k}}\right)}^{\prime }\right]\stackrel{(1)}{z_1}+\left[{\displaystyle \frac{{\tau }^{\prime }{\tau }^2}{k}}-{(k\tau )}^{\prime }-{\left({\displaystyle \frac{{\tau }^{\prime }}{k}}\right)}^{″}\right]\stackrel{(1)}{z_2}\right\}ds\\ & +{\int }_{\mathcal{I}}\{{\displaystyle \frac{\tau }{k}}(2\tau {\stackrel{(1)}{z_1}}^{\prime }+{\tau }^{\prime }\stackrel{(1)}{z_1}+{\stackrel{(1)}{z_2}}^{″}+(k^2-{\tau }^2)\stackrel{(1)}{z_2})-{\displaystyle \frac{2\tau {\tau }^{\prime }\stackrel{(1)}{z_1}}{k}}-{\displaystyle \frac{{\tau }^{\prime }}{k}}{\stackrel{(1)}{z_2}}^{\prime }\\ & +{\left({\displaystyle \frac{{\tau }^{\prime }}{k}}\right)}^{\prime }\stackrel{(1)}{z_2}+{\displaystyle \frac{1}{2}}{\tau }^2\stackrel{(1)}{z}{\}}^{\prime }ds,\end{array}$$

(6)

where k is the curvature, and τ is the torsion of C.

Proof. 

During bending, the torsional energy changes and has the form

$$E_{\tau ϵ}={\displaystyle \frac{1}{2}}{\int }_{\mathcal{I}}{\tau }_{ϵ}^{2}d{s}_{ϵ}={\displaystyle \frac{1}{2}}{\int }_{\mathcal{I}}{(\tau +ϵ\delta \tau +{ϵ}^2{\delta }^2\tau )}^2(ds+ϵ\delta ds+{ϵ}^2{\delta }^{2}ds).$$

Since the variation of the line element is $\delta ds={\delta }^{2}ds=0$, we have

$$E_{{\tau }_{ϵ}}=E_{\tau }+ϵ{\int }_{\mathcal{I}}{\tau }^2\delta \tau ds+{\displaystyle \frac{1}{2}}{ϵ}^2{\int }_{\mathcal{I}}[{(\delta \tau )}^2+2\tau {\delta }^2\tau ]ds,$$

which is obtained after neglecting the terms with ${ϵ}^3$ and ${ϵ}^4$. Therefore,

$$\delta E_{\tau }={\int }_{\mathcal{I}}\tau \delta \tau ds,{\delta }^2{E}_{\tau }={\displaystyle \frac{1}{2}}{\int }_{\mathcal{I}}[{(\delta \tau )}^2+2\tau {\delta }^2\tau ]ds.$$

(7)

According to [12], the first variation of the torsion is

$$\delta \tau ={\tau }^{\prime }\stackrel{(1)}{z}+2k\tau \stackrel{(1)}{z_1}-k^{\prime }\stackrel{(1)}{z_2}+{\left[{\displaystyle \frac{1}{k}}(2\tau {\stackrel{(1)}{z_1}}^{\prime }+{\tau }^{\prime }\stackrel{(1)}{z_1}+{\stackrel{(1)}{z_2}}^{″}+(k^2-{\tau }^2)\stackrel{(1)}{z_2})\right]}^{\prime }.$$

(8)

Thus, the first variation of the torsional energy is

$$\delta E_{\tau }={\int }_{\mathcal{I}}\left\{\tau {\tau }^{\prime }\stackrel{(1)}{z}+2k{\tau }^2\stackrel{(1)}{z_1}-k^{\prime }\tau \stackrel{(1)}{z_2}+\tau {\left[{\displaystyle \frac{1}{k}}(2\tau {\stackrel{(1)}{z_1}}^{\prime }+{\tau }^{\prime }\stackrel{(1)}{z_1}+{\stackrel{(1)}{z_2}}^{″}+(k^2-{\tau }^2)\stackrel{(1)}{z_2})\right]}^{\prime }\right\}ds.$$

Here, we apply the following transformations:

$${\displaystyle \frac{2\tau {\tau }^{\prime }}{k}}{\stackrel{(1)}{z_1}}^{\prime }={\left({\displaystyle \frac{2\tau {\tau }^{\prime }}{k}}\stackrel{(1)}{z_1}\right)}^{\prime }-{\left({\displaystyle \frac{2\tau {\tau }^{\prime }}{k}}\right)}^{\prime }\stackrel{(1)}{z_1},$$

$${\displaystyle \frac{{\tau }^{\prime }}{k}}{\stackrel{(1)}{z_2}}^{″}={\left[{\displaystyle \frac{{\tau }^{\prime }}{k}}{\stackrel{(1)}{z_2}}^{\prime }-{\left({\displaystyle \frac{{\tau }^{\prime }}{k}}\right)}^{\prime }\stackrel{(1)}{z_2}\right]}^{\prime }+{\left({\displaystyle \frac{{\tau }^{\prime }}{k}}\right)}^{\prime \prime }\stackrel{(1)}{z_2},$$

$$\tau {\tau }^{\prime }\stackrel{(1)}{z}={({\displaystyle \frac{1}{2}}{\tau }^2)}^{\prime }\stackrel{(1)}{z}={\left({\displaystyle \frac{1}{2}}{\tau }^2\stackrel{(1)}{z}\right)}^{\prime }-{\displaystyle \frac{1}{2}}{\tau }^2{\stackrel{(1)}{z}}^{\prime }={\left({\displaystyle \frac{1}{2}}{\tau }^2\stackrel{(1)}{z}\right)}^{\prime }-{\displaystyle \frac{1}{2}}{\tau }^{2}k\stackrel{(1)}{z_1},$$

where we keep in mind the first equation in (5), after which we obtain Equation (6). □

Theorem 2.

During the infinitesimal bending of the second order of the curve C, the second variation of the torsional energy is

$${\delta }^2{E}_{\tau }=I_1+I_2+{\int }_{\mathcal{I}}{\left\{\tau c-{\displaystyle \frac{{\tau }^{\prime }}{k}}\tau \stackrel{(2)}{z_1}-{\displaystyle \frac{{\tau }^{\prime }\tau }{k}}\stackrel{(2)}{z_1}-{\displaystyle \frac{{\tau }^{\prime }}{k}}\stackrel{(2)}{z_2}+{\left({\displaystyle \frac{{\tau }^{\prime }}{k}}\right)}^{\prime }\stackrel{(2)}{z_2}\right\}}^{\prime }ds,$$

(9)

$$\begin{array}{ll}{I}_1& ={\int }_{\mathcal{I}}\{{\displaystyle \frac{1}{2}}{\left\{{\tau }^{\prime }\stackrel{(1)}{z}+2k\tau \stackrel{(1)}{z_1}-k^{\prime }\stackrel{(1)}{z_2}+{\left[{\displaystyle \frac{1}{k}}(2\tau {\stackrel{(1)}{z_1}}^{\prime }+{\tau }^{\prime }\stackrel{(1)}{z_1}+{\stackrel{(1)}{z_2}}^{\prime \prime }+(k^2-{\tau }^2)\stackrel{(1)}{z_2})\right]}^{\prime }\right\}}^2\\ & +{\displaystyle \frac{{\tau }^{\prime }}{k^2}}(k^{\prime }\stackrel{(1)}{z}+{\stackrel{(1)}{z_1}}^{″}+(k^2-{\tau }^2)\stackrel{(1)}{z_1}-2\tau {\stackrel{(1)}{z_2}}^{\prime }-{\tau }^{\prime }\stackrel{(1)}{z_2})(k\tau \stackrel{(1)}{z}+2\tau {\stackrel{(1)}{z_1}}^{\prime }+{\tau }^{\prime }\stackrel{(1)}{z_1}+{\stackrel{(1)}{z_2}}^{″}\\ & -{\tau }^2\stackrel{(1)}{z_2})+\tau f(\stackrel{(1)}{z})\}ds,\end{array}$$

(10)

$$I_2={\int }_{\mathcal{I}}\left\{\left[{\displaystyle \frac{3}{2}}k{\tau }^2+{\displaystyle \frac{{\tau }^{\prime 2}}{k}}+2{\left({\displaystyle \frac{{\tau }^{\prime }}{k}}\right)}^{\prime }\tau \right]\stackrel{(2)}{z_1}+\left[{\displaystyle \frac{{\tau }^{\prime }{\tau }^2}{k}}-{\left({\displaystyle \frac{{\tau }^{\prime }}{k}}\right)}^{″}-{(k\tau )}^{\prime }\right]\stackrel{(2)}{z_2}\right\}ds,$$

(11)

$$\begin{array}{ll}f(\stackrel{(1)}{\mathbf{z}})& =-\tau {(k\stackrel{(1)}{z}+{\stackrel{(1)}{z_1}}^{\prime }-\tau \stackrel{(1)}{z_2})}^2+(k^{\prime }\stackrel{(1)}{z}+{\stackrel{(1)}{z_1}}^{″}+(k^2-{\tau }^2)\stackrel{(1)}{z_1}\\ & -2\tau {\stackrel{(1)}{z_2}}^{\prime }-{\tau }^{\prime }\stackrel{(1)}{z_2})({\stackrel{(1)}{z_2}}^{\prime }+\tau \stackrel{(1)}{z_1}),\end{array}$$

(12)

$$\begin{array}{ll}c=& {\displaystyle \frac{1}{k}}[\tau (k\stackrel{(2)}{z}+{\stackrel{(2)}{z_1}}^{\prime }-\tau \stackrel{(2)}{z_2})+{({\stackrel{(2)}{z_2}}^{\prime }+\tau \stackrel{(2)}{z_1})}^{\prime }-{\displaystyle \frac{1}{k}}(k^{\prime }\stackrel{(1)}{z}+{\stackrel{(1)}{z_1}}^{″}+(k^2-{\tau }^2)\stackrel{(1)}{z_1}\\ & -2\tau {\stackrel{(1)}{z_2}}^{\prime }-{\tau }^{\prime }\stackrel{(1)}{z_2})(k\tau \stackrel{(1)}{z}+2\tau {\stackrel{(1)}{z_1}}^{\prime }+{\tau }^{\prime }\stackrel{(1)}{z_1}+{\stackrel{(1)}{z_2}}^{″}-{\tau }^2\stackrel{(1)}{z_2})]-\tau \stackrel{(2)}{z}+k\stackrel{(2)}{z_2},\end{array}$$

(13)

where k is the curvature, and τ is the torsion of C.

Proof. 

Based on paper [12], the second variation of the torsion is

$$\begin{array}{ll}{\delta }^2\tau & =\left\{{\displaystyle \frac{1}{k}}\left[\tau (k\stackrel{(2)}{z}+{\stackrel{(2)}{z_1}}^{\prime }-\tau \stackrel{(2)}{z_2})+{({\stackrel{(2)}{z_2}}^{\prime }+\tau \stackrel{(2)}{z_1})}^{\prime }-{\displaystyle \frac{1}{k}}(k^{\prime }\stackrel{(1)}{z}+{\stackrel{(1)}{z_1}}^{″}+(k^2-{\tau }^2)\stackrel{(1)}{z_1}\right.\right.\\ & {\left.\left.-2\tau {\stackrel{(1)}{z_2}}^{\prime }-{\tau }^{\prime }\stackrel{(1)}{z_2})(k\tau \stackrel{(1)}{z}+2\tau {\stackrel{(1)}{z_1}}^{\prime }+{\tau }^{\prime }\stackrel{(1)}{z_1}+{\stackrel{(1)}{z_2}}^{\prime \prime }-{\tau }^2\stackrel{(1)}{z_2})\right]-\tau \stackrel{(2)}{z}+k\stackrel{(2)}{z_2}\right\}}^{\prime }\\ & +{\tau }^{\prime }\stackrel{(2)}{z}+2k\tau \stackrel{(2)}{z_1}-k^{\prime }\stackrel{(2)}{z_2}+f(\stackrel{(1)}{\mathbf{z}}),\end{array}$$

(14)

where $f(\stackrel{(1)}{\mathbf{z}})$ is given by Equation (12).

Applying Equations (8) and (14) into Equation (7), we obtain

$$\begin{array}{ll}{\delta }^2{E}_{\tau }& ={\int }_{\mathcal{I}}{\displaystyle \frac{1}{2}}{\left\{{\tau }^{\prime }\stackrel{(1)}{z}+2k\tau \stackrel{(1)}{z_1}-k^{\prime }\stackrel{(1)}{z_2}+{\left[{\displaystyle \frac{1}{k}}\left(2\tau {\stackrel{(1)}{z_1}}^{\prime }+{\tau }^{\prime }\stackrel{(1)}{z_1}+{\stackrel{(1)}{z_2}}^{\prime \prime }+(k^2-{\tau }^2)\stackrel{(1)}{z_2}\right)\right]}^{\prime }\right\}}^{2}ds\\ & +{\int }_{\mathcal{I}}\{{(\tau c)}^{\prime }-{\displaystyle \frac{{\tau }^{\prime }}{k}}[\tau (k\stackrel{(2)}{z}+{\stackrel{(2)}{z_1}}^{\prime }-\tau \stackrel{(2)}{z_2})+{({\stackrel{(2)}{z_2}}^{\prime }+\tau \stackrel{(2)}{z_1})}^{\prime }-{\displaystyle \frac{1}{k}}(k^{\prime }\stackrel{(1)}{z}+{\stackrel{(1)}{z_1}}^{″}\\ & +(k^2-{\tau }^2)\stackrel{(1)}{z_1}-2\tau {\stackrel{(1)}{z_2}}^{\prime }-{\tau }^{\prime }\stackrel{(1)}{z_2})(k\tau \stackrel{(1)}{z}+2\tau {\stackrel{(1)}{z_1}}^{\prime }+{\tau }^{\prime }\stackrel{(1)}{z_1}+{\stackrel{(1)}{z_2}}^{″}-{\tau }^2\stackrel{(1)}{z_2})]\\ & +\tau {\tau }^{\prime }\stackrel{(2)}{z}-\tau {\tau }^{\prime }\stackrel{(2)}{z_2}+\tau {\tau }^{\prime }\stackrel{(2)}{z}+2k{\tau }^2\stackrel{(2)}{z_1}-k^{\prime }\tau \stackrel{(2)}{z_2}+\tau f(\stackrel{(1)}{\mathbf{z}})\}ds,\end{array}$$

where c denotes the following expression:

$$\begin{array}{ll}c=& {\displaystyle \frac{1}{k}}[\tau (k\stackrel{(2)}{z}+{\stackrel{(2)}{z_1}}^{\prime }-\tau \stackrel{(2)}{z_2})+{({\stackrel{(2)}{z_2}}^{\prime }+\tau \stackrel{(2)}{z_1})}^{\prime }-{\displaystyle \frac{1}{k}}(k^{\prime }\stackrel{(1)}{z}+{\stackrel{(1)}{z_1}}^{″}+(k^2-{\tau }^2)\stackrel{(1)}{z_1}\\ & -2\tau {\stackrel{(1)}{z_2}}^{\prime }-{\tau }^{\prime }\stackrel{(1)}{z_2})(k\tau \stackrel{(1)}{z}+2\tau {\stackrel{(1)}{z_1}}^{\prime }+{\tau }^{\prime }\stackrel{(1)}{z_1}+{\stackrel{(1)}{z_2}}^{″}-{\tau }^2\stackrel{(1)}{z_2})]-\tau \stackrel{(2)}{z}+k\stackrel{(2)}{z_2}.\end{array}$$

After several transformations, using condition (5) and extracting the terms containing the first-order bending field separately from the terms containing the second-order bending field, as well as the expression that is the total differential, we obtain expression (9) for the second-order variation of the torsional energy. □

In the case of the infinitesimal bending of knots, we specify the condition $\stackrel{(1)}{\mathbf{z}}(0)=\stackrel{(1)}{\mathbf{z}}(L)$, $\stackrel{(2)}{\mathbf{z}}(0)=\stackrel{(2)}{\mathbf{z}}(L)$ for the infinitesimal bending fields in order to obtain a family of closed curves. Also, we suppose that the knot and the infinitesimal bending fields are sufficiently smooth. Keeping this in mind, we have the following corollary.

Corollary 1.

During the infinitesimal bending of the second order of the knot C, the first and the second variations of the torsional energy are, respectively, as follows:

$$\delta E_{\tau }={\int }_{\mathcal{I}}\left\{\left[{\displaystyle \frac{3}{2}}k{\tau }^2+{\displaystyle \frac{{\tau }^{\prime 2}}{k}}+2\tau {\left({\displaystyle \frac{{\tau }^{\prime }}{k}}\right)}^{\prime }\right]\stackrel{(1)}{z_1}+\left[{\displaystyle \frac{{\tau }^{\prime }{\tau }^2}{k}}-{(k\tau )}^{\prime }-{\left({\displaystyle \frac{{\tau }^{\prime }}{k}}\right)}^{″}\right]\stackrel{(1)}{z_2}\right\}ds,$$

$${\delta }^2{E}_{\tau }=I_1+I_2,$$

where k is the curvature, τ is the torsion of C, and $I_1$ and $I_2$ are given by Equations (10) and (11).

Finally, for plane curves, we have the following corollary.

Corollary 2.

The first and second variation of the torsional energy of a plane curve (not necessarily closed) are, respectively, as follows:

$$\delta E_{\tau }=0,$$

$${\delta }^2{E}_{\tau }={\int }_{\mathcal{I}}{\displaystyle \frac{1}{2}}{\left\{-k^{\prime }\stackrel{(1)}{z_2}+{\left[{\displaystyle \frac{1}{k}}\left({\stackrel{(1)}{z_2}}^{\prime \prime }+k^2\stackrel{(1)}{z_2}\right)\right]}^{\prime }\right\}}^{2}ds.$$

We see that, unlike the first variation, the second variation of the torsional energy for a plane curve is non-zero in the general case. In particular, for $\stackrel{(1)}{z_2}=0$, the second variation is zero for any plane curve. In that case, we determine the other components of the fields $\stackrel{(1)}{\mathbf{z}}$ and $\stackrel{(2)}{\mathbf{z}}$ from the equations ${\stackrel{(1)}{z}}^{\prime }-k\stackrel{(1)}{z_1}=0,$ and ${\stackrel{(2)}{z}}^{\prime }-k\stackrel{(2)}{z_1}=-{\displaystyle \frac{1}{2}}{(k\stackrel{(1)}{z}+{\stackrel{(1)}{z_1}}^{\prime })}^2$.

4. Second-Order Infinitesimal Bending of Torus Knots

During infinitesimal bending, the torus knots generally do not stay at the initial torus. In this section, we will examine the conditions under which the second-order infinitesimal bending of torus knots remains at the initial torus with a given precision.

Let

$$\begin{array}{cc}& x(u)=(\cos (qu)+a)·\cos (pu)\\ C:\mathbf{r}(u):& y(u)=(\cos (qu)+a)·sin(pu)\\ & z(u)=-sin(qu)\hfill \end{array}$$

(15)

be a $(p,q)-$ torus knot, $0\le u\le 2\pi$, that lies on the torus

$$S:{(a-\sqrt{x^2+y^2})}^2+z^2=1^2.$$

Let

$$\begin{array}{cc}& x_{ϵ}(u)=(\cos (qu)+a)·\cos (pu)+ϵ\stackrel{(1)}{z_1}(u)+{ϵ}^2\stackrel{(2)}{z_1}(u)\\ C_{ϵ}:{\mathbf{r}}_{ϵ}(u):& y_{ϵ}(u)=(\cos (qu)+a)·sin(pu)+ϵ\stackrel{(1)}{z_2}(u)+{ϵ}^2\stackrel{(2)}{z_2}(u)\\ & z_{ϵ}(u)=-sin(qu)+ϵ\stackrel{(1)}{z_3}(u)+{ϵ}^2\stackrel{(2)}{z_3}(u)\hfill \end{array}$$

(16)

be the infinitesimal bending of C, where $\stackrel{(1)}{\mathbf{z}}(u)=(\stackrel{(1)}{z_1}(u),\stackrel{(1)}{z_2}(u),\stackrel{(1)}{z_3}(u))$ and $\stackrel{(2)}{\mathbf{z}}(u)=(\stackrel{(2)}{z_1}(u),\stackrel{(2)}{z_2}(u),\stackrel{(2)}{z_3}(u))$ are the first- and the second-order infinitesimal bending fields, respectively. According to Equation (3), the necessary and sufficient condition for the infinitesimal bending of the second order reads

$${\mathbf{r}}^{.}·\stackrel{(1)}{{\mathbf{z}}^{.}}=0,2{\mathbf{r}}^{.}·\stackrel{(2)}{{\mathbf{z}}^{.}}+\stackrel{(1)}{{\mathbf{z}}^{.}}·\stackrel{(1)}{{\mathbf{z}}^{.}}=0,$$

(17)

where dot denotes derivative with respect to u.

If we substitute

$$F(x,y,z)={(a-\sqrt{x^2+y^2})}^2+z^2-1^2,$$

then the torus knot satisfies the implicit equation of the torus S,

$$F(x(u),y(u),z(u))=0.$$

We require that the bent curves be at the initial torus S with a given precision, i.e., we set the following condition:

$$F(x_{ϵ}(u),y_{ϵ}(u),z_{ϵ}(u))=o({ϵ}^2),$$

(18)

where $o({ϵ}^2)$ is an infinitesimal of an order higher than 2 with respect to $ϵ$. Using the previous condition, Equation (16), and the Maclaurin series, we obtain the following equations:

$$\cos (qu)(\cos (pu)\stackrel{(1)}{z_1}(u)+sin(pu)\stackrel{(1)}{z_2}(u))-sin(qu)\stackrel{(1)}{z_3}(u)=0,$$

(19)

$$\begin{gathered} \cos (qu)(\cos (pu)\stackrel{(2)}{z_1}(u)+sin(pu)\stackrel{(2)}{z_2}(u))-sin(qu)\stackrel{(2)}{z_3}(u)= \\ ={\displaystyle \frac{a}{2(\cos (qu)+a)}}{(sin(pu)\stackrel{(1)}{z_1}(u)-\cos (pu)\stackrel{(1)}{z_2}(u))}^2-{\displaystyle \frac{1}{2}}{\parallel \stackrel{(1)}{\mathbf{z}}(u)\parallel }^2. \end{gathered}$$

(20)

Thus, we proved the following theorem.

Theorem 3.

The necessary and sufficient conditions for the fields $\stackrel{(1)}{\mathbf{z}}(u)=(\stackrel{(1)}{z_1}(u),\stackrel{(1)}{z_2}(u),\stackrel{(1)}{z_3}(u))$ and $\stackrel{(2)}{\mathbf{z}}(u)=(\stackrel{(2)}{z_1}(u),\stackrel{(2)}{z_2}(u),\stackrel{(2)}{z_3}(u))$ to include $(p,q)$ torus knot (15) into the family of deformed curves on the torus with precision (18) is that Equations (19) and (20) are satisfied.

Now, let us find particular bending fields that satisfy (17). Let us look for a field of the first order in the form

$$\stackrel{(1)}{\mathbf{z}}(u)=(-tan(pu)\stackrel{(1)}{z_2}(u),\stackrel{(1)}{z_2}(u),0).$$

Based on the first equation in (17), we obtain a homogenous linear differential equation

$$\stackrel{(1)}{z_2^{.}}(u)+\left({\displaystyle \frac{qsin(qu)}{\cos (qu)+a}}+{\displaystyle \frac{psin(pu)}{\cos (pu)}}\right)\stackrel{(1)}{z_2}(u)=0$$

whose solution is

$$\stackrel{(1)}{z_2}(u)=c(\cos (qu)+a)\cos (pu),$$

and c is a constant. So,

$$\stackrel{(1)}{\mathbf{z}}(u)=(-csin(pu)(\cos (qu)+a),c\cos (pu)(\cos (qu)+a),0).$$

Let us look for the field of the second order in the form

$$\stackrel{(2)}{\mathbf{z}}(u)=(0,0,\stackrel{(3)}{z}(u))$$

and find $\stackrel{(3)}{z}(u)$. After some calculations in the second equation of (17), we obtain

$$\stackrel{(3)}{z}(u)={\displaystyle \frac{c^2{p}^2}{2q}}\int {\displaystyle \frac{{(\cos (qu)+a)}^2}{\cos (qu)}}du+{\displaystyle \frac{c^{2}q}{2}}\int {\displaystyle \frac{{sin}^2(qu)}{\cos (qu)}}du.$$

Finally, by integration, we obtain

$$\stackrel{(3)}{z}(u)={\displaystyle \frac{c^2}{2}}\left({\displaystyle \frac{p^2}{q^2}}-1\right)sin(qu)+{\displaystyle \frac{c^2{p}^{2}a}{q}}u+{\displaystyle \frac{c^2}{4}}\left({\displaystyle \frac{p^2{a}^2}{q^2}}+1\right)ln|{\displaystyle \frac{1+sin(qu)}{1-sin(qu)}}|+const.$$

It can be shown that all bent curves under these fields are on the initial torus with the precision determined by the equation

$$F(x_{ϵ}(u),y_{ϵ}(u),z_{ϵ}(u))=o(ϵ).$$

Also, it is easy to check that this is the second-order infinitesimal bending, i.e., that conditions (17) are valid.

5. Torsional Energy of Torus Knots—Examples and Visualization

Our topic is knotted curves lying on a torus, defined by a parametric equation. Infinitesimal bending on knots affects their shape as well as on their geometrical magnitudes. Our aim is to calculate and visualize this influence both in deformed shape and belonging to the torsion. We will visualize the shape of knotted curves before and after infinitesimal bending fields deform the curves. We calculate the torsion of curves for basic and deformed curves. Through examples, we give figures containing the presented curves, where we use colors to indicate the values of torsion at different points of the curves. For every example, we calculated a range of torsion values at points and then mapped that range to a color scale. Points on curves are colored according the torsion value mapped to an appropriate color. We also calculated numerically torsional energy for basic and deformed knotted curves.

There are several approaches for calculating and visualizing curves. It is possible to hardcode the curve definition as an appropriate function in a programming code in some programming language, and then manually, on paper, calculate derivations and all necessary mathematical expressions and hardcode them in a program. In this way, for any changes in curve definition, the infinitesimal bending fields, or any mathematical expression, one should again manually calculate and change the program. Another approach suggests using some software package that is capable of carrying out symbolic, numeric, and visualizing activities, like Mathematica or Matlab. We decided to develop our own software that can perform the needed calculations and is capable of carrying out some symbolic and numeric operations, with additional result visualization capabilities.

We intended to obtain flexibility for defining curves and bending fields by allowing the software user to enter strings representing them. Then, the string representations are divided lexically, and then analyzed semantically, and finally, we built the appropriate expression tree for the entered function. An expression tree is built of nodes: one node for each operation, mentioned elementary function, or part of an expression (variables and constants). With some more info of used variables, we built the so-called internal form for every function we had to deal with: curve parametric definitions and the bending fields of the first and second order. We used the obtained expression tree for calculating function values easily and effectively by passing values for variables, and every node in the expression tree can conduct the appropriate calculation, and the result of the calculation is passed up to the parent node and finally to the tree root with the final result. The expression tree is also a kind of object-oriented tree that is capable of two important things: giving a new expression tree that represents a derivative over some variables and giving the string function representation of itself. With these abilities, we can automatize forming necessary functions for unit tangent, binormal, and necessary symbolical calculations. Developed software do not have the ability of symbolical integration, but we solved such tasks using numerical integration.

Such an approach further allowed us to convert a string representation to our internal representation based on the expression tree and vice versa. A software user can enter strings that define curves and bending fields (in parametric representation) that include arbitrary elementary functions. After that, on the user’s demand (on a button click), the software can perform all the other necessary activities: parsing, building expression trees, calculating function values, creating a 3D model of curves, and representing colored curves.

The visualization of an obtained curve is based on a polygonal line that connects points on a curve. At every such point, we should calculate the following functions: the curve; the first, second, and third derivative; and also the local values of torsion. This is necessary to obtain the transformed shape of the curve and for curve coloring. For the purpose of calculating integrals numerically, we also perform the same calculations at every subdivision point. For the sake of efficiency, we transform strings to their internal function form once, and then evaluate it as many times as we need, according to the principle “parse once, evaluate many times”. Our software tool is written in Microsoft Visual C++ (VS 2022). The 3D modeling and visualization with semitransparent objects are carried out in OpenGL (1.5). For better visibility, the curves have a tube around them.

5.1. Torus Knot $p=2$, $q=3$

Let us consider a torus knot for values $p=2$, $q=3$, and $a=2$, which is defined by the following parametric equations: $x(u)=(\cos (3u)+2)·\cos (2u)$, $y(u)=(\cos (3u)+2)·sin(2u)$, $z(u)=-sin(3u)$.

The fields of the first- and second-order infinitesimal bending are given by $\stackrel{(1)}{\mathbf{z}}(u)$$(\stackrel{(1)}{z_1}(u)=(\cos (3u)+2)·sin(2u),\stackrel{(1)}{z_2}(u)=-(\cos (3u)+2)·\cos (2u),\stackrel{(1)}{z_3}(u)=0)$ and $\stackrel{(2)}{\mathbf{z}}(u)$$(\stackrel{(2)}{z_1}(u)=-0.5·(\cos (3u)+2)·\cos (2u),\stackrel{(2)}{z_2}(u)=-0.5·(\cos (3u)+2)·sin(2u),\stackrel{(2)}{z_3}(u)=0)$.

It is easy to check that infinitesimal bending fields satisfy conditions given by (17). The basic $p=2,q=3$ knot and bent curve are shown in Figure 1, Figure 2 and Figure 3. Knots are colored according to the values of torsion mapped to a color on a color scale.

We calculated the torsional energy of the $p=2$, $q=3$ knot, and it is 13.3482 for $ϵ=0$ and 12.9334 for $ϵ=1.0$.

5.2. Torus Knot $p=2$, $q=5$

Let us consider a torus knot for values $p=2$, $q=5$, and $a=2$, which is defined by the following parametric equations: $x(u)=(\cos (5u)+2)·\cos (2u)$, $y(u)=(\cos (5u)+2)·sin(2u)$, $z(u)=-sin(5u)$.

The fields of the first- and second-order infinitesimal bending are given by $\stackrel{(1)}{\mathbf{z}}(u)$$(\stackrel{(1)}{z_1}(u)=(\cos (5u)+2)·sin(2u),\stackrel{(1)}{z_2}(u)=-(\cos (5u)+2)·\cos (2u),\stackrel{(1)}{z_3}(u)=0)$ and $\stackrel{(2)}{\mathbf{z}}(u)$$(\stackrel{(2)}{z_1}(u)=-0.5·(\cos (5u)+2)·\cos (2u),\stackrel{(2)}{z_2}(u)=-0.5·(\cos (5u)+2)·sin(2u),\stackrel{(2)}{z_3}(u)=0)$. The infinitesimal bending fields satisfy conditions given by (17). The basic $p=2$, $q=5$ knot and bent curve are shown in Figure 4, Figure 5 and Figure 6.

The knots are colored according to the values of torsion mapped to a color on a color scale. We calculated the torsional energy of the $p=2$, $q=5$ knot, and it is 10.521 for $ϵ=0$ and 10.522 for $ϵ=0.4$.

5.3. Torus Knot $p=3$, $q=4$

Let us consider a torus knot for values $p=3$, $q=4$, and $a=2$, which is defined by the following parametric equations: $x(u)=(\cos (4u)+2)·\cos (3u)$, $y(u)=(\cos (4u)+2)·sin(3u)$, $z(u)=-sin(4u)$.

The fields of the first- and second-order infinitesimal bending are given by $\stackrel{(1)}{\mathbf{z}}(u)$$(\stackrel{(1)}{z_1}(u)=-sin(4u),\stackrel{(1)}{z_2}(u)=0,\stackrel{(1)}{z_3}(u)=-(\cos (4u)+2)·\cos (3u))$ and $\stackrel{(2)}{\mathbf{z}}(u)$$(\stackrel{(2)}{z_1}(u)=-0.5·(\cos (4u)+2)·\cos (3u),\stackrel{(2)}{z_2}(u)=-0.5·(\cos (4u)+2)·sin(3u),\stackrel{(2)}{z_3}(u)=0)$. It is easy to check that the infinitesimal bending fields satisfy the conditions given by (17). The basic $p=3$, $q=4$ knot and bent curve are shown in Figure 7, Figure 8 and Figure 9.

The knots are colored according to the values of torsion mapped to a color on a color scale. We calculated the torsional energy of the $p=3,q=4$ knot, and it is 21.8222 for $ϵ=0$ and 21.3129 for $ϵ=0.7$.

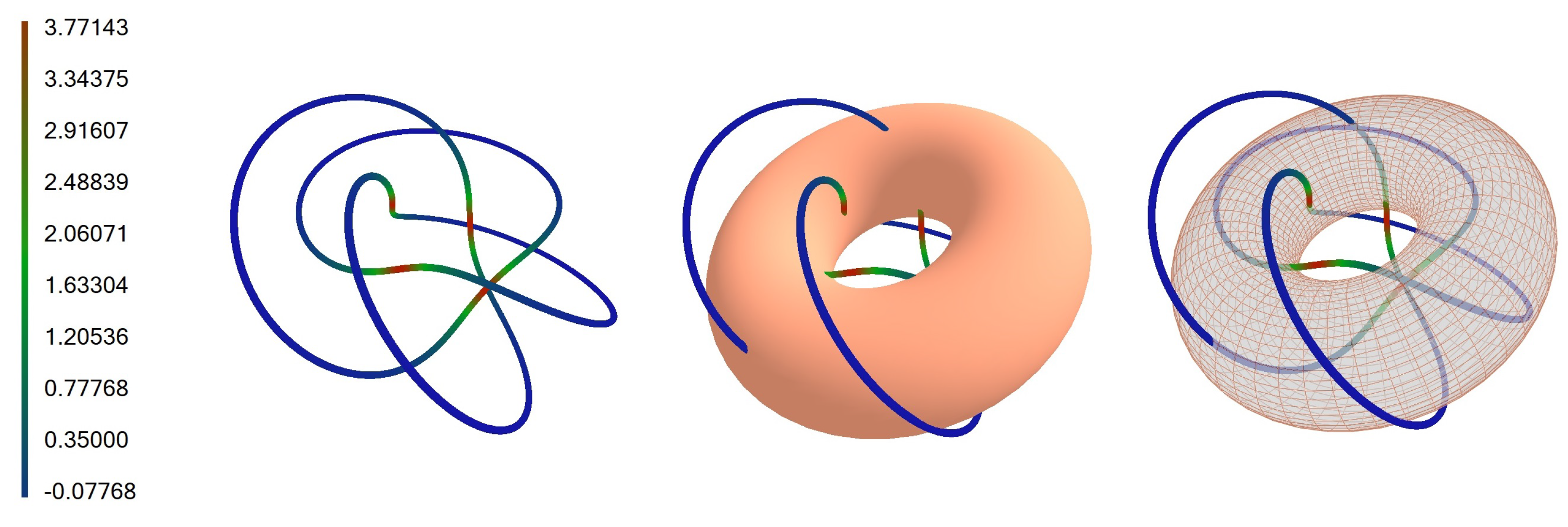
5.4. Torus Knot $p=2$, $q=7$

Let us consider a torus knot for values $p=2$, $q=7$, and $a=2$, which is defined by the following parametric equations: $x(u)=(\cos (7u)+2)·\cos (2u)$, $y(u)=(\cos (7u)+2)·sin(2u)$, $z(u)=-sin(7u)$.

The fields of the first- and second-order infinitesimal bending are given by $\stackrel{(1)}{\mathbf{z}}(u)$$(\stackrel{(1)}{z_1}(u)=(\cos (7u)+2)·sin(2u),\stackrel{(1)}{z_2}(u)=-(\cos (7u)+2)·\cos (2u),\stackrel{(1)}{z_3}(u)=0)$ and $\stackrel{(2)}{\mathbf{z}}(u)$$(\stackrel{(2)}{z_1}(u)=-0.5·(\cos (7u)+2)·\cos (2u),\stackrel{(2)}{z_2}(u)=-0.5·(\cos (7u)+2)·sin(2u),\stackrel{(2)}{z_3}(u)=0)$. The infinitesimal bending fields satisfy the conditions given by (17). The basic $p=2$, $q=7$ knot and bent curve are shown in Figure 10, Figure 11 and Figure 12.

The knots are colored according to the values of torsion mapped to a color on a color scale. We calculated the torsional energy of the $p=2$, $q=7$ knot, and it is 8.657 for $ϵ=0$ and 8.591 for $ϵ=0.95$.

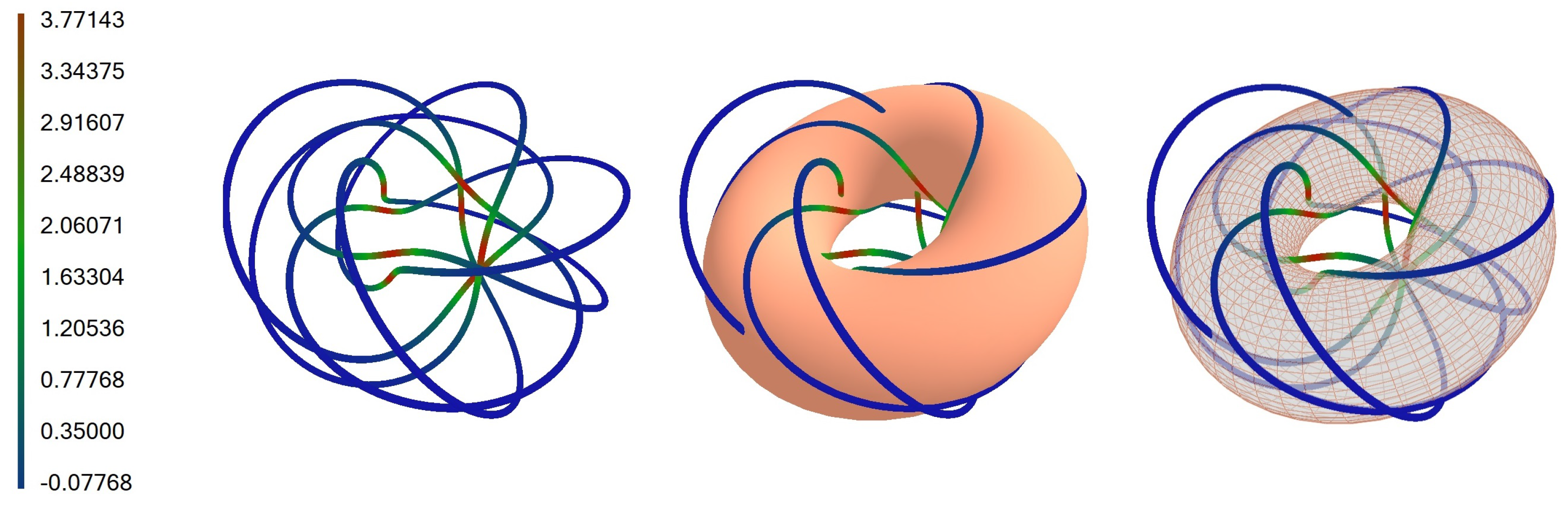
5.5. Torus Knot $p=3$, $q=5$

Let us consider a torus knot for values $p=3$, $q=5$, and $a=2$, which is defined by the following parametric equations: $x(u)=(\cos (5u)+2)·\cos (3u)$, $y(u)=(\cos (5u)+2)·sin(3u)$, $z(u)=-sin(5u)$.

The fields of the first- and second-order infinitesimal bending are given by $\stackrel{(1)}{\mathbf{z}}(u)$$(\stackrel{(1)}{z_1}(u)=(\cos (5u)+2)·sin(3u),\stackrel{(1)}{z_2}(u)=-(\cos (5u)+2)·\cos (3u),\stackrel{(1)}{z_3}(u)=0)$ and $\stackrel{(2)}{\mathbf{z}}(u)$$(\stackrel{(2)}{z_1}(u)=-0.5·(\cos (5u)+2)·\cos (3u),\stackrel{(2)}{z_2}(u)=-0.5·(\cos (5u)+2)·sin(3u),\stackrel{(2)}{z_3}(u)=0)$. The infinitesimal bending fields satisfy the conditions given by (17). The basic $p=3$, $q=5$ knot and bent curve are shown in Figure 13, Figure 14 and Figure 15.

The knots are colored according to the values of torsion mapped to a color on a color scale. We calculated the torsional energy of the $p=3$, $q=5$ knot, and it is 18.975 for $ϵ=0$ and 18.746 for $ϵ=0.85$.

6. Discussion and Conclusions

In this paper, we examined the change in the torsional energy of the curves in the case of infinitesimal bending as a special type of deformation that preserves the arc length with a certain precision. The restriction we set is to preserve the arc length with the adopted accuracy described by Equation (2). This means that the change in the arc length is of an order higher than two with respect to an infinitesimal $ϵ$. We paid special attention to knots, with a more detailed examination of torus knots, which were analyzed both analytically and graphically. In addition to explicitly defined formulas for the variation in torsional energy, we calculated numerical values for specific examples that allow us to better understand the changes in energy that occur during deformation.

Our method is applicable both for arbitrary biregular curves and for knots as closed curves without self-intersection. However, it should be kept in mind that the choice of bending field is not always simple. Namely, under the influence of some fields, the curve may break or self-intersect, which is not always in our interest, especially in the case of knots. This is why it is necessary to take this into account when observing special deformation.

In addition to the mentioned research and obtained results, this paper opens up new research questions. For instance, it would be interesting to consider the torsional energy variations of other space curves and, for example, of some spherical curves or helices. Also, some results and/or conjectures about characterizations of the critical curves of the respected variations could be considered.