Higher-Order INAR Model Based on a Flexible Innovation and Application to COVID-19 and Gold Particles Data
Abstract
:1. Introduction
2. The INAR(1) Process with the PEE Innovations
The PEE-INAR(1) Model
3. The INAR(p) Model with PEE Innovations
4. Estimation
4.1. Conditional Maximum Likelihood
4.2. Conditional Least Squares
5. Simulation Study
6. Empirical Study
- (i)
- INAR model based on the discrete Teissier innovations (DT-INAR), see [29].
- (ii)
- INAR model based on the binomial-discrete Poisson Lindley innovations (BDPL-INAR), see [30].
- (iii)
- INAR model based on the three parameter discrete-Lindley innovations (DLi3-INAR), see [31].
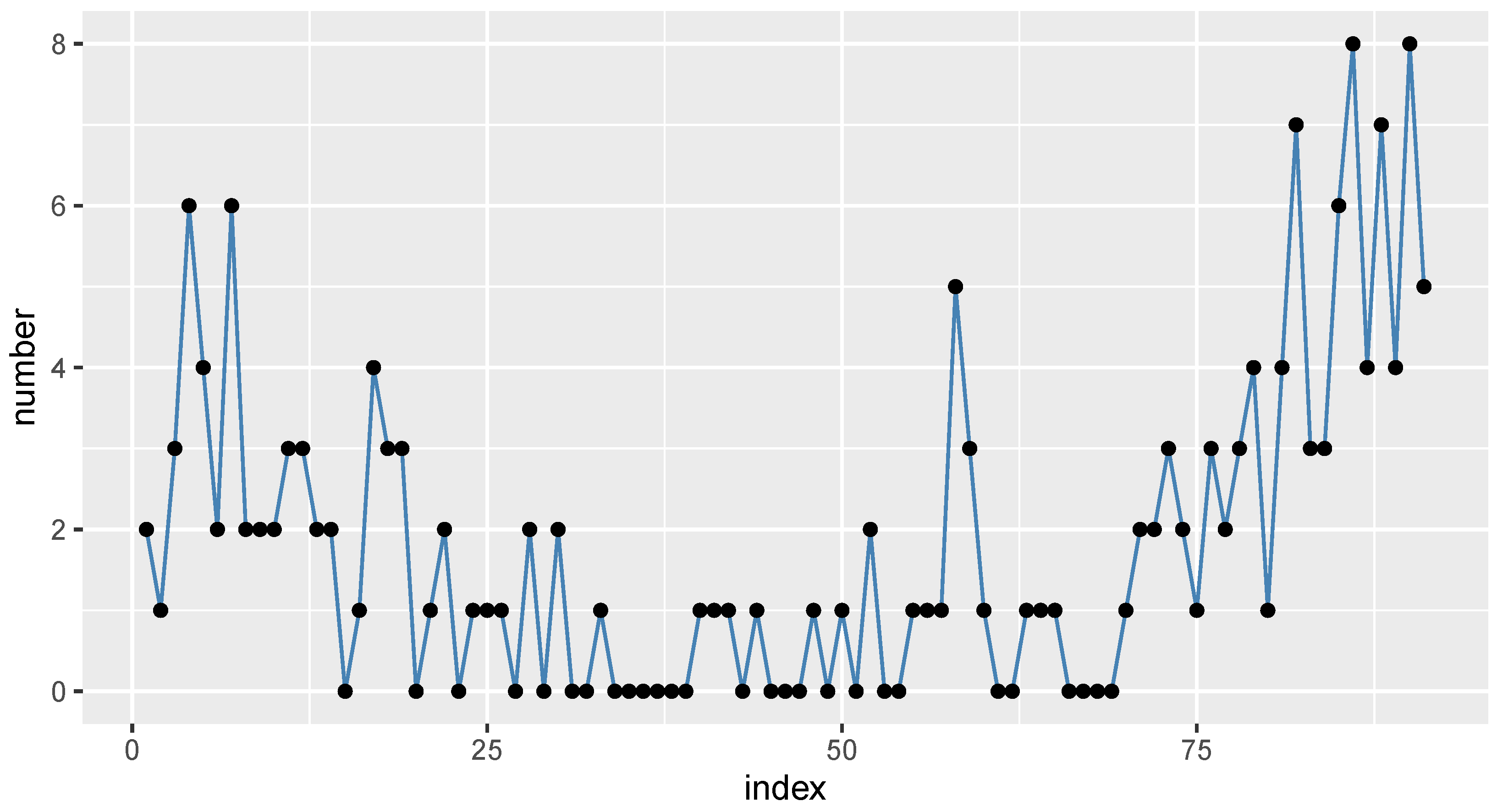
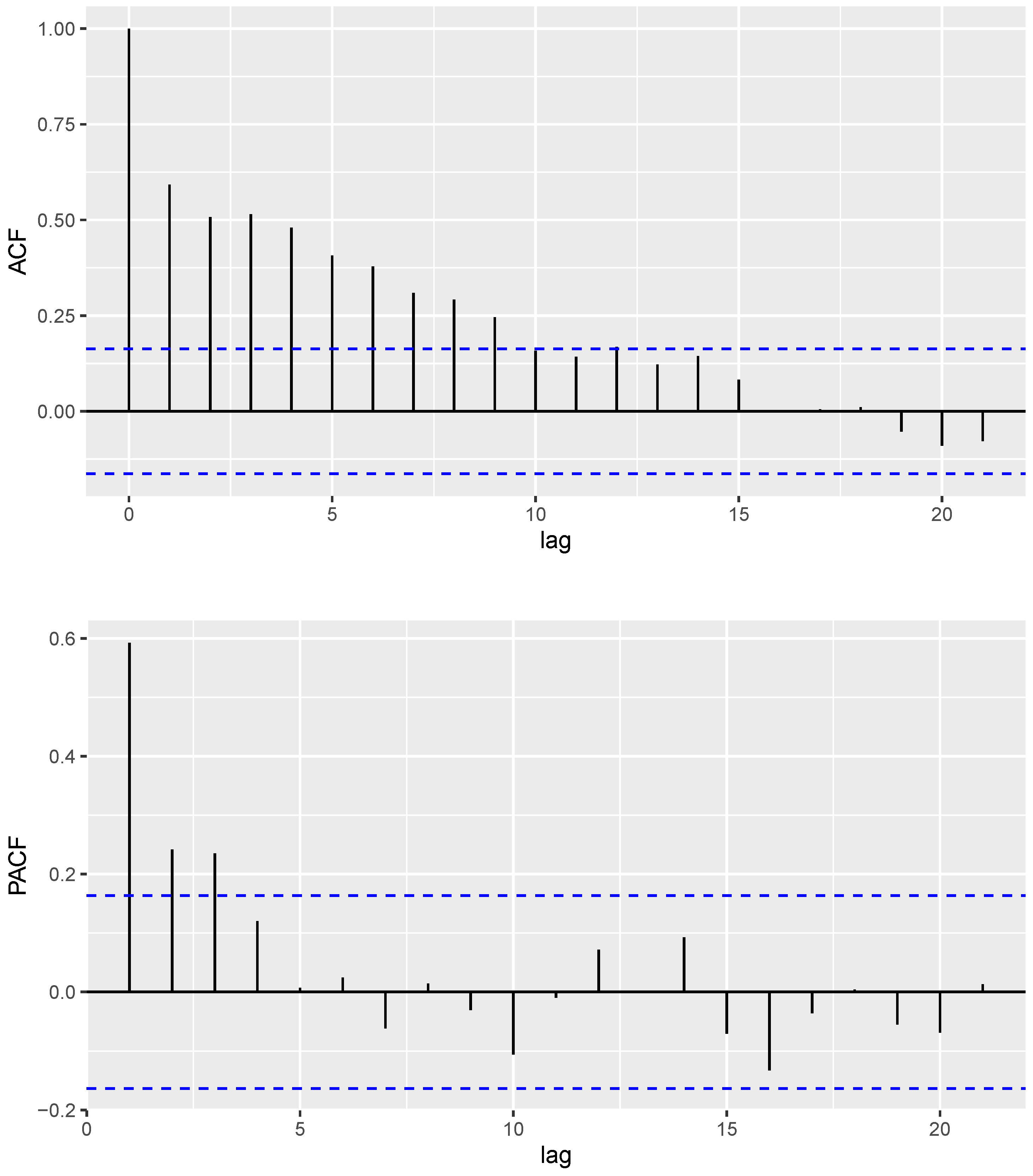
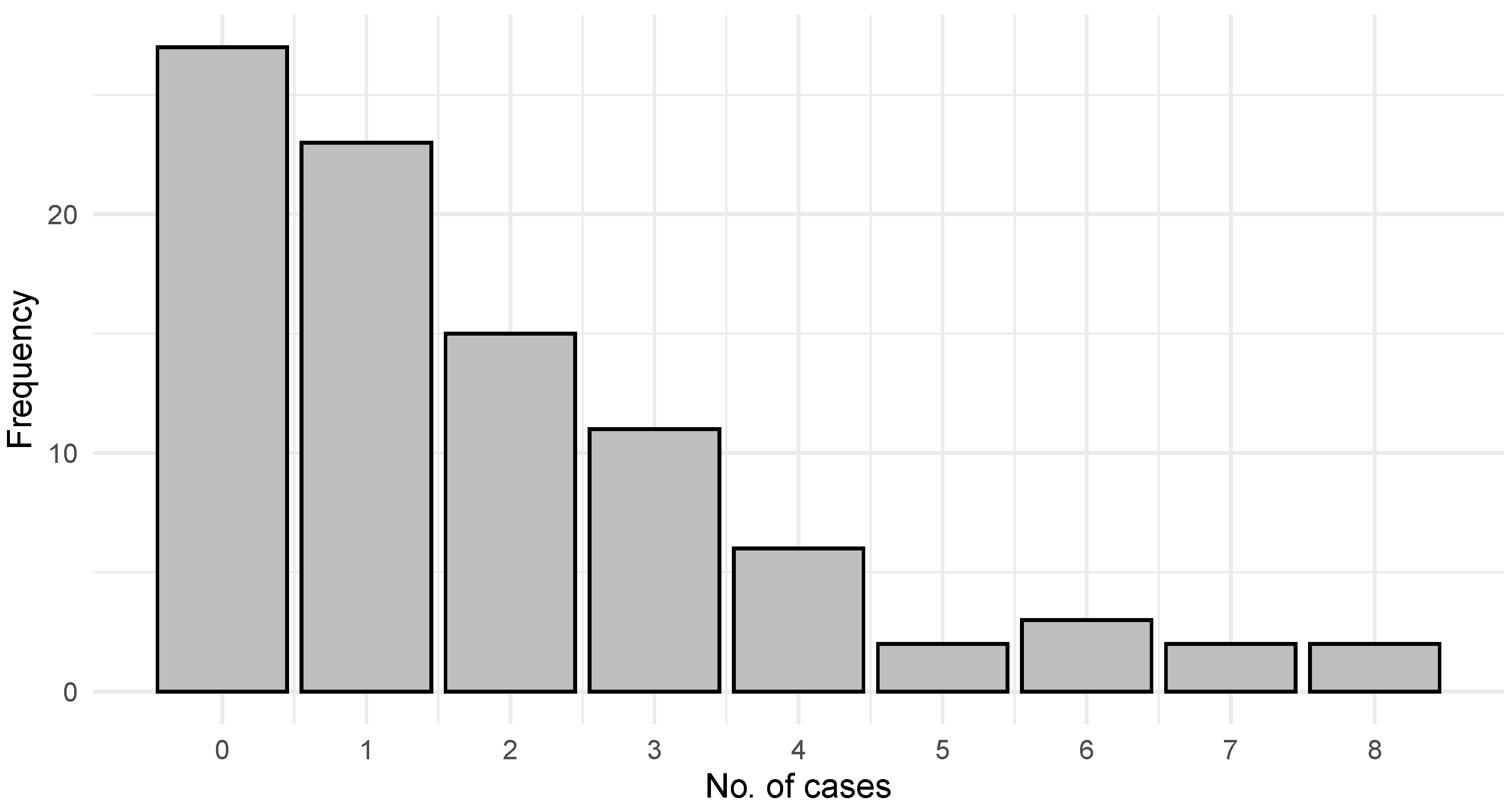
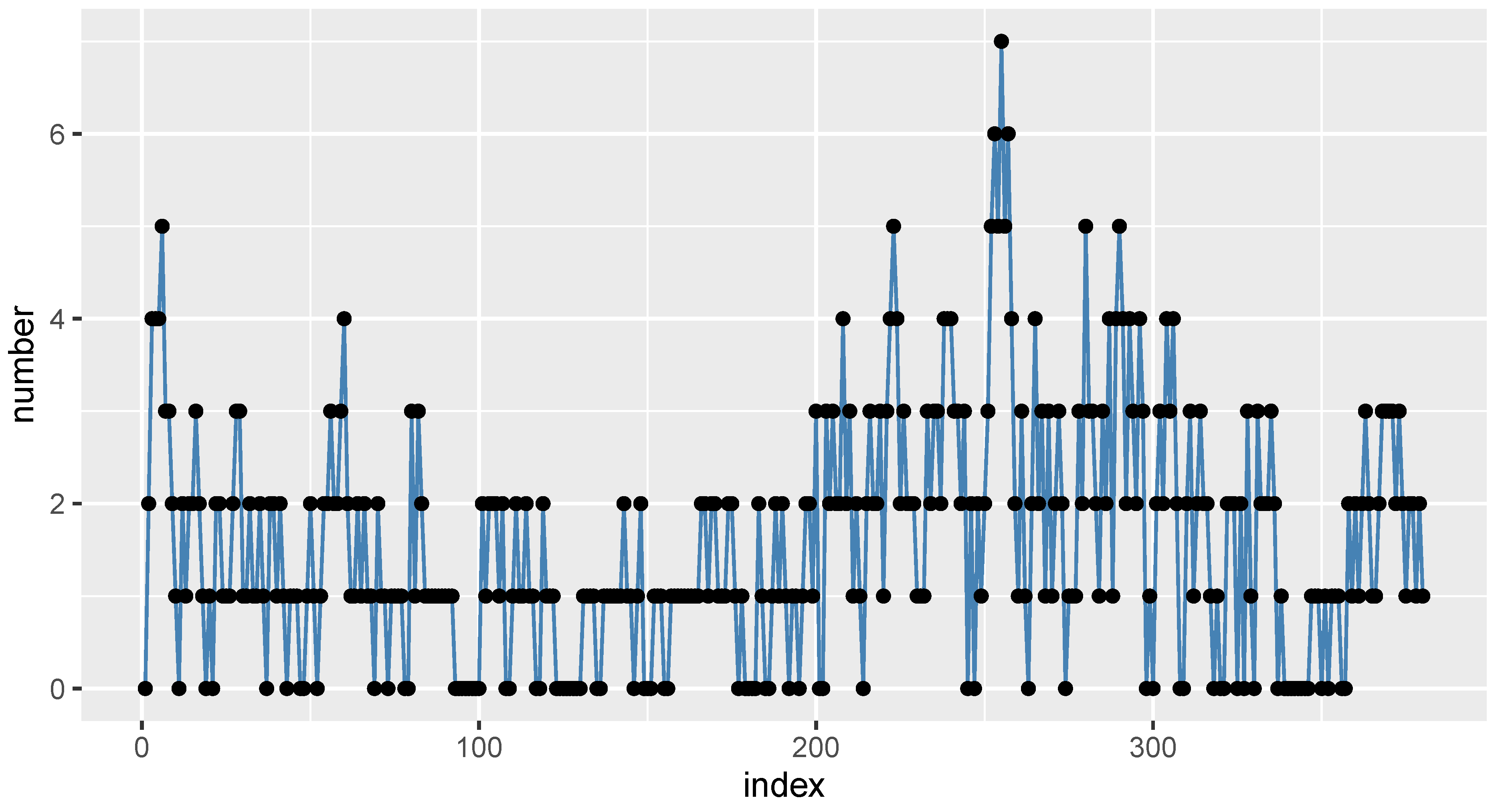
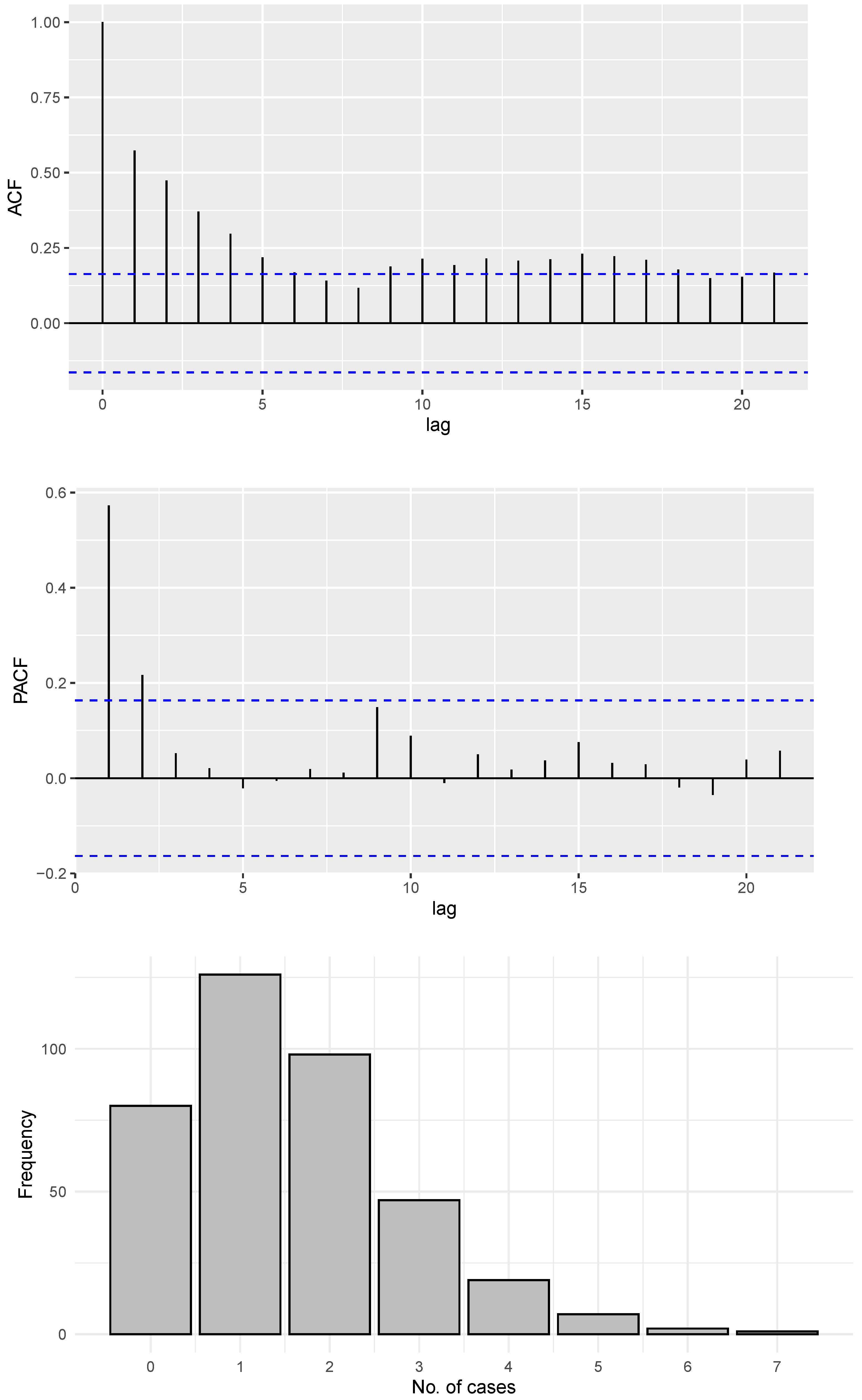
6.1. COVID-19 Data
6.2. Gold Particles Data
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- ppois=function(x,lambda,theta){
- f=1-(((lambda+1)^(-(x+2))∗(lambda+lambda^2+theta+(x+2)∗lambda∗theta)
- )
- /(lambda+theta))
- return(f)
- }
- ppois(2,0.5,1)
- rpois <- function(n, L,T)
- {
- U <- runif(n)
- X <- rep(0,n)
- # loop through each uniform
- for(i in 1:n)
- {
- # first check if you are in the first interval
- if(U[i] < ppois(0,L,T))
- {
- X[i] <- 0
- } else
- {
- # while loop to determine which subinterval,I, you
- are in
- # terminated when B = TRUE
- B = FALSE
- I = 0
- while(B == FALSE)
- {
- # the interval to check
- int <- c( ppois(I, L,T), ppois(I+1,L,T) )
- # see if the uniform is in that interval
- if( (U[i] > int[1]) & (U[i] < int[2]) )
- {
- # if so, quit the while loop and store
- the value
- X[i] <- I+1
- B = TRUE
- } else
- {
- # If not, continue the while loop and
- increase I by 1
- I=I+1
- }
- }
- }
- }
- return(X)
- }
- rpois(50, 1.5, 1.2)
- r.inarp.sim <- function(n, order.max, alpha,lambda,theta){
- x <- rep(NA, times = n)
- error <- rpois(n, lambda, theta)
- for (i in 1:order.max) {
- x[i] <- error[i]
- }
- for (t in (order.max + 1):n) {
- x[t] <- 0
- for (j in 1:order.max) {
- x[t] <- x[t] + rbinom(1, x[t - j], alpha[j])
- }
- x[t] <- x[t] + error[t]
- }
- return(x)
- }
- r.inarp.sim(n = 100, order.max = 2, alpha = c(0.1,0.4),lambda = 2,theta
- =0.5)
References
- McKenzie, E. Some simple models for discrete variate time series 1. Jawra J. Am. Water Resour. Assoc. 1985, 21, 645–650. [Google Scholar] [CrossRef]
- Al-Osh, M.A.; Alzaid, A.A. First-order integer-valued autoregressive (INAR(1)) process. J. Time Ser. Anal. 1987, 8, 261–275. [Google Scholar] [CrossRef]
- McKenzie, E. Some ARMA models for dependent sequences of Poisson counts. Adv. Appl. Probab. 1988, 20, 822–835. [Google Scholar] [CrossRef]
- Ristić, M.M.; Bakouch, H.S.; Nastić, A.S. A new geometric first-order integer-valued autoregressive (NGINAR(1)) process. J. Stat. Plan. Inference 2009, 139, 2218–2226. [Google Scholar] [CrossRef]
- Bakouch, H.S.; Ristić, M.M. Zero truncated Poisson integer-valued AR(1) model. Metrika 2010, 72, 265–280. [Google Scholar] [CrossRef]
- Schweer, S.; Weiß, C.H. Compound Poisson INAR(1) processes: Stochastic properties and testing for overdispersion. Comput. Stat. Data Anal. 2014, 77, 267–284. [Google Scholar] [CrossRef]
- Bourguignon, M.; Vasconcellos, K.L. First order non-negative integer valued autoregressive processes with power series innovations. Braz. J. Probab. Stat. 2015, 29, 71–93. [Google Scholar] [CrossRef]
- Lívio, T.; Khan, N.M.; Bourguignon, M.; Bakouch, H.S. An INAR(1) model with Poisson–Lindley innovations. Econ. Bull. 2018, A, 1505–1513. [Google Scholar]
- Aghababaei Jazi, M.; Jones, G.; Lai, C.D. Integer valued AR(1) with geometric innovations. J. Iran. Stat. Soc. 2012, 11, 173–190. [Google Scholar]
- Altun, E.; Bhati, D.; Khan, N.M. A new approach to model the counts of earthquakes: INARPQX(1) process. Appl. Sci. 2021, 3, 274. [Google Scholar] [CrossRef]
- Altun, E. A new one-parameter discrete distribution with associated regression and integer-valued autoregressive models. Math. Slovaca 2020, 70, 979–994. [Google Scholar] [CrossRef]
- Popović, P.M. A bivariate INAR(1) model with different thinning parameters. Stat. Pap. 2016, 57, 517–538. [Google Scholar] [CrossRef]
- Mohammadpour, M.; Bakouch, H.S.; Shirozhan, M. Poisson–Lindley INAR(1) model with applications. Braz. J. Probab. Stat. 2018, 32, 262–280. [Google Scholar] [CrossRef]
- Alzaid, A.A.; Al-Osh, M. An integer-valued pth-order autoregressive structure (INAR(p)) process. J. Appl. Probab. 1990, 27, 314–324. [Google Scholar] [CrossRef]
- Du, J.-G.; Li, Y. The integer-valued autoregressive (INAR(p)) model. J. Time Ser. Anal. 1991, 12, 129–142. [Google Scholar]
- Drost, F.C.; Van Den Akker, R.; Werker, B.J. Local asymptotic normality and efficient estimation for INAR(p) models. J. Time Ser. Anal. 2008, 29, 783–801. [Google Scholar] [CrossRef]
- Drost, F.C.; Van den Akker, R.; Werker, B.J. Efficient estimation of auto-regression parameters and innovation distributions for semiparametric integer-valued AR(p) models. J. R. Stat. Soc. Ser. Stat. Methodol. 2009, 71, 467–485. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, D.; Zhu, F. Inference for INAR(p) processes with signed generalized power series thinning operator. J. Stat. Plan. Inference 2010, 140, 667–683. [Google Scholar] [CrossRef]
- Gladyshev, E.G. Periodically correlated random sequence. Soviet. Math. 1961, 2, 385–388. [Google Scholar]
- Monteiro, M.; Scotto, M.G.; Pereira, I. Integer-valued autoregressive processes with periodic structure. J. Stat. Plan. Inference 2010, 140, 1529–1541. [Google Scholar] [CrossRef]
- Buteikis, A.; Leipus, R. An integer-valued autoregressive process for seasonality. J. Stat. Comput. Simul. 2020, 90, 391–411. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Q.; Zhu, F. Random environment binomial thinning integer-valued autoregressive process with Poisson or geometric marginal. Braz. J. Probab. Stat. 2020, 34, 251–272. [Google Scholar] [CrossRef]
- Prezotti Filho, P.R.; Reisen, V.A.; Bondon, P.; Ispány, M.; Melo, M.M.; Serpa, F.S. A periodic and seasonal statistical model for non-negative integer-valued time series with an application to dispensed medications in respiratory diseases. Appl. Math. Model. 2021, 96, 545–558. [Google Scholar] [CrossRef]
- Maya, R.; Chesneau, C.; Krishna, A.; Irshad, M.R. Poisson extended exponential distribution with associated INAR(1) process and applications. Stats 2022, 5, 755–772. [Google Scholar] [CrossRef]
- Weiß, C.H. An Introduction to Discrete-Valued Time Series; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Al-Osh, M.; Alzaid, A.A. Integer-valued moving average (INMA) process. Stat. Pap. 1988, 29, 281–300. [Google Scholar] [CrossRef]
- Bu, R.; McCabe, B.; Hadri, K. Maximum likelihood estimation of higher-order integer-valued autoregressive processes. J. Time Ser. Anal. 2008, 29, 973–994. [Google Scholar] [CrossRef]
- Joe, H. Likelihood inference for generalized integer autoregressive time series models. Econometrics 2019, 7, 43. [Google Scholar] [CrossRef]
- Irshad, M.R.; Jodrá, P.; Krishna, A.; Maya, R. On the discrete analogue of the Teissier distribution and its associated INAR(1) process. Math. Comput. Simul. 2023, 214, 227–245. [Google Scholar] [CrossRef]
- Shirozhan, M.; Okereke, E.W.; Bakouch, H.S.; Chesneau, C. A flexible integer-valued AR(1) process: Estimation, forecasting and modeling COVID-19 data. J. Stat. Comput. Simul. 2023, 93, 1461–1477. [Google Scholar] [CrossRef]
- Eliwa, M.S.; Altun, E.; El-Dawoody, M.; El-Morshedy, M. A new three-parameter discrete distribution with associated INAR(1) process and applications. IEEE Access 2020, 8, 91150–91162. [Google Scholar] [CrossRef]


| = 0.5, = 0.3, = 1.6, = 0.7 | |||||
|---|---|---|---|---|---|
| Parameter | n | CML | CLS | ||
| Bias | MSE | Bias | MSE | ||
| 50 | −0.00472 | 0.01616 | −0.05084 | 0.02531 | |
| 100 | −0.00314 | 0.00689 | −0.02297 | 0.01125 | |
| 200 | −0.00184 | 0.00355 | −0.01150 | 0.00573 | |
| 300 | −0.00125 | 0.00226 | −0.00937 | 0.00369 | |
| 400 | −0.00010 | 0.00181 | −0.00432 | 0.00280 | |
| 50 | −0.01962 | 0.01838 | −0.05369 | 0.02129 | |
| 100 | −0.01627 | 0.00868 | −0.03749 | 0.01076 | |
| 200 | −0.00625 | 0.00416 | −0.01619 | 0.00571 | |
| 300 | −0.00504 | 0.00268 | −0.01262 | 0.00362 | |
| 400 | −0.00438 | 0.00208 | −0.01032 | 0.00287 | |
| 50 | −0.09165 | 0.35569 | −0.20154 | 0.37458 | |
| 100 | −0.08853 | 0.18334 | −0.14256 | 0.28982 | |
| 200 | −0.07156 | 0.10112 | −0.13650 | 0.14152 | |
| 300 | −0.06249 | 0.08055 | −0.11754 | 0.10136 | |
| 400 | −0.02908 | 0.06195 | −0.06508 | 0.09931 | |
| 50 | 0.19165 | 0.15335 | −0.19854 | 0.16169 | |
| 100 | 0.15675 | 0.11126 | −0.16944 | 0.15609 | |
| 200 | 0.07935 | 0.05058 | −0.16451 | 0.15126 | |
| 300 | 0.06627 | 0.05003 | −0.13749 | 0.14404 | |
| 400 | 0.05120 | 0.03762 | −0.08557 | 0.11326 | |
| = 0.4, = 0.2, = 1.2, = 0.9 | |||||
|---|---|---|---|---|---|
| Parameter | n | CML | CLS | ||
| Bias | MSE | Bias | MSE | ||
| 50 | 0.00543 | 0.01301 | −0.04288 | 0.02287 | |
| 100 | 0.00470 | 0.00724 | −0.01902 | 0.01254 | |
| 200 | 0.00072 | 0.00322 | −0.01243 | 0.00567 | |
| 300 | 0.00234 | 0.00229 | −0.00677 | 0.00410 | |
| 400 | 0.00113 | 0.00165 | −0.00652 | 0.00286 | |
| 50 | −0.01558 | 0.01382 | −0.04464 | 0.01667 | |
| 100 | −0.00969 | 0.00820 | −0.02861 | 0.01087 | |
| 200 | −0.00204 | 0.00374 | −0.01393 | 0.00536 | |
| 300 | −0.00337 | 0.00251 | −0.01279 | 0.00364 | |
| 400 | −0.00143 | 0.00189 | −0.00873 | 0.00265 | |
| 50 | −0.04760 | 0.11652 | −0.08939 | 0.11574 | |
| 100 | −0.02667 | 0.06381 | −0.08442 | 0.06985 | |
| 200 | −0.00988 | 0.03173 | −0.07852 | 0.04698 | |
| 300 | −0.00879 | 0.01873 | −0.07821 | 0.04034 | |
| 400 | −0.00591 | 0.01515 | −0.02922 | 0.03297 | |
| 50 | −0.24843 | 0.25267 | 0.27138 | 0.37775 | |
| 100 | −0.23901 | 0.24417 | 0.25147 | 0.30304 | |
| 200 | −0.23631 | 0.24380 | 0.24401 | 0.25091 | |
| 300 | −0.23352 | 0.22876 | 0.24300 | 0.23349 | |
| 400 | −0.19476 | 0.22753 | 0.23390 | 0.23187 | |
| Model | Parameter | Estimate | Std Error | log L | AIC | BIC |
|---|---|---|---|---|---|---|
| PEE-INAR(2) | 0.34330 | 0.08397 | −143.33799 | 294.67599 | 304.71942 | |
| 0.29190 | 0.09068 | |||||
| 1.38030 | 1.42716 | |||||
| 0.00010 | 1.39072 | |||||
| PEE-INAR(1) | 0.45897 | 1.05246 | −149.01889 | 304.03779 | 311.57037 | |
| 1.08045 | 1.50832 | |||||
| 0.11301 | 0.06388 | |||||
| DT-INAR(2) | 0.35590 | 0.06094 | −162.03214 | 330.06429 | 337.59686 | |
| 0.27323 | 0.06300 | |||||
| 0.48354 | 0.02498 | |||||
| DT-INAR(1) | 0.40357 | 0.01799 | −181.43955 | 366.87910 | 371.90082 | |
| 0.59686 | 0.05366 | |||||
| BDPL-INAR(2) | 0.34433 | 0.08350 | −143.51806 | 295.03612 | 305.07956 | |
| 0.28807 | 0.09016 | |||||
| 0.99990 | 1.91169 | |||||
| 0.48685 | 1.08893 | |||||
| BDPL-INAR(1) | 0.45899 | 117.11367 | −149.01889 | 304.03779 | 311.57037 | |
| 9.53718 | 116.77791 | |||||
| 8.82505 | 0.06388 | |||||
| DLi3-INAR(2) | 0.34330 | 0.08397 | −143.33799 | 296.67599 | 309.23028 | |
| 0.29190 | 0.09068 | |||||
| 6.70660 | 5.31318 | |||||
| 0.42013 | 0.25201 | |||||
| 0.00010 | 3.91858 | |||||
| DLi3-INAR(1) | 0.45926 | 59.2776 | −149.02031 | 308.04062 | 320.59491 | |
| 0.6639 | 3.2197 | |||||
| 0.0352 | 0.2434 | |||||
| 0.4805 | 0.0638 |
| Model | Parameter | Estimate | Std Error | log L | AIC | BIC |
|---|---|---|---|---|---|---|
| PEE-INAR(2) | 0.49188 | 0.04530 | −522.31596 | 1052.63192 | 1068.39260 | |
| 0.20424 | 0.05276 | |||||
| 4.21543 | 0.58439 | |||||
| 9.9990 | 4.63723 | |||||
| PEE-INAR(1) | 0.57037 | 0.27852 | −534.38144 | 1074.76288 | 1086.58339 | |
| 2.64733 | 7.87235 | |||||
| 9.99000 | 0.03105 | |||||
| DT-INAR(2) | 0.34821 | 0.04483 | −535.07328 | 1076.14657 | 1087.96708 | |
| 0.17003 | 0.04221 | |||||
| 0.46375 | 0.01549 | |||||
| DT-INAR(1) | 0.41251 | 0.01157 | −550.51787 | 1105.03574 | 1112.91608 | |
| 0.51266 | 0.03352 | |||||
| BDPL-INAR(2) | 0.48773 | 0.04601 | −522.46265 | 1052.92530 | 1068.68599 | |
| 0.21088 | 0.05324 | |||||
| 0.06186 | 0.06766 | |||||
| 0.01499 | 0.01673 | |||||
| BDPL-INAR(1) | 0.56887 | 0.03965 | −533.39932 | 1072.79864 | 1084.61915 | |
| 0.04884 | 0.01399 | |||||
| 0.01694 | 0.03114 | |||||
| DLi3-INAR(2) | 0.49812 | 0.04445 | −524.88199 | 1059.76397 | 1079.46483 | |
| 0.22716 | 0.05073 | |||||
| 3.87526 | 2.34043 | |||||
| 0.29820 | 0.04151 | |||||
| 0.23710 | 12.46557 | |||||
| DLi3-INAR(1) | 0.54084 | 3.69433 | −530.72820 | 1071.45641 | 1091.15726 | |
| 0.00856 | 719.40720 | |||||
| 1.66825 | 0.02747 | |||||
| 0.19226 | 0.03634 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almuhayfith, F.E.; Krishna, A.; Maya, R.; Irshad, M.R.; Bakouch, H.S.; Almulhim, M. Higher-Order INAR Model Based on a Flexible Innovation and Application to COVID-19 and Gold Particles Data. Axioms 2024, 13, 32. https://doi.org/10.3390/axioms13010032
Almuhayfith FE, Krishna A, Maya R, Irshad MR, Bakouch HS, Almulhim M. Higher-Order INAR Model Based on a Flexible Innovation and Application to COVID-19 and Gold Particles Data. Axioms. 2024; 13(1):32. https://doi.org/10.3390/axioms13010032
Chicago/Turabian StyleAlmuhayfith, Fatimah E., Anuresha Krishna, Radhakumari Maya, Muhammad Rasheed Irshad, Hassan S. Bakouch, and Munirah Almulhim. 2024. "Higher-Order INAR Model Based on a Flexible Innovation and Application to COVID-19 and Gold Particles Data" Axioms 13, no. 1: 32. https://doi.org/10.3390/axioms13010032
APA StyleAlmuhayfith, F. E., Krishna, A., Maya, R., Irshad, M. R., Bakouch, H. S., & Almulhim, M. (2024). Higher-Order INAR Model Based on a Flexible Innovation and Application to COVID-19 and Gold Particles Data. Axioms, 13(1), 32. https://doi.org/10.3390/axioms13010032







