An Interval Type-2 Fuzzy Logic Approach for Dynamic Parameter Adaptation in a Whale Optimization Algorithm Applied to Mathematical Functions
Abstract
:1. Introduction
2. Related Works
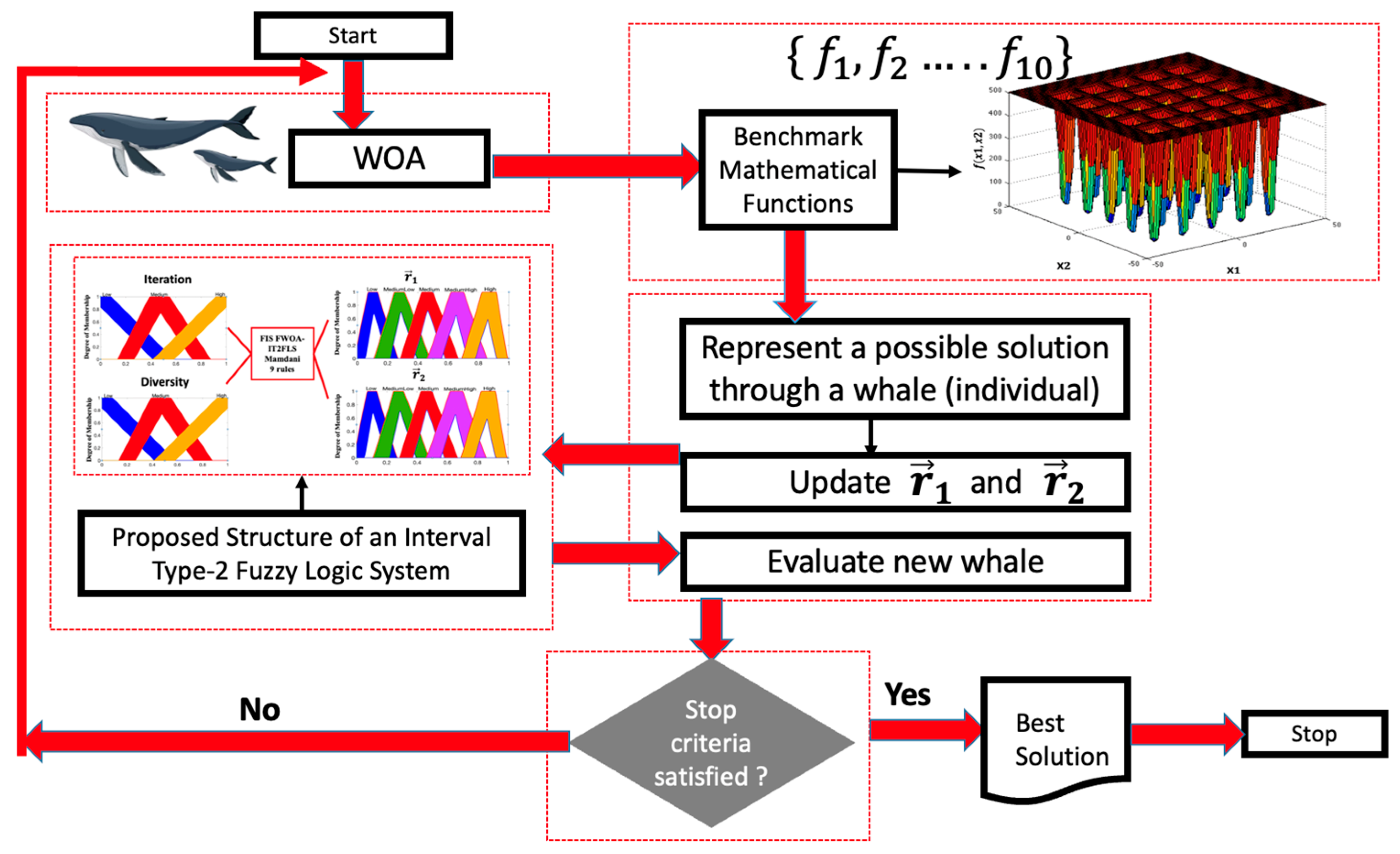
3. Whale Optimization Algorithm
3.1. Original WOA
| Algorithm 1: Pseudo-Code of the WOA Algorithm |
| Initialize the whale population Xi (i = 1, 2,……, n) Calculate the fitness of each search agent X* = the best search agent while (t < maximum number of iterations) for each search agent update a, A, C, l, and p if1 (p < 0.5) if2 () Update the position of the current agent by Equation (1) else if2 () Select a random search agent () Update the position of the current agent by Equation (6) end if2 else if1 (p ) Update the position of the current search by Equation (5) end if1 end for Check if any search agent goes beyond the search space and amend it Calculate the fitness of each search agent Update X* if there is a better solution t = t + 1 end while return X* |
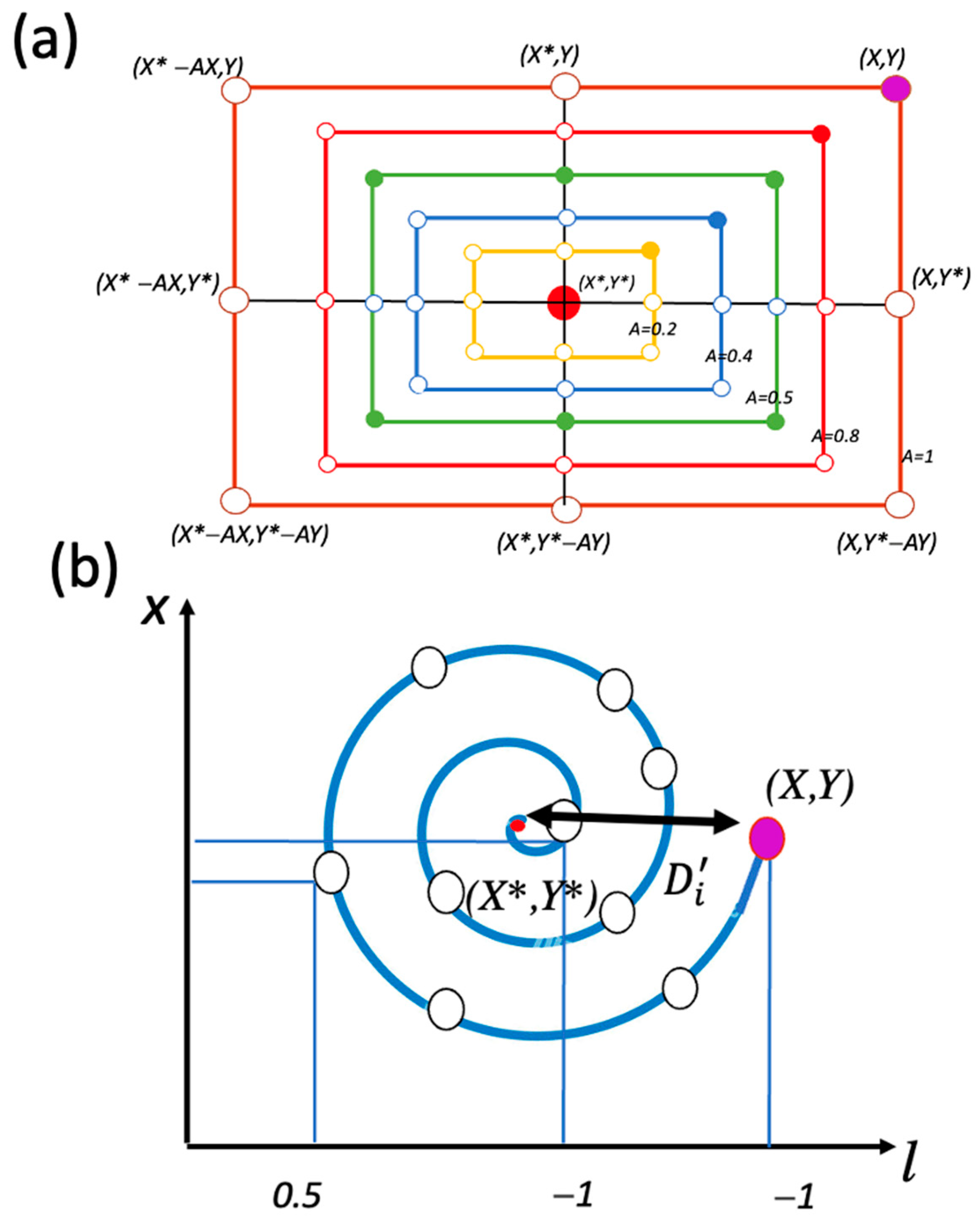
3.1.1. Surround Prey
3.1.2. Bubble-Net Attacking Method
3.1.3. Search for Prey
3.2. Fuzzy WOA
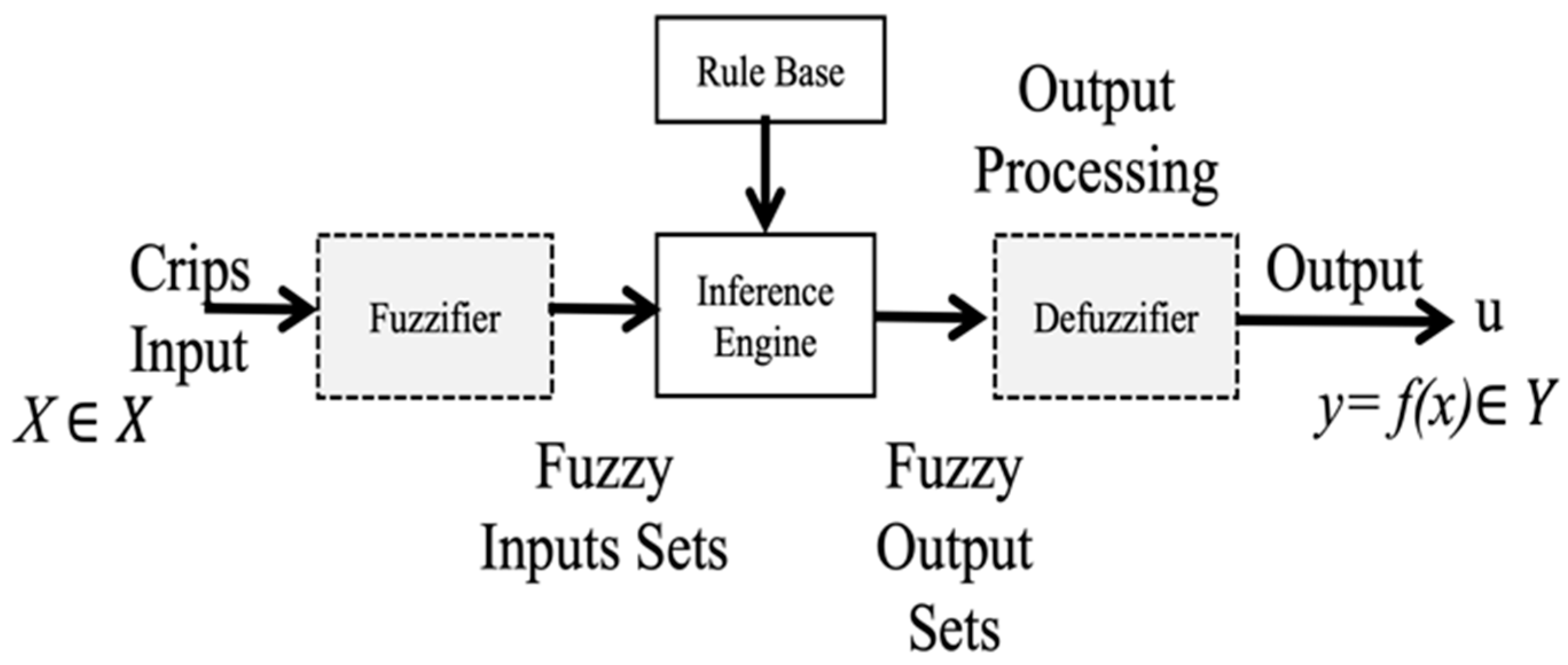
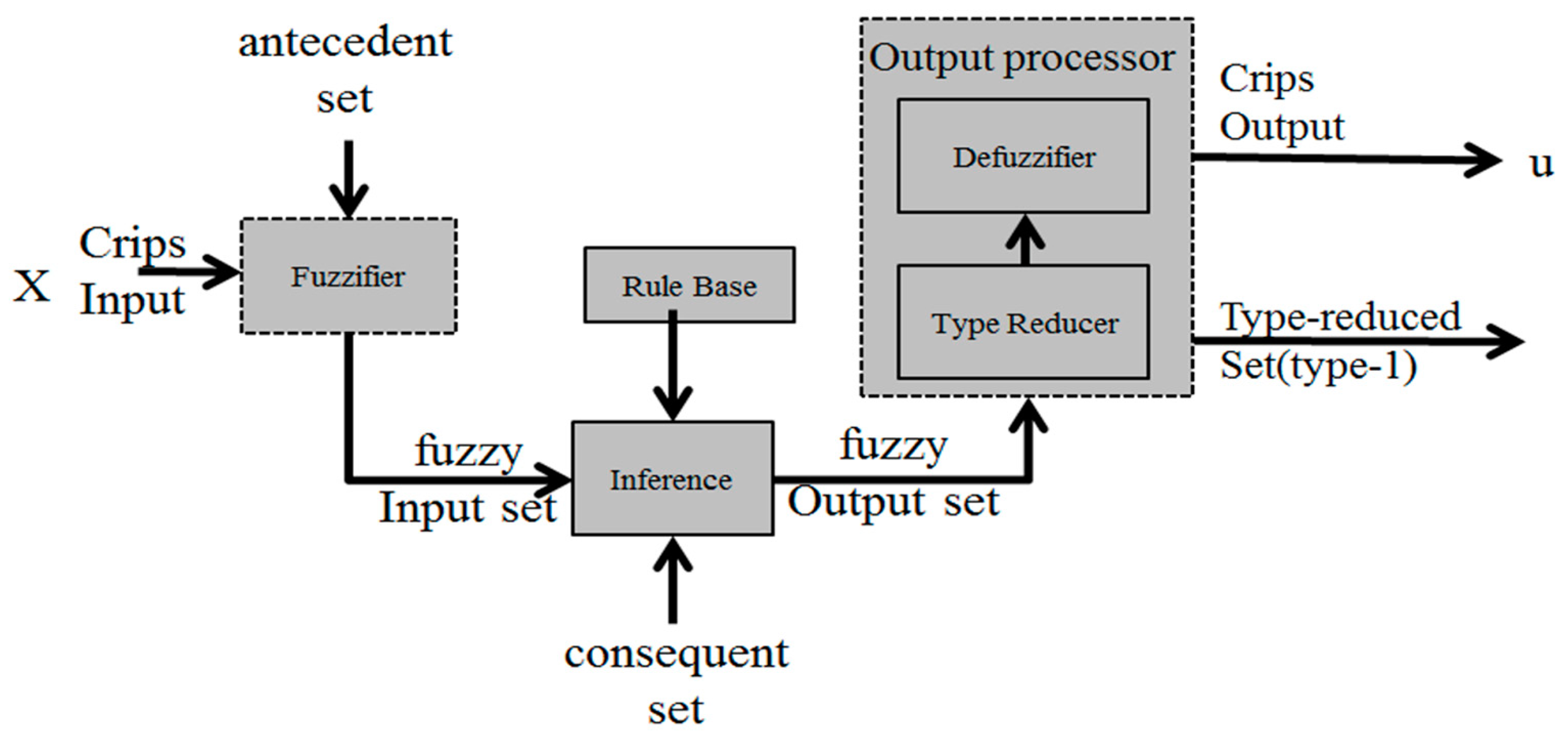
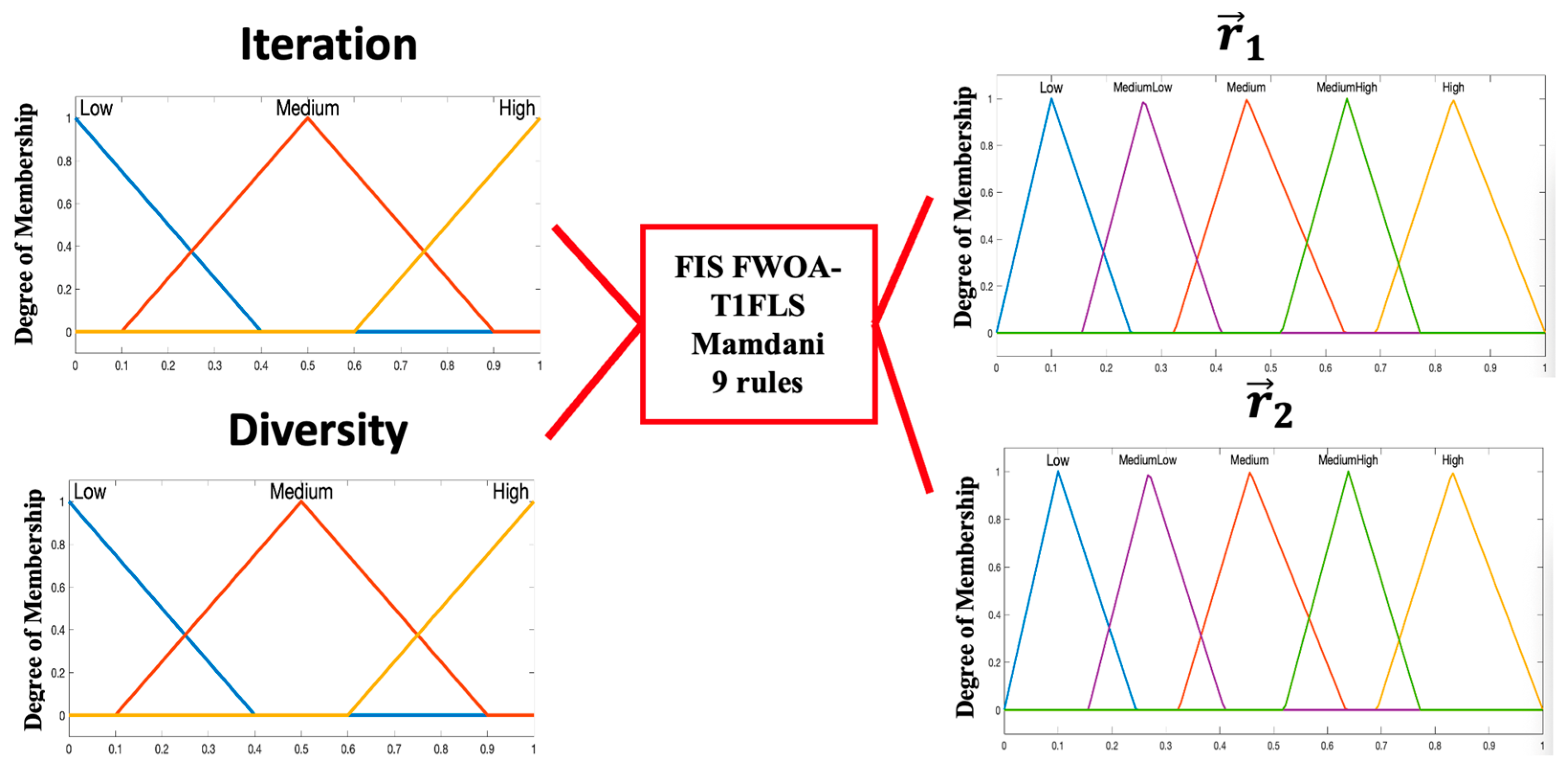
3.2.1. Type-1 Fuzzy Logic System
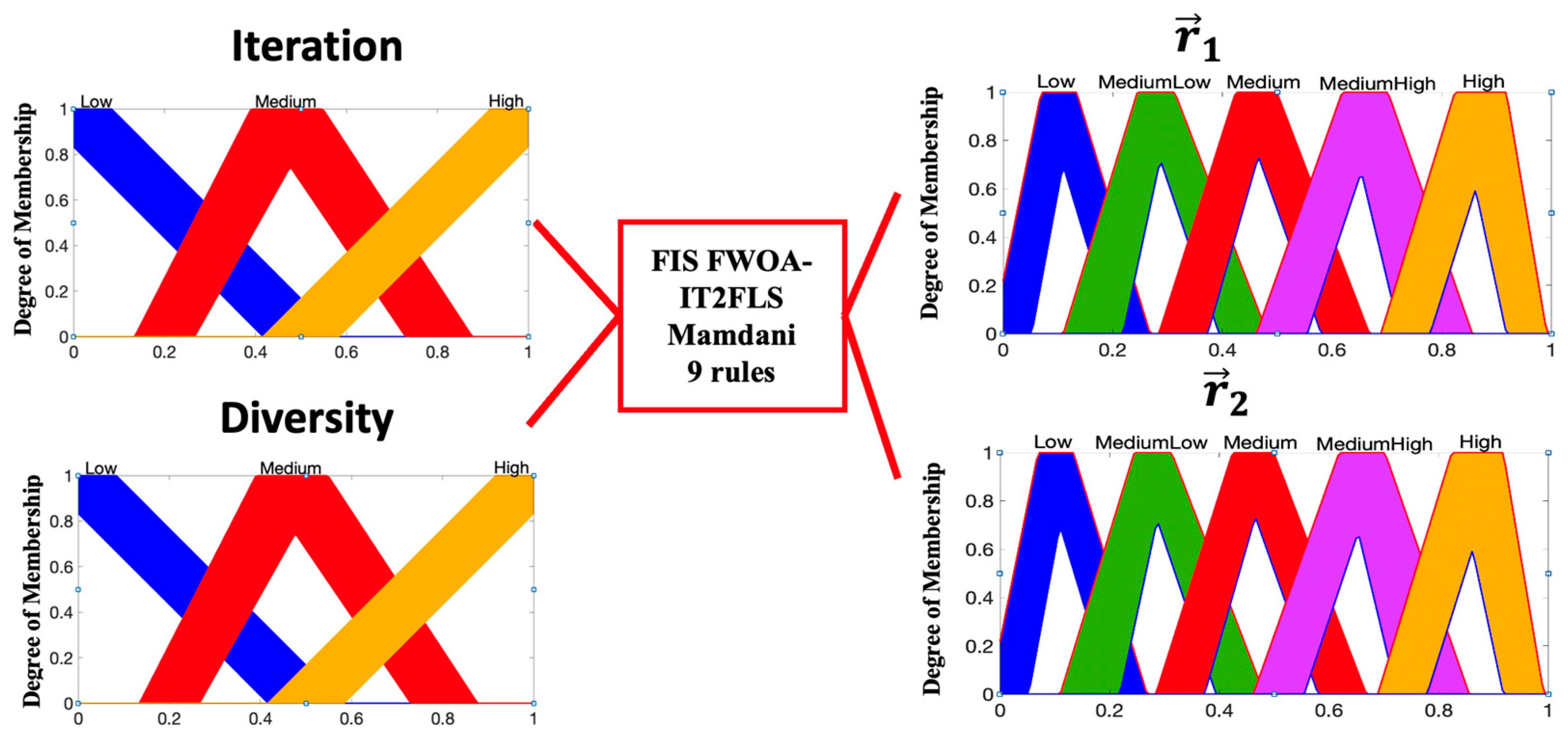
3.2.2. Interval Type-2 Fuzzy System
4. Set of Benchmark Functions
5. Experimental Results
6. Analysis of Results
6.1. Statistical Test
6.2. Discussion of the Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, L.; Hanm, T.; Zhou, H.; Zhang, Z.R.; Han, B.; Tang, A. Tuna swarm optimization: A novel swarm-based metaheuristic algorithm for global optimization. Comput. Intell. Neurosci. 2021, 2021, 9210050. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.B.; Gao, X.Z.; Lu, L.; Liu, Y.; Zhang, H. A new bio-inspired optimisation algorithm: Bird Swarm Algorithm. J. Exp. Theor. Artif. Intell. 2016, 28, 673–687. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Zidan, M.; Jameel, M.; Abouhawwash, M. Mantis Search Algorithm: A novel bio-inspired algorithm for global optimization and engineering design problems. Comput. Methods Appl. Mech. Eng. 2023, 415, 116200. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Jameel, M.; Abouhawwash, M. Exponential distribution optimizer (EDO): A novel math-inspired algorithm for global optimization and engineering problems. Artif. Intell. Rev. 2023, 56, 9329–9400. [Google Scholar] [CrossRef]
- Yuan, Y.; Shen, Q.; Wang, S.; Ren, J.; Yang, D.; Yang, Q.; Mu, X. Coronavirus mask protection algorithm: A new bio-inspired optimization algorithm and its applications. J. Bionic Eng. 2023, 20, 1747–1765. [Google Scholar] [CrossRef] [PubMed]
- Dehghani, M.; Trojovský, P. Osprey optimization algorithm: A new bio-inspired metaheuristic algorithm for solving engineering optimization problems. Front. Mech. Eng. 2023, 8, 1126450. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovský, P.; Malik, O.P. Green Anaconda Optimization: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Biomimetics 2023, 8, 121. [Google Scholar] [CrossRef]
- Miramontes, I.; Melin, P. A Comparative Study Between Bird Swarm Algorithm and Artificial Gorilla Troops Optimizer. In Fuzzy Logic and Neural Networks for Hybrid Intelligent System Design; Springer International Publishing: Cham, Switzerland, 2023; pp. 223–236. [Google Scholar]
- Castillo, O.; Ochoa, P.; Soria, J. Differential evolution with fuzzy logic for dynamic adaptation of parameters in mathematical function optimization. In Imprecision and Uncertainty in Information Representation and Processing: New Tools Based on Intuitionistic Fuzzy Sets and Generalized Nets; Springer International Publishing: Cham, Switzerland, 2016; pp. 361–374. [Google Scholar]
- Kumar, G.V.; Kumar, T.R.; Das, P.R. Improved Bio-Inspired Algorithm Design for Prediction of Heart Diseases. J. Surv. Fish. Sci. 2023, 10, 327–331. [Google Scholar]
- Bulla, C.M.; Birje, M.N. Efficient Resource Management Using Improved Bio-Inspired Algorithms for the Fog Computing Environment. Int. J. Cloud Appl. Comput. (IJCAC) 2022, 12, 1–18. [Google Scholar] [CrossRef]
- Amin, W.; Hussain, F.; Anjum, S. iHPSA: An improved bio-inspired hybrid optimization algorithm for task mapping in Network on Chip. Microprocess. Microsyst. 2022, 90, 104493. [Google Scholar] [CrossRef]
- Yu, W.; Kang, H.; Sun, G.; Liang, S.; Li, J. Bio-inspired feature selection in brain disease detection via an improved sparrow search algorithm. IEEE Trans. Instrum. Meas. 2022, 72, 1–15. [Google Scholar] [CrossRef]
- Agrawal, P.; Ganesh, T.; Mohamed, A.W. Chaotic gaining sharing knowledge-based optimization algorithm: An improved metaheuristic algorithm for feature selection. Soft Comput. 2021, 25, 9505–9528. [Google Scholar] [CrossRef]
- Sayed, G.I.; Tharwat, A.; Hassanien, A.E. Chaotic dragonfly algorithm: An improved metaheuristic algorithm for feature selection. Appl. Intell. 2019, 49, 188–205. [Google Scholar] [CrossRef]
- Ramezani, M.; Bahmanyar, D.; Razmjooy, N. A new improved model of marine predator algorithm for optimization problems. Arab. J. Sci. Eng. 2021, 46, 8803–8826. [Google Scholar] [CrossRef]
- Qiao, W.; Yang, Z. An improved dolphin swarm algorithm based on Kernel Fuzzy C-means in the application of solving the optimal problems of large-scale function. IEEE Access 2019, 8, 2073–2089. [Google Scholar] [CrossRef]
- Ndiaye, A.; Faye, M.; Lefebvre, G.; Tankari, M.A. Adaptive neuro-fuzzy inference system and genetic algorithm (NFGA)-based MPPT controller for PV system: Experimental realization. In Power Electronics Converters and their Control for Renewable Energy Applications; Academic Press: Cambridge, MA, USA, 2023; pp. 265–282. [Google Scholar]
- Siddikov, I.; Porubay, O.; Rakhimov, T. Synthesis of the neuro-fuzzy regulator with genetic algorithm. Int. J. Electr. Comput. Eng. (IJECE) 2024, 14, 184–191. [Google Scholar] [CrossRef]
- Cuevas, F.; Castillo, O.; Cortes-Antonio, P. A New Fuzzy Approach to Dynamic Adaptation of the Marine Predator Algorithm Parameters in the Optimization of Fuzzy Controllers for Autonomous Mobile Robots. In New Perspectives on Hybrid Intelligent System Design Based on Fuzzy Logic, Neural Networks and Metaheuristics; Springer International Publishing: Cham, Switzerland, 2022; pp. 179–204. [Google Scholar]
- Saffari, A.; Khishe, M.; Zahiri, S.H. Fuzzy-ChOA: An improved chimp optimization algorithm for marine mammal classification using artificial neural network. Analog Integr. Circuits Signal Process. 2022, 111, 403–417. [Google Scholar] [CrossRef]
- Kasruddin Nasir, A.N.; Ahmad, M.A.; Tokhi, M.O. Hybrid spiral-bacterial foraging algorithm for a fuzzy control design of a flexible manipulator. J. Low Freq. Noise Vib. Act. Control. 2022, 41, 340–358. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.; Ayob, A.; Mutlag, A.H.; Ustun, T.S. Optimal fuzzy logic controller based PSO for photovoltaic system. Energy Rep. 2023, 9, 427–434. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, D.; Xu, Z.; Heidari, A.A.; Chen, H.; Jiang, X.; Xu, S. bSRWPSO-FKNN: A boosted PSO with fuzzy K-nearest neighbor classifier for predicting atopic dermatitis disease. Front. Neuroinform. 2023, 16, 1063048. [Google Scholar] [CrossRef]
- Bernal, E.; Lagunes, M.L.; Castillo, O.; Soria, J.; Valdez, F. Optimization of type-2 fuzzy logic controller design using the GSO and FA algorithms. Int. J. Fuzzy Syst. 2021, 23, 42–57. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Shadowed Type-2 Fuzzy Sets in Dynamic Parameter Adaption in Cuckoo Search and Flower Pollination Algorithms for Optimal Design of Fuzzy Fault-Tolerant Controllers. Math. Comput. Appl. 2022, 27, 89. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Type-2 fuzzy logic applications designed for active parameter adaptation in metaheuristic algorithm for fuzzy fault-tolerant controller. Int. J. Intell. Comput. Cybern. 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Perez, J.; Valdez, F.; Castillo, O.; Roeva, O. Bat algorithm with parameter adaptation using interval type-2 fuzzy logic for benchmark mathematical functions. In Proceedings of the 2016 IEEE 8th International Conference on Intelligent Systems (IS), Sofia, Bulgaria, 4–6 September 2016; pp. 120–127. [Google Scholar]
- Patel, H.R.; Shah, V.A. A metaheuristic approach for interval type-2 fuzzy fractional order fault-tolerant controller for a class of uncertain nonlinear system. Autom. Časopis Za Autom. Mjer. Elektron. Računarstvo I Komun. 2022, 63, 656–667. [Google Scholar] [CrossRef]
- Valdez, F.; Castillo, O.; Peraza, C. Fuzzy logic in dynamic parameter adaptation of harmony search optimization for benchmark functions and fuzzy controllers. Int. J. Fuzzy Syst. 2020, 22, 1198–1211. [Google Scholar] [CrossRef]
- Amador-Angulo, L.; Mendoza, O.; Castro, J.R.; Rodríguez-Díaz, A.; Melin, P.; Castillo, O. Fuzzy sets in dynamic adaptation of parameters of a bee colony optimization for controlling the trajectory of an autonomous mobile robot. Sensors 2016, 16, 1458. [Google Scholar] [CrossRef] [PubMed]
- Ouali, M.A.; Ladjal, M. Nonlinear Dynamical Systems Modelling and Identification Using Type-2 Fuzzy Logic-Metaheuristic Algorithms Based Approach. In Proceedings of the 2020 International Conference on Electrical Engineering (ICEE), Istanbul, Turkey, 25–27 September 2020; pp. 1–6. [Google Scholar]
- Castillo, O.; Melin, P.; Ontiveros, E.; Peraza, C.; Ochoa, P.; Valdez, F.; Soria, J. A high-speed interval type 2 fuzzy system approach for dynamic parameter adaptation in metaheuristics. Eng. Appl. Artif. Intell. 2019, 85, 666–680. [Google Scholar] [CrossRef]
- Wang, J.; Bei, J.; Song, H.; Zhang, H.; Zhang, P. A whale optimization algorithm with combined mutation and removing similarity for global optimization and multilevel thresholding image segmentation. Appl. Soft Comput. 2023, 137, 110130. [Google Scholar] [CrossRef]
- Zhao, G.; Xiao, L.; Zhou, H. Busbar Voltage Control of DC Microgrid Group Based on Whale Optimization Algorithm and Fuzzy Control. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2023; Volume 2465, p. 012022. [Google Scholar]
- Panigrahi, A.; Pati, A.; Sahu, B.; Das, M.N.; Nayak, D.S.K.; Sahoo, G.; Kant, S. En-MinWhale: An ensemble approach based on MRMR and Whale optimization for Cancer diagnosis. IEEE Access 2023, 11, 113526–113542. [Google Scholar] [CrossRef]
- Dai, Y.; Yu, J.; Zhang, C.; Zhan, B.; Zheng, X. A novel whale optimization algorithm of path planning strategy for mobile robots. Appl. Intell. 2023, 53, 10843–10857. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, T.; Zhang, G.; Wang, D.; Kong, M. Using the Whale Optimization Algorithm to Solve the Optimal Reactive Power Dispatch Problem. Processes 2023, 11, 1513. [Google Scholar] [CrossRef]
- Aihong, A.A.; Ya'u, B.I.; Ali, U.; Ahmad, A. An Optimized Deep Learning Method for Software Defect Prediction Using Whale optimization Algorithm (WOA): A Review. ATBU J. Sci. Technol. Educ. 2023, 11, 159–174. [Google Scholar]
- Mahdavi, E.; Asadpour, S.; Macedo, L.H.; Romero, R. Reconfiguration of Distribution Networks with Simultaneous Allocation of Distributed Generation Using the Whale Optimization Algorithm. Energies 2023, 16, 4560. [Google Scholar] [CrossRef]
- Anvari, S.; Abdollahi Azgomi, M.; Ebrahimi Dishabi, M.R.; Maheri, M. Weighted K-nearest neighbors classification based on Whale optimization algorithm. Iran. J. Fuzzy Syst. 2023, 20, 61–74. [Google Scholar]
- Houssein, E.H.; Sayed, A. Dynamic candidate solution boosted beluga whale optimization algorithm for biomedical classification. Mathematics 2023, 11, 707. [Google Scholar] [CrossRef]
- Tan, W.H.; Mohamad-Saleh, J. A hybrid whale optimization algorithm based on equilibrium concept. Alex. Eng. J. 2023, 68, 763–786. [Google Scholar] [CrossRef]
- Mostafa Bozorgi, S.; Yazdani, S. IWOA: An improved whale optimization algorithm for optimization problems. J. Comput. Des. Eng. 2019, 6, 243–259. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saha, A.K.; Sharma, S.; Chakraborty, R.; Debnath, S. A hybrid whale optimization algorithm for global optimization. J. Ambient Intell. Humaniz. Comput. 2023, 14, 431–467. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saha, A.K.; Chhabra, A. Improving whale optimization algorithm with elite strategy and its application to engineering-design and cloud task scheduling problems. Cogn. Comput. 2023, 15, 1497–1525. [Google Scholar] [CrossRef]
- Mahadeva, R.; Kumar, M.; Gupta, V.; Manik, G.; Patole, S.P. Modified Whale Optimization Algorithm based ANN: A novel predictive model for RO desalination plant. Sci. Rep. 2023, 13, 2901. [Google Scholar] [CrossRef]
- Uzer, M.S.; Inan, O. Application of improved hybrid whale optimization algorithm to optimization problems. Neural Comput. Appl. 2023, 35, 12433–12451. [Google Scholar] [CrossRef]
- Li, M.; Yu, X.; Fu, B.; Wang, X. A modified whale optimization algorithm with multi-strategy mechanism for global optimization problems. Neural Comput. Appl. 2023, 1–14. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, C.; Gharehchopogh, F.S.; Mirjalili, S. An improved whale optimization algorithm based on multi-population evolution for global optimization and engineering design problems. Expert Syst. Appl. 2023, 215, 119269. [Google Scholar] [CrossRef]
- Yang, P.; Wang, T.; Yang, H.; Meng, C.; Zhang, H.; Cheng, L. The Performance of Electronic Current Transformer Fault Diagnosis Model: Using an Improved Whale Optimization Algorithm and RBF Neural Network. Electronics 2023, 12, 1066. [Google Scholar] [CrossRef]
- Singh, H.; Rai, V.; Kumar, N.; Dadheech, P.; Kotecha, K.; Selvachandran, G.; Abraham, A. An enhanced whale optimization algorithm for clustering. Multimed. Tools Appl. 2023, 82, 4599–4618. [Google Scholar] [CrossRef]
- Elmogy, A.; Miqrish, H.; Elawady, W.; El-Ghaish, H. ANWOA: An adaptive nonlinear whale optimization algorithm for high-dimensional optimization problems. Neural Comput. Appl. 2023, 35, 22671–22686. [Google Scholar] [CrossRef]
- UZER, M.S.; Onur, İ.N.A.N. Combining grey wolf optimization and whale optimization algorithm for benchmark test functions. Kahramanmaraş Sütçü İmam Üniversitesi Mühendislik Bilim. Derg. 2023, 26, 462–475. [Google Scholar] [CrossRef]
- Deng, H.; Liu, L.; Fang, J.; Qu, B.; Huang, Q. A novel improved whale optimization algorithm for optimization problems with multi-strategy and hybrid algorithm. Math. Comput. Simul. 2023, 205, 794–817. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi A Zadeh; World Scientific: Singapore, 1996; Volume 6, pp. 394–432. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1995, 8, 338–353. [Google Scholar] [CrossRef]
- Karnik, N.N.; Mendel, J.; Liang, Q. Type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 1999, 7, 643–658. [Google Scholar] [CrossRef]
- Karnik, N.N.; Mendel, J.M. Operations on type-2 fuzzy sets. Int. J. Fuzzy Sets. Syst. 2001, 122, 327–348. [Google Scholar] [CrossRef]
- Castillo, O.; Amador-Angulo, L. A generalized type-2 fuzzy logic approach for dynamic parameter adaptation in bee colony optimization applied to fuzzy controller design. Inf. Sci. 2018, 460, 476–496. [Google Scholar] [CrossRef]

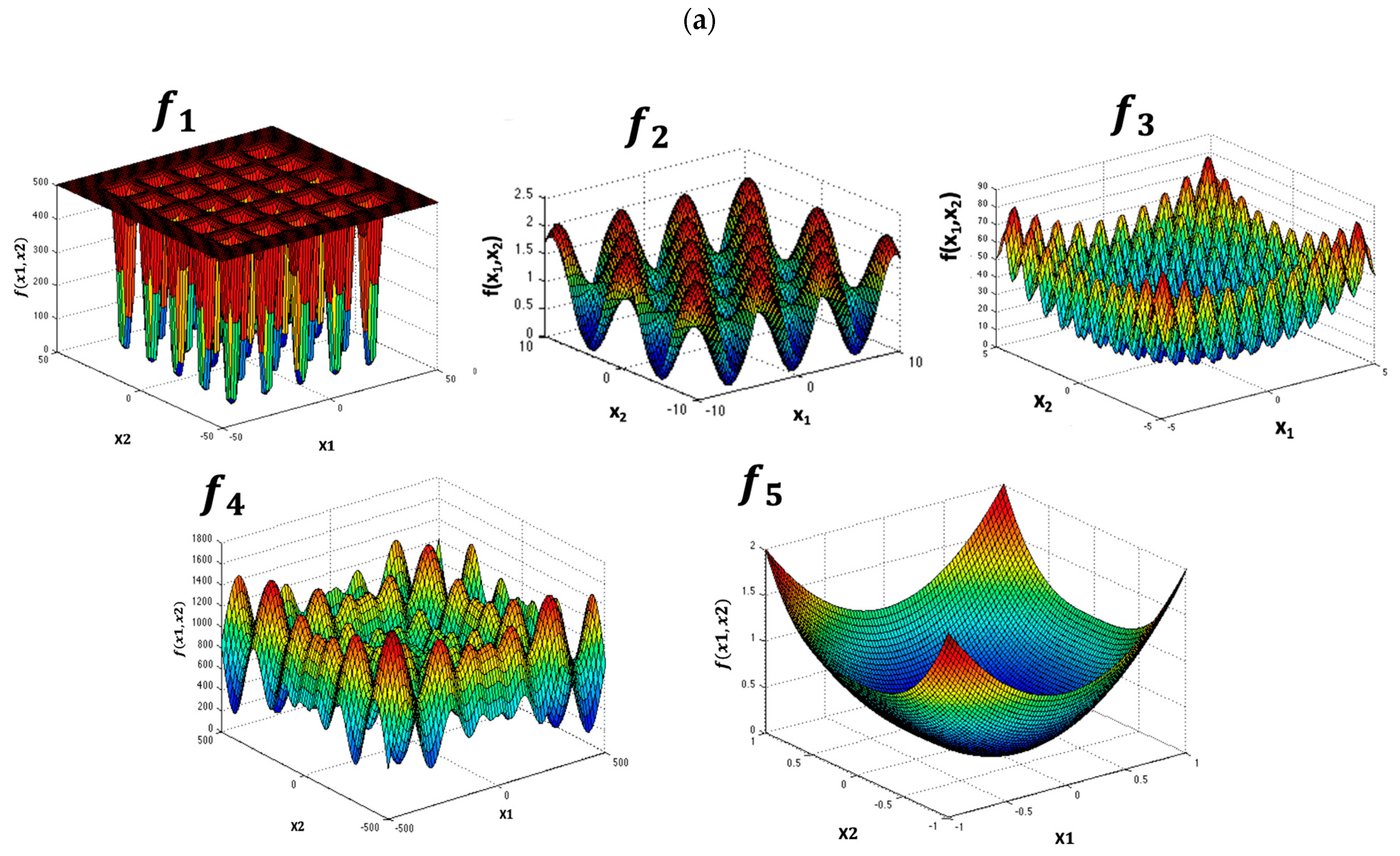
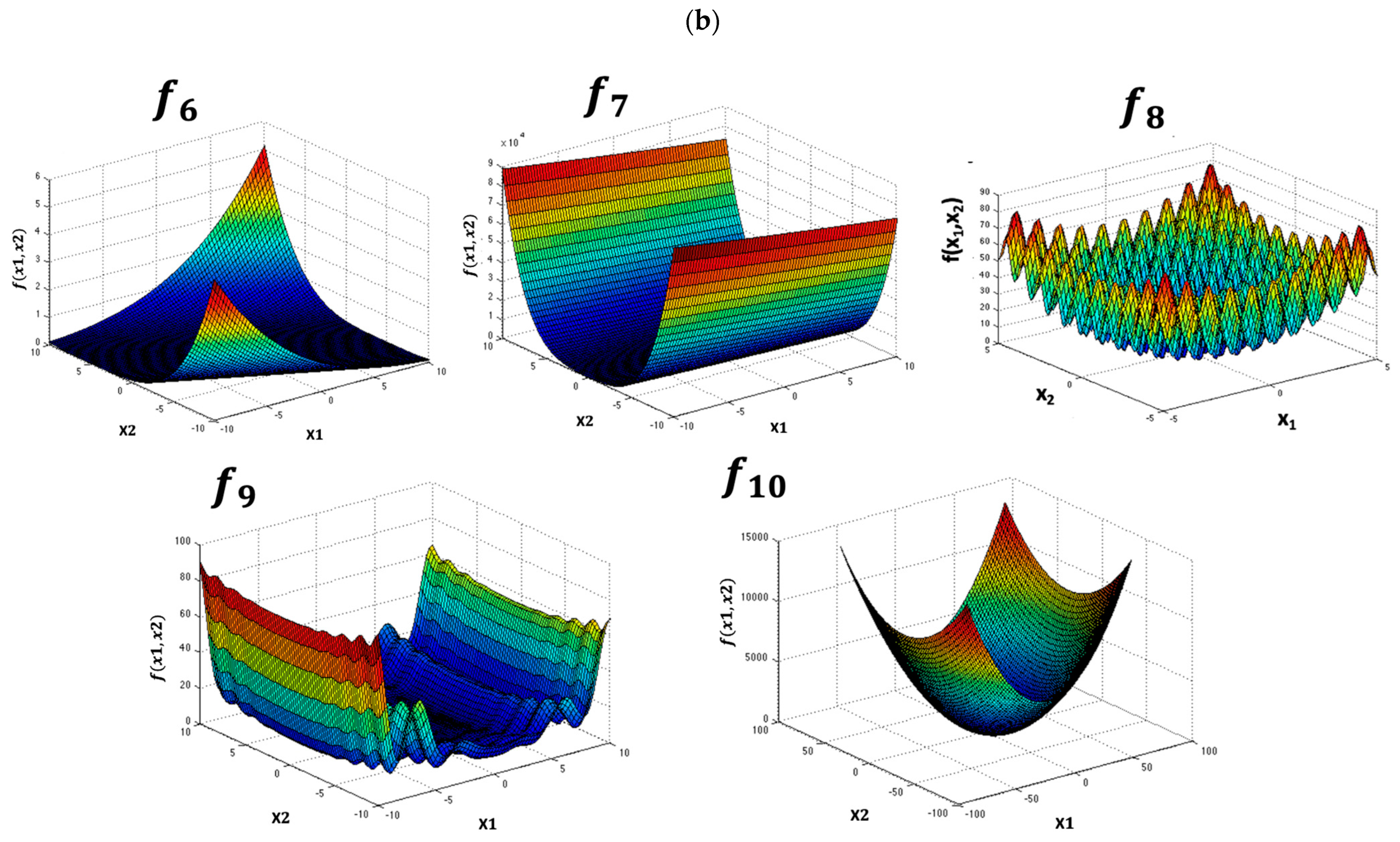

| Name | Search Domain | f Min | Mathematical Representation | |
|---|---|---|---|---|
| F1 | Sphere | 0 | ||
| F2 | Griewangk | 0 | ||
| F3 | Rastringin | 0 | ||
| F4 | Shewefel | −837.9658 | ||
| F5 | Sum of Different Powers | 0 | ||
| F6 | Zakharov | 0 | ||
| F7 | Dixon and Price | 0 | ||
| F8 | Levy | 0 | , for all i = 1,……,n | |
| F9 | Sum of Squares | 0 | ||
| F10 | Rotated Hyper Ellipsoid | 0 |
| Methods | ||||
|---|---|---|---|---|
| Original WOA Fixed | Original WOA Random | FWOA-T1FLS | FWOA-IT2FLS | |
| F1 | 6.92 × 10−51 | 2.49 × 10−1 | 3.41 × 10−1 | 6.29 × 10−53 |
| F2 | 1.61 × 10−9 | 6.99 × 10+1 | 7.72 × 10+6 | 2.91 × 10−9 |
| F3 | 8.79 × 10−10 | 2.15 × 10+1 | 1.71 × 10+13 | 3.74 × 10−10 |
| F4 | 2.91 × 10−2 | 2.15 × 10+1 | 5.00 × 10+2 | 9.88 × 10+1 |
| F5 | 6.35 × 10−35 | 8.21 × 10−2 | −1.69 × 10−15 | 1.86 × 10−28 |
| F6 | 4.54 × 10−1 | 3.06 × 10−1 | 8.96 × 10+13 | 3.97 × 10−1 |
| F7 | 1.20 × 10−2 | 2.90 × 10−2 | 2.90 × 10−2 | 1.26 × 10−2 |
| F8 | 3.97 × 10−1 | 1.16 × 100 | 3.84 × 10+14 | 6.20 × 10−1 |
| F9 | 4.94 × 10−54 | 1.16 × 10−1 | 3.93 × 10−32 | 1.22 × 10−48 |
| F10 | 2.21 × 10−52 | 1.01 × 10+1 | −6.55 × 10+13 | 7.48 × 10−44 |
| Methods | ||||
|---|---|---|---|---|
| Original WOA Random | Original WOA Fixed | FWOA-T1FLS | FWOA-IT2FLS | |
| F1 | 1.18 × 10−70 | 5.26 × 10−1 | 1.06 × 10−41 | 7.57 × 10−60 |
| F2 | 2.57 × 10−9 | 8.75 × 10−1 | 3.33 × 10+6 | 1.75 × 10−10 |
| F3 | 9.47 × 10−10 | 6.70 × 10−1 | 1.17 × 10+13 | 8.22 × 10−12 |
| F4 | 4.06 × 10+2 | 1.33 × 10+1 | 1.40 × 10+13 | 9.20 × 10+1 |
| F5 | 4.15 × 10−49 | 2.43 × 10−2 | 2.25 × 10−36 | 2.97 × 10−42 |
| F6 | 2.17 × 10−1 | 3.29 × 10−1 | 1.22 × 10+13 | 3.88 × 10−1 |
| F7 | 1.13 × 10−2 | 1.06 × 100 | 1.06 × 100 | 1.40 × 10−2 |
| F8 | 8.45 × 10−1 | 1.16 × 100 | 6.27 × 10−1 | 5.67 × 10−1 |
| F9 | 3.17 × 10−72 | 4.03 × 10−1 | 1.21 × 10−52 | 5.25 × 10−55 |
| F10 | 1.16 × 10−71 | 4.19 × 100 | 4.29 × 10−53 | 1.25 × 10−57 |
| Methods | ||||
|---|---|---|---|---|
| Original WOA Random | Original WOA Fixed | FWOA-T1FLS | FWOA-IT2FLS | |
| F1 | 9.58 × 10−84 | 2.39 × 10−1 | 1.20 × 10−51 | 2.84 × 10−59 |
| F2 | 2.57 × 10−9 | 6.35 × 10+1 | 5.60 × 10+5 | 7.22 × 10−9 |
| F3 | 1.36 × 10−10 | 4.36 × 10+2 | 1.17 × 10+13 | 1.39 × 10−9 |
| F4 | 3.76 × 10+2 | 4.39 × 10+2 | 1.40 × 10+13 | 2.23 × 10+2 |
| F5 | 3.75 × 10−54 | 1.03 × 10−1 | 4.47 × 10−27 | 1.56 × 10−42 |
| F6 | 5.65 × 10−1 | 3.73 × 10−1 | 5.65 × 10−1 | 1.24 × 10−1 |
| F7 | 1.39 × 10−2 | 4.50 × 10−1 | 8.01 × 10+5 | 1.31 × 10−2 |
| F8 | 9.39 × 10−1 | 9.35 × 10−1 | 4.77 × 10+14 | 4.32 × 10−1 |
| F9 | 6.38 × 10−81 | 6.65 × 10+1 | −1.28 × 10−62 | 1.19 × 10−61 |
| F10 | 2.14 × 10−78 | 4.60 × 100 | −4.37 × 100 | 7.51 × 10−66 |
| Methods | ||||
|---|---|---|---|---|
| Original WOA Random | Original WOA Fixed | FWOA-T1FLS | FWOA-IT2FLS | |
| F1 | 1.69 × 10−93 | −3.57 × 10−1 | 1.00 × 10−56 | 2.35 × 10−60 |
| F2 | 5.28 × 10−9 | −6.03 × 100 | 1.42 × 106 | 2.15 × 10−9 |
| F3 | 8.64 × 10−10 | 7.55 × 10−2 | 2.16 × 105 | 1.96 × 10−10 |
| F4 | 4.21 × 102 | 1.27 × 102 | 5.00 × 10+2 | 3.03 × 10+2 |
| F5 | 1.55 × 10−64 | 1.00 × 10−1 | 3.91 × 10−38 | 3.50 × 10−42 |
| F6 | 5.65 × 10−1 | 1.71 × 100 | 3.75 × 1013 | 4.35 × 10−1 |
| F7 | 1.12 × 10−2 | 5.63 × 10−1 | 2.28 × 1014 | 1.30 × 10−2 |
| F8 | 9.93 × 10−1 | 7.21 × 10−1 | 3.97 × 1014 | 5.81 × 10−1 |
| F9 | 1.14 × 10−91 | 6.25 × 10−1 | −1.33 × 100 | 4.88 × 10−59 |
| F10 | 1.64 × 10−89 | −2.57 × 100 | −4.37 × 100 | 2.80 × 10−59 |
| Methods | ||||
|---|---|---|---|---|
| Original WOA Random | Original WOA Fixed | FWOA-T1FLS | FWOA-IT2FLS | |
| F1 | 2.34 × 10−101 | 2.68 × 10−1 | 5.17 × 10−63 | 2.63 × 10−59 |
| F2 | 4.00 × 10−9 | 7.57 × 10+1 | 3.44 × 10+5 | 4.59 × 10−10 |
| F3 | 8.19 × 10−10 | 4.53 × 10−1 | 1.17 × 10+13 | 8.94 × 10−10 |
| F4 | 4.21 × 102 | 5.00 × 102 | 1.40 × 10+13 | 4.87 × 10+2 |
| F5 | 2.40 × 10−64 | 7.40 × 10−2 | 7.65 × 10−79 | 2.67 × 10−43 |
| F6 | 5.00 × 100 | 1.61 × 100 | 1.62 × 10+14 | 1.29 × 100 |
| F7 | 1.12 × 10−2 | 1.33 × 100 | 1.33 × 100 | 1.20 × 10−2 |
| F8 | 1.00 × 100 | 6.78 × 10−1 | 7.05 × 10+14 | 4.38 × 10−1 |
| F9 | 2.52 × 10−102 | 2.91 × 100 | 3.33 × 10−1 | 7.47 × 10−59 |
| F10 | 1.03 × 10−98 | −2.17 × 100 | 2.53 × 10−80 | 2.01 × 10−60 |
| Methods | ||||
|---|---|---|---|---|
| FWOA-IT2FLS | Original WOA Random | Z-Value | Evidence | |
| F1 | −2.63 × 10−59 | 2.34 × 10−101 | −1.265 | NS |
| F2 | 4.59 × 10−10 | 4.00 × 10−9 | −1.004 | NS |
| F3 | 8.94 × 10−10 | 8.19 × 10−10 | −3.531 | S |
| F4 | 4.87 × 10+2 | 4.21 × 10+2 | −97.494 | S |
| F5 | 2.67 × 10−43 | 2.40 × 10−64 | 1.281 | NS |
| F6 | 1.29 × 100 | 5.00 × 100 | −0.016 | NS |
| F7 | 1.20 × 10−2 | 1.12 × 10−2 | 0.0543 | NS |
| F8 | 4.38 × 10−1 | 1.00 × 100 | 77.992 | NS |
| F9 | 7.47 × 10−59 | −2.52 × 10−102 | −0.852 | NS |
| F10 | 2.01 × 10−60 | −1.03 × 10−98 | −1.0054 | NS |
| Methods | ||||
|---|---|---|---|---|
| FWOA-T1FLS | Original WOA Random | Z-Value | Evidence | |
| F1 | 5.71 × 10−63 | 2.34 × 10−101 | 0.560 | NS |
| F2 | 3.44 × 10+5 | 4.00 × 10−9 | 3.085 | NS |
| F3 | 1.17 × 10−13 | 8.19 × 10−10 | −2.902 | S |
| F4 | 1.40 × 10+13 | 4.21 × 10+2 | 591.500 | NS |
| F5 | 7.65 × 10−79 | 2.40 × 10−64 | −1.600 | S |
| F6 | 1.62 × 10+14 | 5.00 × 100 | −0.183 | NS |
| F7 | 1.33 × 100 | 1.12 × 10−2 | −1.002 | NS |
| F8 | 7.05 × 10+14 | 1.00 × 100 | −1.686 | S |
| F9 | 3.33 × 10−1 | −2.52 × 10−102 | −1.000 | NS |
| F10 | 2.53 × 10−80 | −1.03 × 10−98 | 3.122 | NS |
| Methods | ||||
|---|---|---|---|---|
| FWOA-IT2FLS | FWOA-T1FLS | Z-Value | Evidence | |
| F1 | 2.63 × 10−59 | 9.04 × 10−62 | −1.265 | NS |
| F2 | −4.59 × 10−10 | 3.44 × 10+5 | −3.09 | S |
| F3 | −8.94 × 10−10 | −2.02 × 10+5 | 2.902 | NS |
| F4 | −4.87 × 10+2 | −5.02 × 10+2 | 1.4388 | NS |
| F5 | 2.67 × 10−43 | 7.65 × 10−79 | 1.281 | NS |
| F6 | 1.29 × 100 | 5.00 × 100 | 0.166 | NS |
| F7 | 1.20 × 10−2 | 1.22 × 10−2 | 1.807 | NS |
| F8 | 4.38 × 10−1 | 9.69 × 10−1 | −8.242 | S |
| F9 | 7.47 × 10−59 | 3.33 × 10−1 | 1.000 | NS |
| F10 | 2.01 × 10−60 | 2.53 × 10−80 | −1.005 | NS |
| Methods | ||||||||
|---|---|---|---|---|---|---|---|---|
| Original WOA Random | Fuzzy WOA-T1FLS | Fuzzy WOA-IT2FLS | FBCO-IT2FLS [61] | |||||
| Best | Worst | Best | Worst | Best | Worst | Best | Worst | |
| F1 | 1.60 × 10−97 | 1.98 × 10−92 | 5. 43 × 10−55 | 2. 23 × 10−55 | 1.74 × 10−59 | 2.94 × 10−60 | 7.74 × 10−8 | 6.94 × 10−7 |
| F2 | 3.57 × 10−8 | 1.32 × 10−8 | 1.04 × 10−8 | 2.34 × 107 | 3.73 × 10−8 | 4.02 × 10−8 | 8.40 × 10−5 | 3.26 × 10−2 |
| F3 | 4.81 × 10−9 | 9.58 × 10−9 | 4.67 × 10+4 | 8.69 × 10+5 | 4.78 × 10−9 | 8.90 × 10−9 | 7.52 × 100 | 1.51 × 10+1 |
| F4 | 4.20 × 102 | 4.22 × 10+2 | 5.00 × 102 | 5.00 × 10+2 | 3.03 × 10+2 | 3.03 × 10+2 | 1.01 × 103 | 2.47 × 10+3 |
| F5 | 3.92 × 10−63 | 3.24 × 10−94 | 5.00 × 102 | 1.35 × 10−36 | 1.77 × 10−86 | 7.93 × 10−41 | 1.87 × 10−10 | 1.08 × 10−6 |
| F6 | 4.92 × 100 | 9.24 × 100 | 8.52 × 10+14 | 7.69 × 10+14 | 4.99 × 100 | 8.53 × 100 | 5.46 × 102 | 7.20 × 10+2 |
| F7 | 2.18 × 10−6 | 3.33 × 10−1 | 1.13 × 10+8 | 1.00 × 10+1 | 4.14 × 10−4 | 3.18 × 10−1 | 1.76 × 100 | 9.06 × 100 |
| F8 | 7.72 × 10−1 | 1.03 × 100 | 1.01 × 10+14 | 9.98 × 10+14 | 9.63 × 10−2 | 1.22 × 100 | 6.37 × 10−7 | 1.04 × 10−5 |
| F9 | 2.96 × 10−90 | 2.56 × 10−90 | 1.00 × 10+1 | 1.63 × 10−7 | 1.70 × 10−57 | 7.68 × 10−58 | 5.10 × 106 | 1.29 × 10−4 |
| F10 | 2.56 × 10−89 | 2.88 × 10−88 | 6.55 × 10+1 | 5.68 × 10−7 | 6.29 × 10−59 | 5.96 × 10−58 | 1.35 × 10−4 | 2.44 × 10−3 |
| Methods | |||
|---|---|---|---|
| Original WOA Random | FWOA-IT2FLS | FBCO-IT2FLS [61] | |
| F1 | 2.34 × 10−101 | 2.63 × 10−59 | 1.74 × 10−7 |
| F2 | 4.00 × 10−9 | 1.36 × 10−8 | 6.12 × 10−3 |
| F3 | 8.19 × 10−10 | 8.14 × 10−10 | 1.98 × 100 |
| F4 | 4.21 × 102 | 3.37 × 10−12 | 3.59 × 10+2 |
| F5 | 2.40 × 10−64 | 2.67 × 10−43 | 2.46 × 10−7 |
| F6 | 5.00 × 100 | 1.29 × 100 | 3.89 × 10+1 |
| F7 | 1.12 × 10−2 | 1.20 × 10−2 | 1.76 × 100 |
| F8 | 1.00 × 100 | 4.38 × 10−1 | 1.91 × 10−6 |
| F9 | 2.52 × 10−102 | 7.47 × 10−59 | 2.50 × 10−5 |
| F10 | 1.03 × 10−98 | 2.01 × 10−60 | 6.83 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amador-Angulo, L.; Castillo, O. An Interval Type-2 Fuzzy Logic Approach for Dynamic Parameter Adaptation in a Whale Optimization Algorithm Applied to Mathematical Functions. Axioms 2024, 13, 33. https://doi.org/10.3390/axioms13010033
Amador-Angulo L, Castillo O. An Interval Type-2 Fuzzy Logic Approach for Dynamic Parameter Adaptation in a Whale Optimization Algorithm Applied to Mathematical Functions. Axioms. 2024; 13(1):33. https://doi.org/10.3390/axioms13010033
Chicago/Turabian StyleAmador-Angulo, Leticia, and Oscar Castillo. 2024. "An Interval Type-2 Fuzzy Logic Approach for Dynamic Parameter Adaptation in a Whale Optimization Algorithm Applied to Mathematical Functions" Axioms 13, no. 1: 33. https://doi.org/10.3390/axioms13010033
APA StyleAmador-Angulo, L., & Castillo, O. (2024). An Interval Type-2 Fuzzy Logic Approach for Dynamic Parameter Adaptation in a Whale Optimization Algorithm Applied to Mathematical Functions. Axioms, 13(1), 33. https://doi.org/10.3390/axioms13010033







